Уравнения с делением: Как решать уравнения с умножением и делением. Правила решения уравнений с умножением

Упрощение уравнений делением.

Когда неизвестное значение умножается на другое любое известное значение, уравнение сокращается делением обеих сторон на это известное значение.

Пример 1. Упростите уравнение      ax + b — 3h = d
  Переносим члены      ax = d + 3h — b
  Делим на a       x = ( + 3h — b)/a.

Пример 2. Упростите уравнение      2x = a/c — d/h + 4b
Избавляемся от знаменателей      2chx = ah — cd + 4bch
Делим на 2ch       x = (ah — cd + 4bch)/2ch.

Если неизвестное значение имеет коэффициенты для нескольких членов, уравнение должно быть разделено на все эти коэффициенты, соединенные их знаками.

Пример 3. Упростите уравнение      ax + x = h — 4
  Делим на a + 1      x = (h — 4)/(a + 1)

Пример 4. Упростите уравнение      x — (x — b)/h = (a + d)/4
  избавляемся от знаменателей     4hx — 4x = ah + dh — 4b
  Делим на 4h — 4      x = (ah + dh -4b)/(4h — 4)

Если любое значение, известное или неизвестное, есть множителем

каждого члена, уравнение может быть разделено на него. С другой стороны, если любое значение есть знаменателем каждого члена уравнения, то уравнение может быть умножено на него. В этом случае, множитель или делимое удаляется с тем, чтобы сделать уравнение более простым.

Пример 5. Упростите уравнение      ax + 3ab = 6ad + a
  Делим на a       x + 3b = 6d + 1
  И        x = 6d + 1- 3b.

Пример 6. Упростите уравнение      x.(a + b) — a — b = d.(a + b)
Делим by a + b     x — 1 = d
И         x = d + 1.

Иногда условия задачи выражены не уравнениям, а пропорцией. Чтобы показать, как это может быть сведено к уравнению, необходимо использовать тему следующего раздела, а пока мы приведем правило, согласно которому «в пропорции с четырьмя значениями, то произведение двух крайних членов равно произведению двух внутренних членов».

     Так, если a:b = c:d,      тогад ad = bc.

     И если 3:4 = 6:8,      тогда 3.8 = 4.6.

Пропорция преобразуется в уравнение путем умножения крайних членов и записью их произведения на одной стороне уравнения и записью произведения внутренних членов пропорций на другой стороне.

Пример 1. Преобразуйте в уравнение      ax:b = ch:d.
Произведение крайних членов есть     adx
Произведение внутренних членов есть      bch
Поэтому уравнение, будет иметь вид      adx=bch.

Пример 2. Преобразуйте в уравнение      a + b:c = h — m:y.
Уравнение будет иметь вид:       ay + by = ch — cm.

С другой стороны, уравнение может быть преобразовано в пропорцию путем записи одной стороны уравнения как произведение двух множителей, как внутренних членов будущей пропорции, и на другой стороне также как произведение двух множителей как внешних членов будущей пропорции.

Так как какая-нибудь величина (или значение) часто может быть записана как различные пары множителей то и разные пропорции могут быть образованы из одного того же самого уравнения.

Пример 1. Преобразуйте в пропорцию      abc = deh.
Сторона abc может быть преобразована к виду     a.bc, или ab.c, или ac.b.
А deh может быть записана как      d. eh, или de.h или dh.e.

Поэтому a:d :: eh:bc      и ac:dh = e:b
Также, ab:de = h:c       и ac:d = eh:b, &c.

для каждого из этих примеров произведение внешних членов есть abc, а произведение внутренних есть deh.

Пример 2. Преобразуйте в пропорцию      ax + bx = cd — ch
Первый член может быть записан как    x.(a + b)
Второй член может быть записан как       c.(d — h)
Поэтому x:c = (d — h):(a + b)
И d — h:x = a + b:c, &c.

Если любой член или любые члены уравнения могут быть заменены таким же самым значением, то уравнение останется верным.

Так, например вместо 16 мы можем записать 2.8, или 64/4, или 25 — 9.

Здесь просто использованы разные формы записи одних и тех же значений.

Обычно, действия по упрощению или решению уравнений делаются в определенном порядке.

Во-первых, избавляемся от знаменателей.
Во-вторых, переносим и проводим операции с членами уравнения.
В третьих, делим на коэффициенты неизвестной величины.

Пример.

1. Решите уравнение      3x/4 + 6 = 5x/8 + 7
Избавление от знаменателей      24x + 192 = 20x + 224
Перенос и объединение членов     4x = 32
Деление на 4       x = 8.

2. Решите уравнение      x/a + h = x/b — x/c + d
Избавление от знаменателей      bcx + abx — acx = abcd — abch

Деление        x = (abcd — abch)/(bc + ab — ac)

3. Решите      40 — 6x — 16 = 120 — 14x.      Ответ: x = 12.

4. Решите      x/3 + x/5 = 20 — x/4.

5. Решите      (1 — a)/x — 4 = 5.

6. Решите      6x/(x + 4) = 1.

7. Решите      x + x/2 + x/3 = 11.

8. Решите      (x — 5)/4 + 6x = (284 — x)/5.

9. Решите      3x + (2x + 6)/5 = 5 + (11x — 37)/2

10. Решите      (6x — 4)/3 — 2 = (18- 4x)/3 + x.

11. Решите      3x — (x — 4)/4 — 4 = (5x + 14)/3 — 1/12.

12. Решите      (7x + 5)/3 — (16 + 4x)/5 + 6 = (3x + 9)/2.

13. Решите      x — (3x — 3)/5 + 4 = (20 — x)/2 — (6x — 8)/7 + (4x — 4)/5.

14. Решите     (6x + 7)/9 + (7x — 13)/(6x + 3) = (2x + 4)/3.

15. Решите      [(5x + 4)/2]:[(18 — x)/4] = 7:4.

Пример решения иррационального уравнения путем деления его обеих частей на одно и то же выражение

Несомненно, сразу можно пробовать уединить радикал, после чего решать иррациональное уравнение методом возведения обеих частей уравнения в квадрат. Такой подход вполне имеет право на существование. Однако видно, что он приведет нас к необходимости решать уравнение четвертой степени. В нашем случае это уравнение имеет два рациональных корня, что позволяет найти все его корни и в итоге получить интересующее нас решение. Однако в общем случае решение уравнений четвертой степени сопряжено со значительными сложностями. Аналогично, к уравнению четвертой степени приводит и введение новой переменной . Так что пока оставим эти пути решения и посмотрим, нет ли альтернативной возможности.

Попробуем решить иррациональное уравнение через проведение преобразований.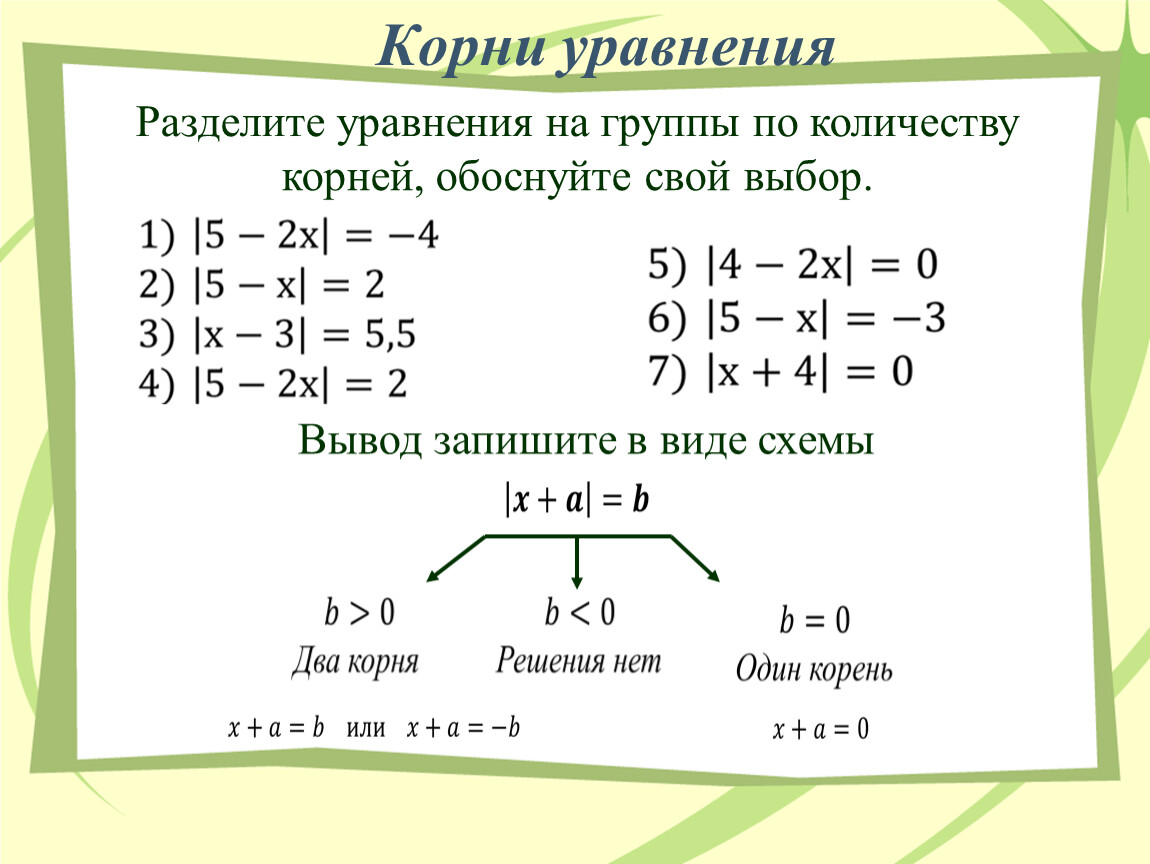 Перепишем уравнение в виде . Проделанное преобразование является равносильным преобразованием уравнения, так как состоит в замене выражения 1+x тождественно равным ему выражением , и при такой замене не изменяется область допустимых значений (она определяется условием 1+x≥0 как для исходного уравнения, так и для полученного). Мы провели это преобразование для того, чтобы отчетливо увидеть, что левая часть уравнения представляет собой некоторый аналог

однородного многочлена 4·x²+12·x·y−27·y². Типичным прием работы с такими многочленами состоит во введении новой переменной . По аналогии будем стремиться ввести новую переменную . Для этого нам нужно обе части иррационального уравнения разделить на одно и то же выражение , то есть, перейти к уравнению . И здесь возникает вопрос, а имеем ли мы право проводить такое деление? Мы знаем, что деление обеих частей уравнения на одно и то же выражение является равносильным преобразованием уравнения, если при этом не изменяется ОДЗ и это выражение не обращается на ней в нуль. Посмотрим, как у нас обстоят дела с этими условиями. При таком переходе у нас сужается ОДЗ: из нее пропадет число −1. А при каких значениях переменной выражение обращается в нуль на ОДЗ переменной x для исходного уравнения? При x=−1. Итак, все наши планы рушит минус единица. Другими словами, если бы область допустимых значений для исходного уравнения была бы не множеством [−1, +∞), а множеством (−1, +∞), то никаких проблем с намеченным делением у нас не было бы. Как же нам быть? Выход такой: отдельно проверить число −1, а дальше работать на множестве (−1, +∞).

Проверим, является ли x=−1 корнем исходного уравнения. Для этого осуществим проверку подстановкой. Имеем

Подстановка дала неверное числовое равенство, следовательно, x=−1 не является корнем решаемого уравнения.

Для остальных значений переменной из ОДЗ, то есть, на множестве (−1, +∞) мы можем проводить намеченное деление, то есть, переходить к уравнению и дальше

Теперь можно обращаться к методу введения новой переменной для решения иррационального уравнения. Принимаем , это дает квадратное уравнение 4·t²+12·t−27=0. Решаем его:

Возврат к старой переменной дает два уравнения: и . Решим их по очереди методом возведения обеих частей уравнений в квадрат:

Уравнение решено, осталось решить уравнение .

Таким образом, исходное иррациональное уравнение имеет два корня и 3.

Уравнения и неравенства — Уравнения деления

Уравнения и неравенства — Уравнения деления — Первый взгляд

Дом | Учитель | Родители | Глоссарий | О нас

Кому решать уравнение деления, используйте обратное операция умножения. Умножьте обе части на такое же количество.

Нажмите уравнение, чтобы посмотреть, как его решить.

Помощь с домашним заданием | Алгебра | Уравнения и неравенства

Отправить эту страницу другу по электронной почте

Поиск   ·   Уравнения деления	Первый Взгляд   В Глубина   Примеры   Тренировка Решение уравнений деления

Использование свойств деления и умножения равенства для решения уравнений

Результаты обучения

• Определить, является ли число решением уравнения
• Проверьте свое решение линейного уравнения, чтобы убедиться в его точности
• Решите уравнения, используя свойства деления и умножения равенства
• Решите уравнения, которые необходимо упростить

Решите алгебраические уравнения, используя свойства равенства умножения и деления

Точно так же, как вы можете складывать или вычитать одну и ту же точную величину с обеих сторон уравнения, вы также можете умножать или делить обе части уравнения на одну и ту же величину, чтобы записать эквивалентное уравнение. Для начала давайте в качестве примера рассмотрим числовое уравнение [латекс]5\cdot3=15[/латекс]. Если вы умножите обе части этого уравнения на  [latex]2[/latex], вы все равно получите верное уравнение.

[латекс]\begin{array}{r}5\cdot 3=15\,\,\,\,\,\,\, \\ 5\cdot3\cdot2=15\cdot2 \\ 30=30\ ,\,\,\,\,\,\,\end{array}[/latex]

Эта характеристика уравнений обобщается в M свойстве равенства умножения .

Давайте рассмотрим свойства деления и умножения равенства, поскольку мы готовимся использовать их для решения одношаговых уравнений.

Свойство равенства деления

Для всех вещественных чисел [latex]a,b,c[/latex] и [latex]c\ne 0[/latex], если [latex]a=b[/latex], затем [latex]\Large\frac{a}{c}\normalsize =\Large\frac{b}{c}[/latex].

Если два выражения равны друг другу, и вы разделите обе части на одно и то же число, не равное нулю, полученные выражения также будут эквивалентны.

Свойство равенства умножения

Для всех действительных чисел [latex]a,b,c[/latex], если [latex]a=b[/latex], то [latex]ac=bc[/latex].

Если два выражения равны друг другу и вы умножаете обе части на одно и то же число, полученные выражения также будут эквивалентны.

Проще говоря, когда вы делите или умножаете обе части уравнения на одну и ту же величину, вы все равно получаете равенство. Когда уравнение включает в себя умножение или деление, вы можете «отменить» эти операции, используя обратную операцию, чтобы изолировать переменную.

В предыдущем примере, чтобы «отменить» умножение, мы разделили. Как вы думаете, как мы «отменяем» деление? Далее мы покажем пример, который требует от нас использования умножения для отмены деления.

пример

Решить: [латекс]\большой\фрак{а}{-7}\нормальный размер =-42[/латекс]

Показать решение

Теперь посмотрите, сможете ли вы решить задачу, требующую умножения для отмены деления. Вспомните правила умножения двух отрицательных чисел — два отрицательных числа при умножении дают положительное.

попробуйте

https://ohm. lumenlearning.com/multiembedq.php?id=141868&theme=oea&iframe_resize_id=mom21

Другой способ думать о решении уравнения, когда операция умножения или деления, состоит в том, что мы хотим умножить коэффициент мультипликативным обратным (обратным), чтобы изменить коэффициент на [латекс]1[/латекс].

В следующем примере мы изменим коэффициент на [latex]1[/latex] путем умножения на мультипликативную обратную величину [latex]\frac{1}{2}[/latex].

В видео ниже вы увидите примеры того, как использовать свойства равенства умножения и деления для решения одношаговых уравнений с целыми числами и дробями.

пример

Решите: [латекс]4x=-28[/латекс]

Решение:

Чтобы решить это уравнение, мы используем свойство равенства деления, чтобы разделить обе части на [латекс]4[/латекс ].

[латекс]4x=-28[/латекс]
Разделите обе части на 4, чтобы отменить умножение.	[латекс]\Large\frac{4x}{\color{red}4}\normalsize =\Large\frac{-28}{\color{red}4}[/latex]
Упрощение.	[латекс]х =-7[/латекс]
Проверьте свой ответ.	[латекс]4x=-28[/латекс]
Пусть [латекс]х=-7[/латекс]. Замените x на [латекс]-7[/латекс].	[латекс]4(\color{red}{-7})\stackrel{\text{?}}{=}-28[/latex]
	[латекс]-28=-28[/латекс]

Поскольку это верное утверждение, [латекс]х=-7[/латекс] является решением [латекс]4х=-28[/латекс].

Теперь вы можете попытаться решить уравнение, которое требует деления и содержит отрицательные числа. Попробовать это похоже на то, что в следующем примере, с отрицательной переменной. Как стандартная практика, хорошо убедиться, что переменные положительны, когда вы решаете уравнения. Следующий пример покажет вам, как это сделать.

пример

Решить: [латекс]-r=2[/латекс]

Показать решение

Теперь можно попробовать решить уравнение с отрицательной переменной. Попробовать сторона знака равенства.

Двухшаговые линейные уравнения

Если уравнение имеет вид [латекс]ах+b=с[/латекс], где [латекс]х[/латекс] — переменная, уравнение можно решить, как и раньше. Сначала «отменить» сложение и вычитание, а затем «отменить» умножение и деление.

Примеры

Решите: [латекс]4x+6=-14[/латекс]

Решение:

В этом уравнении переменная находится только в левой части. Левую часть имеет смысл называть переменной стороной. Следовательно, правая часть будет постоянной стороной.

«>

Поскольку левая сторона переменная, цифра 6 неуместна. Мы должны «отменить» добавление [латекс]6[/латекс], вычитая [латекс]6[/латекс], и чтобы сохранить равенство, мы должны вычесть [латекс]6[/латекс] с обеих сторон. Используйте свойство вычитания равенства.		[латекс]4x+6\цвет{красный}{-6}=-14\цвет{красный}{-6}[/латекс]
Упрощение.		[латекс]4x=-20[/латекс]
Теперь все [latex]x[/latex] слева, а константа справа.
Используйте Свойство Разделения Равенства.		[латекс]\Large\frac{4x}{\color{red}{4}}\normalsize =\Large\frac{-20}{\color{red}{4}}[/latex]
Упрощение.		[латекс]x=-5[/латекс]
Чек:		[латекс]4x+6=-14[/латекс]
Пусть [латекс]х=-5[/латекс] .		[латекс]4(\цвет{красный}{-5})+6=-14[/латекс]
		[латекс]-20+6=-14[/латекс]
		[латекс]-14=-14\четверка\галочка[/латекс]

Решите: [латекс]2y — 7=15[/латекс]

Показать решение

Теперь вы можете попробовать аналогичную задачу.