Определитель равен нулю если: Свойства определителя матрицы | Мозган калькулятор онлайн

определение и свойства (11 шт)

Содержание:

• Определение
• Свойства определителей

Определение

Квадратной матрице $ A=\left( \begin{array}{cccc}{a_{11}} & {a_{12}} & {\dots} & {a_{1 n}} \\ {a_{21}} & {a_{22}} & {\dots} & {a_{2 n}} \\ {\ldots} & {\cdots} & {\cdots} & {\cdots} \\ {a_{n 1}} & {a_{n 2}} & {\dots} & {a_{n n}}\end{array}\right) $ $n$-го порядка ставиться в соответствие число $ |A|=\operatorname{det} A=\left| \begin{array}{cccc}{a_{11}} & {a_{12}} & {\dots} & {a_{1 n}} \\ {a_{21}} & {a_{22}} & {\dots} & {a_{2 n}} \\ {\ldots} & {\ldots} & {\ldots} & {\ldots} \\ {a_{n 1}} & {a_{n 2}} & {\dots} & {a_{n n}}\end{array}\right| $, называемое определителем матрицы или детерминантом.

Замечание

Все что будет сказано относительно строк, будет относиться и к столбцам.

1  При транспонировании квадратной матрицы её определитель не меняется: $ |A|=\left|A^{t}\right| $

Пример

Известно, что определитель матрицы $ A=\left( \begin{array}{ll}{a} & {d} \\ {b} & {c}\end{array}\right) $ равен 3. {3} \cdot|A|=8 \cdot|A|=8 \cdot 3=24 $

Ответ. $ |B|=24 $

4  Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.

$$ \left| \begin{array}{ccc}{b_{11}+c_{11}} & {b_{12}+c_{12}} & {b_{13}+c_{13}} \\ {a_{21}} & {a_{22}} & {a_{23}} \\ {a_{31}} & {a_{32}} & {a_{33}}\end{array}\right|=\left| \begin{array}{ccc}{b_{11}} & {b_{12}} & {b_{13}} \\ {a_{21}} & {a_{22}} & {a_{23}} \\ {a_{31}} & {a_{32}} & {a_{33}}\end{array}\right|+\left| \begin{array}{ccc}{c_{11}} & {c_{12}} & {c_{13}} \\ {a_{21}} & {a_{22}} & {a_{23}} \\ {a_{31}} & {a_{32}} & {a_{33}}\end{array}\right| $$

5  Если две строки определителя поменять местами, то определитель поменяет знак.

Пример

$ \left| \begin{array}{ll}{1} & {1} \\ {2} & {3}\end{array}\right|=-\left| \begin{array}{ll}{2} & {3} \\ {1} & {1}\end{array}\right| $

6  Определитель с двумя равными строками равен нулю.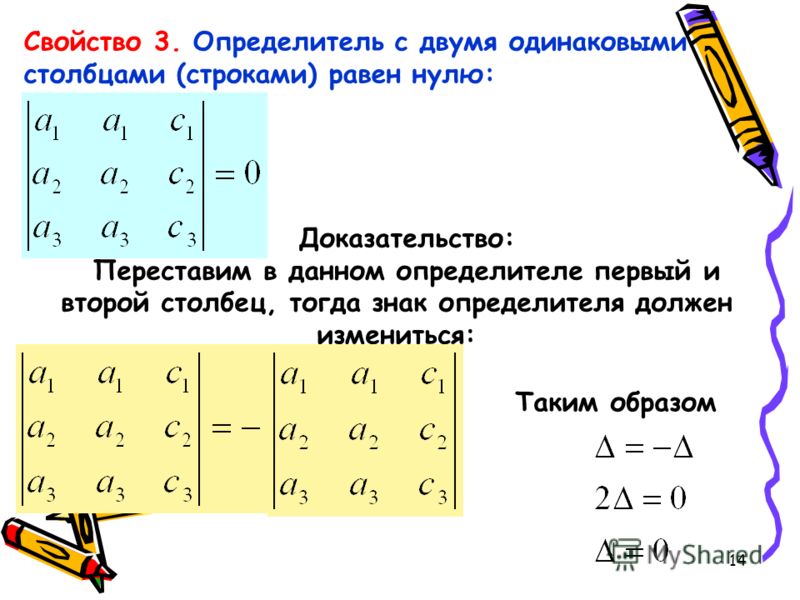

Пример

$ \left| \begin{array}{rrr}{1} & {2} & {3} \\ {1} & {0} & {-7} \\ {1} & {2} & {3}\end{array}\right|=0 $

7  Определитель с двумя пропорциональными строками равен нулю.

Пример

$ \left| \begin{array}{rrr}{1} & {2} & {3} \\ {-1} & {2} & {2} \\ {2} & {4} & {6}\end{array}\right|=\left| \begin{array}{ccc}{1} & {2} & {3} \\ {-1} & {2} & {2} \\ {2 \cdot 1} & {2 \cdot 2} & {2 \cdot 3}\end{array}\right|=0 $

8  Определитель, содержащий нулевую строку, равен нулю.

Пример

$ \left| \begin{array}{rrr}{1} & {-1} & {0} \\ {0} & {0} & {0} \\ {2} & {3} & {1}\end{array}\right|=0 $

9  Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.

Пример

Пусть задан определитель третьего порядка $ \left| \begin{array}{rrr}{1} & {-1} & {0} \\ {1} & {0} & {-1} \\ {2} & {3} & {1}\end{array}\right| $ . Прибавим ко второй строке определителя третью его строку, при этом значение определителя не измениться:

$$ \left| \begin{array}{rrr}{1} & {-1} & {0} \\ {1} & {0} & {-1} \\ {2} & {3} & {1}\end{array}\right|=\left| \begin{array}{ccc}{1} & {-1} & {0} \\ {1+2} & {0+3} & {-1+1} \\ {2} & {3} & {1}\end{array}\right|=\left| \begin{array}{rrr}{1} & {-1} & {0} \\ {3} & {3} & {0} \\ {2} & {3} & {1}\end{array}\right| $$

10  Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.

Пример

$ \left| \begin{array}{rrrr}{1} & {0} & {3} & {0} \\ {0} & {2} & {4} & {1} \\ {0} & {0} & {5} & {1} \\ {0} & {0} & {0} & {-1}\end{array}\right|=1 \cdot 2 \cdot 5 \cdot(-1)=-10 $

11  Определитель произведения матриц равен произведению определителей: $ |A \cdot B|=|A| \cdot|B| $

Читать дальше: минор и алгебраическое дополнение.

08. Свойства определителей

Определение 9. Транспонированием A матрицы называется такое ее преобразование, при котором строки матрицы становятся ее столбцами с теми же самыми номерами.

Матрица транспонированная матрице

A обозначается символом :

.

Свойство 1. Определитель транспонированной матрицы равен определителю исходной матрицы, т. е. .

Доказательство. ОПределителя матрицы А есть алгебраическая сумма N! произведений вида

(11)

Где в каждое произведение входит по одному элементу из каждой строки и каждого столбца матрицы A, со знаком равным знаку подстановки

.

Так как сомножители произведения (11) также находятся по одному в каждом столбце и каждой строке матрицы , то каждое произведение определителя матрицы A входит в определитель матрицы . Отсюда. так как количество слагаемых в и в одинаково, следует, что и в состоят из одних и тех же слагаемых. Для того, чтобы показать, что знаки произведений равны, составим подстановку для произведения (11) в (учитываем, что строки матрицы

А стали столбцами матрицы с теми же номерами). Она равна подтановке:

.

Подстановки иИмеют одинаковое число инверсий, четность и знак.

Таким образом и суммы одних и тех же произведений и поэтому . Свойство доказано.

Замечание 1. Из свойства 1 вытекает, что строки и столбцы матрицы Равноправны, т. е., если какое-нибудь свойство доказано для строк, то оно будет справедливо и для столбцов и обратно. Поэтому дальнейшие свойства формулируются и доказываются только для строк. В дальнейшем под строками и столбцами определителя понимаются строки и столбцы соответствующей матрицы.

Свойство 2. Если в матрице поменять местами две строки, то абсолютная величина определителя не меняется, а знак определителя меняется на противоположный.

Доказательство. Пусть даны исходный и преобразованный определитель:

.

(12)

Определитель Получается из определителя D перестановкой I-й и J-й строк (точками обозначены все остальные строки, которые в D и Совпадают. Требуется доказать, что D= -.

ОПределитель D есть алгебраическая сумма N! произведений вида

, (13)

Где в каждое произведение входит по одному элементу из каждой строки и каждого столбца определителя D, со знаком равным знаку подстановки

.

Так как сомножители произведения (13) также находятся по одному в каждом столбце и каждой строке определителя , то каждое произведение определителя D входит в определитель . Отсюда, так как количество слагаемых в D и одинаково, следует, что D и состоят из одних и тех же произведений, Для того, чтобы показать, что D= —, достаточно показать, что каждое произведение (13) определителях D и Имеет противоположные знаки. Знак произведения (13) в определителе равен знаку подстановки:

(учитываем, что элемент Лежит в определителе в J-й строке в-м столбце, элемент — в I-й строке и в -м столбце). У подстановок и Совпадают вторые строки, а первая строка подстановки Получена из первой строки подстановки транспозицией элементов I и J . Поэтому в силу теоремы 2 подстановки и Имеют противоположную четность и знак. Отсюда образом произведение (13) входит в определители D и с противоположным знаком. Таким образом определители D и суммы одних и тех же произведений, но с противоположными знаками и D= —. . Свойство доказано.

Свойство 3. Если в определителе есть две одинаковые строки, то определитель равен нулю.

Доказательство. Пусть в определителе D I-я строка равна j-й строке. Переставим

I-ю и J-ю строки местами и получим определитель (см.(13)). По свойству 2 D= —. Так как I-я и J-я строки равны, то D= . Из этих равенств находим, что D= 0. Свойство доказано.

Свойство 4. Если в определителе есть нулевая строка, то определитель равен нулю.

Доказательство. Пусть в определителе I-я строка нулевая. По определению определителя он равен алгебраической сумме произведений вида:

.

В каждое произведение входит нулевой элемент I-й строки и поэтому оно равно нулю. Следовательно, и определитель равен нулю. Свойство доказано.

Свойство 5. Если все элементы какой-нибудь строки определителя представлены в виде двух слагаемых, то определитель равен сумме двух определителей, в первом из которых элементы отмеченной строки равны соответствующим первым слагаемым, во втором — вторым слагаемым.

Пусть все элементы I-й строки представлены в виде ; J=1,2,…,N. Тогда свойство перепишется в виде:

=

= .

Доказательство. По формуле (8) находим

= .

Свойство доказано.

Замечание 2. Индукцией по m легко доказать, что свойство 5 справедливо для случая, когда каждый элемент i-й строки сумма m слагаемых, .

Свойство 6. Если все элементы какой-нибудь строки определителя имеют общий множитель, то его можно вынести за знак определителя, т. е., если элементы какой-нибудь строки определителя умножить на число k, то и сам определитель умножится на число k.

.

Доказательство. По формуле (8) находим

Свойство доказано.

Свойство 7. Если в определителе есть две пропорциональны строки, то он равен нулю.

Доказательство. Пусть I-я и J-я строки определителя пропорциональны, т. е. . Вынося из J-й общий множитель K за знак определителя, получим определитель с двумя равными строками, который равен нулю. Поэтому и исходный определитель равен нулю. Свойство доказано.

Свойство 8. Если к какой-нибудь строке определителя прибавить другую строку, умноженную на число k, то определитель от этого не изменится.

Доказательство. Пусть к I-й строке определителя прибавили ее J-ю строку, умноженную на число K . Тогда по свойствам 5 и 7 получаем:

Свойство доказано.

Определение 10. Говорят, что I-я строка матрицы A есть линейная комбинация остальных строк определителя, если существуют такие числа , что каждый элемент I-й строки есть сумма попарных произведений этих чисел на соответствующие элементы остальных строк матрицы, т. е.

Свойство 9. Если какая-нибудь строка определителя есть линейная комбинация остальных строк определителя, то определитель равен нулю.

Доказательство. Если I-я строка определителя есть линейная комбинация остальных строк определителя, то по замечанию 2 определитель равен сумме n-1 определителей с пропорциональными строками, и по свойству 7 все такие определители равны нулю. Тогда и исходный определитель равен нулю. Свойство доказано.

< Предыдущая		Следующая >

линейная алгебра — Что значит иметь определитель равный нулю?

$\begingroup$

После пары часов поиска в своей книге я все еще не понимаю, что означает для $(n\times n)$-матрицы $A$ наличие определителя, равного нулю, $\det(A )=0$.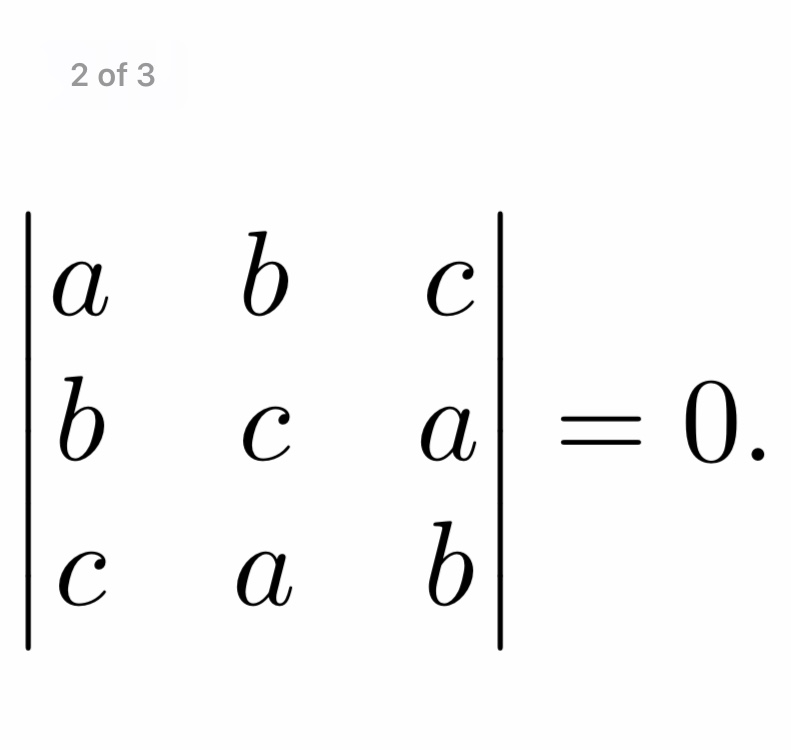

Надеюсь, кто-нибудь объяснит мне это простым языком.

• линейная алгебра
• матрицы
• терминология
• определитель

$\endgroup$ 9$

Матрица необратима.

Объем параллелепипеда, определяемый векторами-столбцами матрицы, равен $0$.

Объем параллелепипеда, определяемый векторами-строками матрицы, равен $0$.

Система однородных линейных уравнений, представленная матрицей, имеет нетривиальное решение.

Определитель линейного преобразования, определяемого матрицей, равен $0$.

Свободный коэффициент в характеристическом многочлене матрицы равен $0$.

В зависимости от определения определителя, которое вы видели, доказательство каждой эквивалентности может быть более или менее сложным.

$\endgroup$

7

$\begingroup$

Для меня это самое наглядное видео в сети, объясняющее детерминанты, и всем, кто хочет глубокого и наглядного понимания этой темы, стоит его посмотреть:

Определитель от 3Blue1Brown

Весь плейлист доступен по этой ссылке:

Суть линейной алгебры от 3Blue1Brown

Ключевая часть серии «Линейные преобразования и матрицы». Если вы это хорошо понимаете, все остальное будет как кусок пирога. Буквально: простой английский + визуальный.

$\endgroup$

5

$\begingroup$

Если определитель квадратной матрицы $n\times n$ $A$ равен нулю, то $A$ необратима . Это важный тест, который помогает определить, является ли квадратная матрица обратимой, т. Е. Есть ли у матрицы обратная. Когда у него есть обратное, это позволяет найти единственное решение, например, уравнения $Ax = b$ при заданном векторе $b$.

Когда определитель матрицы равен нулю, связанная с ним система уравнений линейно зависима; то есть, если определитель матрицы равно нулю , по крайней мере одна строка такой матрицы скалярно кратна другой.

[Когда определитель матрицы отличен от нуля, линейная система, которую она представляет, линейно независима.]

Когда определитель матрицы равен нулю, ее строки являются линейно зависимыми векторами, а ее столбцы являются линейно зависимыми векторами.

$\endgroup$

5

$\begingroup$ 9{-1} = \dfrac{1}{detA} adjA$$

Следовательно, если определитель равен нулю, обратная матрица не существует.

$\endgroup$

9

$\begingroup$

Определитель имеет геометрическую интерпретацию. Помимо интерпретации в другом ответе, еще одной привлекательной, связанной с определителем, является его интерпретация как объема $N$-мерного параллелепипеда. Это более выражено в трехмерном пространстве. Если вы возьмете трехмерные векторы $3$, они могут образовывать или не образовывать углы параллелепипеда, если вы возьмете определитель матрицы с этими тремя векторами в качестве столбцов (или строк), если определитель равен нулю, он означает, что они не образуют вместе параллелепипед, если он отличен от нуля, это означает, что они действительно образуют 3 ребра параллелепипеда с объемом, заданным определителем. Знак значения определителя дает своеобразную информацию об ориентации этого тела.

$\endgroup$

$\begingroup$

Когда вы думаете о матрице как о преобразовании, определитель — это площадь (или объем в более высоком измерении), созданная базисом после преобразования. Этот тип мышления даст вам визуальную помощь. Например, при $n=3$ определитель матрицы равен нулю, значит, отображение по этой матрице переводит плоскость в прямую (площадь основания в преобразованной плоскости равна нулю). Идея может быть обобщена для более высокой размерности.

Обратите внимание, что невозможно сопоставить линию с плоскостью. Значит, обратной матрицы, у которой определитель равен нулю, не существует.

$\endgroup$

$\begingroup$

Возьмите матрицу 2 x 2, назовите ее A, начертите ее в системе координат.

А= [[2,1],[4,2]] . —> Обозначение матрицы Numpy

Следующие два вектора записываются из A

x=[2,4]

y=[1,2]

Если вы построите это, вы увидите, что они находятся в тот же промежуток. Это означает, что векторы x и y не образуют площадь. Следовательно, det(A) равен нулю. Det относится к области, образованной векторами.

$\endgroup$

$\begingroup$

Другими словами:

Если взять $2$ вектора в $2D$ пространстве, можно показать, что площадь образованного параллелограмма является просто определителем матрицы, образованной этими двумя векторами. Это общий результат для $n$-мерностей — определитель матрицы есть объем $n$-параллелограмма, образованного строками матрицы.

Если определитель равен нулю, это означает, что объем равен нулю. Это может произойти только тогда, когда один из векторов «перекрывает» один из других или, более формально, когда два вектора либо линейно зависимы.

$\endgroup$

1

$\begingroup$

С точки зрения исключения Гаусса: для любой матрицы существуют элементарные матрицы $E_r,…,E_1$, соответствующие некоторым элементарным операциям над строками, такие что $$E_r…E_1A=A_{красный}$$ где $A_{red}$ — редуцированная эшелонная форма строк или просто редуцированная форма матрицы.

Если $A$ — квадратная матрица и определитель $A$ равен нулю, то:

1. $A_{red}$ имеет хотя бы одну нулевую строку (внизу).
2. Определитель $A_{red}$ равен нулю.
3. Количество поворотов в $A_{red}$ меньше, чем количество строк в $A$.

$\endgroup$

$\begingroup$

Если матрица A имеет обратную, это означает, что умножение матриц AB = I, единичная матрица. Говоря простым языком, если матрица обратима, то она может иметь решение.

Если определитель матрицы отличен от нуля, матрица может иметь решение. Если определитель равен нулю, то матрица необратима и, следовательно, не имеет решения, поскольку одна из строк может быть удалена заменой другой строки в матрице.

Обычная причина обратимости матрицы заключается в том, что одна или несколько строк в матрице являются скалярами другой.

ПРИМЕР для матрицы 3×3: Строка 1: x + y + z = P по сравнению со строкой 2: Qx + Qy + Qz = QP. Вторая строка может быть переписана как Q*(x + y + z = P) или Q*(Row 1)]

ИЛИ одна из строк может быть создана добавлением двух или более других строк.

ПРИМЕР для матрицы 3×3: Строка 1: x + 2y + 3z = P, Строка 2: 4x + 5y + 6z = Q, Строка 3: 7x + 8y + 9z = P+Q. Вы видите, что Строку 3 можно продублировать, добавив Строку 1 и Строку 2.

Короче говоря, если определитель матрицы равен нулю, матрица не имеет решения, потому что матрицу нельзя инвертировать.

$\endgroup$

линейная алгебра.

Почему определитель равен нулю, если и только если векторы-столбцы линейно зависимы?

Это легко понять, если вы разбираетесь в линейных преобразованиях.

Что такое векторы?

Вот как вы думаете о векторе, верно? Одна стрелка, указывающая в пространство:

$\begin{bmatrix} x\\y\\z \end{bmatrix}$

Но вы также можете описать их как одну стрелку для каждого измерения:

$x\begin{bmatrix } 1\\0\\0\end{bmatrix} + y\begin{bmatrix} 0\\1\\0 \end{bmatrix}+ z\begin{bmatrix} 0\\0\\1\end{bmatrix }$

Здесь мы использовали единичные векторы для каждого измерения в качестве основы.

Что такое линейное преобразование?

С помощью этой модели векторов легко описывать линейные преобразования. Давайте посмотрим на матрицу 3×3 A . Когда вы применяете преобразование A к вектору v , вы получаете новый вектор v’ : Av=v’ . Обычно вы учитесь вычислять его, умножая компоненты каждой строки на компоненты вектора-столбца и добавляя их:

$\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix} \begin{bmatrix}x \\y\\z \end{bmatrix} = \begin{bmatrix}ax+by+cz\\dx+ey+fz\\gx+hy+iz\end{bmatrix}$

Но если вы посмотрите на этот новый вектор справа, вы увидите, что он такой же, как

$x\begin{bmatrix} a\\d\\g\end{bmatrix} + y\begin{bmatrix} b\ \e\\h \end{bmatrix}+ z\begin{bmatrix} c\\f\\i\end{bmatrix}$

Вам это знакомо? Да, матрица представляет собой просто основу из трех векторов-столбцов, с помощью которых вы можете линейно сопоставить все векторы с набором новых векторов, умножив компоненты на векторы, заменяющие исходные единичные векторы. Если это выглядит так:

$\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}$

, что является матрицей идентичности, то, конечно, ничего не произойдет. Вы просто получаете те же векторы, потому что новая база совпадает с исходной базой единичного вектора.

Что означает определитель?

Вероятно, вы знаете, как вычислить определитель, или в любом случае легко найдете его в Интернете. Но что он описывает? В двумерном пространстве два двумерных вектора могут описывать параллелограмм. в трехмерном пространстве три трехмерных вектора могут описывать параллелепипед. У них есть площадь A или объем V соответственно. Теперь определитель матрицы преобразования описывает, насколько площадь или объем будут масштабироваться при применении преобразования к такому набору векторов.

Что означает определитель 0?

Если вы прочитали последний абзац, вы, вероятно, могли бы сделать вывод: определитель нуля означает, что объем или площадь становится равным 0. Когда это происходит? Конечно только при потере хотя бы одного измерения!

Когда это измерение потеряно?

Исходно у нас есть Матрица тождества $\begin{bmatrix} 1&0\\0&1 \end{bmatrix}$, которая состоит из 2-х независимых векторов, натянутых на плоскость, на которой расположены всевозможные параллелограммы.