Задачи по теме теорема синусов и косинусов 9 класс: Решение задач по теме «Теоремы синусов и косинусов» | Методическая разработка по геометрии (9 класс):

Содержание

Решение задач по теме «Теоремы синусов и косинусов» | Методическая разработка по геометрии (9 класс):

Теорема косинусов:

квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

с² = а²+b²- 2аb cos ɣ

cos ɣ=——————

25.09.20 Классная работа

2.10.20. Классная работа

Задача №2

Задан треугольник ABC, где AC=12, BC=10 и ∠ACB=60 ∘ ∠ACB=60∘

Найдите значение AB2

Решение:
По теореме косинусов мы имеем

AB² =AC²+BC² −2.AC∙BC∙cos∠ACB

Подставляя вместо AC, BC и угла их значения, мы получаем: AB² =12² +10²−2∙12∙10∙cos(60◦), или

AB² =144+100−2∙120 ∙

Выполнив арифметические операции на правой стороне уравнения, получим AB² =124.

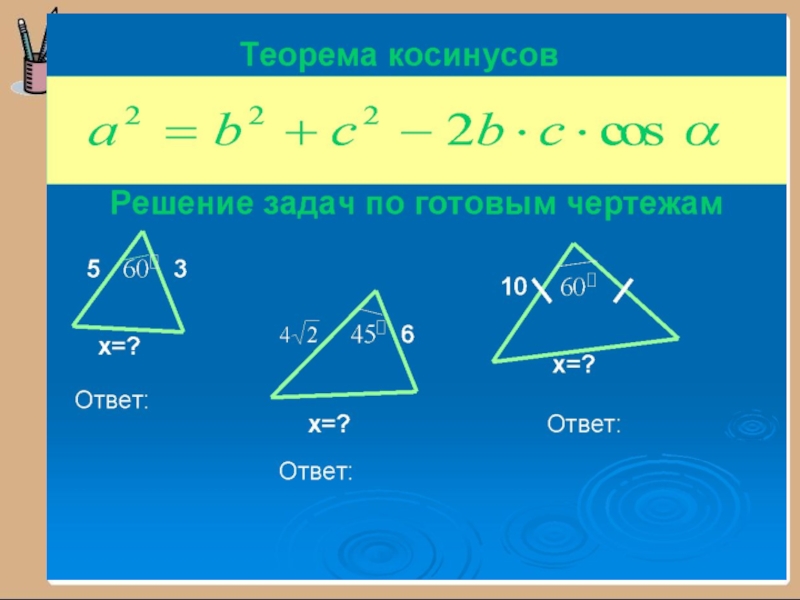
18.09. Классная работа. Записать задачи в тетрадь: Решение задач по теме «Теорема косинусов»

Задача №1

В треугольнике ABC, AC=3, BC=5, AB=6. Найдите cos(∠ACB)
Решение:
По теореме косинусов для треугольника ABC, мы имеем AB²=AC² +BC²−2AC∙BC∙cos(∠ACB).Переставив члены уравнения, мы получим 2AC∙BC∙cos(∠ACB)=AC² +BC² −AB²

Делим обе стороны на 2AC∙BC, получаем cos(∠ACB)=(AC² +BC² −AB²):2AC∙BC =3 2 +5 2 −6 2 2.3.5 =9+25−3630 =−230 =−115

cos⁡(∠ACB)= =(3²+5²−6²):(2∙3∙5)=(9+25−36):30=−2:30=−1/15

Задача №3

Задан треугольник ABC ,AC=17, BC=14 и ∠ACB=60°

Найдите значение AB2

Решение:
По теореме косинусов мы имеем AB² =AC²+BC²−2.AC∙BC∙cos∠ACB

Подставляя вместо AC, BC и угла их значения, мы получаем: AB² =17² +14² −2∙17∙14.cos(60◦)

или AB² =289+196−2∙238∙

После выполнения соответствующих арифметических операций, получаем AB² =247

.Задача №3

Домашняя работа

Решение задач по теме «Теорема косинусов»

Задача №1

В треугольнике ABC, AC=3, BC=5, AB=6. Найдите cos (∠ACB)
Задача №2

Задан треугольник ABC, где AC=12, BC=10 и ∠ACB=60 ∘

Найдите значение AB2

Задача №3

Задан треугольник ABC с AC=17, BC=14 и ∠ACB=60 ∘

Найдите значение AB2

Задача №4

Задан треугольник ABC в котором AC=22, BC=21 и ∠ACB=60 ∘

Найдите значение AB2

9.10. Домашняя работа. Записать задачи в тетрадь

9.10.20 Самостоятельная работа. (распечатать и сделать)

9.10. Записать в тетрадь

25.09. Классная работа. Решение задач по теме: «Теорема синусов»

Стороны треугольника пропорциональны синусам противолежащих углов.

Теорема синусов устанавливает зависимость между сторонами треугольника и противолежащими им углами.

Задание 1. Основание треугольника равно 10 см, один из углов при основании равен , а противолежащий основанию угол равен . Найдите сторону, противолежащую углу в .

Решение. Пусть искомая сторона — см. Тогда по теореме синусов имеем:

(см) Ответ. (см)

Пример

Задание 2. В треугольнике , , . Найти .

Решение. Согласно теореме о сумме углов треугольника

Сторону найдем по теореме синусов:

Ответ.

Задача №3. В треугольнике АВС ∠А=30°,АВ=8, АС=6. Найдите SАВС.

Дано: ∆ АВС, ∠А=30°, АВ=8, АС=6.

Найти: SАВС.

Решение:

Ответ: .

Классная работа. Решение задач по теме: «Площадь треугольника»

2. Найдите площадь треугольника, две стороны которого равны 40 и 20, а угол между ними равен 300.

В данном случае:

Ответ: 200

3. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 300. Боковая сторона треугольника равна 5. Найдите площадь этого треугольника

В данном случае:

Ответ: 6,25

16.10.20. Классная работа. Решение задач по теме: «Площадь треугольника»

формула и примеры решения задач

Содержание:

Формулировка теоремы синусов
Расширенная теорема синусов
Примеры решения задач
Историческая справка

Формулировка теоремы синусов

Теорема

Стороны треугольника пропорциональны синусам противолежащих углов. {\circ}} \Rightarrow$$

$$\Rightarrow \frac{A C}{\frac{\sqrt{3}}{2}}=\frac{4 \sqrt{6}}{\frac{\sqrt{2}}{2}} \Rightarrow A C=\frac{4 \sqrt{18}}{\sqrt{2}}=4 \cdot \sqrt{9}=12$$

Ответ. $A C=12$

Историческая справка

Самое древнее доказательство для теоремы синусов на плоскости описано в книге «Трактат о полном четырёхстороннике» персидского математика, механика и астронома Насира ад-Дина Ат-Туси (1201 — 1274), которая была написана в 13 веке. Теорема синусов для сферического треугольника была доказана математиками средневекового Востока ещё в 10 веке. В труде западноарабского математика, астронома и законоведа Ал-Джайяни (989 — 1050) 11 века «Книга о неизвестных дугах сферы» приводилось общее доказательство теоремы синусов на сфере.

Ручная тригонометрия — Урок — TeachEngineering

Quick Look

Уровень: 11 (9-12)

Необходимое время: 15 минут

Зависимость от урока: Нет

предметных областей: Геометрия, измерение

Доля:

TE Информационный бюллетень

Краткое содержание

Учащиеся изучают концепцию подобных прямоугольных треугольников и то, как они применяются к тригонометрическим отношениям.

Используйте этот урок, чтобы напомнить, что такое коэффициенты срабатывания и как они работают. В дополнение к тригонометрии учащиеся изучают приложение клинометра на устройстве Android® или iOS® и то, как его можно использовать для проверки математики, лежащей в основе тригонометрии. Это готовит учащегося к соответствующей деятельности, во время которой каждая группа проверяет клинометр, чтобы лучше понять тригонометрию.

Инженерное подключение

Некоторые объекты и расстояния в нашем мире очень трудно — даже невозможно — измерить напрямую вручную или с помощью инструментов. Инженеры, которые проектируют различные типы конструкций, невероятно больших или очень маленьких, или машины, которые могут перемещаться на большие расстояния глубоко под водой или далеко в космос, должны иметь точное представление о длинах и размерах, даже если их невозможно измерить. Часто в таких случаях инженеры используют тригонометрию и другие математические соотношения, чтобы найти очень точное приближение к длинам и размерам.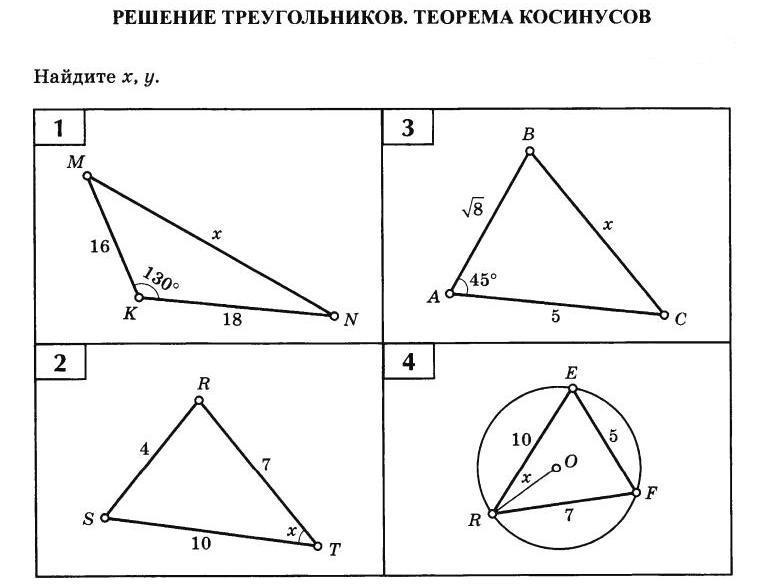 При проектировании больших конструкций инженеры должны обеспечить баланс сил, действующих на конструкцию, чтобы они оставались неподвижными. Инженеры используют тригонометрию для учета вертикальных и горизонтальных составляющих различных сил, действующих на конструкции, таким образом определяя, сможет ли конструкция устоять без разрушения еще до того, как она будет построена. Эти стратегии, основанные на математических знаниях, позволяют инженерам разрабатывать решения проблем, которые иначе были бы неразрешимы.

Цели обучения

После этого урока учащиеся должны уметь:

Опишите, как инженеры могут использовать клинометр.
Используйте клинометр для измерения углов.

Образовательные стандарты

Каждый урок или занятие TeachEngineering соотносится с одной или несколькими науками K-12, технологические, инженерные или математические (STEM) образовательные стандарты.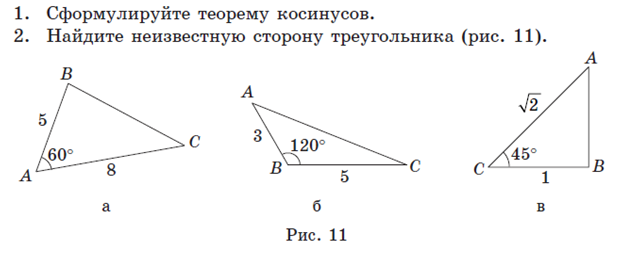

Все более 100 000 стандартов K-12 STEM, включенных в TeachEngineering , собираются, поддерживаются и упаковываются сетью Achievement Standards Network (ASN) , проект D2L (www.achievementstandards.org).
В ASN стандарты структурированы иерархически: сначала по источнику; напр. по штатам; внутри источника по типу; напр. , естественные науки или математика; внутри типа по подтипу, затем по классу, и т. д. .
Общие базовые государственные стандарты — математика
Поймите, что по подобию отношения сторон в прямоугольных треугольниках являются свойствами углов в треугольнике, что приводит к определениям тригонометрических отношений для острых углов. (Оценки 9 — 12) Подробнее
Посмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
Используйте тригонометрические соотношения и теорему Пифагора для решения прямоугольных треугольников в прикладных задачах. (Оценки 9 — 12) Подробнее
Посмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
Международная ассоциация преподавателей технологий и инженерии — Технология
Используйте компьютеры и калькуляторы для доступа, извлечения, организации, обработки, хранения, интерпретации и оценки данных и информации для общения.

(Оценки 9 — 12) Подробнее
Посмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
Используйте различные подходы к информированию о процессах и процедурах использования, обслуживания и оценки технологических продуктов и систем. (Оценки 9 — 12) Подробнее
Посмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
ГОСТ
Предложите выравнивание, не указанное выше
Какое альтернативное выравнивание вы предлагаете для этого контента?
Подписаться

Подпишитесь на нашу рассылку новостей, чтобы получать внутреннюю информацию обо всем, что связано с TeachEngineering, например, о новых функциях сайта, обновлениях учебных программ, выпусках видео и многом другом!
PS: Мы никому не передаем личную информацию и электронные письма.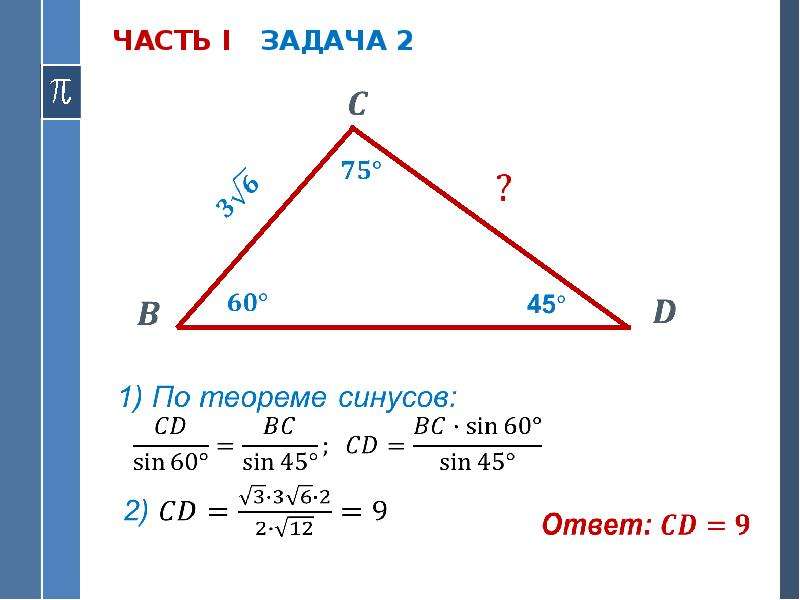
Рабочие листы и вложения
Викторина после урока (docx)
Викторина после урока (pdf)
Ключ для ответов на викторину после урока (docx)
Ключ к ответу на викторину после урока (pdf)
Посетите [www.teachengineering.org/lessons/view/uno_handheld_lesson01], чтобы распечатать или загрузить.
Больше учебных программ, подобных этому
Урок средней школы
Навигация по номерам
Учащиеся узнают, что математика важна в навигации и технике. Они используют теорему Пифагора для решения реальных проблем.
Навигация по номерам
Урок средней школы
Повесть о трениях
Учащиеся старших классов узнают, как инженеры математически проектируют дорожки для американских горок, используя подход, согласно которому криволинейная дорожка может быть аппроксимирована последовательностью множества коротких уклонов. Они применяют основное исчисление и теорему о работе-энергии для неконсервативных сил для количественной оценки трения вдоль кривой…

Сказка о трениях
Урок средней школы
Занятия математикой: анализ сил в ферменном мосту
Изучите основы анализа сил, которые инженеры выполняют в соединениях ферм для расчета прочности ферменного моста, известного как «метод соединений». Найдите растяжения и сжатия для решения систем линейных уравнений, где размер зависит от количества элементов и узлов в ферме…
Занимаемся математикой: анализ сил в ферменном мосту
Деятельность средней школы
У вас есть треугольники!
Учащиеся узнают о тригонометрии, геометрии и измерениях, участвуя в практическом взаимодействии с технологией LEGO® MINDSTORMS®. Сначала они рассматривают основные геометрические и тригонометрические понятия. Затем они оценивают высоту различных объектов с помощью простой тригонометрии. Студенты…
У вас есть треугольники!
Предварительные знания
Учащиеся должны пройти курс геометрии в средней школе и понимать конгруэнтность и подобие геометрических фигур. Студенты также должны иметь начальные знания тригонометрии.
Учитель должен уметь работать с приложением клинометр для iOS или Android. Большинство клинометров говорят сами за себя с небольшим опытом. Если вы используете клинометр с открытым кодом (предложенный в списке материалов), лучше всего держать мобильное устройство вертикально с 0°, отображаемым в верхней части клинометра, а затем поворачивать мобильное устройство влево или вправо так, чтобы верхняя или нижняя часть устройство выравнивается по наклонной стороне измеряемого угла.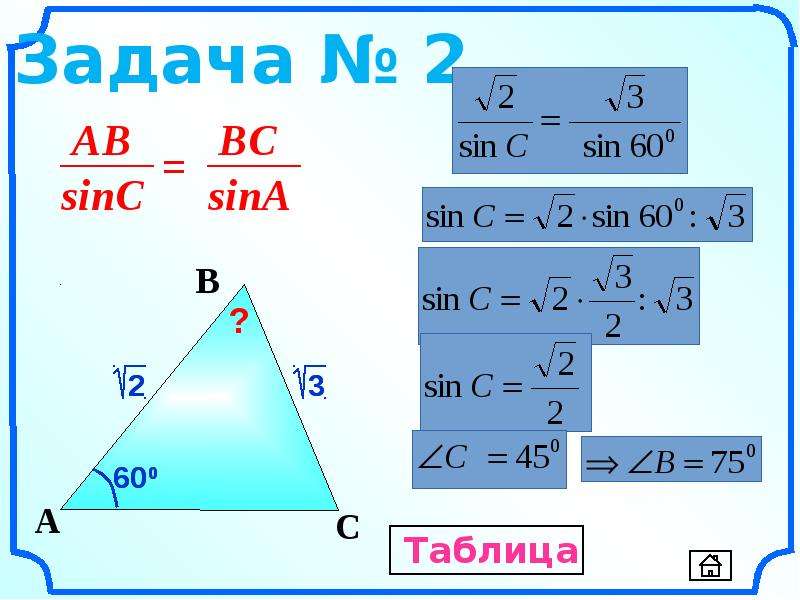 Другая сторона угла должна быть выровнена по горизонтали. Градус, отображаемый на клинометре, является градусной мерой угла. Дополнительная информация представлена в разделе «Основные сведения и концепции для учителей».
Введение/Мотивация
Тригонометрия — это раздел математики, изучающий взаимосвязь между длинами сторон и углов треугольника. Инженеры обычно используют тригонометрические концепции для расчета углов. Инженеры-строители и инженеры-механики используют тригонометрию для расчета крутящего момента и сил на таких объектах, как мосты или строительные балки. Примером может служить расчет статических сил на объект, который не движется, например мост. Причина, по которой мост статичен (не движется), заключается в том, что силы, действующие на него, уравновешиваются (уравновешивают друг друга). Инженеры используют тригонометрию для разложения сил на горизонтальные и вертикальные компоненты, которые можно анализировать.
Понимание сил, действующих на объекты, является важной частью статики, важной области инженерии. Изучение статики и связанные с ней расчеты используются инженерами, чтобы гарантировать, что здания и мосты не рухнут из-за действующих на них сил.
Для начала я хочу, чтобы все нарисовали два прямоугольных треугольника с конгруэнтными соответствующими углами (см. рис. 1), из чего следует, что треугольники подобны . Подобие — это геометрическое понятие, означающее, что все соответствующие углы равны конгруэнтны и отношения соответствующих сторон равны. С точки зрения непрофессионала, подобные фигуры являются большими или меньшими ( в масштабе ) копиями друг друга. От геометрической концепции сходства вы перейдете к тригонометрии. Рис. 1. Подобные прямоугольные треугольники.
Copyright
Copyright © 2014 Scott Burns, College of Information Science & Technology, University of Nebraska-Omaha
Рассмотрите эти вопросы, связанные с вашими нарисованными фигурами:
Запомните три тригонометрических соотношения. (Покажите учащимся рис. 2 при рассмотрении тригонометрических соотношений, используя стороны a, b и c и острый угол θ для моделирования отношений.)
Синус противоположен гипотенузе в прямоугольном треугольнике. Это означает, что sin(θ) = y/r.
Косинус примыкает к гипотенузе. Это означает, что cos(θ) = x/r.
Касательная противоположна смежной в прямоугольном треугольнике. Это означает, что tan(θ) = y/x.
Почему это работает? Подумайте о подобных треугольниках. Помните, что углы равны, а соответствующие стороны находятся в равных отношениях.
Затем извлеките устройство Android или iOS и запустите приложение клинометра (см. рис. 3). Поэкспериментируйте с приложением, чтобы увидеть, что оно делает. Как можно использовать это приложение для изучения триггерных коэффициентов? (Много возможных ответов, но цель состоит в том, чтобы дать учащимся понять, что они могут измерить угол и стороны прямоугольного треугольника и проверить правильность тригонометрических соотношений). Обратитесь к соответствующему упражнению «Тригонометрия через мобильное устройство», чтобы узнать, как интегрировать мобильные устройства с этим уроком.
Рис. 3. Снимок экрана приложения клинометра.
Copyright
Copyright © 2014 Scott Burns, College of Information Science & Technology, University of Nebraska-Omaha
(Чтобы подвести итог введению и заставить учащихся задуматься о возможных применениях тригонометрии и клинометров и о том, как каждый из них может быть применен к инженерному делу, проведите мозговой штурм в классе, ответив на следующие вопросы.) В каких профессиях могут использоваться тригонометрия и клинометры? Где инженеры могут использовать тригонометрию? Для каких типов проектов инженеры могут использовать клинометры?
(После обсуждения попросите пары учащихся воспользоваться Интернетом, чтобы подтвердить свои мысли и/или найти другие возможные ответы. возможные инженерные применения тригонометрии и использование клинометра. )
Предыстория урока и концепции для учителей
Подобные треугольники являются основой тригонометрии прямоугольного треугольника. Поскольку прямые углы конгруэнтны, любые прямоугольные треугольники, у которых есть еще один конгруэнтный соответствующий угол, будут подобны в соответствии с геометрическим постулатом сходства углов. Если треугольники подобны, отношения соответствующих сторон будут равны. Тригонометрия использует это свойство подобных треугольников, вычисляя отношения двух сторон в треугольнике. Например, синус – это отношение катета, противолежащего углу, к гипотенузе в прямоугольном треугольнике. Это означает, что любой прямоугольный треугольник с острым углом 30° будет иметь отношение противоположной стороны к гипотенузе 1:2.
Клинометр — это устройство, которое можно использовать для измерения углов. Приложение на мобильном устройстве позволяет использовать мобильное устройство для измерения углов. Используя приложение в виде простого кода с 0° в верхней части клинометра (как показано на рисунке 3), вы можете использовать верхнюю или нижнюю часть мобильного устройства для измерения угла. Поместив устройство на наклонную поверхность и используя приложение клинометра, можно определить угол наклонной поверхности.
Клинометры
можно использовать для измерения углов между объектами или наклона неподвижного объекта, что позволяет косвенно измерять расстояние с помощью тригонометрии. Устройство Android или iOS должно быть почти вертикально, чтобы использовать функцию измерения угла клинометра, когда оно находится в режиме, соответствующем рисунку 3. Когда приложение клинометра соответствует рисунку 3, с 0° в верхней части клинометра, поверните поворачивайте устройство Android или iOS влево или вправо, пока верхняя или нижняя часть устройства не совпадет с наклонной стороной угла. Другая сторона угла должна быть выровнена по горизонтали. Затем градусную меру угла можно считать с клинометра. На рис. 4 показано выравнивание клинометра при измерении угла. Рис. 4. Измерение угла с помощью приложения клинометра.
авторское право
Copyright © 2014 Скотт Бернс и Брайан Сандалл, Колледж информационных наук и технологий, Университет Небраски, Омаха, и Карли Самсон, Программа ITL, Инженерный колледж, Колорадский университет в Боулдере
Инженерам-строителям часто приходится измерять очень большие объекты, такие как небоскребы и мосты. Нецелесообразно, а часто и невозможно измерять эти объекты рулеткой. Когда прямые измерения невозможны, вместо них используются технологии и математика. Тригонометрия прямоугольного треугольника использует одну известную сторону треугольника в сочетании с известным углом для вычисления других сторон треугольника (которые могут быть, например, высотой или длиной здания). Инженеры используют такие устройства, как клинометры, для измерения угла, необходимого для выполнения тригонометрических вычислений.
Различные определения основных тригонометрических функций
Распознаваемые термины:
Триггерные функции — это отношения катетов и гипотенузы прямоугольных треугольников, используемые в теореме Пифагора. Основные триггерные функции связаны с эталонным углом (данным углом или его эквивалентом).
Концептуально:
Если мы посмотрим на прямоугольную систему координат и поместим угол (θ) так, чтобы его вершина расположена в начале координат, а смежный катет угла лежит на абсциссе, основные тригонометрические функции этого угла определяются как:
Синус – отношение длины катета, противоположного опорному углу, к длине гипотенузы.
Косинус – отношение длины катета, примыкающего к опорному углу, к длине гипотенузы.
Тангенс – отношение длины стороны, противоположной опорному углу, к длине стороны, примыкающей к опорному углу.
В математических терминах:
Основные триггерные функции для угла θ, расположенного, как указано выше, определены следующим образом:
sin θ = г/г
потому что θ = x/r
тангенс θ = у/х
(Помните из теоремы Пифагора, что x ² + y ² = r ² ).
Рис. 5. Прямоугольный треугольник в окружности на координатной плоскости.
Copyright
Copyright © 2014 Карли Самсон, Программа ITL, Инженерный колледж, Колорадский университет в Боулдере
В процессе работы:
На рис. 5 показан прямоугольный треугольник, расположенный на координатной плоскости, одна из вершин которого находится в начале координат на плоскости и в центре окружности. Одна сторона треугольника находится в направлении х, начинается в начале координат и имеет длину х. Другая сторона треугольника находится в направлении y и простирается от точки (x, 0) до (x, y). Гипотенуза имеет длину r и простирается от (0,0) до (x,y). Поскольку тригональные функции угла определяются как указанные выше отношения, и эти отношения не меняются в зависимости от положения точки (x, y) на гипотенузе, синус, косинус и тангенс связаны с углом θ и а не точка (x, y), выбранная для расчета отношений.
Связанные виды деятельности
Тригонометрия с помощью мобильного устройства. Учащиеся исследуют отношения между углами и длинами сторон в прямоугольных треугольниках с помощью материалов, найденных в классе, и электронного устройства. Используя всю или часть измерительной линейки или дюбеля и учебники или другие материалы, учащиеся строят прямоугольные треугольники и измеряют углы с помощью приложения клинометра на устройстве Android (телефон или планшет) или iOS (iPhone® или iPad®). Затем им предлагается составить треугольник с заданной длиной стороны и одним углом. Электронное устройство используется для измерения точности их построения.
Словарь/Определения
клинометр: прибор для измерения углов наклона, возвышения или депрессии объекта по отношению к силе тяжести.
косинус: отношение длины катета, примыкающего к опорному углу, к длине гипотенузы.
синус: Отношение длины катета, противоположного опорному углу, к длине гипотенузы.
Тангенс : Отношение длины стороны, противоположной опорному углу, к длине стороны, прилегающей к опорному углу.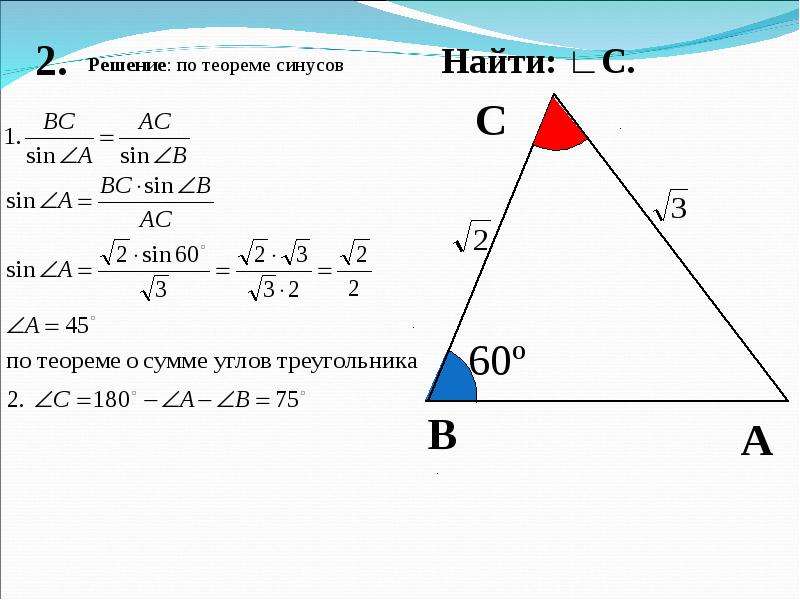
тригонометрия: изучение отношений между углами и сторонами прямоугольных треугольников.
Оценка
Оценка перед уроком
Обсуждение в классе: Задайте классу следующие вопросы, чтобы проверить их знания тригонометрии:
Что вы знаете о тригонометрии? ( Пример ответа: Это предмет изучения математики, в котором содержится информация об отношениях сторон прямоугольных треугольников. )
Какие инструменты доступны для измерения угла наклонной поверхности? ( Возможные ответы: Транспортир, уровень, транзит, клинометр .)
Как можно измерить высоту дерева или флагштока? ( Пример ответа: Измерьте тень очень высокого объекта и измерьте угол от кончика тени до вершины объекта. Затем используйте тангенс триггерной функции, чтобы найти противоположную сторону треугольника [высота объекта ].)
Оценка после внедрения
Наблюдения : Во время урока учащиеся бродят по комнате, задавая вопросы и/или наблюдая за работой учащихся; задайте себе следующие (или похожие) вопросы:
Могут ли учащиеся объяснить, что такое коэффициенты триггера?
Могут ли учащиеся продемонстрировать, что они знают, как подобные треугольники связаны с тригонометрией?
Понимают ли учащиеся, как можно использовать клинометр для решения задач по тригонометрии?
Оценка итогов урока
Тест: Проведите тест после урока, чтобы оценить понимание учащимися тригонометрии, клинометров и того, как инженеры используют тригонометрию и клинометры в реальных проектах.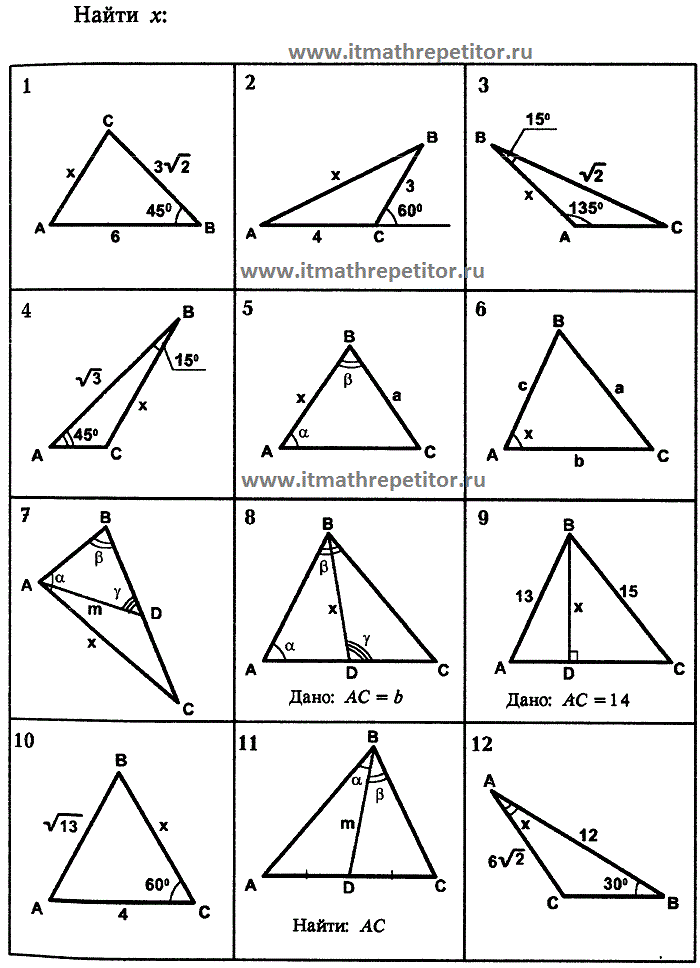
Авторские права
© 2014 Регенты Университета Колорадо; оригинал © 2013 Университет Небраски
Авторы
Скотт Бернс
Программа поддержки
Программа IMPART RET, Колледж информационных наук и технологий, Университет Небраски, Омаха
Благодарности
Содержание этой учебной программы цифровой библиотеки было разработано в рамках сайта RET в области инженерии и компьютерных наук по внедрению прикладных исследований мобильной платформы в программу обучения (IMPART) Университета Небраски в Омахе в рамках гранта Национального научного фонда RET номер CNS 1201136 , Однако это содержание не обязательно отражает политику NSF, и вы не должны исходить из того, что оно одобрено федеральным правительством.
Последнее изменение: 13 июня 2019 г.
Урок 9 | Прямоугольные треугольники и тригонометрия | 10 класс Математика
Цель
Описать и вычислить касательные в прямоугольных треугольниках. Опишите, как изменяется значение тангенса по мере приближения меры угла к 0°, 45° и 90°.
Общие базовые стандарты
Основные стандарты
Основные стандарты, рассмотренные в этом уроке
А628Д5К3-5Б97-4Е03-Б1ЭК-5АД5К66Д8950
G.SRT.C.6 — Поймите, что по подобию отношения сторон в прямоугольных треугольниках являются свойствами углов в треугольнике, что приводит к определениям тригонометрических отношений для острых углов.
G.SRT.C.7 — Объясните и используйте соотношение между синусом и косинусом дополнительных углов.
Основополагающие стандарты
Основополагающие стандарты, рассмотренные в этом уроке
А628Д5К3-5Б97-4Е03-Б1ЭК-5АД5К66Д8950
G. CO.C.10
Критерии успеха
Основные понятия, которые учащиеся должны продемонстрировать или понять для достижения цели урока .
Определить тангенс любого заданного угла в прямоугольном треугольнике как отношение длины противоположной стороны к этому углу прилежащей стороны (TOH).
Объясните, что тангенс любого заданного угла равен между всеми треугольниками с одинаковыми мерами угла, исходя из критерия сходства между углами.
Вычислить тангенс любой градусной меры в треугольнике с помощью научного или графического калькулятора.
Определите и запомните тангенс для обычных угловых мер 0°, 30°, 45°, 60° и 90°.
Объясните, почему тангенс любого угла в 90° не определен.
Определите соотношение между синусом, косинусом и тангенсом и запишите определение тангенса через синус и косинус.
Советы учителям
Рекомендации для учителей по проведению этого урока
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950
Стандарты Common Core не требуют запоминания тангенса для стандартных мер углов.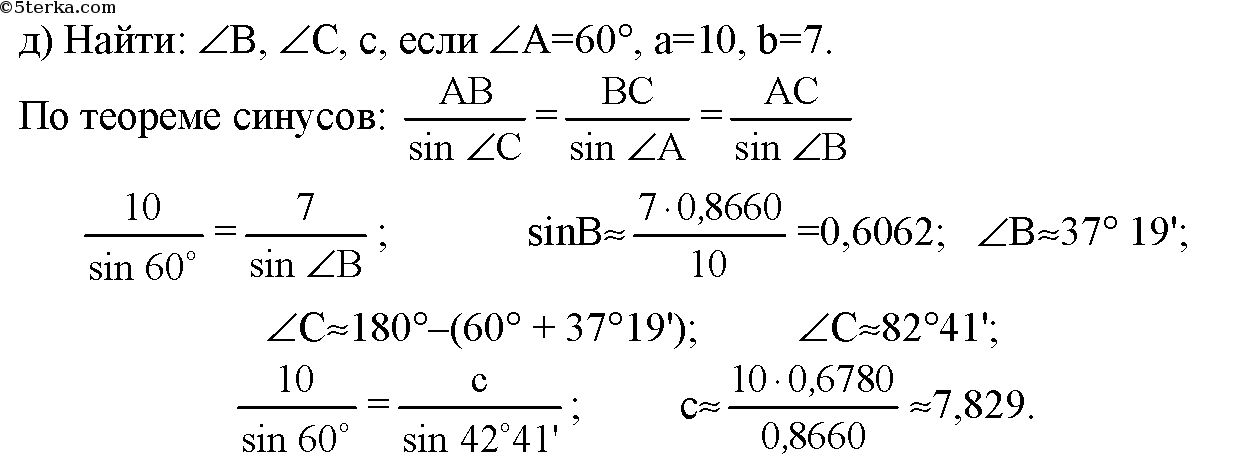 Однако, если учащиеся запомнят эти значения, им будет легче получить доступ к некоторым материалам по алгебре 2 и исчислению AP.
Fishtank Plus
Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.
Проблемы с якорем
Задачи, разработанные для изучения ключевых моментов урока, и наводящие вопросы, помогающие ученикам понять
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950
Проблема 1
Ниже представлен набор подобных прямоугольных треугольников. Найдите отношение длин сторон в каждом треугольнике, описывающих сторону, противоположную отмеченному углу, к стороне, прилегающей к отмеченному углу.
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной проблемы.
Проблема 2
Чему равен тангенс 0°, 45°, 60° и 90°? Объясните, почему тангенс угла 90° не определен.
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.
Проблема 3
Для прямоугольного треугольника всегда, иногда или никогда верно следующее утверждение?
$${\mathrm{tan}\theta=\frac{\mathrm{sin}\theta}{\mathrm{cos}\theta}}$$
Наводящие вопросы
Создайте бесплатную учетную запись или войдите в нее получить доступ к наводящим вопросам для этой якорной проблемы.
Каталожные номера
EngageNY Mathematics Geometry > Модуль 2 > Тема E > Урок 30 — Пример 2
Геометрия > Модуль 2 > Тема E > Урок 30 общей основной учебной программы штата Нью-Йорк по математике от EngageNY и Great Minds. © 2015 Великие умы. Лицензировано EngageNY Департамента образования штата Нью-Йорк в соответствии с лицензией США CC BY-NC-SA 3.0. По состоянию на 2 декабря 2016 г., 17:15.
Изменено Fishtank Learning, Inc.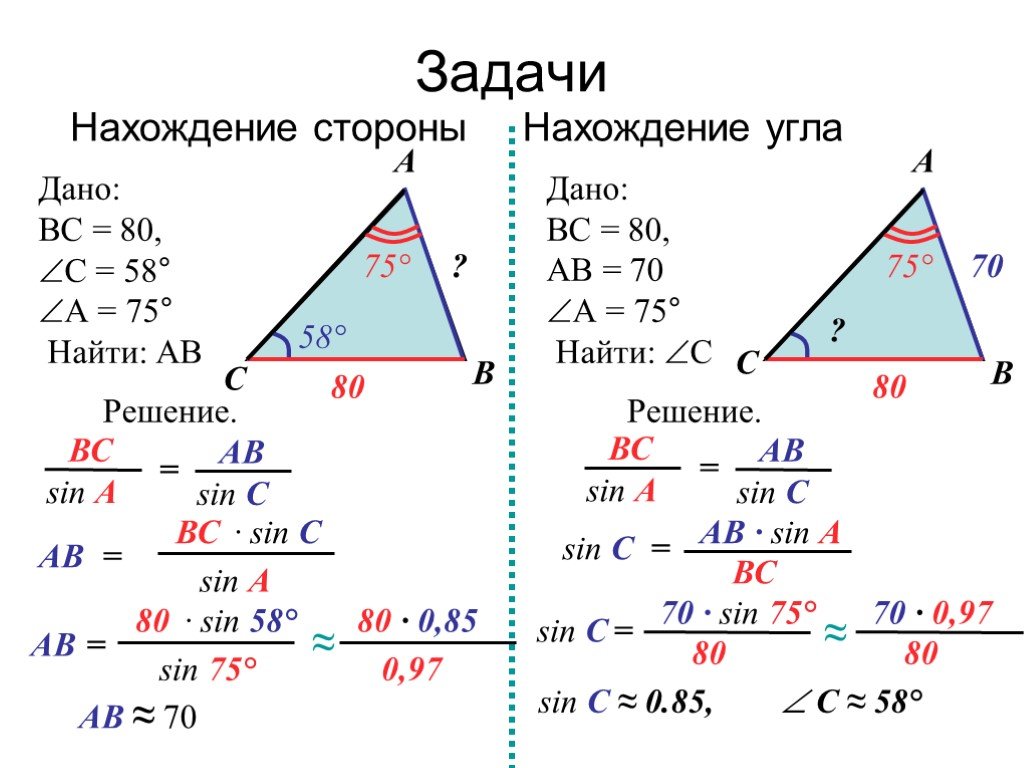
Целевая задача
Задание, которое представляет собой пик мышления урока — мастерство покажет, была ли достигнута цель
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950
\sqrt5}{5}}$$, найдите $${\mathrm{cos}\theta}$$ и $${\mathrm{tan}\theta}$$.
Каталожные номера
EngageNY Mathematics Geometry > Модуль 2 > Тема E > Урок 30 — Набор задач, вопрос №4
Геометрия > Модуль 2 > Тема E > Урок 30 общей основной учебной программы штата Нью-Йорк по математике от EngageNY и Great Minds. © 2015 Великие умы. Лицензировано EngageNY Департамента образования штата Нью-Йорк в соответствии с лицензией США CC BY-NC-SA 3.0. По состоянию на 2 декабря 2016 г., 17:15.
Дополнительная практика
Следующие ресурсы включают задачи и задания, связанные с целью урока, которые можно использовать для дополнительной практики или для создания собственного набора задач.
Включите задачи, в которых учащимся нужно вычислить касательную нестандартных прямоугольных треугольников, а затем проверить, что касательная одинакова для любых подобных треугольников.
No related posts.