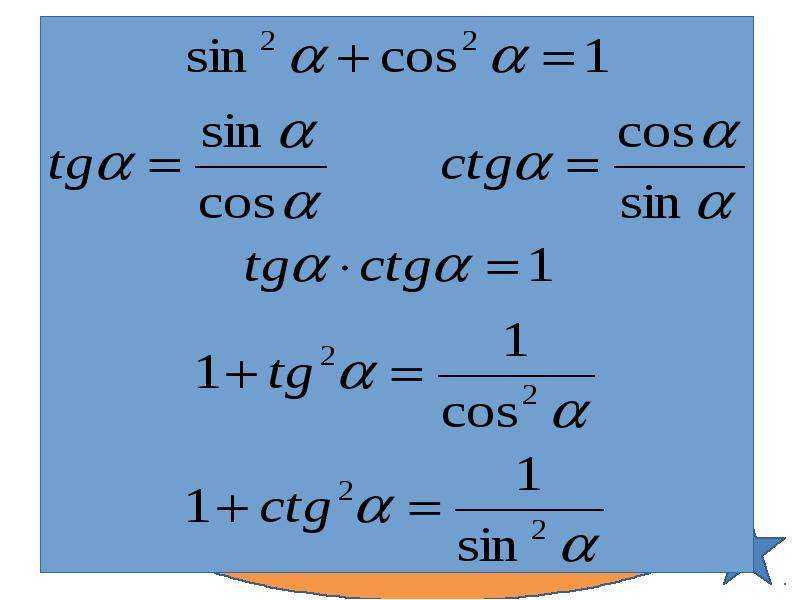Формула тригонометрии: 73 формулы тригонометрии

Содержание

73 формулы тригонометрии

На странице вы найдете все формулы тригонометрии в удобном для использования оформлении. Формулы структурированы в блоки по количеству аргументов, степеням, арифметическим операциям над ними.

Содержание:

Основные тригонометрические тождества
Формулы двойного угла
Формулы тройного угла
Формулы понижения степени
1. Вторая степень
2. Третья степень
3. Четвертая степень
4. Пятая степень
Формулы половинного угла
Формулы понижения степени половинного угла
Формулы сложения аргументов
Формулы вычитания аргументов
Формулы суммы
Формулы разности
Формулы произведения
Формулы произведения в степени
Все формулы на одном листе

Все формулы тригонометрии

Основные тригонометрические тождества

\tg \alpha = \dfrac {\sin \alpha}{ \cos \alpha} = \dfrac{1}{\ctg \alpha}

\ctg \alpha = \dfrac {\cos \alpha}{ \sin \alpha} = \dfrac{1}{\tg \alpha}

\sin ^2 \alpha + \cos ^2 \alpha = 1

1+\tg^2\alpha=\dfrac{1}{\cos^2\alpha}

1+\ctg^2\alpha=\dfrac{1}{\sin^2\alpha}

\tg\alpha \cdot \ctg\alpha=1

Формулы двойного угла (аргумента)

\sin(2\alpha)=2 \cdot \cos \alpha \cdot \sin \alpha

\sin(2\alpha)=\dfrac{2 \cdot \tg \alpha}{1+\tg ^2 \alpha}=\dfrac{2 \cdot \ctg \alpha}{1+\ctg ^2 \alpha}=\dfrac{2}{\tg \alpha + \ctg \alpha}

\cos(2\alpha)=\cos ^2 \alpha- \sin ^2 \alpha = 2 \cdot \cos ^2 \alpha- 1 = 1- 2 \cdot \sin ^2 \alpha

\cos(2\alpha)=\dfrac{1 -\tg ^2 \alpha}{1+\tg ^2 \alpha}=\dfrac{\ctg ^2 \alpha- 1}{\ctg ^2 \alpha +1}=\dfrac{\ctg \alpha-\tg \alpha}{\ctg \alpha + \tg \alpha}

\tg(2\alpha) = \dfrac{2 \cdot \tg \alpha}{1-\tg ^2 \alpha}=\dfrac{2 \cdot \ctg \alpha}{\ctg ^2 \alpha- 1}=\dfrac{2}{\ctg \alpha- \tg \alpha}

\ctg(2\alpha) = \dfrac{\ctg ^2 \alpha-1}{2 \cdot \ctg \alpha}=\dfrac{\ctg \alpha- \tg \alpha}{2}

Формулы тройного угла (аргумента)

\sin(3\alpha)=3 \cdot \sin \alpha- 4 \cdot \sin ^3 \alpha

\cos(3\alpha)= 4 \cdot \cos ^3 \alpha- 3 \cdot \cos \alpha

\tg(3\alpha)= \dfrac{3 \cdot \tg \alpha- \tg ^3 \alpha}{1-3 \cdot \tg ^2 \alpha}

\ctg(3\alpha)= \dfrac{\ctg ^3 \alpha- 3 \cdot \ctg \alpha}{3 \cdot \ctg ^2 \alpha -1}

Формулы понижения степени тригонометрических функций

Вторая степень

\sin ^2 \alpha = \dfrac{1-\cos(2\alpha)}{2}

\cos ^2 \alpha = \dfrac{1+\cos(2\alpha)}{2}

\tg ^2 \alpha = \dfrac{1-\cos(2\alpha)}{1+\cos(2\alpha)}

\ctg ^2 \alpha = \dfrac{1+\cos(2\alpha)}{1-\cos(2\alpha)}

(\sin \alpha- \cos \alpha)^2=1-\sin(2 \alpha)

(\sin \alpha+ \cos \alpha)^2=1+\sin(2 \alpha)

Третья степень

\sin ^3 \alpha = \dfrac{3 \cdot \sin(\alpha)-\sin(3 \alpha)}{4}

\cos ^3 \alpha = \dfrac{3 \cdot \cos(\alpha)+\cos(3 \alpha)}{4}

\tg ^3 \alpha = \dfrac{3 \cdot \sin (\alpha)-\sin(3 \alpha)}{3 \cdot \cos (\alpha)+\cos(3 \alpha)}

\ctg ^3 \alpha = \dfrac{3 \cdot \cos (\alpha)+\cos(3 \alpha)}{3 \cdot \sin (\alpha)-\sin(3 \alpha)}

Четвёртая степень

\sin ^4 \alpha = \dfrac{3-4 \cdot \cos(2 \alpha)+\cos(4 \alpha)}{8}

\cos ^4 \alpha = \dfrac{3+4 \cdot \cos(2 \alpha)+\cos(4 \alpha)}{8}

Пятая степень

\sin ^5 \alpha = \dfrac{10 \cdot \sin(\alpha)-5 \cdot \sin(3 \alpha)+\sin(5 \alpha)}{16}

\cos ^5 \alpha = \dfrac{10 \cdot \cos(\alpha)+5 \cdot \cos(3 \alpha)+\cos(5 \alpha)}{16}

Формулы половинного угла (аргумента)

\sin \Big( \dfrac{\alpha}{2} \Big)=\pm \sqrt{\dfrac{1-\cos \alpha}{2}}

\cos \Big( \dfrac{\alpha}{2} \Big)=\pm \sqrt{\dfrac{1+\cos \alpha}{2}}

\tg \Big( \dfrac{\alpha}{2} \Big)= \dfrac{1-\cos \alpha}{\sin \alpha}= \dfrac{\sin \alpha}{1+\cos \alpha}

\ctg \Big( \dfrac{\alpha}{2} \Big)= \dfrac{1+\cos \alpha}{\sin \alpha}= \dfrac{\sin \alpha}{1-\cos \alpha}

Формулы понижения степени половинного угла (аргумента)

\sin ^2 \Big( \dfrac{\alpha}{2} \Big)=\dfrac{1-\cos \alpha}{2}

\cos ^2 \Big( \dfrac{\alpha}{2} \Big)=\dfrac{1+\cos \alpha}{2}

\tg ^2 \Big( \dfrac{\alpha}{2} \Big)=\dfrac{1-\cos \alpha}{1+\cos \alpha}

\ctg ^2 \Big( \dfrac{\alpha}{2} \Big)=\dfrac{1+\cos \alpha}{1-\cos \alpha}

Формулы сложения аргументов

\sin(\alpha + \beta)=\sin \alpha \cdot \cos \beta + \cos \alpha \cdot \sin \beta

\cos(\alpha + \beta)=\cos \alpha \cdot \cos \beta- \sin \alpha \cdot \sin \beta

\tg(\alpha + \beta)= \dfrac{\tg \alpha + \tg \beta}{1-\tg \alpha \cdot \tg \beta}

\ctg(\alpha + \beta)= \dfrac{\ctg \alpha \cdot \ctg \beta-1}{\ctg \alpha + \ctg \beta}

Формулы вычитания аргументов

\sin(\alpha- \beta)=\sin \alpha \cdot \cos \beta- \cos \alpha \cdot \sin \beta

\cos(\alpha- \beta)=\cos \alpha \cdot \cos \beta+ \sin \alpha \cdot \sin \beta

\tg(\alpha- \beta)= \dfrac{\tg \alpha- \tg \beta}{1+\tg \alpha \cdot \tg \beta}

\ctg(\alpha- \beta)= \dfrac{\ctg \alpha \cdot \ctg \beta+1}{\ctg \beta — \ctg \alpha}

Формулы суммы тригонометрических функций

\sin \alpha+ \sin \beta=2 \cdot \sin \big( \dfrac{\alpha + \beta}{2} \big) \cdot \cos \big( \dfrac{\alpha- \beta}{2} \big)

\cos \alpha+ \cos \beta=2 \cdot \cos \big( \dfrac{\alpha + \beta}{2} \big) \cdot \cos \big( \dfrac{\alpha- \beta}{2} \big)

\tg \alpha + \tg \beta = \dfrac{\sin(\alpha + \beta)}{\cos \alpha \cdot \cos \beta}

\ctg \alpha + \ctg \beta = \dfrac{\sin(\alpha + \beta)}{\cos \alpha \cdot \cos \beta}

\sin (\alpha)+\cos(\alpha)=\sqrt{2} \cdot \sin \Big( \alpha+ \dfrac{\pi}{4} \Big)

Формулы разности тригонометрических функций

\sin \alpha- \sin \beta=2 \cdot \sin \big( \dfrac{\alpha- \beta}{2} \big) \cdot \cos \big( \dfrac{\alpha+ \beta}{2} \big)

\cos \alpha- \cos \beta=-2 \cdot \sin \big( \dfrac{\alpha + \beta}{2} \big) \cdot \sin \big( \dfrac{\alpha- \beta}{2} \big)

\tg \alpha- \tg \beta = \dfrac{\sin(\alpha- \beta)}{\cos \alpha \cdot \cos \beta}

\ctg \alpha- \ctg \beta = \dfrac{\sin(\alpha + \beta)}{\sin \alpha \cdot \sin \beta}

\sin (\alpha)-\cos(\alpha)=\sqrt{2} \cdot \sin \Big( \alpha- \dfrac{\pi}{4} \Big)

Формулы произведения тригонометрических функций

\sin \alpha \cdot \sin \beta = \dfrac{\cos (\alpha- \beta)-\cos(\alpha + \beta)}{2}

\sin \alpha \cdot \cos \beta = \dfrac{\sin (\alpha- \beta)+\sin(\alpha + \beta)}{2}

\cos \alpha \cdot \cos \beta = \dfrac{\cos (\alpha- \beta)+\cos(\alpha + \beta)}{2}

\tg \alpha \cdot \tg \beta = \dfrac{\cos(\alpha- \beta)- \cos(\alpha+\beta)}{\cos(\alpha- \beta)+ \cos(\alpha+\beta)}=\dfrac{\tg \alpha + \tg \beta}{\ctg \alpha + \ctg \beta}

\ctg \alpha \cdot \ctg \beta = \dfrac{\cos(\alpha- \beta)+ \cos(\alpha+\beta)}{\cos(\alpha- \beta)- \cos(\alpha+\beta)}=\dfrac{\ctg \alpha + \ctg \beta}{\tg \alpha + \tg \beta}

\tg \alpha \cdot \ctg \beta = \dfrac{\sin(\alpha- \beta)+ \sin(\alpha+\beta)}{\sin(\alpha+ \beta)- \sin(\alpha-\beta)}

Формулы произведения тригонометрических функций в степени

\sin ^2 (\alpha) \cdot \cos ^2 (\alpha) = \dfrac{1-\cos(4 \alpha)}{8}

\sin ^3 (\alpha) \cdot \cos ^3 (\alpha) = \dfrac{3 \cdot \sin(2 \alpha)- \sin(6 \alpha)}{32}

\sin ^4 (\alpha) \cdot \cos ^4 (\alpha) = \dfrac{3-4 \cdot \cos(4 \alpha)+ \cos(8 \alpha)}{128}

\sin ^5 (\alpha) \cdot \cos ^5 (\alpha) = \dfrac{10 \cdot \sin (2 \alpha)-5 \cdot \sin(6 \alpha)+\sin (10 \alpha)}{512}

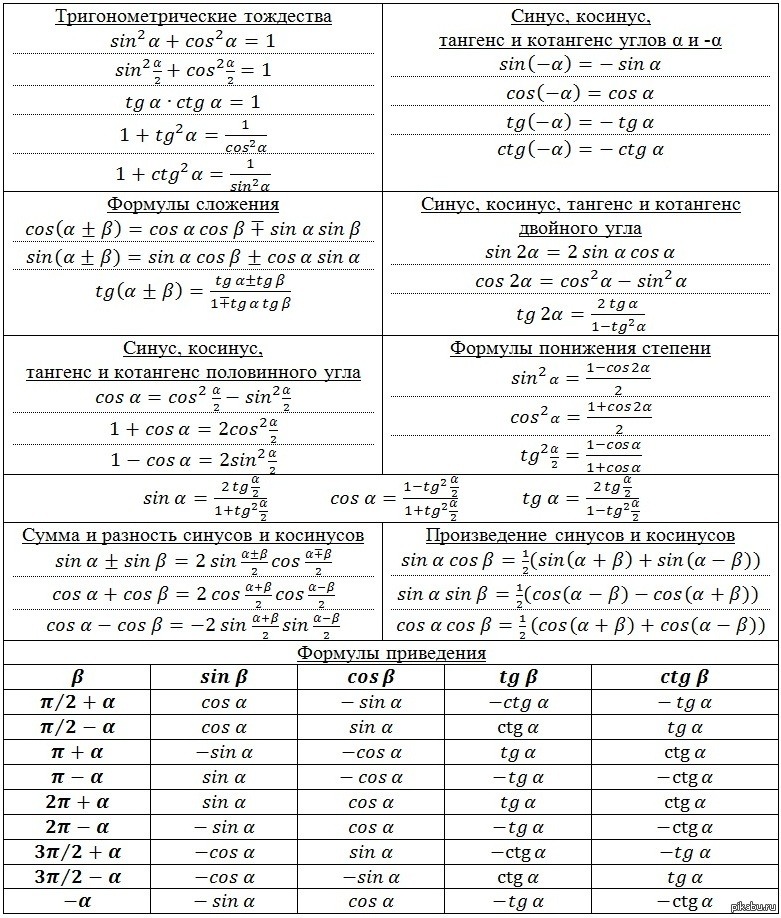
Все формулы тригонометрии на одном листе

На этой картинке собраны все формулы тригонометрии для печати. Лист можно распечатать и использовать при решении задач ЕГЭ или вырезать таблицы и использовать как шпаргалку. Распечатанный лист можно применять как справочный материал при решении задач по тригонометрии в 10 и 11 классе.

Формулы тригонометрии и простейшие уравнения

На этой странице вы узнаете

Как лошадь может помочь в тригонометрии?
Какие знаки принимают функции в разных четвертях?
Что за 6 секретов преобразования тригонометрических выражений помогут нам?

Любые формулы достаточно коварны. Но есть верный способ их одолеть — найти самое сложное и сделать простым. Как добраться до финиша с минимальными потерями? Давайте узнаем в статье.

Формулы тригонометрии

Основное тригонометрическое тождество

sin²x + cos²x = 1

Чтобы доказать данное тождество, рассмотрим прямоугольный треугольник со сторонами a, b, c и углом α

\(sin\: \alpha = \frac{b}{c}\)
\(cos\: \alpha = \frac{c}{b}\)

Запишем теорему Пифагора для прямоугольного треугольника

a² + b² = c² | : c²
\(\frac{a^{2}}{c^{2}} + \frac{b^{2}}{c^{2}} = 1\)

Существует еще несколько основных формул:

tg α * ctg α = 1
\(1 + tg^{2} \alpha = \frac{1}{cos^{2} \alpha}\)
\(1 + ctg^{2} \alpha = \frac{1}{sin^{2} \alpha}\)

А что делать, если угол в тригонометрической функции отложен от вертикальной или горизонтальной оси, например, \(cos (x + \frac{\pi}{2})\) или sin(x + π)?

Для всех таких записей существуют специальные формулы, их называют формулами приведения.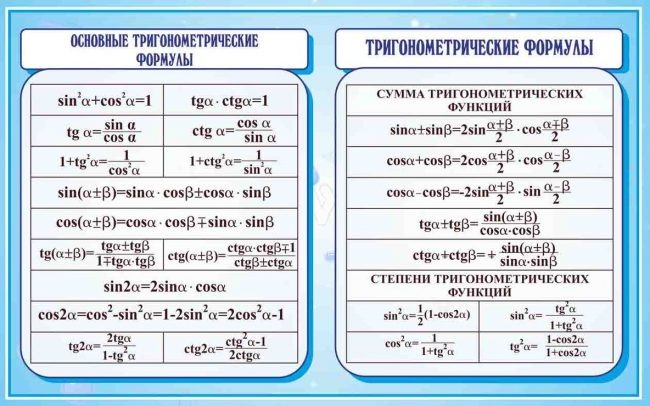 Но запомнить их все достаточно сложно. Поэтому рассмотрим правило, которое поможет вам упростить решение и избавиться от известного слагаемого в угле тригонометрической функции.

Как лошадь может помочь в тригонометрии?

Правило лошади
Формулировка: Если откладывать угол от вертикальной оси, лошадь говорит “да” и кивает, водя головой по вертикальной оси. Тогда значение изначальной функции меняется на кофункцию — функцию противоположную данной. Например, для синуса косинус является кофункцией.
А если откладывать угол от горизонтальной оси, лошадь говорит “нет” и мотает головой, водя по горизонтальной оси, тогда функция не меняется.

Применив правило лошади, нужно обязательно определить знак новой функции от х. Её знак совпадает со знаком изначальной функции.

Нумерация четвертей на окружности идет по часовой стрелке.

Какие знаки принимают функции в разных четвертях?

Теперь давайте рассмотрим на примере применение данного правила:
\(tg(x + \frac{3 \pi}{2})\)

Применим правило лошади и узнаем, меняется ли функция на противоположную.

\(\frac{3 \pi}{2}\) находится на горизонтальной оси, значит лошадь кивает, и функция tg меняется на кофункцию ctg.

Разберемся со знаком.

Так как tg в 4-ой четверти отрицательный, значит перед ctg ставим минус и получим

\(tg(x + \frac{3 \pi}{2}) = -ctg\:x\)

Что за 6 секретов преобразования тригонометрических выражений помогут нам?

Также существуют и другие тригонометрические формулы:

1) Формулы отрицательных углов:

2) Синус, косинус, тангенс и котангенс двойного угла:

3) Формулы сложения и вычитания углов:

4) Формулы понижения степени:

5) Формулы суммы и разности синусов и косинусов:

6) Произведение синусов и косинусов:

Решение простейших тригонометрических уравнений

Тригонометрическое уравнение — это уравнение, в котором переменная содержится под знаком тригонометрической функции.

Чтобы решить такое тригонометрическое уравнение, нужно воспользоваться тригонометрической окружностью, найти значение тригонометрической функции на оси этой функции и записать значения точек с периодом, так как данные функции периодические.

Для этого, возможно, потребуется прочитать статью «Тригонометрическая окружность и графики функций».

Рассмотрим решение таких уравнений на примерах.

Пример 1:
\(cos\:x = -\frac{1}{2}\)

Найдём на тригонометрической окружности точки, для которых значение косинуса равно \(-\frac{1}{2}\)

На окружности есть две таких точки. При этом вторую точку можно отложить на отрицательном направлении, тогда решения можно записать следующим образом:

\(x = \pm \frac{2 \pi}{3} + 2 \pi k, k \in Z\)

Важно: обязательно нужно прописывать период, так как точки на данных местах, находящиеся на всех витках спирали, будут иметь такое значение косинуса.

Пример 2:
\(sin\:x = \frac{1}{2}\)

Проведем перпендикулярную к оси синусов линию через значение \(\frac{1}{2}\). Запишем эти две точки в виде совокупности.

Пример 3:
tg x = 1

Найдем нужное значение на оси тангенсов. Проведем линию и заметим, что в ответ должны идти две диаметрально противоположные точки. Следовательно, можно записать начальную точку, но с периодом в половину окружности, то есть πk, где k ∈ Z

\(x = \frac{\pi}{4} + \pi k, k \in Z\)

Пример 4:
\(ctg\:x = \sqrt{3}\)

Найдем \(\sqrt{3}\) на оси котангенсов и проведём прямую, найденные точки будут диаметрально противоположными. Поэтому запишем первую точку с периодом в половину окружности.

\(x = \frac{\pi}{6} + \pi k, k \in Z\)

Алгоритм решения простейших тригонометрических уравнений:
1) Найти значение тригонометрической функции на оси этой функции на тригонометрической окружности.
2) Отметить точки.
3) Записать точки.

Фактчек

sin²x + cos²x = 1 — основное тригонометрическое тождество.
Формулы приведения применяются, если угол в тригонометрической функции отложен от вертикальной или горизонтальной оси.
Функция меняется на кофункцию в формулах приведения, если угол отложен от вертикальной оси.
Тригонометрическое уравнение — это уравнение, в котором переменная содержится под знаком тригонометрической функции.

Проверь себя

Задание 1.
Чему равно sin(x + π)?

sin x
-sin x
1
cos x

Задание 2.
Чему равно \(ctg(x + \frac{\pi}{2})\)?

tg x
ctg x
— ctg x
— tg x

Задание 3.
Чему равно tg(-2x — π)?

2x
0
-tg(2x)
tg(2x)

Задание 4.
Решите уравнение \(sin(x + \frac{3 \pi}{2}) = 1\)

x = π + 2πk, k ∈ Z
x = π + πk, k ∈ Z
x = 2πk, k ∈ Z
x = -π + 2πk, k ∈ Z

Задание 5.

Решите уравнение cos (2x) = 1

x = -π + πk, k ∈ Z
x = 2πk, k ∈ Z
x = πk, k ∈ Z
x = -π + 2πk, k ∈ Z

Ответы: 1. — 2; 2. — 4; 3. — 3; 4. — 1; 5. — 3

Тригонометрические формулы и тождества — полный список

Последнее обновление Teachoo 30 марта 2023 г. В формулах тригонометрии мы узнаем

Основные формулы
sin, cos tan при 0, 30, 45, 60 градусах
Пифагорейские тождества
Знак греха, потому что, загар в разных квадрантах
радианы
Отрицательные углы (четно-нечетные тождества)
Значение sin, cos, tan повторяется после 2π
Угол сдвига на π/2, π, 3π/2 (тождества кофункций или тождества периодичности)
Тождества суммы и разности углов
Формулы двойного угла
Формулы тройного угла
Идентичности половинного угла (формулы уменьшения мощности)
Sum Identities (сумма идентификаторов продукта)
Идентификаторы продукта (продукт для суммирования идентификаторов)
Закон синуса
Закон косинуса
Что такое обратные тригонометрические функции?
Область и диапазон функций обратной тригонометрии
Обратные тригонометрические формулы
Подстановки обратной тригонометрии

Основные формулы

sin, cos tan при 0, 30, 45, 60 градусах

Пифагорейские тождества

Чтобы узнать знак греха, потому что, загар в разных квадрантах,

мы помним

А дд → С угар → Т о → С кофе

Представление в виде таблицы

	Квадрант я	Квадрант II	Квадрант III	Квадрант IV
грех	+	+	–	–
потому что	+	–	–	–
загар	+	–	+	–

радианы

Радианная мера = π/180 × градусная мера

Также,

1 градус = 60 минут

то есть 1° = 60’

1 минута = 60 секунд

то есть 1’ = 60’’

Отрицательные углы (четно-нечетные тождества)

грех (–х) = – грех х

соз (–х) = соз х

тангенс (–x) = – тангенс х

сек (–x) = сек х

cosec (–x) = – cosec x

детская кроватка (–x) = – детская кроватка x

Значение sin, cos, tan повторяется после 2π

грех (2π + х) = грех х

потому что (2π + х) = потому что х

загар (2π + х) = загар х

Угол сдвига на π/2, π, 3π/2 (тождества кофункций или тождества периодичности)


sin (π/2 – x) = cos x	потому что (π / 2 — х) = грех х
грех (π/2 + х) = потому что х	cos (π/2 + x) = – sin x
sin (3π/2 – x) = – cos x	cos (3π/2 – x) = – sin x
sin (3π/2 + x) = – cos x	потому что (3π/2 + х) = грех х
грех (π — х) = грех х	cos (π – x) = – cos x
грех (π + х) = – грех х	cos (π + x) = – cos x
грех (2π – х) = – грех х	потому что (2π — х) = потому что х
грех (2π + х) = грех х	потому что (2π + х) = потому что х

Тождества суммы и разности углов

Формулы двойного угла

Формулы тройного угла

Идентичности половинного угла (формулы уменьшения мощности)

Sum Identities (сумма идентификаторов продукта)

Идентификаторы продукта (продукт для суммирования идентификаторов)

Продукт для суммирования тождеств

2 cos⁡x cos⁡y = cos⁡ (x + y) + cos⁡(x — y)

-2 sin⁡x sin⁡y = cos⁡ (x + y) — cos⁡(x — y)

2 sin⁡x cos⁡y = sin⁡ (x + y) + sin⁡(x — y)

2 cos⁡x sin⁡y = sin⁡ (x + y) — sin⁡(x — y)

Закон синуса

Здесь

A, B, C — вершины Δ ABC
a — сторона, противоположная A, т. е. BC
b — сторона, противоположная B, т.е. AC
c — сторона, противоположная C, т.е. AB

Закон косинуса

Так же, как закон синуса, у нас есть закон косинуса

Что такое обратные тригонометрические функции

Если грех θ = х

Затем положить грех на правую сторону

θ = грех ^-1 Икс

грех ^-1 х = θ

Таким образом, обратным греху является угол.

Точно так же обратная ко всем функциям тригонометрии угол.

Примечание : Здесь угол измеряется в радианах, а не в градусах.

Итак, у нас есть

грех ^-1 Икс

потому что ^-1 Икс

загар ^-1 Икс

cosec ^-1 Икс

сек ^-1 Икс

загар ^-1 Икс

Область определения и область значений обратных тригонометрических функций

	Домен	Диапазон
грех ^-1	[–1, 1]	[-π/2,π/2]
потому что ^-1	[–1, 1]	[0,π]
загар ^-1	р	(-π/2,π/2)
cosec ^-1	р – (–1, 1)	[π/2,π/2] — {0}
сек ^-1	р – (–1, 1)	[0,π]-{π/2}
детская кроватка ^-1	р	(0, π)

Формулы обратной тригонометрии

Некоторые формулы обратной тригонометрии:

грех ^–1 (–x) = – грех ^-1 Икс

потому что ^–1 (–x) = π – грех ^-1 Икс

загар ^–1 (–x) = – загар ^-1 Икс

cosec ^–1 (–x) = – cosec ^-1 Икс

сек ^–1 (–x) = – сек ^-1 Икс

детская кроватка ^–1 (–x) = π – детская кроватка ^-1 Икс

Замена обратной тригонометрии

Сводка тригонометрических формул

Эти формулы связывают длины и площади определенных кругов или треугольников.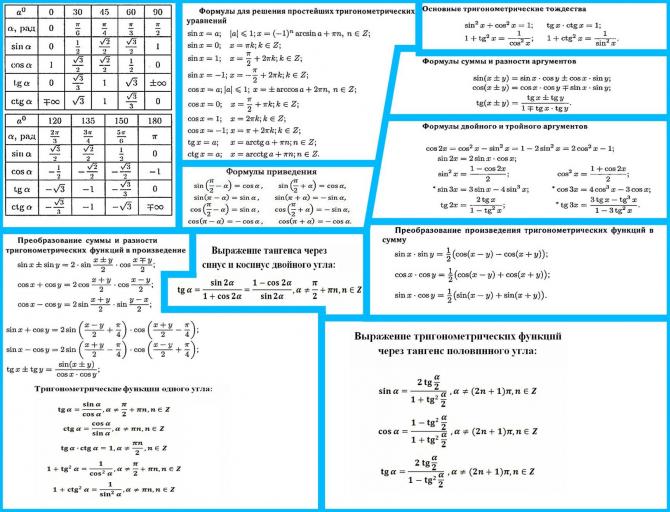 На следующей странице вы найдете личности. Тождества не относятся к конкретным геометрическим фигурам, но справедливы для всех углов.

Формулы для дуг и секторов окружностей

Вы можете легко найти длину дуги и площадь сектора для угла θ в окружности радиусом r .

Длина дуги. Длина дуги равна радиусу r , умноженному на угол θ , где угол измеряется в радианах. Чтобы перевести градусы в радианы, умножьте количество градусов на π /180.
Площадь сектора. Площадь сектора равна половине квадрата радиуса, умноженного на угол, где, опять же, угол измеряется в радианах.

Формулы для прямоугольных треугольников

Наиболее важными формулами тригонометрии являются формулы прямоугольного треугольника. Если θ — один из острых углов в треугольнике, то синус теты — это отношение противолежащего катета к гипотенузе, косинус — отношение прилежащего катета к гипотенузе, а тангенс — это отношение противоположная сторона соседней стороне.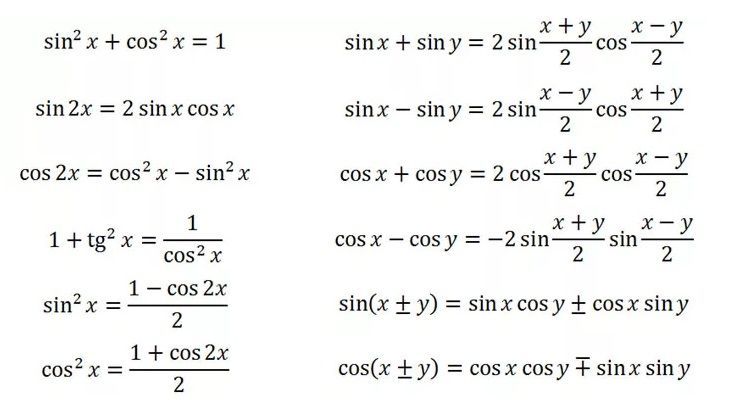

Эти три формулы вместе известны мнемоникой SohCahToa. Кроме того, есть очень важная формула Пифагора, которая гласит, что квадрат гипотенузы равен сумме квадратов двух других сторон.

Зная, что два острых угла дополняют друг друга, то есть дают в сумме 90°, можно решить любой прямоугольный треугольник:

Зная две стороны из трех, можно найти третью сторону и оба острых угла.
Если вы знаете один острый угол и одну из трех сторон, вы можете найти другой острый угол и две другие стороны.

Формулы для косоугольных треугольников

Эти формулы работают для любого треугольника, острого, тупоугольного или прямоугольного. Мы будем использовать стандартные обозначения, в которых три вершины треугольника обозначены прописными буквами A , B и C , а три противоположные им стороны соответственно обозначены строчными буквами а , б и с .

Есть две важные формулы для косых треугольников. Они называются законом косинусов и законом синусов.

Закон косинусов обобщает формулу Пифагора на все треугольники. Он говорит, что c ² , квадрат одной стороны треугольника, равен a ² + b ² , сумма квадратов двух других сторон минус 2. ab cos&nbsp C , удвоенное произведение их на косинус противоположного угла. Когда угол C прямой, он становится формулой Пифагора.

Закон синусов гласит, что отношение синуса одного угла к противоположной стороне одинаково для всех трех углов.

С помощью этих двух формул вы можете решить любой треугольник:

Зная два угла и сторону, можно найти третий угол и две другие стороны.
Если известны две стороны и угол между ними, то можно найти третью сторону и оба других угла.
Если известны две стороны и угол, противолежащий одной из них, то для угла, противолежащего другой, есть два варианта (один острый и один тупой), и для обоих вариантов можно определить оставшийся угол и оставшуюся сторону.
No related posts.