Ни нечетная и ни четная функция: Чётные и нечётные функции — урок. Алгебра, 9 класс.

Чётные и нечётные функции | это… Что такое Чётные и нечётные функции?

Толкование

Чётные и нечётные функции

f(x) = x — пример нечётной функции.

f(x) = x² — пример чётной функции.

f(x) = x³, нечётная

f(x) = x³ + 1 ни чётная, ни нечётная

Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.

Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.

Или по-другому

Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.

Содержание 1 Определения 2 Свойства 3 Примеры 3. 1 Нечётные функции 3.2 Чётные функции 4 Вариации и обобщения

Определения

• Функция называется нечётной, если справедливо равенство

• Функция f называется чётной, если справедливо равенство

• Если не выполняется ни одно из этих равенств, то функция называется функцией общего вида.

Свойства

• График нечётной функции симметричен относительно начала координат O.
• График чётной функции симметричен относительно оси ординат Oy.
• Произвольная функция может быть представлена в виде суммы нечётной и чётной функций:

f(x) = g(x) + h(x),

где

• Функция  — единственная функция, одновременно являющаяся нечётной и чётной.
• Сумма, разность и вообще любая линейная комбинация чётных функций чётна, а нечётных — нечётна.
• Произведение или дробь двух нечётных функций чётно.
• Произведение или дробь двух чётных функций чётно.
• Произведение или дробь нечётной и чётной функций нечётно.
• Композиция двух нечётных функция нечётна.
• Композиция двух чётных функций чётна.
• Композиция чётной функции с нечётной чётна.
• Композиция любой функции с чётной чётна (но не наоборот).
• Функция, обратная чётной, чётна, а нечётной — нечётна.
• Производная чётной функции нечётна, а нечётной — чётна.
  • То же верно про производную третьего, пятого и вообще любого нечётного порядка.
• Производная чётного порядка сохраняет чётность.

Примеры

Нечётные функции

• Нечётная степень где  — произвольное целое число.
• Синус .
• Тангенс .

Чётные функции

• Чётная степень где  — произвольное целое число.
• Косинус .

Вариации и обобщения

• Понятие чётности и нечётности функций естественно обобщаются на случай отображений между векторными пространствами.

Wikimedia Foundation. 2010.

Игры ⚽ Поможем решить контрольную работу

• Чётные числа
• Чётный граф (теория графов)

Полезное

Как определить четность нечетность функции. Нечётные и чётные функции

Функция называется четной (нечетной), если для любогои выполняется равенство

.

График четной функции симметричен относительно оси
.

График нечетной функции симметричен относительно начала координат.

Пример 6.2. Исследовать на четность или нечетность функции

1)
; 2)
; 3)

.

Решение .

1) Функция определена при
. Найдем
.

Т.е.
. Значит, данная функция является четной.

2) Функция определена при

Т.е.
. Таким образом, данная функция нечетная.

3) функция определена для , т.е. для

,
. Поэтому функция не является ни четной, ни нечетной. Назовем ее функцией общего вида.

3. Исследование функции на монотонность.

Функция
называется возрастающей (убывающей) на некотором интервале, если в этом интервале каждому большему значению аргумента соответствует большее (меньшее) значение функции.

Функции возрастающие (убывающие) на некотором интервале называются монотонными.

Если функция
дифференцируема на интервале
и имеет положительную (отрицательную) производную
, то функция
возрастает (убывает) на этом интервале.

Пример 6.3 . Найти интервалы монотонности функций

1)
; 3)
.

Решение .

1) Данная функция определена на всей числовой оси. Найдем производную .

Производная равна нулю, если
и
. Область определения – числовая ось, разбивается точками
,
на интервалы. Определим знак производной в каждом интервале.

В интервале
производная отрицательна, функция на этом интервале убывает.

В интервале
производная положительна, следовательно, функция на этом интервале возрастает.

2) Данная функция определена, если
или

.

Определяем знак квадратного трехчлена в каждом интервале.

Таким образом, область определения функции

Найдем производную
,
, если
, т.е.
, но
. Определим знак производной в интервалах
.

В интервале
производная отрицательна, следовательно, функция убывает на интервале

. В интервале
производная положительна, функция возрастает на интервале
.

4. Исследование функции на экстремум.

Точка
называется точкой максимума (минимума) функции
, если существует такая окрестность точки, что для всех
из этой окрестности выполняется неравенство

.

Точки максимума и минимума функции называются точками экстремума.

Если функция
в точкеимеет экстремум, то производная функции в этой точке равна нулю или не существует (необходимое условие существования экстремума).

Точки, в которых производная равна нулю или не существует называются критическими.

5. Достаточные условия существования экстремума.

Правило 1 . Если при переходе (слева направо) через критическую точку производная
меняет знак с «+» на «–», то в точкефункция
имеет максимум; если с «–» на «+», то минимум; если

не меняет знак, то экстремума нет.

Правило 2 . Пусть в точке
первая производная функции
равна нулю
, а вторая производная существует и отлична от нуля. Если
, то– точка максимума, если
, то– точка минимума функции.

Пример 6.4 . Исследовать на максимум и минимум функции:

1)
; 2)
; 3)
;

4)
.

Решение.

1) Функция определена и непрерывна на интервале
.

Найдем производную
и решим уравнение
, т.е.
.Отсюда
– критические точки.

Определим знак производной в интервалах ,
.

При переходе через точки
и
производная меняет знак с «–» на «+», поэтому по правилу 1
– точки минимума.

При переходе через точку
производная меняет знак с «+» на «–», поэтому
– точка максимума.

,
.

2) Функция определена и непрерывна в интервале
. Найдем производную
.

Решив уравнение
, найдем
и
– критические точки. Если знаменатель
, т.е.
, то производная не существует. Итак,
– третья критическая точка. Определим знак производной в интервалах.

Следовательно, функция имеет минимум в точке
, максимум в точках
и
.

3) Функция определена и непрерывна, если
, т.е. при
.

Найдем производную

.

Найдем критические точки:

Окрестности точек
не принадлежат области определения, поэтому они не являются т. экстремума. Итак, исследуем критические точки
и
.

4) Функция определена и непрерывна на интервале
. Используем правило 2. Найдем производную
.

Найдем критические точки:

Найдем вторую производную
и определим ее знак в точках

В точках
функция имеет минимум.

{2}+1} . Подставьте в нее следующие значения x {\displaystyle x} :

Проверьте, симметричен ли график функции относительно оси Y. Под симметрией подразумевается зеркальное отображение графика относительно оси ординат. Если часть графика справа от оси Y (положительные значения независимой переменной) совпадает с частью графика слева от оси Y (отрицательные значения независимой переменной), график симметричен относительно оси Y. Если функция симметрична относительно оси ординат, такая функция четная.

Проверьте, симметричен ли график функции относительно начала координат. Начало координат – это точка с координатами (0,0). Симметрия относительно начала координат означает, что положительному значению y {\displaystyle y} (при положительном значении x {\displaystyle x} ) соответствует отрицательное значение y {\displaystyle y} (при отрицательном значении x {\displaystyle x} ), и наоборот. Нечетные функции обладают симметрией относительно начала координат.

{2}} . Будучи записанной в такой форме, функция кажется четной, потому что присутствует четный показатель степени. Но этот пример доказывает, что вид функции нельзя быстро определить, если независимая переменная заключена в скобки. В этом случае нужно раскрыть скобки и проанализировать полученные показатели степени.

Четная функция.

Четной называется функция, знак которой не меняется при изменении знака x .

x выполняется равенство f (–x ) = f (x ). Знак x не влияет на знак y .

График четной функции симметричен относительно оси координат (рис.1).

Примеры четной функции:

y = cos x

y = x 2

y = –x 2

y = x 4

y = x 6

y = x 2 + x

Пояснение:
Возьмем функцию y = x 2 или y = –x 2 .
При любом значении x функция положительная.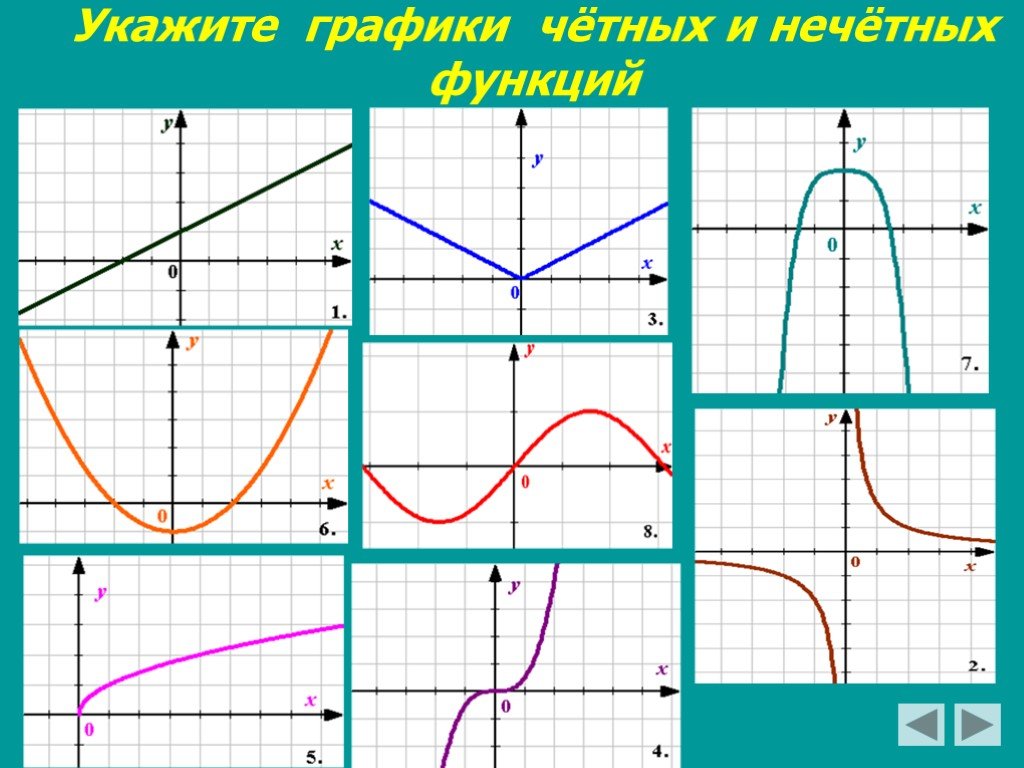 Знак x не влияет на знак y . График симметричен относительно оси координат. Это четная функция.

Нечетная функция.

Нечетной называется функция, знак которой меняется при изменении знака x .

Говоря иначе, для любого значения x выполняется равенство f (–x ) = –f (x ).

График нечетной функции симметричен относительно начала координат (рис.2).

Примеры нечетной функции:

y = sin x

y = x 3

y = –x 3

Пояснение:

Возьмем функцию y = –x 3 .
Все значения у в ней будут со знаком минус. То есть знак x влияет на знак y . Если независимая переменная – положительное число, то и функция положительная, если независимая переменная – отрицательное число, то и функция отрицательная: f (–x ) = –f (x ).
График функции симметричен относительно начала координат. Это нечетная функция.

Свойства четной и нечетной функций:

ПРИМЕЧАНИЕ:

Не все функции являются четными или нечетными. Есть функции, которые не подчиняются такой градации. К примеру, функция корня у = √х не относится ни к четным, ни к нечетным функциям (рис.3). При перечислении свойств подобных функций следует давать соответствующее описание: ни четна, ни нечетна.

Периодические функции.

Как вы знаете, периодичность – это повторяемость определенных процессов с определенным интервалом. Функции, описывающие эти процессы, называют периодическими функциями . То есть это функции, в чьих графиках есть элементы, повторяющиеся с определенными числовыми интервалами.

Которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе.

Определение 1.

Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).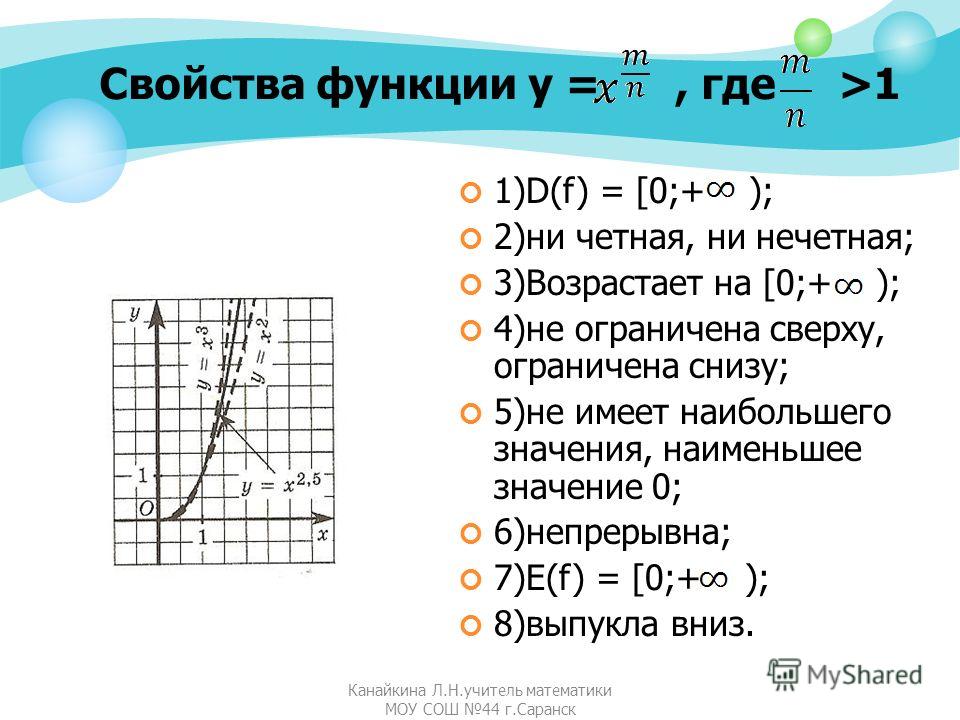

Определение 2.

Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).

Доказать, что у = х 4 — четная функция.

Решение. Имеем: f(х) = х 4 , f(-х) = (-х) 4 . Но (-х) 4 = х 4 . Значит, для любого х выполняется равенство f(-х) = f(х), т.е. функция является четной.

Аналогично можно доказать, что функции у — х 2 ,у = х 6 ,у — х 8 являются четными.

Доказать, что у = х 3 ~ нечетная функция.

Решение. Имеем: f(х) = х 3 , f(-х) = (-х) 3 . Но (-х) 3 = -х 3 . Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной.

Аналогично можно доказать, что функции у = х, у = х 5 , у = х 7 являются нечетными.

Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х 3 , у = х 5 , у = х 7 — нечетные функции, тогда как у = х 2 , у = х 4 , у = х 6 — четные функции. И вообще для любой функции вида у = х» (ниже мы специально займемся изучением этих функций), где n — натуральное число , можно сделать вывод: если n — нечетное число, то функция у = х» — нечетная; если же n — четное число, то функция у = хn — четная.

Существуют и функции, не являющиеся ни четными, ни нечетными. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).

Итак, функция может быть четной, нечетной, а также ни той ни другой.

Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность.

В определениях 1 и 2 речь идет о значениях функции в точках х и -х. Тем самым предполагается, что функция определена и в точке х, и в точке -х. Это значит, что точка -х принадлежит области определения функции одновременно с точкой х. Если числовое множество X вместе с каждым своим элементом х содержит и противоположный элемент -х, то X называют симметричным множеством. Скажем, (-2, 2), [-5, 5], (-оо, +оо) — симметричные множества, в то время как }

Как определить, является ли функция четной, нечетной или ни одной — Криста Кинг Математика

Что такое четные и нечетные функции?

Когда мы говорим о «четном, нечетном или ни одном», мы говорим о симметрии функции. Легче всего визуально увидеть четное, нечетное или ни то, ни другое, глядя на график. Иногда сложно или невозможно построить график функции, поэтому есть и алгебраический способ проверки.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Четные функции

Симметрично относительно оси ???y???

При подключении ???-x??? в функцию, она упростится, чтобы быть такой же, как исходная функция. Это означает, что не имеет значения, подключаете ли вы ???x??? или ???-x???, ваш вывод будет таким же.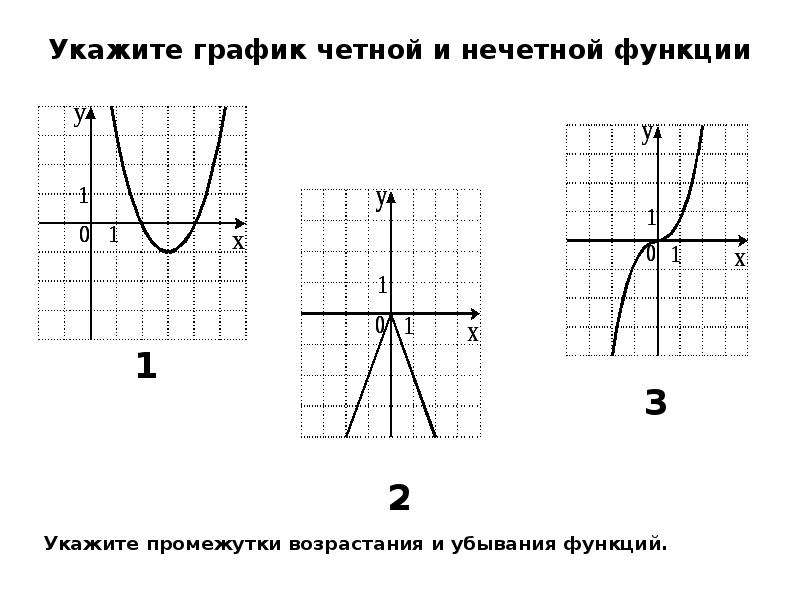 Итак,

???f(-x)=f(x)???

Ниже приведены четные и симметричные относительно оси ???y??? графики.

 Нечетные функции

Симметрично относительно происхождения

При подключении ???-x??? в функцию, это упростит получение отрицательной исходной функции или исходной функции, умноженной на ???-1???. Это означает, что при подключении ???-x??? в функцию, вы получите тот же вывод, что и при подключении ???x???, за исключением того, что он будет отрицательным (или будет иметь противоположный знак, чем исходный вывод). Так

???f(-x)=-f(x)???

Ниже приведены нечетные и симметричные относительно начала координат графики. Обязательно визуально сравните квадранты, расположенные по диагонали друг от друга (квадранты 1 и 3 и квадранты 2 и 4).

Ни четная, ни нечетная

Несимметричная относительно оси ???y??? и несимметричная относительно начала координат

Функция не имеет симметрии.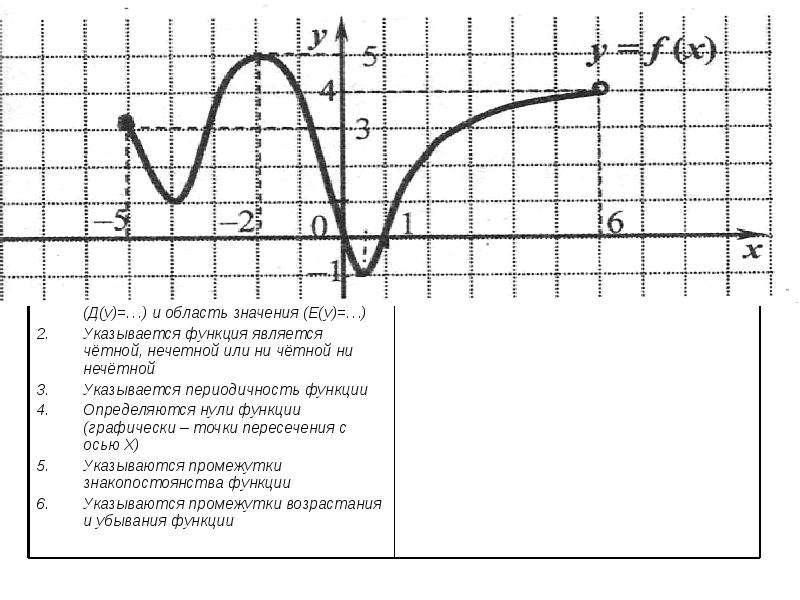 Вполне возможно, что график может быть симметричен относительно оси ???x???, но тогда он не пройдет тест вертикальной линии и, следовательно, не будет функцией.

Как определить, является ли функция четной, нечетной или ни одной из них

Пройти курс

Хотите узнать больше об Алгебре 1? У меня есть пошаговый курс для этого. 🙂

Узнать больше

Является ли полиномиальная функция четной, нечетной или ни одной?

Пример 94???

Поскольку ???f(-x)=f(x)???, функция четная. Мы видим, что график симметричен оси ???y???.

Получить доступ к полному курсу Алгебра 1

Начать

Изучение математикиКриста Кинг 29 января 2021 г. математика, изучение онлайн, онлайн-курс, онлайн-математика, алгебра, алгебра 1, алгебра i, функции, четные, нечетные, ни один, даже нечетный или ни один, симметричные функции, симметричные относительно y- ось, симметричная относительно начала координат, замена -x, замена -x 9{3}\\f(x)=x3

или

f(x)=1xf\left(x\right)=\frac{1}{x}\\f(x)=x1​

были отразив по по обеим осям , результатом будет исходный график.

Рис. 12. (a) Кубическая функция набора инструментов (b) Горизонтальное отражение кубической функции набора инструментов (c) Горизонтальные и вертикальные отражения воспроизводят исходную кубическую функцию.

Мы говорим, что эти графы симметричны относительно начала координат. Функция с графиком, симметричным относительно начала координат, называется 9{x}\\f(x)=2x

не является ни четным, ни нечетным. Кроме того, единственная функция, которая одновременно является четной и нечетной, — это постоянная функция

f(x)=0f\left(x\right)=0\\f(x)=0

.

A Общее примечание: четные и нечетные функции

Функция называется четной, если для каждого входа )=f\left(-x\right)\\f(x)=f(−x)

График четной функции симметричен относительно

y-y\text{-}\\y-

ось.

Функция называется нечетной, если для каждого входа

xx\\x

f(x)=−f(−x)f\left(x\right)=-f\left(-x\right) )\\f(x)=−f(−x)

График нечетной функции симметричен относительно начала координат.

Как: Имея формулу функции, определить, является ли функция четной, нечетной или ни одной из них.

1. Определить, удовлетворяет ли функция

   f(x)=f(−x)f\left(x\right)=f\left(-x\right)\\f(x)=f(−x)

   .

   No related posts.