Круги Эйлера в решении задач
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Решение задач с помощью кругов Эйлера
Круги Эйлера
Смысл логических связок становится более понятным, если
проиллюстрировать их с помощью кругов Эйлера
Круги Эйлера – это геометрическая схема, которая помогает
находить и/или делать более наглядными логические связи
между явлениями и понятиями. А также помогает
изобразить отношения между каким-либо множеством и его
9-ые классы
5-ые классы
Школа
9 «А» класс
Круги Эйлера – это тот метод, который наглядно демонстрирует: лучше один раз увидеть, чем сто раз услышать. Его заслуга
в том, что наглядность упрощает рассуждения и помогает
быстрее и проще получить ответ.
Метод Эйлера является незаменимым при решении
некоторых задач.
Пример.
Конструктор
Игрушка
Заводная
игрушка
Заводной
автомобиль
На рисунке представлено множество – все возможные игрушки.
Некоторые из игрушек являются конструкторами – они
выделены в голубой овал. Это часть большого множества
«игрушки» и одновременно отдельное множество (ведь
конструктором может быть и «Лего», и примитивные
конструкторы из кубиков для малышей). Какая-то часть
большого множества «игрушки» может быть заводными
игрушками. Они не конструкторы, поэтому мы рисуем для них
отдельный овал. Желтый овал «заводной автомобиль»
относится одновременно к множеству «игрушки» и является
частью меньшего множества «заводная игрушка».
Поэтому иизображается внутри обоих овалов сразу.
Задача 1.
«Обитаемый остров» и «Стиляги»
Некоторые ребята из нашего класса любят ходить в
кино. Известно, что 15 ребят смотрели фильм
«Обитаемый остров»
11 человек смотрели фильм «Стиляги», из них 6
смотрели и «Обитаемый остров», и «Стиляги».
Сколько человек смотрели
только фильм «Стиляги»?
Решение:
Решение:
Чертим два множества таким образом:
«Обитаемый
остров»
«Стиляги»
6
6 человек, которые смотрели фильмы «Обитаемый остров» и
«Стиляги», помещаем в пересечение множеств.
15 – 6 = 9 – человек, которые смотрели только «Обитаемый
остров».
11 – 6 = 5 – человек, которые смотрели только «Стиляги».
Получаем:
«Обитаемый
9
6
5
«Стиляги»
Ответ: 5 человек смотрели только «Стиляги».
Задача 3.
«Экстрим»
Из 100 ребят, отправляющихся в детский оздоровительный
лагерь, кататься на сноуборде умеют 30 ребят, на
скейтборде – 28, на роликах – 42.
На скейтборде и на сноуборде умеют кататься 8 ребят, на
скейтборде и на роликах – 10, на сноуборде и на роликах
– 5, а на всех трех – 3.
Сколько ребят не умеют кататься ни на
сноуборде, ни на скейтборде, ни на роликах?
Решение:
Решение:
Скейтборд
Ролики
30
Всеми тремя спортивными снарядами
владеют три человека, значит, в общей
части кругов вписываем число 3. На
скейтборде и на роликах умеют кататься 10
человек, а 3 из них катаются еще и на
сноуборде. Следовательно, кататься только
на скейтборде и на роликах умеют 10-3=7
ребят.
7
2
13
3 5
Сноуборд
20
Аналогично получаем, что только на скейтборде и на сноуборде умеют кататься
8-3=5 ребят, а только на сноуборде и на роликах 5-3=2 человека. Внесем эти
данные в соответствующие части. Определим теперь, сколько человек умеют
кататься только на одном спортивном снаряде. Кататься на сноуборде умеют 30
человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно, только
на сноуборде умеют кататься 20 ребят.
Аналогично получаем, что только наскейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию
задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на
одном спортивном снаряде. Следовательно, 20 человек не умеют кататься ни на
одном спортивном снаряде.
Ответ. 20 человек не умеют кататься ни на одном спортивном снаряде.
Задача 4.
В таблице приведены запросы и количество найденных
Запрос
Найдено страниц (в тыс.)
Крейсер | Линкор
Крейсер
7000
4800
Линкор
4500
Какое количество страниц (в тысячах) будет найдено по
запросу Крейсер &
Линкор?
Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые
слова, не изменялся за время выполнения запросов.
Решение:
Решение:
При помощи кругов Эйлера изобразим условия задачи. При
этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.
линкор
крейсер
1
2
3
Опираясь на условия задачи, составим уравнения:
Крейсер | Линкор: 1 + 2 + 3 = 7000
Крейсер: 1 + 2 = 4800
Линкор: 2 + 3 = 4500
Чтобы найти Крейсер & Линкор (обозначенный на чертеже как область 2),
подставим уравнение (2) в уравнение (1) и выясним, что:
4800 + 3 = 7000, откуда получаем 3 = 2200.
Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:
2 + 2200 = 4500, откуда 2 = 2300.
Ответ: 2300 — количество страниц, найденных по запросу Крейсер & Линкор
English Русский Правила
Применение диаграмм Эйлера-Вена для решения задач математики и информатики.
Муниципальное автономное общеобразовательное учреждение
Средняя школа № 8
Исследовательская работа по информатике
на тему: «Применение диаграмм Эйлера-Вена для решения задач математики и информатики»
Руководитель: Кустова Ю.
Е.
Выполнил: ученик 7 Б класса
Скворцов Н.
г. Бор
2021 год
Содержание
Введение 3
Глава 1 4
1.1 История возникновения кругов Эйлера-Вена 4
1.2 Графическое представление отношения между множествами кругами Эйлера 4
1.3 Практическое применение кругов Эйлера 5
Глава 2 7
2.1 Способы решения задач 7
2.2 Эксперимент в классе на использование кругов Эйлера-Венна 8
Заключение 10
Литература 11
Приложение 1 12
Приложение 2 13
Приложение 3 14
Приложение 4 15
Приложение 5 16
Приложение 6 17
Приложение 7 18
Введение
Актуальность темы учебно-исследовательской работы
На уроках математики мы рассмотрели тему «Множества».
Графически множества удобно представлять с помощью кругов, которые называют кругами Эйлера. В процессе изучения материала учителем моему классу было предложено решить одну задачу. На первый взгляд она показалась нам простой. Однако, легко решить ее математически сразу не удалось. Тогда учитель познакомил нас с графическим способом решения подобных задач с применением кругов Эйлера-Вена. Этот способ я оценил очень увлекательным. Меня заинтересовала эта тема, и я решил узнать побольше.
В наше время вокруг нас собрано огромное количество информации, и разобраться в ней бывает непросто. Находить логические связи между явлениями и понятиями помогают «Круги Эйлера» – это практичный и удобный метод решения логических задач. «Круги Эйлера» находят широкое применение, как в повседневной жизни, так и в науке, поэтому ими стоит уметь пользоваться каждому.
Вышеуказанные причины определили актуальность и важность темы исследовательской работы.
Предмет исследования: решение задач раздела математической логики с использованием кругов Эйлера-Вена
Предметные области: математика, информатика, русский язык, биология и др.
Цель работы – познакомиться с методом решения задач с использованием кругов Эйлера
Задачи:
Познакомиться с литературой по теме: круги Эйлера;
Рассмотреть способы решения задач раздела математической логики в математике и информатике;
Показать наглядность и быстроту способа решения задач с использованием кругов Эйлера
Сделать выводы о проделанной работе
Гипотеза
Применение кругов Эйлера-Вена обеспечивает простоту, наглядность и быстроту решения задач раздела математической логики в математике и информатике.
Глава 1
1.1 История возникновения кругов Эйлера-Вена
Леонард Эйлер (1707 – 1783) (Приложение 1. Рисунок 1) родился в маленькой тихой Швейцарии. Эйлер принадлежит к числу гениев, чьё творчество стало достоянием всего человечества.
До сих пор школьники всех стран изучают некоторые разделы математики в том виде, какой придал им Эйлер. Студенты проходят высшую математику по классической монографии Эйлера. Он был прежде всего математиком. Но всегда подчеркивал практическую деятельность расцвета математики. Он оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных наук. Его называли идеальным математиком 18 века.
Леонард Эйлер написал более 850 научных работ. В одной из них и появились круги. А впервые он их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления». Позднее аналогичный прием использовал ученый Джон Венн — британский логик и философ и этот приём назвали «диаграммы Венна», который используется во многих областях: теория множеств, теория вероятностей, логики, статистики, компьютерных науках.
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов и они получили название «круги Эйлера-Венна».
Этот метод даёт более наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах.
1.2 Графическое представление отношения между множествами
кругами Эйлера
Круги́ Э́йлера — графическая схема, с помощью которой можно изобразить отношения между множествами для наглядного представления.
С множествами можно выполнять определенные операции. Операции над множествами рассматриваются для получения новых множеств из уже существующих. К основным операциям, которые можно выполнять над множествами, относятся следующие:
Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А или В (Приложение 2. рис. 1). Такое отношение существует между объемом понятий «самые умные девочки класса» и «самые умные мальчики класса» образуют новое множество «самые умные ученики класса»
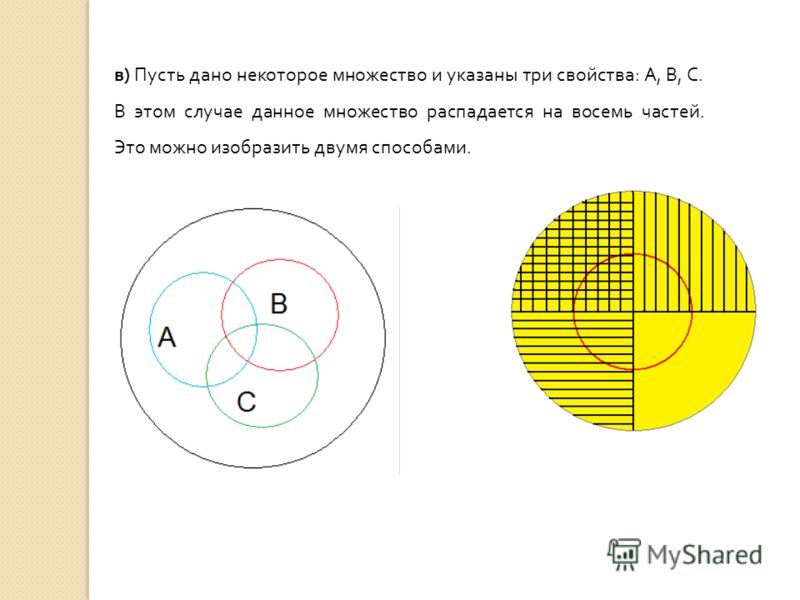
Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (Приложение 2.
рис. 2).
Такое отношение существует между объемом понятий «студент» и «спортсмен». Некоторые (но не все) студенты являются спортсменами; некоторые (но не все) спортсмены являются студентами.
Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (Приложение 2. рис. 3).
Такое отношение существует между объемом понятий «студент» и «спортсмен». И это только та часть студентов, которые действительно не являются спортсменами.
Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В (Приложение 2. рис. 4).
Такое отношение существует между объемом понятий «студент» и «спортсмен». И это только та часть студентов, которые действительно не являются спортсменами или та часть спортсменов, которая не является студентами.
Абсолютным дополнением множества А называется множество всех тех элементов, которые не принадлежат множеству А (Приложение 2.
рис. 5):
Такое именно отношение существует, например, между понятиями «тупоугольный треугольник» и «остроугольный треугольник». В объеме понятия «тупоугольный треугольник» не отображается ни один остроугольный треугольник, а в объеме понятия «остроугольный треугольник» не отображается ни один тупоугольный треугольник.
1.3 Практическое применение кругов Эйлера
Графические изображения, сделанные с использованием кругов Эйлера, существенно упрощают понимание сложных математических формулировок и наглядно отражают суть определений.
Круги Эйлера – метод, позволяющий развивать математические представления и использовать их при изучении окружающего нас мира.
Какие задачи можно решить с помощью кругов Эйлера? Удобнее всего, логические задачи на пересечение и объединение множеств.
Множеств может быть два, а может быть и больше. Чем больше множеств, тем труднее становится решить задачу.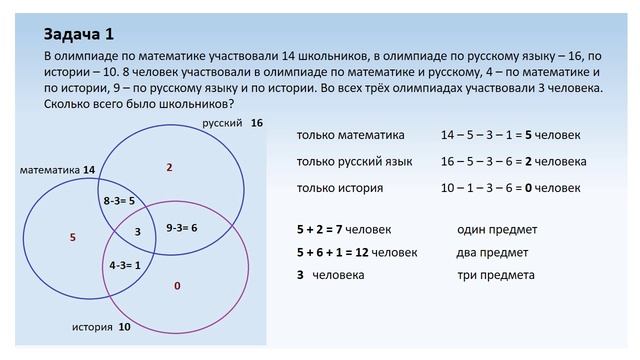
С помощью кругов Эйлера на практике можно решать задачи логики, биологии, философии и других областей. Проиллюстрируем это на примерах.
Например, кругами Эйлера можно изобразить высказывание: «Все квадраты являются прямоугольниками». (Приложение 3. Рис. 6)
Можно проанализировать ситуацию поиска целевой аудитории в каком-то городе людей в возрасте от 18 до 35 лет, зарегистрированных одновременно в известных социальных сетях «В контакте» и «Одноклассники». (Приложение 3. Рис. 7). Искомая область находится на пересечении трех областей.
Применять круги Эйлера удобно в маркетинге и рекламе. В данных областях круги Эйлера могут самым наглядным способом передать важнейшую информацию. (Приложение 3. Рис. 8)
Следовательно, используя круги Эйлера можно решать задачи в различных областях деятельности человека.
Глава 2
2.1 Способы решения задач
Рассмотрим несколько задач, которые могут быть решены с применением кругов Эйлера на уроках математики и информатики.
Задача 1.
В трех седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке – 10 ребят из хора, в хоре – 6 спортсменов, в драмкружке – 8 спортсменов; 3 спортсмена посещают и драмкружок, и хор.
Необходимо выяснить:
Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке?
Сколько ребят занято только спортом?
Решение
Для наглядности приведем два варианта решения: классический и с помощью кругов Эйлера.
Классический метод
Ответ: 10 человек.
Метод с использованием кругов Эйлера (Приложение 4)
По условию задачи известно о 3 кружках: драмкружок, хор, спортивная секция.
Чтобы решать подобные задачи можно придерживаться следующего алгоритма
Изобразить кругами Эйлера заданное по условию задачи количество множеств;
Пронумеровать все полученные сегменты;
Выразить сегментами дано из условия задачи;
Выразить сегментами неизвестное из условия задачи;
Используя полученные уравнения выполнить подстановки и найти результат
Применение кругов Эйлера в информатике
Задача 2.
В информатике с использованием кругов Эйлера можно решать задачи на построение запросов для поисковых систем или подсчитывать количество страниц по запросам.
Следует иметь ввиду, что в языке запросов поискового сервера для обозначения логической операции «ИЛИ» (объединение) используется символ «|», а для обозначения логической операции «И» (пересечение) – символ «&».
Например: в таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
Запрос | Найдено страниц (в тысячах) |
Списывать&(На|ЕГЭ&Запрещено) | 1475 |
Списывать&ЕГЭ&Запрещено | 450 |
Списывать&На | 1400 |
Необходимо найти количество страниц (в тысячах) по запросу:
Списывать&На&ЕГЭ&Запрещено
Из условия задачи известно о четырех множествах: Списывать, На, ЕГЭ, Запрещено
Далее задача решается точно также по алгоритму, описанному выше.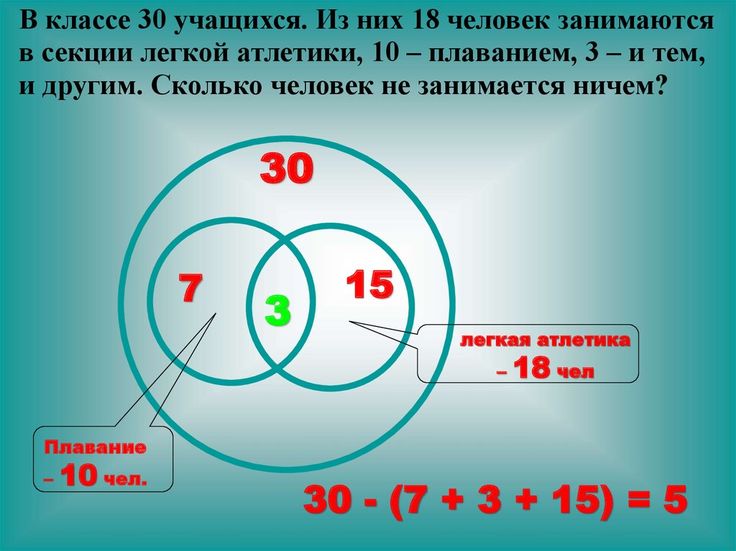
Единственная сложность – появляется приоритет выполнения операций (Приложение 5).
Чем сложнее и запутаннее логическая задача, связанная с множествами, тем полезнее будет нарисовать диаграмму с кругами Эйлера. После этого решение значительно упрощается.
2.2 Эксперимент в классе на использование кругов Эйлера-Венна
При изучении данной темы я решил провести небольшой эксперимент в моем классе и доказать выдвинутую гипотезу – использование кругов Эйлера-Венна обеспечивает простоту, наглядность и быстроту решения задач раздела математической логики в математике и информатике.
В ходе эксперимента я предложил одноклассникам конкретную задачу и попросил ребят ее решить. Однако, на этом этапе поставленная задача у всех одноклассников вызвала затруднение.
На следующем этапе я сначала объяснил ребятам возможность использования кругов Эйлера при решении подобных задач. После этого та самая задача, в условии которой нам было сначала достаточно непросто разобраться, стала понятна и решаема.
На заключительном этапе я предложил еще одну задачу. И ребята, убедившись в простоте и наглядности использования кругов Эйлера-Венна с удовольствием быстро пришли к поставленной цели.
Проведенный эксперимент доказал не только выдвинутую мной гипотезу, но и показал мне возможность использования данного подхода не только в решении задач математики и информатики, а при решении обычных жизненных задач выбора. Например, если человек хочет определить, какая профессия больше ему подходит, он может сначала нарисовать схему в виде кругов Эйлера. Возможно, чертеж этого поможет определиться ему с выбором: Те варианты, которые окажутся на пересечении всех трех кругов, и есть профессия, которая не только сможет обеспечить вам достойную заработную плату, но и будет нравиться. (Приложение 6).
Заключение
В результате проведенного исследования мной были изучены: теоретические основы становления раздела математической логики; изучены основные операции: пересечение, объединение, разность; проиллюстрировано применение кругов Эйлера для решения различных задач; рассмотрены способы решения задач раздела математической логики; подробно рассмотрено применение кругов Эйлера-Вена для решения задач математики и информатики.
В ходе исследования я подтвердил гипотезу и пришел к следующим выводам:
Чем сложнее и запутаннее логическая задача, связанная с множествами, тем полезнее будет нарисовать диаграмму с кругами Эйлера. После этого решение значительно упрощается.
Круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.
Знания по этой теме мне пригодятся при сдаче ОГЭ и ЕГЭ по математике и информатике и при написании олимпиадных работ по данным предметам.
Литература
Список учебной и научной литературы
Депман,И.Я., Виленкин, Н.Я. За страницами учебника математики Пособие для учащихся 5 – 6 кл./И.Я Депман. М.: Просвещение, 1999.
Задачи для внеклассной работы по математике в V – VI классах: Пособие для учителей/ Сост.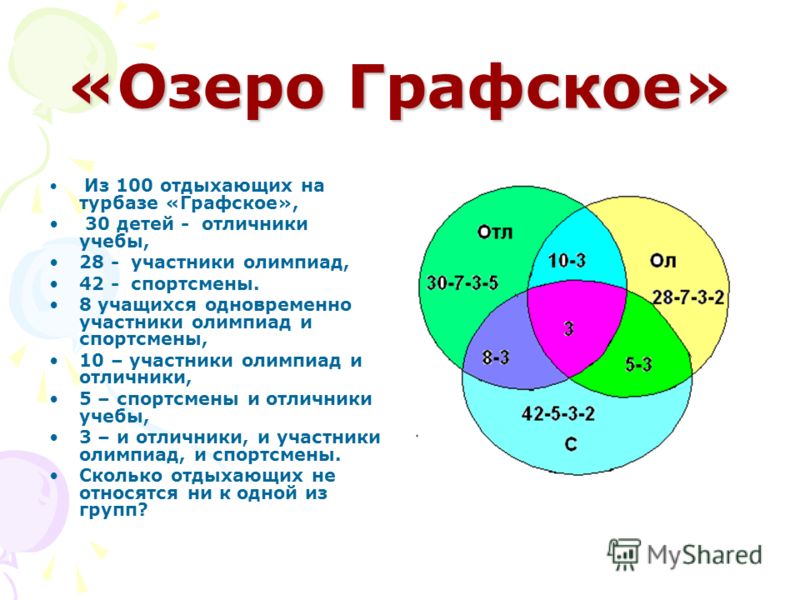
В.Ю. Сафонова. Под ред. Д.Б. Фукса, А. Л. Гавронского. М.: МИРОС, 1993.
Игнатьев. Е.И. В царстве смекалки, или Арифметика для всех: Книга для семьи и школы. Опыт математической хрестоматии в 3 книгах/Худож. Н.Я. Бойко. – Ростов н/Д: Кн. Изд-во, 1995.
Шарыгин И. Ф., Шевкин А. В. Математика: Задачи на смекалку: Учеб. пособие для 5 – 6 кл. общеобразоват. учреждений. – 5-е изд. – М.: Просвещение, 2000. – 95 с.: ил.
Математика: 6 класс: Дидакт. материалы для общеобразова. учеб. заведений/Г.В.Дорофеев, С.Б.Суворова, И.Ф.Шарыгин и др.- М.: Дрофа, 1996.
Фарков, А.В. Математические олимпиады в школе.5–11 классы./А.В. Фарков. М.: Айрис–пресс, 2007.
Интернет-ресурсы:
http://www.tutoronline.ru/blog/krugi-jejlera;
http://logika.vobrazovanie.ru/index.php?link=kr_e.html;
http://mmmf.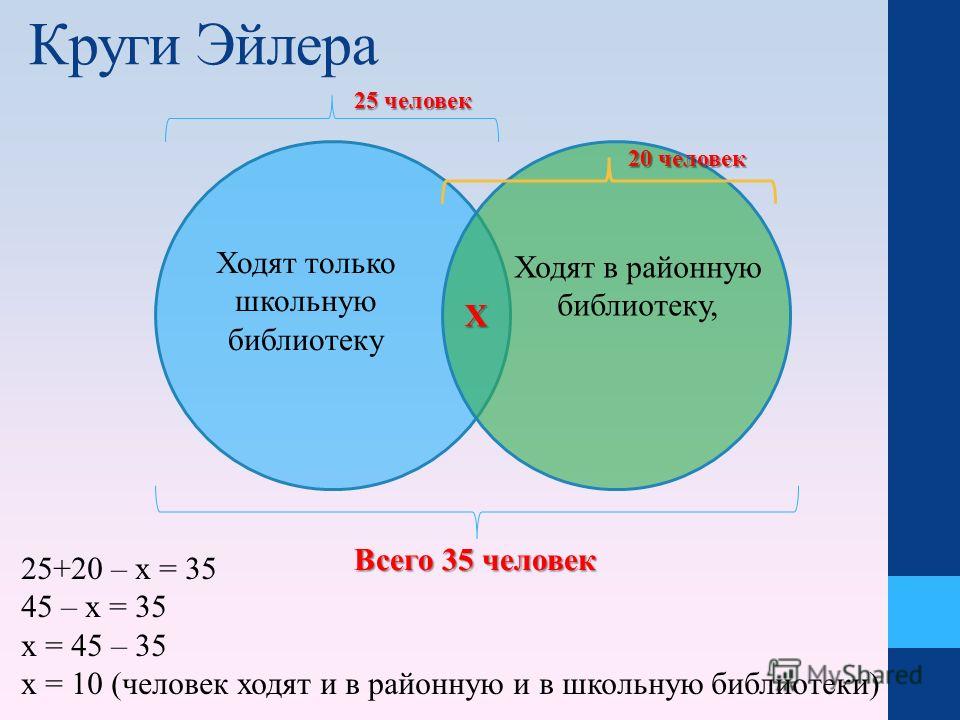
msu.ru/archive/20122013/z5/z5090313.html
Приложения
Приложение 1
Рисунок 1
Приложение 2
В А В А В А В 3 2 1 А Рисунок 1 | операция «объединение» сложение секторов 1+2+3 |
А В Рисунок 2 | операция «пересечение» сектор 2 |
1 2 3 Рисунок 3 | операция «разность» сектор 1 |
1 2 3 Рисунок 4 | сектор 1 или 3 исключаем 2 |
0 Рисунок 5 | сектор 0 исключаем 1, 2, 3 |
Приложение 3
Рисунок 6
Прямоугольники
Квадраты
Отображение отношений между множествами
Рисунок 7
Применение кругов Эйлера в социологическом исследовании
Рисунок 8
Применение кругов Эйлера в маркетинге и рекламе
Приложение 4
1
2
3
4
5
6
Драм
Спорт
7
Хор
Дано: | Найти: |
1 +2+3+4+5+6+7=70 (1) 1+2+4+5=27 (2) 2+3+5+6=22 (3) 4+5+6+7=32 (4) 4+5=10 (5) 5+6=6 (6) 2+5=8 (7) 5=3 (8) | 1+2+3 – Не поют в хоре? 1+4+7 – Не увлекаются спортом? 3+6+7 – Не посещают драмкружок? 3+6 – Заняты только спортом? |
Решение: 1+2+3 – Первое уравнение минус четвертое (70-32=38 человек) 1+4+7 –Первое уравнение минус третье (70-22=48 человек) 3+6+7 – Первое уравнение минус второе (70-27=43 человека) 3+6 – Третье уравнение минус седьмое (22-8=14 человек) | |
Приложение 5
Дано: кол-во страниц по запросам (в тысячах) | Найти: кол-во страниц по запросу (в тысячах) | |||
Списывать&(На|ЕГЭ&Запрещено) | 1475 | Списывать&На&ЕГЭ&Запрещено 9 сектор | ||
Списывать&ЕГЭ&Запрещено | 450 | |||
Списывать&На | 1400 | |||
Приложение 6
Как анализировать аргументы с помощью диаграмм Эйлера
На экзамене по конечной математике вас могут попросить проанализировать аргумент с помощью визуального подхода с использованием диаграммы Эйлера.
Эта изобразительная техника используется для проверки правильности аргумента.Аргумент может быть классифицирован как допустимый или недопустимый. Действительный аргумент возникает в ситуациях, когда, если посылки верны, то и заключение должно быть верным. И аргумент может быть верным, даже если вывод ложный.
Следующий аргумент имеет две предпосылки: (1) «У всех собак есть блохи». (2) «Хэнк — собака». Вывод таков, что, следовательно, у Хэнка блохи.Используя диаграмму Эйлера для анализа этого аргумента, нарисуйте круг, содержащий все объекты, на которых есть блохи. Внутри круга поместите еще один круг, чтобы содержать всех собак. А внутри круга собак посади Хэнка. Рисунок иллюстрирует этот подход.
У бедного Хэнка блохи.
Этот аргумент не обязательно верен, потому что вы знаете, что не у всех собак есть блохи.
Все это показывает, что аргумент равен действительный . Если обе посылки верны, то и заключение должно быть верным.
Теперь рассмотрим аргумент, включающий прямоугольники и треугольники. Многоугольник — это фигура, состоящая из отрезков, соединенных концами.
При анализе правильности этого аргумента диаграмма Эйлера начинается с круга, содержащего все многоугольники, как показано здесь.
Два типа полигонов.
Два круга нарисованы внутри большего круга — один содержит прямоугольники, а другой — треугольники. Два круга не пересекаются, потому что у прямоугольников четыре стороны, а у треугольников три стороны.
Аргумент недействителен . Прямоугольники — это не треугольники, даже иногда.
Аргументы могут иметь более двух посылок. Например:
Одна диаграмма Эйлера, которая может представить эту ситуацию, имеет три пересекающихся круга, как показано здесь.
Президент Авраам Линкольн и другие юристы штата Иллинойс.
Как видно из диаграммы, могут быть президенты, родившиеся в Кентукки, которые не были юристами в Иллинойсе, и могут быть президенты, которые были юристами в Иллинойсе, но не родились в Кентукки. Аргумент равен
Эта статья из книги:
- Конечная математика для чайников,
Об авторе книги:
Мэри Джейн Стерлинг является автором Алгебра I для чайников, Алгебра для чайников, и многих других Для чайников книг. Она преподавала в Университете Брэдли в Пеории, штат Иллинойс, более 30 лет, преподавая алгебру, бизнес-расчеты, геометрию и конечную математику.
Эту статью можно найти в категории:
- Расчет и анализ,
Диаграммы Эйлера и Венна Задания на разминку онлайн
Судя по диаграмме, какое утверждение верно?
Все спортсмены бегуны.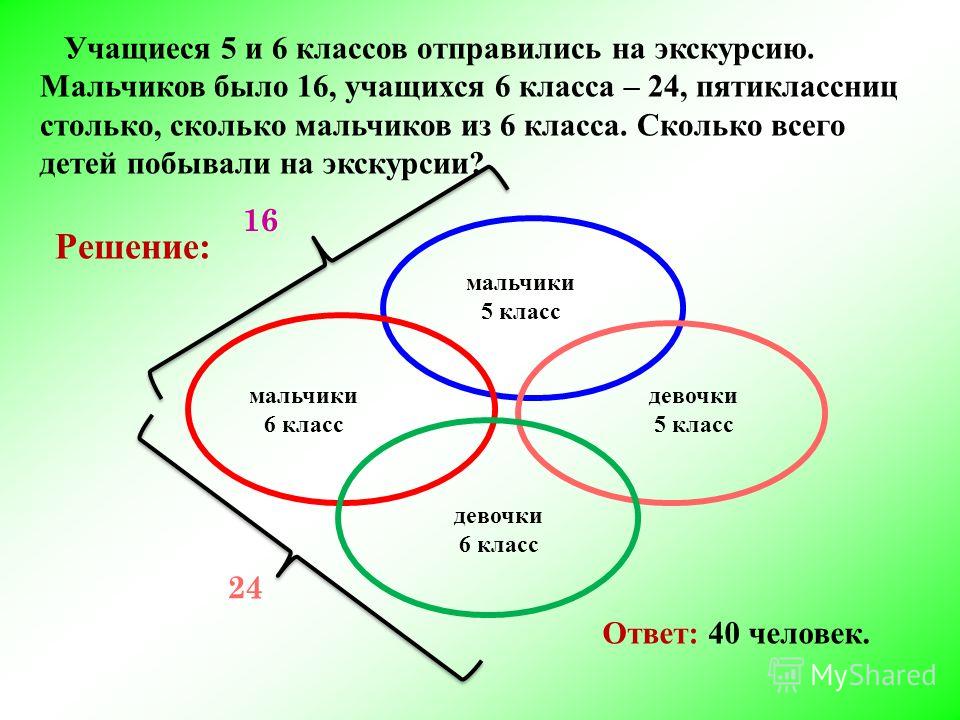
Все бегуны спортсмены.Показать объяснение
Звездочка указывает на людей, которые…
…спортсмены, но не пловцы и не бегуны. … пловцы и спортсмены, но не бегуны. … пловцы, бегуны и спортсмены. … пловцы и бегуны, но не спортсмены. Каждый кружок на диаграмме представляет людей, которым нравятся фильмы определенного типа: ужасы, комедии и мелодрамы.
Однако этикетки были стерты.
Сара любит фильмы ужасов и комедии, но не романтику, и ее местоположение отмечено звездочкой на диаграмме. Таким образом, можно сделать вывод, что кружок C на диаграмме представляет категорию людей, которые __________.\text{\_\_\_\_\_\_\_\_\_\_}.__________.
как романтические фильмы как комедии как фильмы ужасовПоказать объяснение
На картинке выше представлена полная диаграмма Эйлера данных опроса о предпочтениях в отношении мороженого с четырьмя вкусами. В опросе людей просили отметить все вкусы из списка, которые им нравятся. Если бы вы просмотрели опросы, какое максимально возможное количество вкусов предпочитал один человек?
1 2 3 4Показать объяснение
Сколько из этих утверждений верно ?
A.