Теория к данной теме:Базовые задачи по экономике1. Линейная функция спросаУсловие: Дана функция спроса Qd(P) = 100 — 2P, найдите точечную эластичность спроса по цене при P0 = 20. Решение: Мы можем сразу воспользоваться формулой точечной эластичности спроса по цене для непрерывного случая, так как нам известна функция спроса по цене: (1) Edp = Q’p*P0/Q0 Для формулы нам потребуется найти производную функции Qd(P) по параметру P: Q’p = (100 — 2P)’p = -2. Обратите внимание на отрицательный знак производной. Если закон спроса выполняется, то производная функции спроса по цене всегда должна быть отрицательной. Теперь найдем вторую координату нашей точки: Подставляем полученные данные в формулу (1) и получаем ответ: Edp = -2 * 20/60 = -2/3. Ответ: -2/3 Примечание: при решении данной задачи мы можем также воспользоваться формулой эластичности спроса по цене для дискретного случая (см. задачу 5). Для этого нам потребуется зафиксировать координаты точки, в которой мы находимся: (Q0,P0) = (60,20) и просчитать изменение цены на 1%, согласно определению: (Q1,P1) = (59,6;20,2). Подставляем все это в формулу. Ответ получается аналогичным: Edp = (59,6 — 60)/(20.2 — 20) * 20/60 = -2/3. 2. Линейная функция спроса (общий вид)Условие: Дана функция спроса Qd(P) = a — bP, найдите точечную эластичность спроса по цене при P = P0. Решение: Опять воспользуемся формулой (1) точечной эластичности спроса по цене для непрерывного случая. Производная функции Qd(P) по параметру P: Q’p = (a — bP)’p = -b. Знак опять отрицательный, это хорошо, значит мы не допустили ошибки. Вторая координата рассматриваемой точки: Q0(P0) = a — b*P0. В случае, если в формуле присутствуют параметры a и b, не смущайтесь. Они выполняют роль коэффициентов функции спроса. Подставляем найденные значения в формулу (1): (2) Edp = -b*[P0/(a-bP0)] Ответ:-(bP0)/(a-bP0) Примечание: Теперь, зная универсальную формулу эластичности спроса по цене для линейной функции 
3. Функция спроса с постоянной эластичностьюУсловие: Дана функция спроса Qd(P) = 1/P, найдите точечную эластичность спроса по цене при P = P0. Решение: Еще один очень распространенный вид функции спроса — гипербола. Каждый раз, когда спрос задается функционально, используется формула Edp для непрерывного случая: (1) Edp = Q’p*P0/Q0 Прежде, чем перейти к производной, необходимо подготовить исходную функцию: Qd(P) = 1/P = P-1. Тогда Q’p = (P-1)’p = -1*P-2 = -1/P2. При этом не забывайте контролировать отрицательный знак производной. Подставляем полученный результат в формулу: Edp = -P0-2*[P0/(1/P0)] = — P0-2*P02 = -1 Ответ: -1 Примечание: Функции такого вида часто называются «функциями с постоянной эластичность», так как в каждой точке эластичность равняется постоянному значению, в нашем случае это значение равно -1. 4. Функция спроса с постоянной эластичностью (общий вид)Условие: Дана функция спроса Qd(P) = 1/Pn, найдите точечную эластичность спроса по цене при P = P0. Решение: В предыдущей задаче задана гиперболическая функция спроса. Решим ее в общем виде, когда степень функции задана параметром Запишем исходную функцию в виде: Qd(P) = 1/Pn = P-n. Тогда Q’p = (P-n)’p = -n*P-n-1 = -n/Pn+1. Производная отрицательна при всех неотрицательных P. В таком случае эластичность спроса по цене будет: Edp = -nP-n-1*[P/(1/Pn)] = — nP-n-1*Pn+1 = -n Ответ: -1 Примечание: Мы получили общий вид функции спроса с постоянной эластичностью по цене равной {-n}. 5. Эластичность спроса по цене (дискретный случай)Условие: При дискретном случае не дано функции спроса и изменения происходят по точкам. Пусть известно, что если Q0 = 10, то P0 = 100, а при Q1 = 9, P1 = 101. Найдите точечную эластичность спроса по цене.Решение: Используем формулу точечной эластичности спроса по цене для дискретного случая: (3) Edp = ▲Q/▲P * P0/Q0 или Edp = (Q1 — Q0)/(P1 — P0) * P0/Q0 Подставляем в формулу наши значения и получаем: Edp = (9 — 10)/(101 — 100) * 100/10 = -1/1 *10 = -10. Обязательно убеждаемся, что полученно значение эластичности спроса по цене неположительно. Если оно положительное, то 98%, что вы допустили ошибку в вычислениях и 1%, что вы имеете дело с функцией спроса, для которой нарушается закон спроса. Ответ: -10 Примечание: Согласно определению 6. Восстановление функции спроса через эластичностьУсловие: Пусть известно, что если Q0 = 10, то P0 = 100, а значение эластичности в этой точке равно -2. Восстановите функцию спроса на данное благо, если известно, что она имеет линейный вид. Решение: Введем функцию спроса в линейном виде: Qd(P) = a — bP. В таком случае, в точке (Q0, P0) эластичность будет равна Edp = -b * P0/Q0: Edp = -b * 100/10 = — 10b. Через это соотношение находим, что b = 1/5. Чтобы найти параметр a, снова используем координаты точки (Q0, P0): 10 = a — 1/5*100 —> a = 10 + 20 = 30. Ответ: Qd(P) = 30 — 1/5P. Примечание: По схожему принципу можно восстановить функцию спроса с постоянной ценовой эластичностью. База задач будет постоянно пополняться Переход к задачам на Эластичность спроса по доходу Обсуждение задач на форуме |
Теория к данной теме:Урок 2.2. Виды эластичности спроса (в разработке)Базовые задачи по экономике1. Эластичность спроса по доходу (дискретный случай)Условие: Пусть известно, что при I0 = 1000, покупатель готов приобрести 10 ед. Решение: Формула, которая нам понадобится: (1) Edi = ▲Q/▲I * I0/Q0 Координаты первоначальной точки нам уже известны: (Q0;I0) = (10;1000). Найдем изменения дохода и величины спроса, если нам известно, что доход меняется на 2%. Для нахождения точечной эластичности не имеет значения увеличивается или уменьшается доход. Предположим, что доход увеличился на 2% и достиг значение равное: I1 = 1000 + 0,02*1000 = 1020. Так как товар А является нормальным, то при увеличении дохода спрос на него должен тоже увеличиться. В нашем случае, согласно условию, увеличение дохода на 2% увеличит величину спроса на 1 ед. Таким образом, Q1 = 10 + 1 = 11 .
Подставляем координаты новой точки в формулу (1): Edi = (11 — 10)/(1020-1000) * 1000/10 = 1/20 * 100 = 5. Ответ: 5 Примечание: при решении задач на эластичность спроса по доходу следует постоянно следить за знаком, так как для разных категорий товара он может быть как отрицательным, так и положительным. 2. Эластичность спроса по доходу (непрерывный случай)Условие: Дана функция спроса Qd(P,I) = 100 — 2P + 4I. Найдите точечную эластичность спроса по доходу, при P0 = 10, I0 = 20. Решение: Воспользуемся формулой точечной эластичности спроса по доходу для непрерывного случая: (2) Edi = Q’i*I0/Q0  В данном случае, параметр P выступает такой же константой, как и 100, поэтому его производная равна 0. Знак производной по доходу положительный, это говорит о том, что данный товар является нормальным. В данном случае, параметр P выступает такой же константой, как и 100, поэтому его производная равна 0. Знак производной по доходу положительный, это говорит о том, что данный товар является нормальным.
Рассчитаем первоначальную величину спроса: Q0 = 100 — 2*10 + 4*20 = 160. Подставим все известные нам значения в формулу точечной эластичности спроса по доходу для непрерывного случая (2): Edi = 4*20/160 = 0,5. Ответ: 0,5 Примечание: При работе с функциями, зависящих от нескольких параметров, не забывайте четко прописывать с какими параметрами из них вы работаете на данный момент. Чем четче будет ваша запись, тем меньше вероятность совершения ошибок в вычислениях. 3. Комбинация эластичности спроса по цене и доходуУсловие: Точечная эластичность спроса на благо по цене некоторого индивида равна -2, а точеная эластичность спроса по доходу в этой точке равна 0,5. Решение: Эластичности, которые нам даны отражают мгновенную реакцию индивида на изменения дохода и цены. Рассчитаем процентное изменение величины спроса, воспользовавшись следующими формулами: Edp = ▲%Q/▲%P и Edp = ▲%Q/▲%I. Преобразуем их, выразив процентное изменение Q: (3) ▲%Q = Edp * ▲%P и (4) ▲%Q = Edp * ▲%I. Подставим в формулы (3) и (4) данные из условия задачи: ▲%Q1 = -2 * 4% = -8%; ▲%Q2 = 0,5 * 2% = 1%. Так как рассчитанное изменение выражается в процентах, то общее изменение Q будет зависеть от характера изменения цены P и дохода I одновременно или последовательно. Если они изменяются одновременно, то следует рассчитать величину изменения, применив процент к первоначальному значению Q: ▲Q1 = — 0,08*Q0 = -0,08*20 = — 1,6; ▲Q2 = 0,01*Q0 = 0,01*20 = 0,2. Таким образом, общее изменение составит: ▲Q = -1,6 + 0,2 = -1,4. Тогда итоговое Q2 = 20 — 1,4 = 18,6. При последовательном изменении цены и дохода, указанном в условии задачи, сначала необходимо рассчитать реакцию величины спроса на рост P: ▲Q1 = — 0,08*Q0 = -1,6. Следовательно, новое Q1 = 20 — 1,6 = 18,4. Затем рассчитаем последствия увеличения дохода индивида: ▲Q2 = 0,01*Q1 = 0,01*18,4 = 0,184. Получается, что итоговое Q2 = 18,4 + 0,184 = 18,584, а его изменение ▲Q = -1,416. Таким образом, при одновременном и последовательном изменении параметров спроса итоговые результаты отличаются. Ответ: -1,4 и -1,416. Примечание: Чем более значительное изменение параметров P и I, тем более заметна разница двух случаев. Однако, не стоит забывать, что для получения более точных расчетов при сильных изменениях параметров следует использовать дуговую эластичность. База задач будет постоянно пополняться Переход к задачам на Эластичность спроса по цене Обсуждение задач на форуме |
Задачи эластичность спроса
Тема Эластичность спроса и предложения
Задача № 1.
В таблице 1. представлен объём спроса на мороженное при различном уровне цен.
Таблица 1.
|
Цена за порцию (грн.) |
Объём спроса (тыс. порций) |
Расходы (Выручка),тыс грн. |
Коэффициент ценовой эластичности спроса |
|
2,10 |
10 |
— |
— |
|
1,80 |
20 |
— |
— |
|
1,50 |
30 |
— |
— |
|
1,20 |
40 |
— |
— |
|
0,90 |
50 |
— |
— |
|
0,60 |
60 |
— |
— |
|
0,30 |
70 |
— |
— |
а) Начертите кривую спроса обозначив цену на вертикальной оси, а количество порций мороженного на горизонтальной.
б) Предположим, что цена порции мороженного равняется 1.20 грн. Как изменится объём спроса, если цена снизится на 30 коп.?
в) Определите расходы на мороженное при каждом из значений цены. Полученные данные занесите в таблицу.
г) Рассчитайте коэффициент ценовой эластичности для всех указанных интервалов цены. Полученные данные запишите в таблицу.
д) Начертите кривую расходов на мороженное, обозначив сумму расходов на вертикальной оси, а величину спроса на горизонтальной.
е) При какой цене выручка окажется максимальной.
ж) При каких значениях цены спрос является эластичным? Неэластичным?
Задача № 2
В таблице 2 представлены данные об объёме предложения на рынке товара X.
Таблица 2.
|
Коэффициент ценовой эластичности предложения |
Объём предложения (единицы) |
Цена (гр. |
|
— |
0 |
2 |
|
— |
2 |
4 |
|
— |
4 |
6 |
|
— |
6 |
8 |
|
— |
8 |
10 |
|
— |
10 |
12 |
|
— |
12 |
14 |
|
— |
14 |
16 |
а) Рассчитайте коэффициент ценовой эластичности предложения и заполните таблицу 2. 2.
2.
Задание 3.
В таблице 3. представлены данные о структуре расходов семьи за два года (цены на товары а, б, в, г, не меняются). Заполните таблицу 3.
Таблица 3.
|
Покупаемые товары |
Расходы на покупку (грн.) |
Доля в бюджете семьи (%) |
Эластичность спроса по доходу |
Характер товара |
||
|
1 год |
2 год |
1 год |
3 год |
|||
|
Товар А |
30 |
50 |
— |
— |
||
|
Товар Б |
30 |
70 |
— |
— |
||
|
Товар В |
25 |
20 |
— |
— |
||
|
Товар Г |
15 |
60 |
— |
— |
||
|
Итого |
100 |
200 |
100 |
100 |
||
Задание 2.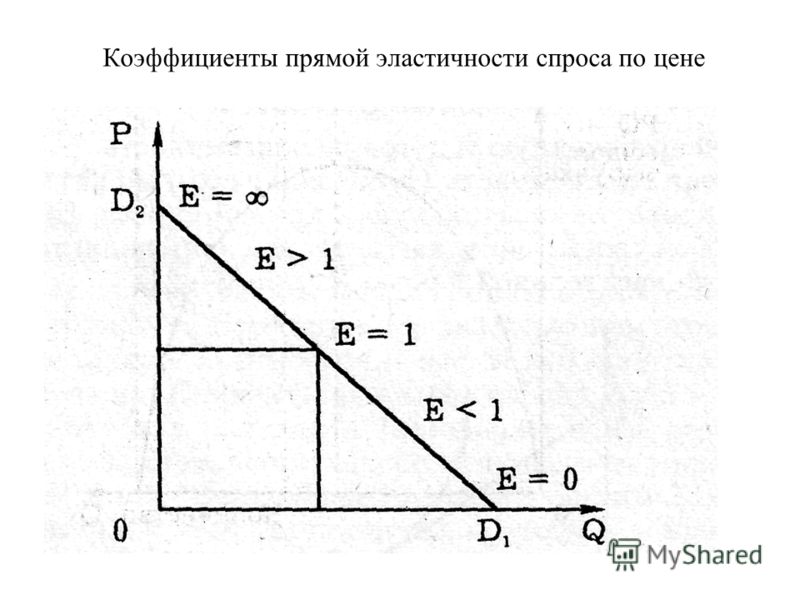 4.
4.
Задача № 4
а) Докажите, что для всех линейных функций спроса с одинаковой запретительной ценой, ценовая эластичность для определения цены Р — совпадает.
б) Какие последствия вытекают отсюда для представления олигополистов об эластичности? Сравните значение эластичности индивидуальной с рыночной функцией спроса.
Решения задач по теме эластичность спроса
и предложенияОтветы.
Решение задачи № 1.
а) См. Рис. 1.
.
Рис.1
б) Так как кривая спроса представляет собой прямую линию, то смещение цены на 30% в любом случае будет сопровождаться увеличением объёма спроса на 10 тыс. порций
в) и г) Смотри таблицу. 4.
Таблица 4.
|
Цена за порцию (грн.) |
Объём спроса (тыс. порций) |
Расходы (выручка) тыс. |
Коэффициент ценовой эластичности |
|
2,10 |
10 |
21 |
4,33 |
|
1,80 |
20 |
36 |
2,21 |
|
1,50 |
30 |
45 |
1,27 |
|
1,20 |
40 |
48 |
0,78 |
|
0,90 |
50 |
45 |
0,50 |
|
0,60 |
60 |
36 |
0,23 |
|
0,30 |
70 |
21 |
— |
д) Смотри рис. 2.
2.
Рис.2.
Кривая выручки.
Е) При цене 1,20
Ж) При цене выше 1,20; ниже 1,20
Решение задачи № 3
Таблица 5.
|
Коэффициент целевой эластичности предложения |
Объём предложения (единиц) |
Цена (грн.) |
|
— |
0 |
2 |
|
3,00 |
2 |
4 |
|
1,40 |
4 |
6 |
|
1,666 |
6 |
8 |
|
1,285 |
8 |
10 |
|
1,222 |
10 |
12 |
|
1,182 |
12 |
14 |
|
1,153 |
14 |
16 |
Решение задачи № 4.
Таблица 6.
|
Покупаемые товары |
Расходы на покупки (грн.) |
Доля в бюджете семьи (%) |
Эластичность спроса по доходу |
Характер товара |
||
|
1 год |
2 год |
1 год |
2 год |
|||
|
Товар А |
30 |
50 |
30 |
25 |
2/3 |
Первой необходимости |
|
Товар Б |
30 |
70 |
30 |
35 |
4/3 |
Роскоши |
|
Товар В |
25 |
20 |
25 |
10 |
-1/5 |
Недоброкаче ственные |
|
Товар Г |
15 |
60 |
15 |
30 |
3 |
Роскоши |
|
Итого |
100 |
200 |
100 |
100 |
||
Решение задачи № 4
а) Исходя из функции спроса р = а-ba отсюда следует dp / dQ = b.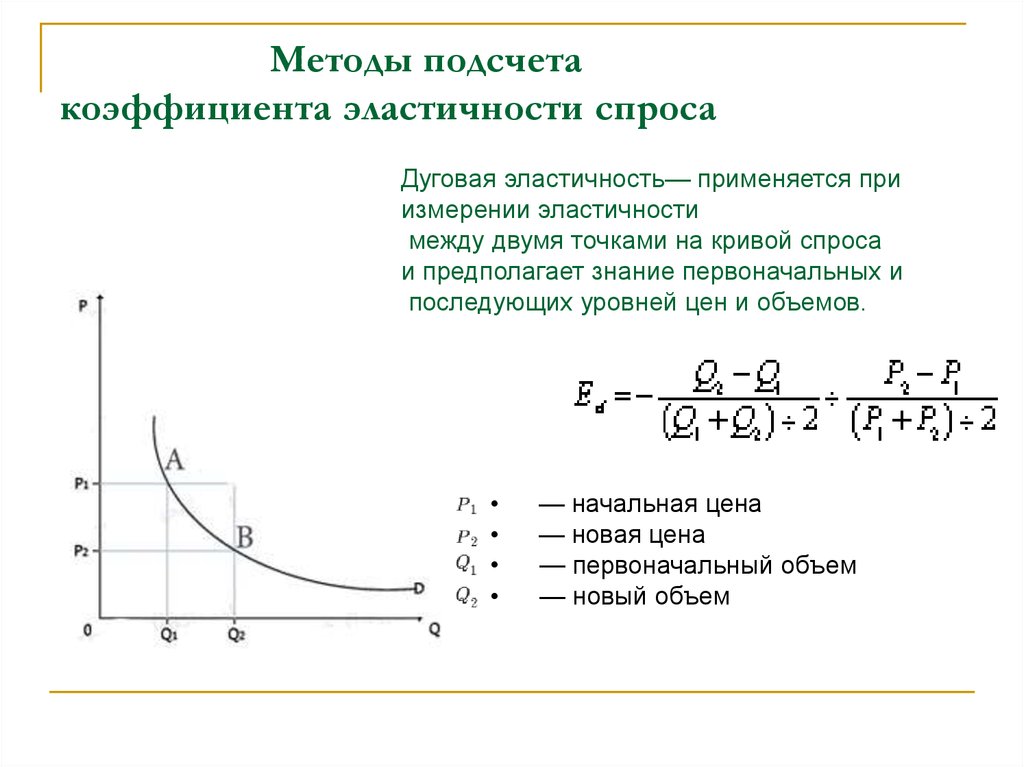 Значит действует только dQ / dp = 1 / b. Подставляя это значение в общее выражение для ценовой эластичности получим: Э Q, р = — lp(-l)/bQ. Далее Q с учётом функции спроса можно заменить выражением: (а — р) / Ь, так что в итоге имеем выражение вида:
Значит действует только dQ / dp = 1 / b. Подставляя это значение в общее выражение для ценовой эластичности получим: Э Q, р = — lp(-l)/bQ. Далее Q с учётом функции спроса можно заменить выражением: (а — р) / Ь, так что в итоге имеем выражение вида:
1P P
Эа, р = ——————— -1 = ——————
b((a-p)/b а-Р
При этом становится очевидным, что ценовая эластичность для определённой цены Р, определяется только запретительной ценой а, но не количеством насыщения (оно зависит только от величины b). Графически это можно представить следующим образом:
Рис. 3.
Из выражения ценовой эластичности Е а, р = р / (а — р) в связи с рисунком 3. становится очевидным, что ценовую эластичность можно определить и геометрическим способом, б) Как видно из рисунка…индивидуальная функция спроса отдельного олигополиста имеет ту же запретительную цену, что и функция рыночного спроса, отсюда следует, что ценовая эластичность установленная отдельным олигополистом исходя из его индивидуальной функции спроса, такая же как и ценовая эластичность, которая определяется объективно на основании функции рыночного спроса.
Эластичность. Решение задач по экономике
Похожие презентации:
Экономика Германии
Бухгалтерский баланс
Экономика Китая
Цифровая экономика
Инфляция и семейная экономика
Экономика Китая
Конкуренция. Виды конкуренции
Казахстанская модель экономического развития
Инфляция (виды, причины и последствия)
Теневая экономика
1. Решение задач по экономике
СоставительЗибарев М.В., 2013 г.
Тесты с ответами http://www.docme.ru/doc/7836/e-konomika—vse-testy
P
β
Q
10. Эластичность спроса -1
Если при росте цены на товар со 100 до 200 ден.
ед., объем спроса сократился с 30 до 20 шт., то
данный товар является …
Дано: Р1 =100, Р2 = 200, Q1 = 30, Q2 = 20.
Применим формулу дуговой эластичности,
так как изменение цены превысило 5%
Е=
Q2 – Q1
20 – 30
(Q2 + Q1) / 2
(30 + 20) / 2
Р2 – Р1
(Р2 + Р1) / 2
-10
=
=
200 – 100
(200 + 100) / 2
25
=
10
150
25
100
100
=
150
Вывод: так как |Е|< 1, (спрос по цене
неэластичный), то данный товар является
товаром неэластичного спроса.

=
2
3
5
2
-3
=
5
11. Эластичность спроса — 2
На рисунке показано изменение спроса на товар
при снижении его цены. Тогда коэффициент
дуговой эластичности спроса по цене равен:
Дано: Р1 = 6, Р2 = 4, Q1 = 3, Q2 = 5.
Решение.
Q2 – Q1
(Q2 + Q1) / 2
Р
6
4
Е=
А
=
Р2 – Р1
Q2 – Q 1
Р2 + Р1
Q2 + Q1
Р2 – Р1
=
(Р2 + Р1) / 2
В
=
D
3 5
Е=
Q
Q 2 – Q1
Р2 + Р1
Р2 – Р1
Q2 + Q1
5–3
4+6
4–6
5+3
=
2
–2
10
8
Е = – 5/4; |Е| > 1. Спрос эластичный
12. Эластичность спроса — 3
Если при снижении цены на 1% величина спроса
выросла на 5%, то спрос …
Q2 – Q1
∆Q
Q1
Q1
Е=
=
Изменение величины спроса, %
=
Р2 – Р1
∆Р
Р1
Р1
Изменение цены, %
Решение: 5% : 1% = 5, /Е/ > 1, спрос эластичный
Ответ: … по цене эластичный.
13. Эластичность предложения — 4
При росте цены с 4 до 10 д.
 е. величина
е. величинапредложения увеличилась с 12 до 16 штук.
Коэффициент дуговой эластичности предложения
равен …
1)
2)
3)
4)
2/3;
1/3;
3;
1.
Решение: Е = 1/3.
Ответ: 2.
14. Эластичность спроса — 5
Эластичность спроса по доходу — 6Если изменение в доходах потребителей с 10 000
до 12 000 д.е. привело к росту объемов спроса на
20 %, то коэффициент эластичности равен …
Эластичность спроса по доходу определяется по формуле:
Q2 – Q1
∆Q
Q1
Q1
Е=
=
R2 – R1
=
Изменение дохода, %
∆R
R1
R1
20%
20%
Е=
Изменение величины спроса, %
=
=
20%
20%
=
12000 – 10000
2000
20
10000
10000
100
= 1
20%
Ответ: эластичность по доходу Е = 1.
Эластичность спроса по доходу — 7
Если рост доходов в 1,2 раза привел к увеличению
спроса на пылесосы на 5%, то эластичность спроса
по доходу на этот товар равна …
∆Q
Изменение величины спроса, %
Q1
Е=
=
Изменение дохода, %
∆R
R1
Решение:
Рост доходов в 1,2 раза означает прирост на 20%
∆Q
Q1
Е=
5%
=
∆R
R1
=
20%
1
4
Ответ: Е = 0,25 ; неэластичный спрос по доходу.

Эластичность спроса по доходу — 8
Если рост дохода на 30% привел к увеличению
спроса на телевизоры на 6%, то эластичность
спроса по доходу на этот товар равна …
1)
2)
3)
4)
1/6;
1/5;
1/3;
5.
∆Q
Изменение величины спроса, %
Q
Е=
=
∆R
R
Е = 6 / 30 = 1 / 5
Ответ : 2.
Изменение дохода, %
∆ Qм
Е=
Изменение величины спроса на товар М, %
Qм
=
Изменение цены на товар С, %
∆ Рс
Рс
Решение:
10%
Е=
2
= 0,4
=
25%
5
Ответ: Е = 0,4
18. Перекрестная эластичность — 9
Цена товара Y выросла на 3%.
Коэффициент перекрестной эластичности
спроса на товар Х по цене товара Y равен
«-1». Тогда величина спроса на товар Х …
∆ QХ
Е=
Изменение величины спроса на товар Х, %
QХ
=
Изменение цены на товар Y, %
∆ РY
РY
Пояснение. Если Е < 0, то это товары комплементы
(используются совместно — мотор и бензин)
∆ QХ
∆ QХ
QХ
QХ
-1=
3%
= — 1 ∙ 3%
= — 3%
Если Е > 0, то это товары субституты (товары
заменяемые — чай, кофе)
Ответ : сократится на 3%
19.
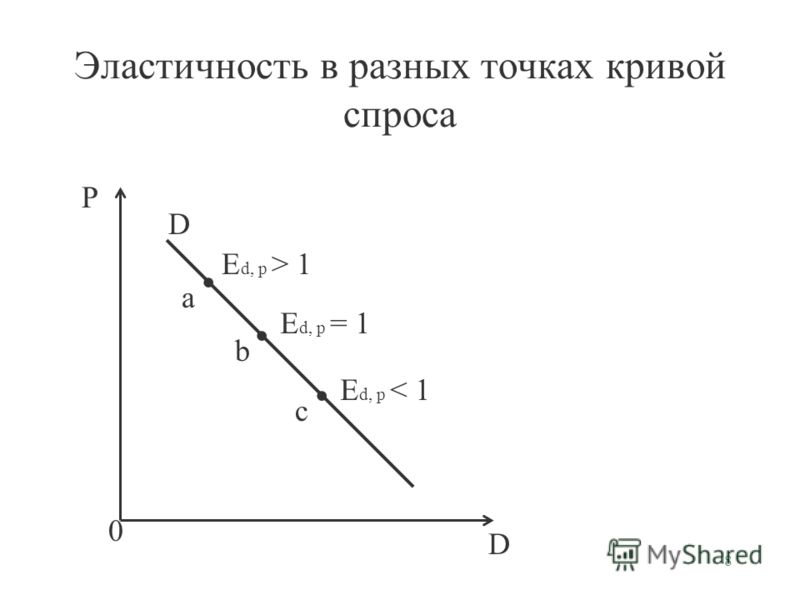 Перекрестная эластичность — 10
Перекрестная эластичность — 10Перекрестная эластичность товара А по цене
товара В равна (-2). Если произойдет рост цены
товара В на 2%, то величина спроса на товар А …
Изменение величины спроса на товар А, %
Е=
Изменение цены на товар В, %
-2=
∆ QА
Если Е < 0, то это товары комплементы (мотор и бензин)
QА
∆ QА
2%
QА
= — 4%
Ответ : величина спроса уменьшится на 4%
20. Перекрестная эластичность — 11
Эластичность спроса — 12Цена упала на 10%, эластичность спроса 0,6.
Изменение спроса, выраженное в процентах
составит …
∆Q
Изменение величины спроса, %
Q1
Е=
=
∆Р
Изменение цены, %
Р1
∆Q
0,6 =
Q1
10 %
∆Q
= 0,6 ∙ 10 % = 0,6 ∙ 0,1 =
0,06 = 6 %
Q1
Ответ: 6.
Точечная эластичность спроса и выручка — 13
Если известно, что при снижении цены на 5%
выручка выросла на 9,25%, то коэффициент
точечной эластичности спроса на товар составит…
∆Q
Выручка = Р ∙ Q
Р
Q1
Р2∙ Q2 = 109,25% Р1∙ Q1
Е=
∆Р
Р1
Р1
95% Р1∙ Q2 = 109,25% Р1∙ Q1
Р2
95 ∙ Q2 = 109,25 ∙ Q1
∆Q
Q1
Е=
Q1 Q2
5%
∆Q
Q1
Q2 / Q1 = 109,25 / 95
Q
Q2/ Q1 = 1,15
= 15%
/Е/ = 15 % / 5 % = 3
Точечная эластичность спроса и выручка — 14
• Определите точечную эластичность спроса, если при
снижении цены на 10% выручка увеличилась на 8%.

∆Q
∆Q
Е=
Q1
=
Q1
Р
Q2 – Q1
Q1
=
Q2
-1
Q1
Выручка = Р ∙ Q
∆Р
Р2∙ Q2 = 108% Р1∙ Q1
Р1
Р1
90% Р1∙ Q2 = 108% Р1∙ Q1
Р2
90 ∙ Q2 = 108 ∙ Q1
∆Q
Q1
Е=
Q1 Q2
10 %
∆Q
Q1
Q2 / Q1 = 108 / 90
Q
Q2/ Q1 = 1,2
= 20
Ответ: /Е/= 2.
Вопрос
Если спрос на данный товар
эластичный, то снижение цены (при
прочих равных условиях) как правило
приводит к …
1) повышению дохода от продажи данного
товара;
2) снижению дохода от продажи данного
товара;
3) не окажет никакого влияния на доход от
продажи данного товара;
4) снижению спроса на данный товар.
Правильный ответ : 1.
English Русский Правила
Задача: Задачи по микроэкономике с решением
Тема: Задачи по микроэкономике с решением
Раздел: Бесплатные рефераты по микроэкономике
Тип: Задача | Размер: 40.14K | Скачано: 279 | Добавлен 15.01.14 в 07:40 | Рейтинг: +1 | Еще Задачи
Эластичность спроса и предложения.
3. Используя данные нижеприведенной табл., определите коэффициент и тип ценовой эластичности спроса на всех участках кривой спроса, ограниченных положениями таблицы. Вычислите валовую выручку (валовой доход) при всех комбинациях, представленных в таблице, и установите зависимость между типом ценовой эластичности спроса и изменением валовой выручки. Определите точку единичной эластичности.
|
№ положения |
Цена за 1 ед. товара (ден. единиц) |
Объем спроса в месяц Qd |
|
1 |
1050 |
2,0 |
|
2 |
900 |
2,4 |
|
3 |
750 |
2,8 |
|
4 |
600 |
3,3 |
|
5 |
450 |
4,0 |
|
6 |
300 |
4,8 |
|
7 |
150 |
5,8 |
Решение.
Степень чувствительности потребителей к изменению цены измеряют с помощью коэффициента ценовой эластичности спроса, представляющего собой отношение процентного изменения количества спрашиваемой продукции к процентному изменению цены, вызвавшему это изменение спроса. Иными словами, коэффициент ценовой эластичности спроса
где Q1 и Q2 — первоначальный и текущий объем спроса; P1 и Р2 — первоначальная и текущая цена.
Различают следующие типы эластичности :
Единичная эластичность, когда на каждый процент изменения цены объем спроса изменяется соответственно на 1 % (Ed = 1).
Эластичный спрос, когда объем спроса в процентах изменяется быстрее, чем изменяется цена в процентах (Ed › 1).
Неэластичный спрос, когда объем спроса в процентах изменяется медленнее, чем изменяется цена в процентах (Ed ‹ 1).
Совершенно неэластичный спрос, когда объем спроса не изменяется при любом изменении цены (Ed = 0).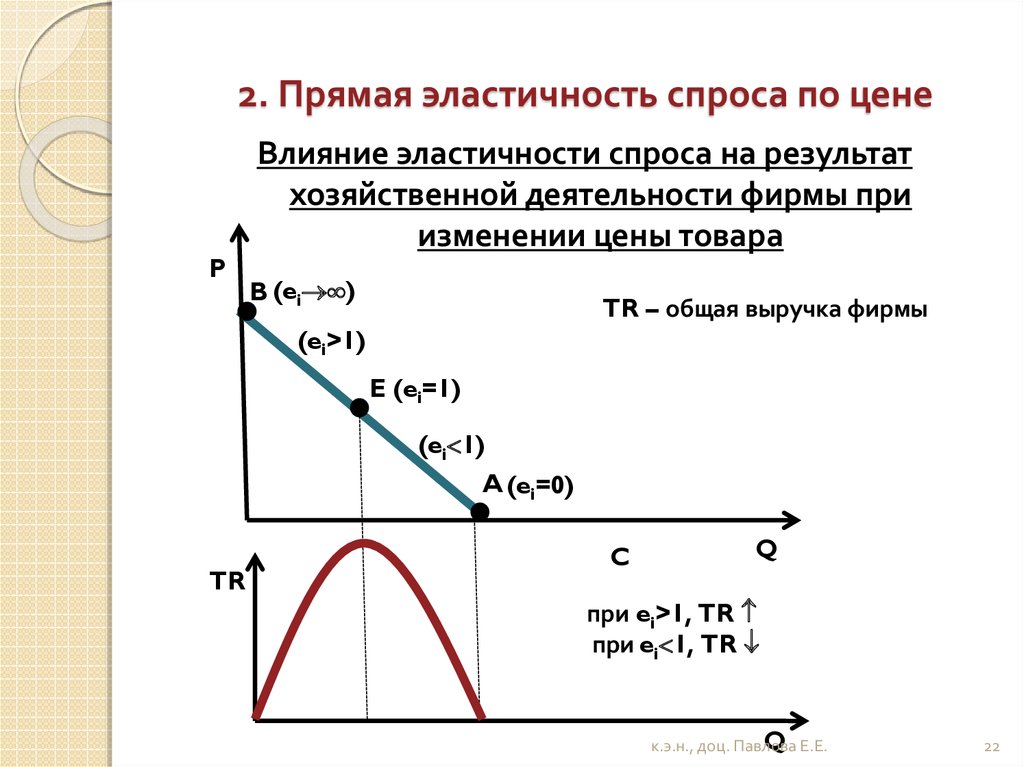
Бесконечно эластичный спрос, когда объем спроса может изменяться до бесконечности при незначительном изменении цены (Ed= ∞).
Рассчитаем коэффициент эластичности на участке 2-1:
вычислений сведем в таблицу.
Валовая выручка – англ. Gross Revenue, является суммой денег, которую получает компания в результате ведения бизнеса, расходы при этом не учитываются.
Валовой доход – выручка компании за вычетом себестоимости проданных товаров.
В нашем случае расходы компании нам неизвестны, поэтому рассчитаваем только валовую выручку по формуле
Аналогично рассчитаем валовую выручку на других участках. Результаты вычислений сведем в таблицу.
|
№ положения |
Цена за 1 ед. товара (ден. единиц) |
Объем спроса в месяц Qd |
Изменение цены, % |
Изменение объема, % |
Коэффициент эластичности |
Тип эластичности |
Валовая выручка |
|
1 |
1050 |
2,0 |
|
|
|
|
2100 |
|
2 |
900 |
2,4 |
-14 |
20 |
1,40 |
Эластичный спрос |
2160 |
|
3 |
750 |
2,8 |
-17 |
17 |
1,00 |
Единичный спрос |
2100 |
|
4 |
600 |
3,3 |
-20 |
18 |
0,89 |
Неэластичный спрос |
1980 |
|
5 |
450 |
4,0 |
-25 |
21 |
0,85 |
Неэластичный спрос |
1800 |
|
6 |
300 |
4,8 |
-33 |
20 |
0,60 |
Неэластичный спрос |
1440 |
|
7 |
150 |
5,8 |
-50 |
21 |
0,42 |
Неэластичный спрос |
870 |
Как видим из таблицы, на участке 2-3 наблюдаем единичную эластичность, т. е. при снижении цены на 3% спрос увеличился также на 3%.
е. при снижении цены на 3% спрос увеличился также на 3%.
На участке 1-2 спрос эластичен, т.к. в результате снижения цены спрос на товар возрос до такого уровня, при котором валовая выручка увеличилась.
На остальных участках снижение цены вызывает увеличение спроса на товар, а общий доход товаропроизводителя понизится, такой спрос на товар является неэластичным.
Определение цены и объема производства.
Максимизация прибыли и минимизация убытка
2. Предположим, что чисто конкурентная фирма в краткосрочном периоде имеет валовые издержки, приведенные в таблице.
|
Количество продукции, ед. |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Валовые издержки, р. |
200 |
240 |
260 |
300 |
360 |
440 |
560 |
710 |
Ответьте на следующие вопросы:
а) используя оба подхода, рассмотренные в теме, какой оптимальный объем производства должна выбрать фирма, если рыночная цена продукта составит: 70 р.; 100 р.; 130 р.; 160 р.?
б) почему фирме не следует закрываться при этих ценах?
в) какую валовую прибыль (валовой убыток) и среднюю прибыль (средний убыток) получит фирма при оптимальном объеме выпуска, если рыночная цена товара составит: 70 р. ; 100 р.; 130 р.; 160 р.?
; 100 р.; 130 р.; 160 р.?
г) каким будет объем рыночного предложения, если в отрасли действуют 2000 одинаковых фирм?
Решение:
К наиболее распространенным методам определения оптимального объема производства относятся:
— метод сопоставления валовых показателей;
— метод сопоставления предельных показателей.
Метод составления валовых показателей предполагает расчет прибыли предприятия при различных объемах производства и реализации продукции. Последовательность расчета такова:
— определяется величина объема производства, при котором достигается нулевая прибыль;
— определяется объем производства с максимальной прибылью
Метод сопоставления предельных показателей позволяет установить до каких пределов рентабельно увеличение производства и реализации. Он основан на сопоставлении предельных издержек и предельного дохода. Если величина предельного дохода на единицу продукции превышает величину предельных издержек на единицу продукции, то увеличение производства и реализации будет рентабельно.
Рассчитаем показатели, необходимые для анализа и сведем их в таблицу.
|
Количество продукции, ед. |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Валовые издержки, р. |
200 |
240 |
260 |
300 |
360 |
440 |
560 |
710 |
|
Постоянные издержки |
200 |
200 |
200 |
200 |
200 |
200 |
200 |
200 |
|
Переменные издержки |
0 |
40 |
60 |
100 |
160 |
240 |
360 |
510 |
|
Средние издержки |
|
240 |
130 |
100 |
90 |
88 |
93,33 |
101,43 |
|
Валовый доход при цене 70 р |
0 |
70 |
140 |
210 |
280 |
350 |
420 |
490 |
|
Валовый доход при цене 100 р |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
|
Валовый доход при цене 130 р |
0 |
130 |
260 |
390 |
520 |
650 |
780 |
910 |
|
Валовый доход при цене 160 р |
0 |
160 |
320 |
480 |
640 |
800 |
960 |
1120 |
|
Предельные издержки |
0 |
40 |
20 |
40 |
60 |
80 |
120 |
150 |
|
Предельный доход при цене 70 р |
|
70 |
70 |
70 |
70 |
70 |
70 |
70 |
|
Предельный доход при цене 100 р |
|
100 |
100 |
100 |
100 |
100 |
100 |
100 |
|
Предельный доход при цене 130 р |
|
130 |
130 |
130 |
130 |
130 |
130 |
130 |
|
Предельный доход при цене 160 р |
|
160 |
160 |
160 |
160 |
160 |
160 |
160 |
|
Валовая прибыль при цене 70 р |
-200 |
-170 |
-120 |
-90 |
-80 |
-90 |
-140 |
-220 |
|
Валовая прибыль при цене 100 р |
-200 |
-140 |
-60 |
0 |
40 |
60 |
40 |
-10 |
|
Валовая прибыль при цене 130 р |
-200 |
-110 |
0 |
90 |
160 |
210 |
220 |
200 |
|
Валовая прибыль при цене 160 р |
-200 |
-80 |
60 |
180 |
280 |
360 |
400 |
410 |
|
Средняя прибыль при цене 70 р |
|
-170 |
-60 |
-30 |
-20 |
-18 |
-23,33 |
-31,43 |
|
Средняя прибыль при цене 100 р |
|
-140 |
-30 |
0 |
10 |
12 |
6,67 |
-1,43 |
|
Средняя прибыль при цене 130 р |
|
-110 |
0 |
30 |
40 |
42 |
36,67 |
28,57 |
|
Средняя прибыль при цене 160 р |
|
-80 |
30 |
60 |
70 |
72 |
66,67 |
58,57 |
Из таблицы видим, что
а), в) при цене 70 р за ед. оптимальный объем производства (в таблице выделено жирным шрифтом) будет составлять 4 ед. при издержках 360 р., так как при этом объеме производства убыток минимален, а предельный доход (70) превышает предельные издержки (60), т.е. производство рентабельно. Далее наращивать объемы производства не стоит. Валовая прибыль составит (-)80, средняя прибыль (-)20.
оптимальный объем производства (в таблице выделено жирным шрифтом) будет составлять 4 ед. при издержках 360 р., так как при этом объеме производства убыток минимален, а предельный доход (70) превышает предельные издержки (60), т.е. производство рентабельно. Далее наращивать объемы производства не стоит. Валовая прибыль составит (-)80, средняя прибыль (-)20.
При цене 100 р за ед. оптимальный объем производства (в таблице выделено жирным шрифтом) будет составлять 5 ед. при издержках 440 р., так как при этом объеме производства прибыль максимальна, а предельный доход (100) превышает предельные издержки (80), т.е. производство рентабельно. При росте производства до 6 ед. валовая прибыль уменьшается, а предельные издержки превышают предельный доход. Валовая прибыль составит 60, средняя прибыль 12.
При цене 130 р за ед. оптимальный объем производства (в таблице выделено жирным шрифтом) будет составлять 6 ед. при издержках 560 р., так как при этом объеме производства прибыль максимальна, а предельный доход (130) превышает предельные издержки (120), т. е. производство рентабельно. При росте производства до 7 ед. валовая прибыль уменьшается, а предельные издержки превышают предельный доход. Валовая прибыль составит 220, средняя прибыль 36,67.
е. производство рентабельно. При росте производства до 7 ед. валовая прибыль уменьшается, а предельные издержки превышают предельный доход. Валовая прибыль составит 220, средняя прибыль 36,67.
При цене 160 р за ед. оптимальный объем производства (в таблице выделено жирным шрифтом) будет составлять 7 ед. при издержках 710 р., так как при этом объеме производства прибыль максимальна, а предельный доход (160) превышает предельные издержки (150), т.е. производство рентабельно. При дальнейшем росте производства может снизится валовая прибыль, т.к. разница между предельными издержками и предельным доходом, а также средняя прибыль снизилась в сравнении с показателями при объеме производства 6 ед. Валовая прибыль при объеме 7 ед. составит 410, средняя прибыль 58,57.
б) При таких ценах фирме не следует закрываться, т.к. фирма максимизирует прибыль при таком объёме, при котором предельные издержки равны предельному доходу (MR=MC). Фирма наращивает производство до тех пор, пока дополнительные затраты, связанные с выпуском ещё одной единицы продукции, не начинают превышать выручку от её реализации. В нашем примере при оптимальном объеме производства предельные издержки всегда меньше предельного дохода, т.е. производство рентабельно. Иначе говоря, фирме следует сопоставлять предельный доход (MR) и предельные издержки (МС) производства каждой последующей единицы продукта. Любую единицу продукта, предельный доход от которой превышает связанные с ней предельные издержки, следует производить, поскольку от продажи каждой такой единицы фирма получает больше дохода, чем добавляет к издержкам, производя эту единицу. Следовательно, такая единица продукта увеличивает совокупные прибыли или сокращает убытки. Точно так же, если предельные издержки производства единицы продукта превышают порождаемый ею предельный доход, фирме следует отказаться от выпуска этой единицы. Она добавит больше к издержкам, чем к доходу; такая единица продукта не окупит себя.
В нашем примере при оптимальном объеме производства предельные издержки всегда меньше предельного дохода, т.е. производство рентабельно. Иначе говоря, фирме следует сопоставлять предельный доход (MR) и предельные издержки (МС) производства каждой последующей единицы продукта. Любую единицу продукта, предельный доход от которой превышает связанные с ней предельные издержки, следует производить, поскольку от продажи каждой такой единицы фирма получает больше дохода, чем добавляет к издержкам, производя эту единицу. Следовательно, такая единица продукта увеличивает совокупные прибыли или сокращает убытки. Точно так же, если предельные издержки производства единицы продукта превышают порождаемый ею предельный доход, фирме следует отказаться от выпуска этой единицы. Она добавит больше к издержкам, чем к доходу; такая единица продукта не окупит себя.
г) Предположим, что в данной отрасли действует 2000 конкурентных фирм и каждая из них несет такие же общие и удельные издержки, что и отдельная фирма, которую мы рассматривали. Исходя из этого, мы можем вычислить величину совокупного, или рыночного, предложения, умножив показатели предложения отдельной фирмы на 2000. Сравнив величины совокупного предложения и совокупного спроса при четырех возможных ценах, мы видим, что равновесная цена и равновесный объем производства равны 3 ед по цене 100 р или 2 ед по цене 130, средний объем производства 2,5 ед при средней цене 115 р. Т.е объем рыночного предложения 5000 ед (или 575000 р).
Исходя из этого, мы можем вычислить величину совокупного, или рыночного, предложения, умножив показатели предложения отдельной фирмы на 2000. Сравнив величины совокупного предложения и совокупного спроса при четырех возможных ценах, мы видим, что равновесная цена и равновесный объем производства равны 3 ед по цене 100 р или 2 ед по цене 130, средний объем производства 2,5 ед при средней цене 115 р. Т.е объем рыночного предложения 5000 ед (или 575000 р).
Экономическое поведение фирмы в условиях чистой монополии.
Экономическое поведение фирмы в условиях олигополии и монополистической конкуренции.
1. Определите предельную выручку монополиста от реализации десятой единицы продукции, если 9 единиц он может продать по цене 230 р., а для продажи десятой единицы должен снизить цену до 200 р. Каково соотношение между предельной выручкой и ценой продукта и почему? Какой тип ценовой эластичности существует на данном участке кривой спроса и почему?
Решение:
Предельный доход определяется как разность общего дохода от продажи n + 1 единиц товара и общего дохода от продажи n товаров, т.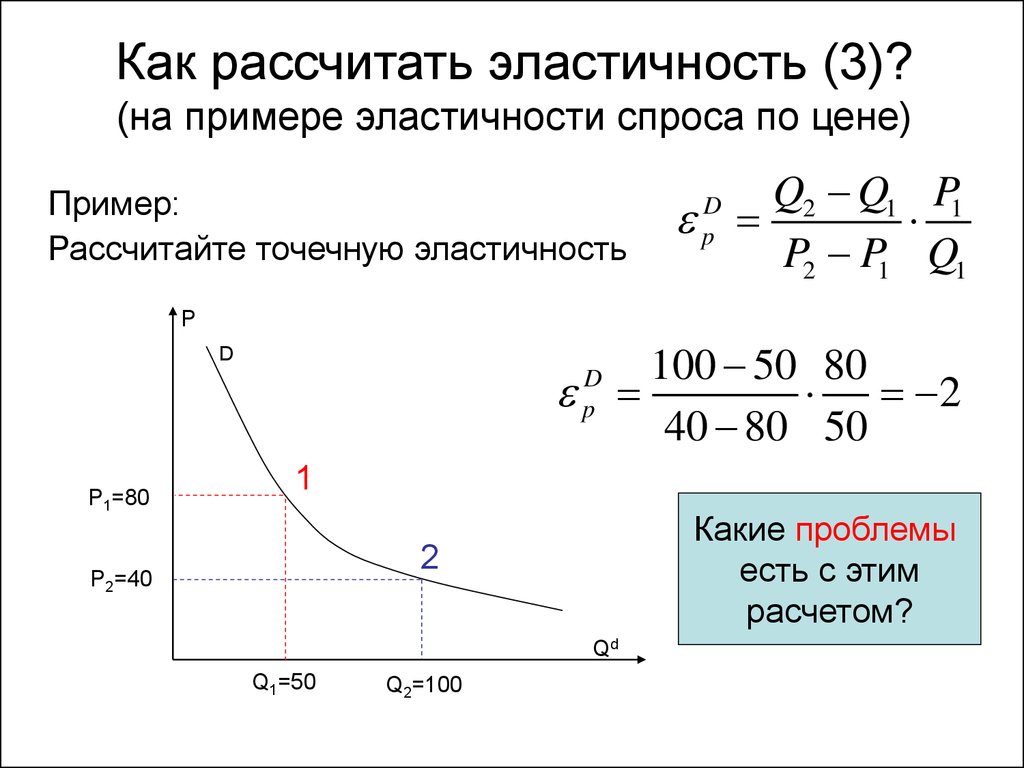 е. в нашем случае
е. в нашем случае
Соотношение между предельной выручкой и ценой продукта: предельная выручка равна цене, так как фирма максимизирует прибыль при таком условии. Однако это справедливо лишь в случае совершенной конкуренции.
Предельный доход фирмы в условиях конкуренции равен цене продукции, так как в условиях конкуренции цена, устанавливаемая каждой конкретной фирмой на свою продукцию, не оказывает существенного влияния на суммарный спрос на продукцию. Таким образом, фирмы в условиях конкуренции могут позволить себе не снижать цену при увеличении количества реализуемого товара.
Монополия предполагает, что одна фирма является единственным производителем какой-либо продукции, не имеющей аналогов. При этом покупатели не имеют возможности выбора и вынуждены приобретать данную продукцию у фирмы-монополиста. Принятие решения об объеме выпуска основывается на том же принципе, что и в случае конкуренции, т.е. на равенстве предельного дохода и предельных издержек. Только в данном случае предельный доход фирмы-монополиста не будет равен цене на товар. Это связано с тем, что фирма-монополист для увеличения количества проданной продукции вынуждена снижать цену всей продукции, а не последней единицы товара. Поэтому предельный доход на единицу продукции равен цене при производстве первой единицы товара и меньше цены товара при продаже всех последующих единиц товара.
Это связано с тем, что фирма-монополист для увеличения количества проданной продукции вынуждена снижать цену всей продукции, а не последней единицы товара. Поэтому предельный доход на единицу продукции равен цене при производстве первой единицы товара и меньше цены товара при продаже всех последующих единиц товара.
Особенностью олигополии является взаимозависимость решений фирм по ценам и объему производства. Действия фирм-конкурентов — это дополнительное ограничение, которое фирмы должны учитывать при определении оптимальных цены и объема производства. Точку равновесия и безубыточности определяют не только издержки и спрос, но и ответная реакция конкурентов.
На данном участке кривой спроса спрос неэластичный, т.к. при снижении цены на 13% объем продаж увеличился на 11%, коэффициент эластичности 0,85.
2. Какое количество продукции следует продавать фирме и по какой цене, если ее валовая выручка TR = 200Q — 4Q2; предельная выручка MR = = 204 — 8Q; предельные издержки МС = 50 + 3Q? Почему данная фирма действует в условиях несовершенной конкуренции?
Решение:
Фирма действует в условиях несовершенной конкуренции, т. к. величина предельной выручки зависит от объема выпуска. Для нахождения оптимального объема приравниваем функции предельной выручки и предельных издержек. Цену находим поделив значение валовой выручки при оптимальной объеме на этот объем
к. величина предельной выручки зависит от объема выпуска. Для нахождения оптимального объема приравниваем функции предельной выручки и предельных издержек. Цену находим поделив значение валовой выручки при оптимальной объеме на этот объем
MR= МС
204 — 8Q =50 + 3Q
204-50 = 3Q + 8Q
Q = 154/11 = 14 — оптимальный объем продаж
Валовая выручка при оптимальном объеме:
TR = 200Q — 4Q2
TR = 200 * 14 — 4* 142 = 2800-784 = 2016
Цена: 2016 руб / 14шт = 144 рубля
3. Предельная выручка фирмы, действующей в условиях монополистической конкуренции, MR = 80 — 4Q, предельные издержки (на восходящем участке) МС = 5Q — 10, а минимальные средние издержки составляют 50 р. Какое количество продукции фирма может продать с наибольшей выгодой? Сколько единиц продукции предлагала бы фирма в положении долгосрочного равновесия, если предположить, что она работает в условиях чистой конкуренции?
Решение:
Фирма, действующая в условиях монополистической конкуренции, не совпадает с целой отраслью и благодаря дифференциации на своём сегменте она — монополист. Здесь кривая спроса приобретает характерный отрицательный наклон: рост объёма реализации достигается за счёт снижения цен. Фирма максимизирует прибыль при таком объёме, при котором предельные издержки равны предельному доходу (MR=MC). Фирма наращивает пр-во до тех пор, пока дополнительные затраты, связанные с выпуском ещё одной единицы продукции, не начинают превышать выручку от её реализации.
Здесь кривая спроса приобретает характерный отрицательный наклон: рост объёма реализации достигается за счёт снижения цен. Фирма максимизирует прибыль при таком объёме, при котором предельные издержки равны предельному доходу (MR=MC). Фирма наращивает пр-во до тех пор, пока дополнительные затраты, связанные с выпуском ещё одной единицы продукции, не начинают превышать выручку от её реализации.
Таким образом, равновесный объем Qравн. при условии максимизации прибыли
МR=MC
80 — 4Q=5Q – 10
Qравн.=10
В случае получения прибылей в краткосрочном периоде можно ожидать, что экономические выгоды привлекут новых конкурентов, поскольку вхождение в отрасль является относительно простым. Что приведет к увеличению предложения. Когда новые конкуренты войдут в отрасль, кривая спроса, с которым сталкивается типичная фирма, сдвинется влево, потому что в этом случае каждая фирма станет обладать меньшей долей совокупного спроса и конкурирует с большим числом продуктов, представляющих собой близкие заменители. Это в свою очередь приводит к исчезновению экономических прибылей. В ходе конкуренции исчезают экономические прибыли и стимул для вхождения в отрасль большего числа фирм. Фирмы постепенно покидают отрасль. Столкнувшись с меньшим количеством продуктов-заменителей и увеличившейся долей совокупного спроса, выжившие фирмы видят, что их убытки прекращаются и постепенно уступают место нормальной прибыли.
Это в свою очередь приводит к исчезновению экономических прибылей. В ходе конкуренции исчезают экономические прибыли и стимул для вхождения в отрасль большего числа фирм. Фирмы постепенно покидают отрасль. Столкнувшись с меньшим количеством продуктов-заменителей и увеличившейся долей совокупного спроса, выжившие фирмы видят, что их убытки прекращаются и постепенно уступают место нормальной прибыли.
Таким образом, для фирм, действующих при монополистической конкуренции, в долгосрочном периоде существует тенденция к получению нормальной прибыли, или к возникновению безубыточности. Эти тенденции, основанные на наличии свойств «чистых конкурентов» и «чистых монополистов», и определяют цены и объемы производства в рассматриваемых условиях.
Для достижения эффективности распределения ресурсов они должны быть распределены между фирмами и отраслями таким образом, чтобы обеспечить производство определенного ассортимента продуктов, которые более всего нужны обществу (потребителям). Эффективность распределения ресурсов достигается, когда невозможно как-либо изменить структуру совокупного продукта, чтобы при этом получать чистую выгоду для общества.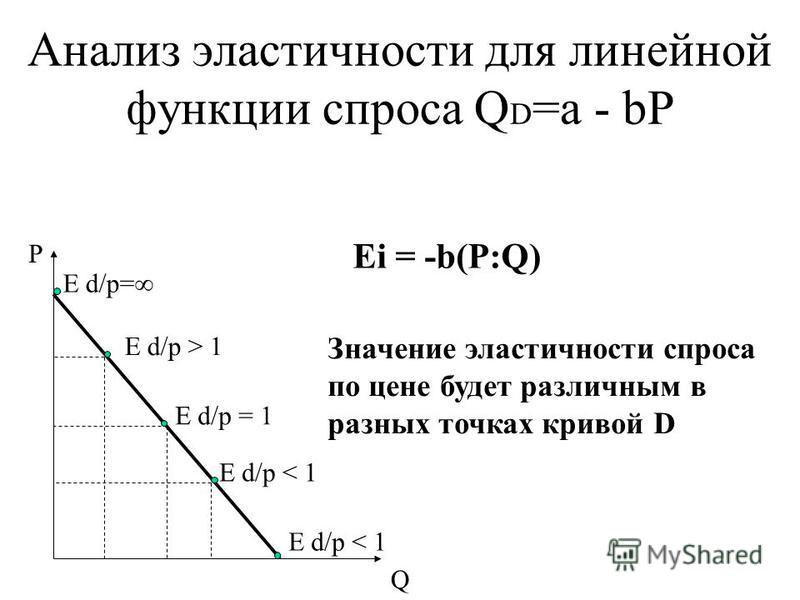
В долгосрочном периоде конкуренция вынуждает фирмы производить такой объем продукции, который приходится на точку минимума средних общих издержек, и устанавливать такую цену, которая соответствует этим издержкам. Это, очевидно, наиболее предпочтительная ситуация для потребителей. Она означает, что фирма должна использовать наилучшую технологию из доступных, иначе она не выживет в конкурентной борьбе. Другими словами, в производстве любого данного количества продукта используется минимум ресурсов.
Р=min (AC)
Так же, как в случае совершенной конкуренции, в долгосрочном периоде при монополистической конкуренции каждая фирма функционирует в точке безубыточности. Однако при совершенной конкуренции, в силу ее специфики, в долгосрочном периоде достигались условия экономической эффективности.
Известно, что экономическая эффективность требует тройного равенства Рх = МС=АТС Равенство Рх = МС отражает эффективное использование ресурсов. Равенство Рх = min АТС определяет высокую производственную эффективность.
Таким образом, в долгосрочном периоде
АТС=МС
50=5Q – 10
Qдолг=12
Ответ: Qравн.=10, Qдолг=12
Чтобы скачать бесплатно Задачи на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.
Важно! Все представленные Задачи для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.
Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.
Если Задача, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.
Примеры решений задач по экономике
Решения задач по экономической теории
В этом разделе вы найдете ссылки на задачи (с решениями и ответами) по разным разделам экономики для студентов ВУЗов. Разобраны и простые типовые задачи, и задачи посложнее.
Все примеры выложены бесплатно онлайн, вы можете их просмотреть, распечатать, изучить. Еще примеры работ экономического направления вы можете скачать тут.
Если вам нужна помощь в выполнении ваших работ по экономике, обращайтесь: экономика на заказ. Решаем задачи, контрольные работы, лабораторные и кейсы, помогаем сдавать тесты.
Если вам нужна помощь в выполнении ваших работ по экономике, обращайтесь экономика на заказ.
Www. matburo. ru
25.06.2020 11:53:07
2020-06-25 11:53:07
Источники:
Https://www. matburo. ru/ex_econ_all. php? p1=economics
Решения задач по экономической теории » /> » /> .keyword { color: red; }
Решения задач по экономической теории
В этом разделе вы найдете подробно решенные задачи с ответами по предмету «Экономическая теория» для студентов. Примеры решений выложены бесплатно для вашего удобства. Если вам нужна помощь с подобными заданиями, обращайтесь: Экономическая теория на заказ.
Экономическая теория: задачи с решениями
Задача 1. Возьмите в качестве примера рынок молока, продаваемого и производимого в вашем регионе. Перечислите детерминанты спроса и предложения по данному товару в вашем регионе, приведите примеры. Охарактеризуйте эластичность спроса и предложения по цене, перекрестную эластичность. Постройте график спроса и предложения молока с учетом эластичности.
Задача 2. Объясните смысл эластичности предложения по цене, приведите примеры. Найдите эластичность спроса по доходу, сделайте выводы на основании имеющихся данных (I*, Q* — доходы и спрос после изменения цен).
Задача 3. Фирма функционирует в условиях совершенной конкуренции.
Q 0 12 30 52 70 81 90 94 95
TC 25 50 75 100 125 150 175 200 225
Р (цена) = 2 ден. ед. Найти: АТС, МС. Построить графики ATС, MС, Р. На графике найти Qmin, Qmax, Qopt, размер прибыли в точке оптимума.
Задача 4. Имеются данные по предприятию «Х»:
Цеховые расходы — 160 тыс. р.; общезаводские расходы — 64 тыс. р.; расходы на реализацию продукции — 85 тыс. р.
р.; общезаводские расходы — 64 тыс. р.; расходы на реализацию продукции — 85 тыс. р.
Найти: себестоимость продукции, используя «котловой» метод распределения косвенных затрат.
В этом разделе вы найдете подробно решенные задачи с ответами по предмету «Экономическая теория» для студентов. Примеры решений выложены бесплатно для вашего удобства. Если вам нужна помощь с подобными заданиями, обращайтесь: Экономическая теория на заказ.
Задача 1. Возьмите в качестве примера рынок молока, продаваемого и производимого в вашем регионе. Перечислите детерминанты спроса и предложения по данному товару в вашем регионе, приведите примеры. Охарактеризуйте эластичность спроса и предложения по цене, перекрестную эластичность. Постройте график спроса и предложения молока с учетом эластичности.
Задача 2. Объясните смысл эластичности предложения по цене, приведите примеры. Найдите эластичность спроса по доходу, сделайте выводы на основании имеющихся данных (I*, Q* — доходы и спрос после изменения цен).
Задача 3. Фирма функционирует в условиях совершенной конкуренции.
Q 0 12 30 52 70 81 90 94 95
TC 25 50 75 100 125 150 175 200 225
Р (цена) = 2 ден. ед. Найти: АТС, МС. Построить графики ATС, MС, Р. На графике найти Qmin, Qmax, Qopt, размер прибыли в точке оптимума.
Задача 4. Имеются данные по предприятию «Х»:
Цеховые расходы — 160 тыс. р.; общезаводские расходы — 64 тыс. р.; расходы на реализацию продукции — 85 тыс. р.
Найти: себестоимость продукции, используя «котловой» метод распределения косвенных затрат.
В этом разделе вы найдете подробно решенные задачи с ответами по предмету Экономическая теория для студентов.
Www. matburo. ru
21.04.2017 22:50:20
2017-04-21 22:50:20
Источники:
Https://www. matburo. ru/ex_econ_all. php? p1=et
Готовые решение задач по экономической теории — скачать бесплатно » /> » /> .keyword { color: red; }
Решения задач по экономической теории
Сделайте индивидуальный заказ на нашем сервисе. Там эксперты помогают с учебой без посредников Разместите задание – сайт бесплатно отправит его исполнителя, и они предложат цены.
Там эксперты помогают с учебой без посредников Разместите задание – сайт бесплатно отправит его исполнителя, и они предложат цены.
Цены ниже, чем в агентствах и у конкурентов
Вы работаете с экспертами напрямую. Поэтому стоимость работ приятно вас удивит
Бесплатные доработки и консультации
Исполнитель внесет нужные правки в работу по вашему требованию без доплат. Корректировки в максимально короткие сроки
Если работа вас не устроит – мы вернем 100% суммы заказа
Техподдержка 7 дней в неделю
Наши менеджеры всегда на связи и оперативно решат любую проблему
Строгий отбор экспертов
К работе допускаются только проверенные специалисты с высшим образованием. Проверяем диплом на оценки «хорошо» и «отлично»
Требуются доработки?
Они включены в стоимость работы
Работы выполняют эксперты в своём деле. Они ценят свою репутацию, поэтому результат выполненной работы гарантирован
Последние размещённые задания
Ежедневно эксперты готовы работать над 1000 заданиями. Контролируйте процесс написания работы в режиме онлайн
Контролируйте процесс написания работы в режиме онлайн
Помощь на экзамене
Онлайн-помощь, Теория автоматического управления
Срок сдачи к 25 июня
Проектирование промышленных зданий
Курсовая, проектирование зданий и сооружений
Срок сдачи к 21 июня
Дать развернутые ответы на вопросы билетов
Ответы на билеты, История теории культуры
Срок сдачи к 21 июня
Контрольная, Управление персоналом
Срок сдачи к 25 июня
Реферат на тему «Современные методы воспитания которые можно применить.
Срок сдачи к 22 июня
Помочь решить 2 билета по мсфо
Решение задач, Бухгалтерский учет
Срок сдачи к 21 июня
Задание: Описать очередь с приоритетами как структуру данных
Реферат, Информатика и программирование
Срок сдачи к 23 июня
Помощь на зачете по физике
Срок сдачи к 25 июня
Выполнить в инвентор
Лабораторная, инженерная и компьютерная графика
Срок сдачи к 23 июня
Помогите решить задачу
Решение задач, Бухгалтерский учет
Срок сдачи к 22 июня
Решить в аналитической форме, тема: «Анализ движения точки, заданного координатным способом»
Контрольная, теоретическая механика
Срок сдачи к 23 июня
Чертеж, Инженерная графика
Срок сдачи к 20 июня
Составить аннотированный список литературы
Подбор литературы, Педагогика
Срок сдачи к 24 июня
Решите пожалуйста вариант 5
Контрольная, Численные методы
Срок сдачи к 21 июня
К/р по физике 11 кл
Срок сдачи к 23 июня
Решите пожалуйста вариант 5
Контрольная, Численные методы
Срок сдачи к 21 июня
Помощь на экзамене
Онлайн-помощь, Высшая математика
Срок сдачи к 21 июня
Маркетинговый анализ рынка на примере Калининградской области.
Срок сдачи к 24 июня
Размещенные на сайт контрольные, курсовые и иные категории работ (далее — Работы) и их содержимое предназначены исключительно для ознакомления, без целей коммерческого использования. Все права в отношении Работ и их содержимого принадлежат их законным правообладателям. Любое их использование возможно лишь с согласия законных правообладателей. Администрация сайта не несет ответственности за возможный вред и/или убытки, возникшие в связи с использованием Работ и их содержимого.
Сделайте индивидуальный заказ на нашем сервисе. Там эксперты помогают с учебой без посредников Разместите задание – сайт бесплатно отправит его исполнителя, и они предложат цены.
Ежедневно эксперты готовы работать над 1000 заданиями. Контролируйте процесс написания работы в режиме онлайн
Требуются доработки? Они включены в стоимость работы
Срок сдачи к 23 июня.
Skachatvs. com
29.06.2019 19:19:00
2019-06-29 19:19:00
Источники:
Https://skachatvs. com/reshenie-zadach/ekonomicheskaya-teoriya
com/reshenie-zadach/ekonomicheskaya-teoriya
4.1 Расчет эластичности – принципы микроэкономики
Цели обучения
К концу этого раздела вы сможете:
- Рассчитать ценовую эластичность спроса
- Рассчитать ценовую эластичность предложения
- Рассчитать эластичность спроса по доходу и перекрестную эластичность спроса по цене
- Применение концепции ценовой эластичности к реальным ситуациям
Сколько будет?
Представьте, что вы идете в свою любимую кофейню, а официант сообщает вам, что цены изменились. Вместо 3 долларов за чашку кофе со сливками и подсластителем теперь вы будете платить 2 доллара за черный кофе, 1 доллар за сливки и 1 доллар за подсластитель на ваш выбор. Если вы хотите заплатить свои обычные 3 доллара за чашку кофе, вы должны выбирать между сливками и подсластителем. Если вы хотите и то, и другое, теперь вам придется заплатить дополнительную плату в размере 1 доллара. Звучит абсурдно? Что ж, именно в такой ситуации оказались клиенты Netflix в 2011 году — повышение цен на 60%, чтобы сохранить тот же сервис.
Звучит абсурдно? Что ж, именно в такой ситуации оказались клиенты Netflix в 2011 году — повышение цен на 60%, чтобы сохранить тот же сервис.
В начале 2011 года потребители Netflix платили около 10 долларов в месяц за пакет, состоящий из потокового видео и проката DVD. В июле 2011 года компания объявила об изменении упаковки. Клиенты, желающие сохранить как потоковое видео, так и аренду DVD, будут платить 15,98 долларов США в месяц, что означает увеличение цены примерно на 60%. В 2014 году Netflix также повысил стоимость подписки на потоковое видео с 7,99 до 8,99 долларов в месяц для новых клиентов из США. Компания также изменила свою политику потокового контента 4K с 9 долларов.от 0,00 до 12,00 долларов в месяц в этом году.
Как отреагировали клиенты 18-летней фирмы? Они отказались от Netflix? Насколько это изменение цены повлияет на спрос на продукты Netflix? Ответы на эти вопросы будут рассмотрены в этой главе с помощью концепции, которую экономисты называют эластичностью.
Нажмите, чтобы прочитать остальную часть истории Netflix
Любой, кто изучал экономику, знает закон спроса: чем выше цена, тем меньше объем спроса. Чего вы можете не знать, так это того, насколько ниже будет требуемое количество. Точно так же закон предложения показывает, что более высокая цена приведет к увеличению объема предложения. Вопрос: насколько выше? В этом разделе объясняется, как ответить на эти вопросы и почему они крайне важны в реальном мире.
Чтобы найти ответы на эти вопросы, нам нужно понять концепцию эластичности. Эластичность – это экономическая концепция, которая измеряет реакцию одной переменной на изменения другой переменной. Предположим, вы уронили два предмета с балкона второго этажа. Первый предмет — теннисный мяч, а второй — кирпич. Что подпрыгнет выше? Очевидно, теннисный мяч. Мы бы сказали, что теннисный мяч обладает большей эластичностью.
Но как эта степень отклика проявляется в наших моделях? Как кривая спроса, так и кривая предложения показывают взаимосвязь между ценой и количеством, и эластичность может улучшить наше понимание этой взаимосвязи.
Собственная ценовая эластичность спроса – это процентное изменение количества спроса товаров или услуг, деленное на процентное изменение цены. Это показывает реакцию величины спроса на изменение цены.
Эластичность предложения по собственной цене является процентным изменением количества поставляемого деленного на процентное изменение цены. Это показывает реакцию количества поставляемого товара на изменение цены.
Наша формула для эластичности [латекс]\frac{\%\Delta Quantity}{\%\Delta Price}[/latex] может использоваться для большинства задач с эластичностью, просто мы используем разные цены и количества для разных ситуаций. .
Почему проценты нелогичны
Напомним, что упрощенная формула для процентного изменения – [латекс]\frac{New\;Value-Old\;Value}{Old\;Value}[/latex], также записывается как [latex ]\frac{\Delta Value}{Старое\;Значение}[/latex].
Предположим, что объем спроса увеличился с 4 до 6 чашек кофе. При расчете процентного изменения ([латекс]\frac{\left(6-4\right)}{4}[/latex]) объем спроса увеличился на 50 %. Используя те же числа, рассмотрите, что произойдет, когда объем спроса уменьшится с 6 до 4 чашек кофе ([латекс]\frac{\left(4-6\right)}{6}[/latex]) это изменение приведет к 33 % уменьшение объема спроса.
При расчете процентного изменения ([латекс]\frac{\left(6-4\right)}{4}[/latex]) объем спроса увеличился на 50 %. Используя те же числа, рассмотрите, что произойдет, когда объем спроса уменьшится с 6 до 4 чашек кофе ([латекс]\frac{\left(4-6\right)}{6}[/latex]) это изменение приведет к 33 % уменьшение объема спроса.
Сразу же следует отметить, что это должно насторожить при расчете эластичности между двумя точками. Если процентное изменение зависит от направления (от А к В или от В к А), то как мы можем обеспечить постоянное значение эластичности?
Рисунок 4.1aРассчитаем эластичность с обеих точек зрения:
Переход от A к B:
%ΔPrice: цена на кофе падает с 4,50 до 3,00 долларов, что означает, что процентное изменение составляет [латекс]\frac{\left( 3,00-4,50\справа)}{4,50}[/латекс] = -33%. Цена упала на 33 %.
%ΔQuantity: количество проданного кофе увеличивается с 4 до 6, что означает процентное изменение [латекс]\frac{\left(6-4\right)}{4}[/latex] = 50%. Количество увеличилось на 50%
Количество увеличилось на 50%
Эластичность: [латекс]\frac{\%\Delta Quantity}{\%\Delta Price}=-\frac{50\%}{33\%}[/latex] = 1,5*
Переход от B к A:
%ΔPrice: цена на кофе повышается с 3,00 до 4,50 долл. США, что означает, что процентное изменение составляет [латекс]\frac{\left(4,50-3,00\right)}{3,00} [/латекс] = 50%. Цена выросла на 50%.
%ΔQuantity:
Количество проданного кофе падает с 6 до 4, что означает процентное изменение [латекс]\frac{\left(4-6\right)}{6}[/latex] = -33%. Количество упало на 33%
Эластичность: [латекс]\frac{\%\Delta Quantity}{\%\Delta Price}=\frac{33\%}{50\%}[/latex] = 0,67
Эти два расчета дают нам разные числа. Этот тип анализа сделал бы эластичность зависимой от направления, что добавило бы ненужных сложностей. Чтобы избежать этого, мы будем полагаться на средние значения.
*Обратите внимание, что эластичность является абсолютной величиной, то есть на нее не влияют положительные или отрицательные значения.
Метод средней точки
Для расчета эластичности вместо простых процентных изменений количества и цены экономисты используют среднее процентное изменение. Это называется методом средней точки эластичности и представлено следующими уравнениями:
[латекс]\begin{array}{r @{{}={}} l}\%\;изменение\;в\;количестве & \frac { { Q }_{ 2 }-{ Q }_{ 1 } }{ ({ Q }_{ 2 }+{ Q }_{ 1 })/2 } \times 100 \\[1em] \%\;изменение\;в\;цене & \frac { { P }_ { 2 }-{ P }_{ 1 } }{ ({ P }_{ 2 }+{ P }_{ 1 })/2 } \times 100 \end{array}[/latex]
Преимущество метода m id-point заключается в том, что можно получить одинаковую эластичность между двумя ценовыми точками независимо от того, происходит ли повышение или снижение цены. Это связано с тем, что знаменатель является средним, а не старым значением.
Использование метода средней точки для расчета эластичности между точками A и B:
[латекс]\begin{array}{r @{{}={}} l}\%\;изменение\;в\;количестве & \frac { { 6 }-{ 4 } }{ ({ 6 }+ { 4 })/2 } \times 100 \\[1em] & \frac { 2 }{ 5 } \times 100 \\[1em] & 40\% \\[1em] \%\;change\;in\ ;цена & \frac { { 3,00 }-{ 4,50 } }{ ({ 3,00 }+{ 4,50 })/2 } \times 100 \\[1em] & \frac { -1,50 }{ 3,75 } \times 100 \\ [1em] & -40\% \\[1em] Цена\;Эластичность\;спроса\;\\frac { 40\% }{ 40\% } \\[1em] & 1 \end{array}[/ латекс]
Этот метод дает нам своего рода среднюю эластичность спроса по двум точкам на нашей кривой.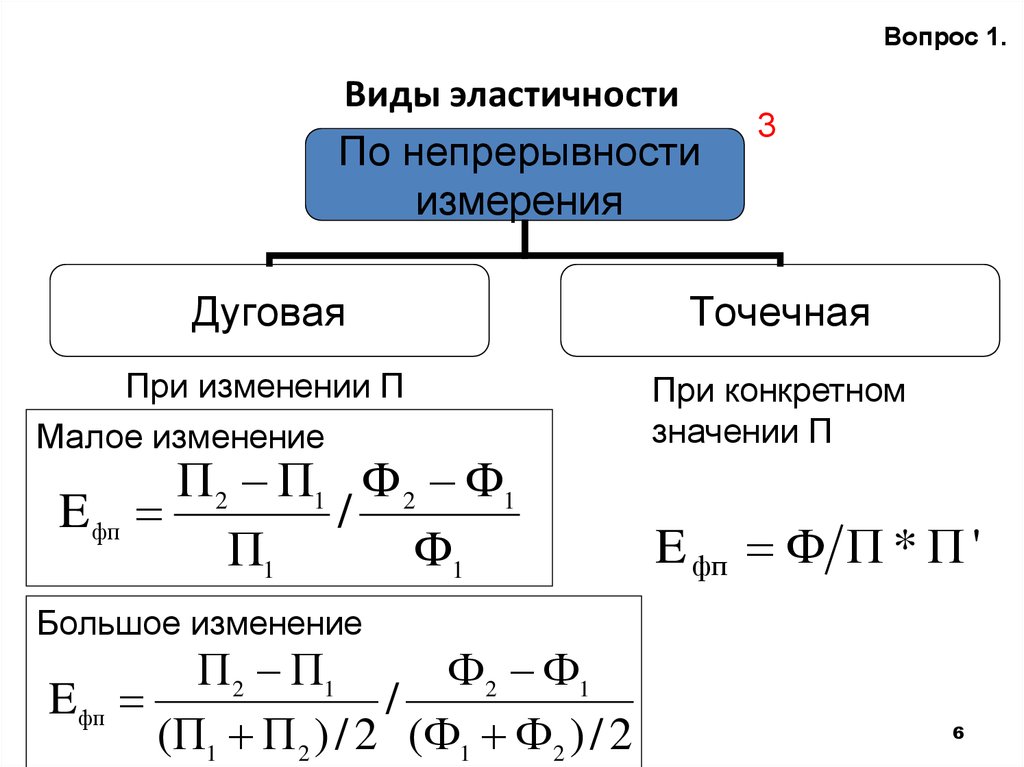 Обратите внимание, что наша эластичность 1 находится между эластичностями 0,67 и 1,52, которые мы рассчитали в предыдущем примере.
Обратите внимание, что наша эластичность 1 находится между эластичностями 0,67 и 1,52, которые мы рассчитали в предыдущем примере.
Формула точки-уклона
На рисунке 4.1а нам были даны две точки, и мы рассмотрели эластичность как движение по кривой. Как мы увидим в Теме 4.3, часто полезно рассматривать эластичность в одной точке. Чтобы вычислить это, мы должны вывести новое уравнение.
[латекс]\frac{\%\Delta Quantity}{\%\Delta Price}=эластичность[/latex]
Поскольку мы знаем, что процентное изменение цены можно переписать как
[латекс]\frac{\Delta Price}{Цена}[/latex]
и процентное изменение количества до
[латекс]\frac{\Delta Quantity}{Количество}[/latex]
, мы можем преобразовать исходное уравнение в
.[латекс]\frac{\frac{\Delta Quantity}{Количество}}{\frac{\Delta Price}{Цена}}[/latex]
это то же самое, что сказать
[латекс]\frac{\Delta Quantity\cdot Price}{\Delta Price\cdot Quantity}=\frac{\Delta Q}{\Delta P}\cdot \frac{P}{Q}[/latex]
Это дает нам нашу формулу точка-наклон . Как мы используем его для расчета эластичности в точке А? Часть P/Q нашего уравнения соответствует значениям в точке, которые составляют 4,5 и 4 доллара. ΔQ/ΔP соответствует обратному наклону кривой . Наклон возврата рассчитывается как подъем/спуск.
Как мы используем его для расчета эластичности в точке А? Часть P/Q нашего уравнения соответствует значениям в точке, которые составляют 4,5 и 4 доллара. ΔQ/ΔP соответствует обратному наклону кривой . Наклон возврата рассчитывается как подъем/спуск.
На рис. 4.1 наклон равен [латекс]\фрак{3-4,5}{6-4}[/латекс] = 0,75, что означает обратное соотношение 1/0,75 = 1,33. Подставив эту информацию в наше уравнение, мы получим:
[латекс]\frac{\Delta Q}{\Delta P}\cdot \frac{P}{Q}[/latex]
[латекс]1,33\cdot \frac{4,5}{4}[/латекс] = 1,5
Этот анализ дает нам эластичность как единую точку. Обратите внимание, что это дает нам то же число, что и при расчете эластичности от точки А до точки Б. Это не совпадение. Когда мы рассчитываем от точки А к точке Б, мы на самом деле просто вычисляем эластичность в точке А, поскольку мы используем значения в точке А в качестве знаменателя для нашего процентного изменения. Точно так же от точки B до точки A мы рассчитываем эластичность в точке B. Когда мы используем метод средней точки, мы просто берем среднее значение двух точек. Это подтверждает тот факт, что в каждой точке нашей линии существует разная эластичность, концепция, которая будет важна, когда мы будем обсуждать доход.
Когда мы используем метод средней точки, мы просто берем среднее значение двух точек. Это подтверждает тот факт, что в каждой точке нашей линии существует разная эластичность, концепция, которая будет важна, когда мы будем обсуждать доход.
Не такой уж и другой
Несмотря на то, что средняя точка и точка-наклон кажутся довольно разными формулами, среднюю точку можно переписать, чтобы показать, насколько они похожи на самом деле.
[латекс]\frac{\frac{\Delta Q}{(Q1+Q2)/2}}{\frac{\Delta P}{(P1+P2)/2}}[/latex] = [латекс] \frac{\frac{\Delta Q}{Q1+Q2}}{\frac{\Delta P}{P1+P2}}[/latex]
Помните, что когда дробь делится на дробь, вы можете преобразовать ее в дробь, умноженную на дробь, обратную знаменателю.
= [латекс]\frac{\Delta Q}{\Delta P}\cdot \frac{\left(P1+P2\right)}{\left(Q1+Q2\right)}[/latex]
Обратите внимание, что по сравнению с точкой-наклоном: [латекс]\frac{\Delta Q}{\Delta P}\cdot \frac{P}{Q}[/latex], единственное отличие состоит в том, что точка-наклон является обратным наклона, умноженного на одну точку, тогда как средняя точка является обратной величиной наклона, умноженной на несколько точек. Это подтверждает вывод о том, что средняя точка представляет собой среднее значение.
Это подтверждает вывод о том, что средняя точка представляет собой среднее значение.
Прочие эластичности
Помните, что эластичность — это реакция одной переменной на изменения другой переменной. Это означает, что его можно применять не только к соотношению цены и количества в нашей рыночной модели. В теме 3 мы обсуждали, как товары могут быть хуже/нормальными или замещающими/дополняющими. Мы рассмотрим это еще подробнее, когда будем знакомить с теорией потребления, а сейчас мы можем развить наше понимание, применяя то, что мы знаем об эластичностях.
Эластичность предложения по собственной цене (e
P С ) Наш анализ эластичности сосредоточен на спросе, но те же принципы применимы и к кривой предложения. В то время как эластичность спроса измеряет реакцию объема спроса на изменение цены, эластичность предложения по собственной цене измеряет реакцию объема предложения. Чем более эластична фирма, тем больше она может увеличивать производство при повышении цен и сокращать производство при падении цен. Наше уравнение выглядит следующим образом:
Наше уравнение выглядит следующим образом:
[латекс]\frac{\%\Delta Q\;Поставляется}{\%\Delta P}[/latex]
Эластичность предложения по собственной цене может быть рассчитана с использованием формулы средней точки и точки-наклона так же, как для e P D .
Перекрестная ценовая эластичность спроса (e
XP D )В то время как эластичность спроса по собственной цене измеряет реакцию количества на собственную цену товара, перекрестная эластичность спроса по цене показывает нам, как количественный спрос реагирует на изменения в цене товара.0039 сопутствующие товары . В то время как раньше мы могли игнорировать положительные и отрицательные стороны эластичности, перекрестной цены, это имеет значение. Наше уравнение выглядит следующим образом:
[латекс]\frac{\%\Delta Q\;Хорошо A}{\%\Delta P\;Хорошо B}[/latex]
Рассмотрим наше обсуждение дополнений и заменителей в теме 3. 3. Мы определили дополнения как товары, которые люди предпочитают потреблять вместе с другим товаром, и заменители как товары, которые люди предпочитают потреблять вместо другого товара. Если цена на дополнение повысится, наш спрос упадет, если цена на заменитель повысится, наш спрос повысится. Для перекрестной ценовой эластичности это означает:
3. Мы определили дополнения как товары, которые люди предпочитают потреблять вместе с другим товаром, и заменители как товары, которые люди предпочитают потреблять вместо другого товара. Если цена на дополнение повысится, наш спрос упадет, если цена на заменитель повысится, наш спрос повысится. Для перекрестной ценовой эластичности это означает:
Дополнение будет иметь отрицательную перекрестную ценовую эластичность , поскольку, если процентное изменение цены положительно, процентное изменение количества будет отрицательным, и наоборот.
Заменитель будет иметь положительную перекрестную эластичность по цене , поскольку, если процентное изменение цены положительно, процентное изменение количества будет положительным и наоборот.
Это добавляет еще одно измерение к нашему обсуждению комплементов/заменителей. Теперь мы можем прокомментировать силу связи между двумя товарами. Например, перекрестная эластичность -4 предполагает, что человек предпочитает потреблять два товара вместе, тогда как перекрестная эластичность -0,5. Это может отражать перекрестную эластичность потребителя хот-дога по отношению к кетчупу и приправам. Потребитель может сильно предпочесть есть хот-доги с кетчупом и в некоторой степени предпочесть приправы.
Это может отражать перекрестную эластичность потребителя хот-дога по отношению к кетчупу и приправам. Потребитель может сильно предпочесть есть хот-доги с кетчупом и в некоторой степени предпочесть приправы.
Эластичность спроса по доходу (e
N D )В Теме 3 мы также объяснили, как товары могут быть нормальными или некачественными в зависимости от того, как потребитель реагирует на изменение дохода. Эта отзывчивость также может быть измерена с помощью эластичности спроса по доходу . Наше уравнение выглядит следующим образом:
[латекс]\frac{\%\Delta Q}{\%\Delta Income}[/latex]
Как и в случае с перекрестной эластичностью, независимо от того, является ли наша эластичность положительной или отрицательной, мы получаем ценную информацию о том, как потребитель относится к товару:
Нормальный товар будет иметь положительную эластичность по доходу , поскольку, если процентное изменение дохода положительно, процентное изменение количества будет положительным и наоборот.
Товар низшего качества будет иметь отрицательную эластичность по доходу , поскольку, если % изменения дохода положительны, % изменения количества будут отрицательными и наоборот.
Значение нашей эластичности покажет, насколько товар реагирует на изменение дохода. Товар с эластичностью спроса по доходу 0,05, хотя технически нормальный товар (поскольку спрос увеличивается после роста дохода), не так чувствителен, как товар с эластичностью спроса по доходу 5,9.0005
Резюме
Эластичность — это мера чувствительности, вычисляемая путем деления процентного изменения одной переменной на процентное изменение другой.
Формулы средней точки и точки-наклона важны для расчета эластичности в различных ситуациях. Средняя точка дает среднее значение эластичности между двумя точками, тогда как точка-наклон дает эластичность в определенной точке. Их можно рассчитать по следующим формулам:
| Базовая формула | Средняя формула | Формула точки-уклона |
| [латекс]\frac{\%\Delta Quantity}{\%\Delta Price}[/latex] | [латекс]\frac{\Delta Q}{\Delta P}\cdot \frac{\left(P1+P2\right)}{\left(Q1+Q2\right)}[/latex] | [латекс]\frac{\Delta Q}{\Delta P}\cdot \frac{P}{Q}[/latex] |
Поскольку эластичность измеряет отзывчивость, ее также можно использовать для измерения эластичности предложения по собственной цене, перекрестной эластичности спроса по ценам и эластичности спроса по доходу. Их можно рассчитать по следующим формулам:
Их можно рассчитать по следующим формулам:
| Эластичность предложения по собственной цене | Перекрестная эластичность спроса | Эластичность спроса по доходу |
| [латекс]\frac{\%\Delta Q\;Поставляется}{\%\Delta P}[/latex] | [латекс]\frac{\%\Delta Q\;Хорошо A}{\%\Delta P\;Хорошо B}[/latex] | [латекс]\frac{\%\Delta Q}{\%\Delta Income}[/latex] |
Глоссарий
- Перекрестная эластичность спроса
- процентное изменение величины спроса на товар А в результате процентного изменения цены товара В
- Эластичность
- экономическая концепция, которая измеряет реакцию одной переменной на изменения другой переменной
- Эластичность спроса по доходу
- процентное изменение объема спроса на товар или услугу в результате процентного изменения дохода
- Эластичность спроса по собственной цене
- процентное изменение величины спроса на товар или услугу, деленное на процентное изменение цены
- Метод средней точки
- Включает умножение обратной величины наклона на значения одной точки.

- Эластичность предложения по собственной цене
- процентное изменение объема поставки, деленное на процентное изменение цены
- Метод наклона точки
- Метод расчета эластичности между двумя точками. Включает расчет процентного изменения цены и количества по отношению к среднему значению двух точек.
Упражнения 4.1
1. Используйте приведенную ниже диаграмму кривой спроса, чтобы ответить на следующий вопрос.
Какова эластичность спроса по собственной цене при повышении цены с 2 до 4 долларов за единицу? Используйте в своих расчетах формулу средней точки.
а) 1/3.
б) 6/10.
в) 2/3.
г) Ничего из вышеперечисленного.
2. Предположим, что увеличение цены на 2% приводит к уменьшению объема спроса на 6%. Эластичность спроса по собственной цене равна:
а) 1/3.
б) 6.
в) 2
г) 3.
3. Если эластичность спроса по собственной цене равна 0,3 по абсолютной величине, то какой процент изменения цены приведет к уменьшению количества на 6% потребовал?
а) 3%
б) 6%
в) 20%.
г) 50%.
4. Предположим, вам сказали, что эластичность предложения по собственной цене равна 0,5. Что из следующего является правильной интерпретацией этого числа?
а) Повышение цены на 1% приведет к увеличению объема предложения на 50%.
б) Повышение цены на 1% приведет к увеличению объема предложения на 5%.
c) Увеличение цены на 1% приведет к увеличению объема предложения на 2%.
d) Увеличение цены на 1% приведет к увеличению объема предложения на 0,5%.
5. Предположим, что увеличение цены на 10 приводит к 50-процентному уменьшению объема спроса. Чему равна (абсолютная величина) собственная ценовая эластичность спроса?
а) 0,5.
б) 0,2.
c) 5.
d) 10.
6. Если товары X и Y являются ЗАМЕНЯЮЩИМИ, то что из следующего может быть значением перекрестной ценовой эластичности спроса на товар Y?
а) -1.
б)-2.
в) Ни а), ни б).
d) Как а), так и б).
7 . Если пицца является нормальным товаром, то что из следующего может быть значением эластичности спроса по доходу?
а) 0.2.
б) 0,8.
в) 1.4
г) Все вышеперечисленное.
8. Если товары X и Y являются ДОПОЛНИТЕЛЬНЫМИ, что из следующего может быть значением перекрестной ценовой эластичности спроса?
а) 0.
б) 1.
в) -1.
г) Все вышеперечисленное может быть величиной перекрестной ценовой эластичности спроса.
4.1 Расчет эластичности – принципы микроэкономики
Цели обучения
К концу этого раздела вы сможете:
- Рассчитать ценовую эластичность спроса
- Рассчитать ценовую эластичность предложения
- Рассчитать эластичность спроса по доходу и перекрестную эластичность спроса по цене
- Применение концепции ценовой эластичности к реальным ситуациям
 0)
0)Сколько будет?
Представьте, что вы идете в свою любимую кофейню, а официант сообщает вам, что цены изменились. Вместо 3 долларов за чашку кофе со сливками и подсластителем теперь вы будете платить 2 доллара за черный кофе, 1 доллар за сливки и 1 доллар за подсластитель на ваш выбор. Если вы хотите заплатить свои обычные 3 доллара за чашку кофе, вы должны выбирать между сливками и подсластителем. Если вы хотите и то, и другое, теперь вам придется заплатить дополнительную плату в размере 1 доллара. Звучит абсурдно? Что ж, именно в такой ситуации оказались клиенты Netflix в 2011 году — повышение цен на 60%, чтобы сохранить тот же сервис.
В начале 2011 года потребители Netflix платили около 10 долларов в месяц за пакет, состоящий из потокового видео и проката DVD. В июле 2011 года компания объявила об изменении упаковки. Клиенты, желающие сохранить как потоковое видео, так и аренду DVD, будут платить 15,98 долларов США в месяц, что означает увеличение цены примерно на 60%. В 2014 году Netflix также повысил стоимость подписки на потоковое видео с 7,99 до 8,99 долларов в месяц для новых клиентов из США. Компания также изменила свою политику потокового контента 4K с 9 долларов.от 0,00 до 12,00 долларов в месяц в этом году.
В 2014 году Netflix также повысил стоимость подписки на потоковое видео с 7,99 до 8,99 долларов в месяц для новых клиентов из США. Компания также изменила свою политику потокового контента 4K с 9 долларов.от 0,00 до 12,00 долларов в месяц в этом году.
Как отреагировали клиенты 18-летней фирмы? Они отказались от Netflix? Насколько это изменение цены повлияет на спрос на продукты Netflix? Ответы на эти вопросы будут рассмотрены в этой главе с помощью концепции, которую экономисты называют эластичностью.
Нажмите, чтобы прочитать остальную часть истории Netflix
Любой, кто изучал экономику, знает закон спроса: чем выше цена, тем меньше объем спроса. Чего вы можете не знать, так это того, насколько ниже будет требуемое количество. Точно так же закон предложения показывает, что более высокая цена приведет к увеличению объема предложения. Вопрос: насколько выше? В этом разделе объясняется, как ответить на эти вопросы и почему они крайне важны в реальном мире.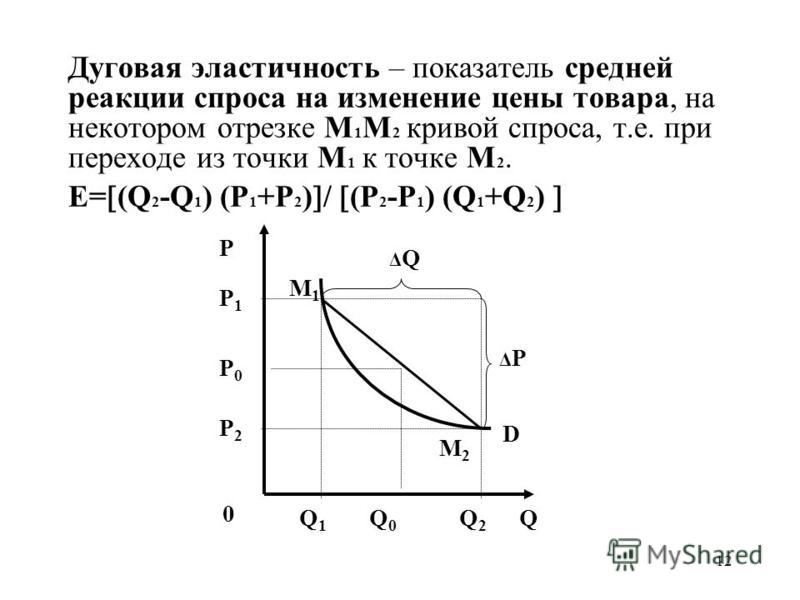
Чтобы найти ответы на эти вопросы, нам нужно понять концепцию эластичности. Эластичность – это экономическая концепция, которая измеряет реакцию одной переменной на изменения другой переменной. Предположим, вы уронили два предмета с балкона второго этажа. Первый предмет — теннисный мяч, а второй — кирпич. Что подпрыгнет выше? Очевидно, теннисный мяч. Мы бы сказали, что теннисный мяч обладает большей эластичностью.
Но как эта степень отклика проявляется в наших моделях? Как кривая спроса, так и кривая предложения показывают взаимосвязь между ценой и количеством, и эластичность может улучшить наше понимание этой взаимосвязи.
Собственная ценовая эластичность спроса – это процентное изменение количества спроса товаров или услуг, деленное на процентное изменение цены. Это показывает реакцию величины спроса на изменение цены.
Эластичность предложения по собственной цене является процентным изменением количества поставляемого деленного на процентное изменение цены. Это показывает реакцию количества поставляемого товара на изменение цены.
Это показывает реакцию количества поставляемого товара на изменение цены.
Наша формула для эластичности [латекс]\frac{\%\Delta Quantity}{\%\Delta Price}[/latex] может использоваться для большинства задач с эластичностью, просто мы используем разные цены и количества для разных ситуаций. .
Почему проценты нелогичны
Напомним, что упрощенная формула для процентного изменения – [латекс]\frac{New\;Value-Old\;Value}{Old\;Value}[/latex], также записывается как [latex ]\frac{\Delta Value}{Старое\;Значение}[/latex].
Предположим, что объем спроса увеличился с 4 до 6 чашек кофе. При расчете процентного изменения ([латекс]\frac{\left(6-4\right)}{4}[/latex]) объем спроса увеличился на 50 %. Используя те же числа, рассмотрите, что произойдет, когда объем спроса уменьшится с 6 до 4 чашек кофе ([латекс]\frac{\left(4-6\right)}{6}[/latex]) это изменение приведет к 33 % уменьшение объема спроса.
Сразу же следует отметить, что это должно насторожить при расчете эластичности между двумя точками. Если процентное изменение зависит от направления (от А к В или от В к А), то как мы можем обеспечить постоянное значение эластичности?
Если процентное изменение зависит от направления (от А к В или от В к А), то как мы можем обеспечить постоянное значение эластичности?
Рассчитаем эластичность с обеих точек зрения:
Переход от A к B:
%ΔPrice: цена на кофе падает с 4,50 до 3,00 долларов, что означает, что процентное изменение составляет [латекс]\frac{\left( 3,00-4,50\справа)}{4,50}[/латекс] = -33%. Цена упала на 33 %.
%ΔQuantity: количество проданного кофе увеличивается с 4 до 6, что означает процентное изменение [латекс]\frac{\left(6-4\right)}{4}[/latex] = 50%. Количество увеличилось на 50%
Эластичность: [латекс]\frac{\%\Delta Quantity}{\%\Delta Price}=-\frac{50\%}{33\%}[/latex] = 1,5*
Переход от B к A:
%ΔPrice: цена на кофе повышается с 3,00 до 4,50 долл. США, что означает, что процентное изменение составляет [латекс]\frac{\left(4,50-3,00\right)}{3,00} [/латекс] = 50%. Цена выросла на 50%.
%ΔQuantity:
Количество проданного кофе падает с 6 до 4, что означает процентное изменение [латекс]\frac{\left(4-6\right)}{6}[/latex] = -33%. Количество упало на 33%
Количество упало на 33%
Эластичность: [латекс]\frac{\%\Delta Quantity}{\%\Delta Price}=\frac{33\%}{50\%}[/latex] = 0,67
Эти два расчета дают нам разные числа. Этот тип анализа сделал бы эластичность зависимой от направления, что добавило бы ненужных сложностей. Чтобы избежать этого, мы будем полагаться на средние значения.
*Обратите внимание, что эластичность является абсолютной величиной, то есть на нее не влияют положительные или отрицательные значения.
Метод средней точки
Для расчета эластичности вместо простых процентных изменений количества и цены экономисты используют среднее процентное изменение. Это называется методом средней точки эластичности и представлено следующими уравнениями:
[латекс]\begin{array}{r @{{}={}} l}\%\;изменение\;в\;количестве & \frac { { Q }_{ 2 }-{ Q }_{ 1 } }{ ({ Q }_{ 2 }+{ Q }_{ 1 })/2 } \times 100 \\[1em] \%\;изменение\;в\;цене & \frac { { P }_ { 2 }-{ P }_{ 1 } }{ ({ P }_{ 2 }+{ P }_{ 1 })/2 } \times 100 \end{array}[/latex]
Преимущество метода m id-point заключается в том, что можно получить одинаковую эластичность между двумя ценовыми точками независимо от того, происходит ли повышение или снижение цены. Это связано с тем, что знаменатель является средним, а не старым значением.
Это связано с тем, что знаменатель является средним, а не старым значением.
Использование метода средней точки для расчета эластичности между точками A и B:
[латекс]\begin{array}{r @{{}={}} l}\%\;изменение\;в\;количестве & \frac { { 6 }-{ 4 } }{ ({ 6 }+ { 4 })/2 } \times 100 \\[1em] & \frac { 2 }{ 5 } \times 100 \\[1em] & 40\% \\[1em] \%\;change\;in\ ;цена & \frac { { 3,00 }-{ 4,50 } }{ ({ 3,00 }+{ 4,50 })/2 } \times 100 \\[1em] & \frac { -1,50 }{ 3,75 } \times 100 \\ [1em] & -40\% \\[1em] Цена\;Эластичность\;спроса\;\\frac { 40\% }{ 40\% } \\[1em] & 1 \end{array}[/ латекс]
Этот метод дает нам своего рода среднюю эластичность спроса по двум точкам на нашей кривой. Обратите внимание, что наша эластичность 1 находится между эластичностями 0,67 и 1,52, которые мы рассчитали в предыдущем примере.
Формула точки-уклона
На рисунке 4.1а нам были даны две точки, и мы рассмотрели эластичность как движение по кривой. Как мы увидим в Теме 4.3, часто полезно рассматривать эластичность в одной точке. Чтобы вычислить это, мы должны вывести новое уравнение.
Чтобы вычислить это, мы должны вывести новое уравнение.
[латекс]\frac{\%\Delta Quantity}{\%\Delta Price}=эластичность[/latex]
Поскольку мы знаем, что процентное изменение цены можно переписать как
[латекс]\frac{\Delta Price}{Цена}[/latex]
и процентное изменение количества до
[латекс]\frac{\Delta Quantity}{Количество}[/latex]
, мы можем преобразовать исходное уравнение в
.[латекс]\frac{\frac{\Delta Quantity}{Количество}}{\frac{\Delta Price}{Цена}}[/latex]
это то же самое, что сказать
[латекс]\frac{\Delta Quantity\cdot Price}{\Delta Price\cdot Quantity}=\frac{\Delta Q}{\Delta P}\cdot \frac{P}{Q}[/latex]
Это дает нам нашу формулу точка-наклон . Как мы используем его для расчета эластичности в точке А? Часть P/Q нашего уравнения соответствует значениям в точке, которые составляют 4,5 и 4 доллара. ΔQ/ΔP соответствует обратному наклону кривой . Наклон возврата рассчитывается как подъем/спуск.
На рис. 4.1 наклон равен [латекс]\фрак{3-4,5}{6-4}[/латекс] = 0,75, что означает обратное соотношение 1/0,75 = 1,33. Подставив эту информацию в наше уравнение, мы получим:
[латекс]\frac{\Delta Q}{\Delta P}\cdot \frac{P}{Q}[/latex]
[латекс]1,33\cdot \frac{4,5}{4}[/латекс] = 1,5
Этот анализ дает нам эластичность как единую точку. Обратите внимание, что это дает нам то же число, что и при расчете эластичности от точки А до точки Б. Это не совпадение. Когда мы рассчитываем от точки А к точке Б, мы на самом деле просто вычисляем эластичность в точке А, поскольку мы используем значения в точке А в качестве знаменателя для нашего процентного изменения. Точно так же от точки B до точки A мы рассчитываем эластичность в точке B. Когда мы используем метод средней точки, мы просто берем среднее значение двух точек. Это подтверждает тот факт, что в каждой точке нашей линии существует разная эластичность, концепция, которая будет важна, когда мы будем обсуждать доход.
Не такой уж и другой
Несмотря на то, что средняя точка и точка-наклон кажутся довольно разными формулами, среднюю точку можно переписать, чтобы показать, насколько они похожи на самом деле.
[латекс]\frac{\frac{\Delta Q}{(Q1+Q2)/2}}{\frac{\Delta P}{(P1+P2)/2}}[/latex] = [латекс] \frac{\frac{\Delta Q}{Q1+Q2}}{\frac{\Delta P}{P1+P2}}[/latex]
Помните, что когда дробь делится на дробь, вы можете преобразовать ее в дробь, умноженную на дробь, обратную знаменателю.
= [латекс]\frac{\Delta Q}{\Delta P}\cdot \frac{\left(P1+P2\right)}{\left(Q1+Q2\right)}[/latex]
Обратите внимание, что по сравнению с точкой-наклоном: [латекс]\frac{\Delta Q}{\Delta P}\cdot \frac{P}{Q}[/latex], единственное отличие состоит в том, что точка-наклон является обратным наклона, умноженного на одну точку, тогда как средняя точка является обратной величиной наклона, умноженной на несколько точек. Это подтверждает вывод о том, что средняя точка представляет собой среднее значение.
Прочие эластичности
Помните, что эластичность — это реакция одной переменной на изменения другой переменной. Это означает, что его можно применять не только к соотношению цены и количества в нашей рыночной модели. В теме 3 мы обсуждали, как товары могут быть хуже/нормальными или замещающими/дополняющими. Мы рассмотрим это еще подробнее, когда будем знакомить с теорией потребления, а сейчас мы можем развить наше понимание, применяя то, что мы знаем об эластичностях.
Эластичность предложения по собственной цене (e
P С ) Наш анализ эластичности сосредоточен на спросе, но те же принципы применимы и к кривой предложения. В то время как эластичность спроса измеряет реакцию объема спроса на изменение цены, эластичность предложения по собственной цене измеряет реакцию объема предложения. Чем более эластична фирма, тем больше она может увеличивать производство при повышении цен и сокращать производство при падении цен. Наше уравнение выглядит следующим образом:
Наше уравнение выглядит следующим образом:
[латекс]\frac{\%\Delta Q\;Поставляется}{\%\Delta P}[/latex]
Эластичность предложения по собственной цене может быть рассчитана с использованием формулы средней точки и точки-наклона так же, как для e P D .
Перекрестная ценовая эластичность спроса (e
XP D )В то время как эластичность спроса по собственной цене измеряет реакцию количества на собственную цену товара, перекрестная эластичность спроса по цене показывает нам, как количественный спрос реагирует на изменения в цене товара.0039 сопутствующие товары . В то время как раньше мы могли игнорировать положительные и отрицательные стороны эластичности, перекрестной цены, это имеет значение. Наше уравнение выглядит следующим образом:
[латекс]\frac{\%\Delta Q\;Хорошо A}{\%\Delta P\;Хорошо B}[/latex]
Рассмотрим наше обсуждение дополнений и заменителей в теме 3. 3. Мы определили дополнения как товары, которые люди предпочитают потреблять вместе с другим товаром, и заменители как товары, которые люди предпочитают потреблять вместо другого товара. Если цена на дополнение повысится, наш спрос упадет, если цена на заменитель повысится, наш спрос повысится. Для перекрестной ценовой эластичности это означает:
3. Мы определили дополнения как товары, которые люди предпочитают потреблять вместе с другим товаром, и заменители как товары, которые люди предпочитают потреблять вместо другого товара. Если цена на дополнение повысится, наш спрос упадет, если цена на заменитель повысится, наш спрос повысится. Для перекрестной ценовой эластичности это означает:
Дополнение будет иметь отрицательную перекрестную ценовую эластичность , поскольку, если процентное изменение цены положительно, процентное изменение количества будет отрицательным, и наоборот.
Заменитель будет иметь положительную перекрестную эластичность по цене , поскольку, если процентное изменение цены положительно, процентное изменение количества будет положительным и наоборот.
Это добавляет еще одно измерение к нашему обсуждению комплементов/заменителей. Теперь мы можем прокомментировать силу связи между двумя товарами. Например, перекрестная эластичность -4 предполагает, что человек предпочитает потреблять два товара вместе, тогда как перекрестная эластичность -0,5. Это может отражать перекрестную эластичность потребителя хот-дога по отношению к кетчупу и приправам. Потребитель может сильно предпочесть есть хот-доги с кетчупом и в некоторой степени предпочесть приправы.
Это может отражать перекрестную эластичность потребителя хот-дога по отношению к кетчупу и приправам. Потребитель может сильно предпочесть есть хот-доги с кетчупом и в некоторой степени предпочесть приправы.
Эластичность спроса по доходу (e
N D )В Теме 3 мы также объяснили, как товары могут быть нормальными или некачественными в зависимости от того, как потребитель реагирует на изменение дохода. Эта отзывчивость также может быть измерена с помощью эластичности спроса по доходу . Наше уравнение выглядит следующим образом:
[латекс]\frac{\%\Delta Q}{\%\Delta Income}[/latex]
Как и в случае с перекрестной эластичностью, независимо от того, является ли наша эластичность положительной или отрицательной, мы получаем ценную информацию о том, как потребитель относится к товару:
Нормальный товар будет иметь положительную эластичность по доходу , поскольку, если процентное изменение дохода положительно, процентное изменение количества будет положительным и наоборот.
Товар низшего качества будет иметь отрицательную эластичность по доходу , поскольку, если % изменения дохода положительны, % изменения количества будут отрицательными и наоборот.
Значение нашей эластичности покажет, насколько товар реагирует на изменение дохода. Товар с эластичностью спроса по доходу 0,05, хотя технически нормальный товар (поскольку спрос увеличивается после роста дохода), не так чувствителен, как товар с эластичностью спроса по доходу 5,9.0005
Резюме
Эластичность — это мера чувствительности, вычисляемая путем деления процентного изменения одной переменной на процентное изменение другой.
Формулы средней точки и точки-наклона важны для расчета эластичности в различных ситуациях. Средняя точка дает среднее значение эластичности между двумя точками, тогда как точка-наклон дает эластичность в определенной точке. Их можно рассчитать по следующим формулам:
| Базовая формула | Средняя формула | Формула точки-уклона |
| [латекс]\frac{\%\Delta Quantity}{\%\Delta Price}[/latex] | [латекс]\frac{\Delta Q}{\Delta P}\cdot \frac{\left(P1+P2\right)}{\left(Q1+Q2\right)}[/latex] | [латекс]\frac{\Delta Q}{\Delta P}\cdot \frac{P}{Q}[/latex] |
Поскольку эластичность измеряет отзывчивость, ее также можно использовать для измерения эластичности предложения по собственной цене, перекрестной эластичности спроса по ценам и эластичности спроса по доходу. Их можно рассчитать по следующим формулам:
Их можно рассчитать по следующим формулам:
| Эластичность предложения по собственной цене | Перекрестная эластичность спроса | Эластичность спроса по доходу |
| [латекс]\frac{\%\Delta Q\;Поставляется}{\%\Delta P}[/latex] | [латекс]\frac{\%\Delta Q\;Хорошо A}{\%\Delta P\;Хорошо B}[/latex] | [латекс]\frac{\%\Delta Q}{\%\Delta Income}[/latex] |
Глоссарий
- Перекрестная эластичность спроса
- процентное изменение величины спроса на товар А в результате процентного изменения цены товара В
- Эластичность
- экономическая концепция, которая измеряет реакцию одной переменной на изменения другой переменной
- Эластичность спроса по доходу
- процентное изменение объема спроса на товар или услугу в результате процентного изменения дохода
- Эластичность спроса по собственной цене
- процентное изменение величины спроса на товар или услугу, деленное на процентное изменение цены
- Метод средней точки
- Включает умножение обратной величины наклона на значения одной точки.

- Эластичность предложения по собственной цене
- процентное изменение объема поставки, деленное на процентное изменение цены
- Метод наклона точки
- Метод расчета эластичности между двумя точками. Включает расчет процентного изменения цены и количества по отношению к среднему значению двух точек.
Упражнения 4.1
1. Используйте приведенную ниже диаграмму кривой спроса, чтобы ответить на следующий вопрос.
Какова эластичность спроса по собственной цене при повышении цены с 2 до 4 долларов за единицу? Используйте в своих расчетах формулу средней точки.
а) 1/3.
б) 6/10.
в) 2/3.
г) Ничего из вышеперечисленного.
2. Предположим, что увеличение цены на 2% приводит к уменьшению объема спроса на 6%. Эластичность спроса по собственной цене равна:
а) 1/3.
б) 6.
в) 2
г) 3.
3. Если эластичность спроса по собственной цене равна 0,3 по абсолютной величине, то какой процент изменения цены приведет к уменьшению количества на 6% потребовал?
а) 3%
б) 6%
в) 20%.
г) 50%.
4. Предположим, вам сказали, что эластичность предложения по собственной цене равна 0,5. Что из следующего является правильной интерпретацией этого числа?
а) Повышение цены на 1% приведет к увеличению объема предложения на 50%.
б) Повышение цены на 1% приведет к увеличению объема предложения на 5%.
c) Увеличение цены на 1% приведет к увеличению объема предложения на 2%.
d) Увеличение цены на 1% приведет к увеличению объема предложения на 0,5%.
5. Предположим, что увеличение цены на 10 приводит к 50-процентному уменьшению объема спроса. Чему равна (абсолютная величина) собственная ценовая эластичность спроса?
а) 0,5.
б) 0,2.
c) 5.
d) 10.
6. Если товары X и Y являются ЗАМЕНЯЮЩИМИ, то что из следующего может быть значением перекрестной ценовой эластичности спроса на товар Y?
а) -1.
б)-2.
в) Ни а), ни б).
d) Как а), так и б).
7 . Если пицца является нормальным товаром, то что из следующего может быть значением эластичности спроса по доходу?
а) 0.2.
б) 0,8.
в) 1.4
г) Все вышеперечисленное.
8. Если товары X и Y являются ДОПОЛНИТЕЛЬНЫМИ, что из следующего может быть значением перекрестной ценовой эластичности спроса?
а) 0.
б) 1.
в) -1.
г) Все вышеперечисленное может быть величиной перекрестной ценовой эластичности спроса.
5.1 Эластичность спроса по цене – принципы экономики
Цели обучения
- Объяснить концепцию эластичности спроса по цене и ее расчет.

- Объясните, что означает неэластичность спроса по цене, эластичность по цене за единицу товара, эластичность по цене, совершенно неэластичность по цене и совершенно эластичность по цене.
- Объясните, как и почему значение ценовой эластичности спроса изменяется вдоль линейной кривой спроса.
- Понять взаимосвязь между общим доходом и ценовой эластичностью спроса.
- Обсудите детерминанты ценовой эластичности спроса.
Из закона спроса мы знаем, как величина спроса отреагирует на изменение цены: она изменится в противоположном направлении. Но насколько сильно изменит? Кажется разумным ожидать, например, что 10-процентное изменение цены, взимаемой за визит к врачу, приведет к другому процентному изменению величины спроса, чем 10-процентное изменение цены Ford Mustang. Но насколько велика эта разница?
Чтобы показать, насколько величина спроса реагирует на изменение цены, мы применяем понятие эластичности. Ценовая эластичность спроса на товар или услугу, e D , представляет собой процентное изменение количества спроса на конкретный товар или услугу, деленное на процентное изменение цены этого товара или услуги, при прочих равных условиях. Таким образом, мы можем написать
Таким образом, мы можем написать
Уравнение 5.2
[latex]e_D = \frac{\%\изменение\в\количество\спрос }{\%\изменение\в\цена}[/latex]
Поскольку эластичность спроса по цене показывает реакцию объема спроса на изменение цены, при условии, что другие факторы, влияющие на спрос, неизменны, она отражает движение вдоль кривой спроса. При нисходящей кривой спроса цена и объем спроса движутся в противоположных направлениях, поэтому эластичность спроса по цене всегда отрицательна. Положительное процентное изменение цены предполагает отрицательное процентное изменение величины спроса, и наоборот. Иногда вы увидите абсолютное значение показателя ценовой эластичности. В сущности, знак «минус» игнорируется, так как ожидается, что будет отрицательная (обратная) связь между величиной спроса и ценой. Однако в этом тексте мы сохраним знак «минус» в описании ценовой эластичности спроса и будем говорить «абсолютное значение ценовой эластичности спроса», когда мы описываем именно это.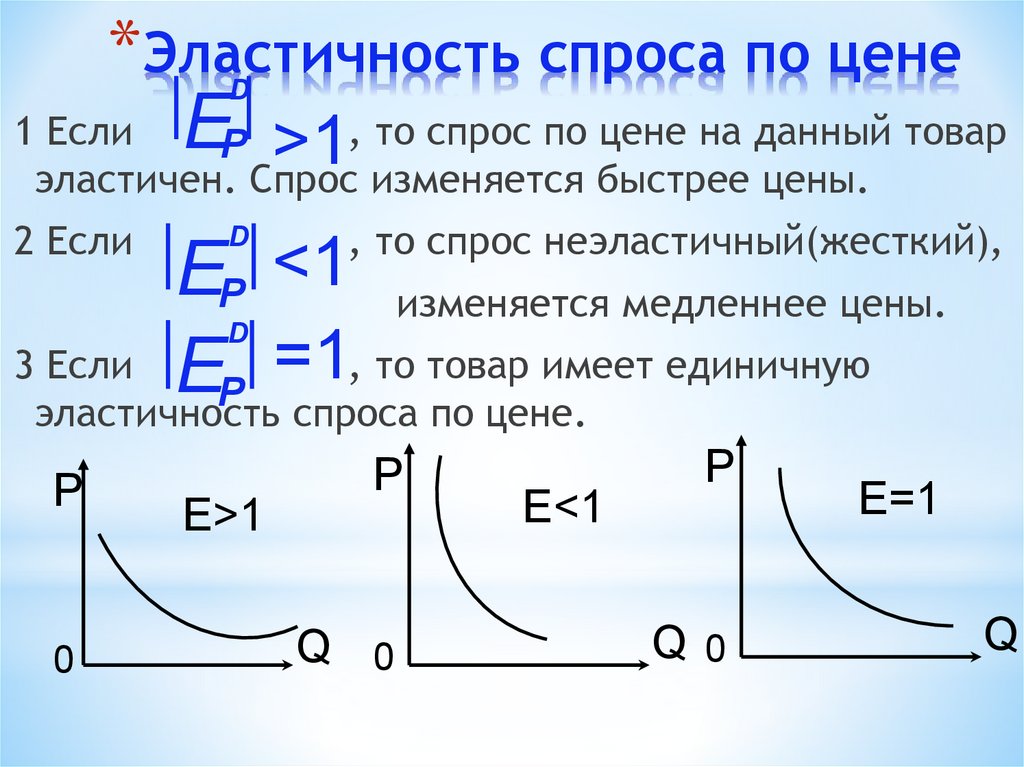
Внимание!
Будьте осторожны, не путайте эластичность с уклоном. Наклон линии — это изменение значения переменной по вертикальной оси, деленное на изменение значения переменной по горизонтальной оси между двумя точками. Эластичность – это отношение процентных изменений. Наклон кривой спроса, например, представляет собой отношение изменения цены к изменению количества между двумя точками кривой. Эластичность спроса по цене – это отношение процентного изменения количества товара к процентному изменению цены. Как мы увидим, при расчете эластичности в разных точках линейной кривой спроса наклон остается постоянным, то есть не меняется, но значение эластичности будет меняться.
Вычисление эластичности спроса по цене
Чтобы найти эластичность спроса по цене, необходимо сначала вычислить процентные изменения цены и величины спроса. Мы рассчитываем эти изменения между двумя точками на кривой спроса.
На рис. 5.1 «Реагирование и спрос» показана конкретная кривая спроса, линейная кривая спроса на поездки в общественном транспорте. Предположим, что начальная цена составляет 0,80 доллара США, а объем спроса составляет 40 000 поездок в день; мы находимся в точке А на кривой. Теперь предположим, что цена падает до 0,70 долл., и мы хотим сообщить об ответной реакции величины спроса. Мы видим, что при новой цене объем спроса возрастает до 60 000 поездок в день (точка B). Чтобы вычислить эластичность, нам нужно рассчитать процентное изменение цены и объема спроса между точками А и В.
Предположим, что начальная цена составляет 0,80 доллара США, а объем спроса составляет 40 000 поездок в день; мы находимся в точке А на кривой. Теперь предположим, что цена падает до 0,70 долл., и мы хотим сообщить об ответной реакции величины спроса. Мы видим, что при новой цене объем спроса возрастает до 60 000 поездок в день (точка B). Чтобы вычислить эластичность, нам нужно рассчитать процентное изменение цены и объема спроса между точками А и В.
Рисунок 5.1 Реакция и спрос
Кривая спроса показывает, как изменения цены приводят к изменениям величины спроса. Движение из точки А в точку Б показывает, что снижение цены на 0,10 доллара увеличивает количество поездок в день на 20 000. Движение от B к A означает увеличение цены на 0,10 доллара, что снижает спрос на 20 000 поездок в день.
Мы измеряем процентное изменение между двумя точками как изменение переменной, деленное на среднее значение переменной между двумя точками. Таким образом, процентное изменение количества между точками А и В на рис. 5.1 «Отзывчивость и спрос» вычисляется относительно средних значений количества в точках А и В: (60 000 + 40 000)/2 = 50 000. Таким образом, процентное изменение количества составляет 20 000/50 000, или 40%. Точно так же процентное изменение цены между точками A и B основано на среднем двух цен: (0,80 долл. + 0,70 долл.)/2 = 0,75 долл., поэтому процентное изменение составляет −0,10/0,75, или −13,33. %. Ценовая эластичность спроса между точками A и B, таким образом, составляет 40% / (-13,33%) = -3,00.
5.1 «Отзывчивость и спрос» вычисляется относительно средних значений количества в точках А и В: (60 000 + 40 000)/2 = 50 000. Таким образом, процентное изменение количества составляет 20 000/50 000, или 40%. Точно так же процентное изменение цены между точками A и B основано на среднем двух цен: (0,80 долл. + 0,70 долл.)/2 = 0,75 долл., поэтому процентное изменение составляет −0,10/0,75, или −13,33. %. Ценовая эластичность спроса между точками A и B, таким образом, составляет 40% / (-13,33%) = -3,00.
Эта мера эластичности, основанная на процентных изменениях относительно среднего значения каждой переменной между двумя точками, называется дуговой эластичностью. Метод дуговой эластичности имеет то преимущество, что он дает одинаковую эластичность независимо от того, идем ли мы из точки А в точку В или из точки В в точку А. Именно этот метод мы будем использовать для вычисления эластичности.
Для метода дуговой эластичности мы рассчитываем ценовую эластичность спроса, используя среднее значение цены, $$ \bar{P} $$ , и среднее значение объема спроса, $$ \bar{Q} $$. Мы будем использовать греческую букву Δ для обозначения «изменения», поэтому изменение количества между двумя точками равно Δ Q и изменение цены Δ P . Теперь мы можем записать формулу ценовой эластичности спроса как
Мы будем использовать греческую букву Δ для обозначения «изменения», поэтому изменение количества между двумя точками равно Δ Q и изменение цены Δ P . Теперь мы можем записать формулу ценовой эластичности спроса как
Уравнение 5.3
[латекс] \ displaystyle e_D = \ frac {\ Delta Q / \ bar {Q}} {\ Delta P / \ bar {P}} [/latex]
Ценовая эластичность спроса между точками A и B равна: ( \$ 0,80 + \$ 0,70)/2}} = \frac{40 \% }{-13,33 \% } = -3,00[/latex]
С формулой упругости дуги эластичность одинакова, независимо от того, двигаемся ли мы из точки A в точку B или из точки B в точку A. Если мы начнем с точки B и перейдем к точке A, мы получим:
[латекс]e_D = \frac{\frac{-20 000}{(60 000+40 000)/2}}{\frac{ \$ 0,10}{( \$ 0,80 + \$ 0,70)/2}} = \ frac{-40 \% }{13,33 \% } = -3,00[/latex]
Метод дуговой эластичности дает нам оценку эластичности. Он дает значение эластичности в средней точке в диапазоне изменений, таких как движение между точками A и B. Для точного расчета эластичности нам нужно будет рассмотреть реакцию зависимой переменной на чрезвычайно небольшое изменение в независимая переменная. Тот факт, что эластичности дуг являются приблизительными, предполагает важное практическое правило при расчете эластичностей дуг: мы должны учитывать только небольшие изменения независимых переменных. Мы не можем применить концепцию упругости дуги к большим изменениям.
Для точного расчета эластичности нам нужно будет рассмотреть реакцию зависимой переменной на чрезвычайно небольшое изменение в независимая переменная. Тот факт, что эластичности дуг являются приблизительными, предполагает важное практическое правило при расчете эластичностей дуг: мы должны учитывать только небольшие изменения независимых переменных. Мы не можем применить концепцию упругости дуги к большим изменениям.
Еще один аргумент в пользу учета лишь небольших изменений при расчете эластичности спроса по цене станет очевидным в следующем разделе. Мы исследуем, что происходит с ценовой эластичностью при движении от одной точки к другой вдоль линейной кривой спроса.
Внимание!
Обратите внимание, что в формуле дуговой эластичности метод вычисления процентного изменения отличается от стандартного метода, с которым вы, возможно, знакомы. Этот метод измеряет процентное изменение переменной относительно ее исходного значения. Например, используя стандартный метод, когда мы идем из точки А в точку Б, мы вычисляем процентное изменение количества как 20 000/40 000 = 50%. Процентное изменение цены составит -0,10 долл. США/0,80 долл. США = -12,5%. Ценовая эластичность спроса тогда будет 50% / (-12,5%) = -4,00. Однако переход из точки В в точку А даст другую эластичность. Процентное изменение количества составит -20 000/60 000, или -33,33%. Процентное изменение цены составит 0,10 долл. США/0,70 долл. США = 14,29.%. Таким образом, эластичность спроса по цене составит -33,33% / 14,29% = -2,33. Используя среднее количество и среднюю цену для расчета процентных изменений, подход дуговой эластичности позволяет избежать необходимости указывать направление изменения и, таким образом, дает нам один и тот же ответ, независимо от того, идем ли мы от А к В или от В к А.
Процентное изменение цены составит -0,10 долл. США/0,80 долл. США = -12,5%. Ценовая эластичность спроса тогда будет 50% / (-12,5%) = -4,00. Однако переход из точки В в точку А даст другую эластичность. Процентное изменение количества составит -20 000/60 000, или -33,33%. Процентное изменение цены составит 0,10 долл. США/0,70 долл. США = 14,29.%. Таким образом, эластичность спроса по цене составит -33,33% / 14,29% = -2,33. Используя среднее количество и среднюю цену для расчета процентных изменений, подход дуговой эластичности позволяет избежать необходимости указывать направление изменения и, таким образом, дает нам один и тот же ответ, независимо от того, идем ли мы от А к В или от В к А.
Ценовая эластичность вдоль линейной кривой спроса
Что происходит с ценовой эластичностью спроса, когда мы перемещаемся вдоль кривой спроса? Ответ зависит от характера самой кривой спроса. На линейной кривой спроса, такой как на рис. 5.2 «Эластичность спроса по цене для линейной кривой спроса», эластичность становится меньше (в абсолютном значении) по мере движения вниз и вправо.
Рис. 5.2 Ценовая эластичность спроса для линейной кривой спроса
Ценовая эластичность спроса изменяется между различными парами точек на линейной кривой спроса. Чем ниже цена и чем больше объем спроса, тем меньше абсолютное значение ценовой эластичности спроса.
На рис. 5.2 «Эластичность спроса по цене для линейной кривой спроса» показана та же кривая спроса, которую мы видели на рис. 5.1 «Реакция и спрос». Мы уже рассчитали ценовую эластичность спроса между точками А и В; он равен −3,00. Обратите внимание, однако, что когда мы используем тот же метод для вычисления ценовой эластичности спроса между другими наборами точек, наш ответ меняется. Для каждой из показанных пар точек изменения цены и объема спроса одинаковы (снижение цены на 0,10 доллара и 20 000 дополнительных поездок в день соответственно). Но при высоких ценах и низких количествах в верхней части кривой спроса процентное изменение количества относительно велико, тогда как процентное изменение цены относительно невелико. Таким образом, абсолютная величина ценовой эластичности спроса относительно велика. По мере продвижения вниз по кривой спроса одинаковые изменения количества представляют все меньшие и меньшие процентные изменения, в то время как равные изменения цены представляют все большие и большие процентные изменения, а абсолютное значение показателя эластичности снижается. Например, между точками C и D эластичность спроса по цене составляет -1,00, а между точками E и F эластичность спроса по цене составляет -0,33.
Таким образом, абсолютная величина ценовой эластичности спроса относительно велика. По мере продвижения вниз по кривой спроса одинаковые изменения количества представляют все меньшие и меньшие процентные изменения, в то время как равные изменения цены представляют все большие и большие процентные изменения, а абсолютное значение показателя эластичности снижается. Например, между точками C и D эластичность спроса по цене составляет -1,00, а между точками E и F эластичность спроса по цене составляет -0,33.
На линейной кривой спроса ценовая эластичность спроса меняется в зависимости от интервала, в котором мы ее измеряем. Для любой линейной кривой спроса абсолютное значение ценовой эластичности спроса будет падать по мере нашего движения вниз и вправо по кривой.
Ценовая эластичность спроса и изменения общего дохода
Предположим, что управление общественного транспорта рассматривает вопрос о повышении платы за проезд. Будет ли его общий доход расти или падать? Общий доход – это цена за единицу, умноженная на количество проданных единиц 1 . В этом случае стоимость проезда умножается на количество пассажиров. Транзитное управление, безусловно, захочет знать, приведет ли повышение цены к увеличению или падению его общего дохода. На самом деле определение влияния изменения цены на общий доход имеет решающее значение для анализа многих проблем в экономике.
В этом случае стоимость проезда умножается на количество пассажиров. Транзитное управление, безусловно, захочет знать, приведет ли повышение цены к увеличению или падению его общего дохода. На самом деле определение влияния изменения цены на общий доход имеет решающее значение для анализа многих проблем в экономике.
Мы проведем два быстрых вычисления, прежде чем обобщим применяемый принцип. Учитывая кривую спроса, показанную на рисунке 5.2 «Эластичность спроса по цене для линейной кривой спроса», мы видим, что при цене 0,80 доллара транспортное управление будет продавать 40 000 поездок в день. Общий доход составит 32 000 долларов в день (0,80 доллара умножить на 40 000). Если бы цена была снижена на 0,10 доллара до 0,70 доллара, объем спроса увеличился бы до 60 000 поездок, а общий доход увеличился бы до 42 000 долларов (0,70 доллара умножить на 60 000). Снижение стоимости проезда увеличивает общий доход на . Однако, если первоначальная цена составляла 0,30 доллара, а администрация транзита снизила ее на 0,10 доллара до 0,20 доллара, общий доход уменьшился бы с 42 000 долларов (0,30 доллара умножить на 140 000) до 32 000 долларов (0,20 доллара умножить на 160 000). Таким образом, оказывается, что влияние изменения цены на общий доход зависит от начальной цены и, как следствие, исходной эластичности. Мы обобщаем этот пункт в оставшейся части этого раздела.
Таким образом, оказывается, что влияние изменения цены на общий доход зависит от начальной цены и, как следствие, исходной эластичности. Мы обобщаем этот пункт в оставшейся части этого раздела.
Проблема при оценке влияния изменения цены на общий доход от товара или услуги заключается в том, что изменение цены всегда изменяет величину спроса в противоположном направлении. Повышение цены уменьшает объем спроса, а снижение цены увеличивает объем спроса. Вопрос в том, сколько. Поскольку общий доход определяется путем умножения цены за единицу товара на величину спроса, неясно, приведет ли изменение цены к увеличению или падению общего дохода.
Мы уже говорили об этом в контексте управления транзитом. Рассмотрим следующие три примера роста цен на бензин, пиццу и диетическую колу.
Предположим, что требуется 1000 галлонов бензина в день по цене 4 доллара за галлон. Таким образом, общий доход от бензина составляет 4000 долларов в день (= 1000 галлонов в день, умноженных на 4 доллара за галлон). Если увеличение цены на бензин до 4,25 доллара снижает объем спроса до 950 галлонов в день, общий доход возрастает до 4037,50 доллара в день (=9).50 галлонов в день умножить на 4,25 доллара за галлон). Несмотря на то, что люди потребляют меньше бензина по цене 4,25 доллара, чем по цене 4 доллара, общий доход увеличивается, потому что более высокая цена более чем компенсирует падение потребления.
Если увеличение цены на бензин до 4,25 доллара снижает объем спроса до 950 галлонов в день, общий доход возрастает до 4037,50 доллара в день (=9).50 галлонов в день умножить на 4,25 доллара за галлон). Несмотря на то, что люди потребляют меньше бензина по цене 4,25 доллара, чем по цене 4 доллара, общий доход увеличивается, потому что более высокая цена более чем компенсирует падение потребления.
Далее рассмотрим пиццу. Предположим, требуется 1000 пицц в неделю по цене 9 долларов за пиццу. Общий доход от пиццы составляет 9 000 долларов в неделю (= 1 000 пицц в неделю умножить на 9 долларов за пиццу). Если увеличение цены на пиццу до 10 долларов за пиццу уменьшит объем спроса до 900 пицц в неделю, общий доход по-прежнему будет составлять 9 долларов.000 в неделю (=900 пицц в неделю умножить на 10 долларов за пиццу). Опять же, когда цена растет, потребители покупают меньше, но на этот раз общий доход не меняется.
Теперь рассмотрим диетическую колу. Предположим, требуется 1000 банок диетической колы в день по цене 0,50 доллара за банку. Общий доход от диетической колы составляет 500 долларов в день (= 1000 банок в день умножить на 0,50 доллара за банку). Если повышение цены на диетическую колу до 0,55 доллара за банку снижает объем спроса до 880 банок в месяц, общий доход от диетической колы упадет до 484 долларов в день (= 880 банок в день умножить на 0,55 доллара за банку). Как и в случае с бензином, люди будут покупать меньше диетической колы, когда цена вырастет с 0,50 до 0,55 доллара, но в этом примере общий доход падает.
Общий доход от диетической колы составляет 500 долларов в день (= 1000 банок в день умножить на 0,50 доллара за банку). Если повышение цены на диетическую колу до 0,55 доллара за банку снижает объем спроса до 880 банок в месяц, общий доход от диетической колы упадет до 484 долларов в день (= 880 банок в день умножить на 0,55 доллара за банку). Как и в случае с бензином, люди будут покупать меньше диетической колы, когда цена вырастет с 0,50 до 0,55 доллара, но в этом примере общий доход падает.
В нашем первом примере увеличение цены увеличило общий доход. Во втором случае повышение цен оставило общий доход без изменений. В третьем примере рост цен уменьшил общую выручку. Есть ли способ предсказать, как изменение цены повлияет на общий доход? Есть; эффект зависит от ценовой эластичности спроса.
Эластичный, единично эластичный и неэластичный спрос
Чтобы определить, как изменение цены повлияет на общий доход, экономисты распределяют эластичность спроса по цене по трем категориям на основе их абсолютного значения. Если абсолютное значение эластичности спроса по цене больше 1, спрос называется эластичным по цене. Если он равен 1, спрос эластичен по цене за единицу товара. А если он меньше 1, то спрос неэластичен по цене.
Если абсолютное значение эластичности спроса по цене больше 1, спрос называется эластичным по цене. Если он равен 1, спрос эластичен по цене за единицу товара. А если он меньше 1, то спрос неэластичен по цене.
Связь эластичности с изменениями общего дохода
Когда цена товара или услуги изменяется, объем спроса изменяется в противоположном направлении. Общий доход будет двигаться в направлении переменной, которая изменяется на больший процент. Если переменные изменяются на один и тот же процент, общий доход остается прежним. Если объем спроса изменяется на больший процент, чем цена (т. е. если спрос эластичен по цене), общий доход будет изменяться в направлении изменения количества. Если цена изменяется на больший процент, чем величина спроса (т. е. если спрос неэластичен по цене), общий доход будет двигаться в направлении изменения цены. Если цена и объем спроса изменяются на один и тот же процент (т. е. если спрос эластичен по цене за единицу), то общий доход не меняется.
Когда спрос неэластичен по цене, заданное процентное изменение цены приводит к меньшему процентному изменению величины спроса. Это означает, что общий доход будет двигаться в направлении изменения цены: снижение цены уменьшит общий доход, а повышение цены увеличит его.
Рассмотрим ценовую эластичность спроса на бензин. В приведенном выше примере каждый день покупалось 1000 галлонов бензина по цене 4 доллара за галлон; повышение цены до 4,25 доллара за галлон уменьшило спрос до 950 галлонов в день. Таким образом, у нас было среднее количество 975 галлонов в день и средняя цена 4,125 доллара. Таким образом, мы можем рассчитать дуговую эластичность спроса на бензин по цене:
| Процентное изменение количества спроса = -50/975 = -5,1% |
| Процентное изменение цены = 0,25/4,125 = 6,06% |
| Ценовая эластичность спроса = -5,1%/6,06% = -0,084 |
Спрос на бензин неэластичен по цене, и общий доход движется в направлении изменения цены. Когда цена растет, общая выручка увеличивается. Напомним, что в нашем примере выше общие расходы на бензин (которые равны общей выручке продавцов) выросли с 4000 долларов в день (= 1000 галлонов в день, умноженных на 4,00 доллара) до 4037,50 долларов в день (= 9).50 галлонов в день умножить на 4,25 доллара за галлон).
Когда цена растет, общая выручка увеличивается. Напомним, что в нашем примере выше общие расходы на бензин (которые равны общей выручке продавцов) выросли с 4000 долларов в день (= 1000 галлонов в день, умноженных на 4,00 доллара) до 4037,50 долларов в день (= 9).50 галлонов в день умножить на 4,25 доллара за галлон).
Когда спрос неэластичен по цене, заданное процентное изменение цены приводит к меньшему процентному изменению величины спроса. Это означает, что общий доход будет двигаться в направлении изменения цены: повышение цены увеличит общий доход, а снижение цены уменьшит его.
Рассмотрим снова пример пиццы, который мы рассмотрели выше. При цене 9 долларов за пиццу требовалось 1000 пицц в неделю. Общий доход составил 9 долларов США.000 в неделю (= 1000 пицц в неделю умножить на 9 долларов за пиццу). Когда цена поднялась до 10 долларов, объем спроса упал до 900 пицц в неделю. Общий доход остался на уровне $9000 в неделю (=900 пицц в неделю умножить на $10 за пиццу).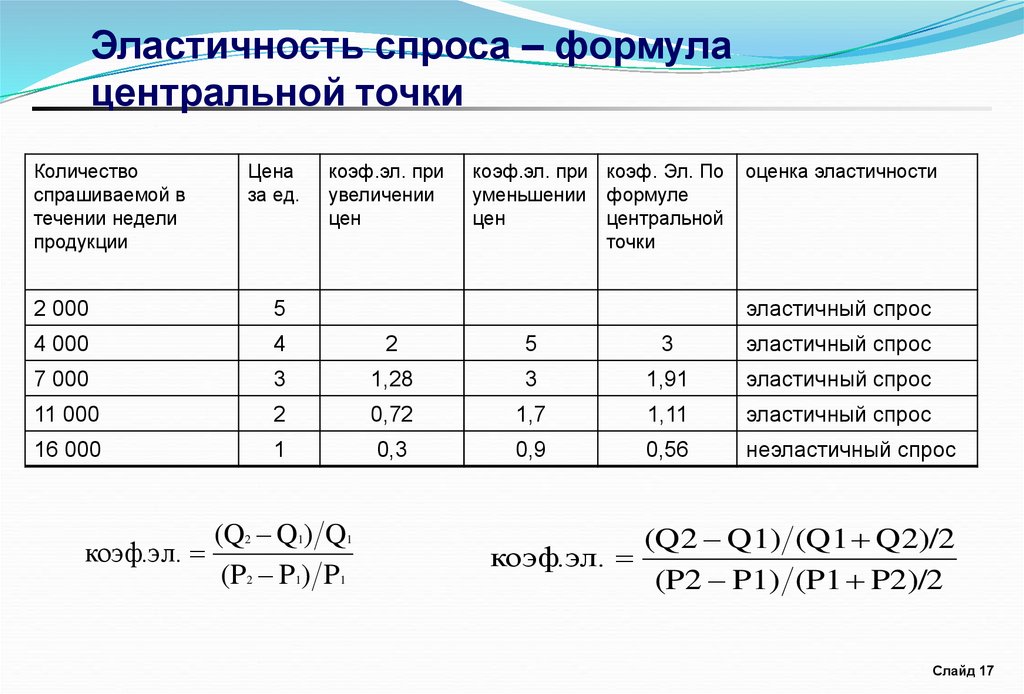 Опять же, у нас есть среднее количество 950 пицц в неделю и средняя цена 9,50 долларов. Используя метод упругости дуги, мы можем вычислить:
Опять же, у нас есть среднее количество 950 пицц в неделю и средняя цена 9,50 долларов. Используя метод упругости дуги, мы можем вычислить:
Процентное изменение требуемого количества = -100/950 = -10,5% |
Процентное изменение цены = 1,00 долл. США/9,50 долл. США = 10,5% |
Ценовая эластичность спроса = -10,5%/10,5% = -1,0 |
Спрос эластичен по цене за единицу, а общий доход остается неизменным. Объем спроса падает на тот же процент, на который увеличивается цена.
Рассмотрим следующий пример спроса на диетическую колу. По цене 0,50 доллара за банку каждый день покупали 1000 банок диетической колы. Таким образом, общий доход составил 500 долларов в день (= 0,50 доллара за банку, умноженное на 1000 банок в день). Повышение цены до 0,55 доллара снизило спрос до 880 банок в день. Таким образом, мы имеем среднее количество 940 банок в день по средней цене 0,525 доллара за банку. Вычисляя ценовую эластичность спроса на диетическую колу в этом примере, мы имеем:
Вычисляя ценовую эластичность спроса на диетическую колу в этом примере, мы имеем:
Процентное изменение требуемого количества = -120/940 = -12,8% |
Процентное изменение цены = 0,05 долл. США/0,525 долл. США = 9,5% |
Ценовая эластичность спроса = -12,8%/90,5% = -1,3 |
Спрос на диетическую колу эластичен по цене, поэтому общий доход движется в направлении изменения количества. Он падает с 500 долларов в день до повышения цен до 484 долларов в день после повышения цен.
Кривая спроса также может использоваться для отображения изменений общего дохода. На рис. 5.3 «Изменения общего дохода и линейная кривая спроса» показана кривая спроса из рис. 5.1 «Реагирование и спрос» и рис. 5.2 «Эластичность спроса по цене для линейной кривой спроса». В точке A общий доход от поездок на общественном транспорте определяется площадью прямоугольника, нарисованного с точкой A в верхнем правом углу и началом в нижнем левом углу. Высота прямоугольника — цена; его ширина — это количество. Мы уже видели, что общий доход в точке А составляет 32 000 долларов (0,80 доллара × 40 000). Когда мы снижаем цену и перемещаемся в точку B, прямоугольник, показывающий общий доход, становится короче и шире. Обратите внимание, что площадь, полученная при переходе к прямоугольнику в точке B, больше, чем потерянная площадь; общий доход возрастает до 42 000 долларов (0,70 доллара × 60 000). Напомним, что на рис. 5.2 «Эластичность спроса по цене для линейной кривой спроса» показано, что спрос эластичен между точками А и В. В общем случае спрос эластичен в верхней половине любой линейной кривой спроса, поэтому общий доход движется в направлении изменение количества.
Высота прямоугольника — цена; его ширина — это количество. Мы уже видели, что общий доход в точке А составляет 32 000 долларов (0,80 доллара × 40 000). Когда мы снижаем цену и перемещаемся в точку B, прямоугольник, показывающий общий доход, становится короче и шире. Обратите внимание, что площадь, полученная при переходе к прямоугольнику в точке B, больше, чем потерянная площадь; общий доход возрастает до 42 000 долларов (0,70 доллара × 60 000). Напомним, что на рис. 5.2 «Эластичность спроса по цене для линейной кривой спроса» показано, что спрос эластичен между точками А и В. В общем случае спрос эластичен в верхней половине любой линейной кривой спроса, поэтому общий доход движется в направлении изменение количества.
Рисунок 5.3. Изменения общего дохода и линейная кривая спроса
Перемещение из точки А в точку В подразумевает снижение цены и увеличение объема спроса. Между этими двумя точками спрос эластичен. Общий доход, показанный площадями прямоугольников, проведенных из точек А и В к началу координат, увеличивается. Когда мы перемещаемся из точки E в точку F, которая находится в неэластичной области кривой спроса, общий доход падает.
Когда мы перемещаемся из точки E в точку F, которая находится в неэластичной области кривой спроса, общий доход падает.
Движение из точки E в точку F также показывает снижение цены и увеличение количества спроса. Однако на этот раз мы находимся в неэластичной области кривой спроса. Общая выручка теперь движется в направлении изменения цены — она падает. Обратите внимание, что прямоугольник, проведенный из точки F, меньше по площади, чем прямоугольник, проведенный из точки E, что еще раз подтверждает наш предыдущий расчет.
Рисунок 5.4
Мы отметили, что линейная кривая спроса более эластична, когда цены относительно высоки, а объемы относительно низки, и менее эластична, когда цены относительно низки, а объемы относительно велики. Мы можем быть еще более конкретными. Для любой линейной кривой спроса спрос будет эластичен по цене в верхней половине кривой и неэластичен по цене в нижней половине. В средней точке линейной кривой спроса спрос эластичен по цене за единицу товара.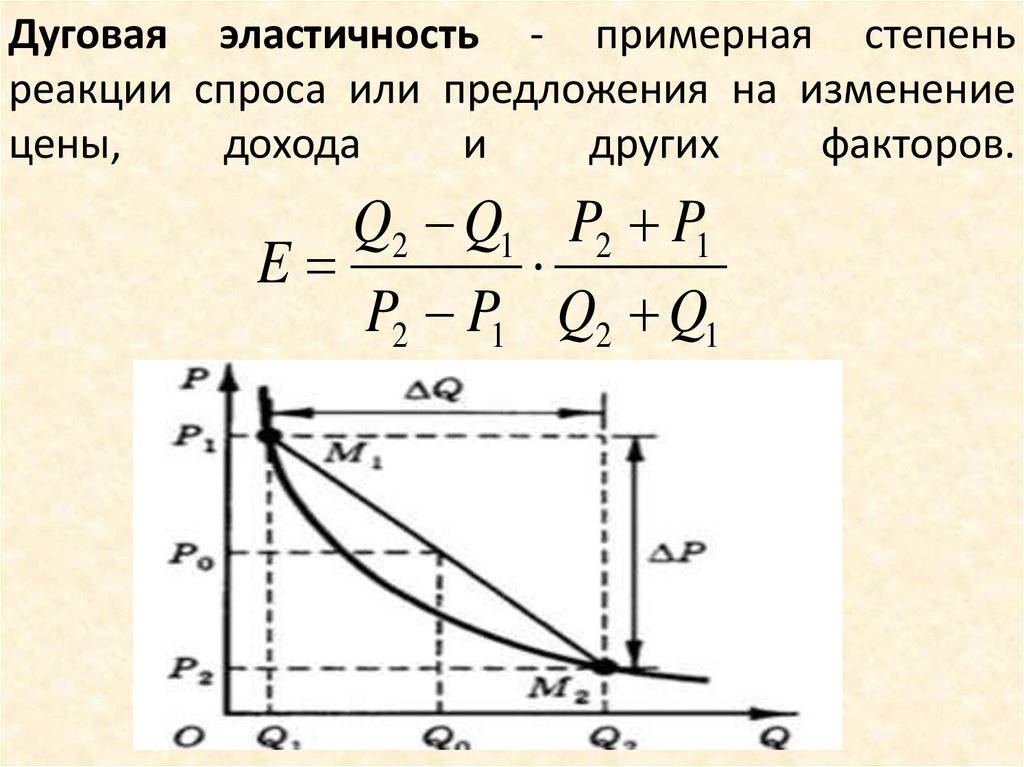
Эластичность кривых спроса по цене
На рисунке 5.5 «Кривые спроса с эластичностью спроса по постоянной цене» показаны четыре кривые спроса, на которых эластичность спроса по цене одинакова во всех точках. Кривая спроса на графике (а) вертикальна. Это означает, что изменение цены не влияет на величину спроса. Числитель формулы, приведенной в уравнении 5.2 для ценовой эластичности спроса (процентное изменение величины спроса), равен нулю. Следовательно, ценовая эластичность спроса в этом случае равна нулю, и говорят, что кривая спроса совершенно неэластична. Это теоретически крайний случай, и никакие товары, изученные эмпирически, точно не соответствуют ему. Товаром, который приближается, по крайней мере, в определенном ценовом диапазоне, является инсулин. Диабетик не будет потреблять больше инсулина, когда его цена упадет, но в некотором ценовом диапазоне будет потреблять количество, необходимое для контроля болезни.
Рисунок 5.5 Кривые спроса с эластичностью по постоянной цене
Кривая спроса на рисунке (a) абсолютно неэластична. Кривая спроса на графике (b) абсолютно эластична. Эластичность спроса по цене составляет -1,00 на всем протяжении кривой спроса на графике (c), тогда как она составляет -0,50 на всем протяжении кривой спроса на графике (d).
Кривая спроса на графике (b) абсолютно эластична. Эластичность спроса по цене составляет -1,00 на всем протяжении кривой спроса на графике (c), тогда как она составляет -0,50 на всем протяжении кривой спроса на графике (d).
Как показано на рис. 5.5 «Кривые спроса с эластичностью по постоянной цене», несколько других типов кривых спроса имеют одинаковую эластичность в каждой точке на них. Кривая спроса на графике (b) горизонтальна. Это означает, что даже самые незначительные изменения цен оказывают огромное влияние на величину спроса. Знаменатель формулы, приведенной в уравнении 5.2 для ценовой эластичности спроса (процентное изменение цены), приближается к нулю. Таким образом, ценовая эластичность спроса в этом случае бесконечна, и говорят, что кривая спроса абсолютно эластична. Это тип кривой спроса, с которой сталкиваются производители стандартизированных продуктов, таких как пшеница. Если пшеница других ферм продается по 4 доллара за бушель, типичная ферма может продать столько пшеницы, сколько захочет, по 4 доллара, но ничего по более высокой цене, и у нее не будет причин предлагать свою пшеницу по более низкой цене.
Нелинейные кривые спроса на рисунках (c) и (d) имеют отрицательную ценовую эластичность спроса; но, в отличие от линейной кривой спроса, рассмотренной выше, значение ценовой эластичности постоянно на всем протяжении каждой кривой спроса. Кривая спроса на графике (c) имеет ценовую эластичность спроса, равную −1,00 во всем диапазоне; на панели (d) ценовая эластичность спроса равна -0,50 во всем диапазоне. Эмпирические оценки спроса часто показывают кривые, подобные кривым на рисунках (c) и (d), которые имеют одинаковую эластичность в каждой точке кривой.
Внимание!
Не путайте неэластичный по цене спрос и совершенно неэластичный спрос. Совершенно неэластичный спрос означает, что изменение количества равно нулю при любом процентном изменении цены; кривая спроса в этом случае вертикальна. Неэластичный спрос по цене означает только то, что процентное изменение количества меньше, чем процентное изменение цены, а не то, что изменение количества равно нулю. При неэластичном по цене (в отличие от совершенно неэластичного) спросе сама кривая спроса по-прежнему имеет нисходящий наклон.
Детерминанты эластичности спроса по цене
Чем больше абсолютное значение эластичности спроса по цене, тем больше реакция величины спроса на изменение цены. Что определяет, является ли спрос более или менее эластичным по цене? Наиболее важными факторами, определяющими ценовую эластичность спроса на товар или услугу, являются наличие заменителей, важность статьи в бюджете домохозяйства и время.
Наличие заменителей
Ценовая эластичность спроса на товар или услугу будет больше по абсолютной величине, если для них доступно много близких заменителей. Если существует множество заменителей определенного товара или услуги, то потребители легко переключаются на эти заменители, когда цена на этот товар или услугу повышается. Предположим, например, что цены на автомобили Ford растут. Есть много близких заменителей Ford — Chevrolet, Chrysler, Toyota и так далее. Доступность близких заменителей обычно делает спрос на автомобили Ford более эластичным по цене.
Если у товара нет близких заменителей, спрос на него, вероятно, будет менее эластичен по цене. Например, нет близких заменителей бензина. Ценовая эластичность спроса на бензин в среднесрочной перспективе, скажем, в три-девять месяцев обычно оценивается примерно в -0,5. Поскольку абсолютное значение ценовой эластичности меньше 1, это ценовая неэластичность. Однако мы ожидаем, что спрос на конкретную марку бензина будет гораздо более эластичен по цене, чем спрос на бензин в целом.
Например, нет близких заменителей бензина. Ценовая эластичность спроса на бензин в среднесрочной перспективе, скажем, в три-девять месяцев обычно оценивается примерно в -0,5. Поскольку абсолютное значение ценовой эластичности меньше 1, это ценовая неэластичность. Однако мы ожидаем, что спрос на конкретную марку бензина будет гораздо более эластичен по цене, чем спрос на бензин в целом.
Важность в семейном бюджете
Одна из причин, по которой изменения цен влияют на объем спроса, заключается в том, что они изменяют то, сколько потребитель может купить; изменение цены товара или услуги влияет на покупательную способность дохода потребителя и, таким образом, влияет на количество товара, которое потребитель купит. Этот эффект сильнее, когда товар или услуга важны для бюджета типичного домохозяйства.
Например, изменение цены на джинсы, вероятно, важнее для вашего бюджета, чем изменение цены на карандаши. Предположим, что цены на оба продукта удвоились. В этом году вы планировали купить четыре пары джинсов, но теперь можете решить обойтись двумя новыми парами. Изменение цен на карандаши, напротив, может привести к очень незначительному сокращению объема спроса просто потому, что карандаши вряд ли будут занимать большое место в семейном бюджете. Чем выше значение статьи в бюджетах домохозяйств, тем больше, вероятно, будет абсолютное значение ценовой эластичности спроса.
Изменение цен на карандаши, напротив, может привести к очень незначительному сокращению объема спроса просто потому, что карандаши вряд ли будут занимать большое место в семейном бюджете. Чем выше значение статьи в бюджетах домохозяйств, тем больше, вероятно, будет абсолютное значение ценовой эластичности спроса.
Время
Предположим, завтра утром подорожает электричество. Что произойдет с объемом спроса?
Ответ во многом зависит от того, сколько времени мы отводим на ответ. Если мы заинтересованы в снижении спроса к завтрашнему дню, мы можем ожидать, что отклик будет очень небольшим. Но если мы даем потребителям год на то, чтобы отреагировать на изменение цены, мы можем ожидать, что реакция будет намного сильнее. Мы ожидаем, что абсолютное значение эластичности спроса по цене будет выше, чем больше времени будет отведено для реакции потребителей.
Рассмотрим ценовую эластичность спроса на сырую нефть. Экономист Джон К.Б. Купер оценил эластичность спроса на сырую нефть по цене в краткосрочном и долгосрочном периоде для 23 промышленно развитых стран за период 1971–2000 гг. Профессор Купер обнаружил, что практически для каждой страны ценовая эластичность была отрицательной, а долгосрочная ценовая эластичность, как правило, была намного выше (по абсолютной величине), чем краткосрочная ценовая эластичность. Его результаты представлены в таблице 5.1 «Краткосрочная и долгосрочная ценовая эластичность спроса на сырую нефть в 23 странах». Как видите, результаты исследования были опубликованы в журнале ОПЕК (Организация стран-экспортеров нефти), организации, члены которой извлекли большую выгоду из неэластичности спроса на их продукцию. Ограничивая предложение, ОПЕК, производящая около 45% мировой нефти, может оказывать повышательное давление на цены на сырую нефть. Это увеличивает общие доходы ОПЕК (и всех других производителей нефти) и снижает общие затраты.
Профессор Купер обнаружил, что практически для каждой страны ценовая эластичность была отрицательной, а долгосрочная ценовая эластичность, как правило, была намного выше (по абсолютной величине), чем краткосрочная ценовая эластичность. Его результаты представлены в таблице 5.1 «Краткосрочная и долгосрочная ценовая эластичность спроса на сырую нефть в 23 странах». Как видите, результаты исследования были опубликованы в журнале ОПЕК (Организация стран-экспортеров нефти), организации, члены которой извлекли большую выгоду из неэластичности спроса на их продукцию. Ограничивая предложение, ОПЕК, производящая около 45% мировой нефти, может оказывать повышательное давление на цены на сырую нефть. Это увеличивает общие доходы ОПЕК (и всех других производителей нефти) и снижает общие затраты.
Таблица 5.1 Краткосрочная и долгосрочная ценовая эластичность спроса на сырую нефть в 23 странах
| Страна | Краткосрочная ценовая эластичность спроса | Эластичность спроса по цене в долгосрочном периоде |
|---|---|---|
| Австралия | −0,034 | −0,068 |
| Австрия | −0,059 | −0,092 |
| Канада | −0,041 | −0,352 |
| Китай | 0,001 | 0,005 |
| Дания | −0,026 | −0,191 |
| Финляндия | −0,016 | −0,033 |
| Франция | −0,069 | −0,568 |
| Германия | −0,024 | −0,279 |
| Греция | −0,055 | −0,126 |
| Исландия | −0,109 | −0,452 |
| Ирландия | −0,082 | −0,196 |
| Италия | −0,035 | −0,208 |
| Япония | −0,071 | −0,357 |
| Корея | −0,094 | −0,178 |
| Нидерланды | −0,057 | −0,244 |
| Новая Зеландия | −0,054 | −0,326 |
| Норвегия | −0,026 | −0,036 |
| Португалия | 0,023 | 0,038 |
| Испания | −0,087 | −0,146 |
| Швеция | −0,043 | −0,289 |
| Швейцария | −0,030 | −0,056 |
| Соединенное Королевство | −0,068 | −0,182 |
| США | −0,061 | −0,453 |
Для большинства стран ценовая эластичность спроса на сырую нефть имеет тенденцию быть выше (по абсолютной величине) в долгосрочной перспективе, чем в краткосрочной.
Источник: Джон С. Б. Купер, «Эластичность спроса на сырую нефть по цене: оценки из 23 стран», Обзор ОПЕК: экономика энергетики и смежные вопросы , 27:1 (март 2003 г.): 4. Оценки основаны на данных. за период 1971–2000 гг., за исключением Китая и Южной Кореи, где период равен 1979–2000. Хотя ценовые эластичности для Китая и Португалии были положительными, они не были статистически значимыми.
Ключевые выводы
- Ценовая эластичность спроса измеряет реакцию величины спроса на изменения цены; он рассчитывается путем деления процентного изменения объема спроса на процентное изменение цены.
- Спрос неэластичен по цене, если абсолютное значение эластичности спроса по цене меньше 1; он эластичен по цене за единицу, если абсолютное значение равно 1; эластичность по цене, если абсолютное значение больше 1,9.0008
- Спрос эластичен по цене в верхней половине любой линейной кривой спроса и неэластичен по цене в нижней половине. Эластична по цене за единицу в средней точке.

- Когда спрос неэластичен по цене, общий доход движется в направлении изменения цены. Когда спрос эластичен по цене за единицу, общий доход не меняется в ответ на изменение цены. Когда спрос эластичен по цене, общий доход движется в направлении изменения количества.
- Абсолютное значение ценовой эластичности спроса больше, когда доступны заменители, когда товар занимает важное место в бюджете домохозяйства и когда у покупателей есть больше времени, чтобы приспособиться к изменениям цены товара.
Показательный пример: эластичность и стоп-сигналы
Рисунок 5.6
Ruin Raider — остановка движения — CC BY-NC-ND 2.0.
Мы все сталкиваемся с ситуацией каждый день. Вы приближаетесь к перекрестку. Загорается желтый свет. Вы знаете, что должны замедлиться, но вы немного торопитесь. Итак, вы немного ускоряетесь, чтобы попытаться сделать свет. Но красный свет мигает прямо перед тем, как вы доберетесь до перекрестка. Стоит ли рискнуть и пройти?
Многие люди, столкнувшиеся с такой ситуацией, делают рискованный выбор. В 1998 году 2000 человек в США погибли из-за того, что водители проезжали перекрестки на красный свет. Чтобы уменьшить количество водителей, делающих такой выбор, во многих районах на перекрестках установлены камеры. Водителей, которые проезжают на красный свет, фотографируют, и они получают штрафы по почте. Этот метод правоприменения вместе с недавним увеличением штрафов за проезд на красный свет на перекрестках привел к интригующему применению концепции эластичности. Экономисты Авнер Бар-Илан из Хайфского университета в Израиле и Брюс Сакердот из Дартмутского университета оценили эластичность цен на проезд через светофоры по отношению к дорожным штрафам на перекрестках в Израиле и Сан-Франциско.
В 1998 году 2000 человек в США погибли из-за того, что водители проезжали перекрестки на красный свет. Чтобы уменьшить количество водителей, делающих такой выбор, во многих районах на перекрестках установлены камеры. Водителей, которые проезжают на красный свет, фотографируют, и они получают штрафы по почте. Этот метод правоприменения вместе с недавним увеличением штрафов за проезд на красный свет на перекрестках привел к интригующему применению концепции эластичности. Экономисты Авнер Бар-Илан из Хайфского университета в Израиле и Брюс Сакердот из Дартмутского университета оценили эластичность цен на проезд через светофоры по отношению к дорожным штрафам на перекрестках в Израиле и Сан-Франциско.
В декабре 1996 года в Израиле резко увеличили штраф за проезд на красный свет. Старый штраф в 400 шекелей (в то время это было равно 122 долларам в США) был увеличен до 1000 шекелей (305 долларов). В январе 1998 года Калифорния увеличила штраф за это правонарушение со 104 до 271 доллара. В Израиле и городе Сан-Франциско камеры установлены на нескольких перекрестках. Водители, которые проигнорировали светофоры, сфотографировались и автоматически получили штрафы, налагающие новые более высокие штрафы.
В Израиле и городе Сан-Франциско камеры установлены на нескольких перекрестках. Водители, которые проигнорировали светофоры, сфотографировались и автоматически получили штрафы, налагающие новые более высокие штрафы.
Мы можем думать о проезде на красный свет как о деятельности, на которую есть спрос — в конце концов, игнорирование красного сигнала светофора ускоряет поездку. Это также может вызвать удовлетворение у людей, которым нравится не соблюдать правила дорожного движения. Концепция эластичности позволяет нам показать, насколько водители отреагировали на увеличение штрафов.
Профессора Бар-Илан и Сакердот получили информацию обо всех водителях, упомянутых на 73 перекрестках в Израиле и восьми перекрестках в Сан-Франциско. Для Израиля, например, определили период 19 января92 по июнь 1996 года как период «до». Они сравнили количество нарушений в предшествующий период с количеством нарушений с июля 1996 г. по декабрь 1999 г. — период «после» — и обнаружили, что количество штрафов на одного водителя сократилось на 31,5%. В частности, среднее количество штрафов на одного водителя составляло 0,073 в период до повышения; он упал до 0,050 после повышения. Увеличение штрафа составило 150 процентов. (Обратите внимание, что, поскольку они производили расчеты «до» и «после», авторы использовали стандартный метод, описанный в главе «Осторожно!», для расчета процентного изменения, т. е. вместо этого они вычисляли процентные изменения по сравнению с исходными значениями. от среднего значения переменных.) Таким образом, эластичность штрафов по отношению к штрафу составила -0,21 (= -31,5%/150%).
В частности, среднее количество штрафов на одного водителя составляло 0,073 в период до повышения; он упал до 0,050 после повышения. Увеличение штрафа составило 150 процентов. (Обратите внимание, что, поскольку они производили расчеты «до» и «после», авторы использовали стандартный метод, описанный в главе «Осторожно!», для расчета процентного изменения, т. е. вместо этого они вычисляли процентные изменения по сравнению с исходными значениями. от среднего значения переменных.) Таким образом, эластичность штрафов по отношению к штрафу составила -0,21 (= -31,5%/150%).
Экономисты оценили эластичность для определенных групп людей. Например, у молодых людей (17–30 лет) эластичность составляла -0,36; люди старше 30 лет имели эластичность -0,16. В целом эластичность по абсолютной величине снижалась по мере роста дохода. Для Сан-Франциско и Израиля вместе взятых эластичность составляла от -0,26 до -0,33.
В целом результаты показали, что люди рационально отреагировали на увеличение штрафов. Повышение цены определенного поведения снижает частоту этого поведения. Исследование также указывает на эффективность камер как метода принуждения. С камерами нарушители могут быть уверены, что их процитируют, если они проигнорируют красный свет. И сокращение числа людей, проезжающих на красный свет, явно спасает жизни.
Повышение цены определенного поведения снижает частоту этого поведения. Исследование также указывает на эффективность камер как метода принуждения. С камерами нарушители могут быть уверены, что их процитируют, если они проигнорируют красный свет. И сокращение числа людей, проезжающих на красный свет, явно спасает жизни.
Источник: Авнер Бар-Илан и Брюс Сакердот. «Ответ преступников и не преступников на штрафы». Журнал права и экономики , 47: 1 (апрель 2004 г.): 1–17.
1 Обратите внимание, что, поскольку количество проданных единиц товара равно количеству купленных единиц, определение общего дохода можно также использовать для определения общих расходов. Какой термин мы используем, зависит от рассматриваемого вопроса. Если мы пытаемся определить, что происходит с доходами продавцов, то мы спрашиваем об общем доходе. Если мы пытаемся определить, сколько потребители тратят, то мы спрашиваем об общих расходах.
2 Деление на ноль дает неопределенное решение. Утверждение, что ценовая эластичность спроса бесконечна, требует, чтобы мы сказали, что знаменатель «приближается» к нулю.
Утверждение, что ценовая эластичность спроса бесконечна, требует, чтобы мы сказали, что знаменатель «приближается» к нулю.
Как рассчитать ценовую эластичность спроса [+Примеры]
В основе маркетинга лежит прогнозирование того, как потребители будут реагировать на различные формы стимулов. Насколько повысит продажи продукт, если Райан Гослинг (или герой Патрика Хэл Вэриан) одобрит продукт? Как потребители отнесутся к плюшевому мишке в маркетинговом электронном письме или на упаковке? Хотя компании никогда не могут быть на 100% уверены в том, как отреагирует потребитель, цель каждой команды по маркетингу и продукту — увеличить конверсию, использование и положительное отношение к бренду.
Ценообразование, а точнее стратегия ценообразования вашей компании, — это единственная область, применимая к маркетингу и продукту, которая все еще содержит много предположений. Феноменальный маркетинг и разработка продукта могут привести к увеличению ваших цен при сохранении того же уровня конверсии. Эти две области вашего бизнеса также могут подорвать вашу конверсию, если все сделано неправильно. Тем не менее, установление цены и сообщение ценности не должны быть игрой вслепую. Точно так же оптимизация и изменения цен не должны быть случайными.
Эти две области вашего бизнеса также могут подорвать вашу конверсию, если все сделано неправильно. Тем не менее, установление цены и сообщение ценности не должны быть игрой вслепую. Точно так же оптимизация и изменения цен не должны быть случайными.
К счастью, есть способ управлять этим процессом. Одним из краеугольных камней стратегии ценообразования, микроэкономики и отличной основы для маркетинга/товаров является теория ценовой эластичности спроса, также известная просто как ценовая эластичность. Давайте изложим основы ценовой эластичности и то, как вы можете увеличить спрос, сделав предложение вашего продукта более неэластичным с помощью маркетинга и разработки продукта.
Что такое ценовая эластичность спроса? Эластичность спроса по цене (PED) является важным понятием в законе спроса. Это измерение того, как спрос на товар будет зависеть от изменения его цены. Другими словами, PED — это способ выяснить реакцию потребителей на колебания цен, в отличие от ценовой эластичности предложения, которая определяет реакцию предложения на цену.
Хотя уравнения иногда могут быть сложными, это очень простое и легкое.
Как рассчитать ценовую эластичность спроса
Вот основная формула ценовой эластичности спроса, которую вы можете использовать:
Ценовая эластичность спроса = (% изменения объема спроса)/(% изменения цены)
Поскольку объем спроса обычно уменьшается с ростом цены, коэффициент ценовой эластичности почти всегда отрицателен. Экономисты, будучи лентяями, обычно выражают коэффициент как положительное число, даже если его значение противоположно. Мы довольно трудный народ. Однако важно отметить, что уменьшение объема спроса не означает автоматически, что выручка уменьшается. Дополнительный размер прибыли может компенсировать небольшое снижение объемов закупок.
Когда ценовая эластичность товара меньше 1, он считается неэластичным. Это означает, что увеличение цены на одну единицу привело к уменьшению спроса менее чем на одну единицу. С другой стороны, если коэффициент (абсолютное значение) больше 1, товар эластичный. Это означает, что увеличение цены на единицу приведет к еще большему падению спроса. Теоретически общий доход будет максимальным, когда ценовая эластичность товара равна 1, или, другими словами, когда спрос является единично эластичным.
Это означает, что увеличение цены на единицу приведет к еще большему падению спроса. Теоретически общий доход будет максимальным, когда ценовая эластичность товара равна 1, или, другими словами, когда спрос является единично эластичным.
Я просто выбросил много слов, таких как «единица», «эластичность», «коэффициент», «ленивый» и т. д. Да, экономисты любят использовать причудливые слова, чтобы оттолкнуть эти политологи или коммуникаторы (шучу, конечно), так что давайте немного разберем это с некоторыми примерами ценовой эластичности спроса.
Цена и спрос обычно движутся в противоположном направлении, но кривая спроса сильно различается в зависимости от продукта (особенно от того, насколько продукт необходим). Когда вы смотрите на что-то вроде бака с бензином, влияет ли увеличение на 0,50 доллара за галлон на то, будете ли вы заправляться или нет? Как правило, кроме того, что это раздражает вас, ответ отрицательный, потому что многие жители пригородной зоны полагаются на бензин, чтобы добраться до работы или с работы. Таким образом, бензин считается неэластичным, поскольку для действительного снижения спроса требуется резкое повышение цены. Бостонская MBTA недавно увидела это с повышением цен, когда цена выросла, но количество пассажиров на самом деле не пострадало.
Таким образом, бензин считается неэластичным, поскольку для действительного снижения спроса требуется резкое повышение цены. Бостонская MBTA недавно увидела это с повышением цен, когда цена выросла, но количество пассажиров на самом деле не пострадало.
И наоборот, если кусок пиццы, который вы покупаете каждый день на обед, подорожает на 0,50 доллара, повлияет ли это на вашу покупку? Если вы не слишком привязаны к пицце и у вас есть другие варианты (подробнее об этом ниже), вы, вероятно, перейдете в другое заведение. Пицца и продукты питания в целом имеют тенденцию к эластичности, когда даже незначительное повышение цены может вызвать изменение спроса.
Как определить ценовую эластичность спроса на ваш продукт
Очевидно, по крайней мере надеюсь, что вы хотите, чтобы ваш бизнес приносил как можно больше денег. Таким образом, вам нужно сделать свой продукт максимально неэластичным, увеличивая спрос, независимо от того, насколько дорогим вы делаете продукт. По сути, вы хотите, чтобы ваши клиенты, будь то благодаря определенным функциям, вашим услугам или маркетингу мирового класса, не могли жить без вашего бизнеса. Входные данные, необходимые для возникновения этого явления, будут корректироваться в зависимости от сегментов клиентов, но мыслительный процесс для каждого сегмента остается одним и тем же. Так как же определить эластичность вашего продукта для каждого сегмента и использовать это знание в своих интересах? Вот несколько вещей, о которых следует подумать:
По сути, вы хотите, чтобы ваши клиенты, будь то благодаря определенным функциям, вашим услугам или маркетингу мирового класса, не могли жить без вашего бизнеса. Входные данные, необходимые для возникновения этого явления, будут корректироваться в зависимости от сегментов клиентов, но мыслительный процесс для каждого сегмента остается одним и тем же. Так как же определить эластичность вашего продукта для каждого сегмента и использовать это знание в своих интересах? Вот несколько вещей, о которых следует подумать:
Предметы первой необходимости, как правило, неэластичны (бензин, электричество, вода и т. д.), а предметы роскоши — наоборот (шоколад, еда, развлечения и т. д.), потому что от них легче отказаться, когда дела идут плохо. Например, вы, вероятно, не перестанете покупать лампочки, если цена вырастет на несколько процентов, но вы можете не заказать круиз на Багамы, если стоимость вырастет. В этом случае можно было бы предсказать, что лампочки будут относительно неэластичными, а круизы, к сожалению, нет.
В этом случае можно было бы предсказать, что лампочки будут относительно неэластичными, а круизы, к сожалению, нет.
Google отлично справился со своей платформой AdWords, стимулируя спрос, потому что значительное количество компаний используют свою рекламу для поддержания всего своего бизнеса. Конечно, конкуренты подкрадываются, но ваш маркетинг и реальный продукт делают ваше предложение необходимостью. Вы должны найти ответ на вопрос: если доходы наших клиентов иссякли (B2B) или доходы потребителей сократились вдвое (B2C), что в нашем предложении делает нас последней вещью, которую они исключают из своей жизни?
2. Насколько доступны близкие заменители? Я ем много бутербродов (не судите строго). Если цена на нарезку «Голова кабана» поднимется, я легко могу переключиться на «Грудку индейки Сары Ли». Существует множество других марок мясного ассорти, поэтому, если голова кабана не убедит меня, что его качество стоит повышения цены, я, вероятно, перестану покупать их мясо.
Если у вашего продукта много похожих конкурентов, повышение цен, скорее всего, оттолкнет потребителей. Я просто хочу кратко рассказать о дифференциации продукта. В сфере SaaS и программного обеспечения дифференцировать продукты намного проще, чем если бы вы продавали пылесосы. Поэтому создавайте неотъемлемые функции, которые важны для клиента и которых нет у ваших конкурентов. В качестве альтернативы, станьте частью предыстории вашего клиента, где затраты на переход от вас были бы настолько высоки, что переход не стоил бы. Мы используем Hubspot на хардкорном уровне. Переход на другую платформу был бы неудобен с тактической и процедурной точки зрения. Конечно, конкурент с учетом этого мог бы создать простое решение, но это сомнительно (бостонская любовь!).
3. Сколько на самом деле стоит ваш продукт? Я говорю не о сравнении с товарами вашего конкурента, а о том, сколько стоит ваш товар. Вы можете продавать одни из самых дешевых автомобилей, но даже дешевое транспортное средство стоит дорого. Чем выше цена, тем она эластичнее из-за психологического ценообразования. Например, вы, вероятно, даже не знаете, сколько стоит эта упаковка ручек Paper Mate, поэтому, когда цена вырастет на 10% (всего несколько центов), вы, скорее всего, этого не заметите. Но если цена нового автомобиля, который вы хотите, упадет на 10% (сотни или тысячи долларов), вы обязательно это заметите.
Чем выше цена, тем она эластичнее из-за психологического ценообразования. Например, вы, вероятно, даже не знаете, сколько стоит эта упаковка ручек Paper Mate, поэтому, когда цена вырастет на 10% (всего несколько центов), вы, скорее всего, этого не заметите. Но если цена нового автомобиля, который вы хотите, упадет на 10% (сотни или тысячи долларов), вы обязательно это заметите.
Вы можете воспользоваться фактическим номером на наклейке для ваших продуктов, предоставляя предложения на малых, средних и высоких уровнях. Вы не собираетесь предлагать автомобиль за 50 долларов (если только это не настоящий драндулет), но вы можете предложить программу проката автомобилей, которая позволит вам иметь меньшую цену. Zipcar отлично справляется с этим благодаря своим почасовым и дневным ставкам. Конкурировать еще лучше с SKU электронной коммерции в дополнение к их планам корпоративного уровня.
4. Как долго продлится изменение цены? Все товары со временем становятся более эластичными. Со временем можно найти замену или научиться жить без чего-то, когда это было невозможно под давлением времени. Классический пример – масло. Если в краткосрочной перспективе (скажем, завтра) цена на нефть вырастет, люди будут ворчать за завтраком пару дней, но все равно наполнят свои баки. Однако люди могут покупать гибриды или автомобили меньшего размера, которые в долгосрочной перспективе потребляют меньше топлива. Поэтому, даже если вы определили, что ваш продукт неэластичен, будьте осторожны с последствиями изменения цены (даже небольшого процентного изменения) в будущем.
Со временем можно найти замену или научиться жить без чего-то, когда это было невозможно под давлением времени. Классический пример – масло. Если в краткосрочной перспективе (скажем, завтра) цена на нефть вырастет, люди будут ворчать за завтраком пару дней, но все равно наполнят свои баки. Однако люди могут покупать гибриды или автомобили меньшего размера, которые в долгосрочной перспективе потребляют меньше топлива. Поэтому, даже если вы определили, что ваш продукт неэластичен, будьте осторожны с последствиями изменения цены (даже небольшого процентного изменения) в будущем.
Например, компания Rackspace долгое время могла устанавливать премиальные цены, потому что хостинговые решения премиум-класса были недоступны даже для небольших веб-приложений. С появлением облака цены стали более конкурентоспособными, и Rackspace потеряла часть своих недорогих клиентов. Carbonite также сталкивается с этим явлением благодаря большому количеству решений для резервного копирования на рынке.
В целом ценовая эластичность должна быть важным фактором при разработке вашего продукта и маркетинговых стратегий, в дополнение к тому, что она является основным строительным блоком вашего ценообразования. Огромный фактор, который я повторю, заключается в том, что ценовая эластичность для разных потребительских сегментов будет разной. Таким образом, ваш маркетинг, ценообразование и комплектация должны различаться. В конце концов, помните, ценообразование — это процесс, который вы должны интегрировать в траекторию развития вашей компании.
Чтобы узнать больше о стратегии ценообразования, загрузите нашу электронную книгу «Стратегия ценообразования» или ознакомьтесь с тем, что мы можем сказать о нашем программном обеспечении для оптимизации цен.
Ценовая эластичность спроса Часто задаваемые вопросы
Какие бывают виды ценовой эластичности?
Существует два типа ценовой эластичности спроса: эластичный спрос и неэластичный спрос. Эластичный спрос возникает, когда спрос на товары изменяется, чувствителен к изменениям цен. Неэластичный спрос – это когда изменение цены не сильно влияет на спрос на товары. На товары первой необходимости спрос эластичный, а на товары первой необходимости неэластичный.
Неэластичный спрос – это когда изменение цены не сильно влияет на спрос на товары. На товары первой необходимости спрос эластичный, а на товары первой необходимости неэластичный.
Что является примером эластичного спроса?
Эластичный спрос используется для описания сценария, в котором изменение спроса чувствительно к небольшому изменению цены. Например, если мы увидим значительное изменение цен на чипсы Lays, потребители с большей вероятностью перейдут на другую марку, что приведет к снижению спроса, и наоборот. Это означает, что чипы имеют эластичный спрос из-за наличия близких заменителей.
Что является примером неэластичного спроса?
Неэластичный спрос описывает сценарий, при котором колебания цены не меняют спрос на товар. Например, газ необходим для движения автомобилей, и альтернативы газу нет. Это означает, что любой, у кого есть машина, должен будет платить за бензин независимо от того, насколько высоки цены, что делает спрос неэластичным.
Почему ценовая эластичность спроса важна?
Знание ценовой эластичности может дать представление о том, как рынок будет реагировать на изменения цен. Это важно для предприятий, которые принимают решения о ценообразовании, поскольку повышение или понижение цен напрямую повлияет на количество продаж. Факторинг ценовой эластичности спроса является ключевым шагом для компаний при определении правильных целей ценообразования в своей нише.
Это важно для предприятий, которые принимают решения о ценообразовании, поскольку повышение или понижение цен напрямую повлияет на количество продаж. Факторинг ценовой эластичности спроса является ключевым шагом для компаний при определении правильных целей ценообразования в своей нише.
Деловой расчет
Приближение касательной линии
Когда мы впервые подумали о производной, мы использовали наклон секущих на крошечных интервалах для аппроксимации производной: \[ f'(a)\приблизительно \frac{\Delta y}{\Delta x}=\frac{ f(x)-f(a)}{x-a}\]
Теперь, когда у нас есть другие способы нахождения производных, мы можем использовать это приближение, чтобы пойти другим путем. Решите приведенное выше выражение для \(f(x)\), и вы получите аппроксимацию касательной:
Аппроксимация касательной линии (TLA) (или
Linear Approximation)
Чтобы аппроксимировать значение \(f(x)\) с помощью TLA, найдите некоторое \(a\), где
- \(a\) и \(x\)
близки,
и - Вы знаете точные значения как \(f(a)\), так и \(f'(a)\).

Тогда \[f(x) \приблизительно f(a)+f'(a)(x-a).\]
Другой способ взглянуть на ту же формулу: \[\Delta y\приблизительно f'(a) \Delta x\]
Насколько близко близко? Это зависит от формы графика \(f\). В общем, чем ближе, тем лучше.
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, поддерживающего видео HTML5
Попробуйте сами, используя этот апплет (нажмите кнопку рядом с L(x), если строка не отображается):
Пример 1
Предположим, мы знаем, что \(g(20) = 5\) и \(g'(20) = 1,4\). Используйте эту информацию для аппроксимации \(g(23)\) и \(g(18)\).
Используя аппроксимацию касательной: \[ \begin{выравнивание*} г(23)\приблизительно & 5 + (1,4)(23 — 20) = 9.2\\ г(18)\приблизительно & 5 + (1,4)(18 — 20) = 2,2 \end{выравнивание*} \]
Обратите внимание, что мы не знаем, близки ли эти приближения, но это лучшее, что мы можем сделать с ограниченной информацией, с которой мы имеем дело. Обратите также внимание, что 18 и 23 близки к 20, так что мы можем надеяться, что эти приближения довольно хороши. Мы чувствовали бы себя более уверенно, используя эту информацию для аппроксимации \(g(20,003)\). Мы бы чувствовали себя очень неуверенно, используя эту информацию для аппроксимации \(g(55)\).
Обратите также внимание, что 18 и 23 близки к 20, так что мы можем надеяться, что эти приближения довольно хороши. Мы чувствовали бы себя более уверенно, используя эту информацию для аппроксимации \(g(20,003)\). Мы бы чувствовали себя очень неуверенно, используя эту информацию для аппроксимации \(g(55)\).
Эластичность
Мы знаем, что функции спроса убывают, поэтому, когда цена увеличивается, объем спроса уменьшается. Но как насчет выручки = цена \(\раз\) количество? Когда цены повысятся, упадет ли выручка из-за того, что спрос так сильно упал? Или выручка увеличится, потому что спрос не сильно упал?
Эластичность спроса — это мера того, как спрос реагирует на изменение цены. Это нормализовано — это означает, что конкретные цены и количества не имеют значения, и все рассматривается как изменение в процентах. Формула эластичности спроса включает производную, поэтому мы обсуждаем ее здесь.
Эластичность спроса
При заданной функции спроса, которая дает \(q\) через \(p\) (так что \(q=D(p)\)), эластичность спроса равна \[ \begin{выравнивание*} E &= \left|\frac{p}{q}\cdot \frac{dq}{dp}\right|\\ &= \left|\frac{p\cdot D'(p)}{D(p)}\right| \end{выравнивание*} \]
Обратите внимание, что поскольку спрос [обычно] является убывающей функцией \(p\), производная [обычно] отрицательна. Вот почему у нас есть абсолютное значение: так что \(E\) всегда будет положительным. Это означает, что мы также можем писать \(E\) как \(-\dfrac{p}{q}\cdot \dfrac{dq}{dp}\) или \(-\dfrac{p\cdot D'(p) {Д(р)}\). С этими формами легче работать при решении, когда \(E=1\).
Вот почему у нас есть абсолютное значение: так что \(E\) всегда будет положительным. Это означает, что мы также можем писать \(E\) как \(-\dfrac{p}{q}\cdot \dfrac{dq}{dp}\) или \(-\dfrac{p\cdot D'(p) {Д(р)}\). С этими формами легче работать при решении, когда \(E=1\).
- Если \(E \lt 1\), мы говорим, что спрос неэластичен. В этом случае повышение цен увеличивает выручку.
- Если \(E \gt 1\), мы говорим, что спрос эластичен. В этом случае повышение цен снижает выручку.
- Если \(E = 1\), мы говорим, что спрос унитарный. \(E = 1\) в критических точках функции дохода.
Интерпретация эластичности
Если цена увеличится на 1%, спрос уменьшится на Е%.
Пример 2
Компания продает \( q \) устройств для намотки ленты в год по цене $\( p \) за устройство для намотки ленты. Функция спроса на ленточные намоточные машины определяется выражением \(p=300-0,02q \). Найдите эластичность спроса при цене 70 долларов за штуку. Приведет ли рост цены к увеличению выручки?
Во-первых, нам нужно решить уравнение спроса, чтобы оно давало \( q \) через \( p \), чтобы мы могли найти \( \frac{dq}{dp} \): \( p= 300-0,02q\), значит \(q=15000-50p\). Тогда \( \frac{dq}{dp}=-50 \).
Тогда \( \frac{dq}{dp}=-50 \).
Нам нужно найти \( q \) при \( p = 70 \): \[ q = 11500. \]
Теперь вычислите \[ E=\left| \frac{p}{q}\cdot\frac{dq}{dp} \right|=\left| \frac{70}{11500}\cdot(-50) \right| \ приблизительно 0,3 \]
\(E \lt 1\), поэтому спрос неэластичен. Повышение цены на 1% вызовет падение спроса всего на 0,3%. Повышение цены приведет к увеличению выручки, поэтому кажется, что компания должна увеличить свою цену.
Спрос на продукты, которые люди должны покупать, такие как лук, имеет тенденцию быть неэластичным. Даже если цена вырастет, людям все равно придется покупать примерно такое же количество лука, и выручка не уменьшится. Спрос на товары, без которых люди могут обойтись или отложить покупку, например автомобили, имеет тенденцию к эластичности. Если цена вырастет, люди просто не будут покупать машины прямо сейчас, и доходы упадут. 92=&400\\ p = & \ sqrt {\ frac {400} {3}} \ приблизительно 11,55. \end{выравнивание*} \]
Цена в 11,55 долларов максимизирует доход.
Формула эластичности спроса по доходу
Формула эластичности спроса по доходу (содержание)
- Формула
- Примеры
- Калькулятор
Термин «эластичность по доходу» показывает, как меняется спрос на определенный товар при изменении реального дохода потребителя. Другими словами, это мера реакции спроса на товар на изменения реального дохода. Формулу эластичности спроса по доходу можно получить, разделив процентное изменение величины спроса на товар (∆D/D) на процентное изменение реального дохода потребителя, который его покупает (∆I/I). Математически это представляется как
Эластичность спроса по доходу = процентное изменение объема спроса (∆D/D) / процентное изменение дохода (∆I/I)
Однако формулу эластичности спроса по доходу можно расширить следующим образом: Эластичность спроса по доходу = (D 1 – D 0 ) / (D 1 + D 0 ) / (I 1 – I 0 + I 1906 0 )
где,
- D 0 = Требуемое начальное количество
- D 1 = Требуемое окончательное количество
- I 0 = Начальный реальный доход
- I 1 = Окончательный реальный доход
Давайте рассмотрим пример, чтобы лучше понять расчет эластичности спроса по доходу.
Вы можете скачать этот шаблон Excel с формулой эластичности спроса по доходу здесь — Формула эластичности спроса по доходу, шаблон Excel
Формула эластичности спроса по доходу – Пример №1
Возьмем в качестве примера экзотическую кухню. Предположим, что за последнее время средний уровень доходов вырос на 75%, что привело к дополнительным деньгам, что в итоге привело к увеличению потребления экзотических кухонь на 25%. Рассчитайте эластичность спроса по доходу на основе имеющейся информации.
Решение:
Эластичность спроса по доходу рассчитывается по приведенной ниже формуле
Эластичность спроса по доходу = Процентное изменение объема спроса (∆D/D) / Процентное изменение дохода (∆I/I) Следовательно, эластичность спроса на экзотическую кухню по доходу равна 0,33, т.е. это нормальный товар. Возьмем в качестве примера дешевую одежду. Решение: . 0 ) / (I 1 — I 0 ) / (I 1 + I 0 ) Формула эластичности спроса по доходу – Пример №2
 Еженедельный спрос на дешевую одежду снизился с 4000 до 2500 штук, поскольку уровень реального дохода в экономике увеличился с 75 до 125 долларов в день. Причина в смещении предпочтений из-за наличия дополнительных денег на фоне повышения уровня доходов. Рассчитайте эластичность спроса по доходу на основе имеющейся информации.
Еженедельный спрос на дешевую одежду снизился с 4000 до 2500 штук, поскольку уровень реального дохода в экономике увеличился с 75 до 125 долларов в день. Причина в смещении предпочтений из-за наличия дополнительных денег на фоне повышения уровня доходов. Рассчитайте эластичность спроса по доходу на основе имеющейся информации.
- Эластичность спроса = [(25 500 — 4 000) / (2,500 + 4000). ] / [(125 – 75 долл. США) / (125 долл. США + 75 долл. США)]
- Эластичность спроса по доходу = -0,92
Следовательно, эластичность спроса на дешевую одежду по доходу равна -0,92, т. е. это товар низшего качества.
Объяснение
Формулу эластичности спроса по доходу можно вывести, выполнив следующие шаги:
Шаг 1: Во-первых, определите начальный реальный доход и объем спроса при этом уровне дохода, которые обозначены I 0 и D 0 соответственно. Аналогично определите конечный реальный доход и спрос, обозначенные I 1 и D 1 соответственно.
Аналогично определите конечный реальный доход и спрос, обозначенные I 1 и D 1 соответственно.
Шаг 2: Затем рассчитайте изменение объема спроса путем вычитания начального количества из конечного количества. Теперь процентное изменение количества спроса рассчитывается путем деления изменения количества спроса на среднее конечного и начального количества, т.е. 2 * (D 1 – D 0 ) / (D 1 + D 0 ).
Шаг 3: Затем рассчитайте изменение реального дохода, вычитая первоначальный доход из конечного дохода. Теперь процентное изменение реального дохода рассчитывается путем деления изменения реального дохода на среднее значение конечного и начального доходов, т. е. 2 * (I 1 – Я 0 ) / (Я 1 + Я 0 ).
Шаг 4: Наконец, формула эластичности спроса по доходу может быть получена путем деления процентного изменения величины спроса на товар (шаг 2) на процентное изменение реального дохода потребителя, который его покупает (шаг 3). ) как показано ниже.
) как показано ниже.
Эластичность спроса по доходу = (D 1 – D 0 ) / (D 1 + D 0 ) / (I 1 – I 0 ) / (I 1 + I 0 ),
Актуальность и использование формулы эластичности спроса по доходу
Важно понимать концепцию эластичности спроса по доходу, поскольку она помогает предприятиям прогнозировать влияние экономические циклы продаж своей продукции. Основываясь на значении эластичности спроса по доходу, предприятия делят товары на две широкие категории — обычные товары и товары низшего качества.
Нормальные товары демонстрируют значение эластичности спроса по доходу больше нуля, что указывает на то, что объем спроса на нормальные товары увеличивается с увеличением уровня дохода. Товары первой необходимости — это тип обычных товаров, значение эластичности спроса по доходу которых находится в диапазоне от нуля до единицы и относятся к группе товаров и услуг, которые покупаются независимо от изменения уровня доходов. С другой стороны, предметы роскоши — это тип обычных товаров, у которых значение эластичности спроса по доходу больше единицы.
С другой стороны, предметы роскоши — это тип обычных товаров, у которых значение эластичности спроса по доходу больше единицы.
Некачественные товары демонстрируют значение эластичности спроса по доходу меньше нуля, что указывает на то, что количество требуемого некачественных товаров уменьшается с увеличением уровня дохода из-за смещения потребительских предпочтений от более дешевых продуктов и услуг к более качественным.
Калькулятор формулы эластичности спроса по доходу
Вы можете использовать следующий калькулятор эластичности спроса по доходу:
| Процентное изменение требуемого количества (∆D/D) | |
| Percentage Change in Income (∆I/I) | |
| Income Elasticity of Demand | |
| Income Elasticity of Demand = |
|
|
Рекомендуемые статьи
Это руководство по формуле эластичности спроса по доходу.






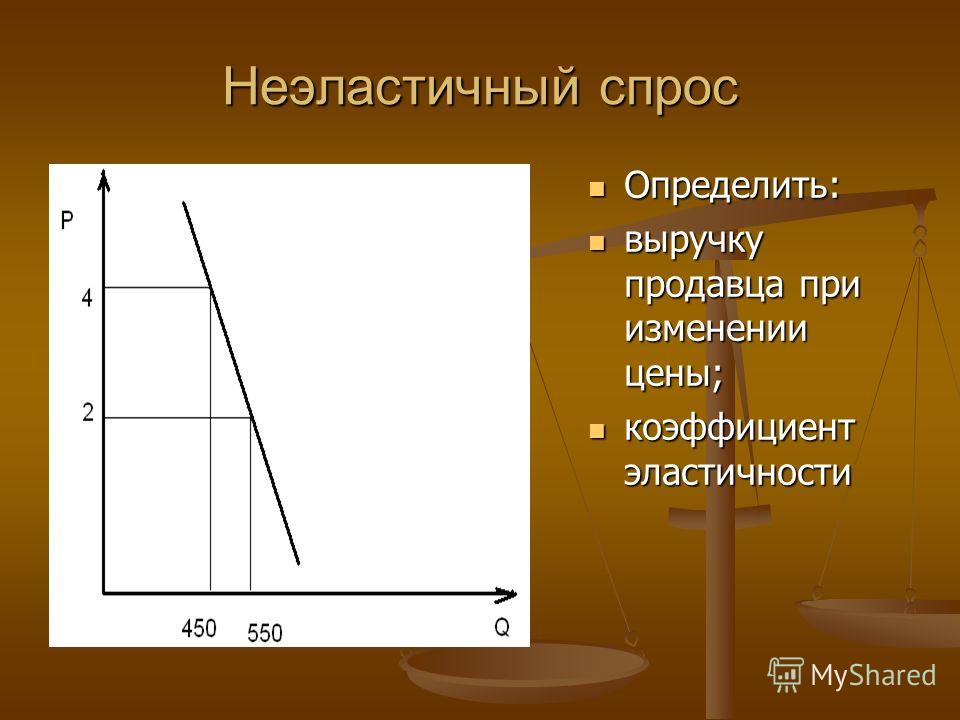 товара A (Q0), при изменении дохода на 2%, величина спроса изменится на 1 ед. Найдите эластичность спроса по доходу (E
товара A (Q0), при изменении дохода на 2%, величина спроса изменится на 1 ед. Найдите эластичность спроса по доходу (E В данный момент индивид потребляет 20 ед. блага (Q0). Как изменится величина его спроса (Q), если одновременно цена товара (P) вырастет на 4%, а доход индивида (I) вырастет на 2%. Найдите изменение Q, если сначала произойдет рост цены, а доход индивида вырастет лишь через некоторое время.
В данный момент индивид потребляет 20 ед. блага (Q0). Как изменится величина его спроса (Q), если одновременно цена товара (P) вырастет на 4%, а доход индивида (I) вырастет на 2%. Найдите изменение Q, если сначала произойдет рост цены, а доход индивида вырастет лишь через некоторое время.

 )
)
 грн
грн




