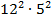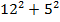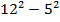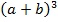Урок алгебры в 7 классе «Все действия со степенями»
1. Древние славяне тоже умели записывать большие числа, для этого у них были специальные названия для большого счета
«тысяща» =
«легион» =
«ворон» =
«колода» =
Наш мозг состоит из нервных клеток и способен ежедневно
запомнить единиц информации. К концу жизни наша память
может хранить около единиц информации — число, о котором пока даже не мечтают создатели компьютерной техники.
Легенда о шахматной доске
Шахматы —одна из самых древних игр. Она существует уже многие века, и не удивительно, что с нею связаны предания, правдивость которых за давностью времени невозможно проверить. Одну из подобных легенд я и хочу рассказать. Чтобы понять ее, не нужно вовсе уметь играть в шахматы — достаточно знать, что игра происходит на доске, разграфленной на 64 клетки (попеременно черные и белые).
Шахматная игра была придумана в Индии, и когда индийский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений. Узнав, что игра изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку.
Изобретатель — его звали Сета — явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников.
— Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал,— сказал царь.
Мудрец поклонился.
— Я достаточно богат, чтобы исполнить самое смелое твое пожелание,— продолжал царь.— Назови награду, которая тебя удовлетворит, и ты получишь ее.
Сета молчал.
— Не робей,— ободрил его царь.— Выскажи свое желание. Я не пожалею ничего, чтобы исполнить его!
— Велика доброта твоя, повелитель. Но дай срок обдумать ответ. Завтра, по зрелом размышлении, я сообщу тебе мою просьбу.
Когда на другой день Сета снова явился к ступеням трона, он удивил царя беспримерной скромностью своей просьбы.
— Повелитель,— сказал Сета,— прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.
— Простое пшеничное зерно? — изумился царь.
— Да, повелитель. За вторую клетку прикажи выдать два зерна, за третью — четыре, за четвертую — 8, за пятую— 16, за шестую — 32…
— Довольно! — с раздражением прервал его царь.— Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию: за каждую вдвое больше против предыдущей. Но знай, что просьба твоя недостойна моей щедрости. Прося такую ничтожную награду, ты непочтительно пренебрегаешь моей милостью. Поистине, как учитель, ты мог бы показать лучший пример уважения к доброте своего государя. Ступай! Слуги мои вынесут тебе мешок с пшеницей.
Сета улыбнулся, покинул залу и стал дожидаться у ворот дворца.
За обедом царь вспомнил об изобретателе шахмат и послал узнать, унес ли уже безрассудный Сета свою жалкую награду.
— Повелитель,— был ответ,— приказание твое, исполняется. Придворные математики исчисляют число следуемых зерен.
Царь нахмурился — он не привык, чтобы повеления его исполнялись так медлительно.
Вечером, отходя ко сну, царь Шерам еще раз осведомился, давно ли Сета со своим мешком пшеницы покинул ограду дворца.
— Повелитель,— ответили ему,— математики твои трудятся без устали и надеются еще до рассвета закончить подсчет.
— Почему медлят с этим делом?! — гневно воскликнул царь.— Завтра, прежде чем я проснусь, всё до последнего зерна должно быть выдано Сете. Я дважды не приказываю!
Утром царю доложили, что старшина придворных математиков просит выслушать важное донесение. Царь приказал ввести его.
— Прежде чем скажешь о твоем деле,— объявил Шерам.— я желаю услышать, выдана ли наконец Сете та ничтожная награда, которую он себе назначил.
— Ради этого я и осмелился явиться перед тобой в столь ранний’ час,— ответил старик.— Мы добросовестно исчислили все количество зерен, которое желает получить Сета. Число это так велико…
— Как бы велико оно ни было,— надменно перебил царь,— житницы мои не оскудеют! Награда обещана и должна быть выдана…
— Не в твоей власти, повелитель, исполнять подобные желания. Во всех амбарах твоих нет такого числа зерен, какое потребовал Сета. Нет его и в житницах целого царства. Не найдется такого числа зерен и на всем пространстве Земли. И если желаешь непременно выдать обещанную награду, то прикажи превратить земные царства в пахотные поля, прикажи осушить моря и океаны, прикажи растопить льды и снега, покрывающие далекие северные пустыри. Пусть все пространство их сплошь будет засеяно пшеницей. И все то, что родится на этих полях, прикажи отдать Сете. Тогда он получит свою награду.
С изумлением внимал царь словам старца.
— Назови же мне это чудовищное число,—сказал он в раздумье.
— Восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот сорок четыре триллиона семьдесят три биллиона семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать, о повелитель!
Такова легенда. Действительно ли было то, что здесь рассказано, неизвестно, но что награда, о которой говорит предание, должна была выразиться именно таким числом, в этом вы сами можете убедиться терпеливым подсчетом. Начав с единицы, нужно сложить числа: 1, 2, 4, 8 и т. д.
Искомое число зерен: 18 446 744 073 709 551615.
Если желаете представить себе всю огромность этого числового великана, прикиньте, какой величины амбар потребовался бы для вмещения подобного количества зерен. Известно, что кубический метр пшеницы вмещает около 15 миллионов зерен. Значит, награда шахматного изобретателя должна была бы занять объем примерно в 12 000 000 000 000 куб. м, или 12 000 куб. км. При высоте амбара 4 м и ширине 10 м длина его должна была бы простираться на 300 000 000 км, то есть вдвое дальше, чем от Земли до Солнца!
Алгебра, 7 класс: уроки, тесты, задания
Информация о разделе
Математический язык. Математическая модель
-
Числовые и алгебраические выражения
-
Что такое математический язык
-
-
Линейное уравнение с одной переменной
-
Координатная прямая
Линейная функция
-
Координатная плоскость
-
Линейное уравнение с двумя переменными и его график
-
Линейная функция y = kx + m и её график
-
-
Взаимное расположение графиков линейных функций
Системы двух линейных уравнений с двумя переменными
-
Основные понятия
-
Метод подстановки
-
Метод алгебраического сложения
-
Системы двух линейных уравнений с двумя неизвестными как математические модели реальных ситуаций
Степень с натуральным показателем и её свойства
-
Что такое степень с натуральным показателем
-
Таблица основных степеней
-
Свойства степени с натуральным показателем
-
Умножение и деление степеней с одинаковым показателем
-
Степень с нулевым показателем
Одночлены. Арифметические операции над одночленами
-
Понятие одночлена. Стандартный вид одночлена
-
Сложение и вычитание одночленов
-
Умножение одночленов. Возведение одночлена в натуральную степень
-
Деление одночлена на одночлен
Многочлены. Арифметические операции над многочленами
-
Основные понятия
-
Сложение и вычитание многочленов
-
Умножение многочлена на одночлен
-
Умножение многочлена на многочлен
-
Формулы сокращённого умножения
-
Деление многочлена на одночлен
Разложение многочлена на множители
-
Что такое разложение на множители
-
Вынесение общего множителя за скобки
-
Способ группировки
-
Разложение многочлена на множители с помощью формул сокращённого умножения
-
Разложение многочлена на множители с помощью комбинации различных приёмов
-
Сокращение алгебраических дробей
-
Тождества
Квадратичная функция y = x²
-
Квадратичная функция и её график
-
Графическое решение уравнений
-
Что означает в математике запись у = f(x)
Задания для текущего контроля знаний, алгебра 7 класс
Задания для текущего контроля знаний , алгебра 7 класс
Предлагаю задания для организации контроля знаний учащихся, которые содержат вопросы по теории (В), задания для устного решения (У), задания для письменного решения (П) и дополнительные задания (Д).Предлагаемые задания можно использовать при актуализации знаний, организации работы в парах или в группах, при подготовке к контрольной работе.
Тема «Числовые выражения и выражения с переменными»
Приведите примеры числовых выражений и выражений с переменными.Какие знаки используют для сравнения значений выражений?
Привесимте пример двойного неравенства и прочитайте его
Приведите примеры строгих и нестрогих неравенств
Какие свойства действий над числами вы знаете?
Приведите пример тождества
Какие статистические характеристики вы знаете? Как их находят? Приведите пример их практического применения.
1.Вычислите:
а) 1,6+3,4 б) 5-6,5
в) -4,2+6,2 г) (-0,3)2
д)  е)
е) 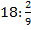
ж) 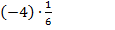 з)
з) 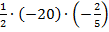
2.Используя термины сумма, разность, произведение, частное, прочитайте выражения:
а)my б) n-m
в) a+b г) 4: n-3
д) 3x+9 е) (a+y)c
ж) (2-a)(2+a) з)ac+cd
3.Найдите среднее арифметическое, моду и медиану выборки:
-4; -2; 2; 2; 4; 6
П (задания для письменного решения)
Д (дополнительные задания).
1.Найдите значение выражения:
а) 0,5x+1,8 при x=-4
б) a2 -8a+16 при a=-0,5
в) xy – yz при 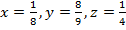
2.Запишите в виде неравенства:
а) х меньше или равно 12
б) с неотрицательное число
3.Запишите в виде двойного неравенства:
а) а больше -5 и меньше или равно 7
б) с неположительное число, больше -5
4.Упростите выражение:
а) 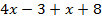
б) 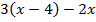
в) 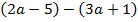
5.Найдите среднее арифметическое, размах, медиану и моду выборки:
а) 18; 24; 18; 15; 19;
б) 10; 9; 15; 17; 12; 13; 11
1.Упростите выражение:
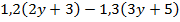
2.Вычислите наиболее рациональным способом:
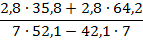
Тема «Степень с натуральным показателем»
Сформулируйте определение степени с натуральным показателем. Приведите примеры степени с натуральным показателем, назовите в каждом из них основание и показатель степени.Сформулируйте основное свойство степени.
Сформулируйте правило умножения степеней с одинаковыми основаниями. Приведите примеры.
Сформулируйте правило деления степеней с одинаковыми основаниями. Приведите примеры.
1.Какие из выражений являются степенями:
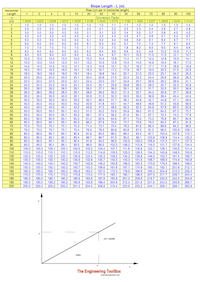
а) 52 б) 5∙3
в) 52+32 г) (-3)2
д) е)
е) 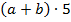
2.Прочитайте степень, назовите основание и показатель степени:
а)m2 б) 310
в) (a+b)3 г) -40
д) (4,5)2 е) 121
ж) -96 з) 012
3.Прочитайте выражения, используя слова сумма, разность, произведение, квадрат, куб:
П (задания для письменного решения)
Д (дополнительные задания).
1.Вычислите:
а) 32 б) 23 в) (-2)4+32 г) (-5)4+(-1)7
д) (-0,4)3 + (-0,2)3 е) (73:200-0,42): (-0,5)3
2.Найдите значение выражения:
а) 14х3 при х= 0; 2; -0,5
б) х3-х2 при х=0,1
в) (х+а)5 при х=-0,8 а=-0,6
3.Представьте в виде степени выражение:
а) 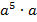
б) 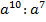
в)(x5)3
г) (-3a)2∙(3a)3
4.Вычислите:
а) 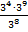
б) 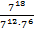
1.Представьте в виде степени:
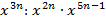
2.Докажите, что значение выражения 39100 делится нацело на 10


| 1. |
Сравнение степеней (отрицательные целые числа)
Сложность: лёгкое |
1 |
| 2. |
Сравнение степеней (десятичная дробь)
Сложность: лёгкое |
3 |
| 3. |
Сравнение степеней (смешанное число и обыкновенная дробь)
Сложность: лёгкое |
2 |
| 4. |
Сравнение степеней (обыкновенная дробь и -1)
Сложность: лёгкое |
3 |
| 5. |
Действия со степенями (основание — бином)
Сложность: среднее |
3 |
| 6. |
Действия со степенями (основание — обыкновенная дробь)
Сложность: среднее |
5 |
| 7. |
Действия со степенями, основание — отрицательный одночлен (целые числа и переменные)
Сложность: среднее |
3 |
| 8. |
Значение выражения (обыкновенные дроби)
Сложность: среднее |
6 |
| 9. |
Значение выражения (целые числа и дроби)
Сложность: среднее |
7 |
| 10. |
Числовое значение дроби
Сложность: среднее |
6 |
Самостоятельная работа по теме «Действия со степенями», 7 класс.
Самостоятельная работа. Вариант 1.
1. Записать формулу возведения в степень произведения множителей.
2. Упростите:
а. a5.a4.a3:a7= г. (c2)3.c5:(c4)2=
б. x4😡3.x7= д. (2ab)4=
в. (a2)3= е. (5a3. b5)4=
3. Вычислите:
а. 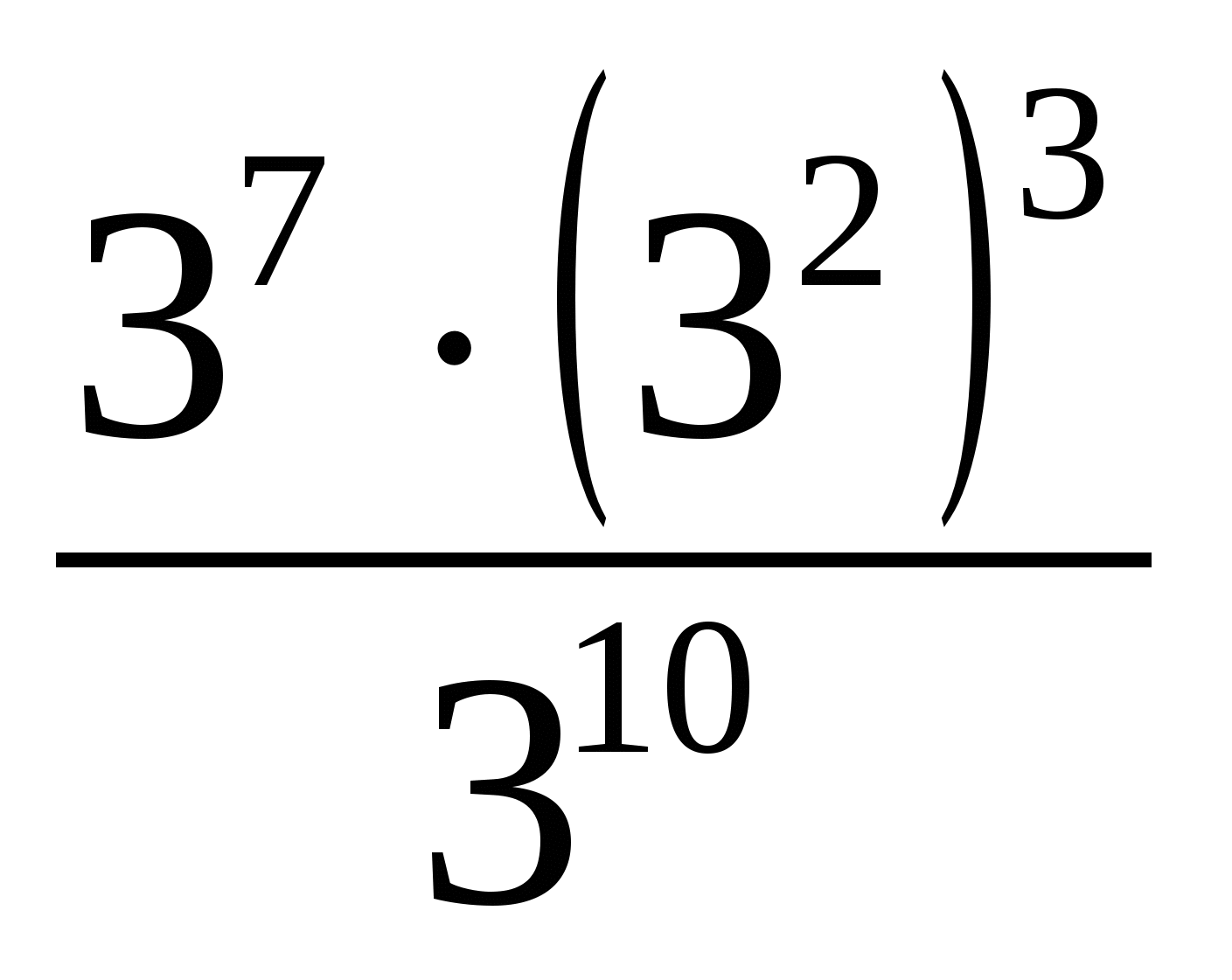 = в. 27.34=
= в. 27.34=
б. 55.0,25.45=
Самостоятельная работа. Вариант 2.
1. Записать формулу возведения степени в степень.
2. Упростите:
а. b4.b6.b3:b5= г. (c5)3.c4:(c7)2=
б. x7.x3😡5= д. (3x.y)3=
в. (a4)6= е. (2a2.b6)5=
3. Вычислите:
а. 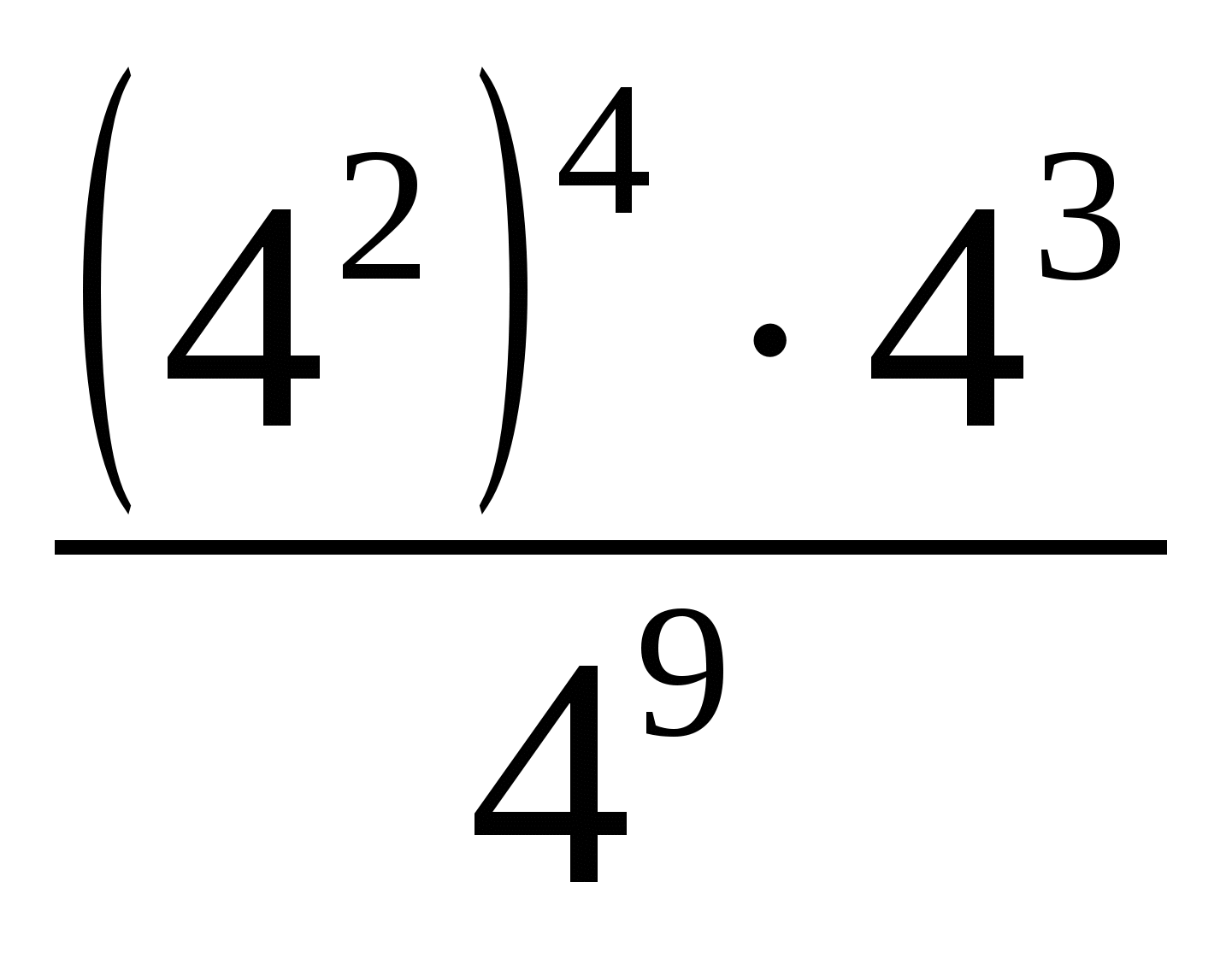 = в. 8.24=
= в. 8.24=
б. 103.0,13.53=
Самостоятельная работа. Вариант 3.
1. Записать формулу умножения степеней.
2. Упростите:
а. a4.a7.a5:a8= г. (c8)3.c4:(c2)5=
б. x11😡6.x4= д. (6ab)3=
в. (a7)9= е. (2a6. b7)3=
3. Вычислите:
а. 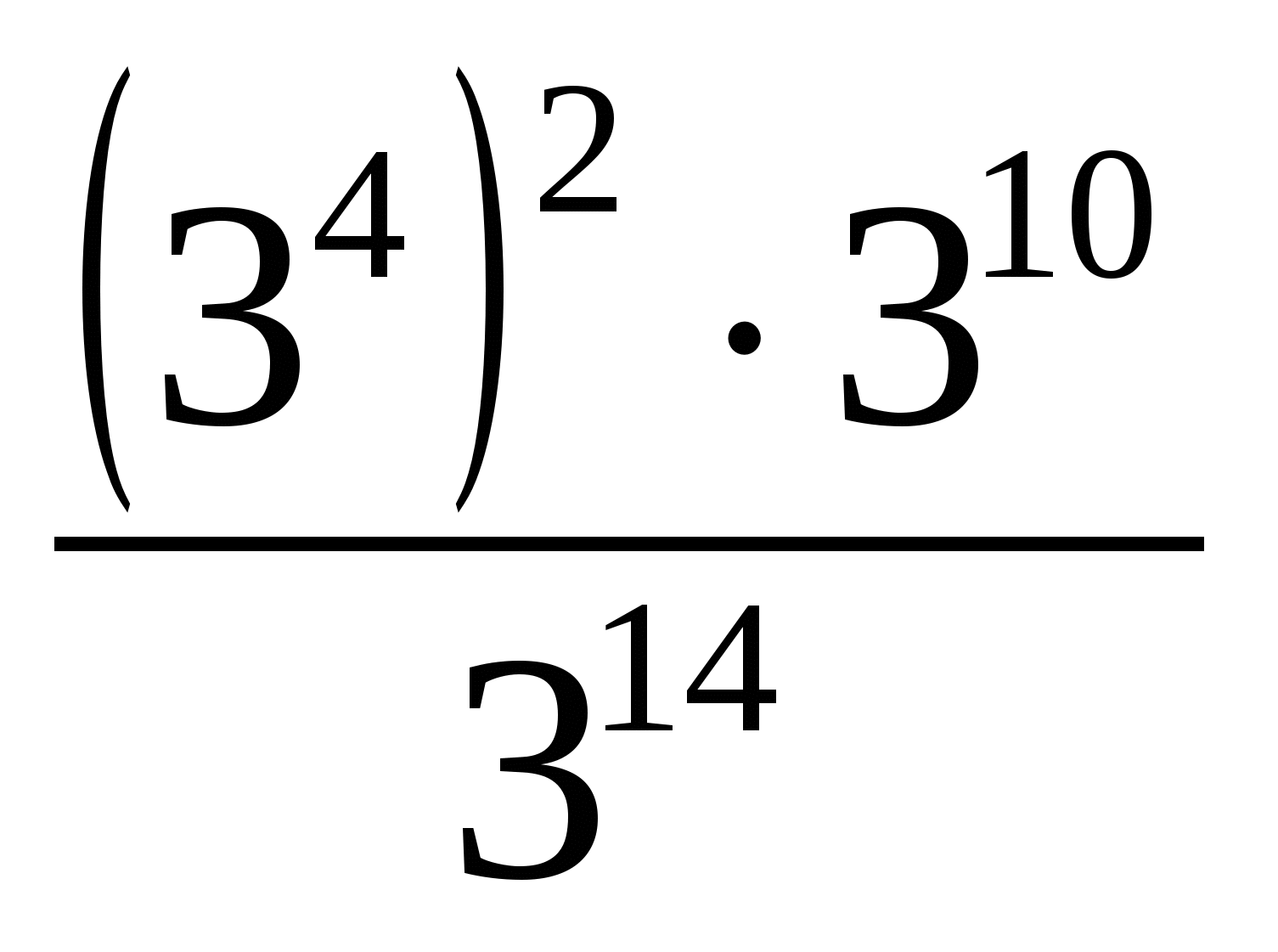 = в. 81.33=
= в. 81.33=
б. 56.0,26.36=
Самостоятельная работа. Вариант4.
1. Записать формулу деления степеней.
2. Упростите:
а. b6.b7.b2:b8= г. (c5)3.c4:(c4)2=
б. x9.x5😡3= д. (4x.y)3=
в. (a3)7= е. (3a4.b6)3=
3. Вычислите:
а. 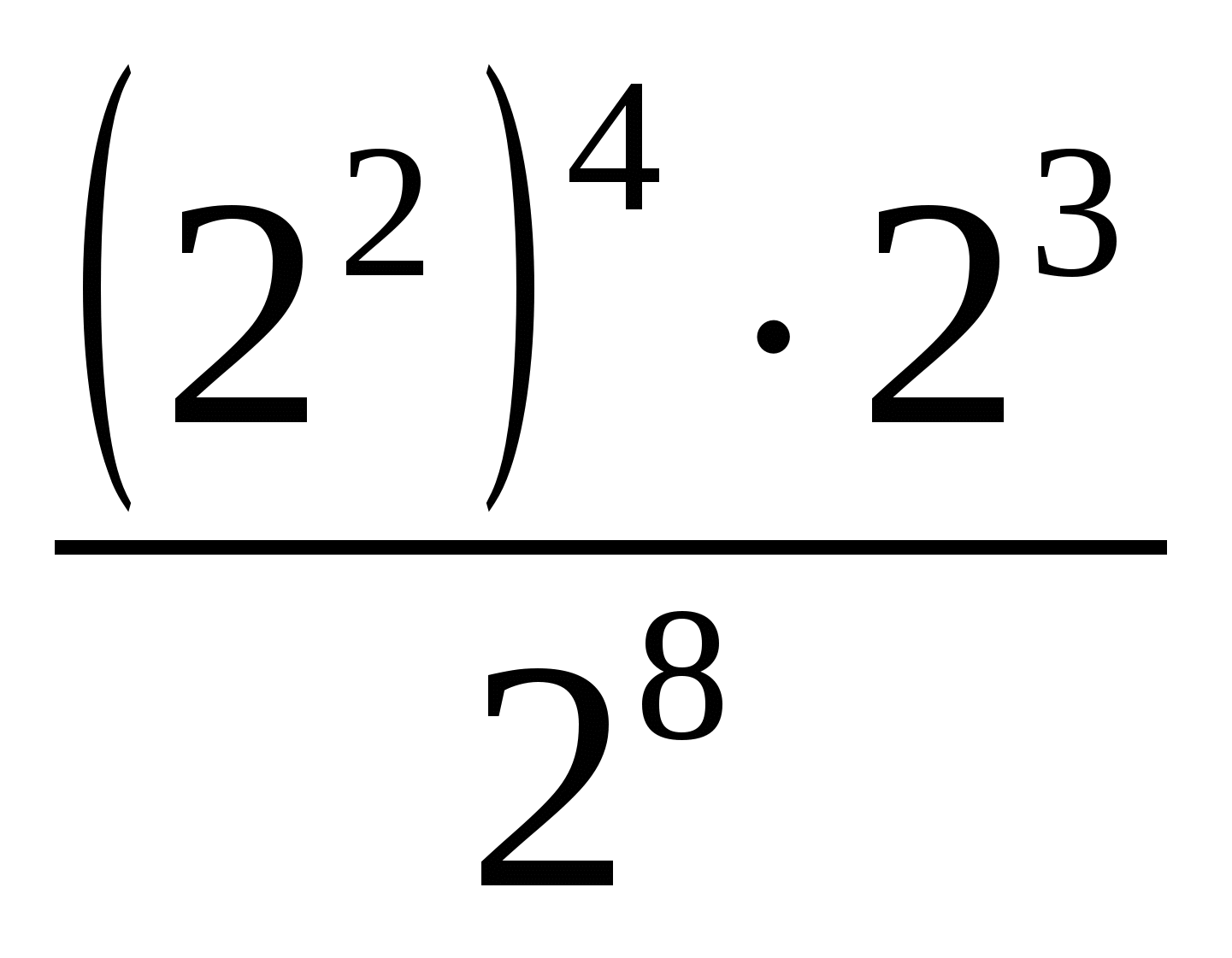 =
=
б. 105.0,15.35=
в. 16.24=
Самостоятельная работа. Вариант 1.
1. Записать формулу возведения в степень произведения множителей.
2. Упростите:
а. a5.a4.a3:a7= г. (c2)3.c5:(c4)2=
б. x4😡3.x7= д. (2ab)4=
в. (a2)3= е. (5a3. b5)4=
3. Вычислите:
а. 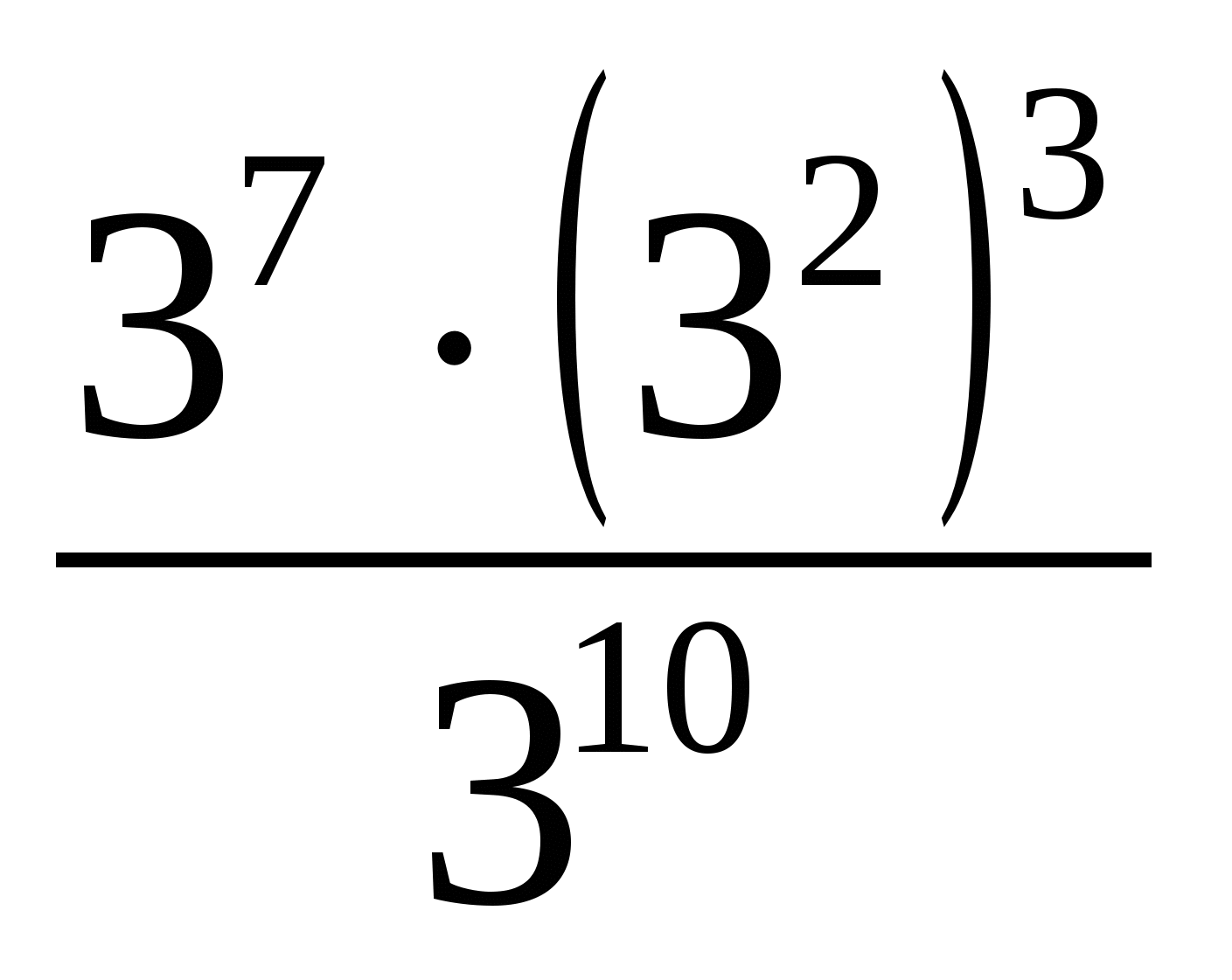 = в. 27.34=
= в. 27.34=
б. 55.0,25.45=
Самостоятельная работа. Вариант 2.
1. Записать формулу возведения степени в степень.
2. Упростите:
а. b4.b6.b3:b5= г. (c5)3.c4:(c7)2=
б. x7.x3😡5= д. (3x.y)3=
в. (a4)6= е. (2a2.b6)5=
3. Вычислите:
а. 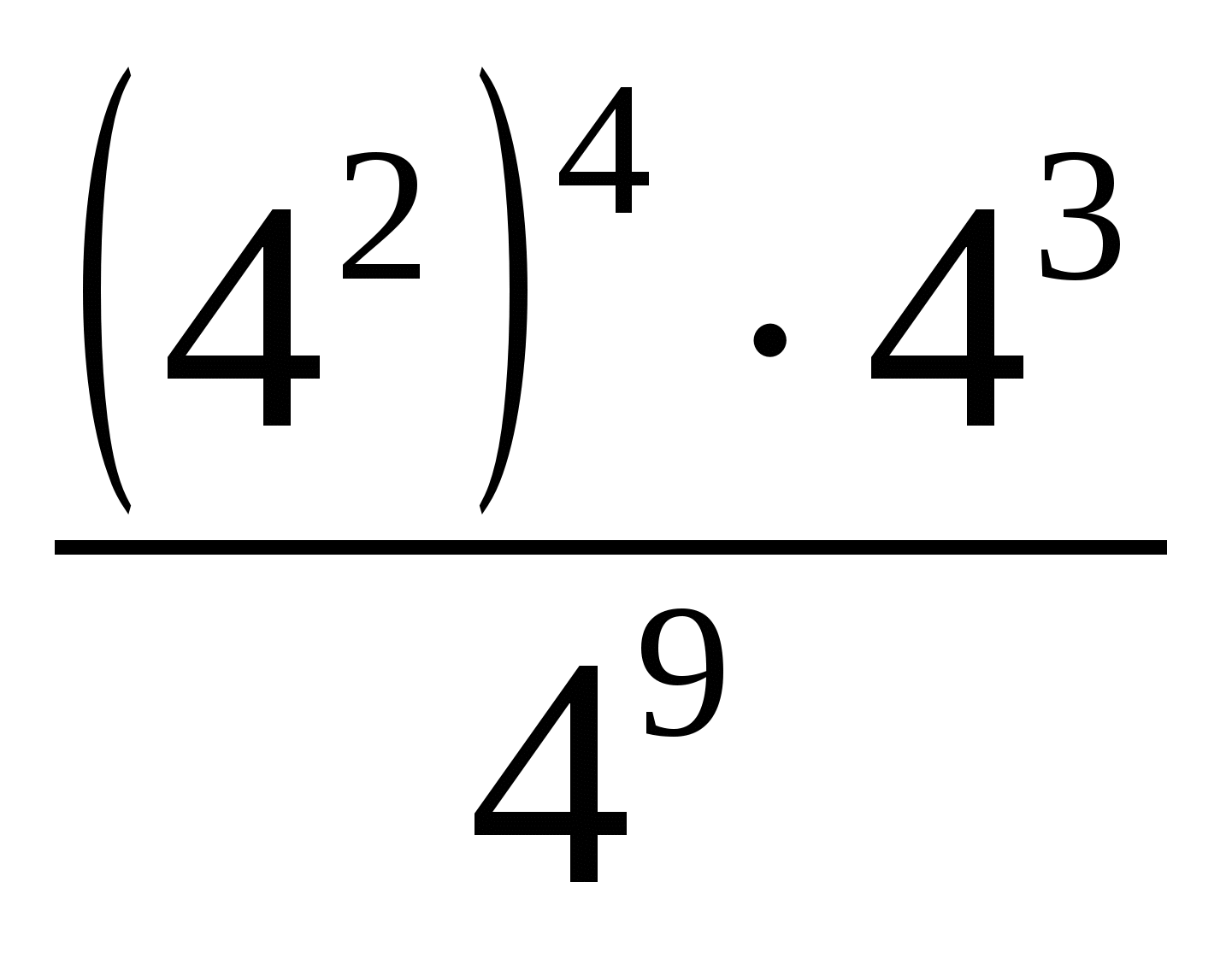 = в. 8.24=
= в. 8.24=
б. 103.0,13.53=
Самостоятельная работа. Вариант 3.
1. Записать формулу умножения степеней.
2. Упростите:
а. a4.a7.a5:a8= г. (c8)3.c4:(c2)5=
б. x11😡6.x4= д. (6ab)3=
в. (a7)9= е. (2a6. b7)3=
3. Вычислите:
а. 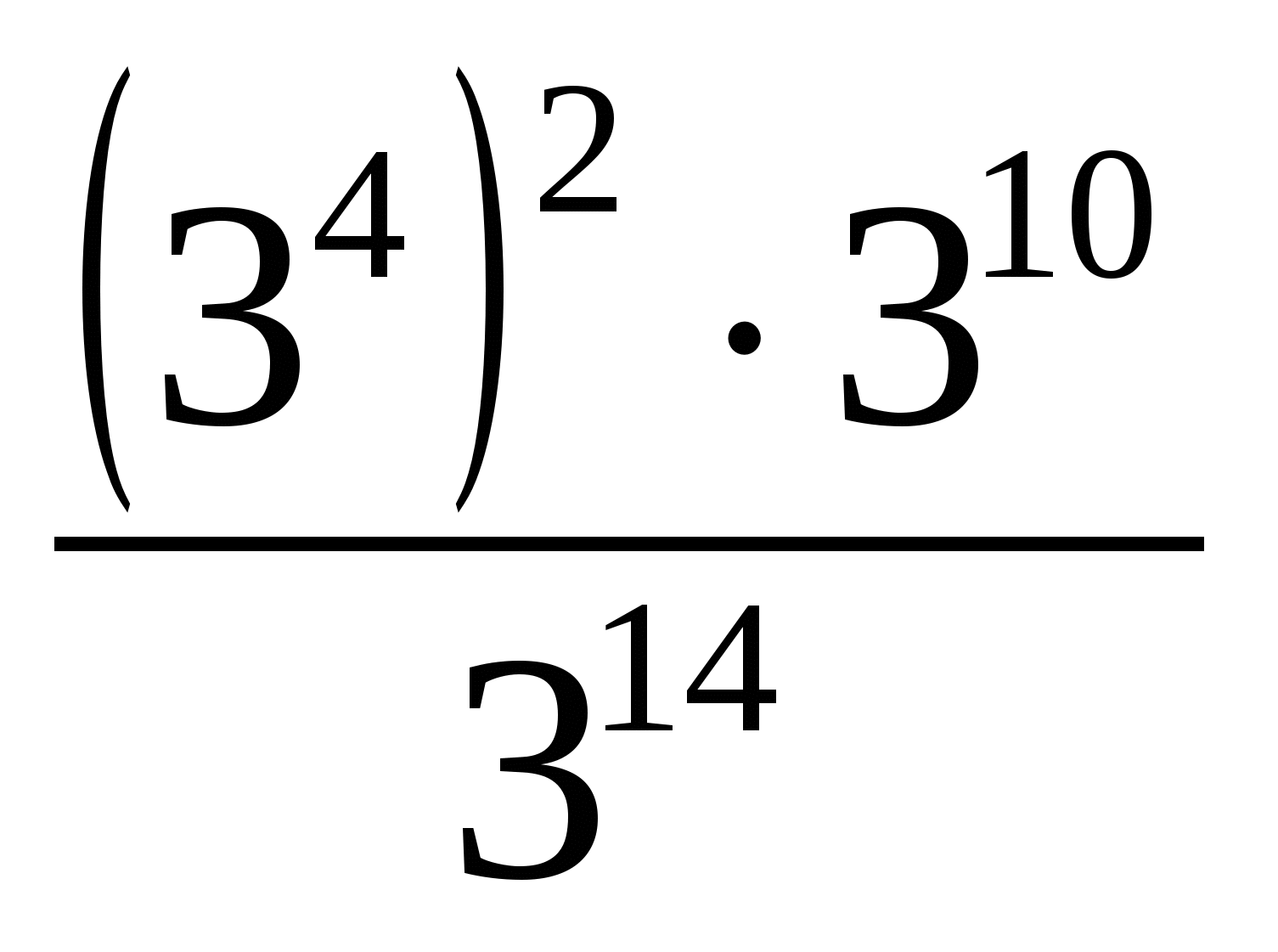 = в. 81.33=
= в. 81.33=
б. 56.0,26.36=
Самостоятельная работа. Вариант4.
1. Записать формулу деления степеней.
2. Упростите:
а. b6.b7.b2:b8= г. (c5)3.c4:(c4)2=
б. x9.x5😡3= д. (4x.y)3=
в. (a3)7= е. (3a4.b6)3=
3. Вычислите:
а. 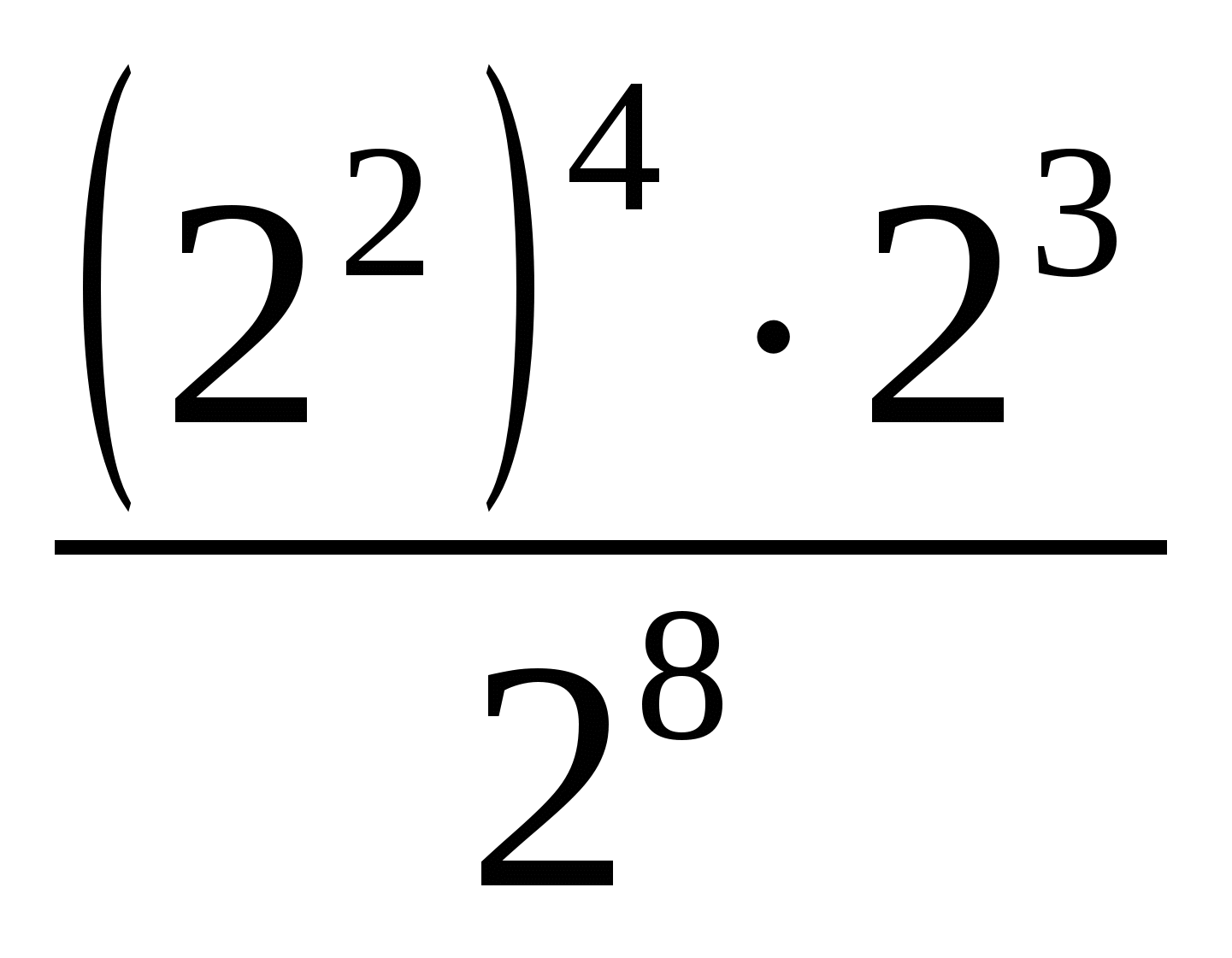 =
=
б. 105.0,15.35=
в. 16.24=
| 1. |
Произведение в виде степени (положительные числа)
Сложность: лёгкое |
3,5 |
| 2. |
Основание и показатель степени (числа)
Сложность: лёгкое |
3 |
| 3. |
Степень бинома
Сложность: лёгкое |
1,5 |
| 4. |
Основание и показатель степени (бином)
Сложность: лёгкое |
2 |
| 5. |
Произведение одинаковых множителей (одночлен)
Сложность: лёгкое |
1 |
| 6. |
Произведение одинаковых множителей (бином)
Сложность: лёгкое |
1 |
| 7. |
Степень числа (показатель степени — n)
Сложность: лёгкое |
2 |
| 8. |
Степень числа (основание)
Сложность: лёгкое |
2 |
| 9. |
Значение степени (обыкновенная дробь)
Сложность: лёгкое |
2 |
| 10. |
Площадь квадрата
Сложность: лёгкое |
2 |
| 11. |
Квадрат числа (минус перед числом)
Сложность: лёгкое |
2 |
| 12. |
Числовые неравенства, сравнение
Сложность: лёгкое |
1 |
| 13. |
Возведение в степень десятичных дробей
Сложность: лёгкое |
1 |
| 14. |
Возведение в степень целых чисел
Сложность: лёгкое |
1 |
| 15. |
Возведение в степень дробей (смешанных чисел)
Сложность: среднее |
2 |
| 16. |
Произведение степеней и простых чисел
Сложность: среднее |
3 |
| 17. |
Произведение (целые числа)
Сложность: среднее |
3 |
| 18. |
Частное (чётная степень)
Сложность: среднее |
3 |
| 19. |
Дробь
Сложность: среднее |
3 |
| 20. |
Разность произведений
Сложность: среднее |
4 |
| 21. |
Сумма произведений
Сложность: среднее |
5 |
| 22. |
Уравнение
Сложность: среднее |
5 |
| 23. |
Убывание (возрастание) степеней
Сложность: среднее |
4 |
7 Уравнения высоких степеней
Навигация Математушка- Наши выпускники
- Оставить заявку
- ЕГЭ
- Статьи
- Контакты
- Цены
- Заочное обучение
- Войти
7 Уравнения высоких степеней
Задача № 1

Ответ:

Решение:

Ответ:

Задача № 2

Ответ:

Решение:

Ответ:

Задача № 3

Ответ:

Решение:

Ответ:

Задача № 4

Ответ:

Решение:

Ответ:

Задача № 5

Ответ:

Решение:

Ответ:

Задача № 6

Ответ:

Решение:

Ответ:

Задача № 7

Ответ:

Решение:

Ответ:

Задача № 8

Ответ:

Решение:

Ответ:

Задача № 9

Ответ:

Решение:

Ответ:

Задача № 10

Ответ:

Решение:

Ответ:

Задача № 11

Ответ:

Решение:

Ответ:

Задача № 12

Ответ:

Решение:

Ответ:

Задача № 13

Ответ:

Решение:

Ответ:

Задача № 14

Ответ:

Решение:

Ответ:

Задача № 15

Ответ:

Решение:

Ответ:

Задача № 16

Ответ:

Решение:

Ответ:

Задача № 17

Ответ:

Решение:

Ответ:

Задача № 18

Ответ:

Решение:

Ответ:

Задача № 19

Ответ:

Решение:

Ответ:

Задача № 20

Ответ:

Решение:

Ответ:

Задача № 21

Ответ:

Решение:

Ответ:

Задача № 22

Ответ:

Решение:

Ответ:

Задача № 23

Ответ:

Решение:

Ответ:

Задача № 24

Ответ:

Решение:

Ответ:

Задача № 25

Ответ:

Решение:

Ответ:

Задача № 26

Ответ:
Стандарты общего ядра 7 класса
Вот Общие основные стандарты для 7-го класса со ссылками на ресурсы, которые их поддерживают. Мы также поощряем много упражнений и книжную работу.
7 класс | Соотношения и пропорциональные отношения
Анализируйте пропорциональные отношения и используйте их для решения реальных и математических задач.
7.RP.A.1 Вычислить удельные веса, связанные с соотношениями долей, включая соотношения длин, площадей и других величин, измеренных в одинаковых или разных единицах.Например, если человек проходит 1/2 мили за каждые 1/4 часа, вычислите единичную скорость как сложную долю (1/2) / (1/4) миль в час, что эквивалентно 2 милям в час.
Соотношение — Рецепт шоколадных чипсов Соотношение — приготовить шоколадные чипсы 7.RP.A.2 Распознавать и представлять пропорциональные отношения между количествами.
а. Решите, находятся ли две величины в пропорциональном отношении, например, проверив эквивалентные отношения в таблице или построив график на координатной плоскости и наблюдая, является ли график прямой линией, проходящей через начало координат.
г. Определите константу пропорциональности (единицу измерения) в таблицах, графиках, уравнениях, диаграммах и словесных описаниях пропорциональных отношений.
г. Изобразите пропорциональные отношения уравнениями. Например, если общая стоимость t пропорциональна количеству n товаров, купленных по постоянной цене p, связь между общей стоимостью и количеством товаров может быть выражена как t = pn.
г. Объясните, что означает точка (x, y) на графике пропорциональной зависимости с точки зрения ситуации, уделяя особое внимание точкам (0, 0) и (1, r), где r — удельная ставка.
7.RP.A.3 Используйте пропорциональные отношения для решения многошаговых задач с соотношением шагов и процентов. Примеры: простые проценты, налог, наценки и уценки, чаевые и комиссии, сборы, увеличение и уменьшение процентов, ошибка в процентах.
Разница в процентах Процент ошибок Изменение в процентахКласс 7 | Система счисления
Применяйте и расширяйте предыдущие представления об операциях с дробями для сложения, вычитания, умножения и деления рациональных чисел.
7.NS.А.1 Применять и расширять предыдущие представления о сложении и вычитании для сложения и вычитания рациональных чисел; представляют собой сложение и вычитание на горизонтальной или вертикальной числовой линейной диаграмме.
а. Опишите ситуации, в которых противоположные количества объединяются, чтобы получить 0. Например, атом водорода имеет нулевой заряд, потому что его две составляющие заряжены противоположно.
г. Под p + q понимается число, находящееся на расстоянии | q | от p в положительном или отрицательном направлении в зависимости от того, положительный или отрицательный q.Докажите, что сумма числа и его противоположности равна 0 (аддитивно противоположны). Интерпретируйте суммы рациональных чисел, описывая контексты реального мира.
г. Под вычитанием рациональных чисел понимается добавление обратного аддитивного числа p — q = p + (-q). Покажите, что расстояние между двумя рациональными числами на числовой прямой является абсолютной величиной их разницы, и примените этот принцип в контексте реального мира.
г. Применяйте свойства операций как стратегии для сложения и вычитания рациональных чисел.
7.NS.A.2 Применяйте и расширяйте предыдущие представления об умножении, делении и дробях для умножения и деления рациональных чисел.
а. Поймите, что умножение расширяется от дробей до рациональных чисел, требуя, чтобы операции продолжали удовлетворять свойствам операций, в частности свойству распределения, что приводит к таким произведениям, как (-1) (- 1) = 1, и правилам умножения чисел со знаком.Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.
г. Поймите, что целые числа можно делить при условии, что делитель не равен нулю, и каждое частное целых чисел (с ненулевым делителем) является рациональным числом. Если p и q целые числа, то — (p / q) = (-p) / q = p / (- q). Интерпретируйте частные рациональных чисел, описывая контексты реального мира.
г. Применяйте свойства операций как стратегии умножения и деления рациональных чисел.
г. Преобразуйте рациональное число в десятичное с помощью длинного деления; знайте, что десятичная форма рационального числа оканчивается нулями или в конечном итоге повторяется.
7.NS.A.3. Решение реальных и математических задач с использованием четырех операций с рациональными числами. (Вычисления с рациональными числами расширяют правила манипулирования дробями до сложных дробей.)
7 класс | Выражения и уравнения
Используйте свойства операций для создания эквивалентных выражений.
7.EE.A.1 Применяйте свойства операций как стратегии для сложения, вычитания, разложения и расширения линейных выражений с рациональными коэффициентами.
7.EE.A.2. Поймите, что переписывание выражения в различных формах в контексте проблемы может пролить свет на проблему и на то, как соотносятся количества в ней. Например, a + 0,05a = 1,05a означает, что «увеличить на 5%» — это то же самое, что «умножить на 1,05».
Десятичные дроби и процентыРешайте реальные и математические задачи, используя числовые и алгебраические выражения и уравнения.
7.EE.B.3 Решайте многоступенчатые реальные и математические задачи, поставленные с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), используя инструменты стратегически.Применяйте свойства операций как стратегии для вычислений с числами в любой форме; конвертировать между формами по мере необходимости; и оценить разумность ответов с помощью мысленных вычислений и стратегий оценки. Например: если женщина, зарабатывающая 25 долларов в час, получает прибавку на 10%, она будет дополнительно получать 1/10 своей зарплаты в час, или 2,50 доллара, с новой зарплаты в 27,50 долларов. Если вы хотите разместить штангу для полотенец длиной 9 3/4 дюйма в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить штангу на расстоянии примерно 9 дюймов от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.
7.EE.B.4. Используйте переменные для представления величин в реальных или математических задачах и создавайте простые уравнения и неравенства для решения проблем, рассуждая о величинах. 7 класс | Геометрия Рисуйте, конструируйте и описывайте геометрические фигуры и описывайте отношения между ними. 7.G.A.1. Решение проблем, связанных с масштабными чертежами геометрических фигур, включая вычисление фактических длин и площадей на основе масштабного чертежа и воспроизведение масштабного чертежа в другом масштабе. Ниже приведены необходимые навыки со ссылками на ресурсы, которые помогут с этим навыком. Мы также поощряем много упражнений и книжную работу. Curriculum Home Важно: это только руководство. 7 класс | Division ☐ Понять и уметь использовать Long Division 7 класс | Числа ☐ Различать различные подмножества действительных чисел (подсчет / натуральные числа, целые числа, целые числа, рациональные числа и иррациональные числа) ☐ Определите факторизацию данного числа на простые множители и запишите в экспоненциальной форме ☐ Упростите выражения, используя порядок операций (Примечание: выражения могут включать абсолютное значение, квадратные корни и / или целые показатели степени больше 0.) ☐ Сложение, вычитание, умножение и деление целых чисел ☐ Сложить два целых числа (с числовой строкой и без нее) ☐ Развить концептуальное понимание отрицательных и нулевых показателей степени с основанием из десяти и относящихся к дробям и десятичным знакам (например, 10 -2 = 0,01 = 1/100) ☐ Распознавать и указывать значение квадратного корня из полного квадрата (до 225) ☐ Определите квадратный корень из неполных квадратов (или более сложных полных квадратов) с помощью калькулятора ☐ Классифицируйте иррациональные числа как неповторяющиеся / не завершающие десятичные дроби ☐ Определите два последовательных целых числа, между которыми лежит квадратный корень из неполного квадратного целого числа меньше 225 (с использованием числовой прямой и без нее) ☐ Признайте разницу между рациональными и иррациональными числами (например,g., исследуйте различные приближения числа пи) ☐ Разместите рациональные и иррациональные числа (приближения) на числовой прямой и выровняйте расположение. ☐ Записывайте числа в экспоненциальном представлении ☐ Заменить числа, записанные в экспоненциальном представлении, на обычные числа Наклон или градиент линии описывает направление и крутизну линии. Наклон может быть выражен в углах, уклонах или ступенях. S угол = tan -1 (y / x) (1) где S угол = угол (рад, градусы (°)) x = горизонтальный участок (м, фут..) y = вертикальный подъем (м, футы …) Наклон как угол для отметки 1 м на расстоянии 2 м можно вычислить как S угол = тангаж -1 ((1 м) / (2 м)) = 26,6 ° S уклон (%) = (100%) y / x (2) где S уклон (%) = уклон (%) Уклон как уклон для отметки 1 м на расстоянии 2 м можно рассчитать как S уклон (%) = (1 м) / (2 м) = 50 (%) Уклон кровли — это уклон, создаваемый стропилами.Вы можете найти уклон крыши в виде x: 12, например 4/12 или 9/12. Уклон кровли в форме x: 12 может быть выражен в ступенях как S, уклон (%) = (100%) x / 12 (3) S уклон (%) = (100%) 4/12 = 33,3% Уклон крыши на форме x: 12 может быть выражен в углах как S угол = tan -1 (x / 12) (3b) S угол = tan -1 (4/12) = 18.4 ° Расчет угловых градусов, уклона и длины уклона. y — вертикальный подъем (м, футы, дюймы ….) x — горизонтальный проход (м, футы, дюймы ….) (включить всплывающее окно) Используйте эту диаграмму для оценки наклона или уклона. Измерьте горизонтальный пробег и вертикальный подъем и проведите линии на диаграмме, чтобы оценить наклон.
а. Решайте задачи со словами, приводящие к уравнениям вида px + q = r и p (x + q) = r, где p, q и r — конкретные рациональные числа. Бегло решать уравнения этих форм. Сравните алгебраическое решение с арифметическим, определяя последовательность операций, используемых в каждом подходе.Например, периметр прямоугольника 54 см. Его длина 6 см. Какая у него ширина?
г. Решите проблемы со словами, приводящие к неравенствам вида px + q> r или px + q 7 класс Учебная программа
Обратитесь в местный орган управления образованием, чтобы узнать их требования. градусов, градиент и преобразователь уклона
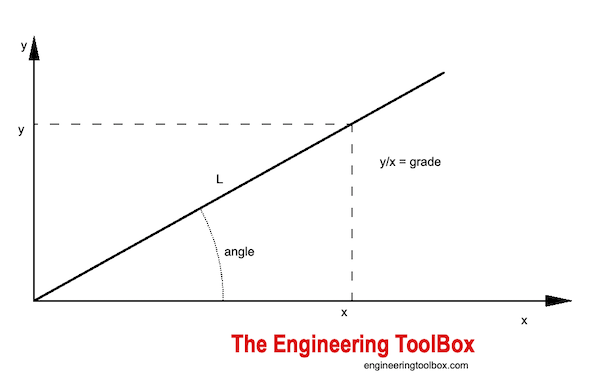
Наклон, выраженный как Угол
Пример — уклон как угол
Наклон, выраженный как уклон
Пример — уклон как уклон
Наклон и Уклон кровли
Пример — Изображение крыши 4/12 для степени
Пример — пик крыши 4/12 как угол
Калькулятор наклона или уклона
Диаграмма наклона или уклона
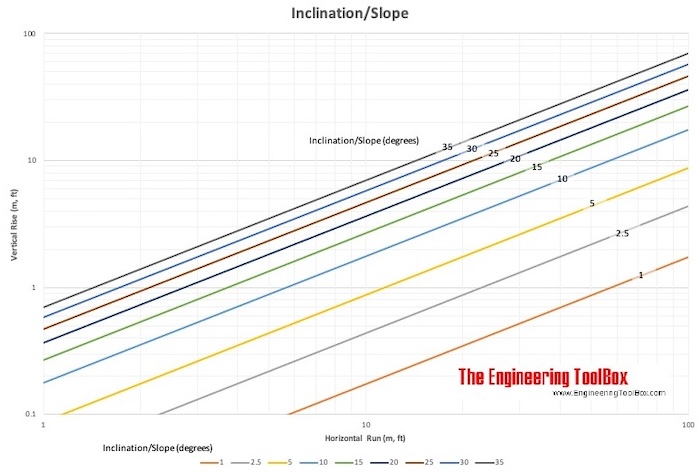
Уклоны в зависимости от уклонов и% уклонов
Уклон Угол
(градусы) Уклон Уклон
(%) X 0,1 1 573,0 0,17 0,2 1 286,5 0.35 0,3 1 191,0 0,52 0,4 1 143,2 0,70 0,5 1 100 1 0,6 1 95,49 1,05 0,7 1 81.85 1,22 0,8 1 71,62 1,40 0,9 1 63,66 1,57 9064 2 1 28,64 3,49 3 1 19,08 5,24 4 1 14.30 6,99 5 1 11,43 8,75 5,74 1 10 10 7 1 8,144 12,3 8 1 7,115 14,1 9 1 6.314 15,8 10 1 5,671 17,6 11 1 5,145 19,4 13 1 4,331 23,1 14 1 4,011 24,9 15 1 3.732 26,8 16 1 3,487 28,7 17 1 3,271 30,6 3,0 19 1 2,904 34,4 20 1 2,747 36,4 21 1 2.605 38,4 22 1 2,475 40,4 23 1 2,356 42,4 25 1 2,145 46,6 26 1 2,050 48,8 27 1 1.963 51,0 28 1 1,881 53,2 29 1 1,804 55,4 31 1 1,664 60,1 32 1 1,600 62,5 33 1 1.540 64,9 34 1 1,483 67,5 35 1 1,428 70,0 37 1 1,327 75,4 38 1 1,280 78,1 39 1 1.235 81,0 40 1 1,192 83,9 41 1 1,150 86,9 43 1 1,072 93,3 44 1 1,036 96,6 45 1 1.000 100,0 46 1 0,9657 103,6 47 1 0,9325 107,2 49 1 0,8693 115,0 50 1 0,8391 119,2 51 1 0.8098 123,5 52 1 0,7813 128,0 53 1 0,7536 132,7 55 1 0,7002 142,8 56 1 0,6745 148,3 57 1 0.6494 154,0 58 1 0,6249 160,0 59 1 0,6009 166,4 61 1 0,5543 180,4 62 1 0,5317 188,1 63 1 0.5095 196,3 64 1 0,4877 205,0 65 1 0,4663 214,5 67 1 0,4245 235,6 68 1 0,4040 247,5 69 1 0.3839 260,5 70 1 0,3640 274,7 71 1 0,3443 290,4 73 1 0,3057 327,1 74 1 0,2867 348,7 75 1 0.2679 373,2 76 1 0,2493 401,1 77 1 0,2309 433,1 79 1 0,1944 514,5 80 1 0,1763 567,1 81 1 0.1584 631,4 82 1 0,1405 711,5 83 1 0,1228 814,4 85 1 0,08749 1143 86 1 0,06993 1430 87 1 0.05241 1908 88 1 0,03492 2864 89 1 0,01746 5729 Вертикальный подъем, горизонтальный ход и длина наклона