Научно-исследовательская работа на тему: «тригонометрия в нашей жизни»
III-я региональная научно-практическая конференция
для старшеклассников школ Челябинской области
Тригонометрия в нашей жизни
секция «Математика»
Автор: Суворова Анастасия, 10 класса
МОУ Кременкульской СОШ
с. Кременкуль
Научный руководитель:
Грязнова Татьяна Александровна,
учитель математики,
МОУ Кременкульской СОШ
с. Долгодеревенское, 2019
Содержание
Введение | 3 |
I. |
|
1.1 История возникновения | 4 |
1.2 Архитектура | 7 |
1.3 Медицина и биология | 8 |
1.4 Измерительные работы | 9 |
II. Практическая часть |
|
2.1. Исследование и создание своего графика биоритмов жизни | 10 |
III. Заключение |
|
3.1 Описание аналитической части | 11 |
3. | 11 |
3.3. Выводы и предложения | 11 |
Список литературы | 12 |
Приложение 1 | 13 |
Приложение 2 | 14 |
Введение
Актуальность:
Данная тема является одной из самых актуальных. Она находит широкое применение в разных разделах математики, и других областях науки, а также тесно связана с деятельностью человека. Имеет теоретическую и практическую значимость.
Объект исследования: Тригонометрия.
Предмет исследования: Графики тригонометрической функции
Цель:
Узнать
о способах применения графиков тригонометрических функции в жизни человека.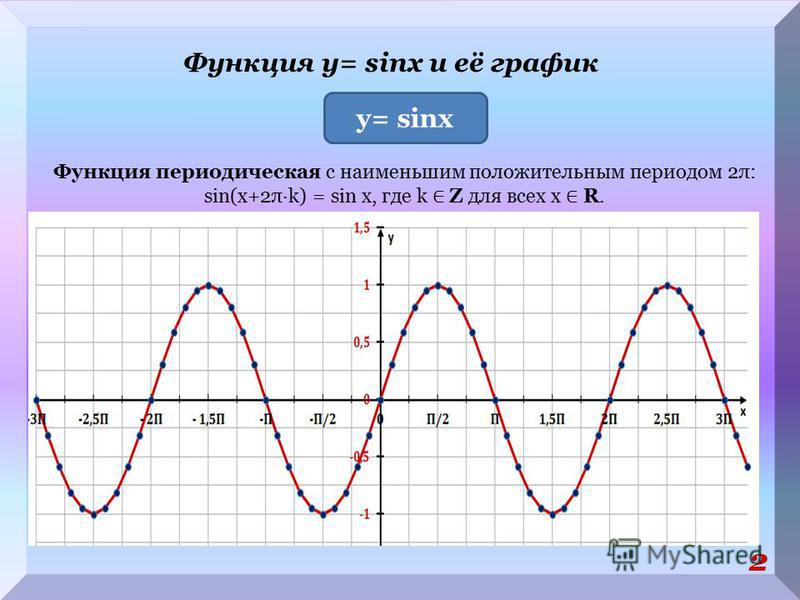
Задачи:
1. Изучить теорию.
2. Составить историческую справку о графиках тригонометрических функций.
3. Описать применение графиков тригонометрических функций в окружающем нас мире и различных отраслях.
4. Вывести свой биоритм жизни.
5. Изготовить демонстрационную модель движения графика синуса.
Методы:
1. Теоретический.
2. Аналитический.
Гипотеза:
Графики тригонометрических функций широко применяются человеком, начиная с древности, и заканчивая настоящим временем.
I. Теоретическая часть
Многие задаются вопросами: зачем нужна тригонометрия? Как она используется в нашем мире? С чем может быть связана тригонометрия? И вот ответы на эти вопросы.
Тригонометрия
или тригонометрические функции используются в астрономии (особенно для расчётов
положения небесных объектов), когда требуется сферическая тригонометрия, в
акустике, в оптике, в анализе финансовых рынков, в статистике, в биологии, в
медицинской визуализации, например, компьютерной томографии и ультразвук, в
химии (Приложение 1, рис. 1), в сейсмологии (Приложение 1, рис.2), в
метеорологии, в океанографии (Приложение 1, рис.3), в архитектуре (Приложение
1, рис.4), в экономике, в компьютерной графике, в кристаллографии (Приложение
1, рис.5) и многих других областях.
1), в сейсмологии (Приложение 1, рис.2), в
метеорологии, в океанографии (Приложение 1, рис.3), в архитектуре (Приложение
1, рис.4), в экономике, в компьютерной графике, в кристаллографии (Приложение
1, рис.5) и многих других областях.
Часто с синусами и косинусами приходится сталкиваться геодезистам. Они имеют специальные инструменты для точного измерения углов. При помощи синусов и косинусов углы можно превратить в длины или координаты точек на земной поверхности.
1.1. История возникновения
Зачатки тригонометрии можно найти в математических рукописях Древнего Египта, Вавилона и Древнего Китая (Приложение 2, рис.1) . 56-я задача из папируса Ринда (II тысячелетие до н. э.) предлагает найти наклон пирамиды, высота которой равна 250 локтей, а длина стороны основания — 360 локтей.
Дальнейшее
развитие тригонометрии связано с именем астронома Аристарха Самосского
(III век до н. э.). В его трактате «О величинах и расстояниях Солнца
и Луны» ставилась задача об определении расстояний до небесных тел; эта задача
требовала вычисления отношения сторон прямоугольного треугольника при
известном значении одного из углов.
Несколько
десятилетий спустя Клавдий Птоломей в своих трудах «География»,
«Аналемма» и «Планисферий» даёт подробное изложение тригонометрических
приложений к картографии, астрономии и механике. Среди прочего,
описана стереографическая проекция, исследованы несколько практических
задач, например: определить высоту и азимут небесного светила по
его склонению и часовому углу. С точки зрения тригонометрии, это
значит, что надо найти сторону сферического треугольника по другим двум
сторонам и противолежащему углу.
В общем, можно сказать, что тригонометрия использовалась для:
· точного определения времени суток; (Приложение 2, рис. 3)
· вычисления будущего расположения небесных светил, моментов их восхода и заката, затмений Солнца и Луны;
· нахождения географических координат текущего места;
· вычисления расстояния между городами с известными географическими координатами.
Гномон— древнейший астрономический инструмент, вертикальный предмет (стела, колонна, шест), позволяющий по наименьшей длине его тени (в полдень)
определить угловую высоту солнца. Так, под котангенсом понималась длина тени от вертикального гномонавысотой 12 (иногда 7) единиц; первоначально эти понятия использовались для расчёта солнечных часов. Тангенсом называлась тень от горизонтального гномона. Косекансом и секансом назывались гипотенузы соответствующих прямоугольных треугольников (отрезки AO на рисунке слева)
Тригонометри́ческие
фу́нкции (Приложение 2, рис. 5) — элементарные функции, которые
исторически возникли при рассмотрении прямоугольных треугольников и
выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе (или,
что равнозначно, зависимость хорд и высот от центрального
угла (дуги) в круге). Эти функции нашли широчайшее применение в самых
разных областях науки. Впоследствии определение тригонометрических функций было
расширено, их аргументом теперь может быть произвольное вещественное или
даже комплексное число. Наука, изучающая свойства тригонометрических
функций, называется тригонометрией.
5) — элементарные функции, которые
исторически возникли при рассмотрении прямоугольных треугольников и
выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе (или,
что равнозначно, зависимость хорд и высот от центрального
угла (дуги) в круге). Эти функции нашли широчайшее применение в самых
разных областях науки. Впоследствии определение тригонометрических функций было
расширено, их аргументом теперь может быть произвольное вещественное или
даже комплексное число. Наука, изучающая свойства тригонометрических
функций, называется тригонометрией.
Синус и косинус относятся к прямым тригонометрическим функциям.
Линия
синуса у индийских математиков первоначально называлась «арха-джива»
(«полутетива», то есть половина хорды данной дуги, поскольку дуга с
хордой напоминает лук с тетивой). Затем слово «арха» было отброшено и линию
синуса стали называть просто «джива». Арабские математики, переводя индийские
книги с санскрита, не перевели слово «джива» арабским словом «ватар»,
обозначающим тетиву и хорду, а транскрибировали его арабскими буквами
и стали называть линию синуса «джиба» (جيب). Так как в арабском
языке краткие гласные не обозначаются, а долгое «и» в слове «джиба»
обозначается так же, как полугласная «й», арабы стали произносить название
линии синуса как «джайб», что буквально обозначает «впадина», «пазуха». При
переводе арабских сочинений на латынь европейские переводчики
перевели слово «джайб» латинским словом sinus — «синус», имеющим то
же значение (следует отметить, что именно в этом значении оно применяется как
анатомический термин синус). Термин «косинус» (лат. Cosinus) —
это сокращение от лат. Complementi
sinus — дополнительный синус.
Так как в арабском
языке краткие гласные не обозначаются, а долгое «и» в слове «джиба»
обозначается так же, как полугласная «й», арабы стали произносить название
линии синуса как «джайб», что буквально обозначает «впадина», «пазуха». При
переводе арабских сочинений на латынь европейские переводчики
перевели слово «джайб» латинским словом sinus — «синус», имеющим то
же значение (следует отметить, что именно в этом значении оно применяется как
анатомический термин синус). Термин «косинус» (лат. Cosinus) —
это сокращение от лат. Complementi
sinus — дополнительный синус.
Первый
график синусоиды (Приложение 2, рис. 6) появился в
книге Альбрехта Дюрера (Приложение 2, рис. 4) «Руководство к
измерению циркулем и линейкой» (нем. Underweysung der Messung mit dem
Zirkel und Richtscheyt, 1525 год). В 1630-х годах, Жиль Роберваль (Приложение
2, рис. 7), в ходе своих исследований циклоиды, независимо вычертил синусоиду,
он же опубликовал формулу тангенса двойного угла. Джон Валлис (Приложение
2, рис. 8) в своей «Механике» (1670), опередив своё время, правильно
указал знаки синуса во всех квадрантах и указал, что у синусоиды
бесконечно много «оборотов». График тангенса для первого квадранта впервые
начертил Джеймс Грегори (1668) (Приложение 2, рис. 9).
8) в своей «Механике» (1670), опередив своё время, правильно
указал знаки синуса во всех квадрантах и указал, что у синусоиды
бесконечно много «оборотов». График тангенса для первого квадранта впервые
начертил Джеймс Грегори (1668) (Приложение 2, рис. 9).
В настоящее время график синуса можно встретить в следующих моментах нашей жизни.
1.2. Архитектура
Широко используется тригонометрия в строительстве, а особенно в архитектуре. Большинство композиционных решений и построений
рисунков проходило именно с помощью геометрии. Но теоретические данные мало что значат. Хочу привести пример на построение одной скульптуры французского мастера Золотого века искусства.
Пропорциональное соотношение в построении статуи было идеально. Однако при поднятии статуи на высокий пьедестал, она смотрелась уродливой.
Скульптором
не было учтено, что в перспективе к горизонту уменьшаются многие детали и при
взгляде снизу вверх уже не создается впечатления ее идеальности.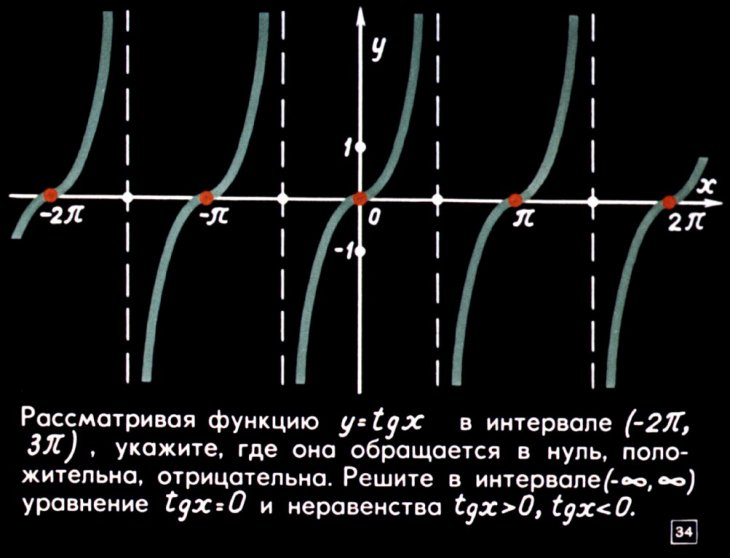 Велось множество
расчетов, чтобы фигура с большой высоты смотрелась пропорционально. В основном
они были основаны на методе визирования, то есть приблизительного измерения, на
глаз. Однако коэффициент разности тех или иных пропорций позволили сделать
фигуру приближенной к идеалу. Таким образом, зная примерное расстояние от
статуи до точки зрения, а именно от верха статуи до глаз человека и высоту
статуи, можно рассчитать синус угла падения взгляда с помощью таблицы (то же
самое мы можем сделать и с нижней точкой зрения), тем самым найдем точку
зрения
Велось множество
расчетов, чтобы фигура с большой высоты смотрелась пропорционально. В основном
они были основаны на методе визирования, то есть приблизительного измерения, на
глаз. Однако коэффициент разности тех или иных пропорций позволили сделать
фигуру приближенной к идеалу. Таким образом, зная примерное расстояние от
статуи до точки зрения, а именно от верха статуи до глаз человека и высоту
статуи, можно рассчитать синус угла падения взгляда с помощью таблицы (то же
самое мы можем сделать и с нижней точкой зрения), тем самым найдем точку
зрения
Ситуация меняется, так как статую поднимают на высоту, поэтому расстояние от верхушки статуи до глаз человека увеличивается, следовательно и синус угла падения увеличивается. Сравнив изменения расстояния от верхушки статуи до земли в первом и во втором случаи, можно найти коэффициент пропорциональности. Впоследствии мы получим чертеж, а потом скульптуру, при поднятии которой зрительно фигура будет приближена к идеалу.
1.3. Медицина и биология.
Модель биоритмов (Приложение 2, рис.11), которые в свою очередь подразумевают цикличность процессов в живом организме можно построить с помощью тригонометрических функций. Для построения модели биоритмов необходимо ввести дату рождения человека, дату отсчета (день, месяц, год) и длительность прогноза (кол-во дней).
Формула сердца. В результате исследования, проведенного студентом иранского университета Шираз Вахидом-Резой Аббаси, медики впервые получили возможность упорядочить информацию, относящуюся к электрической активности сердца или, другими словами, электрокардиографии.
Формула
представляет собой комплексное алгебраически-тригонометрическое равенство,
состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая
несколько дополнительных для расчетов в случаях аритмии. Как утверждают медики,
эта формула в значительной степени облегчает процесс описания основных параметров,
деятельности сердца, ускоряя, тем самым, постановку диагноза и начало
собственно лечения.
Также тригонометрия помогает нашему мозгу определять расстояния до объектов.
Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения. Строго говоря, идея «измерения углов» не является новой. Еще художники Древнего Китая рисовали удаленные объекты выше в поле зрения, несколько пренебрегая законами перспективы. Сформулировал теорию определения расстояния по оценке углов арабский ученый XI века Альхазен. После долгого забвения в середине прошлого столетия идею реанимировал психолог Джеймс Гибсон (James Gibson), строивший свои выводы на основе опыта работы с пилотами военной авиации. Однако после того о теории вновь позабыли.
Движение рыб в воде и полёт птиц (Приложение 2, рис. 10) происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения. При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.
1.4. Измерительные работы
Измерительные работы
Тригонометрией пользуются при измерении расстояния между точек на местности. Предположим, что нам надо найти расстояние d от пункта А до недоступного пункта «дерево». На местности можно выбрать точку B, и измерить длину с отрезка АВ. Затем измерим, например, с помощью астролябии, углы A и B. Эти данные, т.е. c, a и b позволяют решить треугольник АВС и найти искомое расстояние d = AC. Сначала находим угол С, sinC: С=180-а-b, sinC=sin(180-a-b)=sin(a+b). Затем с помощью теоремы синусов находим d.
II. Практическая часть
Больше всего моё внимание зацепило использование графика синусоиды для изображения биоритмов человека.
Мне
захотелось рассчитать свои три основных биоритма: физический, эмоциональный и интеллектуальный.
Для этого я воспользовалась онлайн—программой для расчета биоритмов. В
таблице я указала проценты трех биоритмов на 02.03.19г, который мне показали 5
разных сайтов. Так вышло, что только лишь в двух случаях мне выдали одинаковый
результат.
В
таблице я указала проценты трех биоритмов на 02.03.19г, который мне показали 5
разных сайтов. Так вышло, что только лишь в двух случаях мне выдали одинаковый
результат.
| Сайт №1 | Сайт №2 | Сайт №3 | Сайт №4 | Сайт №5 |
Физический | 27% | 73,4% | 99,77% | 98% | 99,77% |
Эмоциональный | 90% | 55,9% | 78,18% | 90% | 78,18% |
Интеллектуальный | —91% | 55% | —18,93% | —37% | —18,93% |
После
того, как я увидела, что результаты настолько разные, я решила, что хочу сама
рассчитать проценты всех трех биоритмов. На просторах интернета я нашла вот
такую вот формулу:
На просторах интернета я нашла вот
такую вот формулу:
B = (sin (2pi*t/P))*100%, где:
P = {23(физический), 28(эмоциональный), 33(интеллектуальный)}
B – состояние биоритма в % либо может выражаться как состояние относительно нуля, а также состояния нарастания или спадания.
Pi – число π, принимаем равным 3,14.
t – количество дней, прошедших с даты рождения до текущего момента.
P – фаза биоритма.
Для начала нужно посчитать, сколько дней прошло с момента моего рождения. Чтобы это сделать, можно воспользоваться каким-нибудь онлайн-калькулятором или же посчитать вручную. Для второго способа нам потребуется таблица високосных годов и вот такая вот формула:
t = y*365+v+o, где
y – количество прожитых лет (полных) на сегодняшний день.
v – количество прожитых високосных лет на сегодняшний день.
o– количество дней, прошедших со дня рождения по сегодняшнюю дату (всегда меньше года).
После подставила свои данные и получила:
16*365+4+325 = 6169.
В онлайн-калькуляторе у меня также получилось 6169.
Теперь осталось только подставить все известные данные в первую формулу.
Физический биоритм:
(sin(2 × π × 6169 / 23)) × 100 = 99,77%
Эмоциональный биоритм:
(sin(2 × π × 6169 /28)) × 100 = 78,18%
Интеллектуальный биоритм:
(sin(2 × π × 6169 / 33)) × 100 = -18,93%
Таким образом, производя в ручную расчеты собственного биоритма на ближайший месяц, у меня получился график синусоид (прил.1, рис.12).
III. Заключение
3.1. Описание аналитической части
Изучив
графики тригонометрических функций – синусоиду и косинусоиду, можно сделать
вывод, что тригонометрия тесно связана с жизнью человека и его деятельностью,
начиная с древности, и заканчивая настоящим временем.
Исследовав аналитический материал, мы выяснили, что тригонометрия присутствует во многих областях науки.
Дали строгие определения тригонометрии и тригонометрическим функциям.
Определили сферы применения синусоиды и косинусоиды, а также подтвердили значимость математики в окружающем нас мире. В ходе практического исследования применили полученные знания..
3.2. Вывод:
Мы убедились, что выдвинутая нами гипотеза подтвердилась и графики тригонометрических функций – синусоида и косинусоида действительно являются яркими представительницами в окружающем нас мире, а не только линиями в тетради. Они являются замечательными кривыми, которые практически всегда рядом с нами.
Хочется, чтобы данное исследование оказалось не только интересным, но и полезным. А демонстрационная модель будет служить наглядностью на уроках математики при изучении этих функций. Имеет метапредметную связь с другими областями науки.
Список литературы
1. https://ru.wikipedia.org/wiki
https://ru.wikipedia.org/wiki
2. https://ru.wikipedia.org/wiki
3. http://www.math34.ru
4. https://lyna.info/pravilnyj-algoritm-rascheta-bioritmov/
5. http://geocult.ru/bioritmyi-online-raschet
6. http://bio-ritm.ru/
7. https://psi-technology.net/bioritm.php
8. https://progman-soft.ru/bioritm.php
9. https://planetcalc.ru/274/
Приложение 1.
|
| |||
| |||
| |||||
| |||||
| |||||
Приложение 2
| ||||
| ||||
|
|
| |||||
| ||||||
|
|
|
| ||||
| ||||
Темы исследовательских проектов по математике в 10 классе
В этом разделе учащимся предлагается выбрать темы проектов по математике для 10 класса школы. Данными темами предусматривается выполнение исследовательской деятельности, связанной с исследованием числовых функций, с тригонометрическими функциями, тригонометрическими уравнениями и выражениями.
Любая выбранная вами тема проекта по математике для 10 класса может быть видоизменена в зависимости от сложности и объемности темы и проблематики проекта, по согласованию с руководителем.
Представленные темы исследовательских работ по математике для 10 класса дают возможность автору проекта в процессе своего исследования всесторонне изучить производную и её применение при исследовании функций, выяснить геометрический и механический смысл производной.
Темы исследовательских работ по математике в 10 классе
Примерные темы исследовательских работ по математике для учащихся 10 класса:
Алгоритмы решения тригонометрических уравнений и систем уравнений.
Великие математики древности
Великое искусство и жизнь Джероламо Кардано.
Геометрические модели в естествознании.
Геометрия Евклида как первая научная система.
Геометрия Лобачевского
Геометрия многогранников
Графический метод решения тригонометрических уравнений и неравенств.
Графический подход к решению некоторых тригонометрических уравнений.
Графики элементарных функций в рисунках
Диофантовы уравнения.
Диофантовы уравнения.
Загадки пирамиды
Загадочные графики тригонометрических функций.
Задачи на производную.
Замечательные неравенства, их обоснование и применение. Великие математики и их великие теоремы.
Замечательные математические кривые: розы и спирали.
Золотая пропорция
Интерактивные тесты по теме «Производная функции».
Иррациональные алгебраические задачи.
Использование графиков функций для решения задач.
Исследование графика тригонометрической функции
Касательные к графикам функций и их уравнения.
Касательные к тригонометрическим функциям.
Красивые задачи в математике
К неравенству Митриновича.
Комплексные и гиперкомплексные числа.
Лобачевский Н.И. «Коперник геометрии»
Математика и философия
Методы построения графиков тригонометрических функций.
Методы решения тригонометрических уравнений
Метод математической индукции как эффективный метод доказательства гипотез.
Нахождение значения тригонометрических единиц, нахождение площади треугольника, движения.
Нестандартные способы решения тригонометрических уравнений
Объемы и площади поверхностей правильных многогранников и тел вращения
Периодичность тригонометрических функций.
Поверхности многогранников
Построение графиков обратных тригонометрических функций
Построение графиков сложных функций.
Построение графиков тригонометрических функций.
Темы проектов по математике для 10 классе
Примерные темы проектов по математике для учащихся 10 класса:
Предыстория математического анализа. Значение производной в различных областях науки.
Применение производной
Производная в экономике и биологии.
Производная и ее практическое применение
Путешествия по тригонометрической функции y=cosx
Путешествие в мир фракталов
Развертка
Развитие тригонометрии как науки
Разработка логических игр.
Свойства тригонометрических функций: гармонические колебания
Сложные проценты в реальной жизни.
Способы построения графиков тригонометрических функций.
Тригонометрическая функция у=sin x
Тригонометрия вокруг нас.
Формула для нахождения корней кубического уравнения. Уравнения четвертой степени и методы их решения.
Формула сложных процентов и ее применение.
Функции в жизни человека
Функции и их графики
Функция у=cosx и окружающий нас мир.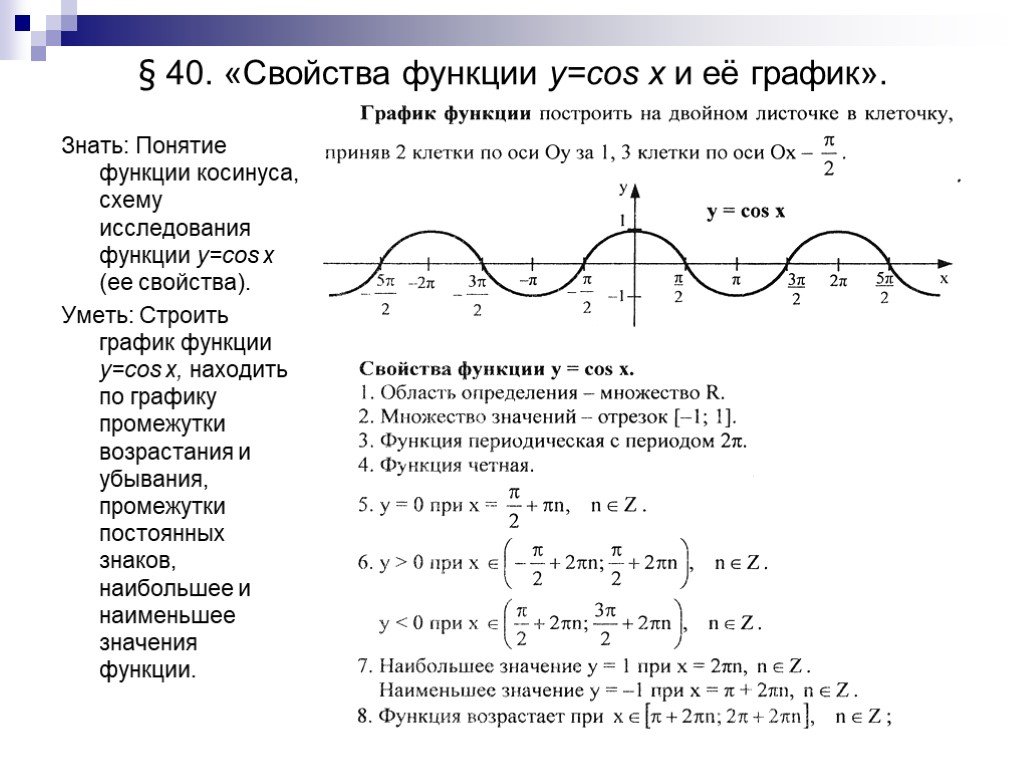
Функционально-графический подход к решению задач.
Фракталы: геометрия красоты
«Числа не управляют миром, но показывают, как управляется мир» (И.В. Гете).
Перейти в раздел:
Ученические работы по математике
Тему проекта по математике
Если страница Вам понравилась, поделитесь в социальных сетях:
калькулятор функций упорядоченных пар — Googlesuche
AlleBilderShoppingVideosMapsNewsBücher
suchoptionen
упорядоченные пары — Tiger Algebra Solver
Решатель алгебры и калькулятор алгебры, показывающий пошаговые решения. … Упорядоченные пары Упорядоченная пара (a, b) — это пара объектов.
Представляют ли набор упорядоченных пар {(2,6),(-3,6),(4,9),(2,10)} fu
www.mathcelebrity.com › search
Проверяет, представляет ли набор упорядоченных пар функцию. Этот калькулятор имеет 1 вход. Какая 1 формула используется для калькулятора функционального теста?
Калькулятор упорядоченных пар — MathCelebrity
www. mathcelebrity.com › упорядоченная пара
mathcelebrity.com › упорядоченная пара
Этот калькулятор выполняет следующие преобразования: * Оценка упорядоченных пар и симметричные точки, включая абциссу и ординату * Полярные координаты …
Ähnliche Fragen
Как найти функцию упорядоченных пар?
Как найти недостающую заказанную пару?
Калькулятор упорядоченных пар онлайн — Cuemath
www.cuemath.com › калькуляторы › расчет упорядоченных пар…
«Калькулятор упорядоченных пар» — это бесплатный онлайн-инструмент, который вычисляет упорядоченные пары для заданного уравнения . В этом калькуляторе вы можете ввести уравнение …
Предварительные алгебраические примеры | Нахождение упорядоченных парных решений — Mathway
www.mathway.com › примеры › предварительная алгебра › найти…
Выберите любое значение x x, которое находится в домене, чтобы подставить его в уравнение. Шаг 2. Выберите 0 0 вместо x x, чтобы найти упорядоченную пару.
Калькулятор упорядоченных пар — mathmusic. org
org
mathmusic.org › наименьшая общая мера › упорядоченный-…
вычислитель выражений; построение графика квадратичных функций+игра; план урока алгебры из фольги; математические дроби; решение и ответы по алгебре 2; решить мое свойство нулевого продукта …
Калькулятор поиска упорядоченной пары — Factoring-polynomials.com
factoring-polynomials.com › точка-наклон › найти-или…
калькулятор поиска упорядоченной пары? Ниже приведен ряд ключевых слов, которые посетители использовали в последнее время, чтобы попасть на наш сайт. Как это может быть полезно?
Калькулятор решения упорядоченных пар — Алгебратор
softmath.com › math-book-ответы › сумма кубов
Это помогает изучить функции каждого метода решения. Перри Хьюз, Кентукки. Спасибо! Это новое программное обеспечение является реальной помощью. Мой сын умеет по-настоящему …
Калькулятор функций — Symbolab
www.symbolab. com › … › Функции › Функции
com › … › Функции › Функции
Бесплатный калькулятор \mathrm{Is a Function} — шаг за шагом проверяйте, является ли ввод действительной функцией .
Калькулятор упорядоченных пар — Бесплатный онлайн-калькулятор — Byju’s
byjus.com › Калькуляторы › Математические калькуляторы
Калькулятор упорядоченных пар — это бесплатный онлайн-инструмент, который отображает упорядоченную пару для данного уравнения. Инструмент онлайн-калькулятора заказанных пар BYJU делает …
Калькулятор суммирования 5 чисел: Двоичный калькулятор
Калькулятор дробей с переменными: Калькулятор комбинирования подобных терминов
Калькулятор правил трапеций: Сложение — калькулятор 3 цифр
Калькулятор углов: Калькулятор импульса со скоростью
Калькулятор упорядоченных пар — mathpapa
Найти упорядоченную пару
Найти неравенство упорядоченных пар Калькулятор
Калькулятор упорядоченных пар линейных уравнений
Find ordered pair from equation
ordered pair calculator — symbolab
Determine the missing coordinate in the ordered pair calculator
graphing-tides-worksheet-answers — Google Suche
AlleBilderShoppingVideosMapsNewsBücher
Suchoptionen
Bilder
Alle anzeigen
Alle anzeigen
[PDF] 6e Qa+r#
www. frsd.k12.nj.us › Домен › Tides_Baja_Graph_Lab_ANSWERS
frsd.k12.nj.us › Домен › Tides_Baja_Graph_Lab_ANSWERS
Рабочий лист «Приливы». Прочтите приведенные ниже абзацы и просмотрите таблицу на листе… Изобразите свой график на миллиметровой бумаге и ответьте на письменные вопросы на этом листе.
graphing_the_tides — График приливов: В этом упражнении вы построите …
www.coursehero.com › файл › graphing-the-tides данные о приливах и использовать полученный график для ответов на вопросы. 1. Изучите.
[PDF] Приливы в Атлантик-Сити, штат Нью-Джерси — январь 2015 г. — высота прилива (футы)
www.cusd80.com › Centricity › Домен › Графики приливов и отливов с образцом
Добавьте ключ к графику. Анализ: ответьте на приведенные ниже вопросы, используя диаграмму данных и график. Обязательно перечислите рабочий лист … Tides Лиз ЛаРоса.
[PDF] Таблица приливов и отливов KEY
nckingtides.web.unc.edu › 2018/02 › Рабочий лист 4-го класса KEY
02.01.2018 · Раздел 3: Анализ данных о приливах. 1. Выберите один день на графике приливов и запишите оба прилива и отлива в этот день.
1. Выберите один день на графике приливов и запишите оба прилива и отлива в этот день.
[PDF] Составление карты приливов. Рабочий лист KEY
nckingtides.web.unc.edu › 2018/02 › 6th-Class-Worksheet-KEY
18.12.2017 · Раздел 3: Анализ данных о приливах. 1. Выберите один день на графике приливов и запишите оба прилива и оба отлива в этот день.
Ответы на рабочий лист Graphing The Tides — Фазы Луны — Pinterest в котором перечислены задачи для ученых …
[PDF] Graphing Tides Lab
www.chemistar.com › EnviroGeo › GeoHandouts › GraphingTidesLa…
Вопросы: (Ответьте ПОЛНЫМ и ПОЛНЫМ предложениями). 1. Опишите, что происходит с линией прилива (т. е. она увеличивается/уменьшается до… затем). 2. Сколько пиков …
Ähnliche Fragen
Что вызывает приливы?
Что вызывает приливы в океане Newsela ответы?
Есть ли формула приливов и отливов?
Tides Worksheet — Studylib
studylib.

 Теоретическая часть
Теоретическая часть 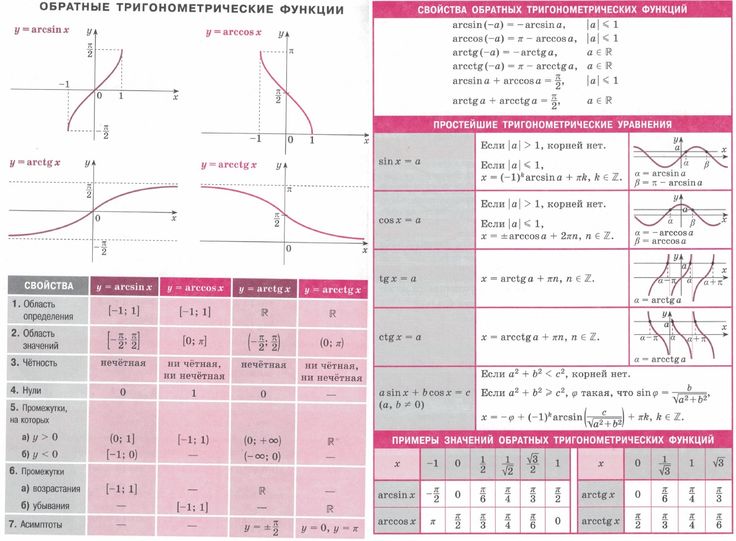 2
Вывод
2
Вывод 1
1 5
5 1
1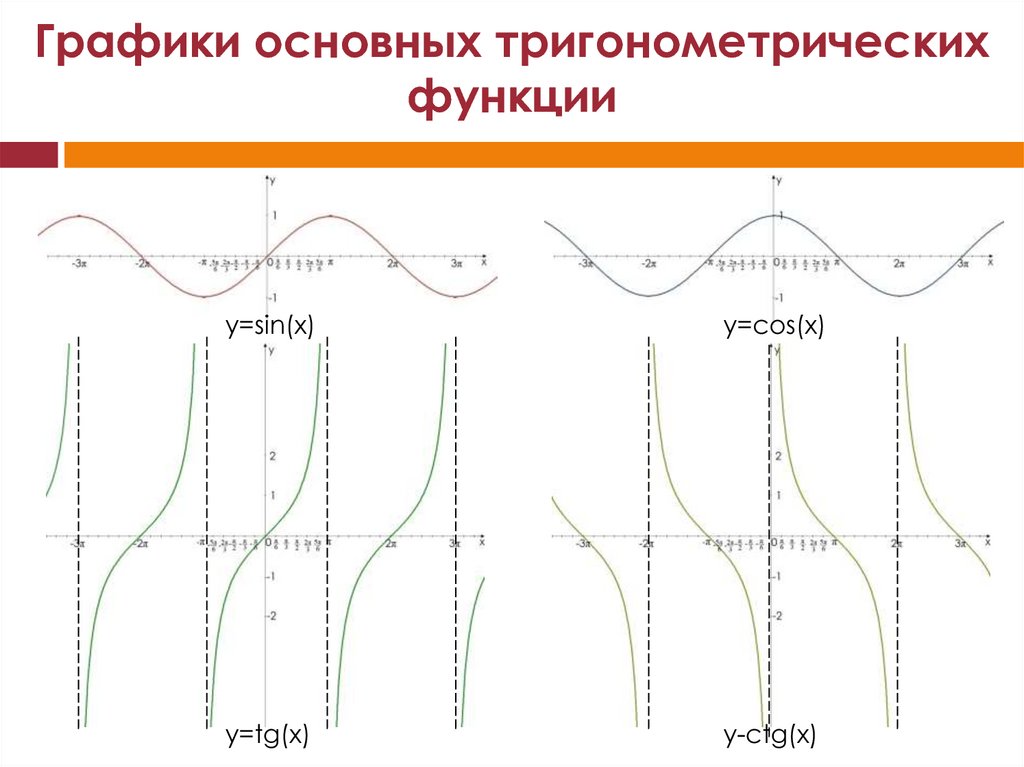 6
6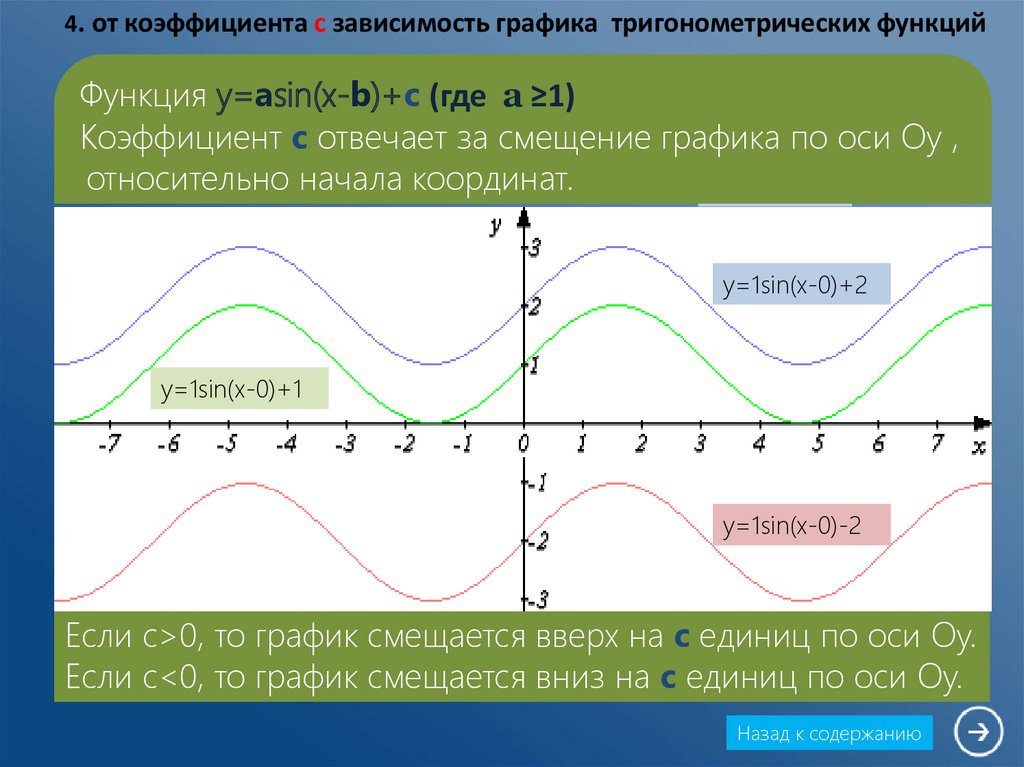 10
10