Асимптота графика функции онлайн: Асимптоты функции | Онлайн калькулятор

Содержание

Асимптоты графика функции — презентация онлайн

Похожие презентации:

Асимптоты графика функции

Исследование функции и построение ее графика

Асимптоты графика функции

Исследование функций и построение графиков

Приложение производной к исследованию функции

Схема исследования функции и построение графика

Исследование функции и построение графиков

Схема исследования функций и построение графиков

Исследование функции с помощью производной

Исследование и построение графиков функции

Асимптоты графика функции.
Опр. Асимптотой графика функции y=f(x)
называется прямая, к которой неограниченно
приближается точка графика функции при
неограниченном удалении от начала координат.
вертикальная асимптота
горизонтальные асимптоты
наклонные асимптоты
Асимптоты графика функции.
Теорема 1. Если
то прямая x=a является вертикальной асимптотой
графика функции y=f(x).
Асимптоты графика функции.

Cледствие. Вертикальные асимптоты следует
искать в точках разрыва области определения и
на концах ее области определения (если
область определения имеет вид
(a,b), (a,+∞), (-∞,b)).
Примеры вертикальных асимптот.
Пример1.
Примеры вертикальных асимптот.
Пример1.
-3
вертикальная
асимптота
Примеры вертикальных асимптот.
Пример 2.
Асимптоты графика функции.
Теорема 2. Если
, то прямая y=a
является горизонтальной асимптотой.
Примеры горизонтальных асимптот.
Пример1.
Примеры горизонтальных асимптот.
Пример1.
горизонтальная
асимптота
-3
Асимптоты графика функции.
Теорема 3. Если
,
то прямая y=ax+b является наклонной асимптотой.
Примеры наклонных асимптот.
Пример1.
Примеры наклонных асимптот.
Пример1.
Примеры наклонных асимптот.
Пример1.
наклонная асимптота
-3
Замечание. Горизонтальная асимптота является частным случаем

наклонной асимптоты
y=ax+b
Если а=0, то наклонная асимптота становится горизонтальной.

Поэтому горизонтальные асимптоты можно не искать,
сразу искать наклонные.
Общая схема исследования
функций.
1. Область определения.
2. Исследование на четность-нечетность.
3. Асимптоты.
4. Экстремумы и интервалы монотонности.
5. Точки перегиба и интервалы выпуклости.
6. Точки пресечения с осями координат.
7. График функции.
Пример
1. Область определения
Пример
1. Область определения
Пример
2. Исследование на четность-нечетность.
f(-x)=……
Пример
2. Исследование на четность-нечетность.
Функция общего вида
Пример
3. Асимптоты
А) вертикальные
x=3 – точка разрыва
Пример
3. Асимптоты
А) вертикальные
x=3 – точка разрыва
x=3 – вертикальная асимптота
Пример
3. Асимптоты
б) горизонтальные и наклонные y=ax+b
Пример
3. Асимптоты
в) наклонные y=ax+b
Пример
3. Асимптоты
в) наклонные y=ax+b
Пример
3. Асимптоты
в) наклонные y=ax+b
y=x-3 – наклонная асимптота,
горизонтальных асимптот нет
Пример
4.

Экстремумы и интервалы монотонности
Пример
4. Экстремумы и интервалы монотонности
Пример
4. Экстремумы и интервалы монотонности
Пример
4. Экстремумы и интервалы монотонности
+
1
т. max
+
3
5
т. min
Пример
4. Экстремумы и интервалы монотонности
+
1
т. max
+
3
5
т. min
Пример
5. Точки перегиба и интервалы выпуклости
Пример
5. Точки перегиба и интервалы выпуклости
Пример
5. Точки перегиба и интервалы выпуклости
Решений нет
Точек перегиба нет
+
3
Пример
6. Точки пересечения с осями координат.

С осью OX y=0
Пример
6. Точки пересечения с осями координат.
С осью OX y=0
Точек пересечения с OX нет
Пример
6. Точки пересечения с осями координат.
С осью OY x=0
Пример
6. Точки пересечения с осями координат.
С осью OY x=0
Пример
7. График функции. Сначала строим асимптоты
x=3
y=x-3
3
-3
Пример
7.

График функции. Отмечаем точки экстремума
x=3
y=x-3
4
1
-3
-4
3
5
Пример
7. График функции. Отмечаем точки пересечения с осями и строим
график
x=3
y=x-3
4
1
-3
-4
3
5

English Русский Правила

Асимптоты. Практикум по математическому анализу. Урок 58

Высшая математика / Практикум по математическому анализу

02.11.201718.11.2017

Асимптотой кривой называется такая прямая, к которой неограниченно приближается тонка кривой при неограниченном удалении ее от начала координат.
Кривая может приближаться к своей асимптоте теми же способами, как и переменная к своему пределу: оставаясь с одной стороны от асимптоты, как, например, в задаче 1 (1) или с разных сторон, бесчисленное множество раз пересекая асимптоту и переходя с одной ее стороны на другую, как, например, в задаче 1 (3).
Для нахождения асимптот пользуются следующими положениями:
а) если при х = а кривая y = f(x) имеет бесконечный разрыв, т. е. если при

или при функция f(x) стремится к бесконечности (того или иного знака), то прямая х=a является ее вертикальной асимптотой;
б) невертикальные асимптоты кривой y = f(x), если они существуют, имеют уравнения вида y=kx+b, где параметры k и b определяются формулами

при одинаковом в обеих формулах поведении х, т. е. в обеих формулах

или .
Задача 1. Найти асимптоты кривых:
1) ; 2) ; 3) ; 4) ; 5) .
Решение.
1) (а) При х=3 данная кривая имеет бесконечный разрыв. Поэтому прямая х=3 есть ее вертикальная асимптота;
(б) далее ищем невертикальные асимптоты:

Подставляя найденные значения k и b в уравнение y=kx+b, получим уравнение невертикальной асимптоты: y=x-3.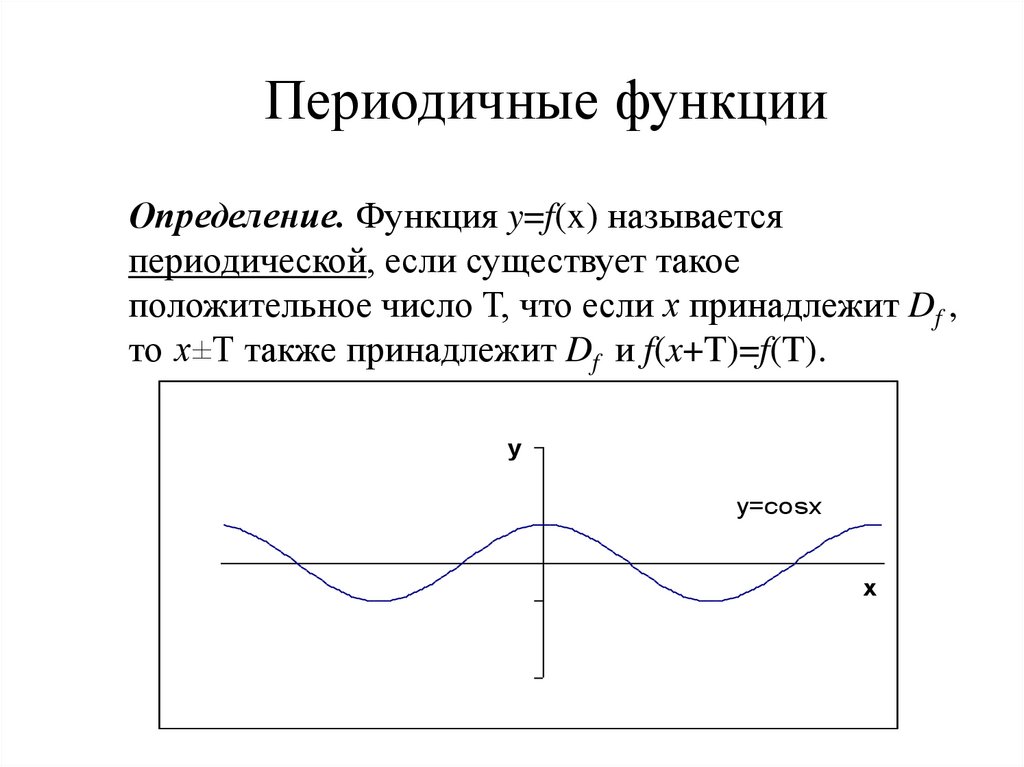 Других невертикальных асимптот кривая не имеет, так как при

значения k и b будут те же самые. Кривая (гипербола) изображена на рис. 63.

Рис.63

2) (а) Кривая не имеет вертикальных асимптот, так как она всюду непрерывна;
(б)

т. е. при угловой коэффициент асимптоты не существует, вследствие чего при кривая не имеет асимптоты;

(Здесь применено правило Лопиталя.)
Следовательно, при

кривая имеет невертикальную асимптоту y=0 (ось Ox).
3) (а) Кривая не имеет бесконечных разрывов, поэтому не имеет и вертикальных асимптот;
(б) так как ;
.
При параметры асимптоты имеют те же значения. Следовательно, при и при кривая имеет асимптоту у=х. Эта кривая бесчисленное множество раз пересекает свою асимптоту, переходя с одной ее стороны на другую (рис.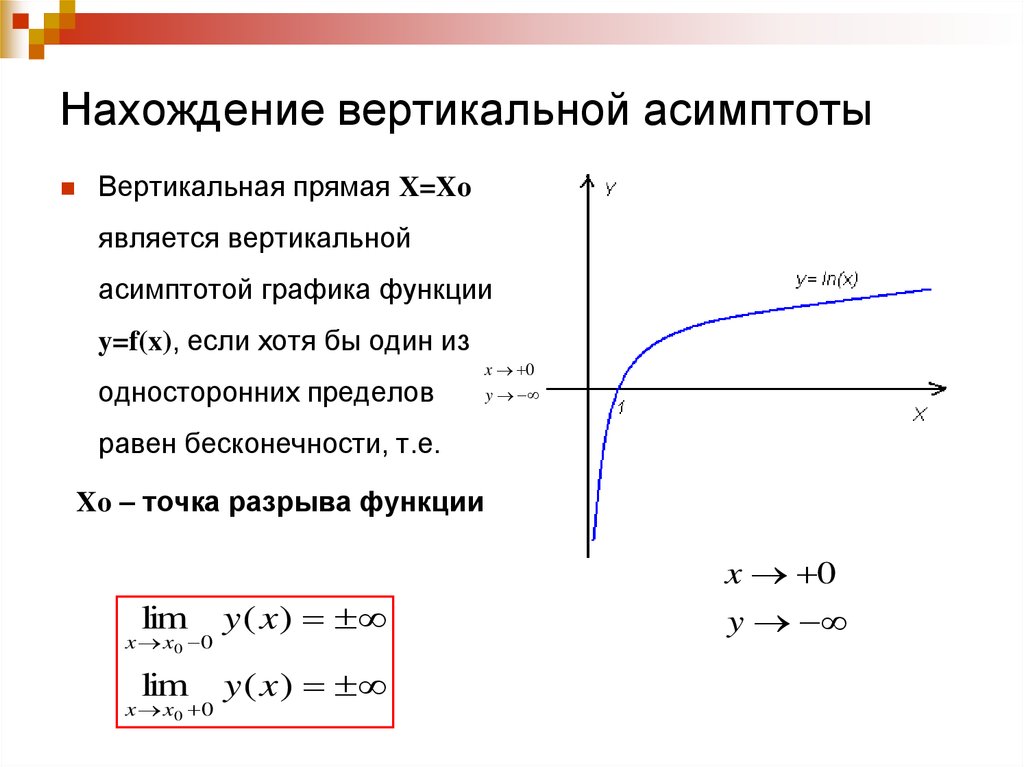 64).

Способ приближения кривой к своей невертикальной асимптоте определяется путем исследования знака разности ординат кривой и асимптоты. Здесь эта разность бесчисленное множество раз меняет свой знак в точках, где .
4)(а) Кривая не имеет вертикальных асимптот, так как она всюду непрерывна;
(б)

Применяя правило Лопиталя дважды, получим

Следовательно, при кривая имеет асимптоту у = 1:
;

Следовательно, при кривая имеет асимптоту (рис. 65).

5) (а) Кривая имеет две вертикальные асимптоты х=-2 и x=2, так как при х=±2 она имеет бесконечные разрывы;
(б) невертикальных асимптот кривая не имеет, ибо ее областью расположения является интервал —2 и поэтому x не может стремиться к бесконечности (рис. 66).

Тегиасимптотаасимптоты графикаасимптоты графика онлайнасимптоты графика функцииасимптоты кривойасимптоты функцииасимптоты функции онлайнвертикальная асимптотавертикальными асимптотами функциигоризонтальная асимптотакак найти асимптотыкак найти асимптоты функциинайти асимптоты графика функциинаклонная асимптотанаклонными асимптотами функциинахождение асимптотправило лопиталя

Асимптота: вертикальная, горизонтальная и косая

Содержание (Нажмите, чтобы перейти к этому разделу):

Что такое асимптота?
типов асимптот (и как их найти)
1. Горизонтальная асимптота
  - Две горизонтальные асимптоты
2. Вертикальная асимптота
3. Наклонная (наклонная) асимптота

Асимптота — это линия на графике, к которой приближается функция, стремясь к бесконечности. Расстояние между графиком функции и асимптотой стремится к нулю, поскольку оба стремятся к бесконечности, но никогда не сливаются.
Вертикальная асимптота. Функция приближается к синей пунктирной линии; Хотя кажется, что он касается, на самом деле это никогда не происходит.

Посмотрите видео с определением и несколькими примерами нахождения асимптот:

Что такое асимптоты?

Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.

Слева направо: горизонтальная, вертикальная и наклонная асимптоты.

Существует три типа асимптот:

A 9Горизонтальная асимптота 0003 — это просто прямая горизонтальная линия на графике. Его можно выразить как y = a, где a — некоторая константа. Когда x стремится к (отрицательной или положительной) бесконечности, значение функции приближается к a.
Вертикальная асимптота — вертикальная линия на графике; линия, которая может быть выражена x = a, где a — некоторая константа. Когда x приближается к этому значению, функция стремится к бесконечности.
Наклонная или наклонная асимптота , как следует из названия, представляет собой наклонную линию на графике. С технической точки зрения, это любая асимптота, не параллельная ни горизонтальной, ни вертикальной оси. Его можно выразить уравнением y = bx + a. При приближении x к бесконечности график функции приближается к этой линии.

Функция может иметь любое количество вертикальных асимптот: даже бесконечное число. Он может иметь только две горизонтальные асимптоты.

Функции не пересекают свои вертикальные асимптоты, но могут пересекать свои горизонтальные асимптоты.

Горизонтальная асимптота — это воображаемая горизонтальная линия на графике. Он показывает общее направление того, куда может быть направлена функция. В отличие от вертикальных асимптот, которые нельзя коснуться или пересечь, горизонтальная асимптота просто показывает общий тренд в определенном направлении.

Как найти горизонтальную асимптоту рациональной функции вручную

Чтобы найти горизонтальную асимптоту рациональной функции, вы должны знать несколько терминов:

1/x или [(x – 6) / (x ² – 8x + 12)])
степень многочлена является числом, «возведенным до». Например, вторая степень (х ²), третья степень (х ³) или 99-я степень (х ⁹⁹).
Коэффициент — это число перед «х». Например, коэффициент 5x ² равен 5; коэффициент 102x ³ равен 102.

Как найти горизонтальную асимптоту, зависит от того, как выглядит ваша функция/уравнение: сравните многочлен высшей степени в числителе с полиномом высшей степени в знаменателе. Выберите один из следующих:

Они одной степени.
Знаменатель имеет высшую степень.
Знаменатель имеет наименьшую степень.

Разделить коэффициенты членов с высшей степенью.
Пример :

Члены высшей степени (т. е. члены с наивысшей степенью) 8x ² вверху и 2x ² внизу, поэтому:

8/ 2 = 4.
горизонтальная асимптота при y = 4. Следующий график подтверждает расположение асимптоты:

Если многочлен в знаменателе имеет более высокую степень, чем числитель, ось x (y = 0) является горизонтальной асимптотой. Например, на следующем графике показано, что ось X является горизонтальной асимптотой для 8x ² /2x ⁴ :

График (8x ² )/(2x ⁴ ) с горизонтальной асимптотой, выделенной желтым цветом .

Если многочлен в знаменателе меньше степени числителя, то горизонтальной асимптоты нет.

Как найти горизонтальные асимптоты на TI-89: Шаги

Примечание. Убедитесь, что вы находитесь на главном экране. Если вы не на главном экране, нажмите кнопку «Домой».

Шаг 1: Посмотрите на показатели степени в знаменателе и числителе.

Если наибольший показатель числителя больше наибольшего показателя знаменателя, асимптоты нет. Вот и все! Готово!

Если наибольший показатель знаменателя функции больше наибольшего показателя числителя, перейти к шагу 2.
Если экспоненциальные степени совпадают в числителе и знаменателе, перейти к шагу 3.

Шаг 2: Горизонтальная асимптота будет y = 0. Вот и все! Готово!

Шаг 3: Введите вашу функцию в y=редактор . Например, у вас может быть функция f(x) = (2x ² – 4) / (x ² + 4). Чтобы ввести функцию в редактор y=, выполните шаги 4 и 5.

Шаг 4: Нажмите кнопку с ромбом, а затем F1, чтобы войти в редактор y=. 92 + 4 ), затем ENTER.

Шаг 6: Нажмите кнопку с ромбом и F5, чтобы просмотреть таблицу значений функции.

Шаг 7: Прокрутите таблицу вниз и посмотрите значения y. Вы заметите, что по мере увеличения x график становится все ближе и ближе к y=2, но не достигает этого значения. График даже достигает y = 1,999999. Горизонтальная асимптота равна y = 2.

Горизонтальная асимптота возникает, когда график x очень близок к горизонтальной линии (т. е. он сглаживается и проходит почти параллельно оси x), когда он стремится к бесконечности. Поскольку есть только два способа «направиться к бесконечности» на графике (один в положительном направлении и один в отрицательном направлении), максимальное количество горизонтальных асимптот, которое может иметь любая функция, равно двум. Многие различные типы функций могут иметь две горизонтальные асимптоты.

Какие виды функций имеют две горизонтальные асимптоты?

Некоторые рациональные функции могут иметь две горизонтальные асимптоты; Их пределы всегда одинаковы, поэтому если есть горизонтальная асимптота с одной стороны, то она должна быть и с другой.

Функции абсолютного значения и радикала/корня также могут иметь две горизонтальные асимптоты, которые могут быть одинаковыми или разными.

А вертикальная асимптота — это вертикальная линия на графике рациональной функции .

Асимптота — это линия, к которой приближается функция; Даже если на графике может показаться, что он достигает этой точки, на самом деле он никогда не достигает этой линии. Асимптоты могут быть вертикальными (прямо вверх) и горизонтальными (прямо поперек).
Рациональная функция представляет собой дробь двух полиномиальных функций, таких как 1/x или [(x – 6) / (x ² – 8x + 12)].)

Как найти вертикальные асимптоты

Любую дробь нельзя делить на ноль. Сюда входят рациональные функции, поэтому, если на графике есть область, где знаменатель равен нулю, у вас будет вертикальная асимптота.

Чтобы узнать, имеет ли рациональная функция какие-либо вертикальные асимптоты, приравняйте знаменатель к нулю, затем найдите x.

Пример от руки

Найдите вертикальные асимптоты следующей функции:
f(x) = (x ² ) / (x ² – 8x + 12)

мест на графике, где не может быть х :

Факторинг (х ² – 8х + 12) =
(х – 2)(х – 6)
х = 2 или х = 6

Построив график функции (я воспользовался бесплатным графическим калькулятором HRW), мы видим, что есть, как и ожидалось, вертикальные асимптоты при x=2 и x=6:

Если вы не можете найти ноль, то нет вертикальных асимптот. Например, предположим, что ваш знаменатель равен х ² + 9:
х ² + 9 = 0
х ² = –9
.

Если у вас есть графический калькулятор, вы можете найти вертикальные асимптоты за секунды.

Пример задачи: Найдите вертикальную асимптоту на TI89 для следующего уравнения:
f(x) = (x ² ) / (x ² – 8x + 12) 92-8x+12),x для входа в функцию.

Шаг 3 : Нажмите ), чтобы закрыть правую скобку.

Шаг 4 : Нажмите Enter.

Шаг 5 : Посмотрите на результаты. Результирующие нули для этой рациональной функции будут иметь вид: (2,6) Это означает, что существует либо вертикальная асимптота, либо отверстие при x = 2 и x = 6.

Шаг 5 : Вставка значения из шага 5 в калькулятор, чтобы отметить разницу в между вертикальной асимптотой и отверстием. Числитель равен x-6, поэтому нажмите 2, -, -4, а затем нажмите Enter, чтобы получить 6. Это означает, что f(2) = 6, что подтверждает наличие вертикальной асимптоты при x = -4. Когда x = 0, числитель равен -6. Это подтверждает наличие дыры в графике при x = -6. Если числитель всегда равен нулю, это означает, что в графике есть дыра, а не вертикальная асимптота.

Вот как найти вертикальную асимптоту на TI89!

Вы можете перепроверить свой ответ с помощью этого калькулятора от Symbolab.

Наклонная асимптота (также называемая нелинейной или наклонной асимптотой ) — это асимптота , не параллельная оси y или оси x.

У вас есть несколько вариантов нахождения наклонных асимптот:

Вручную (длинное деление)
TI-89 Propfrac команда

1. Вручную

Вы можете найти косые асимптоты на длинное деление . Это не рекомендуется, в основном потому, что вы рискуете допустить арифметические и алгебраические ошибки вручную. Но если вам нужно найти наклонную асимптоту вручную, вы можете найти полную процедуру в этом pdf.

Вы также можете найти нелинейные асимптоты на графическом калькуляторе TI-89 , используя команду propFrac( , которая переписывает рациональную функцию как полиномиальную функцию плюс правильную дробь. Части правильной дроби дают вам информацию о нелинейные асимптоты для функции

Пример 1

Пример задачи: Найдите наклонную асимптоту для следующей функции:
f(x) = (x ² – 3x + 5) / (x + 4)

Шаг 1: Нажмите кнопку ДОМОЙ 92 – 3 х + 5) ÷ (х + 4)).

Шаг 4: Нажмите клавишу ВВОД.

Результатом является сумма правильной дроби (33 / x + 4) и функции линейного полинома (x – 7). Линейная функция y = x – 7 есть уравнение наклонной асимптоты. Вы можете использовать этот метод, чтобы найти любую наклонную асимптоту на TI-89.

Вот оно! Готово!

Найти нелинейные асимптоты: Пример 2

Пример задачи: Найти нелинейные асимптоты для функции: f(x) = 92 + х + 1 0 ) ÷ ( х – 6 ) ).

Шаг 4: Нажмите клавишу ВВОД.
Результат представляет собой сумму правильной дроби ( ^-56 ⁄ _{x ² – 2x – 11} ) и квадратичной функции (x ² – 2x – 11). Квадратичная функция y = x ² – 2x – 11 есть уравнение нелинейной асимптоты. Вы можете использовать этот метод, чтобы найти любую нелинейную асимптоту на TI-89.

Вот и все! Готово!

Совет: Убедитесь, что все уравнение заключено в круглые скобки, иначе вы не получите правильный результат для команды propfrac(команда.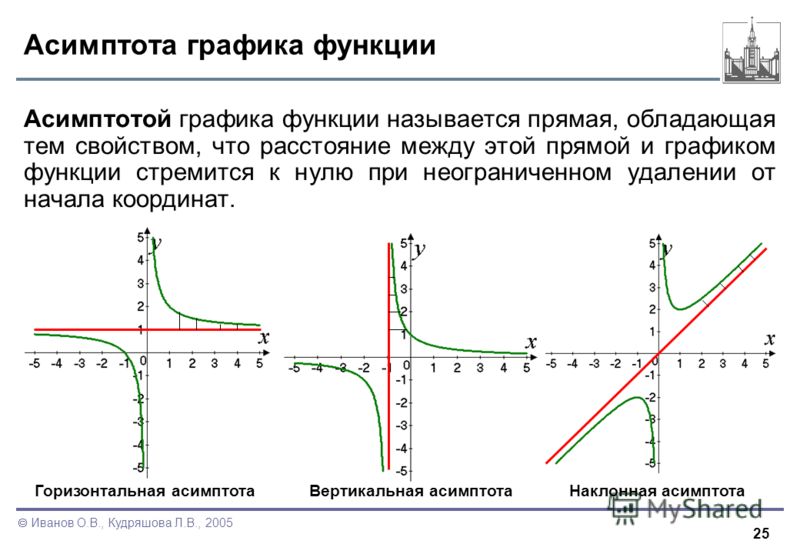

Правильная дробь имеет числитель, который меньше ее знаменателя и представляет величину меньше целого, или < 1: 1/5, 2/5, 3/5 и 4/5 являются правильными дробями.

Литература

Асимптоты рациональных функций. Получено 16 сентября 2019 г. с: https://www.austincc.edu/pintutor/pin_mh/_source/Handouts/Asymptotes/Horizontal_and_Slant_Asymptotes_of_Rational_Functions.pdf
Kmiecik, Joan. Получите ваши перехваты асимптот здесь. Учитель математики, Vol. 83, № 5 (19 МАЯ90), стр. 402-404 Опубликовано: Национальный совет учителей математики
Получено с https://www.jstor.org/stable/27966722 21 сентября 2018 г.
Osikiewicz, Beth-Allyn. Раздаточный материал для класса Math 11012: Вертикальные и горизонтальные асимптоты. Получено с http://www.personal.kent.edu/~bosikiew/Math21012/vertical-horizontal.pdf 21 сентября 2018 г.
Стерлинг, Мэри Джейн. Наклонные асимптоты. Дополнение к рабочей тетради по алгебре II для чайников. Получено с https://www. dummies.com/education/math/алгебра/oblique-asymptotes/ 21 сентября 2018 г.

УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Асимптота: вертикальная, горизонтальная и косая» из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/calculus-definitions/asymptote-vertical-horizontal-oblique/

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

lib › Centricity › Domain › Extra Practice of R…

Worksheet by Kuta Software LLC … Для каждой функции определите пробелы, пересечения, горизонтальную и вертикальную асимптоты и домен. Затем нарисуйте график.

[PDF] Программное обеспечение Kuta — Бесконечное предварительное исчисление — Графики рациональных функций

msmillersmathclasses. weebly.com › kuta_graphs_of_rat_fns_key

Программное обеспечение Kuta — Бесконечное предварительное исчисление. Графики рациональных функций. Для каждой функции определите точки разрыва, дыры, пересечения, …

[PDF] Графики рациональных функций — Kuta Software

cdn.kutasoftware.com › Рабочие листы › Precalc › 02 — Графики рациональных значений..

Kuta Software — Бесконечный предварительный расчет. Графики рациональных функций… Для каждой функции определите точки разрыва, пробелы, точки пересечения, …

[PDF] Рациональные функции — Предварительное исчисление Раздел 2.3 — Математика 1330

online.math.uh.edu › Math2330-unpaid › 1330_Ch3_Section3

(b) Используйте квадратичную формулу, чтобы найти вертикальные асимптоты функции, а затем используйте калькулятор, чтобы округлить эти ответы до ближайшей десятой. График …

[PDF] ПК — Раздел 1.7 — Рабочий лист 1 — KEY.pdf

www.cbsd.org › cms › lib › Centricity › Домен › ПК — Раздел 1. 7 — …

Pre-Calculus/Trig 3. ЧАСТЬ 1: Повторение алгебры II. РАЗДЕЛ 7. РАБОЧИЙ ЛИСТ №1 … Ответьте в форме y = mx + b … ГРАФИК РАЦИОНАЛЬНЫХ ФУНКЦИЙ.

[PDF] Предварительное исчисление с отличием

mi01000971.schoolwires.net › cms › lib › Centricity › Domain › Lim…

Предварительное исчисление с отличием. Изучение графиков рациональных функций. III. Постройте график следующей рациональной функции, чтобы найти область определения, диапазон, точки пересечения, асимптоты …

6.3 Графики рациональных функций — предварительное исчисление

precalculus.flippedmath.com › 63-graphing-rational…

Прикладные решения доступны для покупки! кликните сюда. Корректирующее задание. pc_ca_6.3.pdf. Размер файла: 275 кб. Файл …

[PDF] Asymptotes of Rational Functions Answer Key.pdf

www.birmingham.k12.mi.us › cms › lib › Centricity › Domain › Asy…

иметь горизонтальную или наклонную асимптоту, то найти ее.