Замечательные пределы с примерами решения
Содержание:
- Примеры с решением
Многие задачи математического анализа связаны с первым замечательным пределом.
Рассмотрим в координатной плоскости окружность единичного радиуса с центром в начале координат (рис. 5.1).
Обозначим через,где , величину острого угла в радианах. Тогда длина дуги равна. Пусть — площади треугольника АОВ, сектора АОВ и треугольника СОВ соответственно, причем
. Очевидно, что площади связаны соотношением или
Отсюда. Если , то
Следовательно, или
Полученные неравенства справедливы и при в силу четности функций и. Так как , то по теореме 4.16 о пределе промежуточной функции имеем (5.1)
этот предел и называют замечательным пределом.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Приведем некоторые пределы, который можно свести к пределу (5.
1) после перехода к новой переменной (см. теорему 4.3):
- 1)
- 2)
- 3) в некоторой окрестности точки .
| Термин «Замечательные пределы» широко используется в учебниках и учебниках для обозначения важных идентичностей, которые могут значительно упростить задачу поиска ограничений. |
Возможно вам будут полезны данные страницы:
Метод наименьших квадратов примеры решения |
Векторное произведение примеры решения |
Первый замечательный предел: пример решения |
Второй замечательный предел: пример решения |
Примеры с решением
Пример 1.
Найти .
Решение:
В данном случае имеем неопределенность вида .
Преобразуем дробь и воспользуемся замечанием 4.
5 о пределе степенной функции:
Ко второму замечательному пределу приходят, рассматривая числовую последовательность Доказано, что эта последовательность имеет пределом иррациональное число,
обозначаемое буквой , т. е. где Доказано также, что предел функции при тоже равен , т.е. (5.2)
Этот предел называют вторым замечательным пределом. Величина может быть определена численным методом с любой степенью точности.
Если положить , то предел (5.2) можно записать в виде (5.3)
Заметим, что показательную функцию с основанием , т.е. функцию , часто записывают в виде . В частности,
Рассмотрим функцию . Пусть при и в некоторой окрестности точки Тогда, переходя к новой переменной получим
(5.4)
Пример 2.
Преобразуем дробь, выделяя единицу в данной неправильной дроби: Запишем показатель функции, стоящей под знаком предела, в виде
. Обозначая , где при и учитывая замечание 4.5, найдем
Пусть — показательно-степенная функция,
, — число или один из символов .
Можно доказать, что
1) (5.5)
2) (5.6)
3) (5.7)
Если , то имеет место неопределенность вида (см. замечание 4.1). Эту неопределенность можно раскрыть, используя второй замечательный предел. Полагаем , где при и в некоторой окрестности точки. Преобразуя функцию под знаком предела и учитывая формулу (5.4), получим
Пример 3.
Имеем неопределенность вида . Преобразуем функцию под знаком предела:
Полагая , где при, получим
так как
Второй замечательный предел, примеры нахождения, задачи и подробные решения — Мегаобучалка
Второй замечательный предел имеет вид:
или в другой записи
В случае второго замечательного предела имеем дело с неопределенностью вида единица в степени бесконечность .
Разберем несколько примеров нахождения предела по второму замечательному пределу сподробным оприсанием решения.
Пример.
Вычислить предел
Решение.
Подставляем бесконечность:
Пришли к неопределенности единица в степени бесконечность. Смотрим в таблицу неопределенностей для определения метода решения и останавливаемся на применении второго замечательного предела.
Сделаем замену переменных. Пусть
Если , то
Исходный предел после замены примет вид:
Ответ:
Пример.
Вычислить предел
Решение.
Подставляем бесконечность:
Пришли к неопределенности единица в степени бесконечность, которая указывает на применение второго замечательного предела. Выделим целую часть в основании показательно степенной функции:
Тогда предел запишется в виде:
Сделаем замену переменных. Пусть
Если , то
Исходный предел после замены примет вид:
В преобразованиях были использованы свойства степени и свойства пределов.
Ответ:
Пример.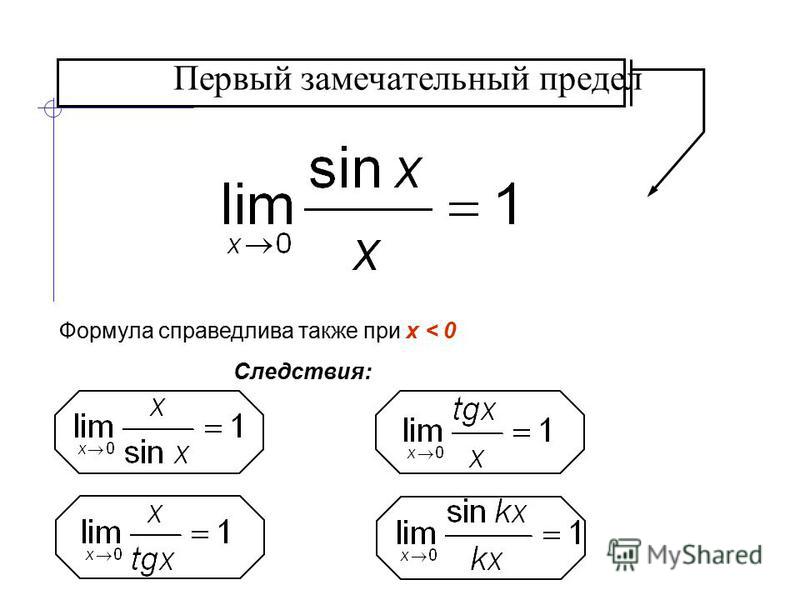
Вычислить предел
Решение.
Преобразуем функцию, чтобы применить второй замечательный предел:
Сейчас домножим показатель на и разделим на это же выражение, затем используем свойства степени:
Так как показатели степени числителя и знаменателя дроби одинаковые (они равны 6), то предел этой дроби на бесконечности равен отношению коэффициентов при старших степенях (см. непосредственное вычисление пределов):
Если произвести замену , то получим второй замечательный предел в чистом виде, следовательно,
Ответ:
39.
Пусть и – бесконечно малые функции при . Предел отношения этих величин может принимать любые значения – в зависимости от быстроты убывания одной величины относительно другой. Для сопоставления скоростей убывания этих величин при стремлении x точке a можно использовать предел отношения
Если этот предел представляет собой конечное ненулевое число, то и называются бесконечно малыми одного и того же порядка. Особый интерес представляет частный случай, когда λ = 1. Тогда говорят, что и являются эквивалентными бесконечно малыми при и записывают это утверждение в виде
Если λ = 0, то говорят, что является бесконечно малой более высокого порядка по сравнению с при а функция имеет меньший порядок малости. Термин “порядок малости” допускает уточнение, если и представляют собой бесконечно малые одного и того же порядка. В этом случае говорят, что является бесконечно малой n-го порядка по сравнению с . Например, функция является бесконечно малой 4-го порядка по сравнению с при x → 0. Если λ = ∞, то бесконечно малые и как бы меняются своими ролями. В этом случае функция является бесконечно малой более высокого порядка по сравнению с при . Сформулируем некоторые полезные свойства эквивалентных бесконечно малых.
|
40.
Limits — Ferguson Math
Что такое лимит?Представьте, если хотите, функцию, которая не определена в определенной точке, скажем, в x=5 . Для каждого значения x, кроме 5, функция существует, но в этой единственной точке x=5 на графике есть дыра. Предел — это, по сути, способ измерения того, какой была бы эта точка , если бы мы могли подставить значение x=5 в уравнение. Предел измеряет, к какому значению функция приближается как с левой, так и с правой стороны в определенной точке x. Сначала это может показаться запутанным, но на самом деле это довольно просто по своей природе. Посмотрите на этот график нашей функции. Обратите внимание на дыру в графике x=5 . Обозначение предела Это все прекрасно, но как записать это математически? Что ж, общепринятое обозначение пределов выглядит следующим образом: Где a — это значение, к которому вы обычно приближаетесь, а f(x) — это функция графика, которую вы пытаетесь измерить. В нашем примере это будет следующее: Довольно просто, да? Мы просто подставили значение x, к которому мы приближаемся, вместо a, и, поскольку мы не знаем фактическую функцию f(x), мы просто сохраняем ее как f(x). Пределы решения алгебраически Что делать, если у нас нет графика функции, и мы не можем решить ее, просто взглянув на нее? Что, если нам просто дана функция графика? Мы просто сдаемся? Если вы хотите идти вперед, но это не невозможно. Скажем, нам дали функцию: И нас попросили найти значение: Что ж, самое замечательное в ограничениях то, что иногда они могут быть такими элементарными, как может показаться. Чтобы найти пределы алгебраически, первое, что мы делаем, это пытаемся подставить значение a, которое в данном случае равно 3, в уравнение и посмотрим, что оно выдаст! Наш процесс выглядит так: Ну, это terwonderful (Потрясающе + Чудесно), потому что на самом деле это так же просто, как подставить значение a в уравнение, которое у нас есть для функции. Но что происходит, когда мы не можем просто сделать это? Есть определенные ситуации, когда подстановка значения a в уравнение создаст нам проблему или будет неопределенным. Если бы мы просто подставили x=3 в эту функцию, мы получили бы 0/0, значение которого мы не знаем и не можем знать. Всякий раз, когда мы получаем что-либо, деленное на 0, у нас возникает проблема; его нельзя вычислить, так как мы не можем делить на 0. Итак, как же нам обойти это? Что ж, мы должны использовать некоторые хитрые приемы, чтобы избавиться от x-3 внизу. Давайте попробуем применить идею разности квадратов к вершине, чтобы мы выполнили то, что я только что сказал: Хотя это может быть не решением всех проблем, с которыми мы сталкиваемся с ограничениями, общий принцип каждый раз остается одним и тем же: вынести знаменатель из числителя, чтобы создать сокращение, и устранить проблему деления на 0. Давайте посмотрим на другой пример: Если мы попытаемся подставить x=0 в уравнение, мы снова получим 0/0. Несмотря на то, что это было много работы, было также включено много шагов, которые не являются необходимыми, а это означает, что объем работы, которую вы вкладываете в самостоятельное решение ограничения, значительно сокращается. Обратите внимание, что в итоге мы сделали то же самое, что и в предыдущем примере: мы получили х вверху и х внизу, чтобы создать отмену, вызывающую проблему 0/0. Это главный пункт решения всех ограничений, которые могут быть разрешены. Свойства пределов Ограничения – замечательные друзья, потому что они обладают многими свойствами, которые по своей природе являются очень мягкими и не ограничивающими. Это должно быть очевидным, потому что значение функции никогда не меняется ни при каком значении x. Если у вас есть функция y = 5, независимо от того, какое значение вы введете для x, значение y всегда будет равно 5, а это означает, что предел, когда x приближается к любому значению, всегда будет оцениваться как 5, поскольку значение функции никогда не меняется. Второе свойство также должно быть очень очевидным: Это очевидно просто потому, что прямая подстановка даст одно и то же значение для любого значения x. Теперь о том, что не так очевидно. Начнем со сложения/вычитания двух пределов: Этот тоже прост, но не так очевиден, как два предыдущих. В основном говорится, что предел двух функций, добавляемых/вычитаемых друг к другу, равен пределу двух функций, добавляемых/вычитаемых друг к другу по отдельности. И просто для удовольствия, вот пример с показателями (Ура!): Теперь это замечательно, потому что позволяет нам находить пределы, не зная конкретных функций, таких как f(x) или g(x). Хотите доказательства этого? Я продемонстрирую. Скажем, мы хотели найти для: И нам дали следующие утверждения: Теперь наши методы решения по пределу бесполезны для нас, потому что мы не знаем f(x) или g(x). Так что же нам делать? Мы используем наши супер-пупер предельные свойства, чтобы преодолеть это препятствие! Видите? Очень полезно иметь эти свойства, так как они позволяют нам выполнять манипуляции, даже не зная, что такое f(x)! Вторая часть информации, которую нам дали, касающаяся g(x), на самом деле не имела к этому никакого отношения. Извините за случайность, но часто в математике вам приходится иметь дело с тем, что вам дают больше информации, чем необходимо. Несуществующие пределы Ранее мы имели дело только с существующими пределами, которые не являются бесконечностью. К сожалению, это не всегда так. Говорят, что предел не существует, если предел как функция, приближающаяся к значению x слева, не равна пределу, когда функция приближается к значению справа. Другими словами, левый предел не равен правому пределу. Что это означает? Ну, это просто. Когда у вас есть предел, скажите тот, который мы использовали в первом примере: Посмотреть, к чему приближается значение, можно как с левой стороны (в данном случае при x<5), так и с правой стороны (в данном случае при x>5). Когда эти два значения не совпадают, предела не существует. Когда это может произойти? Так бывает и с кусочными функциями, например в следующей ситуации: Как видите, при x=3 функция распадается на две разные функции. Когда вы смотрите на предел слева, кажется, что значение y приближается к y=1. Существует обозначение, указывающее, приближается ли используемый вами предел слева или справа, и оно выглядит следующим образом: Первое обозначение используется для указания предела, приближающегося слева, поэтому — знак. Второй используется для обозначения предела, приближающегося к a справа. Третий — это предел функции в точке a, которая является значением, к которому они приближаются. Если первые два не совпадают или один из первых двух не существует, то третий не существует и не может быть определен. Пределы, связанные с бесконечностью Мы редко когда-либо работаем с концепцией бесконечности в математике. Сочетание этого факта с идеей о том, что ограничения — это совершенно новая концепция со своими собственными проблемами, делает ограничения, связанные с бесконечностью, пугающей идеей. Это выглядит намного сложнее, чем есть на самом деле. Помните, что на самом деле означает предел; это означает значение y, к которому мы приближаемся по мере приближения к определенному значению x. Давайте просто посмотрим на несколько чисел для x, для которых это будет работать, и посмотрим, что произойдет:
Просто взглянув на эти цифры, кажется, что когда мы увеличиваем значение x, f(x) становится все меньше и меньше, все ближе и ближе к числу 0. Для ЛЮБОГО значения k, кроме бесконечности. Почему? Ну, просто потому, что неважно, насколько велико число k сверху, пока оно конечно, оно всегда станет бесконечно малым, если его разделить на бесконечность. Даже если k равно миллиарду триллионов квадриллионов, оно все равно станет 0, если оно делится на бесконечность, или, по крайней мере, оно будет приближаться к 0, то есть. Теперь нужно ввести еще одну концепцию, потому что в большинстве случаев мы будем получать функцию от x как в числителе, так и в знаменателе, что немного усложняет процесс. Поверите ли вы мне, если я скажу вам, что это правда? Большинство людей, вероятно, сказали бы, что нет. В конце концов, похоже, что знаменатель будет расти гораздо быстрее, чем числитель, верно? Ну не совсем. Когда вы начинаете работать с бесконечностью, значение 50х становится настолько малым по сравнению с х в квадрате, что его невозможно даже рассматривать. Теперь это становится гораздо более очевидным для человека, который смотрит на это с новой точки зрения. По сути, вы просто смотрите на наивысшую степень как числителя, так и знаменателя. Если высшая степень x принадлежит знаменателю, то предел при приближении x к бесконечности становится равным 0. Если высшая степень находится в числителе, то пределом является также бесконечность, которая, как мы говорим, не существует просто из-за своей природы. Если в числителе и знаменателе имеется одинаковая степень, то предел равен просто коэффициенту наибольшей степени числителя, деленному на коэффициент наибольшей степени знаменателя. ВАУ, это выглядит ужасно. Однако это не так. Помните концепцию, согласно которой х в пятерке — это единственное, о чем мы беспокоимся, так как он растет намного быстрее, чем остальная часть как в числителе, так и в знаменателе, что остальное не имеет значения. Мы действительно можем сократить это до следующего: |
У нас есть значение y для каждого значения x, кроме x=5. Когда мы смотрим на предел для x=5 , мы в основном пытаемся измерить, к какому значению y приближается, когда мы приближаемся к x=5. Что ж, с этим графиком все довольно просто: по мере того, как x приближается к 5, y становится все ближе и ближе к 50. Несмотря на то, что в графике есть дыра, предел все еще существует в этой точке, поскольку предел на самом деле не измеряет то, что график ЕСТЬ в этой точке, а скорее таким, каким он должен быть. 
Самый распространенный пример этого — когда вы получаете 0 в качестве знаменателя уравнения, которое мы не можем решить, так как мы ни в коем случае не можем делить на 0. Давайте посмотрим на пример этого события:
Итак, как мы можем решить эту проблему? Ну и еще одна популярная техника, используемая для решения задач с радикалами, — это умножение и верха, и низа на сопряжение части с радикалом. Это удалит радикал и часто вызывает отмену всего за один простой шаг. Давайте попробуем это, умножив верх и низ на сопряженное число числителя:
Самая первая, которая должна быть совершенно очевидной, выглядит следующим образом:
Вот еще один, с умножением и делением:
Однако, если посмотреть на функцию справа от x=3, кажется, что функция приближается к y=4. Поскольку два предела не совпадают, предела при x=3 не существует. Помните, что предел не совпадает со значением функции в точке: когда x=3, y=1. Это можно сказать с уверенностью, в отличие от предела, которого не существует.
На самом деле это довольно просто и требует очень мало математики при работе с ними. Возьмем, к примеру, следующий предел:
Итак, когда мы получаем число для x, которое бесконечно велико, то f(x) становится бесконечно малым, что переводится в 0. Это дает нам понятие, что: 
50x будет увеличиваться очень быстро, когда вы начнете превращать х в бесконечность, но х в квадрате увеличивается с невероятно высокой скоростью, и в конце концов, когда вы начнете достигать бесконечности, х в квадрате будет единственным членом, на который вы смотрите, поскольку по отношению к нему 50x + 20 не имеет значения. Это может показаться странным, но это правда. Когда вы имеете дело с пределами, уходящим в бесконечность с помощью этого уравнения, вы, по сути, работаете с этим:
Давайте посмотрим на другой пример:Исчисление 1 Пределы — Видеокурс
- домашняя страница
- Пределы исчисления 1 — видеоучебник C . . .
Этот курс посвящен самой первой теме, изучаемой в исчислении — теории пределов.
Мы вводим понятие предела с помощью простых графиков и практических примеров, а не длинного формального определения. Затем мы работаем с многочисленными примерами задач, чтобы закрепить концепции, прежде чем перейти к теоремам и определениям, которые должны усвоить все, кто изучает математический анализ при изучении пределов.
Мы рассмотрим определение предела, методы решения пределов, предельные законы, непрерывность и многое другое.
Урок 3: Оценка пределов с помощью факторинга, часть 1
На этом уроке учащиеся узнают, как решать пределы с помощью факторинга и упрощения…. Просмотреть урок
Урок 4: Оценка пределов с помощью факторинга, часть 2
На этом уроке учащиеся узнают, как находить пределы с помощью факторинга и упрощения…. Посмотреть урок
Урок 5: Пределы с использованием триггерных функций
В этом уроке На этом уроке учащиеся узнают, как находить пределы, включающие триггерные функции…. Посмотреть урок
Урок 6. Касательные линии, скорость и пределы
На этом занятии учащиеся узнают, как можно использовать предел для найти прямую, касательную кривой, и почему это понятие важно…. Посмотреть урок
Урок 7: Формальное определение предела
В этом уроке учащиеся узнают, что такое формальное определение предела и что оно означает.