основы. Алгебраическая и тригонометрическая форма комплексного числа
Комплексные числа — это числа вида a + bi, где a и b — действительные числа, а i — число особого рода, квадрат которого равен минус единице: i²=−1.
Действия над комплексными числами выполняются по таким же правилам, что и над многочленами, при этом i² заменяют на −1.
Комплексные числа вводятся в связи с тем, что действительных чисел недостаточно, чтобы решить любое квадратное уравнение с действительными коэффициентами. Простейшее из квадратных уравнений, не имеющих корней среди действительных чисел, есть
x² + 1 = 0.
Задача такова: нужно расширить систему действительных чисел до такой системы чисел, в которой это уравнение обладало бы корнем.
Решение: x² = — 1, x =√-1,
где √-1 — квадратный корень
из минус единицы — мнимая единица, обозначаемая буквой 
Название «мнимые числа» ввёл в 1637 году французский математик и философ Р. Декарт. А в 1777 году один из крупнейших математиков того времени Л. Эйлер предложил использовать первую букву французского слова «imaginaire» (мнимый) для обозначения числа √-1 «мнимой единицы».
Продвинемся ещё на шаг к алгебрической форме записи комплексных чисел. Квадратное уравнение
имеет корни и , где i = √-1 — квадратный корень из минус единицы.
Таким образом, у комплексных чисел есть действительная и мнимая части. В алгебраической записи комплексного числа a + bi есть действительная часть a и мнимая часть bi.
В литературе наиболее часто встречается именно такая обобщённая алгебраическая форма
комплексного числа: z = a + bi.
Но сейчас мы применим запись z = x + yi только для того, чтобы было более понятно отображение комплексного числа в привычной
системе координат с осями x и y.
Отображая на плоскости горизонтальную ось x как ось действительных чисел, а вертикальную ось y как ось мнимых чисел, можно любое комплексное число z = x + yi отобразить как точку P в декартовой системе координат (рисунок ниже).
Поэтому возможна и запись комплексного числа в тригонометрической форме:
,
где — модуль комплексного числа, (аргумент комплексного числа) — угол, который радиус-вектор образует с осью Ox. Теперь мы видим, что более подходящим является сравнение записи комплексного числа в тригонометрической форме с отображением точки в
Обобщим ещё раз понятие модуля и аргумента комплексного числа. Модуль комплексного числа — это расстояние от начала координат до точки, в виде которой
отображается комплексного числа или, что то же самое — длина радиус-вектора
. Аргумент комплексного числа — это угол, который радиус-вектор
образует с осью Ox.
Аргумент комплексного числа — это угол, который радиус-вектор
образует с осью Ox.
Теперь о том, как перейти от алгебраической формы комплексного числа к тригонометрической. Доказано, что
и
.
Поэтому можем легко найти косинус и синус аргумента комплексного числа:
, .
Пример 1.
Найти тригонометрическую форму числа .Решение. Сначала найдём модуль комплексного числа. Для этого в соответствии с обобщенной записью числа z = a + bi запишем данное число как z = 1 + 1i, где a = 1 и b = 1. Из этого получаем модуль данного числа — квадратный корень из 1 + 1 = 2, что равно . Чтобы определить аргумент числа, учтём, что и . То есть, значение угла равно . Поэтому получаем тригонометрическую форму данного комплексного числа:
.
Пример 2. Найти тригонометрическую форму комплексного числа 1.
Возможны возражения: 1 — это же обычное, точнее, действительное число. Это так. Но это число можно представить и как комплексное число , то есть, комплексное число, в котором a
Решение. Модуль данного числа . Чтобы определить аргумент числа, найдём и . Следовательно, аргумент комплексного числа . Получили тригонометрическую форму данного комплексного числа:
.
Пройти тест по теме Комплексные числа
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пример 3. Найти тригонометрическую форму комплексного числа .
Решение. Модуль данного числа
. Чтобы
определить аргумент числа, найдём и
.
Для нахождения угла с таким косинусом и таким синусом повернём воображаемый циркуль
от угла 0 до
и ещё на . Получаем .
Следовательно, аргумент комплексного числа .
Получили тригонометрическую форму данного комплексного числа:
Получаем .
Следовательно, аргумент комплексного числа .
Получили тригонометрическую форму данного комплексного числа:
.
Пример 4. Найти тригонометрическую форму комплексного числа .
Решение. Модуль данного числа . Чтобы определить аргумент числа, найдём и . Аргумент, то есть угол, у которого найденный косинус и найденный синус, определяется однозначно: . Получили тригонометрическую форму данного комплексного числа:
.
Пример 5. Найти тригонометрическую форму комплексного числа -3.
Решение. Модуль данного числа . Чтобы определить аргумент числа, найдём и . Аргумент, то есть угол, у которого найденный косинус и найденный синус, определяется однозначно: . Получили тригонометрическую форму данного комплексного числа:
.
Пример 6. Найти тригонометрическую форму
комплексного числа .
Решение. Модуль данного числа . Чтобы определить аргумент числа, найдём и . Чтобы найти угол, у которого найденный косинус и найденный синус, отвыкшим от школьных лет и тригонометрии, возможно, придётся чуть побольше попыхтеть, вращая воображаемый циркуль по координатной плоскости. Вот они, шаги вычисления угла: поворачиваем циркуль на , затем на и на Получаем . Получили тригонометрическую форму данного комплексного числа:
.
Пример 7. Найти тригонометрическую форму комплексного числа .
Решение. Модуль данного числа . Чтобы определить аргумент числа, найдём и . Шаги вычисления угла, то есть аргумента: поворачиваем циркуль на , затем на и на Получаем . Получили тригонометрическую форму данного комплексного числа:
.
Пройти тест по теме Комплексные числа
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
О множествах чисел
Множества и операции над множествамиVII.
 1. Формы записи комплексных чисел и действия над ними
1. Формы записи комплексных чисел и действия над ними(схема 43)
Комплексным числом называется выражение вида z=x+iy, (7.1) где x и y – действительные числа, а i так называемая мнимая единица. Соотношение для мнимой единицы i2=–1. (7.2) Если x=0, то число 0+iy=iy называется чисто мнимым; если y=0, то число x+i∙0=x отождествляется с действительным числом  Число x называется действительной частью комплексного числа z и обозначается x=Re z, а y – мнимой частью комплексного числа z и обозначается y=Im z. Два комплексных числа z1=x1+iy1 и z2=x2+iy2 называются равными (z1=z2) тогда, когда равны их действительные и мнимые части: x1=x2, y1=y 2. В частности, комплексное число z=x+iy равно нулю, когда x=y=0. Понятия «больше» и «меньше» для комплексных чисел не вводятся. Числа z=x+iy и называются комплексно сопряженными. Всякое комплексное число z=x+iy можно изобразить точкой M(x;y) плоскости x0y такой,
что x=Re z, y=Im z. Плоскость, на которой изображаются комплексные числа, называется Комплексное
число z=x+iy можно задавать с помощью радиус-вектора . Длина вектора , изображающего комплексное число z, называется модулем этого числа и обозначается |z| или r. Величина
угла между положительным направлением действительной оси и вектором называется аргументом комплексного
числа, обозначается Arg z или φ. Для комплексного числа z=0 аргумент не определен. Аргумент комплексного числа – величина многозначная и определяется с точностью до слагаемого 2πk (k=0;–1;1;–2;2…): , где arg z – главное значение аргумента, заключенное в промежутке (–π;π). Иногда в качестве главного значения аргумента берут величину, принадлежащую промежутку [0;2π). Алгебраической формой комплексного числа называется запись числа z в виде z=x+iy. Модуль r и аргумент φ можно рассматривать как полярные координаты вектора , изображающего комплексное число z=x+iy (см. рис. 7.1). Тогда из соотношений сторон в прямоугольном треугольнике получаем . Следовательно, комплексное число z=x+iy можно записать в виде или . Равенство (7.3) есть тригонометрическая форма комплексного числа. Модуль r=|z| однозначно определяется по формуле . (7.4) Аргумент определяется из формул: . (7.5) При переходе от
алгебраической формы комплексного числа к тригонометрической достаточно
определить главное значение аргумента комплексного числа z, то есть
считать φ=arg z. Знаки полученных значений cos φ и sin φ по
формулам (7. Используя формулу Эйлера , (7.6) комплексное число можно записать в так называемой показательной (или экспоненциальной) форме z=reiφ, (7.7) где r=|z| — модуль комплексного числа, а угол (k=0;–1;1;–2;2…). Функция eiφ – периодическая с основным периодом 2π, поэтому для записи комплексного числа в показательной форме по формуле 7. Пример 7.1. Записать комплексные числа в тригонометрической и показательной формах. Решение. Для z1 имеем . Поэтому . Для действительного числа . Поэтому На множестве комплексных чисел определен ряд операций. 1. Суммой двух комплексных чисел z1=x1+iy1 и z2=x2+iy2 называется комплексное число, определяемое равенством . (7.8) Из (7.8) следует, что геометрически комплексные числа складываются как
векторы, причем сумма комплексных чисел интерпретируется как диагональ
параллелограмма, построенного на векторах, представляющих слагаемые (рис. 2. Вычитание комплексных чисел определяется как действие, обратное сложению. Разностью двух комплексных чисел z1 и z2 называется такое комплексное число z, которое, будучи сложенным с z2, дает число z1, то есть z= z1 – z2, если z+z2=z1. Если z1=x1+iy1, z2=x2+iy2, то из этого определения получаем: (7.9) Из равенства (7.9) следует, что геометрически
комплексные числа вычитаются как векторы. При этом число z= z1 – z2 изображается вектором, соединяющим концы векторов , и исходящим из конца
вычитаемого в конец уменьшаемого (см. . (7.10) 3. Произведением комплексных чисел z1=x1+iy1 и z2=x2+iy2 называется комплексное число, определяемое равенством . (7.11) Из (7.11) следует важнейшее соотношение i2= –1. Действительно, . Найдем произведение комплексных чисел и . . (7.12) Видно, что при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множителей. Нетрудно видеть, что если есть n множителей и все они одинаковые, то частным случаем равенства (7.12) является формула возведения комплексного числа в натуральную степень: . (7.13) (7.13)
называется первой формулой Муавра. Произведение двух комплексных чисел в показательной (экспоненциальной) форме имеет вид: . (7.14) 4. Частным двух комплексных чисел z1 и называется комплексное число z, которое, будучи умноженным на z2, дает число z1, то есть , если . Пусть , тогда с использованием этого определения получаем: . (7.15) На практике при нахождении частного двух комплексных чисел
удобно умножить числитель и знаменатель дроби на число, сопряженное
знаменателю, с дальнейшим применением равенства i2= –1 и формулы разности квадратов. Деление комплексных чисел осуществляется также и в тригонометрической форме, при этом имеет место формула: . (7.16) Видно, что при делении комплексных чисел их модули делятся, а аргументы вычитаются соответственно. Частное двух комплексных чисел в показательной (экспоненциальной) форме имеет вид: . (7.17) Пример 7.2. Найти сумму, разность, произведение и частное комплексных чисел . Решение. По формуле (7.8) сумма заданных чисел равна . Согласно формуле (7.9) разность заданных чисел равна . Пользуясь формулой (7.11), вычислим их произведение . На основании формулы (7. Пример 7.3. Найти произведение и частное комплексных чисел , представив их в тригонометрической и показательной форме. Решение. Используя (7.4) и (7.5), получаем: . Следовательно, на основе формул (7.3) и (7.7) число z1 имеет тригонометрическую и показательную форму . Аналогично, для z2 можно записать: . Отсюда . По формулам (7.12) и (7.16) получим в тригонометрической форме: Пользуясь формулами (7.14) и (7.17), получим в показательной форме: 5. Извлечение корня n-ой степени – операция, обратная возведению в натуральную степень, определенному ранее формулой (7.13). Корнем n-ой степени из комплексного числа z называется комплексное число ω, удовлетворяющее равенству ωn=z, то есть , если ωn=z. Пусть , тогда по данному определению и формуле (7.13) Муавра можно записать: . Сравнивания части этого равенства, получим: . Отсюда (корень арифметический). Окончательно получаем: . (7.18) (7.18) называется второй формулой Муавра. Видно, что для любого корень n-ой степени из комплексного числа z имеет равно n различных значений. Пример 7.4. Найти все корни уравнения z4+16=0. Решение. Запишем уравнение в виде z4=–16+0∙i. Отсюда по формуле (7.18) получим: . Рассмотрим различные значения k=0;1;2;3. Корни z1 и z4, а также z2 и z3 являются
комплексно сопряженными.
Сформулируем несколько иначе основную теорему алгебры 3.2 над полем комплексных чисел. Теорема 7.1 (основная теорема алгебры). Для всякого многочлена с комплексными коэффициентами степени n>0 существует точка , в которой P(z0)=0 Приведем еще одну теорему, имеющую место над множеством комплексных чисел. Теорема 7.2. Если многочлен Pn(x) с действительными коэффициентами имеет комплексный корень a+ib, то он имеет и сопряженный корень a–ib В разложение
многочлена комплексные корни
входят сопряженными парами. Пусть корни многочлена x1=a+ib и x2=a–ib. Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами, а соответствующее квадратное уравнение будет иметь отрицательный дискриминант.
Вопросы для самопроверки |
комплексных чисел | Алгебра и тригонометрия
Цели обучения
В этом разделе вы будете:
- Складывать и вычитать комплексные числа.
- Умножать и делить комплексные числа.
- Упростите степени [latex]i[/latex].
Рисунок 1.
Обнаруженное Бенуа Мандельбротом примерно в 1980 году, множество Мандельброта является одним из самых узнаваемых фрактальных изображений. Изображение построено на теории самоподобия и операции итерации. Увеличение фрактального изображения преподносит много сюрпризов, особенно высокий уровень повторения деталей, появляющийся при увеличении увеличения. Уравнение, порождающее это изображение, оказывается довольно простым.
Изображение построено на теории самоподобия и операции итерации. Увеличение фрактального изображения преподносит много сюрпризов, особенно высокий уровень повторения деталей, появляющийся при увеличении увеличения. Уравнение, порождающее это изображение, оказывается довольно простым.
Чтобы лучше понять это, нам нужно ознакомиться с новым набором чисел. Имейте в виду, что изучение математики постоянно опирается на себя. Отрицательные целые числа, например, заполняют пустоту, оставленную набором положительных целых чисел. Множество рациональных чисел, в свою очередь, заполняет пустоту, оставленную множеством целых чисел. Множество действительных чисел заполняет пустоту, оставленную множеством рациональных чисел. Неудивительно, что множество действительных чисел также имеет пустоты. В этом разделе мы рассмотрим набор чисел, который заполняет пустоты в наборе действительных чисел, и узнаем, как с ним работать.
Выражение квадратных корней из отрицательных чисел в виде кратных [latex]\,i[/latex]
Мы знаем, как найти квадратный корень из любого положительного действительного числа. Аналогичным образом мы можем найти квадратный корень из любого отрицательного числа. Отличие в том, что рут не настоящий. Если значение подкоренной черты отрицательное, корень называется мнимым числом . Мнимое число[латекс]\,i\,[/латекс] определяется как квадратный корень из [латекс]\,-1.[/латекс]
Аналогичным образом мы можем найти квадратный корень из любого отрицательного числа. Отличие в том, что рут не настоящий. Если значение подкоренной черты отрицательное, корень называется мнимым числом . Мнимое число[латекс]\,i\,[/латекс] определяется как квадратный корень из [латекс]\,-1.[/латекс]
[латекс]\sqrt{-1}=i[/ латекс] 9{2}=-1[/latex]
Мы можем записать квадратный корень из любого отрицательного числа как кратное [latex]\,i.\,[/latex]Рассмотрим квадратный корень из [latex]\,- 49.[/latex]
[латекс]\begin{array}{ccc}\hfill \sqrt{-49}& =& \hfill \sqrt{49\cdot \left(-1\right)}\\ & =& \sqrt{49}\sqrt{-1}\hfill \\ & =& 7i\hfill \end{array}[/latex]
Мы используем [latex]\,7i\,[/latex], а не [латекс]\,-7i\,[/латекс], потому что главный корень [латекс]\,49\,[/латекс] является положительным корнем.
Комплексное число — это сумма действительного числа и мнимого числа. Комплексное число выражается в стандартной форме при записи [латекс]\,а+би\,[/латекс], где [латекс]\,а\,[/латекс] — действительная часть, а [латекс]\,b\, [/latex] — мнимая часть. Например, [латекс]\,5+2i\,[/латекс] — комплексное число. Так же и is[latex]\,3+4i\sqrt{3}.[/latex]
Например, [латекс]\,5+2i\,[/латекс] — комплексное число. Так же и is[latex]\,3+4i\sqrt{3}.[/latex]
Мнимые числа отличаются от действительных чисел тем, что квадрат мнимого числа дает отрицательное действительное число. Напомним, что при возведении в квадрат положительного действительного числа результатом является положительное действительное число, а при возведении в квадрат отрицательного действительного числа результатом также является положительное действительное число. Комплексные числа состоят из действительных и мнимых чисел.
Мнимые и комплексные числа
Комплексное число — это число вида [латекс]\,а+би\,[/латекс], где
- [латекс]а\,[/латекс] — действительная часть комплексное число.
- [латекс]b\,[/латекс] — мнимая часть комплексного числа.
Если[латекс]\,b=0,[/латекс],то[латекс]\,а+би\,[/латекс]является действительным числом. Если [латекс]\,а=0\,[/латекс]и[латекс]\,b\,[/латекс]не равно 0, комплексное число называется чисто мнимым числом. Мнимое число – это четный корень из отрицательного числа.
Мнимое число – это четный корень из отрицательного числа.
How To
Имея мнимое число, представьте его в стандартной форме комплексного числа.
- Написать[латекс]\,\sqrt{-a}\,[/latex]как[латекс]\,\sqrt{a}\sqrt{-1}.[/latex]
- Экспресс[латекс]\,\sqrt{-1}\,[/латекс]как[латекс]\,я.\,[/латекс]
- Напишите [латекс]\,\sqrt{a}\cdot i\,[/латекс] в простейшей форме.
Выражение мнимого числа в стандартной форме
Выразите[latex]\,\sqrt{-9}\,[/latex]в стандартной форме.
Показать решение
Попробуйте
Express[latex]\,\sqrt{-24}\,[/latex]в стандартной форме.
Показать решение
Нанесение комплексного числа на комплексную плоскость
Мы не можем наносить на числовую прямую комплексные числа, как настоящие числа. Однако мы все еще можем представить их графически. Чтобы представить комплексное число, нам нужно обратиться к двум компонентам числа. Мы используем комплексную плоскость, которая представляет собой систему координат, в которой горизонтальная ось представляет действительную составляющую, а вертикальная ось представляет мнимую составляющую. Комплексные числа — это точки на плоскости, выраженные в виде упорядоченных пар [латекс]\,\слева (а,б\справа),[/латекс], где [латекс]\,а\,[/латекс] представляет собой координату для горизонтальная ось, а [латекс]\,b\,[/латекс] представляет собой координату вертикальной оси.
Мы используем комплексную плоскость, которая представляет собой систему координат, в которой горизонтальная ось представляет действительную составляющую, а вертикальная ось представляет мнимую составляющую. Комплексные числа — это точки на плоскости, выраженные в виде упорядоченных пар [латекс]\,\слева (а,б\справа),[/латекс], где [латекс]\,а\,[/латекс] представляет собой координату для горизонтальная ось, а [латекс]\,b\,[/латекс] представляет собой координату вертикальной оси.
Рассмотрим число[латекс]\,-2+3i.\,[/латекс]Действительная часть комплексного числа равна [латекс]\,-2\,[/латекс], а мнимая часть равна 3. Мы строим упорядоченную пару [латекс]\,\левый(-2,3\правый)\,[/латекс] для представления комплексного числа[латекс]\,-2+3i,[/латекс], как показано на (рис. ) .
Рис. 2.
Сложная плоскость
На комплексной плоскости горизонтальная ось является реальной осью, а вертикальная ось — мнимой осью, как показано на (Рисунок).
Рис. 3.
Как
Для заданного комплексного числа представить его компоненты на комплексной плоскости.
- Определите действительную и мнимую части комплексного числа.
- Перемещайтесь по горизонтальной оси, чтобы показать действительную часть числа.
- Перемещение параллельно вертикальной оси для отображения мнимой части числа.
- Нанесите точку.
Нанесение комплексного числа на комплексную плоскость
Нанесите комплексное число[latex]\,3-4i\,[/latex] на комплексную плоскость.
Показать решение
Попробуйте
Нанесите комплексное число[латекс]\,-4-i\,[/латекс] на комплексную плоскость.
Показать решение
Сложение и вычитание комплексных чисел
Как и с действительными числами, мы можем выполнять арифметические операции над комплексными числами. Чтобы сложить или вычесть комплексные числа, мы объединяем действительные части, а затем объединяем мнимые части.
Чтобы сложить или вычесть комплексные числа, мы объединяем действительные части, а затем объединяем мнимые части.
Комплексные числа: сложение и вычитание
Добавление комплексных чисел:
[латекс]\влево(а+би\вправо)+\влево(с+ди\вправо)=\влево(а+с\вправо)+\влево(b+d\вправо) i[/latex]
Вычитание комплексных чисел:
[латекс]\left(a+bi\right)-\left(c+di\right)=\left(a-c\right)+\left(b-d\right) )i[/latex]
How To
Даны два комплексных числа, найдите их сумму или разность.
- Определите действительную и мнимую части каждого числа.
- Добавить или вычесть действительные части.
- Сложить или вычесть мнимые части.
Сложение и вычитание комплексных чисел
Сложение или вычитание, как указано.
- [латекс]\влево(3-4i\вправо)+\влево(2+5i\вправо)[/латекс]
- [латекс]\влево(-5+7i\вправо)-\влево(-11+2i\вправо)[/латекс]
Показать решение
Попробуйте
Вычтите [латекс]\,2+5i\,[/латекс]из [латекс]\,3–4i. [/латекс]
[/латекс]
Показать решение
Умножение комплексных чисел
Умножение комплексных чисел очень похоже на умножение двучленов. Основное отличие состоит в том, что мы работаем с реальной и мнимой частями отдельно.
Умножение комплексного числа на вещественное число
Начнем с умножения комплексного числа на действительное число. Мы распределяем действительное число так же, как и биномиальное. Рассмотрим, например, [латекс]\,3\влево(6+2i\вправо)[/латекс]:
Как сделать
Учитывая комплексное и действительное число, умножьте их, чтобы найти произведение.
- Использовать свойство дистрибутива.
- Упростить.
Умножение комплексного числа на действительное число
Найти продукт[латекс]\,4\левый(2+5i\правый).[/латекс]
Показать решение
Попробуйте
Найдите продукт:[латекс]\,\frac{1}{2}\left(5-2i\right). {2},[/латекс] он равен [латекс]\,-1.[/латекс] 9{2}=-1.[/латекс]
{2},[/латекс] он равен [латекс]\,-1.[/латекс] 9{2}=-1.[/латекс]
Умножение комплексного числа на комплексное число
Умножение: [латекс]\,\влево(4+3i\вправо)\влево(2-5i\вправо).[/латекс]
Показать решение
Попробуйте
Умножить:[латекс]\,\влево(3-4i\вправо)\влево(2+3i\вправо).[/латекс]
Показать решение
Деление комплексных чисел
Деление двух комплексных чисел сложнее, чем сложение, вычитание или умножение, потому что мы не можем делить на мнимое число, а это означает, что любая дробь должна иметь знаменатель действительного числа, чтобы записать ответ в стандартной форме[латекс ]\,a+bi.\,[/latex]Нам нужно найти член, на который мы можем умножить числитель и знаменатель, который исключит мнимую часть знаменателя, чтобы мы получили действительное число в качестве знаменателя . Этот член называется комплексно-сопряженным знаменателем, который находится при изменении знака мнимой части комплексного числа. Другими словами, комплексное сопряжение [латекс]\,а+би\,[/латекс] равно [латекс]\,а-би.\,[/латекс]Например, произведение [латекс]\,а +bi\,[/latex] и [латекс]\,a-bi\,[/latex] равно 9{2}\hfill \end{массив}[/latex]
Другими словами, комплексное сопряжение [латекс]\,а+би\,[/латекс] равно [латекс]\,а-би.\,[/латекс]Например, произведение [латекс]\,а +bi\,[/latex] и [латекс]\,a-bi\,[/latex] равно 9{2}\hfill \end{массив}[/latex]
Результатом является действительное число.
Обратите внимание, что комплексные сопряжения имеют обратную связь: комплексное сопряжение [латекс]\,а+би\,[/латекс]является [латекс]\,а-би,[/латекс], а комплексное сопряжение [латекс ]\,a-bi\,[/latex]is[latex]\,a+bi.\,[/latex] Далее, когда квадратное уравнение с действительными коэффициентами имеет комплексные решения, решения всегда комплексно сопряжены друг другу .
Предположим, мы хотим разделить [латекс]\,с+ди\,[/латекс] на [латекс]\,а+би,[/латекс], где ни [латекс]\,а\,[/латекс]ни [латекс]\,b\,[/латекс] равно нулю. Сначала запишем деление в виде дроби, затем найдем комплексно-сопряженную часть знаменателя и умножим. 9{2}}\hfill \end{array}[/latex]
Комплексное сопряжение
Комплексно-сопряженное число комплексного числа[латекс]\,а+би\,[/латекс]является[латекс]\,а -bi. \,[/latex]Оно находится при смене знака мнимой части комплексного числа. Действительная часть числа остается неизменной.
\,[/latex]Оно находится при смене знака мнимой части комплексного числа. Действительная часть числа остается неизменной.
- Когда комплексное число умножается на его комплексно-сопряженное, результатом является действительное число.
- Когда комплексное число добавляется к его комплексно-сопряженному, результатом является действительное число.
Нахождение комплексно-сопряженных чисел
Нахождение комплексно-сопряженных чисел каждого числа.
- [латекс]2+i\sqrt{5}[/латекс]
- [латекс]-\frac{1}{2}i[/латекс]
Показать решение
Анализ
Хотя мы видели, что мы можем найти комплексно-сопряженные числа мнимого числа, на практике мы обычно находим комплексно-сопряженные только комплексные числа с вещественной и мнимой компонентами. Чтобы получить действительное число из мнимого, мы можем просто умножить на[latex]\,i.[/latex]
Попробуйте
Найдите комплексно-сопряженное число [латекс]\,-3+4i. [/латекс]
[/латекс]
Показать решение
Как сделать
Даны два комплексных числа, разделите одно на другое.
- Запишите задачу деления в виде дроби.
- Определите комплексное сопряжение знаменателя.
- Умножить числитель и знаменатель дроби на комплексное сопряжение знаменателя.
- Упростить.
Деление комплексных чисел 9{19}[/латекс]
Каждый из них в конечном итоге приведет к ответу, который мы получили выше, но может потребовать несколько дополнительных шагов, чем наш предыдущий метод.
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики работы с комплексными числами.
- Сложение и вычитание комплексных чисел
- Умножение комплексных чисел
- Умножение комплексных конъюгатов
- Повышение и до степени
Ключевые понятия
- Квадратный корень из любого отрицательного числа может быть записан как кратное [латекс]\,i.
 \,[/латекс]См. (рисунок).
\,[/латекс]См. (рисунок). - Чтобы построить комплексное число, мы используем две числовые линии, которые пересекаются, образуя комплексную плоскость. Горизонтальная ось — это реальная ось, а вертикальная ось — воображаемая ось. См. (Рисунок).
- Комплексные числа можно складывать и вычитать, комбинируя действительные части и комбинируя мнимые части. См. (Рисунок).
- Комплексные числа можно умножать и делить.
- Чтобы умножить комплексные числа, распределите так же, как и многочлены. См. (Рисунок) и (Рисунок) .
- Чтобы разделить комплексные числа, умножьте числитель и знаменатель на комплексное сопряжение знаменателя, чтобы исключить комплексное число из знаменателя. См. (Рисунок) и (Рисунок) .
- Степени [latex]\,i\,[/latex]циклические, повторяющиеся каждые четвертые. См. (Рисунок).
Раздел Упражнения
Verbal
Объясните, как складывать комплексные числа. {2}+x-4,[/latex]вычислить[латекс]\,y\,[/latex]данные[латекс]\,x=2i.[ /латекс] 9{2}+x-3,[/latex]вычислить[латекс]\,y\,[/latex]данные[латекс]\,x=2-3i.[/latex]
{2}+x-4,[/latex]вычислить[латекс]\,y\,[/latex]данные[латекс]\,x=2i.[ /латекс] 9{2}+x-3,[/latex]вычислить[латекс]\,y\,[/latex]данные[латекс]\,x=2-3i.[/latex]
If[латекс]\,y =\frac{x+1}{2-x},[/latex]evaluate[latex]\,y\,[/latex]данные[latex]\,x=5i.[/latex]
Показать решение
Если[латекс]\,y=\frac{1+2x}{x+3},[/latex]вычислить[латекс]\,y\,[/latex]данные[латекс]\,x=4i. [/latex]
Графический
Для следующих упражнений нанесите комплексные числа на комплексную плоскость.
[латекс]1-2i[/латекс]
Показать решение
[латекс]-2+3i[/латекс]
[латекс]i[/латекс]
Показать решение
[латекс]-3-4i[/латекс]
Числовой
Для следующих упражнений выполните указанную операцию и представьте результат в виде упрощенного комплексного числа.
[латекс]\влево(3+2i\вправо)+\влево(5-3i\вправо)[/латекс]
Показать решение
[латекс]\влево(-2-4i\вправо)+\влево(1+6i\вправо)[/латекс]
[латекс]\влево(-5+3i\вправо)-\влево(6- i\right)[/latex]
Показать решение
[латекс]\влево(2-3i\вправо)-\влево(3+2i\вправо)[/латекс]
[латекс]\влево(-4+4i\вправо)-\влево(-6+9i\вправо)[/латекс]
Показать решение
[латекс]\влево(2+3i\вправо)\влево(4i\вправо)[/латекс]
[латекс]\влево(5-2i\вправо)\влево(3i\вправо)[/латекс]
Показать решение
[латекс]\влево(6-2i\вправо)\влево(5\вправо)[/латекс]
[латекс]\влево(-2+4i\вправо)\влево(8\вправо)[/латекс ]
Показать решение
[латекс]\влево(2+3i\вправо)\влево(4-i\вправо)[/латекс]
[латекс]\влево(-1+2i\вправо)\влево(-2+3i\ справа)[/латекс]
Показать решение
[латекс]\влево(4-2i\вправо)\влево(4+2i\вправо)[/латекс]
[латекс]\влево(3+4i\вправо)\влево(3-4i\вправо) [/latex]
Показать решение
[латекс]\frac{3+4i}{2}[/latex]
[латекс]\frac{6-2i}{3}[/latex]
Показать решение
[латекс]\frac{-5+3i}{2i}[/latex]
[латекс]\frac{6+4i}{i}[/latex]
Показать решение
[латекс]\frac{2-3i}{4+3i}[/latex]
[латекс]\frac{3+4i}{2-i}[/latex] 9{2}}[/latex]
Показать решение
[латекс]\frac{3+2i}{2+i}+\left(4+3i\right)[/latex]
[латекс]\frac{4+i}{i}+\frac{ 3-4i}{1-i}[/latex]
Показать решение
[латекс]\frac{3+2i}{1+2i}-\frac{2-3i}{3+i}[/latex]
Глоссарий
- комплексное сопряжение
- комплексное число, содержащее те же элементы, что и другое комплексное число, но с обратным оператором.
 Умножение комплексного числа на его сопряженное дает действительное число.
Умножение комплексного числа на его сопряженное дает действительное число.
- комплексный номер
- сумма действительного числа и мнимого числа; стандартная форма: [латекс]\,а+би,[/латекс], где a — действительная часть, а [латекс]\,b\,[/латекс] — сложная часть.
- сложный самолет
- координатная плоскость, в которой горизонтальная ось представляет действительную составляющую комплексного числа, а вертикальная ось представляет мнимую составляющую, обозначенную i .
- мнимое число 913 в алгебраической форме.
- Курс
- NCERT
- Класс 12
- Класс 11
- Класс 10
- Класс 9
- Класс 8
- 08
- 0 Класс 8 0008
- ИИТ ЕГЭ
- NCERT
- Экзамен
- JEE MAINS
- JEE ADVANCED
- X BOARDS
- XII BOARDS
- NEET
- Neet Предыдущий год (по годам)
- Физика Предыдущий год
- Химия0008
- Биология Предыдущий год
- Новый Все образцы работ
- Образцы работ по биологии
- Образцы работ по физике
- Образцы работ по химии
6
- Класс 12
- Класс 11
- Класс 10
- Класс 9
- Класс 8
- Класс 7
- Класс 6
- Экзаменационный уголок
- Онлайн-класс
- Викторина
- Задать вопрос в WhatsApp
- Поиск Doubtnut
- Английский словарь
- Toppers 006
- Блог
- О нас
- Карьера
- Скачать
- Получить приложение
Toppers
Вопрос
Обновлено: 03.
 01.2019
01.2019Рекомендуемые вопросы
9 видеоРЕКЛАМА
Ab Padhai каро бина объявления ке
Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!
Похожие видео
Комплексное число, z=(−√3+3i)(1−i)(3+√3i)(i)(√3+√3i)
642546907
03:17
Запишите следующее комплексное число в полярной форме:
−3√2+3√2i642551067
02:24
Найдите полярную форму комплексного числа z=−1+√3i
5 04062929044 2 :24
Запишите число z=(i−√3)13 в алгебраической форме.
645248998
06:10
Комплексное число, z=(−√3+3i)(1−i)(3+√3i)(i)(√3+√3i)
645285694
:21
Напишите алгебраическое выражение для:
z умножается на -3 и вычитается из 13.645591074
01:22
െ ശ്രേണിയുടെ ബീജഗണിതരൂപം എഴുതുക.
646246955
02:36
Комплексное число, z=(−√3+3i)(1−i)(3+√3i)(i)(√3+√3i) 913 в алгебраической форме.

- Курс

 Верно и обратное: каждую точку M(x;y) координатной
плоскости можно рассматривать как образ комплексного числа z=x+iy (рис. 7.1).
Верно и обратное: каждую точку M(x;y) координатной
плоскости можно рассматривать как образ комплексного числа z=x+iy (рис. 7.1).
 (7.3)
(7.3) 5), дают возможность определить, какой координатной четверти
принадлежит угол φ.
5), дают возможность определить, какой координатной четверти
принадлежит угол φ. 7 достаточно найти главное значение его аргумента, то есть считать φ=arg z.
7 достаточно найти главное значение его аргумента, то есть считать φ=arg z. 7.2).
7.2). рис. 7.2).
Таким образом, модуль разности двух комплексных чисел равен расстоянию d между
точками, изображающими эти числа на плоскости:
рис. 7.2).
Таким образом, модуль разности двух комплексных чисел равен расстоянию d между
точками, изображающими эти числа на плоскости: Производя все необходимые выкладки согласно формуле (7.11),
получим формулу произведения комплексных чисел, заданных в тригонометрической форме:
Производя все необходимые выкладки согласно формуле (7.11),
получим формулу произведения комплексных чисел, заданных в тригонометрической форме:

 14) вычислим их частное
14) вычислим их частное
 Таким образом, корнями заданного уравнения z4+16=0
являются комплексные числа
Таким образом, корнями заданного уравнения z4+16=0
являются комплексные числа 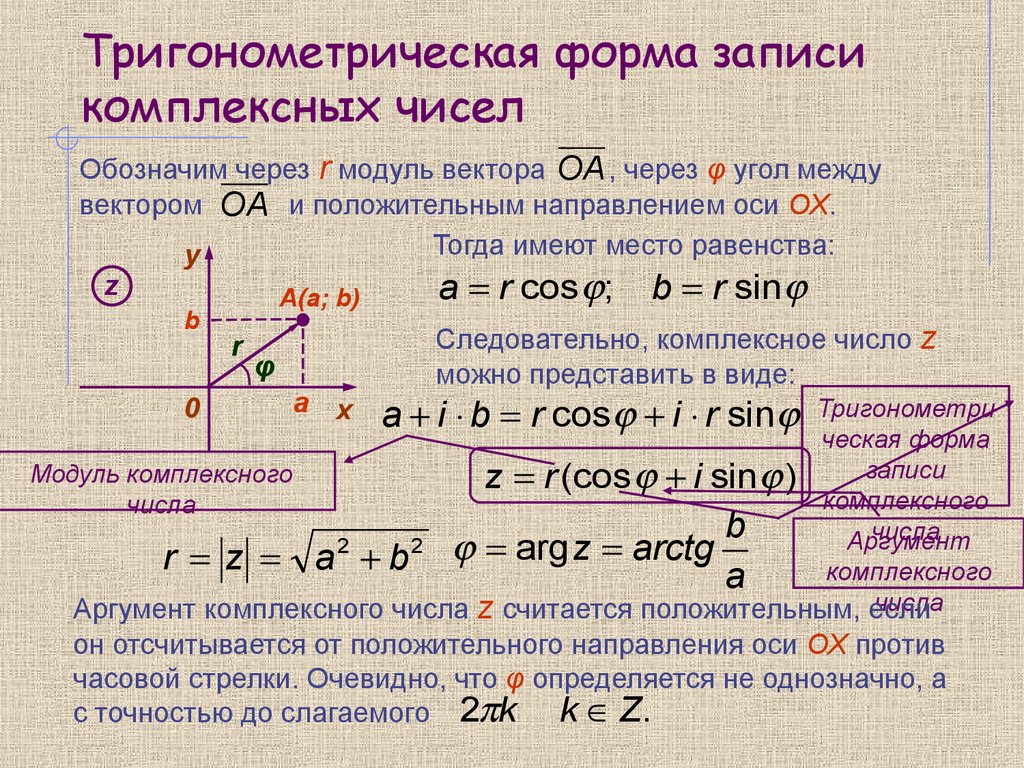 Перемножив линейные множители
разложения , получим трехчлен второй степени с действительными
коэффициентами x2+px+q и
отрицательным дискриминантом. Действительно,
Перемножив линейные множители
разложения , получим трехчлен второй степени с действительными
коэффициентами x2+px+q и
отрицательным дискриминантом. Действительно, \,[/латекс]См. (рисунок).
\,[/латекс]См. (рисунок). Умножение комплексного числа на его сопряженное дает действительное число.
Умножение комплексного числа на его сопряженное дает действительное число. 01.2019
01.2019