Записать в тригонометрической форме: Тригонометрическая форма комплексного числа

Тригонометрическая форма комплексного числа

Также, в зависимости от решаемой задачи, вы можете перевести комплексное число в алгебраическую или показательную форму.

Геометрическое представление комплексного числа

Если рассмотреть плоскость с прямоугольной системой координат, то любому комплексному числу можно сопоставить точку на этой плоскости с соответствующими координатами , и радиус-вектор комплексного числа, т.е. вектор, соединяющий начало координат с точкой на плоскости, соответствующей числу (рис. 1). Данная плоскость называется комплексной. Действительные числа располагаются на горизонтальной (вещественной) оси, мнимые части – на вертикальной (мнимой) оси.

Модуль и аргумент комплексного числа

Если является действительным числом, то его модуль равен абсолютной величине этого действительного числа.

Например.

Свойства модуля

2. в том и только том случае, если
6. , т.е. модуль разности комплексных чисел равен расстоянию между этими числами на комплексной плоскости.

Свойства аргумента

2. Для комплексного числа аргумент определяется с точностью до .
   Для значение аргумента не определено.
3. Главным значением аргумента называется число . Для обратного числа выполняется свойство: .

Действия над комплексными числами в тригонометрической форме

Сравнение

Два комплексных числа и называются равными, если

Умножение

Для произведения комплексных чисел в тригонометрической форме верно равенство:

   

Подробнее про умножение комплексных чисел читайте в отдельной статье: Умножение комплексных чисел.

Деление

Частное комплексных чисел в тригонометрической форме выполняется по формуле:

   

Возведение в степень

Для возведения в степень комплексных чисел в тригонометрической форме верна формула:

   

Подробнее про возведение в степень читайте в отдельной статье: Возведение в степень комплексного числа.

Понравился сайт? Расскажи друзьям!

Тригонометрическая форма комплексного числа

Рассмотрим комплексное число, заданной в обычной (алгебраической) форме:

Задача заключается в представлении комплексного числа (1) в тригонометрической форме. Для этого на комплексной плоскости введем полярные координаты. Примем за полюс начало координат, а за полярную ось вещественную ось R.

Как известно, полярными координатами точки z являются длина r ее радиус-вектора, равной расстоянию от точки

z до полюса, и величина ее полярного угла, т.е. угла, образованного между полярной осью и вектором-радиусом точки z. Отметим, что направление отсчета угла берется от полярной оси до вектора-радиуса против часовой стрелки (Рис.1, Рис.2).

На Рис.3 изображено комплексное число z. Координаты этого числа в декартовой системе координат (a, b). Из определения функций sin и cos любого угла, следует:

Откуда имеем:

Подставляя (2) в (1), получим:

Эта форма записи называется тригонометрической формой записи комплексного числа.

Уравнения (2) возведем в квадрат и сложим:

Откуда:

r−длина радиус-вектора комплексного числа z называется модулем комплексного числа и обозначается |z|. Очевидно |z|≥0, причем |z|=0 тогда и только тогда, когда z=0.

Величина полярного угла точки, соответвующей комплексному числу z, т.е. угла φ, называется аргументом этого числа и обозначается

arg z. Заметим, что arg z имеет смысл лишь при z≠0. Аргумент комплексного числа 0 не имеет смысла.

Аргумент комплексного числа определен неоднозначно. Если φ аргумент комплексного числа, то φ+2πk, k=0,1,… также является аргументом комплексного числа, т.к. cos(φ+2πk)=cosφ, sin(φ+2πk)=sinφ.

Приведение комплексного числа из алгебраической формы в тригонометрическую

Пусть комплексное число представлено в алгебраической форме: z=a+bi. Представим это число в тригонометрической форме. Вычисляем модуль комплексного числа: . Вычисляем аргумент φ комплексного числа из выражений или . Полученные значения вставляем в уравнение (3).

Пример 1. Представить комплексное число

z=1 в тригонометрической форме.

Решение. Комплексное число z=1 можно представить так: z=1+0i. Вычислим модуль этого числа: . Вычислим аргумент этого числа: cosφ=1/1. Откуда имеем φ=0. Подставляя значения модуля и аргумента в (3), получим: z=1(cos0+isin0).

Ответ. z=1(cos0+isin0).

Пример 2. Представить комплексное число z=i в тригонометрической форме.

Решение. Комплексное число z=i можно представить так: z=0+1i. Вычислим модуль этого числа: . Вычислим аргумент этого числа: cosφ=0/1. Откуда имеем φ=π/2. Подставляя значения модуля и аргумента в (3), получим: .

Ответ.

.

Пример 3. Представить комплексное число z=4+3i в тригонометрической форме.

Решение. Вычислим модуль этого числа: . Вычислим аргумент этого числа: cosφ=4/5. Откуда имеем φ=arccos(4/5). Подставляя значения модуля и аргумента в (3), получим: .

Ответ. , где φ=arccos(4/5).

Умножение комплексных чисел в тригонометрической форме записи

Пусть заданы комплексные числа z₁=r₁(cosφ₁+i sinφ₁) и z₂=r₂(cosφ₂+i sinφ₂). Перемножим эти числа:

или

В результате умножения комплексных чисел в тригонометрической форме мы получили комплексное число в тригонометрической форме, следовательно |

z₁z₂|=r₁r₂, или

т.е. модуль произведения комплексных чисел равен произведению модулей сомножителей.

Далее имеем arg(z₁z₂)=φ₁+φ₂ или

т.е. аргумент произведения комплексных чисел равен сумме аргументов сомножителей.

Пример 4. Умножить комплексные числа и .

Решение. Воспользуемся формулой (5):

Ответ. .

Деление комплексных чисел в тригонометрической форме записи

Пусть заданы комплексные числа z₁=r₁(cosφ₁+i sinφ₁

) и z₂=r₂(cosφ₂+i sinφ₂) и пусть z₂≠0, т.е. r₂≠0. Вычислим z₁/z₂:

Получили

Отсюда следует, что или

Далее , или

Следовательно, модуль частного двух комплексных чисел равен модулю делимого, деленному на модуль делителя, а аргумент частного двух комплексных чисел получается вычитанием аргумента делителя от аргумента делимого.

Пример 5. Делить комплексные числа и .

Решение. Воспользуемся формулой (8):

Ответ.

.

Геометрический смысл умножения и деления

На рисунке Рис.4 представлено умножение комплексных чисел z₁ и z₂. Из (6) и (7) следует, что для получения произведения z₁z₂, нужно вектор-радиус точки z₁ повернуть против часовой стрелки на угол φ₂ и растянуть в |z₂| раз (при 0z₂|

Рассмотрим, теперь, деление комплексного числа z₁z₂ на z₁ (Рис.4). Из формулы (8) следует, что модуль искомого числа равен частному от деления модуля числа z₁z₂ на модуль числа z₁, а аргумент равен: φ₂=φ−φ₁. В результате деления получим число z₂.

Смотрите также:

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(60)
4	Найти точное значение	sin(30 град. )
5	Найти точное значение	sin(60 град. )
6	Найти точное значение	tan(30 град. )
7	Найти точное значение	arcsin(-1)
8	Найти точное значение	sin(pi/6)
9	Найти точное значение	cos(pi/4)
10	Найти точное значение	sin(45 град. )
11	Найти точное значение	sin(pi/3)
12	Найти точное значение	arctan(-1)
13	Найти точное значение	cos(45 град. )
14	Найти точное значение	cos(30 град. )
15	Найти точное значение	tan(60)
16	Найти точное значение	csc(45 град. )
17	Найти точное значение	tan(60 град. )
18	Найти точное значение	sec(30 град. )
19	Преобразовать из радианов в градусы	(3pi)/4
20	График	y=sin(x)
21	Преобразовать из радианов в градусы	pi/6
22	Найти точное значение	cos(60 град. )
23	Найти точное значение	cos(150)
24	Найти точное значение	tan(45)
25	Найти точное значение	sin(30)
26	Найти точное значение	sin(60)
27	Найти точное значение	cos(pi/2)
28	Найти точное значение	tan(45 град. )
29	График	y=sin(x)
30	Найти точное значение	arctan(- квадратный корень 3)
31	Найти точное значение	csc(60 град. )
32	Найти точное значение	sec(45 град. )
33	Найти точное значение	csc(30 град. )
34	Найти точное значение	sin(0)
35	Найти точное значение	sin(120)
36	Найти точное значение	cos(90)
37	Преобразовать из радианов в градусы	pi/3
38	Найти точное значение	sin(45)
39	Найти точное значение	tan(30)
40	Преобразовать из градусов в радианы	45
41	Найти точное значение	tan(60)
42	Упростить	квадратный корень x^2
43	Найти точное значение	cos(45)
44	Упростить	sin(theta)^2+cos(theta)^2
45	Преобразовать из радианов в градусы	pi/6
46	Найти точное значение	cot(30 град. )
47	Найти точное значение	arccos(-1)
48	Найти точное значение	arctan(0)
49	График	y=cos(x)
50	Найти точное значение	cot(60 град. )
51	Преобразовать из градусов в радианы	30
52	Упростить	( квадратный корень x+ квадратный корень 2)^2
53	Преобразовать из радианов в градусы	(2pi)/3
54	Найти точное значение	sin((5pi)/3)
55	Упростить	1/( кубический корень от x^4)
56	Найти точное значение	sin((3pi)/4)
57	Найти точное значение	tan(pi/2)
58	Найти угол А	tri{}{90}{}{}{}{}	
59	Найти точное значение	sin(300)
60	Найти точное значение	cos(30)
61	Найти точное значение	cos(60)
62	Найти точное значение	cos(0)
63	Найти точное значение	arctan( квадратный корень 3)
64	Найти точное значение	cos(135)
65	Найти точное значение	cos((5pi)/3)
66	Найти точное значение	cos(210)
67	Найти точное значение	sec(60 град. )
68	Найти точное значение	sin(300 град. )
69	Преобразовать из градусов в радианы	135
70	Преобразовать из градусов в радианы	150
71	Преобразовать из радианов в градусы	(5pi)/6
72	Преобразовать из радианов в градусы	(5pi)/3
73	Преобразовать из градусов в радианы	89 град.
74	Преобразовать из градусов в радианы	60
75	Найти точное значение	sin(135 град. )
76	Найти точное значение	sin(150)
77	Найти точное значение	sin(240 град. )
78	Найти точное значение	cot(45 град. )
79	Преобразовать из радианов в градусы	(5pi)/4
80	Упростить	1/( кубический корень от x^8)
81	Найти точное значение	sin(225)
82	Найти точное значение	sin(240)
83	Найти точное значение	cos(150 град. )
84	Найти точное значение	tan(45)
85	Вычислить	sin(30 град. )
86	Найти точное значение	sec(0)
87	Упростить	arcsin(-( квадратный корень 2)/2)
88	Найти точное значение	cos((5pi)/6)
89	Найти точное значение	csc(30)
90	Найти точное значение	arcsin(( квадратный корень 2)/2)
91	Найти точное значение	tan((5pi)/3)
92	Найти точное значение	tan(0)
93	Вычислить	sin(60 град. )
94	Найти точное значение	arctan(-( квадратный корень 3)/3)
95	Преобразовать из радианов в градусы	(3pi)/4
96	Вычислить	arcsin(-1)
97	Найти точное значение	sin((7pi)/4)
98	Найти точное значение	arcsin(-1/2)
99	Найти точное значение	sin((4pi)/3)
100	Найти точное значение	csc(45)

Тригонометрическая и показательная формы комплексного числа.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Тригонометрическая форма комплексного числа:

Для всякого  комплексного числа $z=x+iy$ справедливо равенство $$z=|z|(\cos\varphi+i\sin\varphi).\qquad\qquad\qquad (1)$$ Здесь $|z|=\sqrt{x^2+y^2},$ a $\varphi$ удовлетворяет условиям: $$\cos\varphi=\frac{x}{\sqrt{x^2+y^2}},\qquad \sin\varphi=\frac{y}{\sqrt{x^2+y^2}},\qquad \varphi\in[0, 2\pi).$$  

Равенство (1) называют тригонометрической формой комплексного числа $z.$  

 Примеры:

Следующие комплексные числа представить в тригонометрической форме и изобразить точками на комплексной плоскости:

1.435. $-i$

Решение.

Пусть $z=x+iy=-i,$ то есть $x=0,\,\, y=-1.$ Тогда $$|z|=\sqrt{x^2+y^2}=\sqrt 1=1.$$

$$\cos\varphi=\frac{0}{1}=0,\qquad \sin\varphi=\frac{-1}{1}=-1\Rightarrow \varphi=\frac{3\pi}{2}.$$ 

Таким образом, $z=\cos\frac{3\pi}{2}+i\sin\frac{3\pi}{2}.$

Ответ: $\cos\frac{3\pi}{2}+i\sin\frac{3\pi}{2}.$

 

1.438. $\frac{1-i}{1+i}.$

Решение.

Запишем число $z=\frac{1-i}{1+i}$ в алгебраической форме:

$$\frac{1-i}{1+i}=\frac{(1-i)(1-i)}{(1+i)(1-i)}=\frac{1-2i+i^2}{1-i^2}=\frac{1-2i-1}{1+1}=\frac{-2i}{2}=-i.$$

Тригонометрическая форма числа $-i$ найдена в предыдущемпримере (1.435):

$z=-i=\cos\frac{3\pi}{2}+i\sin\frac{3\pi}{2}.$

Ответ: $\cos\frac{3\pi}{2}+i\sin\frac{3\pi}{2}.$

 

1.441. $1+\cos\frac{\pi}{7}+i\sin\frac{\pi}{7}.$

Решение.

Пусть $z=x+iy=1+\cos\frac{\pi}{7}+i\sin{\pi}{7},$ то есть $x=1+\cos\frac{\pi}{7},\,\, y=\sin{\pi}{7}.$ Тогда $$|z|=\sqrt{x^2+y^2}=\sqrt {\left(1+\cos\frac{\pi}{7}\right)^2+\sin^2\frac{\pi}{7}}=$$ $$=\sqrt{1+2\cos\frac{\pi}{7}+\cos^2\frac{\pi}{7}+\sin^2\frac{\pi}{7}}=\sqrt{2+2\cos\frac{\pi}{7}}=$$ $$=\sqrt{4\cos^2\frac{\pi}{14}}=2\cos\frac{\pi}{14}.$$

$$\cos\varphi=\frac{x}{|z|}=\frac{1+\cos\frac{\pi}{7}}{2\cos\frac{\pi}{14}}=\frac{2\cos^2\frac{\pi}{14}}{2\cos\frac{\pi}{14}}=\cos\frac{\pi}{14}.$$

$$\sin\varphi=\frac{y}{|z|}=\frac{sin\frac{\pi}{7}}{2\cos\frac{\pi}{14}}=\frac{2\cos\frac{\pi}{14}\sin\frac{\pi}{14}}{2\cos\frac{\pi}{14}}=\sin\frac{\pi}{14}.$$

Таким образом, $\varphi=\frac{\pi}{14}.$

Отсюда находим показательную форму комплексного числа $z=x+iy=1+\cos\frac{\pi}{7}+i\sin{\pi}{7}:$

$$z=2\cos\frac{\pi}{14}\left(\cos\frac{\pi}{14}+i\sin\frac{\pi}{14}\right).$$

Ответ: $2\cos\frac{\pi}{14}\left(\cos\frac{\pi}{14}+i\sin\frac{\pi}{14}\right).$

 

Показательная форма комплексного числа:

Символом $e^{i\varphi}$ обозначается комплексное число $\cos\varphi+i\sin\varphi.$ С помощью этого обозначения всякое комплексное число $z=|z|(\cos\varphi+i\sin\varphi)$ может быть представлено в показательной форме $$z=|z|e^{i\varphi}.$$

Примеры.

Представить в показательной форме следующие комплексные числа:

1.475. $\frac{7+24i}{5}.$

Решение. 

Приведем число $z=\frac{7+24i}{5}$ к алгебраическому виду:

$$z=x+iy=\frac{7+24i}{5}=\frac{7}{5}+\frac{24}{5}i.$$

$$|z|=\sqrt{\left(\frac{7}{5}\right)^2+\left(\frac{24}{5}\right)^2}=\sqrt{\frac{49+576}{25}}=\sqrt{\frac{625}{25}}=\sqrt{25}=5.$$

$$tg\varphi=\frac{y}{x}=\frac{\frac{24}{5}}{\frac{7}{5}}=\frac{24}{7}.$$ Поскольку число $z$ принадлежит первой четверти, то $\varphi=arctg\frac{24}{7}.$

Таким образом, $z=5e^{i arctg\frac{24}{7}}.$

Ответ: $z=5e^{i arctg\frac{24}{7}}.$

  {jumi[*4]}

1.479. $\sin\alpha-i\cos\alpha.$

Решение.

$$z=x+iy=\sin\alpha-i\cos\alpha\Rightarrow \,\,x=\sin\alpha,\,\,y=-cos\alpha.$$

$$|z|=\sqrt{x^2+y^2}=\sqrt{\sin^2\alpha+\cos^2\alpha}=1.$$

$$tg\varphi=\frac{y}{x}=\frac{-\cos\alpha}{\sin\alpha}=-ctg\alpha=tg(\alpha+\frac{\pi}{2})=tg(\alpha+\frac{3\pi}{2}).$$

Кроме этого должны выполняться условия 

$$\cos\varphi=\frac{x}{|z|}=\sin\alpha;\qquad \sin\varphi=\frac{y}{|z|}=\cos\alpha.$$

Отсюда находим

$$\varphi=\alpha+\frac{3\pi}{2}.$$

Таким образом, $$z=\sin\alpha-i\cos\alpha=e^{i\left(\alpha+\frac{3\pi}{2}\right)}.$$

Ответ: $e^{i\left(\alpha+\frac{3\pi}{2}\right)}.$

 

1.482 (а). Данные числа $z_1$ и $z_2$ представить в показательной форме и выполнить указанные действия над ними:

$z_1z_2;$ $\frac{z^2_1}{z_2},$ если $z_1=2\sqrt 3-2i,$ $z_2=3-3\sqrt 3i.$

Решение.

Запишем числа $z_1$ и $z_2$ в показательной форме:

$$|z_1|=\sqrt{x^2+y^2}=\sqrt{(2\sqrt 3)^2+(-2)^2}=\sqrt{16}=4.$$

$$tg\varphi=\frac{y}{x}=\frac{-2}{2\sqrt 3}=-\frac{1}{\sqrt 3}.$$

Поскольку число $z_1$ принадлежит четвертой четверти, то $\varphi_1=arctg{-\frac{1}{\sqrt 3}}=-\frac{\pi}{6}.$

Отсюда $$z_1=4e^{-i\frac{\pi}{6}}.$$

$$|z_2|=\sqrt{x^2+y^2}=\sqrt{3^2+(-3\sqrt 3)^2}=\sqrt{36}=6.$$

$$tg\varphi=\frac{y}{x}=\frac{-3\sqrt 3}{3}=-\sqrt 3.$$

Поскольку число $z_2$ принадлежит четвертой четверти, то $\varphi_2=arctg{\sqrt 3}=-\frac{\pi}{3}.$

Отсюда $$z_2=6e^{-i\frac{\pi}{3}}.$$

Далее находим $z_1z_2$ и $\frac{z^2_1}{z_2}:$

 $$z_1z_2=4e^{-i\frac{\pi}{6}}6e^{-\frac{\pi}{3}}=24e^{i\left(\frac{-\pi}{6}-\frac{\pi}{3}\right)}=24e^{-i\frac{\pi}{2}}=$$

$$=24\left(\cos\left(-\frac{\pi}{2}\right)+i\sin\left(-\frac{\pi}{2}\right)\right)=24(0-1)=-24.$$ 

$$\frac{z^2_1}{z_2}=\frac{(4e^{-i\frac{\pi}{6}})^2}{6e^{-\frac{\pi}{3}}}=\frac{16}{6}e^{i\left(\frac{-2\pi}{6}+\frac{\pi}{3}\right)}=\frac{8}{3}e^{i\cdot 0}=\frac{8}{3}.$$

Ответ: $-24, \frac{8}{3}.$

 

Домашнее задание.

Следующие комплексные числа представить в тригонометрической форме и изобразить точками на комплексной плоскости:

1.436. $1-i\sqrt 3.$

Ответ: $2\left(\cos\frac{5\pi}{3}+i\sin\frac{5\pi}{3}\right).$

 

1.437. $-\frac{1}{2}+i\frac{\sqrt 3}{2}.$

Ответ: $\cos\frac{2\pi}{3}+i\sin\frac{2\pi}{3}.$

 

1.440. $\sin\frac{\pi}{3}+i\cos\frac{\pi}{3}.$

Ответ: $\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}.$

 

 

Представить в показательной форме следующие комплексные числа:

1.476. $5-12i.$

Ответ: $13e^{-i arctg\left(-\frac{12}{5}\right)}.$

 

1.477. $-3-4i.$

Ответ:  $5e^{i arctg\left(\frac{4}{3}+\pi\right)}.$

 

 

1.479.$\sin\alpha-i\cos\alpha.$

Ответ:  $e^{i \left(\alpha+\frac{3\pi}{2}\right)}.$

 

 

1.480. $\sin\alpha+i(1-\cos\alpha).$

Ответ:  $2\sin\frac{\pi}{2}e^{i \frac{\alpha}{2}}.$

 

1.482 (б). Данные числа $z_1$ и $z_2$ представить в показательной форме и выполнить указанные действия над ними:

$z^2_1\overline z_2;$ $\frac{\overline z_2}{z_1},$ если $z_1=-\sqrt 3+i\sqrt 2,$ $z_2=\sqrt 8-\sqrt 8.$

Ответ:  $16e^{i\frac{7\pi}{4}}; 2e^{-i\frac{\pi}{2}}.$

 

 

 

Как записать комплексное число в алгебраической и тригонометрической форме

Комплесное число имеет три формы записи: алгебраическую, показательную и тригонометрическую. Проиллюстрируем на примере методы записи комплексного числа в алгебраической и тригонометрической форме и их использование для решения уравнений.    

 

Дано комплексное число z. Требуется:

1. записать число z в алгебраической и тригонометрической формах;
2. найти все корни уравнения \(ɷ^3-z=0\)

                                                         \({z}={{-2{\sqrt2}}\over1+i}\)

Решение:

1) Комплексное число z в алгебраической форме имеет вид: z=а+bi;

 в тригонометрической форме: z=r(cosj+i×sinj), где и r=\({ \sqrt{a^2+b^2}}\) и j=\(arctg {b \over a}\)

Для тог чтобы записать \({z}={{-2{\sqrt2}}\over1+i}\) в алгебраической форме, умножим числитель и знаменатель на сопряженное к знаменателю, т. е. на 1- i.

.

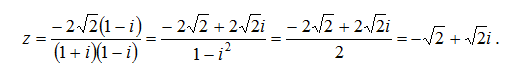
 \(z=-{\sqrt2}+{\sqrt2}i\)- алгебраическая форма.

 

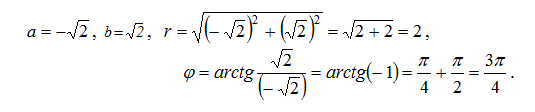
\(z=2{(cos{3π\over4}}+i sin{{3π\over4}})\)- тригонометрическая форма.

 

 

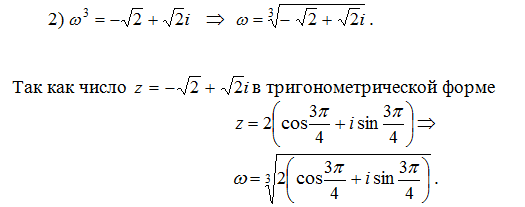
Применяя формулу для извлечения корня из комплексного числа:

 

Автор: Дмитрий Айстраханов

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

1.4.3. Тригонометрическая форма записи комплексных чисел

Глава 1. Арифметика

1.4.

1.4.3.

Та запись комплексного числа, которую мы использовали до сих пор, называется алгебраической формой записи комплексного числа. Часто бывает удобна немного другая форма записи комплексного числа. Пусть и φ = arg z. Тогда по определению аргумента имеем:

Отсюда получается

z = a + bi = r(cos φ + i sin φ).

Такая форма называется тригонометрической формой записи комплексного числа. Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов. Пример 1

Записать число в тригонометрической форме.

Арифметические действия над комплексными числами, записанными в тригонометрической форме, производятся следующим образом. Пусть z₁ = r₁(cos φ₁ + i sin φ₁) и z₂ = r₂(cos φ₂ + i sin φ₂). Имеем:

Видно, что в тригонометрической форме операции умножения и деления производятся особенно просто: для того, чтобы перемножить (разделить) два комплексных числа, нужно перемножить (разделить) их модули и сложить (вычесть) их аргументы.

Отсюда следует, что для того чтобы перемножить n комплексных чисел, нужно перемножить их модули и сложить аргументы: если φ₁, φ₂, …, φ_n – аргументы чисел z₁, z₂, …, z_n, то

В частности, если все эти числа равны между собой, то получим формулу, позволяющую возводить комплексное число в любую натуральную степень.

Первая формула Муавра:

Число z называется корнем степени  из комплексного числа w, если Корень степени обозначается Пусть теперь число w фиксировано. Найдём z из уравнения

Если w = 0, то у уравнения существует единственное решение z = 0.

Если w ≠ 0, то положим, что нам известно тригонометрическое представление числа w = r₀(cos φ₀ + i sin φ₀), и будем искать число z также в тригонометрической форме: z = r(cos φ + i sin φ). Из определения аргумента и геометрической интерпретации комплексных чисел следует, что два комплексных числа, записанных в тригонометрической форме, равны тогда и только тогда, когда равны их модули, а аргументы отличаются на угол, кратный 2π. Имеем:

откуда получается:
Итак, все решения уравнения задаются формулой
Заметим, что если в эту формулу подставлять натуральные числа k, то при k = 0, 1, …, n мы будем получать разные комплексные числа, а при k = n имеем:
Значит, и в дальнейшем значения корней будут повторяться. Следовательно, существует ровно n корней уравнения и все они задаются одной формулой.

Вторая формула Муавра:

Пример 3

Найти



Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(60)
4	Найти точное значение	sin(30 град. )
5	Найти точное значение	sin(60 град. )
6	Найти точное значение	tan(30 град. )
7	Найти точное значение	arcsin(-1)
8	Найти точное значение	sin(pi/6)
9	Найти точное значение	cos(pi/4)
10	Найти точное значение	sin(45 град. )
11	Найти точное значение	sin(pi/3)
12	Найти точное значение	arctan(-1)
13	Найти точное значение	cos(45 град. )
14	Найти точное значение	cos(30 град. )
15	Найти точное значение	tan(60)
16	Найти точное значение	csc(45 град. )
17	Найти точное значение	tan(60 град. )
18	Найти точное значение	sec(30 град. )
19	Преобразовать из радианов в градусы	(3pi)/4
20	График	y=sin(x)
21	Преобразовать из радианов в градусы	pi/6
22	Найти точное значение	cos(60 град. )
23	Найти точное значение	cos(150)
24	Найти точное значение	tan(45)
25	Найти точное значение	sin(30)
26	Найти точное значение	sin(60)
27	Найти точное значение	cos(pi/2)
28	Найти точное значение	tan(45 град. )
29	График	y=sin(x)
30	Найти точное значение	arctan(- квадратный корень 3)
31	Найти точное значение	csc(60 град. )
32	Найти точное значение	sec(45 град. )
33	Найти точное значение	csc(30 град. )
34	Найти точное значение	sin(0)
35	Найти точное значение	sin(120)
36	Найти точное значение	cos(90)
37	Преобразовать из радианов в градусы	pi/3
38	Найти точное значение	sin(45)
39	Найти точное значение	tan(30)
40	Преобразовать из градусов в радианы	45
41	Найти точное значение	tan(60)
42	Упростить	квадратный корень x^2
43	Найти точное значение	cos(45)
44	Упростить	sin(theta)^2+cos(theta)^2
45	Преобразовать из радианов в градусы	pi/6
46	Найти точное значение	cot(30 град. )
47	Найти точное значение	arccos(-1)
48	Найти точное значение	arctan(0)
49	График	y=cos(x)
50	Найти точное значение	cot(60 град. )
51	Преобразовать из градусов в радианы	30
52	Упростить	( квадратный корень x+ квадратный корень 2)^2
53	Преобразовать из радианов в градусы	(2pi)/3
54	Найти точное значение	sin((5pi)/3)
55	Упростить	1/( кубический корень от x^4)
56	Найти точное значение	sin((3pi)/4)
57	Найти точное значение	tan(pi/2)
58	Найти угол А	tri{}{90}{}{}{}{}	
59	Найти точное значение	sin(300)
60	Найти точное значение	cos(30)
61	Найти точное значение	cos(60)
62	Найти точное значение	cos(0)
63	Найти точное значение	arctan( квадратный корень 3)
64	Найти точное значение	cos(135)
65	Найти точное значение	cos((5pi)/3)
66	Найти точное значение	cos(210)
67	Найти точное значение	sec(60 град. )
68	Найти точное значение	sin(300 град. )
69	Преобразовать из градусов в радианы	135
70	Преобразовать из градусов в радианы	150
71	Преобразовать из радианов в градусы	(5pi)/6
72	Преобразовать из радианов в градусы	(5pi)/3
73	Преобразовать из градусов в радианы	89 град.
74	Преобразовать из градусов в радианы	60
75	Найти точное значение	sin(135 град. )
76	Найти точное значение	sin(150)
77	Найти точное значение	sin(240 град. )
78	Найти точное значение	cot(45 град. )
79	Преобразовать из радианов в градусы	(5pi)/4
80	Упростить	1/( кубический корень от x^8)
81	Найти точное значение	sin(225)
82	Найти точное значение	sin(240)
83	Найти точное значение	cos(150 град. )
84	Найти точное значение	tan(45)
85	Вычислить	sin(30 град. )
86	Найти точное значение	sec(0)
87	Упростить	arcsin(-( квадратный корень 2)/2)
88	Найти точное значение	cos((5pi)/6)
89	Найти точное значение	csc(30)
90	Найти точное значение	arcsin(( квадратный корень 2)/2)
91	Найти точное значение	tan((5pi)/3)
92	Найти точное значение	tan(0)
93	Вычислить	sin(60 град. )
94	Найти точное значение	arctan(-( квадратный корень 3)/3)
95	Преобразовать из радианов в градусы	(3pi)/4
96	Вычислить	arcsin(-1)
97	Найти точное значение	sin((7pi)/4)
98	Найти точное значение	arcsin(-1/2)
99	Найти точное значение	sin((4pi)/3)
100	Найти точное значение	csc(45)

Как записать комплексное число в тригонометрической форме 6-7i?

Тригонометрия

Наука

• Анатомия и физиология
• Астрономия
• Астрофизика
• Биология
• Химия
• наука о планете Земля
• Наука об окружающей среде

.

Как написать тригонометрическую форму 2 + 2i?

Precalculus

Наука

• Анатомия и физиология
• Астрономия
• Астрофизика
• Биология
• Химия
• наука о планете Земля
• Наука об окружающей среде
• Органическая химия
• Физика

Математика

.

Введение в 6 функций тригонометрии

Введение в 6 тригонометрических функций — Открытый справочник по математике

В основе тригонометрии лежат шесть функций. Вам необходимо полностью понять три основных вопроса:

• Синус (грех)
• Косинус (cos)
• Касательная (загар)

Остальные три используются не так часто и могут быть производными от трех основных функций.Поскольку их легко получить, в калькуляторах и электронных таблицах их обычно нет.

• Секанс (сек)
• Косеканс (csc)
• Котангенс (детская кроватка)

Все шесть функций имеют трехбуквенные сокращения (показаны в скобках выше).

Определения шести функций

Рассмотрим прямоугольный треугольник выше. Для каждого угла P или Q есть шесть функций, каждая функция — это соотношение двух сторон треугольника. Единственная разница между шестью функциями заключается в том, какую пару сторон мы используем.

В следующей таблице

• a — длина стороны a , расположенной рядом с рассматриваемым углом (x).
• o — длина стороны o p, угол наклона.
• h — длина ч ypotenuse.

« x » представляет собой меру угла в градусах или радианах.

В следующей таблице обратите внимание, как каждая функция является обратной величиной одной из основных функций sin, cos, tan.

Например, на рисунке выше косинус x — это сторона, примыкающая к x (обозначенная a) над гипотенуза (помечено h): Если a = 12 см и h = 24 см, то cos x = 0,5 (12 на 24).

Soh Cah Toa

Эти 9 букв помогают запомнить соотношения трех основных функций — sin, cos и tan.Произносится как «соака-тава». См. Sohcahtoa.

Передаточные числа постоянные

Поскольку функции имеют соотношение двух сторон, они всегда дают одинаковый результат для заданного угла, независимо от размера треугольника.

На рисунке выше перетащите точку C. Треугольник изменится так, чтобы угол C оставался равным 30 °. Обратите внимание, как соотношение сторона, противоположная гипотенузе, не меняется, даже если их длина. Из-за этого не меняется и синус 30 °.Всегда 0,5.

Помните: Когда вы применяете функцию триггера к заданному углу, она всегда дает один и тот же результат. Например, тангенс угла 60 ° всегда равен 1,732.

С помощью калькулятора

В большинстве калькуляторов есть кнопки для определения sin, cos и tan угла. Обязательно установите калькулятор в режим градусов или радианов в зависимости от того, какие единицы вы используете.

Обратные функции

Для каждой из шести функций существует обратная функция, которая работает в обратном порядке.Перед обратной функцией стоят буквы «ARC».

Например, функция, обратная COS, — это ARCCOS. В то время как COS сообщает вам косинус угла, ARCCOS сообщает вам, какой угол имеет данный косинус. См. Обратные тригонометрические функции.

В калькуляторах и таблицах обратные функции иногда написано acos (x) или cos ^-1 (x) .

Тригонометрические функции больших и / или отрицательных углов

Шесть функций также можно определить в прямоугольном система координат.Это позволяет им выходить за рамки прямоугольных треугольников, где углы могут иметь любую меру, даже за 360 °, и может быть как положительным, так и отрицательным. Подробнее об этом см. Тригонометрические функции больших и отрицательных углов.

Identities — замена функции другими

Тригонометрические тождества — это просто способы написания одной функции с использованием других. Например, из таблицы выше мы видим, что Эта эквивалентность называется тождеством. Если бы у нас было уравнение с сек x в нем, мы могли бы заменить сек x с
на один больше cos x , если это помогает нам достичь наших целей.Таких отождествлений много. Для получения дополнительной информации см. Тригонометрические тождества.

Не только прямоугольные треугольники

Эти функции определены с помощью прямоугольного треугольника, но их можно использовать и в других треугольниках. Например, Закон синуса и Закон косинусов можно использовать для решить любой треугольник, а не только прямоугольные.

Графическое изображение функций

Функции можно изобразить в виде графиков, а некоторые, особенно функция SIN, создают формы, которые часто встречаются в природе.Например, см. График функции SIN, часто называемой синусоидой, выше. Подробнее см.

Чистые звуковые тона и радиоволны являются синусоидальными волнами в соответствующей среде.

Производные триггерных функций

Каждую из функций можно дифференцировать в исчислении. Результатом является другая функция, которая указывает скорость ее изменения (наклон) при определенных значениях x . Эти производные функции выражаются в терминах других триггерных функций.Подробнее об этом см. Производные тригонометрических функций. См. Также Оглавление по исчислению.

Другие темы по тригонометрии

Уголки

Тригонометрические функции

Решение задач тригонометрии

Исчисление

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

.

Как написать тригонометрическую форму числа 3-3i?

Precalculus

Наука

• Анатомия и физиология
• Астрономия
• Астрофизика
• Биология
• Химия
• наука о планете Земля
• Наука об окружающей среде
• Органическая химия
• Физика

Математика

.