Двоичная система счисления
☰
В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, десятичная двойка является основанием двоичной системы счисления, аналогично тому, как в десятичной системе основанием является число десять.
Чтобы научиться считать в двоичной системе счисления, рассмотрим, как формируются числа в привычной для нас десятичной.
В десятичной системе счисления мы располагаем десятью знаками-цифрами: от 0 до 9. Когда счет достигает числа 9, вводится новый более старший разряд – десятки. При этом разряд единиц обнуляется и счет в этом разряде опять начинается с нуля. После числа 19 разряд десятков увеличивается на 1, а разряд единиц снова обнуляется. Получается число 20. Когда десятки дойдут до 9, впереди них появится третий разряд – сотни.
Формирование каждого последующего числа в двоичной системе счисления аналогично тому, как это происходит в десятичной за исключением того, что используются всего-лишь две цифры: 0 и 1.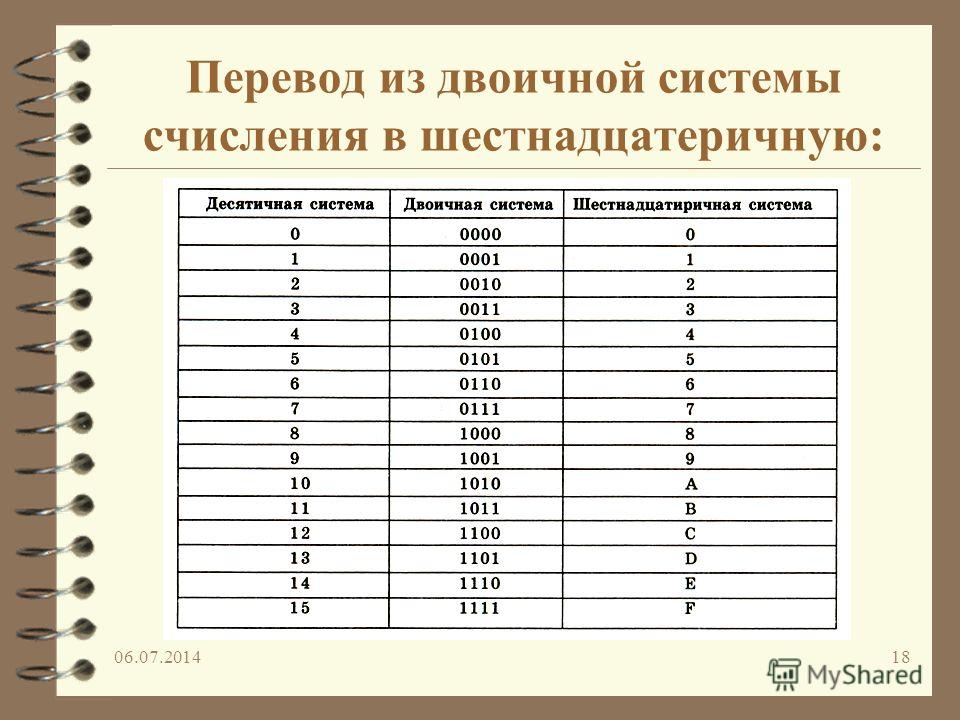
0 1 10 11 100 101 110 111
Итак, число три в двоичной системе записывается как 11, в десятичной – как 3. Количественно это одинаковые числа. Это одно и то же число, выраженное в различных системах счисления. Если есть вероятность неоднозначной трактовки числа, к нему приписывается нижний индекс в десятичной системе счисления, обозначающий, в какой системе счисления выражено данное число:
112 = 310
Индекс для числа, выраженного в десятичной системе, обычно опускается.
Перевод чисел из двоичной системы счисления в десятичную
В двоичной системе счисления с увеличением значения количество разрядов растет очень быстро. Как определить, что значит двоичное число 10001001? Нам сложно понять, сколько это, мы привыкли мыслить в десятичной системе. Поэтому часто используется перевод двоичных чисел в десятичные.
В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и так далее. Например:
5476 = 5000 + 400 + 70 + 6
Можно пойти еще дальше и разложить число, используя основание системы счисления, возводимое в показатель степени, равный разряду цифры, уменьшенному на единицу:
5476 = 5 * 103 + 4 * 102 + 7 * 101 + 6 * 100
После равенства числа 5, 4, 7 и 6 – это набор цифр из которых состоит число 5476. Все эти цифры умножаются на десять, возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы. Так, например, 6 находится в первом разряде, поэтому она умножается на 10(1-1). Натуральное число в нулевой степени равно единице. Таким образом, мы умножаем 6 на 1.
Точно также производится разложение числа в двоичной системы счисления, кроме того, что основанием выступает двойка, а не десятка.
Здесь до знака равенства число представлено в двоичной системе счисления, после «равно» запись идет в десятичной:
10001001 = 1 * 27 + 0 * 26 + 0 * 25 + 0 * 24 + 1 * 23 + 0 * 22 + 0 * 21 + 1 * 20
Результат вычислений дает десятичное число, количественно равное двоичному 10001001:
1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20 =
= 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137
То есть число 10001001 по основанию 2 равно числу 137 по основанию 10:
100010012 = 13710
Почему двоичная система счисления так распространена?
Дело в том, что двоичная система счисления – это язык современной вычислительной техники.
Когда любые данные сохраняются на компьютере, они кодируются числами. С числами же компьютер выполняет операции, изменяя эти данные.
Допустим, у нас есть десятичное число 14, которое требуется сохранить в компьютерной памяти. Мы задействуем участок памяти, в данном случае состоящий как минимум из двух элементов, отводимых под разряды. В одном из разрядов мы сохраняем десятичное число 1, в другом – число 4.
Элемент памяти – это физическое устройство. Если проектировать его для хранения десятичной цифры, потребуется создать такое устройство, которое может находиться в десяти разных физических состояниях и способно переключаться между ними. Каждое из этих состояний будет соответствовать числу от 0 до 9.
Создать такой элемент памяти возможно, однако сложнее и дороже, чем создать элемент, способный находиться только в двух состояниях. Одно состояние сопоставить нулю, второе – единице. Кроме того, подобное хранение данных является более надежным.
Поэтому оказалось проще перевести число 14 в двоичную систему счисления, получив число 1110, и именно его сохранить в памяти. И пусть даже при этом будут задействованы не два, а четыре разряда, то есть четыре элементарных единиц памяти.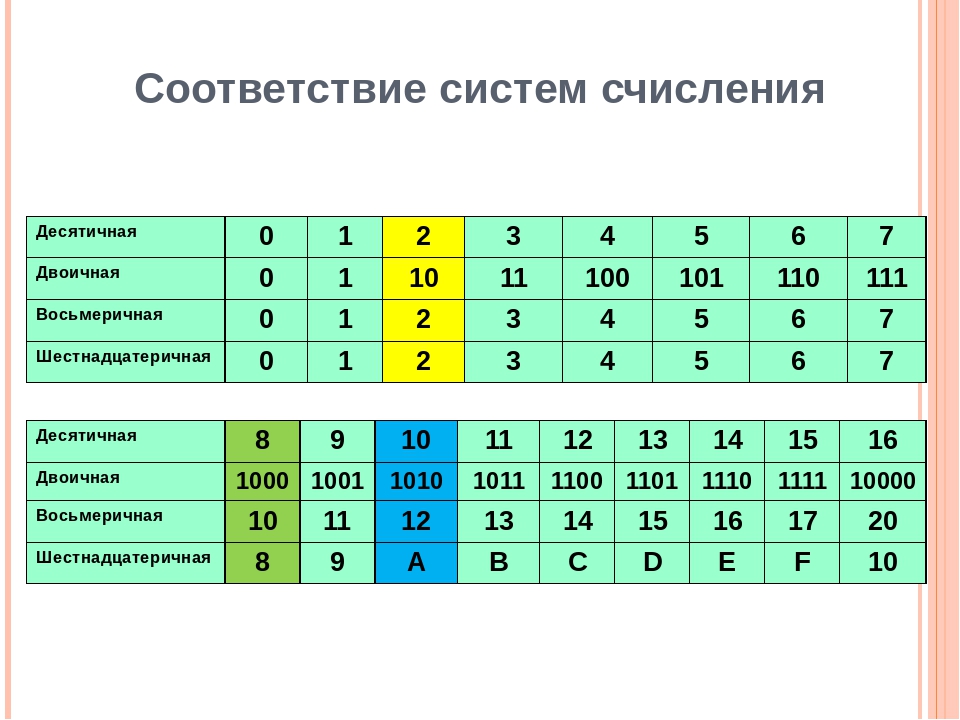
Перевод десятичного числа в двоичное
Одним из алгоритмов перевода десятичного числа в двоичное является деление нацело на два с последующим «сбором» двоичного числа из остатков. Переведем таким образом число 14 в двоичное представление.
14 / 2 = 7, остаток 0 7 / 2 = 3, остаток 1 3 / 2 = 1, остаток 1 1 / 2 = 0, остаток 1
Собирать остатки надо с конца, то есть с последнего деления. Получаем 1110.
Выполним то же самое для числа 77:
77 / 2 = 38, остаток 1 38 / 2 = 19, остаток 0 19 / 2 = 9, остаток 1 9 / 2 = 4, остаток 1 4 / 2 = 2, остаток 0 2 / 2 = 1, остаток 0 1 / 2 = 0, остаток 1
Собираем остатки вместе, начиная с конца: 1001101.
Проверим, выполнив обратный перевод:
1001101 = 1*26 + 0*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77
Информатика — Двоичная система счисления
В этом разделе всюду речь идет о двоичной записи чисел.
Главное: Двоичная запись числа N означает представление этого числа в виде суммы степеней двойки. Места, на которых стоит 1, показывают, какие степени двойки нужно брать. Номер места отсчитывается справа налево и начиная с 0.
Примеры.
1) 25 = 16+8+1 = 24 + 23 + 20 . Поэтому 25 = 110012 .
2) 66 = 64 + 2 = 26
Как переводить числа из десятичной системы в двоичную можно посмотреть, например, здесь. Хорошая книга лежит здесь. Непонятно — пишите.
Другие свойства следуют из этого свойства. Вот несколько примеров.
1. Четные числа оканчиваются на 0, нечетные – на 1.
2. Число 2k в двоичной системе счисления записывается единицей и k нулями. Например, 32 = 25 в двоичной системе счисления записывается так: 100000
3.
Число N делится на 2k <===> число N оканчивается на k нулей 4. Число 2k – 1 в двоичной системе счисления записывается k единицами. Например, 31 = 25 – 1 в двоичной системе счисления записывается так: 11111 5. Двоичная запись числа N содержит ровно k цифр тогда и только тогда, когда Число N принадлежит интервалу 2k-1 ≤ N ≤ 2k — 1 Действительно, пусть, например, k=5. Наименьшее число, которое записывается 5-ю цифрами – это число 100002 = 24 = 1610. А наибольшее число, которое записывается 5-ю цифрами – это число 111112 = 24+ 23+ 22+ 21+ 20 = 1610+810+410+210+110= 3110 = 32 – 1 = 25 – 1.
Еще один пример. Для числа 67 имеем: 64 = 26 ≤ 67 ≤ 27 — 1 = 127. Двоичная запись числа 67 содержит 7 цифр: 64
Что думаете?
Системы счисления. Перевод из одной системы в другую.
1. Порядковый счет в различных системах счисления.
В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.
Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.
Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 10 | 3 |
| 4 | 100 | 11 | 4 |
| 5 | 101 | 12 | 10 |
| 6 | 110 | 20 | 11 |
| 7 | 111 | 21 | 12 |
| 8 | 1000 | 22 | 13 |
| 9 | 1001 | 100 | 14 |
| 10 | 1010 | 101 | 20 |
| 11 | 1011 | 102 | 21 |
| 12 | 1100 | 110 | 22 |
| 13 | 1101 | 111 | 23 |
| 14 | 1110 | 112 | 24 |
| 15 | 1111 | 120 | 30 |
Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита.
Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | |
| 11 | |
| 12 | 10 |
| 13 | 11 |
| 14 | 12 |
| 15 | 13 |
2.Перевод из десятичной системы счисления в любую другую.
Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания.
В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
Пример 1. Переведем десятичное число 46 в двоичную систему счисления.
Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.
Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.
3. Перевод из любой системы счисления в десятичную.
Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.
Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:
Это и есть десятичная запись нашего числа, т.
е.
Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.
Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.
4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).
Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.
Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:
Таблицу соответствия мы научились строить в п.1.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Т.
е.
Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.
Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.
Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.
Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:
Системы счисления
Основные понятия систем счисления
Система счисления — это совокупность правил и приемов записи чисел с помощью набора цифровых знаков. Количество цифр, необходимых для записи числа в системе, называют основанием системы счисления. Основание системы записывается в справа числа в нижнем индексе: ; ; и т. д.
Различают два типа систем счисления:
позиционные, когда значение каждой цифры числа определяется ее позицией в записи числа;
непозиционные, когда значение цифры в числе не зависит от ее места в записи числа.
Примером непозиционной системы счисления является римская: числа IX, IV, XV и т.
д. Примером позиционной системы счисления является десятичная система, используемая повседневно.
Любое целое число в позиционной системе можно записать в форме многочлена:
где S — основание системы счисления;
— цифры числа, записанного в данной системе счисления;
n — количество разрядов числа.
Пример. Число запишется в форме многочлена следующим образом:
Виды систем счисления
Римская система счисления является непозиционной системой. В ней для записи чисел используются буквы латинского алфавита. При этом буква I всегда означает единицу, буква — V пять, X — десять, L — пятьдесят, C — сто, D — пятьсот, M — тысячу и т.д. Например, число 264 записывается в виде CCLXIV. При записи чисел в римской системе счисления значением числа является алгебраическая сумма цифр, в него входящих. При этом цифры в записи числа следуют, как правило, в порядке убывания их значений, и не разрешается записывать рядом более трех одинаковых цифр.
В том случае, когда за цифрой с большим значением следует цифра с меньшим, ее вклад в значение числа в целом является отрицательным. Типичные примеры, иллюстрирующие общие правила записи чисел в римской система счисления, приведены в таблице.
Таблица 2. Запись чисел в римской системе счисления
|
1 |
2 |
3 |
4 |
5 |
|
I |
II |
III |
IV |
V |
|
6 |
7 |
8 |
9 |
10 |
|
VI |
VII |
VIII |
IX |
X |
|
11 |
13 |
18 |
19 |
22 |
|
XI |
XIII |
XVIII |
XIX |
XXII |
|
34 |
39 |
40 |
60 |
99 |
|
XXXIV |
XXXIX |
XL |
LX |
XCIX |
|
200 |
438 |
649 |
999 |
1207 |
|
CC |
CDXXXVIII |
DCXLIX |
CMXCIX |
MCCVII |
|
2045 |
3555 |
3678 |
3900 |
3999 |
|
MMXLV |
MMMDLV |
MMMDCLXXVIII |
MMMCM |
MMMCMXCIX |
Недостатком римской системы является отсутствие формальных правил записи чисел и, соответственно, арифметических действий с многозначными числами.
По причине неудобства и большой сложности в настоящее время римская система счисления используется там, где это действительно удобно: в литературе (нумерация глав), в оформлении документов (серия паспорта, ценных бумаг и др.), в декоративных целях на циферблате часов и в ряде других случаев.
Десятичня система счисления – в настоящее время наиболее известная и используемая. Изобретение десятичной системы счисления относится к главным достижениям человеческой мысли. Без нее вряд ли могла существовать, а тем более возникнуть современная техника. Причина, по которой десятичная система счисления стала общепринятой, вовсе не математическая. Люди привыкли считать в десятичной системе счисления, потому что у них по 10 пальцев на руках.
Древнее изображение десятичных цифр (рис. 1) не случайно: каждая цифра обозначает число по количеству углов в ней. Например, 0 — углов нет, 1 — один угол, 2 — два угла и т.д. Написание десятичных цифр претерпело существенные изменения. Форма, которой мы пользуемся, установилась в XVI веке.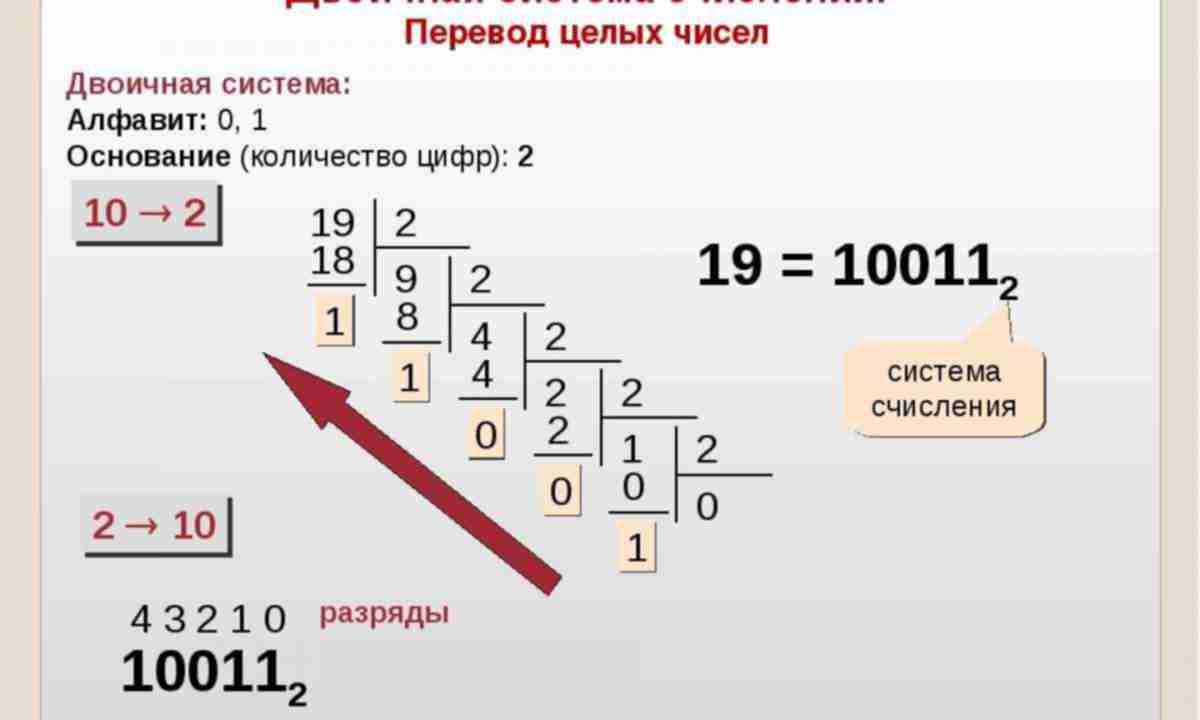
Десятичная система впервые появилась в Индии примерно в VI веке новой эры. Индийская нумерация использовала девять числовых символов и нуль для обозначения пустой позиции. В ранних индийских рукописях, дошедших до нас, числа записывались в обратном порядке — наиболее значимая цифра ставилась справа. Но вскоре стало правилом располагать такую цифру с левой стороны. Особое значение придавалось нулевому символу, который вводился для позиционной системы обозначений. Индийская нумерация, включая нуль, дошла и до нашего времени. В Европе индусские приёмы десятичной арифметики получили распространение в начале ХIII в. благодаря работам итальянского математика Леонардо Пизанского (Фибоначчи). Европейцы заимствовали индийскую систему счисления у арабов, назвав ее арабской. Это исторически неправильное название удерживается и поныне.
Десятичная система использует десять цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, а также символы “+” и “–” для обозначения знака числа и запятую или точку для разделения целой и дробной частей числа.
В вычислительных машинах используется двоичная система счисления, её основание — число 2. Для записи чисел в этой системе используют только две цифры — 0 и 1. Вопреки распространенному заблуждению, двоичная система счисления была придумана не инженерами-конструкторами ЭВМ, а математиками и философами задолго до появления компьютеров, еще в ХVII — ХIХ веках. Первое опубликованное обсуждение двоичной системы счисления принадлежит испанскому священнику Хуану Карамюэлю Лобковицу (1670 г.). Всеобщее внимание к этой системе привлекла статья немецкого математика Готфрида Вильгельма Лейбница, опубликованная в 1703 г. В ней пояснялись двоичные операции сложения, вычитания, умножения и деления. Лейбниц не рекомендовал использовать эту систему для практических вычислений, но подчёркивал её важность для теоретических исследований. Со временем двоичная система счисления становится хорошо известной и получает развитие.
Выбор двоичной системы для применения в вычислительной технике объясняется тем, что электронные элементы — триггеры, из которых состоят микросхемы ЭВМ, могут находиться только в двух рабочих состояниях.
С помощью двоичной системы кодирования можно зафиксировать любые данные и знания. Это легко понять, если вспомнить принцип кодирования и передачи информации с помощью азбуки Морзе. Телеграфист, используя только два символа этой азбуки — точки и тире, может передать практически любой текст.
Двоичная система удобна для компьютера, но неудобна для человека: числа получаются длинными и их трудно записывать и запоминать. Конечно, можно перевести число в десятичную систему и записывать в таком виде, а потом, когда понадобится перевести обратно, но все эти переводы трудоёмки. Поэтому применяются системы счисления, родственные двоичной — восьмеричная и шестнадцатеричная. Для записи чисел в этих системах требуется соответственно 8 и 16 цифр. В 16-теричной первые 10 цифр общие, а дальше используют заглавные латинские буквы. Шестнадцатеричная цифра A соответствует десятеричному числу 10, шестнадцатеричная B – десятичному числу 11 и т. д. Использование этих систем объясняется тем, что переход к записи числа в любой из этих систем от его двоичной записи очень прост.
Ниже приведена таблица соответствия чисел, записанных в разных системах.
Таблица 3. Соответствие чисел, записанных в различных системах счисления
|
Десятичная |
Двоичная |
Восьмеричная |
Шестнадцатеричная |
|
1 |
001 |
1 |
1 |
|
2 |
010 |
2 |
2 |
|
3 |
011 |
3 |
3 |
|
4 |
100 |
4 |
4 |
|
5 |
101 |
5 |
5 |
|
6 |
110 |
6 |
6 |
|
7 |
111 |
7 |
7 |
|
8 |
1000 |
10 |
8 |
|
9 |
1001 |
11 |
9 |
|
10 |
1010 |
12 |
A |
|
11 |
1011 |
13 |
B |
|
12 |
1100 |
14 |
C |
|
13 |
1101 |
15 |
D |
|
14 |
1110 |
16 |
E |
|
15 |
1111 |
17 |
F |
|
16 |
10000 |
20 |
10 |
Правила перевода чисел из одной системы счисления в другую
Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики.
Рассмотрим основные правила перевода.
1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней двойки:
Таблица 4. Степени числа 2
|
n (степень) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
Пример .
Число перевести в десятичную систему счисления.
2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней восьмерки:
Таблица 5. Степени числа 8
|
n (степень) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
8 |
64 |
512 |
4096 |
32768 |
262144 |
Пример .
Число перевести в десятичную систему счисления.
3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней числа 16:
Таблица 6. Степени числа 16
|
n (степень) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
16 |
256 |
4096 |
65536 |
1048576 |
16777216 |
Пример .
Число перевести в десятичную систему счисления.
4. Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в двоичную систему счисления.
5. Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в восьмеричную систему счисления.
6. Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15.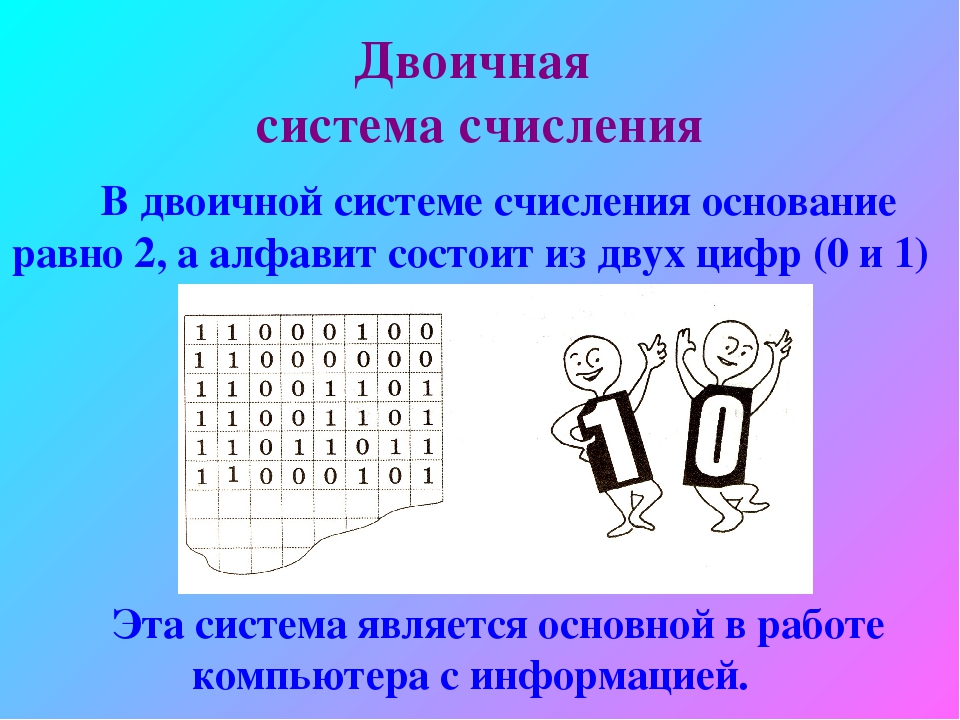
Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в шестнадцатеричную систему счисления.
7. Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 3).
Пример. Число перевести в восьмеричную систему счисления.
8. Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой (табл. 3).
Пример. Число перевести в шестнадцатеричную систему счисления.
9. Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.
Пример. Число перевести в двоичную систему счисления.
10. Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.
Пример. Число перевести в двоичную систему счисления.
11. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
Пример 1. Число перевести в восьмеричную систему счисления.
Пример 2. Число перевести в шестнадцатеричную систему счисления.
Системы счисления
Кодирование информации — представление информации в той или иной стандартной форме.
Например, письменность и арифметика — кодирование речи и числовой информации, музыку кодируют с помощью нот.
Чтобы использовать числа их нужно как-то записывать и называть.
Самые первые системы нумерации возникли в древнем Египте и Месопотамии — применяли иероглифы.
Системы счисления — способы кодирования числовой информации, то есть способ записи чисел с помощью некоторого алфавита, символы которого называют цифрами.
В древнем Вавилоне делили час на 60 минут, угол на 360 градусов, англосаксы начали делить год на 12 месяцев, сутки на два периода по 12 часов, продолжительность года 360 суток.
В Риме семь чисел обозначают буквами. 1-I, 5-V, 10-X, 50- L,100-C, 500-D, 1000-M.
IV (4=5-1)
VI (6=5+1)
Значение числа определяется как сумма или разность цифр числа. Это непозиционная система счисления.
Славяне числа кодировали буквами А=1, В=2, Г=3; чтобы избежать путаницы ставился специальный знак ~ титло. Алфавитная система счисления. Славянская нумерация сохранялась до конца XVII века.
При Петре I возобладала так называемая арабская нумерация. Славянская нумерация сохранилась в богослужебных книгах.
Самой популярной системой кодирования чисел оказалась позиционная, десятичная.
Используются десять цифр. Значение каждой определяется той позицией, которую цифра занимает в записи числа.
Эта система пришла из Индии, где она появилась не позднее VI века, европейцы заимствовали ее у арабов, назвав ее арабской. Из арабского языка заимствовано слово «цифра». Причина ее возникновения анатомическая — 10 пальцев. Анатомическая система счисления (существовали пятеричные, двадцатеричные системы счисления).
Например, 23 — три единицы, два десятка 32 — две единицы, три десятка 400 — 4 сотни, два 0 вклад в число не дают, нужны для того, чтобы указывать позицию 4.
В десятичной позиционной системе особую роль играет число 10 и его степени, например, 1996 — 6 единиц, 9 десятков, 9 сотен 1 тысяча или 1996=6+9*10+9*100+1*1000, т.к.1000=103, 100=102, 10=101, таким образом, 1996=1*103 + 9*102 + 9*101 +6*100.
Любое число в нулевой степени равно единице 0,10 = 1
То есть любое 4-х значное число можно записать в следующем виде:
N=a3*103+a2*102+a1*101+a0*100
a3, a2, a1, a0-десятичные цифры, от 1 до 9 или коэффициенты 3 2 1 0 — разряды, степени числа 10 со степенями называют основанием системы счисления.
Но основанием системы может быть не обязательно число 10, мы можем записать число в р-ичной системе, где основанием будут степени числа р. Любое число N в р-ичной системе мы можем представить в виде формулы:
N=an*Pn+an-1*Pn-1+…+a1*P1+a0*P0
Если взять за основание 60, то придется использовать 60 разных цифр. Такая система была в Древнем Вавилоне. Если основанием возьмем 2, получим систему всего с двумя цифрами 0 и 1. К сожалению, в этой системе даже небольшие числа записываются слишком длинно, так 1995 в двоичной системе записывается 199510=111110010112
Система счисления, где 2 является основанием системы называется двоичной системой счисления, относится к машинной системе счисления, к машинным системам счисления относятся и восьмеричная и шестнадцатеричная. Таким образом существуют следующие системы счисления: вавилонская, римская, алфавитные, анатомические, машинные.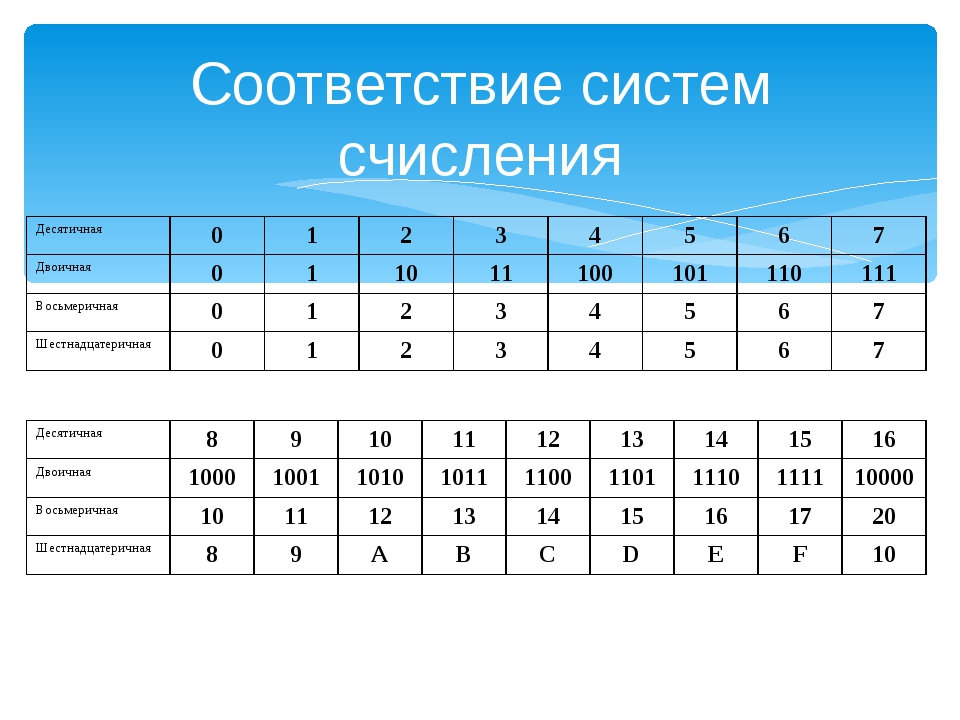
Системы счисления делятся также на позиционные и непозиционные.
Перевод из двоичной системы счисления в десятичную.
Как узнать чему равно девятизначное двоичное число N=1111101002
Подпишем сверху каждый разряд
87654321010 — 1 разряды (степени двойки)
1111101002
В двоичной системе особую роль играет двойка и ее степени.
Таким образом:
111110100=1*28 +1*27 +1*26 +1*25 +1*24 +0*23 +1*22 +0*21 +0*20 =1*256+1*128+1*64 +1*32 +1*16 +0*8 +1*4 +0*2 +0*1=256 + 128 + 64 + 32 + 16 + 0 + 4 + 0 +0 =500
Перевод из десятичной системы счисления в двоичную.
Пусть нужно перевести в двоичную систему число 234. Будем делить 234 последовательно на 2 и запоминать остатки, не забывая про нулевые.
Выписав все остатки, начиная с последнего 3 в обратном порядке, получим двоичное разложение числа.
23410 = 111010102
Восьмеричная и шестнадцатеричная системы счисления.
Запись числа в двоичной системе удобна для компьютера, но громоздка для человека. На помощь приходят системы, родственные двоичной восьмеричная система счисления использует 8 цифр: 0,1,2,3,4,5,6,7.
Единица, записанная в самом младшем разряде означает просто единицу (1*8 в нулевой степени), та же единица в следующем разряде обозначает 8 (1*8 в первой степени), в следующем 64 (1*8 во второй степени) и так далее.
2 1 0 1 — разряды (степени восьмерки)
1008 = 1*82 + 0*81 + 0*80 = 1*64 + 0 + 0 = 6410
8 — это 2 в третьей степени. При переводе в восьмеричную систему двоичное число из трех цифр записывается одной цифрой.
Восьмеричная запись | Двоичное представление |
впереди стоящий 0 ничего не значит |
0 | 000 | |
1 | 001 | |
2 | 010 | |
3 | 011 | |
4 | 100 | |
5 | 101 | |
6 | 110 | |
7 | 111 |
Для перевода из двоичной в восьмеричную число, записанное в двоичной системе делим на триады справа налево
Например, 11011100011=11 011 100 011 и заменить каждую группу одной восьмеричной цифрой 2 2 4 2 и получим 22428
Для перевода числа из восьмеричной системы в двоичную достаточно заменить каждую цифру на ее перевод в двоичную систему, представив каждую цифру в виде триады (1 в двоичной системе 1 добавляем до триады впереди 00)
Еще компактней выглядит запись двоичного числа в шестнадцатеричной системе счисления.
Для первых 10 из 16 шестнадцатеричных цифр используются привычные цифры 0 1 2 3 4 5 6 7 8 9, а для остальных используют первые буквы латинского алфавита
A-10 D-13
B-11 E-14
C-12 F-15
Цифра 1 в самом младшем разряде означает 1, в следующем разряде означает 16 (в первой степени), в следующем разряде 16*16 (162)=256, в следующем разряде 1*163 и так далее.
10016 =25610
Цифра F, записанная в самом младшем разряде означает 15 в десятичной системе, F в следующем разряде означает 15*16 в первой степени в десятичной системе и т.д.
2 1 0 — 1 разряды (степени числа 16)
Число 21016=10*162+15*161+0*160
21016=10*256+240+0*1=2560+240+0=280010
2 1 0
BAD16=11*162+1 0*161+13*1 60 = 11 * 256+10 *16+13*1=2816+160+13=298910
16 — это 2 в четвертой степени.
При переводе из двоичной системы в шестнадцатеричную число двоичное число из 4-х цифр кодируется числом из одной цифры в шестнадцатеричной системе.
Для перевода числа из шестнадцатеричной системы в двоичную достаточно заменить каждую цифру на ее перевод в двоичную, представив каждую цифру в виде сочетания четырех 1 и 0
A | O | F | AOF16 |
1010 | 0000 | 1111 |
Как осуществить перевод чисел из двоичной системы в шестнадцатеричную? Необходимо разбить число, записанное в двоичной системе на группы по 4 разряда справа налево, заменив каждую группу одной шестнадцатеричной цифрой.
1101 | 1010 | 1101 | в двоичной |
11 | 10 | 13 | в десятичной |
B | A | D | в шестнадцатеричной |
10 | 2 | 8 | 16 |
| 0 | 000 | 0 | 0 |
| 1 | 001 | 1 | 1 |
| 2 | 010 | 2 | 2 |
| 3 | 011 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Быстро учимся считать в двоичной и шестнадцатеричной системе
Введение
Иногда возникает потребность быстро прочитать или записать числа в двоичной или шестнадцатеричной системе счисления, например, работая с различными байтовыми редакторами,при расчете формул с побитовыми операциями или работе с цветом.
Часто в таких ситуациях нет возможности долго переводить числа с помощью формул или калькулятора. О быстрых способах перехода между системами счисления пойдет речь в данной статье.
Переход от десятичной системы к двоичной
Первый случай – считаем от десятичной системы к двоичной. Основное, что нужно помнить в данном случае – это ряд степеней двойки (1, 2, 4, 8, 16, 32, 64, 128 и т.д.). Даже если его вы не знаете, то ничего не стоит каждое следующее число умножать на двойку. Так как младшие разряды идут справа, а старшие – слева, то будем их записывать в обратном порядке справа налево.
Для примера будем переводить число 115. Дальше смотрим, если значение разряда помещается в число, то вычитаем из него это значение и ставим в этом разряде 1, иначе ставим 0.
Обратный перевод еще проще – нужно просуммировать все значения разрядов, которые отмечены единичками: 64+32+16+2+1 = 115.
Переход к шестнадцатеричной системе
Теперь давайте разберемся с шестнадцатеричной системой.
Имея ввиду то, что количество чисел, которые кодируются тетрадой (4 бита) и одним шестнадцатеричным символом совпадают, то соответственно каждый символ кодирует одну двоичную тетраду.
В результате получили число 0х73. Главное помнить, что А = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Если есть потребность перевести десятичное число в шестнадцатеричное или наоборот, то здесь проще всего будет сначала перевести число в двоичное представление, а затем только в шестнадцатеричное или десятеричное соответственно.
В итоге мы научились быстро переводить числа из одной системы счисления в другую. Главное, что нужно помнить — степени двойки и уметь хорошо складывать и вычитать. Детальнее о машинной математике вы можете узнать во втором уроке курса C# Стартовый.
Попрактикуйтесь самостоятельно и переведите несколько чисел из одной системы в другую, сверяясь с калькулятором. Немного практики — и вы всему научитесь.
Перевод из одной системы счисления в другую
Для перевода чисел из одной системы счисления в другую необходимо владеть основными сведениями о системах счисления и
форме представления чисел в них.
Количество s различных цифр, употребляемых в системе счисления, называется основанием, или базой системы счисления. В общем случае положительное число X в позиционной системе с основанием s может быть представлено в виде полинома:
где s — база системы счисления, — цифры, допустимые в данной системе счисления . Последовательность образует целую часть X, а последовательность — дробную часть X.
В вычислительной технике наибольшее применение нашли двоичная (BIN — binary), и двоично кодированные системы счисления: восьмеричная (OCT — octal), шестнадцатеричная (HEX — hexadecimal) и двоично-кодированная десятичная (BCD — binary coded decimal).
В дальнейшем для обозначения используемой системы счисления число будет заключаться в скобки, а
в индексе указано основание системы. Число X по основанию s будет обозначено
.
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.
Основанием системы счисления служит число 2 (s = 2) и для записи чисел используются только две цифры: 0 и 1. Чтобы представить любой разряд двоичного числа, достаточно иметь физический элемент с двумя чётко различными устойчивыми состояниями, одно из которых изображает 1, а другое 0.
Прежде чем заняться переводом из любой системы счисления в двоичную, нужно внимательно изучить пример записи числа в двоичной системе счисления:
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.
Эти системы счисления относятся к двоично-кодированным, в которых основание системы счисления
представляет собой целую степень двойки: —
для восьмеричной и — для шестнадцатеричной.
В восьмеричной системе счисления(s = 8) используются 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7.
Прежде чем заняться переводом из любой системы счисления в восьмеричную, нужно внимательно изучить пример записи числа в восьмеричной системе:
В шестнадцатеричной системе счисления (s = 16) используются 16 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Пример записи числа в шестнадцатеричной системе:
Широкое применение восьмеричной и шестнадцатеричной систем счисления обусловлено двумя факторами.
Во-первых, эти системы позволяют заменить запись двоичного числа более компактным представлением
(запись числа в восьмеричной и шестнадцатеричной системах будет соответственно в 3 и 4 раза короче двоичной записи этого числа).
Во-вторых, взаимное преобразование чисел между двоичной системой с одной стороны и восьмеричной и шестнадцатиречной — с другой
осуществляется сравнительно просто.
Действительно, поскольку для восьмеричного числа каждый разряд представляется
группой из трёх двоичных разрядов (триад), а для шестнадцатеричного — группой из четырёх двоичных разрядов (тетрад),
то для преобразования двоичного числа достаточно объединить его цифры в группы по 3 или 4 разряда соответственно, продвигаясь от
разделительной запятой вправо и влево. При этом, в случае необходимости, добавляют нули слева от целой части
и/или справа от дробной части и каждую такую группу — триаду или тетраду — заменяют эвивалентной восьмеричной или
шестнадцатеричной цифрой (см. таблицу).
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.
Соответствие между цифрами в различных системах счисления| DEC | BIN | OCT | HEX | BCD |
| 0 | 0000 | 0 | 0 | 0000 |
| 1 | 0001 | 1 | 1 | 0001 |
| 2 | 0010 | 2 | 2 | 0010 |
| 3 | 0011 | 3 | 3 | 0011 |
| 4 | 0100 | 4 | 4 | 0100 |
| 5 | 0101 | 5 | 5 | 0101 |
| 6 | 0110 | 6 | 6 | 0110 |
| 7 | 0111 | 7 | 7 | 0111 |
| 8 | 1000 | 10 | 8 | 1000 |
| 9 | 1001 | 11 | 9 | 1001 |
| 10 | 1010 | 12 | A | 0001 0000 |
| 11 | 1011 | 13 | B | 0001 0001 |
| 12 | 1100 | 14 | C | 0001 0010 |
| 13 | 1101 | 15 | D | 0001 0011 |
| 14 | 1110 | 16 | E | 0001 0100 |
| 15 | 1111 | 17 | F | 0001 0101 |
Для обратного перевода каждая OCT или HEX цифра заменяется соответственно триадой или тетрадой
двоичных цифр, причём незначащие нули слева и справа отбрасываются.
Для рассмотренных ранее примеров это выглядит следующим образом:
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.
В двоично-десятичной системе вес каждого разряда равен степени 10, как в десятичной системе, а каждая десятичная цифра кодируется четырьмя двоичными цифрами. Для записи десятичного числа в BCD-системе достаточно заменить каждую десятичную цифру эквивалентной четырёхразрядной двоичной комбинацией:
Любое десятичное число можно представить в двоично-десятичной записи, но следует помнить, что это не двоичный эквивалент числа. Это видно из следующего примера:
Пусть X — число в системе счисления с основанием s, которое требуется
представить в системе с основанием h.
Удобно различать два случая.
В первом случае и, следовательно, при переходе к основанию h можно использовать арифметику этой системы. Метод преобразования состоит в представлении числа в виде многочлена по степеням s, а также в вычислении этого многочлена по правилам арифметики системы счисления с основанием h. Так, например, удобно переходить от двоичной или восьмеричной системы счисления к десятичной. Описанный приём иллюстрируют следующие примеры:
.
.
В обоих случаях арифметические действия выполняются по правилам системы счисления с основанием 10.
Во втором случае ()
удобнее пользоваться арифметикой по основанию s. Здесь следует учитывать, что перевод целых чисел
и правильных дробей производится по различным правилам. При переводе смешанных дробей целая и дробная части
переводятся каждая по своим правилам, после чего полученные числа записываются через запятую.
Перевод целых чисел
Правила перевода целых чисел становится ясным из общей формулы записи числа в произвольной позиционной системе. Пусть число в исходной системе счисления s имеет вид . Требуется получить запись числа в системе счисления с основанием h:
.
Для нахождения значений разделим этот многочлен на h:
.
Как видно, младший разряд , то есть , равен первому остатку. Следующий значащий разряд определяется делением частного на h:
.
Остальные также вычисляются путём деления частных до тех пор, пока не станет равным нулю.
Для перевода целого числа из s-ичной системы счисления в h-ичную
необходимо последовательно делить это число и получаемые частные на h (по правилам системы счисления с основанием h)
до тех пор, пока частное не станет равным нулю.
Старшей цифрой в записи числа с основанием h служит
последний остаток, а следующие за ней цифры образуют остатки от предшествующих делений, выписываемые в
последовательности, обратной их получению.
Пример 1. Перевести число 75 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы.
Решение:
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.
Перевод правильных дробей
Правильную дробь , имеющую в системе с основанием s вид , можно выразить в системе счисления с основанием h как многочлен вида
Старшая цифра может быть найдена умножением этого многочлена на h, т.е.
Если это произведение меньше 1, то цифра равна 0,
если же оно больше или равно 1, то цифра равна
целой части произведения.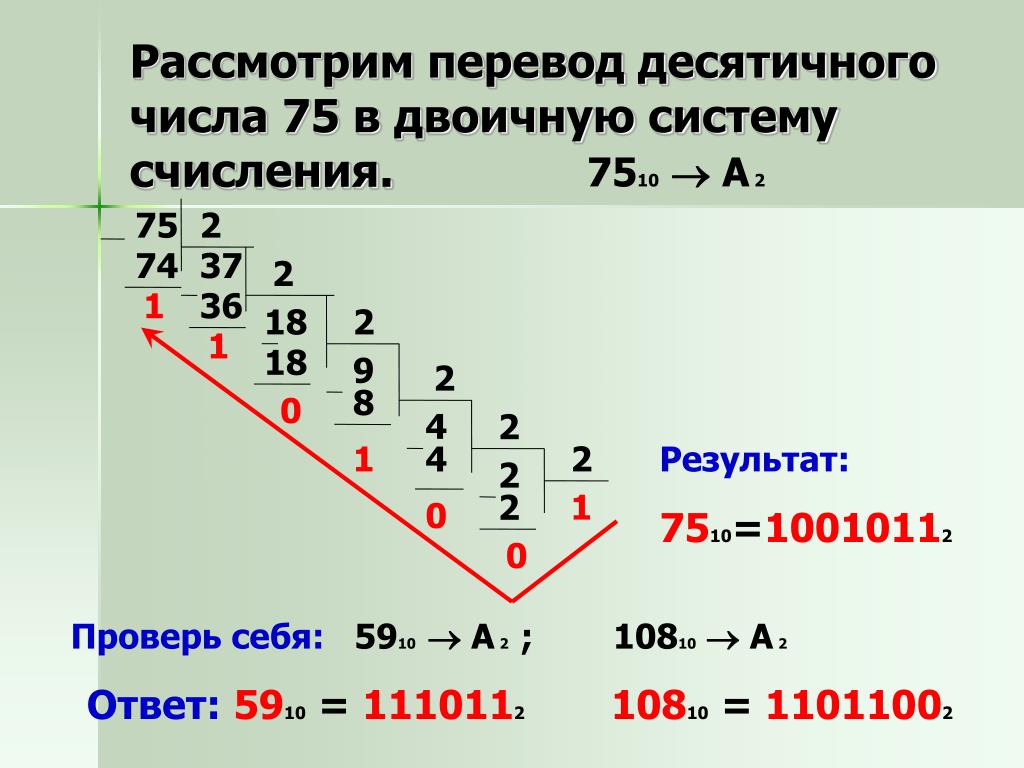
Следующая цифра справа
определяется путём умножения дробной части указанного выше произведения на h и выделения
его целой части и т.д. Процесс может оказаться бесконечным, т.к. не всегда можно представить дробь
по основанию h конечным набором цифр.
Для перевода правильной дроби из системы счисления с основанием s в систему счисления с основанием h нужно умножать исходную дробь и дробные части получающихся произведений на основание h (по правилам «старой» s-системы счисления). Целые части полученных произведений дают последовательность цифр дроби в h-системе счисления.
Описанная процедура продолжается до тех пор, пока дробная часть очередного произведения
не станет равной нулю либо не будет достигнута требуемая точность изображения числа X в
h-ичной системе счисления. Представлением дробной части числа X в новой системе счисления
будет последовательности целых частей полученных произведений, записанных в порядке их получения и
изображённых h-ичной цифрой.
Абсолютная погрешность перевода числа X при p
знаков после запятой равняется .
Пример 2. Перевести правильную дробь 0,453 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.
* В двоичную систему:
Ответ:
** В восьмеричную систему:
Ответ:
*** В шестнадцатеричную систему:
Ответ: так как , то
Поделиться с друзьями
Перевести бренды в ° | двоичная степень в градусы
Количество: 1 двоичный градус углаРавно: Угол 1,41 градуса (°)
Преобразование двоичных градусов в значение градусов в шкале угловых единиц.
TOGGLE: из градусов в двоичные градусы наоборот.
CONVERT: между другими угловыми измерительными устройствами — полный список.
Сколько градусов в 1 двоичной степени? Ответ: 1 брэд равен 1.41 °
1,41 ° преобразовано в 1 из чего?
Число 1,41 ° градуса преобразуется в 1 брэд, один двоичный градус. Это РАВНОЕ значение угла, равное 1 двоичному градусу, но в альтернативных единицах измерения угла.
| результат преобразования угла штифт / ° | ||||
| Из | Символ | Равно | Результат | Символ |
| 1 | brad | = | 1.41 | ° |
Таблица преобразования —
двоичных градусов от до градусов1 двоичный градус в градусы = 1,41 °
2 двоичных градуса в градусы = 2,81 °
3 двоичных градуса в градусы = 4,22 °
4 двоичных градуса в градусы = 5,63 °
5 двоичных градусов в градусы = 7,03 °
6 двоичных градусов в градусы = 8,44 °
7 двоичных градусов в градусы = 9,84 °
8 двоичных градусов в градусы = 11.
25 °
9 двоичных градусов в градусы = 12,66 °
10 двоичных градусов в градусы = 14,06 °
11 двоичных градусов в градусы = 15,47 °
12 двоичных градусов в градусы = 16,88 °
13 двоичных градусов в градусы = 18,28 °
14 двоичных градусов в градусы = 19,69 °
15 двоичных градусов в градусы = 21,09 °
Категория : главное меню • угловое меню • двоичные градусы
Преобразование угла двоичных градусов (шр.) и градусов (°) единиц в обратном порядке из градусов в двоичные градусы.
Уголки
Калькулятор основан на пересчете двух угловых единиц. Угол состоит из двух лучей (как стороны угла, имеющие общую вершину или иначе называемые конечной точкой). Некоторые из них относятся к измерениям вращения — сферические углы, измеряемые длинами дуг, направленных от центра, плюс радиус. Чтобы получить полный набор нескольких угловых единиц на одной странице, попробуйте этот инструмент Multiunit Converter, который встроил все варианты угловых единиц.
Страница с индивидуальными угловыми единицами.
Первая единица: двоичный градус (штифт) используется для измерения угла.
Секунда: градус (°) — единица измерения угла.
ВОПРОС :
15 brad =? °
ОТВЕТ :
15 brad = 21.09 °
Сокращение или префикс двоичной степени:
brad
Сокращенное обозначение степени:
°
Другие применения этого калькулятора углов …
Благодаря вышеупомянутой услуге вычисления с двумя единицами, которую он предоставляет, этот преобразователь углов оказался полезным также в качестве обучающего инструмента:
1.в практике обмена двоичными градусами и градусами (брэд против °).
2. для коэффициентов пересчета между парами единиц измерения.
3. Работа со значениями и свойствами углов.
Конвертировать двоичные радианы град. в градусы
Конвертировать двоичные радианы град. в градусы | преобразование угла (плоских углов) Преобразовать двоичный радиан град.
(brad) по сравнению с градусов (° — deg)
в обратном направлении с заменой мест
из градусов в двоичные радианы град.
Или используйте страницу использованного конвертера с многофункциональным конвертером углов
| результат преобразования для двух единиц угла (плоских углов): | ||
| От единицы Символ | Равно результат | К единице Символ |
| 1 двоичный радиан град. штифт | = 1,41 | градус ° — град |
Каково международное сокращение для каждой из этих двух единиц угла (плоских углов)?
Префикс или символ двоичного радиана град.есть: brad
Префикс или символ градуса: ° — град
Инструмент для преобразования технических единиц измерения углов (плоских углов). Обмен чтением в двоичных радианах град.
единица измерения на градусов единица ° — градус как в эквивалентном результате измерения (две разные единицы, но одно и то же физическое общее значение, которое также равно их пропорциональным частям при делении или умножении).
Один двоичный радиан град.преобразовано в градусы = 1,41 ° — град
1 штифт = 1,41 ° — град.
Поиск страниц при преобразовании в с помощью системы пользовательского поиска Google в Интернете
Двоичный код
радиан град. — Для страницы перевода единиц — градусы — ° — deg требуется активный JavaScript в вашем браузере. Вот конкретные инструкции о том, как включить JS на вашем компьютере. Как включить JavaScriptИли для вашего удобства загрузите браузер Google Chrome для просмотра веб-страниц в высоком качестве.
- стр.
- Разное
- Интернет и компьютеры
Сколько градусов содержится в одном двоичном радиан градусе? Для привязки к этому углу (плоские углы) — двоичных радиан град.
в градусы единиц конвертера, только вырежьте и вставьте следующий код в свой html.
Ссылка появится на вашей странице как: в веб-конвертере единиц измерения из двоичных радиан град. (brad) в градусы (° — deg)
Бинарные радианы онлайн град. калькулятор преобразования в градусы | convert-to.com конвертеры единиц © 2021 | Политика конфиденциальности
Преобразовать градусы в двоичные радианы град.
Преобразование градусов в двоичные радианы град. | преобразование угла (плоских углов)Преобразование градусов (° — градус) по сравнению с двоичных радианов град.(brad)
в обратном направлении
от двоичных радианов град. до градусов
Или используйте страницу использованного конвертера с многофункциональным конвертером углов
| результат преобразования для двух единиц угла (плоских углов): | ||
| От единицы Символ | Равно результат | К единице Символ |
| 1 градус ° — град | = 0,71 | двоичные радианы град. штифт |
Каково международное сокращение для каждой из этих двух единиц угла (плоских углов)?
Префикс или символ градуса: ° — град
Префикс или символ двоичного радиана град. есть: brad
Инструмент для преобразования технических единиц измерения углов (плоских углов). Обменять показания в единицах градусов ° — градусах на двоичных радианов град. единица brad как в эквивалентном результате измерения (две разные единицы, но одно и то же идентичное физическое общее значение, которое также равно их пропорциональным частям при делении или умножении).
Один градус преобразован в двоичный радиан град. равно = 0,71 brad
1 ° — град = 0,71 шпонка
Поиск страниц при преобразовании в с помощью системы пользовательского поиска Google в Интернете
градусов — ° — deg в двоичных радианах deg. — Для страницы конвертера единиц brad требуется активный JavaScript в вашем браузере.
Вот конкретные инструкции о том, как включить JS на вашем компьютере. Как включить JavaScriptИли для вашего удобства загрузите браузер Google Chrome для просмотра веб-страниц в высоком качестве.
- стр.
- Разное
- Интернет и компьютеры
Сколько двоичных радианов град. содержатся в одной степени? Для привязки к этому углу (плоские углы) — градусов в двоичных радианах град. Конвертер единиц , только вырежьте и вставьте следующий код в свой html.
Ссылка будет отображаться на вашей странице как: в Интернете конвертер единиц из градуса (° — градус) в двоичные радианы град. (штифт)
Онлайн градусы в двоичные радианы град. калькулятор преобразования | convert-to.com конвертеры единиц © 2021 | Политика конфиденциальности
Глава 7.
5.3. — Двоичная угловая мера Эта книга представляет собой введение в системы реального времени. Он задуман не как поваренная книга,
, а, скорее, как стимул для того, чтобы думать об аппаратном и программном обеспечении по-другому,
.Это обязательно шире, чем глубоко. Это обзорная книга, предназначенная для
повышения осведомленности читателя о проблемах в реальном времени.
Эта книга является кульминацией более чем 20-летнего опыта создания, изучения и обучения
систем реального времени. Поездки автора привели его в НАСА, UPS,
Lockheed Martin, Силы обороны Канады и Австралии, лаборатории Чарльза
Старка Дрейпера Массачусетского технологического института и многие другие места. Эти посещения и взаимодействие с
буквально сотнями студентов из таких мест, как Boeing, Motorola и Siemens
, привели к более широкому пониманию систем реального времени и, в частности, их реального применения.Эта книга
, по сути, представляет собой сборник этих опытов.
Автор намерен предоставить практическую среду
для разработчиков программного обеспечения для разработки и внедрения систем реального времени. Этот подход
несколько отличается от других текстов по этой теме.
Из-за прагматического подхода некоторые результаты и точки зрения, представленные в книге
, могут быть противоречивыми. Автор адаптировал многие формальные определения из их традиционной жесткой формы
в слова, которые более совместимы с практическим дизайном.Во многих местах
опущены теоретические методы, которые могут затруднить понимание прикладных результатов. В этих случаях читатель отсылается к
дополнительным материалам для чтения. Этот автор очень верит в исследования в этой области, и во многих местах
указывает, где исследования должны быть выполнены или проводятся.
Хотя книга может показаться упрощенной, она несколько сложна. Рассмотрим семафорные операторы. Их
можно написать с минимальным объемом кода, но они чреваты опасностью для проектировщика реального времени.
Точно так же в этой книге есть что-то вроде дзен-простоты и сложности: инь и янь.
Сравнение приближений степеней свободы знаменателя для обобщенной линейной смешанной модели при анализе бинарных исходов в малых выборочных кластерно-рандомизированных испытаниях | BMC Medical Research Methodology
Обобщенные линейные смешанные модели и тест Wald
FGLMM является расширением GLM путем введения случайных эффектов в линейный предсказатель GLM [16,17].{-1} \ left ({X} _i \ beta + {Z} _i {b} _i \ right) + {\ epsilon} _i \ kern0.75em i = 1, \ dots, K $$
(1)
где
Y i — это n i Вектор ответа × 1 для кластера i th ;
g — 1 (·) — обратная функция дифференцируемой монотонной функции связи;
X i — это n i × p матрица фиксированных ковариат;
β — вектор p × 1 параметров регрессии с фиксированными эффектами;
Z i — это n i × v — расчетная матрица случайных эффектов, где v — расчетный параметр;
b i — вектор v × 1 случайных эффектов, специфичных для кластера;
ϵ i — это n i Вектор ошибок × 1.
{- 1 } L \ widehat {\ beta} $$
(2)
, где L — это r × p Матрица с рангом r ≤ p для общей линейной гипотезы, \ (\ widehat {\ beta} \) — оценка β по некоторой оценке метод и \ (\ widehat {Y} \ left (\ widehat {\ beta} \ right) \) — это оценочная матрица ковариации дисперсии \ (\ widehat {\ beta} \).2 \ влево (\ widehat {\ beta} \ right) / r $$
(3)
со степенями свободы числителя r и приблизительным DDF, скажем d . Предположим, мы собираемся проверить нулевую гипотезу об отсутствии эффекта вмешательства, статистика Wald F \ (F \ left ({\ widehat {\ beta}} _ T \ right) \) будет иметь приблизительное распределение F с 1 числитель степеней свободы и d DDF, которые необходимо указать или оценить.K \;} {n} _i \), общее количество участников во всех кластерах.
Сдерживание DDF
Метод сдерживания выбирает DDF как наименьший ранговый вклад случайных эффектов, которые содержат фиксированные эффекты, в матрицу плана при проектировании с разделением участков [15].
Такой выбор DDF соответствует тестам, проводимым для сбалансированных проектов, и может быть адекватным для умеренно несбалансированных проектов [15]. В рамках CRT, если эффект лечения фиксирован и не содержится в каких-либо случайных эффектах, DDF сдерживания рассчитывается по N — K .
Между-внутри DDF
Шлухтер и Элашофф [18] делят остаточные степени свободы на части между кластерами и внутри кластера и предполагают, что в смешанной модели, если фиксированный эффект изменяется в пределах любого кластера, степени внутри кластера свободы следует отнести к эффекту; в противном случае эффекту следует присвоить степени свободы между кластерами. В ЭЛТ для проверки эффекта вмешательства в кластерах будут применяться степени свободы между кластерами и рассчитываться как K — ранг [ X ].{\ prime} \) — собственный вектор м th и U м — приблизительные степени свободы для m th независимая одиночная степень свободы t статистика.
{\ prime} \ right] \) аппроксимируется с использованием многомерного дельта-метода.2 \ frac {r + d-2} {r \ left (d-4 \ right)}. $
(5)
Полученное таким образом значение d является K-R DDF. Для r = 1 K-R DDF то же самое, что и DDF Саттертуэйта, но приближение K-R генерирует более консервативный тест, раздувая матрицу дисперсии-ковариации на φ .
Моделирование данных
Мы провели исследования моделирования на основе конструкции двуручной ЭЛТ с двоичными результатами. Для простоты, но без потери обобщаемости, мы предполагаем, что контрольная и интервенционная руки содержат равное количество кластеров и не содержат ковариант.Коррелированные бинарные ответы генерируются с использованием бета-биномиального метода [20], с помощью которого доля событий в кластере является случайной выборкой из бета-версии (a, b). Можно показать, что предельная доля событий в кластере определяется как \ (\ mu = \ frac {a} {a + b} \), а ICC — это \ (\ rho = \ frac {1} {1 + a + b} \).
2 \ right), $$
(6)
где x i — это двоичный предсказатель на уровне кластера, указывающий лечебные руки ( x i = 0 для управления и x i = 1 для активного вмешательства), i = 1,…, K и j = 1,…, n i и b i Предполагается, что имеют нормальное распределение.Предельное среднее значение было установлено как { μ i | x i = 0} = 0,25. τ определяется бета-биномиальным методом с определенным предельным средним и выбранной внутриклассовой корреляцией ( ρ ) . При наших настройках моделирования приблизительные значения τ 2 равны 0,12, 0,17, 0,44 и 0,81 для ICC, равных 0,001, 0,01, 0,05 и 0,1 соответственно.
Эти значения ICC отражают уровни, часто встречающиеся на практике [4,5,21].Чтобы проверить, генерирует ли бета-биномиальный метод нормально распределенные b i в логит-шкале, графики Q-Q были созданы для моделирования данных. Графики Q-Q для b i предполагают, что предположение нормального распределения выполняется. Размеры выборки в нашем моделировании установлены как 10, 20 и 30 полных кластеров ( K ) с 20, 50 и 100 наблюдениями в среднем на кластер \ (\ left (\ overline {n} \ right) \).Точное количество наблюдений, n i , для каждого кластера i = 1,…, K , выбирается случайным образом и округляется от нормального распределения со средним значением, равным \ (\ overline {n} \), и дисперсией, равной σ 2 . Изменение размеров кластера можно измерить с помощью коэффициента вариации ( cv ), который представляет собой отношение стандартного отклонения размеров кластера к среднему значению размеров кластера.
2 \). В нашем моделировании cv находится в диапазоне от 0 до 1. Чтобы избежать невозможной ситуации, когда количество наблюдений в кластере отрицательно или равно нулю, мы ограничили наименьший размер кластера равным 1. При этих настройках DDF равен различные методы аппроксимации перечислены в таблице 1. Для каждого сценария создается 5000 независимых повторов для вычисления ошибки типа I и 1000 независимых повторов для расчета мощности. Все симуляции и анализы проводятся с использованием SAS 9.3 (Кэри, Северная Каролина).
Частота ошибок типа I каждого приближения DDF рассчитывается путем вычисления наблюдаемой доли тестов Wald F , отклоняющих нулевую гипотезу ( H o : β = 0), когда нулевая гипотеза верна.
На номинальном уровне 0,05 и 5000 симуляций мы ожидаем, что имитируемая частота ошибок типа I будет между 0,044 и 0,056 (95% доверительный интервал), и любая процедура с частотой ошибок типа I ниже этого диапазона будет считаться консервативной, выше этого диапазона будет считается либеральным, и в этом диапазоне будет рассматриваться как имеющий номинальный коэффициент ошибок типа I. Мощность рассчитывается путем вычисления наблюдаемой доли тестов Wald F , отклоняющих нулевую гипотезу ( H o : β = 0), когда истинное значение β равно log1.5 (т.е. отношение шансов 1,5).
Иллюстрация реальных данных
Все пять методов аппроксимации DDF проиллюстрированы с использованием реальной CRT, исследующей, улучшило ли вмешательство в общей практике последующее посещение скрининга груди среди женщин, которые не ответили на их первоначальное приглашение в районе Ньюхэм в Восточном Лондоне [ 22,23]. Среди участвовавших практик 12 были рандомизированы в группу вмешательства и 14 — в контрольную группу.
Персонал приемной общей врачебной практики, выделенный в интервенционную группу, провел обучение, как обращаться к не посещающим обследование груди.Практикам контроля не давали никакого обучения или советов. В исследование были включены в общей сложности 995 женщин, участвовавших в интервенционной практике, и 1069 женщин, участвовавших в контрольной практике. Интересным результатом явилось посещение скрининга груди среди женщин, которые не ответили на их первоначальное приглашение на плановое обследование груди. Практика вмешательства, как правило, имела более высокий уровень посещаемости по сравнению с практикой контроля, хотя уровень посещаемости значительно варьировался в зависимости от практики.Следует отметить, что ключевой особенностью этого испытания является небольшое количество кластеров ( K = 26) с сильно изменяющимися размерами кластеров ( cv ≈ 0,71).
Углы, направления и их двоичное представление — GameDev
То, с чем, вероятно, каждый разработчик игр когда-то работал — а некоторые из нас могут работать с этим ежедневно — это угла .
Углы используются для представления направлений и поворотов, и особенно в 2D, они представляют собой простой способ сделать это, поскольку для представления ориентации требуется только одно число.
В 3D нам нужно три угла — тангаж, рыскание и крен — что немного усложняет задачу.
В этом посте я хочу исследовать способ представления концепций угла , направления , ориентации и поворота .
Мы будем:
- посмотрите, как эти концепции обычно представлены в коде;
- указывает на некоторые недостатки в представлении;
- исследовать семантические различия — если таковые имеются — между концепциями, как с математической, так и с геометрической точки зрения;
- предлагает лучшее решение, основанное на семантических требованиях, переводя их в подходящее двоичное представление.
В этом посте мы будем смотреть только на отдельные углы в 2D-плоскости.
Простая реализация.
Обычно мы представляем углы в радианах с помощью чисел с плавающей запятой.
На первый взгляд это отличное решение:
Арифметика с плавающей запятой очень быстрая, поддерживается практически любым оборудованием и имеет огромный диапазон возможных значений. Кроме того, тригонометрические функции низкого уровня обычно принимают и возвращают числа с плавающей запятой.
Однако и у этого подхода есть некоторые проблемы.
Упаковка
Обычный — обертка. Если мы используем угол для представления ориентации — например, направление, в котором смотрит персонаж, — значимы только углы от 0 до 360 градусов.
Фактически, углы 0 и 360 градусов в этом случае функционально идентичны. В общем случае любые два угла a и b со значениями a = b + 360 * n — n — любое целое число — здесь эквивалентны.
Это может быть проблемой не для всех приложений, например, вычисление вектора вдоль направления с использованием синуса и косинуса значения вернет правильный результат.
Однако нет тривиального способа получить угол между двумя такими ориентациями. После вычитания двух значений мы должны проверить, не выходит ли значение за пределы диапазона [-180, 180], и если да, найти эквивалентный угол внутри этого интервала (используя то же отношение эквивалентности, которое только что упомянуто).
Если мы забудем об этом, в результате объекты могут вращаться неправильно или более чем на полный оборот, чтобы принять желаемую ориентацию.
Погрешность с плавающей запятой (дюйм)
Другая проблема может быть связана с природой двоичных представлений с плавающей запятой. Поплавки имеют заданное количество точных цифр и используют экспоненциальный множитель для переключения между нижним и верхним диапазонами.
В большинстве случаев это прекрасно.
Однако при работе с углами нам может понадобиться представлять углы только в диапазоне [0, 360] или [-180, 180].
В этом случае мы теряем много из возможного диапазона нашего числа с плавающей запятой, и распределение точности очень сильно смещается в сторону меньших числовых значений.
Однако, если мы думаем о направлениях, не имеет смысла представлять одни диапазоны направлений с большей точностью, чем другие.
Представленный ассортимент
Говоря о диапазонах, следует ли представлять направления в виде значений от 0 до 360 или от -180 до 180 градусов?
Оба могут быть полезны для некоторых приложений.Однако для преобразования между ними требуется ветвь (оператор if), что обычно не идеально для низкоуровневого кода.
Кроме того, нам всегда нужно отслеживать, какое представление мы используем, и обязательно применять его вручную, чтобы не получить нежелательных результатов.
Кроме того, могут ли вращения — подумайте об угловых скоростях — теперь иметь значения за пределами этого диапазона?
Если мы будем использовать один и тот же тип данных — float — для всего этого, мы неизбежно столкнемся с проблемами. У меня, безусловно, были самые странные ошибки, возникающие из-за того, что я не решал эти проблемы должным образом
Что здесь происходит?
Я надеюсь, что изложенное выше убедило вас в том, что есть по крайней мере несколько проблем, которые мы должны учитывать при работе с углами.
Но что здесь происходит на самом деле? Почему у нас вообще эти проблемы?
Эти проблемы могут быть вызваны двумя причинами:
- Мы путаем две разные вещи: относительные углы и абсолютные направления;
- Мы используем тип данных без семантики для представления значений с очень строгой семантикой и особыми свойствами.
1. Углы и направления
Разница между тем, что я назову углами и направлениями, с этого момента может быть выражена как в геометрических, так и в математических терминах:
Математически направление — это набор с элементами, семантически соответствующими (полуоткрытому) интервалу [0, 360 [градусов или точкам на окружности.
Геометрически направление — это абсолютное направление или ориентация в 2D-плоскости при заданной фиксированной системе отсчета (нулевое направление , ).
Математически угол — это одномерное векторное пространство с естественным определением сложения, вычитания и скалярного умножения.
Геометрически угол — это разница между двумя направлениями . Таким образом, он также может представлять вращение из одного направления в другое.
Обратите внимание, что с точки зрения операций с элементами этих двух наборов, у нас есть те, которые присущи векторному пространству углов, но нет внутри набора направлений.
Однако у нас есть по крайней мере одна операция между двумя направлениями, чтобы получить угол между ними. Казалось бы, эту операцию можно инвертировать, добавив угол к направлению, чтобы получить другое направление.
Обратите внимание, что из-за эквивалентности направлений, указанных выше, эти две операции на самом деле не являются обратными друг другу.Однако они обратны для подмножества углов.
Какое это подмножество, зависит от точного определения операции между двумя направлениями. Как мы увидим ниже, существует несколько допустимых определений.
Для полноты, имейте в виду, что хотя набор направлений кажется ограниченным, а набор углов кажется бесконечным, оба имеют одинаковую мощность (в частности, | ℝ |, мощность континуума).
2. Тип данных
Поскольку углы являются одномерным векторным пространством, как описано выше, их представление с использованием чисел с плавающей запятой имеет смысл.
Мы могли бы возразить, что использование одного и того же типа данных для углов и скаляров несколько сомнительно, но мы не будем этого делать в этой публикации.
При этом мы создадим собственный тип для наших углов, чтобы обеспечить безопасное и недвусмысленное использование ниже.
Что нас больше беспокоит, так это особый характер направлений. Как описано, у них есть очень разные свойства, которые плохо представлены числами с плавающей запятой.
Тип, который мы создадим для представления направлений, является основным содержанием этого поста, и затем мы определим точные свойства, которые мы хотим, чтобы этот тип имел.
Требования к лучшему представлению Дирекции
На основе семантики, объясненной выше, следующие требования для точного представления концепции направления :
- Наше представление должно обрабатывать обертку или отношение эквивалентности направлений;
- Направления и углы должны быть различимы, и их нельзя легко перепутать;
- Мы хотели бы иметь различные полезные функции, например:
- преобразование направления в направленный вектор и обратно,
- — угол между двумя направлениями,
- все операции, описанные выше, как в векторном пространстве углов, так и между наборами углов и векторов,
- и, возможно, больше…
- В идеале наше представление должно быть полностью типобезопасным, чтобы им нельзя было злоупотреблять неявно.
В более практическом смысле мы не хотим думать о нашем базовом представлении и его крайних случаях каждый раз, когда мы его используем, как мы должны делать это при использовании простых чисел с плавающей запятой для углов и направлений.
Например, при реализации эффекта самонаведения для снаряда мы хотим иметь возможность написать код, который, очевидно, эквивалентен следующему псевдокоду.
Он должен быть легко читаемым и не требовать дополнительных проверок.
Реализация
Ключевым ограничением для нашего представления является поведение упаковки.
В принципе, мы могли бы по-прежнему использовать число с плавающей запятой для внутреннего хранения значения и включать проверки в каждую из наших пользовательских операций.
Хотя это, казалось бы, предотвращает проблемы, описанные выше, это приводит к потенциально значительной потере производительности, а также по-прежнему тратит впустую большой диапазон представлений с плавающей запятой.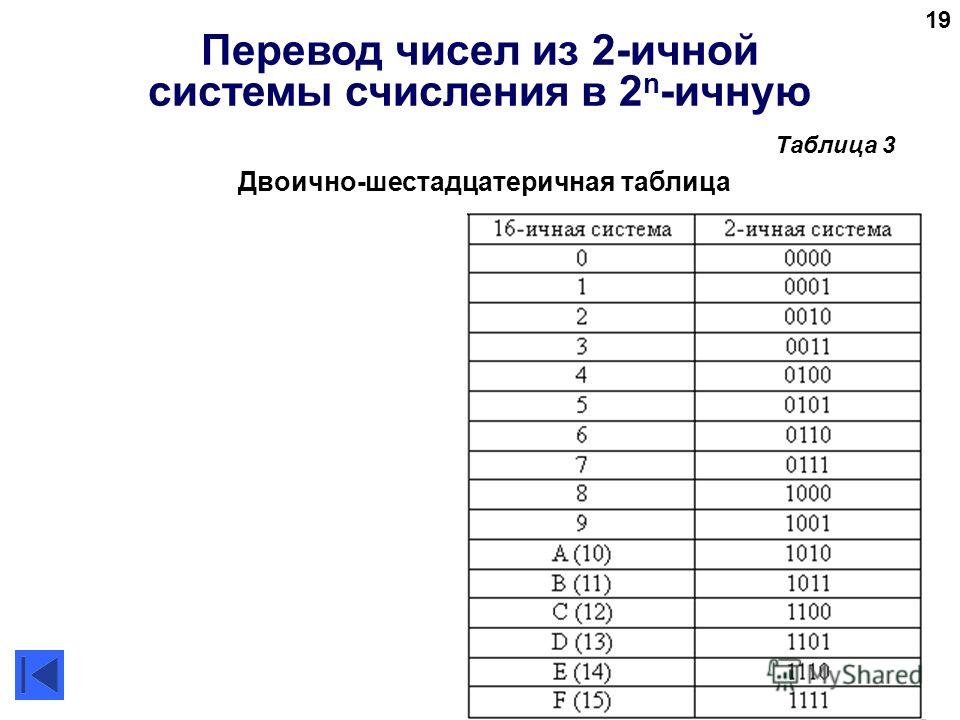
В идеале мы должны использовать двоичное представление, которое изначально поддерживает наши основные требования.
Как оказалось, есть тип данных, который выполняет: целых .
Целые числа демонстрируют переполнение, когда при увеличении их максимального значения они возвращаются к своему минимальному просто в результате их двоичного представления. Это именно то поведение, которое мы ищем.
Этот подход отнюдь не нов.
Фактически, в первые дни разработки игр это был предпочтительный способ управления направлениями. Также см. Этот пост Шона Харгривза по теме: Углы, целые числа и арифметика по модулю.
Этот пост включает небольшую функцию для преобразования угла числа с плавающей запятой в короткое (16-битное) целое число.Уловка заключается в том, что мы приравниваем угол 0 к целочисленному значению 0, а угол в 360 градусов — к целочисленному значению 2 16 .
Точно так же все углы между ними линейно представлены этим диапазоном целочисленных значений.
Оказывается, если мы попытаемся присвоить 2 16 короткому целому числу, это вызовет переполнение и приведет к 0, что нам и нужно.
Другими словами, мы (ab) используем арифметику по модулю, присущую двоичному представлению целого числа, чтобы обеспечить соблюдение классов эквивалентности по направлениям.
Некоторые возражения
Может показаться нелогичным использовать целое число в качестве значения — в данном случае направления — которое в действительности не имеет дискретных шагов. Мы хотим иметь возможность отображать любые углы, а не только их фиксированное количество.
Однако числа с плавающей запятой также имеют ограниченное количество значений, которые они могут представлять. Биты экспоненты числа с плавающей запятой, особенно когда они ограничены небольшим диапазоном, бесполезны для нас, и у нас остается около семи десятичных знаков точности мантиссы с плавающей запятой.
Использование короткого целого числа дает нам точность менее пяти десятичных знаков.
Однако для большинства приложений этого более чем достаточно, и мы можем просто использовать 32-битное целое число для девяти десятичных цифр.
Кроме того, при использовании целых чисел наши доступные значения распределяются равномерно в диапазоне доступных направлений, вместо того, чтобы смещаться в сторону низких числовых значений, как объяснено выше.
Код
Основной код нашего представления направлений прост.
Обратите внимание, что все следующие фрагменты являются (частично измененными) выдержками из полной реализации, которая находится в свободном доступе как часть общей библиотеки утилит C # Bearded.Utilities.
Полный код можно найти в типах Angle и Direction2 в src / Math.
Обратите внимание, что здесь используется точность 32 бита. Для большинства приложений 16 бит может быть более чем достаточно, и мы могли бы привести аргумент, что меньшие типы хороши для двоичной сериализации, например, для их отправки по сети.
Однако, если нет особых ограничений, 32 бита — беспроигрышный вариант.
В дальнейшем мы можем использовать следующие методы для преобразования между направленными векторами и направлениями.
Ниже следует основной тип, который мы будем использовать для представления углов.
Затем мы добавляем следующие перегрузки операторов к нашему типу направления, чтобы иметь возможность определять угол разницы между двумя направлениями и добавлять направление к углу. Здесь целочисленное представление показывает свои преимущества.
С помощью этой настройки мы можем реализовать метод TurnedTowards , который поворачивает направление к другому с заданным максимальным шагом.
Для того, что делает этот метод, он очень короткий и лаконичный. Воспользовавшись нашим целочисленным представлением, он также не требует дополнительных проверок на перенос и почти тривиально возвращает правильный результат.
Обратите внимание, что полная реализация еще более лаконична за счет использования большего количества настраиваемых операторов и методов.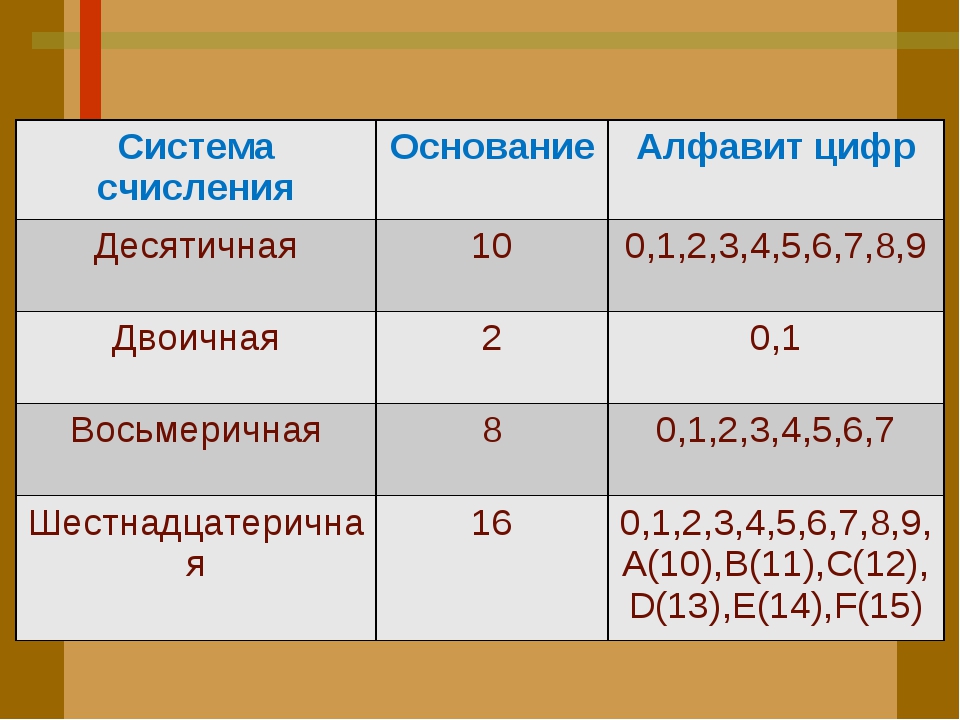
Результат
Используя только что созданные настраиваемые типы, приведенный выше пример псевдокода можно реализовать следующим образом.
Этот код ясно показывает наши намерения и читается практически так же, как наш псевдокод.
Нам не нужны дополнительные проверки — ни в этом коде, ни в базовых вызовах — и хотя я для краткости использую ключевое слово var , наш код полностью типобезопасен и семантически соответствует тому, что мы пытаемся выразить с его помощью.
Недостатки
Я уверен, что из сказанного выше ясно, что я — решительный сторонник этого подхода. Наряду с переносом направлений я считаю безопасность типов одной из самых сильных сторон.
Однако есть и недостатки.
Во-первых, такие типы нужно использовать неукоснительно, чтобы они действительно стоили того. Частое преобразование между безопасными и небезопасными универсальными типами может легко привести к раздуванию и сделать соответствующий код менее понятным.
Во-вторых, как показывают приведенные выше фрагменты, этот подход требует преобразования между целыми числами и числами с плавающей запятой для многих операций. Хотя это очень быстрое преобразование, оно может складываться и приводить к тому, что код может работать значительно медленнее.
Для большинства приложений последнее значение не имеет. Однако для кода, критичного к производительности, следует провести тщательные измерения, чтобы выяснить, перевешивает ли отсутствие проверок переноса большое количество приведений.
Тем не менее, если не удастся определить отрицательное влияние на производительность, я считаю этот возможный компромисс целесообразным.
Для меня повышенная читабельность и безопасность типов возвышают этот подход по сравнению с более простым использованием поплавков.
Заключение
Я хотел бы верить, что вышесказанное является хорошим аргументом в пользу описанного подхода.
Пожалуйста, дайте мне знать, что вы думаете в комментариях.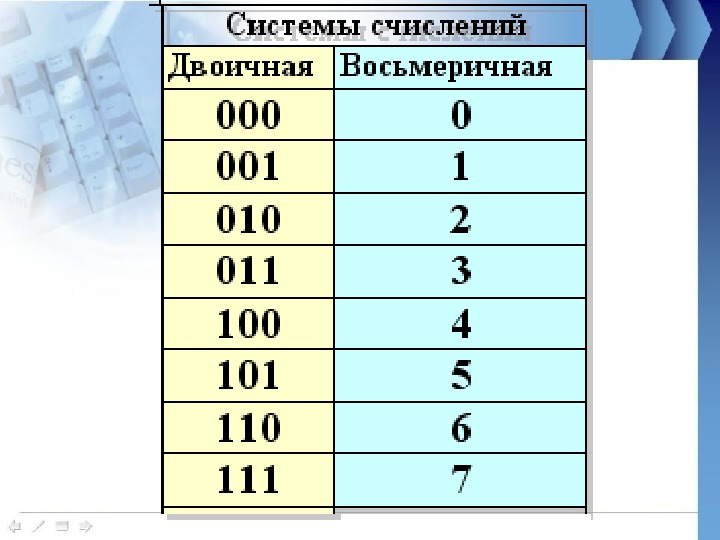
Особенно, если у вас есть опыт такого рода представительств и / или у вас есть аргументы за или против, которые я не упомянул выше, не стесняйтесь делиться ими ниже.
Если вас интересует более полная реализация с большим количеством дополнительных функций, обязательно ознакомьтесь с типами Angle и Direction2 в Bearded.Utilities.Math.
Этот код опубликован под лицензией MIT, так что можете использовать его как хотите.
Наслаждайтесь пикселями!
конвертировать двоичные градусы в обороты
конвертировать двоичные градусы в обороты и многое другое. Кроме того, изучите множество других конвертеров единиц измерения или узнайте больше о преобразовании единиц измерения угла, Сколько двоичных градусов в оборотах
таблица преобразования / таблица преобразования
1 двоичный градус = 0,0039 оборота
2 двоичных градуса = 0,0078 оборота
3 двоичных градуса = 0,0117 оборота
4 двоичных градуса = 0,0156 оборота
5 двоичных градусов = 0.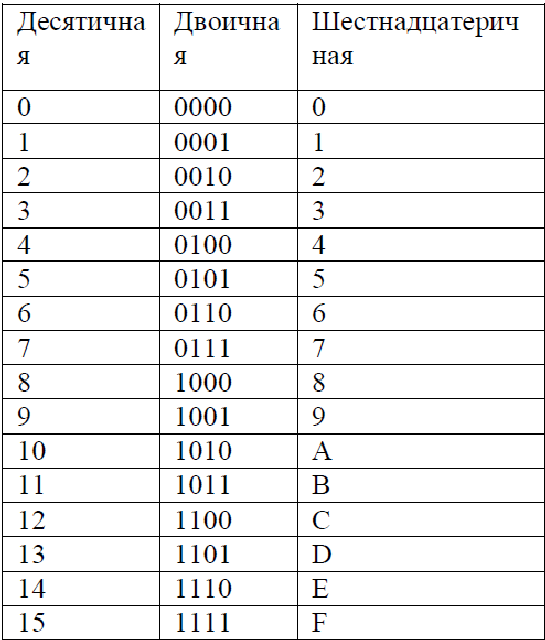
0195 Оборотов
6 двоичных градусов = 0,0234 оборота
7 двоичных градусов = 0,0273 оборота
8 двоичных градусов = 0,0312 оборота
9 двоичных градусов = 0,0351 оборота
10 двоичных градусов = 0,039 оборота
11 двоичных градусов = 0,0429 оборота
12 двоичных градусов = 0,0468 оборотов
13 двоичных градусов = 0,0507 оборота
14 двоичных градусов = 0,0546 оборота
15 двоичных градусов = 0,0585 оборота
16 двоичных градусов = 0.0624 Обороты
17 двоичных градусов = 0,0663 оборота
18 двоичных градусов = 0,0702 оборота
19 двоичных градусов = 0,0741 оборота
20 двоичных градусов = 0,078 оборота
21 двоичный градус = 0,0819 оборота
22 двоичных градуса = 0,0858 оборотов
23 двоичных градуса = 0,0897 оборота
24 двоичных градуса = 0,0936 оборота
25 двоичных градусов = 0,0975 оборота
26 двоичных градусов = 0,1014 оборотов
27 двоичных градусов = 0.
1053 витков
28 двоичных градусов = 0,1092 оборота
29 двоичных градусов = 0,1131 оборота
30 двоичных градусов = 0,117 оборота
31 двоичный градус = 0,1209 оборота
32 двоичных градуса = 0,1248 оборота
33 двоичных градуса = 0,1287 оборота
34 двоичных градуса = 0,1326 оборотов
35 двоичных градусов = 0,1365 оборотов
36 двоичных градусов = 0,1404 оборота
37 двоичных градусов = 0,1443 оборота
38 двоичных градусов = 0.1482 витков
39 двоичных градусов = 0,1521 оборот
40 двоичных градусов = 0,156 оборотов
41 двоичный градус = 0,1599 оборотов
42 двоичных градуса = 0,1638 оборотов
43 двоичных градуса = 0,1677 оборотов
44 двоичных градуса = 0,1716 оборотов
45 двоичных градусов = 0,1755 оборотов
46 двоичных градусов = 0,1794 оборота
47 двоичных градусов = 0,1833 оборота
48 двоичных градусов = 0,1872 оборота
49 двоичных градусов = 0.
1911 Оборотов
50 двоичных градусов = 0,195 оборота
50 двоичных градусов = 0,195 оборота
51 двоичных градусов = 0,1989 оборота
52 двоичных градуса = 0,2028 оборота
53 двоичных градуса = 0,2067 оборота
54 двоичных градусов = 0,2106 оборота
55 двоичных градусов 14 9145 Двоичные градусы = 0,2184 оборота
57 двоичных градусов = 0,2223 оборота
58 двоичных градусов = 0,2262 оборота
59 двоичных градусов = 0.2301 оборот
60 двоичных градусов = 0,234 оборота
61 двоичный градус = 0,2379 оборота
62 двоичных градуса = 0,2418 оборота
63 двоичных градуса = 0,2457 оборота
64 двоичных градуса = 0,2496 оборота
65 двоичных градусов = 0,2496 оборота
65 двоичных градусов = 0,2496 оборота
65 двоичных градусов
66 двоичных градусов = 0,2574 оборота
67 двоичных градусов = 0,2613 оборота
68 двоичных градусов = 0,2652 оборота
69 двоичных градусов = 0,2691 оборота
70 двоичных градусов = 0.
273 оборота
71 двоичный градус = 0,2769 оборота
72 двоичных градуса = 0,2808 оборота
73 двоичных градуса = 0,2847 оборота
74 двоичных градуса = 0,2886 оборота
75 двоичных градусов = 0,2925 оборота
76 двоичных градусов = 0,2925 оборота
77 двоичных градусов = 0,3003 оборота
78 двоичных градусов = 0,3042 оборота
79 двоичных градусов = 0,3081 оборота
80 двоичных градусов = 0,312 оборота
81 двоичных градусов = 0.3159 оборотов
82 двоичных градуса = 0,3198 витков
83 двоичных градуса = 0,3237 витков
84 двоичных градусов = 0,3276 витков
85 двоичных градусов = 0,3315 витков
86 двоичных градусов = 0,3354 витков
87 двоичных градусов = 0,3354 витков
87 двоичных градусов
88 двоичных градусов = 0,3432 оборота
89 двоичных градусов = 0,3471 оборота
90 двоичных градусов = 0,351 оборота
91 двоичных градусов = 0,3549 оборота
92 двоичных градусов = 0.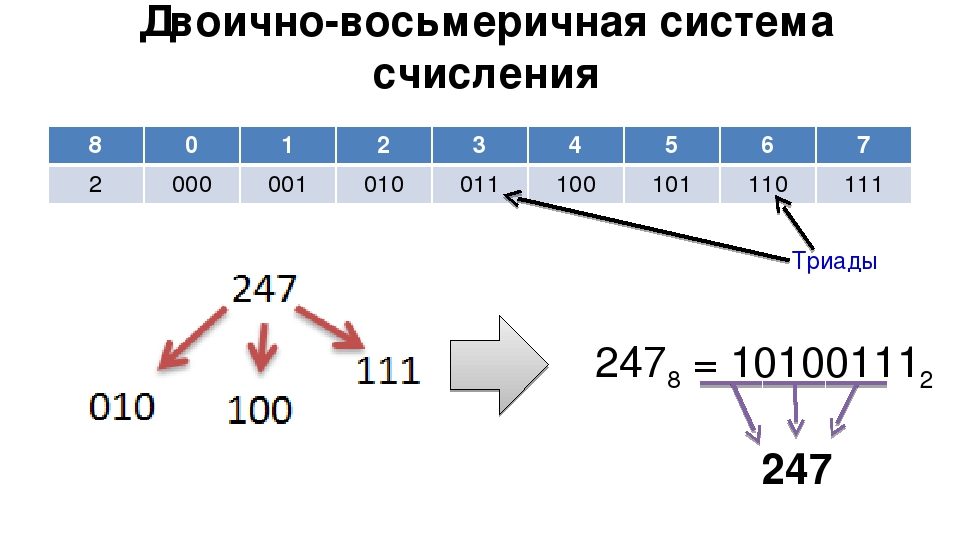
3588 оборотов
93 двоичных градуса = 0,3627 оборотов
94 двоичных градусов = 0,3666 оборотов
95 двоичных градусов = 0,3705 оборотов
96 двоичных градусов = 0,3744 оборотов
97 двоичных градусов = 0,3783 оборотов
97 двоичных градусов = 0,3783 оборотов
99 двоичных градусов = 0,3861 оборота
100 двоичных градусов = 0,39 оборота
101 двоичный градус = 0,3939 оборота
102 двоичный градус = 0,3978 оборота
103 двоичный градус = 0.4017 оборотов
104 двоичных градуса = 0,4056 оборотов
105 двоичных градусов = 0,4095 витков
106 двоичных градусов = 0,4134 витков
107 двоичных градусов = 0,4173 витков
108 двоичных градусов = 0,4212 витков
109 двоичных градусов = 0,4212 витков
109 двоичных градусов
110 двоичных градусов = 0,429 оборота
111 двоичных градусов = 0,4329 оборота
112 двоичных градусов = 0,4368 оборота
113 двоичных градусов = 0,4407 оборота
114 двоичных градусов = 0.
4446 оборотов
115 двоичных градусов = 0,4485 оборотов
116 двоичных градусов = 0,4524 витков
117 двоичных градусов = 0,4563 витков
118 двоичных градусов = 0,4602 витков
119 двоичных градусов = 0,4641 витков
120 двоичных градусов = 0,4641 витков
120 двоичных градусов
121 двоичный градус = 0,4719 оборота
122 двоичный градус = 0,4758 оборота
123 двоичный градус = 0,4797 оборота
124 двоичный градус = 0,4836 оборота
125 двоичных градусов = 0.4875 оборотов
126 двоичных градусов = 0,4914 витков
127 двоичных градусов = 0,4953 витков
128 двоичных градусов = 0,4992 витков
129 двоичных градусов = 0,5031 витков
130 двоичных градусов = 0,507 витков
131 двоичных градусов = 0,507 витков
131 двоичных градусов
132 двоичных градуса = 0,5148 оборота
133 двоичных градуса = 0,5187 оборота
134 двоичных градусов = 0,5226 оборота
135 двоичных градусов = 0,5265 оборота
136 двоичных градусов = 0.
5304 оборота
137 двоичных градусов = 0,5343 оборота
138 двоичных градусов = 0,5382 оборота
139 двоичных градусов = 0,5421 оборота
140 двоичных градусов = 0,546 оборота
141 двоичных градусов = 0,5499 оборотов
141 двоичных градусов = 0,5499 оборотов
14
143 двоичных градуса = 0,5577 оборота
144 двоичных градусов = 0,5616 оборота
145 двоичных градусов = 0,5655 оборота
146 двоичных градусов = 0,5694 оборота
147 двоичных градусов = 0.5733 витков
148 двоичных градусов = 0,5772 витков
149 двоичных градусов = 0,5811 витков
150 двоичных градусов = 0,585 витков
сколько двоичных градусов в оборотах
преобразовать двоичные градусы
витков
.