Значение косинуса: В прямоугольном треугольнике ABC угол C равен 90 градусов. Найдите значение косинуса угла А, если…

2

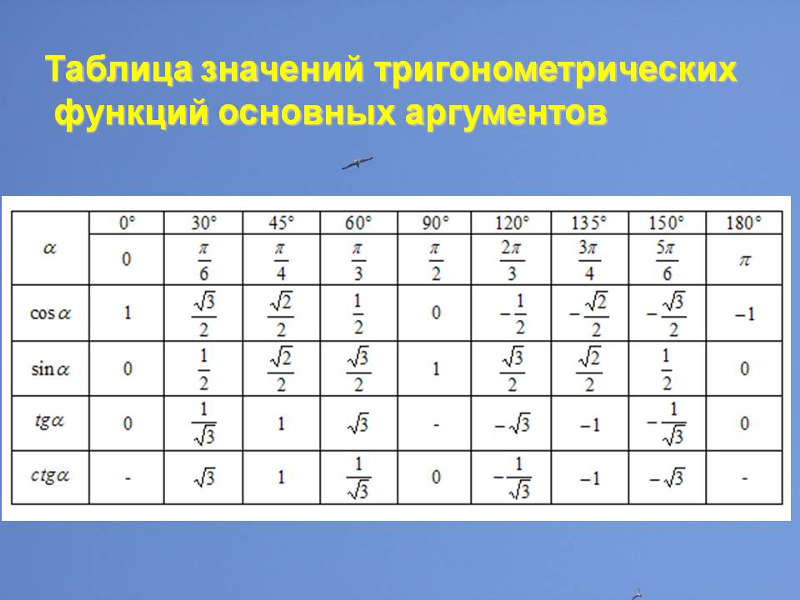
свойства и значения функции косинус

Оглавление

Время чтения:  4 минуты

803

Определения

Синусом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу катета к гипотенузе.

Синус угла А обозначается sin A.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к гипотенузе.

Косинус угла А обозначается cos A.

Наглядно это видно на следующем рисунке:

Функция косинуса: свойства и значения функции косинус

Определение

Функцией косинуса называют элементарную тригонометрическую функцию, выражающую зависимость угла при вершине треугольника от отношения прилежащей его стороны к гипотенузе.

• Основные свойства функции косинус следующие:
  1. Область определения функции косинуса (значений, которые может принимать аргумент x) – множество всех действительных чисел;
  2. Значения функции косинус – это (+1) и (-1) и множество действительных чисел между ними.
  3. Наименьшее значение функции косинус равно 1, а наибольшее – (-1);
  4. Функция чётная, т. е. cos(-x) = cos(x);
  5. Функция периодическая. Её период равен 2π;
  6. Наибольшего своего значения функция косинус x достигает в точках x=2πk;
  7. Наименьшее значение функции косинус x будет в точках x= π/2+2πk;
  8. Область возрастания функции cos(x): -π+2πk<=x<=2πk;
  9. Область убывания функции cos(x): 2πk<= π+2πk;
  10. Функция не имеет разрывов, т. е. непрерывна.

График функции косинус

Графиком функции является косинусоида. Он получается из графика синуса с помощью параллельного переноса на расстояние \[\frac{\pi}{2}\] влево. Он выглядит следующим образом:

Как построить график функции косинус икс

График функции косинуса можно построить следующим образом:

Используем данные единичной окружности, приведённой на рисунке выше.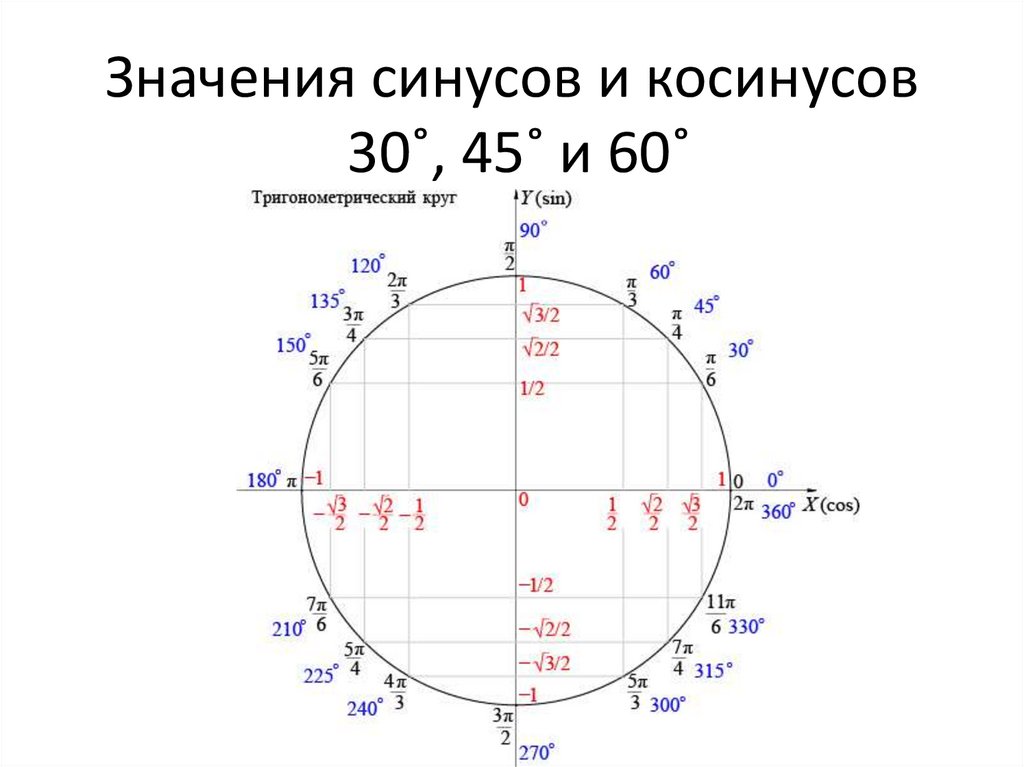

Из рисунка единичной окружности видно, что в точке ноль ордината функции равна единице. В точке π/2 по оси X значение Y равно 0. В точке π по оси X ордината равна (-1). В точке 3π/2 значение функции снова равно 0, а в точке 2π значение по оси X равно 1. Отметим все названные точки.

Соединим их плавной линией

Т. к. наша функция чётная (свойство №4), её график симметричен оси Y. Зеркально отразим его. Помимо этого нам известно, что период функции равен 2π. Из данного свойства следует неограниченная повторяемость кусочка функции между 0 и 2π в обе стороны вдоль оси X. График функции косинус x построен.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Как найти значение функции косинуса при x равном 45 градусам

Построим прямоугольный треугольник с катетами, равняющимися единице.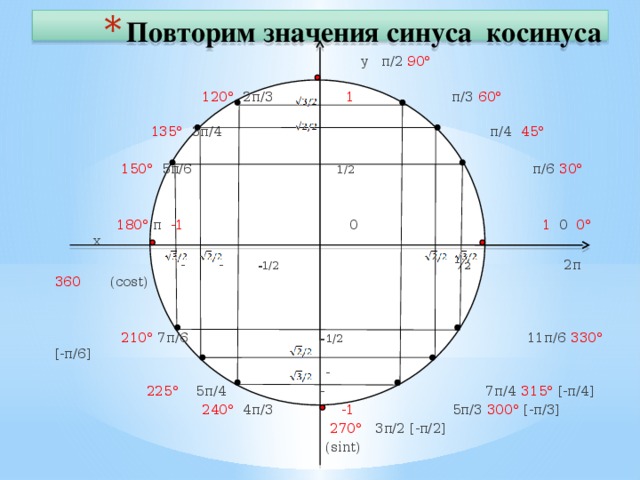 {2}}=\sqrt{1+1}=\sqrt{2}\]

Из определения косинуса находим \[\cos (a)=1 / \sqrt{2}\]

После вычисления и округления числа получим 0,7071. Это и есть косинус 45 градусов.

Оценить статью (0 оценок):

Поделиться

Федор Разовский — Кандидат математических наук

Популярные статьи

Выполнение любых работ по математике

Каковы выходные значения косинуса? (5 ключевых значений, которые нужно знать) — JDM Educational

В тригонометрии иногда встречаются общие входные углы (например, 45 или 90 градусов) для функции косинуса. Полезно знать соответствующие выходные данные для этих углов, чтобы быстрее выполнять расчеты.

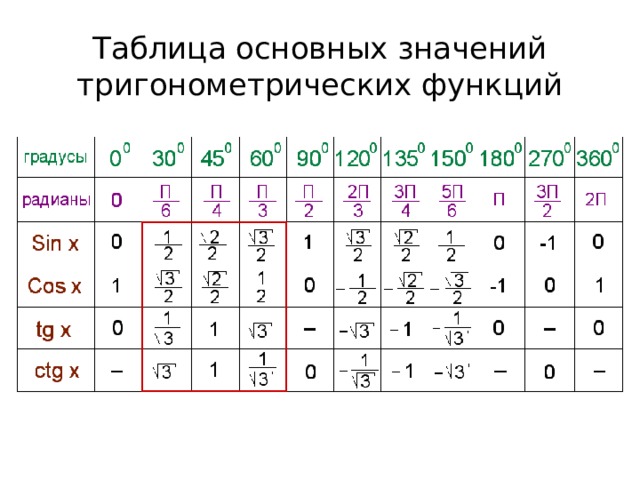
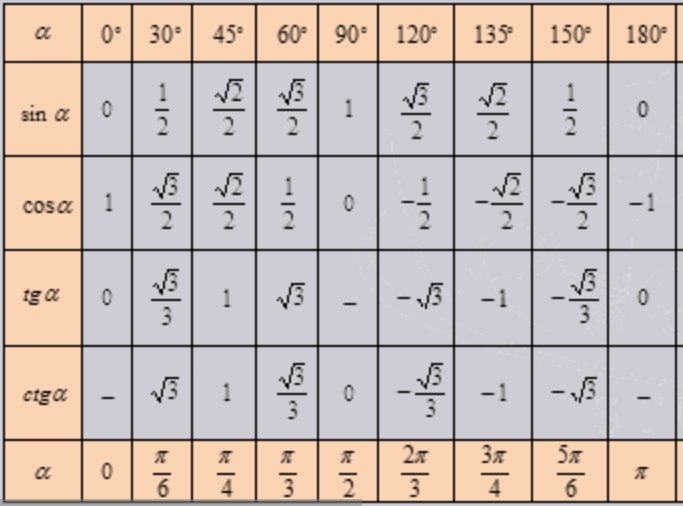
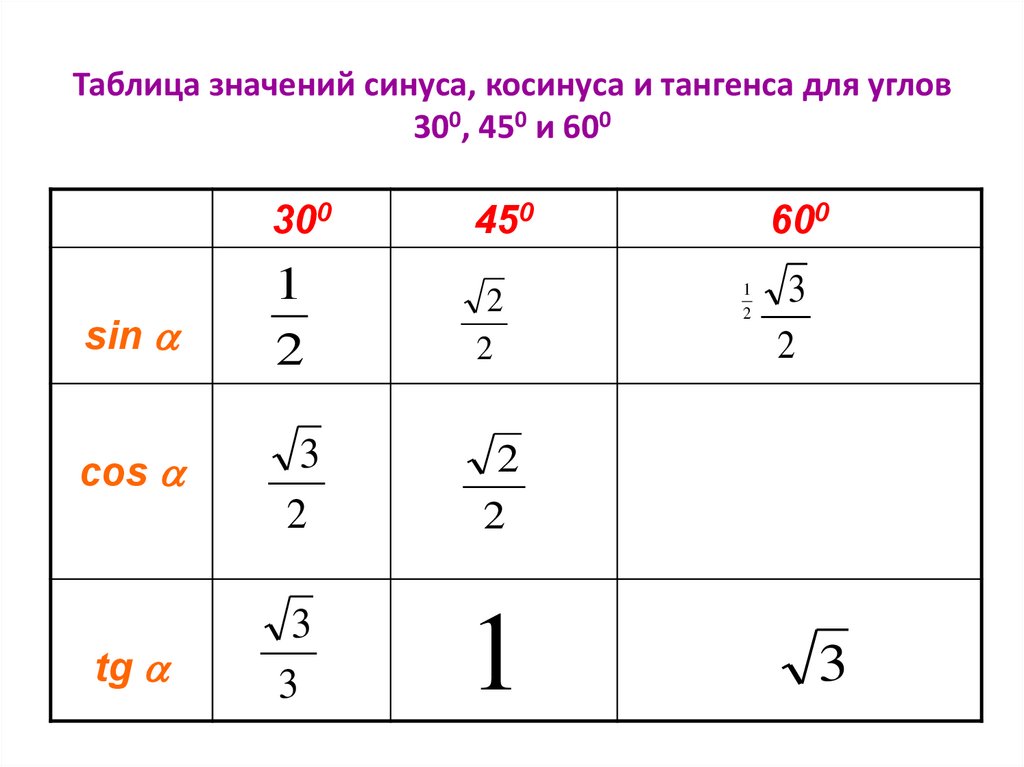
Итак, каковы выходные значения косинуса? Вы должны знать пять выходных значений косинуса: cos(0) = 1, cos(π/6) = √3/2, cos(π/4) = √2/2, cos(π/3) = 1/ 2, а cos(π/2) = 0 Эти выходные значения соответствуют общепринятым степенным мерам 0 ^или , 30 ^или , 45 ^или , 60 ^или , и 90 ^или . Использование отрицательного значения этих углов в качестве входных данных дает нам те же выходные данные.

Конечно, когда входной угол для косинуса находится в квадрантах 2 или 3 (углы между 90 ^o и 270 ^o , или от π/2 до 3π/2 радиан), мы получаем отрицательные значения для косинуса. Когда входной угол для косинуса находится в квадрантах 1 или 4 (углы между 0 ^o и 90 ^o или 270 ^o и 360 ^o ), мы получаем положительные значения косинуса.

В этой статье мы поговорим о некоторых выходных значениях косинуса и о том, как запомнить 5 распространенных из них, которые мы перечислили выше. Мы также рассмотрим знаки выходов для косинуса и когда они положительные, отрицательные или нулевые.

Начнем.

Какие выходные значения косинуса?

Выходные значения косинуса приведены в таблице ниже для 5 общих значений:

Угол [A]	Выход Значение из косинус [COS (A)]
0	1
30	a /2
60	1/2
90	0

Эта таблица показывает 5 общих
углов в 1 -м квадранте
и соответствующей выходе
значений.

В качестве простого способа запомнить значения обратите внимание, что каждое выходное значение имеет вид √n/2, где n изменяется от 4 до 0 по мере того, как мы переходим от градусных мер от 0 к 9.0 ^o (от 0 до π/2 радиан):

• Для 0 ^o : используйте n = 4, поэтому вывод будет sin(0 ^o ) = √4/2 = 2/2 = 1
• Для 30 ^o : используйте n = 3, поэтому результат будет sin(30 ^o ) = √3/2.
• Для 45 ^o : используйте n = 2, поэтому результат будет sin(45 ^o ) = √2/2.
• Для 60 ^o : используйте n = 1, поэтому результат будет sin(60 ^o ) = √1/2 = 1/2.
• Для 90 ^o : используйте n = 0, поэтому результат будет sin(90 ^o ) = √0/2 = 0/2 = 0.

Помните, что мы измеряем исходные углы от x оси, чтобы получить острый угол (менее 90 градусов).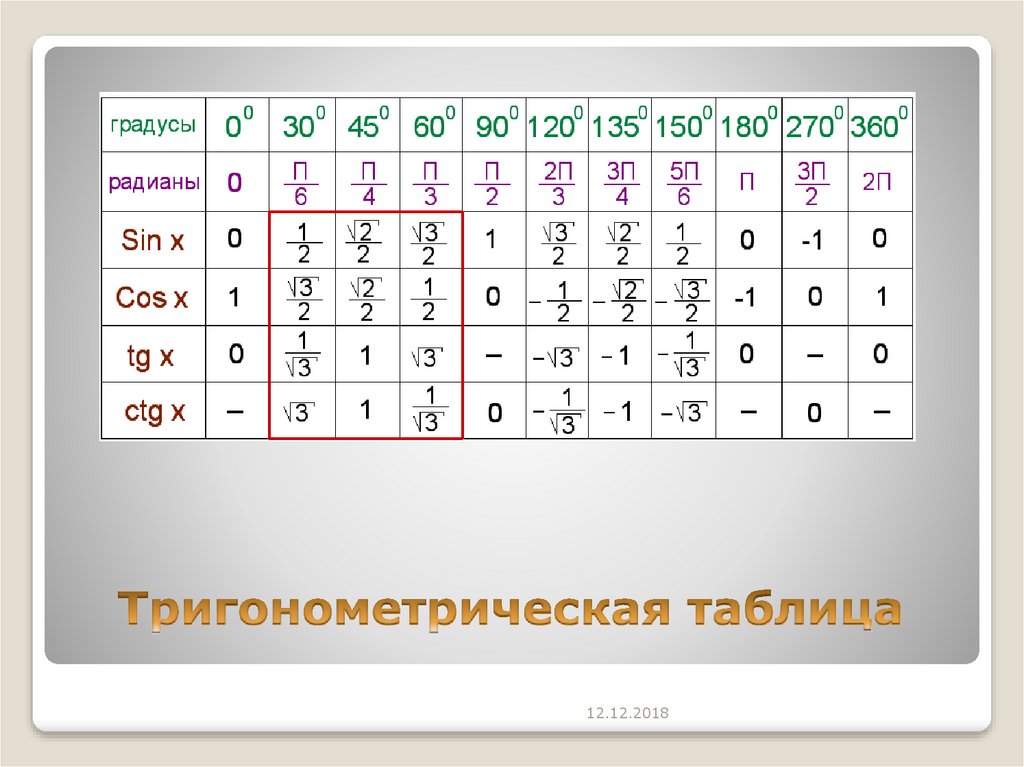 Это означает, что во 2-м квадранте мы вычитаем угол из 180 градусов (π радиан), чтобы получить исходный угол.

Что не может быть многочленом?

Пожалуйста, включите JavaScript

Что не может быть многочленом?

Также имейте в виду, что выходные значения косинуса отрицательны во 2-м квадранте.

Таким образом, в квадранте 2 ^и мы получим следующие исходные углы и выходные значения для косинуса:
Of
Cosine
[cos(A)] 180 0 -1 150 30 -√3/2 135 45 -√2/2 120 60 -1/2 90 90 0. функция.

В квадранте 3 ^rd мы вычитаем 180 градусов (π радиан) из угла, чтобы получить исходный угол.

Кроме того, выходные значения косинуса отрицательны в 3-м квадранте.

Итак, в 3-м квадранте мы получим следующие исходные углы и выходные значения для косинуса:

Angle [A]	Reference Angle [A’]	Output Value Of Cosine [cos(A)]
180	0	-1
210	30	-√3/2
225	45	-√2/2
240	60	-1/2
270	90	0

В этой таблице показаны 5 общих углов в третьем квадранте
и соответствующие эталонные углы
и выходные значения для функции косинуса.

В квадранте 4 ^th мы вычитаем угол из 360 градусов (2π радиан), чтобы получить исходный угол.

Кроме того, выходные значения косинуса положительны в 4-м квадранте.

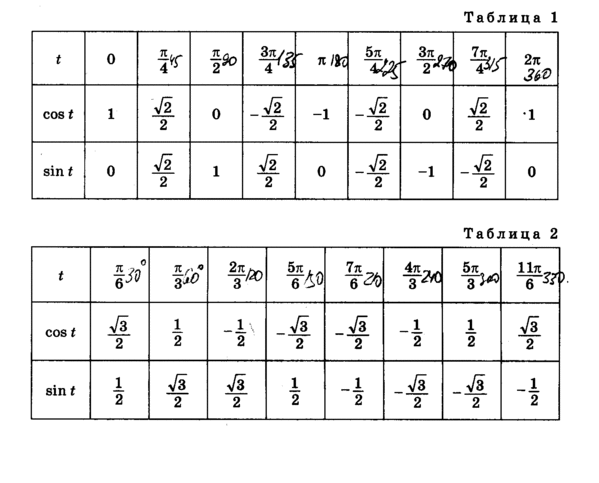
В четвертом квадранте мы получим следующие исходные углы и выходные значения для косинуса:

Angle [A]	Reference Angle [A’]	Output Value Of Cosine [cos(A)]
360	0	1
330	30	√3/2
315	45	√2/2
300	60	1/2
270	90	0

Эта таблица показывает 5 общих углов в
4-й квадрант и соответствующие опорные
углы и выходные значения для функции косинуса.

Наконец, помните, что для отрицательного угла мы добавляем 360 градусов (2π радиан), пока не получим угол между 0 ^o и 360 ^o .

Для угла больше 360 ^o делаем обратное и вычитаем 360 градусов (2π радиан), пока не получим угол между 0 ^o и 360 ^o .

Примеры выходных значений косинуса

Давайте рассмотрим несколько примеров, чтобы показать, как найти выходные значения косинуса для различных входных углов.

Пример 1: косинус в первом квадранте

Допустим, у нас есть угол A = 60 ^o , который находится в первом квадранте (он находится между 0 ^o и 90 ^o ).

Угол 60 градусов находится в первом квадранте (квадрант I). Мы можем посмотреть значение косинуса для 60 градусов в таблице.

Чтобы найти косинус угла A, все, что нам нужно сделать, это найти значение в первой таблице выше.

SO:

• COS (A)
• = COS (60 ^O )
• = 1/2

Пример 2: косини.

имеют угол A = 150 ^o , который находится во втором квадранте (между 90 ^o и 180 ^o ).

Чтобы найти косинус угла A, нам сначала нужно найти опорный угол A’. Во втором квадранте вычисляем

• a ’= 180 ^O —
• A’ = 180 ^O — 150 ^O
• A ’= 30 ^O

Угол 150 градусов находится во втором квадрате (квадрант II). Мы можем найти выходное значение опорного угла (30 градусов) в таблице косинусов.

Кроме того, мы знаем, что косинус имеет отрицательный выход в квадранте 2 ^и . Теперь нам нужно найти значение в первой таблице выше.

Итак:

• cos(A)
• = COS (150 ^O )
• = -COS (30 ^O ) [Используя наш контрольный угол, A ‘= 30 ^O , а косинус отрицательный в 2 ^ND ]
• = -√3/2   [cos(30 ^o ) = √3/2, из приведенной выше таблицы]

Пример 3.

Косинус в третьем квадранте

Предположим, что у нас есть угол A = 225 ^o , что находится в третьем квадранте (между 180 ^o и 270 ^или ).

Чтобы найти косинус угла A, нам сначала нужно найти опорный угол A’. В третьем квадранте мы рассчитываем

• a ‘= a — 180 ^O
• A’ = 225 ^O — 180 ^O
• A ‘= 45 ^O

A 225 Угла наклона 225 Угла. третий квадрант (квадрант III). Мы можем посмотреть значение опорного угла (45 градусов) в таблице косинусов.

Также мы знаем, что косинус имеет отрицательный выход в 3-м квадранте. Теперь нам нужно найти значение в первой таблице выше.

SO:

• COS (A)
• = COS (225 ^O )
• = -cos (45 ^O ) [Использование нашего опорного угла, A ‘= 45 ^O. , а косинус отрицателен в квадранте 3 ^rd ]
• =-√2/2   [cos(45 ^o ) = √2/2, из таблицы выше]

Пример 4: косинус В четвертом квадранте

Допустим, у нас есть угол A = 330 ^o , который находится в четвертом квадранте (он находится между 270 ^или и 360 ^или ).

Чтобы найти косинус угла A, нам сначала нужно найти опорный угол A’. В четвертом квадранте мы рассчитываем

• a ‘= 180 ^O —
• A’ = 360 ^O — 330 ^O
• A ‘= 30 ^O

Алгла 330 Угла Угла 330 степени четвертый квадрант (квадрант IV). Мы можем посмотреть значение опорного угла (30 градусов) в таблице косинусов.

Также мы знаем, что косинус имеет положительный выход в 4-м квадранте. Теперь нам нужно найти значение в первой таблице выше.

SO:

• COS (A)
• = COS (330 ^O )
• = COS (30 ^O ) [Использование нашего контрольного угла, A ‘= 30 0006 O ) , а косинус положителен в четвертом квадранте ^th ]
• =√3/2   [cos(30 ^o ) = √3/2, из таблицы выше]

Пример 5. Косинус A Отрицательный угол

Допустим, у нас есть угол A = -150 ^o , который является отрицательным. Итак, мы добавим 360 ^o , пока не получим угол между 0 ^o и 360 ^o .

Это дает нам B = -150 ^o + 360 ^o = 210 ^o .

Чтобы найти косинус угла A = -150 ^o , мы можем найти косинус угла B = 210 ^o (обратите внимание, что B = 210 ^o находится в квадранте 3 ^rd , так как это находится между 180 ^o и 270 ^o ).

Во-первых, нам нужно найти опорный угол B’. В третьем квадранте мы вычисляем

• B ‘= B -180 ^O
• B’ = 210 ^O -180 ^O
• B ‘= 30 ^O

A -150 Угол находится в третьем квадрате (четырех ) и эквивалентен углу в 210 градусов. Мы можем посмотреть значение опорного угла (30 градусов) в таблице косинусов.

Также мы знаем, что косинус имеет отрицательный выход в 3-м квадранте. Теперь нам нужно найти значение в первой таблице выше.

Итак:

• COS (A)
• = COS (B)
• = COS (210 ^O )
• = -COS (30 ^O ) [Используя наш контрольный угол, b ‘ = 30 ^o , а косинус отрицателен в квадранте 3 ^rd ]
• = -√3/2   [cos(30 ^o ) = √3/2, из таблицы выше] Пример 6. Косинус угла больше 360 ^o

  Допустим, угол A = 630 ^o , что больше 360 ^o . Итак, мы будем вычитать 360 ^o , пока не получим угол между 0 ^o и 360 ^o .

  Это дает нам B = 630 ^o – 360 ^o = 270 ^o .

  Чтобы найти косинус угла A = 630 ^o , мы можем найти косинус угла B = 270 ^o (обратите внимание, что B = 270 ^o находится на границе между 3 ^rd и 4 ^-й квадрантов, начиная с 270 ^или — это пороговое значение).

  Во-первых, нам нужно найти опорный угол B’. Мы рассчитываем

  • B ‘= B — 180 ^O
  • B’ = 270 ^O — 180 ^O
  • B ‘= 90 ^O
  Угол 630 градусов находится в третьем квадрате (квадрант. III) и эквивалентен углу в 270 градусов. Мы можем посмотреть значение опорного угла (90 градусов) в таблице косинусов.

  Также мы знаем, что косинус имеет отрицательный выход в 3-м квадранте. Теперь нам нужно найти значение в первой таблице выше.

  SO:

  • COS (A)
  • = COS (B)
  • = COS (270 ^O )
  • = -COS (90⁾
  • = -COS (90 ^O ) опорный угол, B’ = 90 ^o , а косинус в 3 ^rd квадранте отрицателен]
  • =0   [cos(90 ^o ) = 0, из таблицы выше]

  Вывод

  Теперь вы знаете больше о выходных значениях косинуса и о том, как они меняются при изменении входных углов. Вы также знаете, как определить знак выходных значений на основе квадранта входного угла.

  Здесь вы можете узнать о выходных значениях синуса.

  Вы можете узнать о выходных значениях тангенса здесь.

  Подробнее об использовании триггерных функций можно узнать здесь.

  Здесь вы можете научиться строить графики синусоидальных функций.

  Надеюсь, эта статья оказалась вам полезной. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.

  Не забудьте подписаться на наш канал YouTube и получать обновления о новых математических видео!

  Подпишитесь на наш канал на YouTube!

  ---

  значений комплексного косинуса

  Поскольку функция комплексного косинуса  z↦cos⁡z  имеет простой период2⁢π, косинус достигает всех своих возможных значений в одной из своих полос периодов, например, в полосе периодов

  {z∈ℂ⋮-π≦Re(z)<π}.

  (1)

  Чтобы выяснить, каких значений может достигать функция косинуса в полосе периодов, решаем уравнение  cos⁡z=w,  где w — любое комплексное число. Используя формулу Эйлера (http://planetmath.org/ComplexSineAndCosine)

  cos⁡z=ei⁢z+e-i⁢z2,

  уравнение может быть записано как

  (ei⁢z)2-2⁢w⁢ei⁢z+1= 0,

  (2)

  Это квадратное уравнение относительно ei⁢z, откуда мы получаем два корня (http://planetmath.

  org/Equation)

  ei⁢z=w±w2-1.

  Произведение корней равно 1, поэтому корни отличны от нуля при всех значениях w. Если мы поставим

  w+w2-1=rei⁢φ (-π≦φ<π),

  второй корень является обратным числом

  w-w2-1=1r⁢e-i⁢φ.

  Решение уравнения

  ei⁢z=r⁢ei⁢φ

  получается комплексным логарифмированием

  z=z1=1ilog(rei⁢φ)=φ-ilnr+n⋅2π (n∈ℤ),

  , а другое решение (2) равно

  z=z2=-φ+ilnr+n⋅2π (n∈ℤ).

  В полосе периодов (1) у нас есть одно решение z1 и одно решение z2, оба получены со значением  n=0  (за исключением z2 в случае  φ=-π  с  n=-1). В (1) точки z1 и z2 расположены симметрично относительно начала координат. В случаях   w=1  и   w=-1,  уравнение (2) имеет двойные корни  z=0  и   z=-π,  соответственно; то можно сказать, что z1 и z2 совпадают.

  Во всяком случае, у нас есть

  Теорема. В каждой полосе периодов косинус принимает любое комплексное значение в двух точках.
  

  Пример. Решение уравнения  cos⁡z=2  получается из  ei⁢z=2±3. В полосе периодов (1) получаем

  z=1i⁢log⁡(2±3)=-i⁢ln⁡(2±3)+0⋅2⁢π.

  Так как  2±3  являются обратными числами друг к другу, то мы имеем чисто мнимые числа z=±i⁢ln⁡(2+3).
  

  Из тригонометрии мы знаем, что действительные нули косинуса являются нечетными кратными π2; из этих точек ±π2 принадлежат полосе периодов (1). Таким образом, ±π2 — единственные точки (1), где косинус обращается в нуль. Поэтому, согласно предыдущей теореме, известные точки

  (2n+1)π2 (n= 0,±1,±2,…)

  — единственные нули функции косинуса на всей комплексной плоскости.
  

  Значения функции комплексного косинуса могут быть переведены в функцию комплексного синуса с помощью формулы дополнения

  sin⁡z=cos⁡(π2-z). No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт