Значение косинусов и синусов на окружности: Тригонометрические функции на единичной окружности. Синус и косинус — урок. Алгебра, 10 класс.

Onlinebrückenkurs Mathematik Abschnitt 5.6.3 Тригонометрия в единичном круге

• 5.6.1 Введение
• 5.6.2 Треугольник
• 5.6.3 Единичный круг
• 5.6.4 Упражнения

Глава 5 Геометрия

Раздел 5.6 Тригонометрические функции: синус и т. д.

В предыдущем разделе тригонометрические функции были представлены с помощью прямоугольного треугольника. Следовательно, описанные выше свойства справедливы для угла в диапазоне от 0° до 9°.0∘ или от 0 до π2 соответственно.
Чтобы распространить полученные знания на углы, превышающие π/2, особенно полезно исследовать так называемую единичную окружность.

Единичная окружность — это окружность с радиусом 1. Ее центр расположен в начале координат в декартовой системе координат. Рассмотрим отрезок длины 1, начинающийся из центра. Из своего горизонтального начального положения на положительной оси x этот сегмент теперь вращается против часовой стрелки, то есть в математическом положительном направлении, вокруг своего центра.

В этом процессе его вращающаяся конечная точка проходит по единичной окружности, охватывающей угол φ с положительной осью x. При вращении угол φ увеличивается от 0 до 2π или 360∘ соответственно. Таким образом, любому углу φ соответствует точка с координатами xφ и yφ на единичной окружности.
Для φ от 0 до π2 отрезок прямой, соответствующий отрезок на оси x и соответствующий отрезок на оси y можно рассматривать как прямоугольный треугольник. Гипотенуза — это отрезок длины 1, точка пересечения с осью X — это прилежащая сторона, а точка пересечения с Y — это противоположная сторона. Это соответствует ситуации, описанной в предыдущем разделе.
Следовательно, синус угла φ равен

sin(φ)=yφ1=yφ

, а косинус равен

cos(φ)=xφ1=xφ .

Основываясь на приведенном выше описании, эти определения теперь действительны и для углов φ>

π/2. Здесь значения xφ и yφ также могут быть отрицательными, следовательно, синус и косинус также могут быть отрицательными.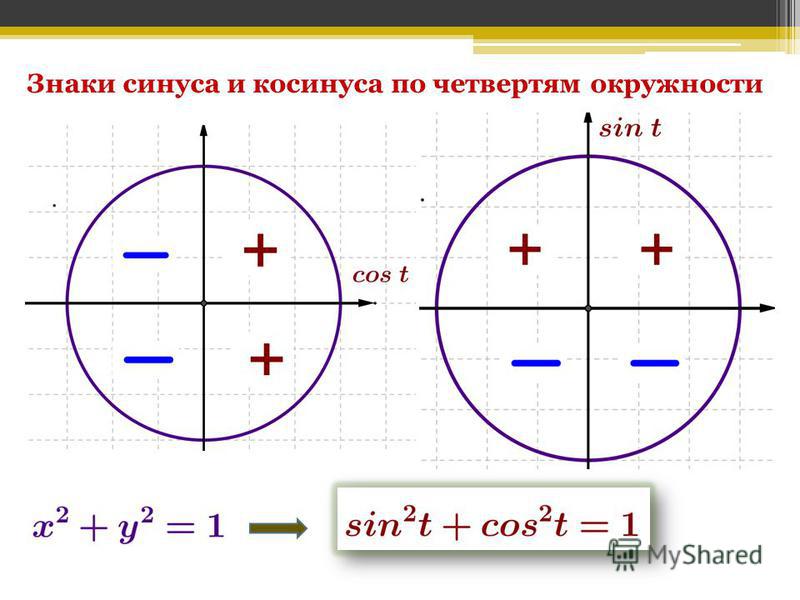 Если значения y нанести на график в зависимости от угла φ, можно получить для функции синуса синюю кривую. Откладывая значения y в зависимости от угла φ, можно получить для функции косинуса зеленую кривую. Если сегмент линии повернут в противоположном направлении, значения для отрицательных углов могут быть определены соответствующим образом.
Кроме того, по теореме Пифагора имеем

xφ2+yφ2=1 .

Замена xφ и yφ соответствующими соотношениями к тригонометрическим функциям приводит для любого φ к важному соотношению

sin2(φ)+cos2(φ)=1 .

Кроме того, из описания функции синуса и косинуса видно, что значения функции косинуса не изменяются, если отрезок линии отражается по оси x. Следовательно, значение косинуса угла φ равно значению косинуса угла -φ (обозначено на рисунке ниже зеленой линией). Для синусоидальной функции отражение поперек оси x приводит к изменению знака значения синуса (обозначено на рисунке ниже синей линией и фиолетовой линией соответственно)

Выраженное в формулах, это

cos(-φ)=cos(φ)      и      sin(-φ)=-sin(φ)

для каждого угла φ.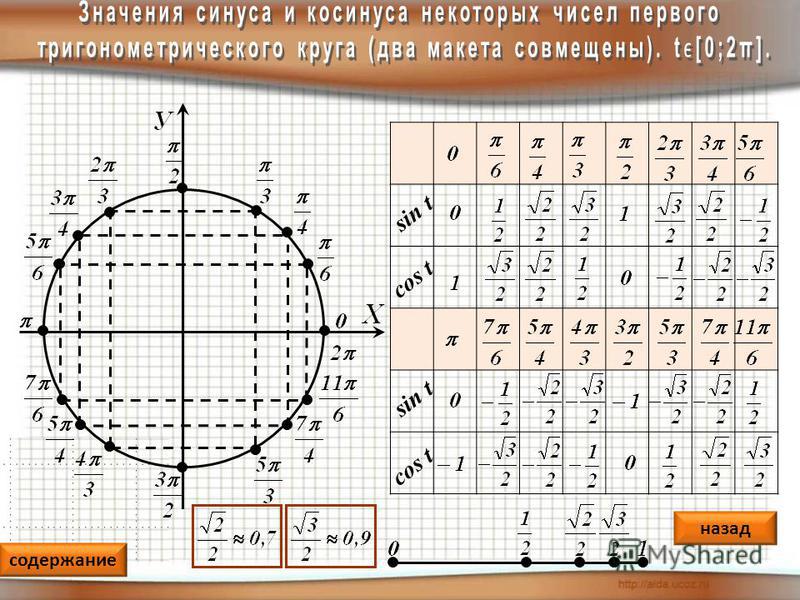 Эти свойства симметрии полезны для многих вычислений. Элементарным примером является вычисление угла между осью x и линией, соединяющей начало координат с точкой в ​​декартовой системе координат (см. также упражнение 5.6.9).

Пример 5.6.8

Найдите значения функции синуса, косинуса и тангенса угла α=315∘.
При α=315∘ точка Pα лежит в четвертом квадранте. На единичной окружности он также описывается отрицательным углом φ=315∘-360∘=-45∘. Таким образом, мы имеем sin(315∘)=sin(-45∘)=-sin(45∘)=122 и cos(315∘)=cos(-45∘)=cos(45∘)=122, а также tan (315∘)=загар(-45∘)=-1.

:

• Базовый
• Декартова система координат
• Косинус
• Определение
• Линейный сегмент
• Ордината
• Происхождение
• Пифагор
• Квадрант
• Отражение
• Прямоугольный треугольник
• Синус
• Тангенс
• Теорема
• Треугольник
• Тригонометрические функции
• Значение

Единица измерения Окружность Круговое определение (синус/косинус)

Отчет

• Детали
• Стандарты
• Библиотека ресурсов

Автор:

Энн Браун

Тема:

Средняя математика

Тип материала:

Урок

Уровень:

Средняя школа

Теги:

Единичный круг или тригонометрия

Войдите, чтобы добавить теги к этому элементу.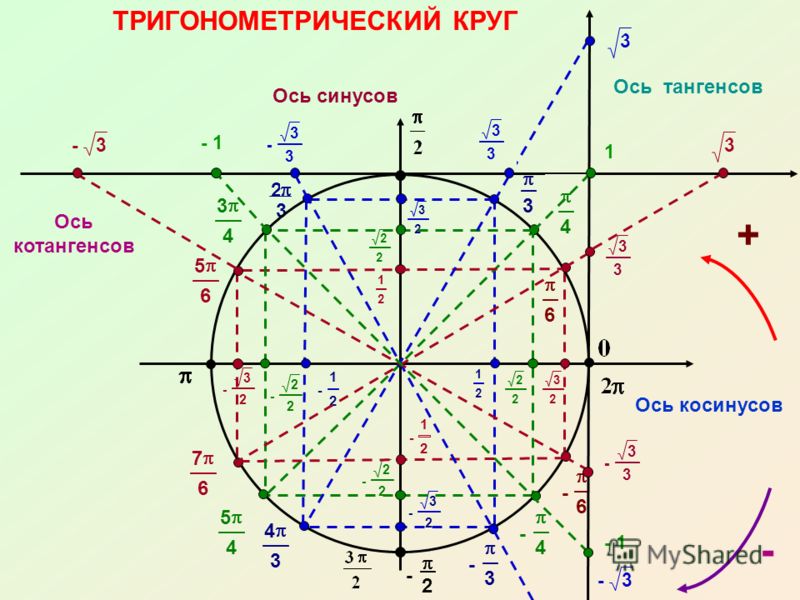

Лицензия:

Язык:

Форматы носителей:

Показать больше Скрыть

UT.MATH.III.F.TF.3 9–12 классы

Область обучения: Средняя математика III

Стандарт: Функции — тригонометрические функции

Индикатор: Используйте специальные треугольники для геометрического определения значений синуса, косинуса, тангенса для π/3, π/4 и π6 и используйте единичный круг, чтобы выразить значения синуса, косинуса и тангенса для π — x, π + x и 2π — x через их значения для x, где x — любое действительное число.

Этот урок предназначен для закрепления знаний учащихся с использованием кругового определения единичного круга. Студенты будут изучать и практиковать функции синуса и косинуса, чтобы найти их точные значения. Лицом к лицу или адаптируется для синхронного. Перед этим уроком учащиеся должны знать 2 специальных прямоугольных треугольника 30-60-90 и 45-45-90 и длины соответствующих сторон в общем виде.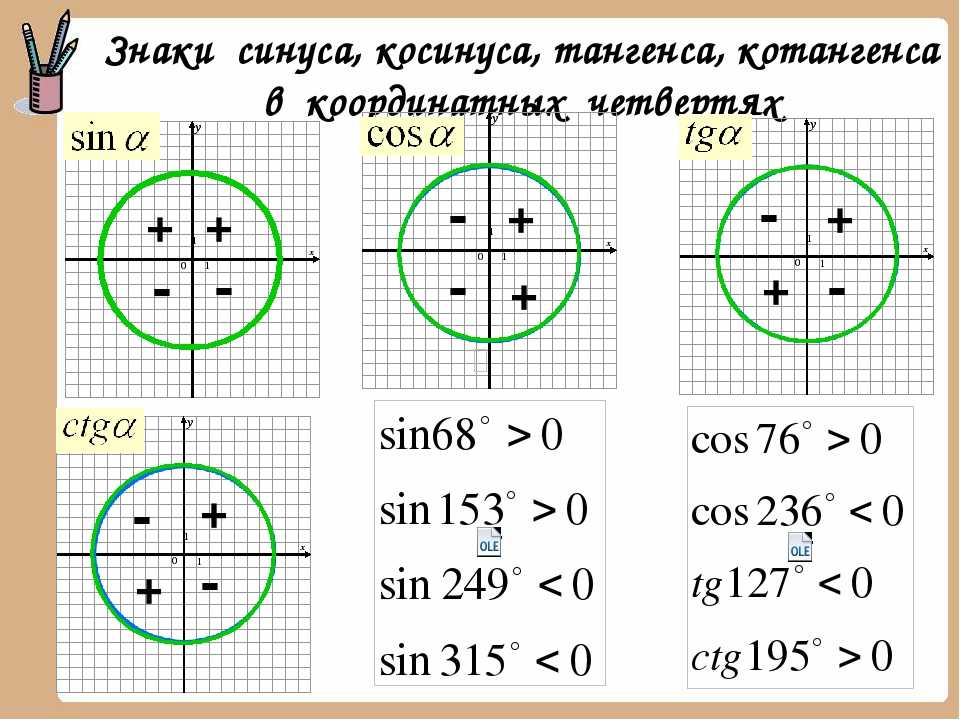 Учащиеся также должны знать градусы и радианы единичного круга. Для разных учащихся вы можете захотеть иметь шаблон двух специальных прямоугольных треугольников и использовать их, чтобы показать развитие точных значений во время проведения урока.

Резюме:

Этот урок предназначен для формирования знаний учащихся с использованием кругового определения единичного круга. Студенты будут изучать и практиковать функции синуса и косинуса, чтобы найти их точные значения.

Лицом к лицу или с возможностью адаптации для синхронного обучения

Справочная информация для учителей:

Для проведения этого урока учащимся потребуется доступ к онлайн-технологиям.

Учащиеся должны предварительно знать единичный круг в радианах, используя тригнометрию прямоугольного треугольника.

Приложены инструкции и ключ в качестве ссылки в Разделе 3 Инструкции.

Круговое определение единицы измерения (синус/косинус) Энн Браун имеет отметку CC0 1.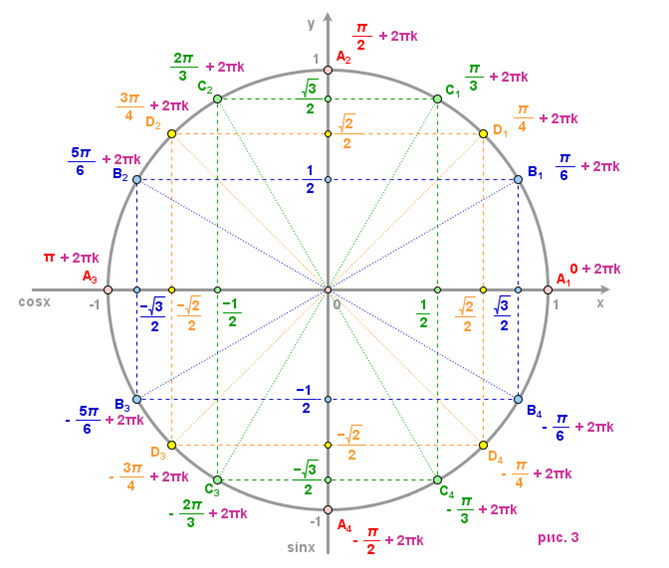 0.

Основные стандарты штата Юта по математике. используйте единичный круг, чтобы выразить эти значения.

 

Критерии обучения:

Учащиеся смогут связать особые прямоугольные треугольники с единичным кругом.

Критерии успеха:

Учащиеся смогут точно распознавать точные значения синуса и косинуса на единичном круге.

Инструкция по планированию:

До этого урока учащиеся должны знать 2 специальных прямоугольных треугольника 30-60-90 и 45-45-90 и длины соответствующих сторон в общем виде . Учащиеся также должны знать градусы и радианы единичного круга.

Для разных учащихся вы можете захотеть иметь шаблон 2 специальных прямоугольных треугольников и использовать их, чтобы показать развитие точных значений во время преподавания урока.

Время урока:

50-60 минут (может варьироваться в зависимости от времени обсуждения)

1) Время в малых группах: дайте учащимся время изучить, как создаются точные значения на единичном круге

• Как запомнить единичный круг (видео на YouTube)
• Ключ подсказки (см.

  No related posts.