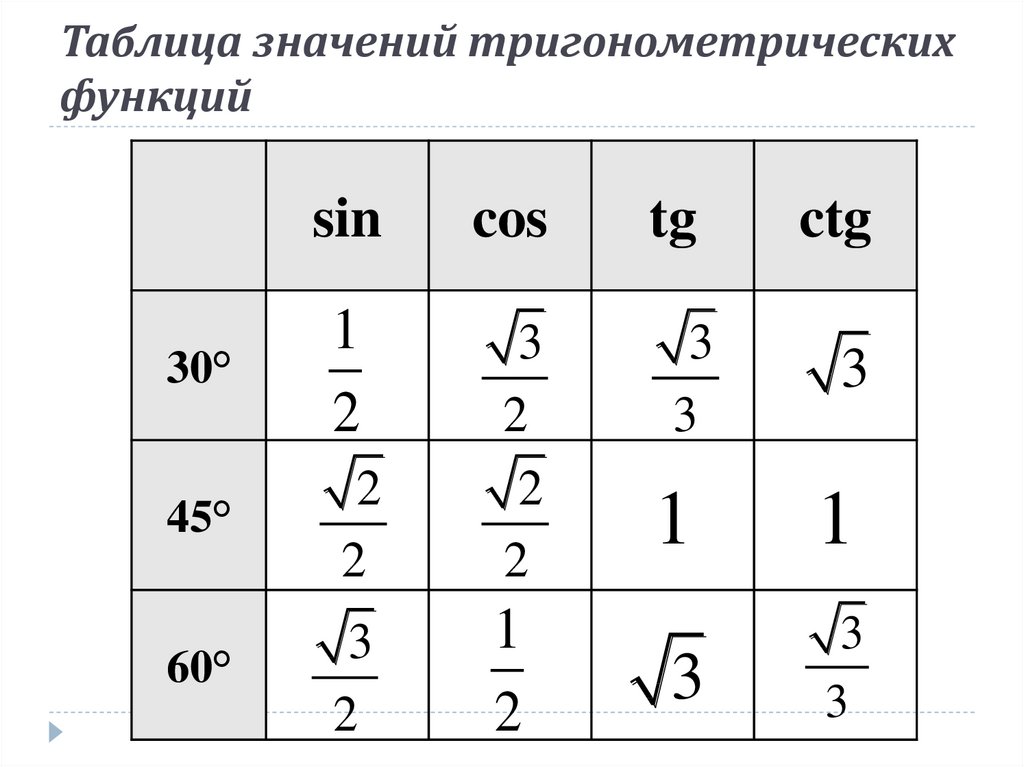
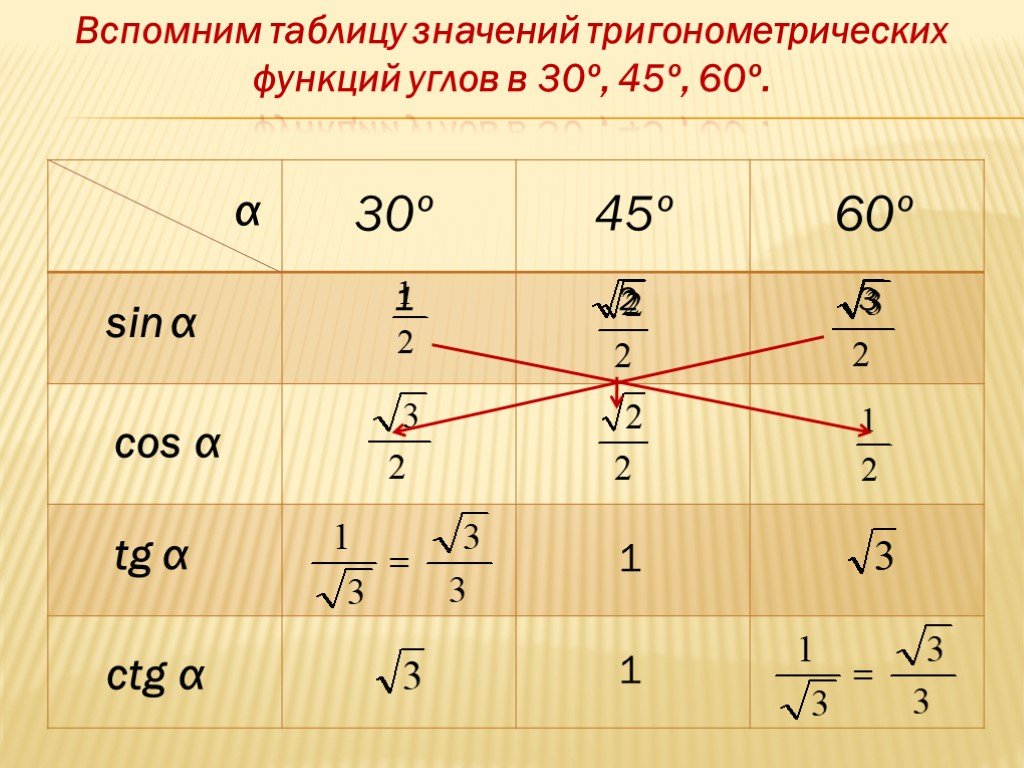
Тест на значения тригонометрических функций. по геометрии за 9 класс
Зарегистрируйся и получи 7 дней бесплатного доступа к тренажерам и персональный план прокачки знаний до 100%!
Вопросов в тесте: 18
Среднее время прохождения: ~10:00
Зарегистрируйся и получи персональный план прокачки знаний до 100%!
Как работает платформа Skills4u
Тестирование по предмету за класс
Платформа определит, какие темы сформированы слабо и составит индивидуальный план обучения
Персональный план обучения
План обучения и повторений поможет ученику в закреплении всех необходимых тем по предмету
Закрепление темы на 100%
Платформа напомнит и проконтролирует все повторения для закрепления каждой темы на 100%
Проработка слабых тем с предыдущих классов
Чтобы идеально овладеть предметом, рекомендуем закрепить пробелы, начиная с самых простых тем
Почему нужно пройти общее тестирование по геометрии за 9 класс, а не по отдельной теме «Значения тригонометрических функций.
Пройдя тестирование за класс вы получите ПОЛНУЮ КАРТИНУ ЗНАНИЙ ПО ВСЕМ ТЕМАМ.
Такой подход позволит глубинно проанализировать знания, вывести успеваемость и понимание предмета на качественно новый уровень.
Пройдя тестирование по одной теме вы получите РЕЗУЛЬТАТ ЗНАНИЙ ТОЛЬКО ЭТОЙ ТЕМЫ, которая, возможно, плохо изучена. Такой метод не является комплексным и дает лишь точечное понимание знаний по предмету.
Зарегистрироваться и пройти тестирование
Как растут результаты учеников
после занятий на тренажерах Skills4u
Занятия
на Skills4u
Занятия
с учебником
Успеваемость
Мотивация
Внимательность
Скорость
Самостоятельность
Запоминание
Первичный Тест «Значения тригонометрических функций.» по геометрии за 9 класс онлайн и бесплатно предоставляется всем желающим.
Советуем пройти тестирование за весь 9 класс по геометрии, чтобы узнать пробелы в знаниях по всем темам и получить индивидуальный план обучения.
После регистрации вы получите 7 дней бесплатного доступа, чтобы увидеть первые результаты занятий и оценить эффективность тренажеров.
Зарегистрироваться и пройти тестирование
А для комплексного результата пройдите общее тестирование за
класс! Узнайте пробелы в знаниях по всем темам
Ученик
Занимайся 20 минут в день и прокачай знания по школьной программе за месяц!
Родитель
Наслаждайтесь прогрессом вашего ребенка в школе и на платформе
Учитель/
репетитор
Зарегистрироваться и пройти тестирование
63055
учеников уже занимаются с нами
Числа рациональные и иррациональные
Числа рациональные и иррациональные
ОглавлениеОт редактораВведение ГЛАВА I. Натуральные и целые числа § 1. Простые числа § 2. Единственность разложения на простые множители § 3. Целые числа § 4. Четные и нечетные целые числа § 5. Свойства замкнутости § 6. Замечания о природе доказательства ГЛАВА II. Рациональные числа § 1. Определение рациональных чисел § 2. 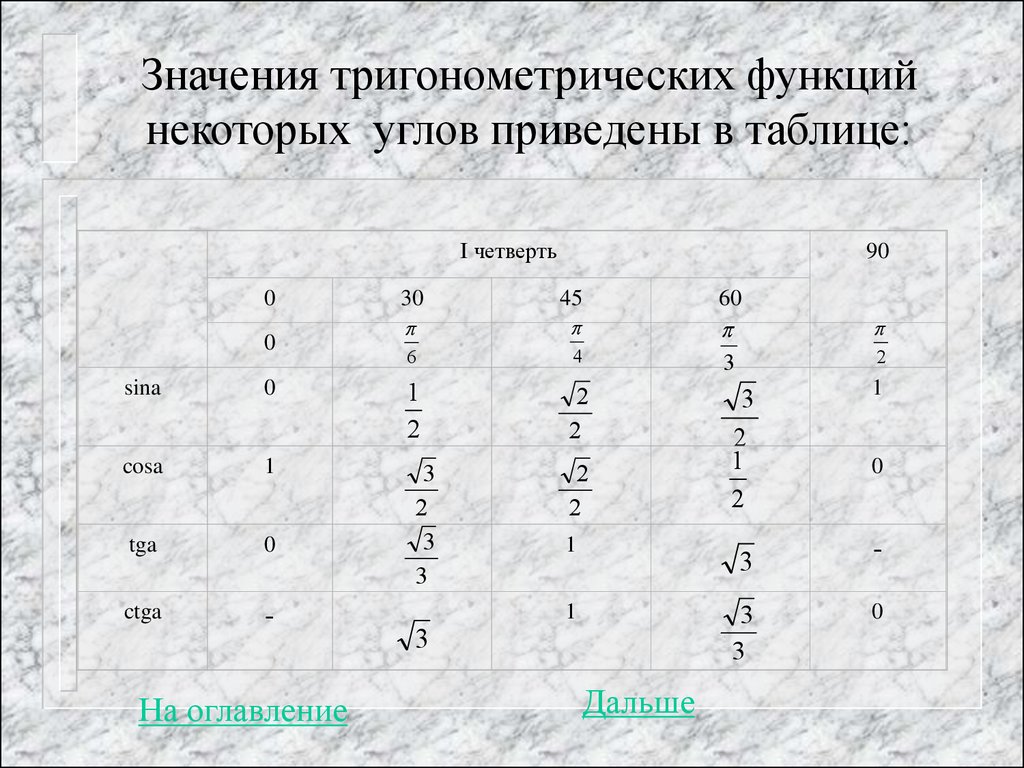 Конечные и бесконечные десятичные дроби§ 3. Различные сгюсобы формулировки и доказательства предложений § 4. Периодические десятичные дроби § 5. Всякую конечную десятичную дробь можно представить в виде периодической десятичной дроби ГЛАВА III. Действительные числа § 1. Геометрическая точка зрения § 2. Десятичные представления § 3. Иррациональность числа V2 § 4. Иррациональность числа V3 § 5. Иррациональность чисел V6 и V2+V3 § 6. Слова, которыми мы пользуемся § 7. Приложение к геометрии § 8. Краткие выводы ГЛАВА IV. Иррациональные числа § 1. Свойства замкнутости § 2. Алгебраические уравнения § 3. Рациональные корни алгебраических уравнений § 4. Дальнейшие примеры § 5. Краткие выводы ГЛАВА V. Значения тригонометрических и логарифмической функций § 1. Иррациональные значения тригонометрических функций § 2. Одно общее правило § 3. Иррациональные значения десятичных логарифмов § 4.  Трансцендентные числа§ 5. Три знаменитые задачи на построение § 6. Дальнейший анализ числа V2 § 7. Краткие выводы ГЛАВА VI. Приближение иррациональных чисел рациональными § 1. Неравенства § 2. Приближение целыми числами § 3. Приближение рациональными числами § 4. Лучшие приближения § 5. Приближения с точностью до 1/n2 § 6. Ограничения точности приближений § 7. Краткие выводы ГЛАВА VII. Существование трансцендентных чисел § 1. Предварительные сведения из алгебры § 2. Один способ приближения числа а § 3. План доказательства § 4. Свойства многочленов § 5. Трансцендентность числа а § 6. Краткие выводы ПРИЛОЖЕНИЕ А. Доказательство бесконечности числа простых чисел ПРИЛОЖЕНИЕ Б. Доказательство основной теоремы арифметики ПРИЛОЖЕНИЕ В. Доказательство Кантора существования трансцендентных чисел ПРИЛОЖЕНИЕ Г. Доказательство иррациональности значений тригонометрических фуннций И. М. Яглом Ответы и указания к упражнениям ПРИЛОЖЕНИЕ В Литература |
Числа рациональные и иррациональные
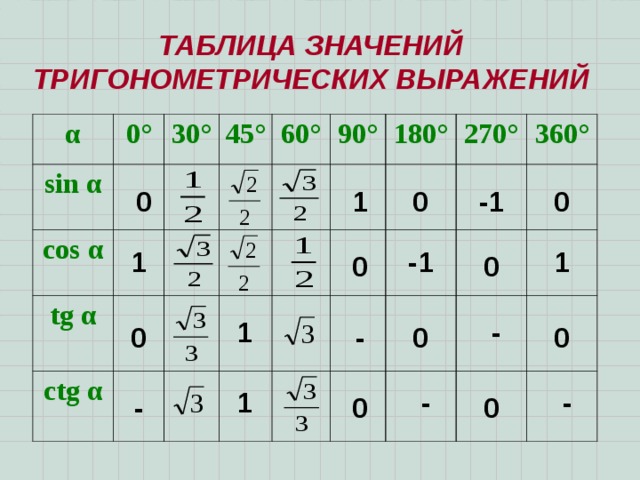
триггерных значений, кратных $\dfrac{\pi}{2}$
| $\тета$ | $\sin\тета$ | $\cos\тета$ | $\загар\тета$ | $\кот\тета$ | $\сек\тета$ | $\csc\тета$ |
| 0 | 0 | 1 | 0 | не определено | 0 | не определено |
| $\dfrac{\pi}{2}$ | 1 | 0 | не определено | 0 | не определено | 0 |
| $\пи$ | 0 | $-1$ | 0 | не определено | $-1$ | не определено |
| $\dfrac{3\pi}{2}$ | $-1$ | 0 | не определено | 0 | не определено | $-1$ |
Доказательство: Поскольку длина окружности равна
задается формулой $C=2\pi r$, длина окружности единичного круга равна $2\pi$.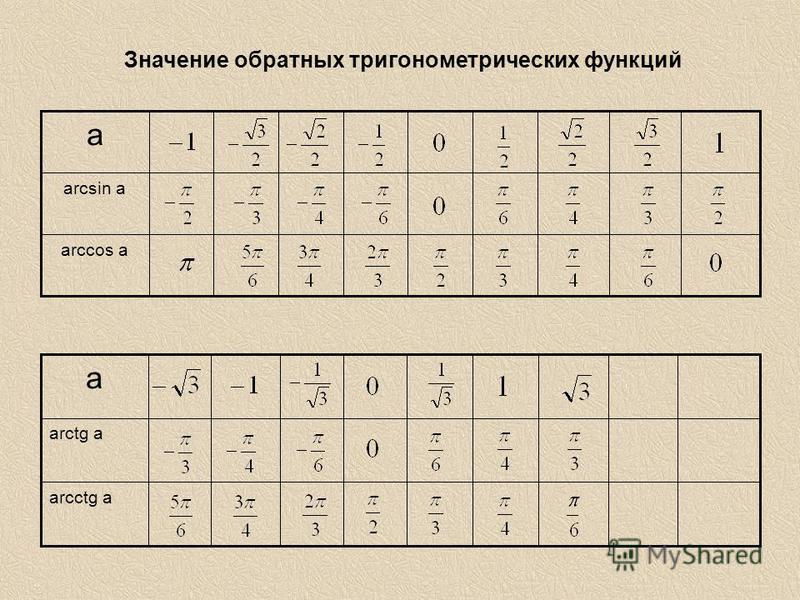
Одна четвертая часть этого расстояния, $\dfrac{\pi}{2}$, будет длиной дуги окружности между соседними осями координат. Следовательно, точка с координатами
$(0,1)$ будет соответствовать длине дуги $\dfrac{\pi}{2}$, а
Определение единичной окружности предоставит значения шести тригонометрических функций $\dfrac{\pi}{2}$. Доказательства для других длин дуг аналогичны.♦ 9\circ$. Потому что ни один из
эти значения являются острым углом, нет доказательства с участием треугольников
для этих значений.
триггерных значений кратных $\dfrac{\pi}{4}$
| $\тета$ | $\sin\тета$ | $\cos\тета$ | $\кот\тета$ | $\сек\тета$ | $\csc\тета$ | |||||||||||||||||
| $\dfrac{\pi}{4}$ | $\dfrac{\sqrt{2}}{2}$ 9\circ$. Предположим, что сторона $AC$ имеет длину 1. Тогда сторона $BC$ также имеет длину 1, и
по теореме Пифагора сторона $AC$ имеет длину $\sqrt{2}$. Ценности
для шести тригонометрических функций следует теорема о соотношениях треугольников.♦триггерных значений, кратных $\dfrac{\pi}{6}$
Доказательство: Пусть $A$ будет точкой $(1,0)$
на единичной окружности и выбираем точки $B$ и $C$
в первом квадранте так, что длина дуги $AB$ равна $\dfrac{\pi}{6}$, а длина дуги $AC$ равна $\dfrac{\pi}{3}$. Альтернативное доказательство: Пусть $ABC$ будет равносторонний треугольник. Пусть точка $D$ будет пересечением сторона $BC$ с высотой от вершины $A$. Посредством Теорема о гипотенузе-ноге геометрии, треугольники $ABD$ и $ACD$ конгруэнтны. Поэтому высота из $A$ делится пополам сторона $BC$. Если сторона $AB$ имеет длину 2, то $BD$ имеет длину 1, и по теореме Пифагора сторона $AD$ имеет длина $\sqrt{3}$. Шесть тригонометрических функций будут следовать теореме об отношениях треугольников.♦ В дополнение к этим основным значениям мы также можем определить точные значения функции синуса под углами, кратными 15 градусам и кратными 18 градусам. Все тригонометрические значения для прямоугольного треугольникаВсе тригонометрические значения для прямоугольного треугольника | Каналы Pearson+Последние каналы
Химия
Biology
Math
Физика
Бизнес
Социальные науки
Начните вводить текст, затем используйте стрелки вверх и вниз, чтобы выбрать вариант из списка.
by patrickJMT Похожие видео Родственные практики Тригонометрические функции для нахождения неизвестных сторон прямоугольных треугольников by patrickJMT 152views Что такое Soh-Cah-Toa? от Tammy Grigsby 323Views Тригонометрические функции: SINE, COSINE, TANGENT, COSECANT, SECANT и COTANGENT от профессора Дэйв. 201 просмотров Определение высоты объекта с помощью тригонометрии by patrickJMT 182views Тригонометрические функции: основы! от Patrickjmt 222Views Нахождение значений тригонометрических функций, приведенных в одном значении тригея в правом треугольнике от PatrickJMT 79Views Введение в тригонометрические функции с использованием Triangles . |
2=1$. Решение этой системы дает \
$\left(\dfrac{\sqrt{3}}{2},\dfrac12\right)$ как координаты точки $B$. Определение и основные
затем тождества производят значения шести тригонометрических
функции.♦
