Формула
Арксинус:
\[(y = arcsin x )\]
это функция, обратная к синусу ( x = sin y )
| Свойства функции | Функции y=arcsin х |
| E(f) | \[-1 \leq x \leq-1\] |
| D(f) | \[-\frac{\pi}{2}<y<\frac{\pi}{2}\] |
| наличие четности | Нечётная, т.к. arcsin(-x)= — arcsin x |
| характер графика направление | возрастание |
Формула
Арккосинус:
\[(y = arccos x )\]
это функция, обратная к косинусу ( x = cos y)
| Свойства | Функции y=arccos х |
| E(f) | \[-1 \leq x \leq-1\] |
| D(f) | \[0 \leq y \leq \pi\] |
| Чётность | Данное свойство ей не характерно. Иными словами, отсутствует. |
| Монотонность | Убывающая |
Формулы
Арктангенс:
\[(y = arctg x)\]
это функция, обратная к тангенсу (x = tg y)
Арккотангенс:
\[(y = arcctg x)\]
это функция, обратная к котангенсу ( x = ctg y)
| Свойства | y=arctg х | y=arcctg х |
| E(f) | R | R |
| D(f) | \[\left(-\frac{\pi}{2} ; \frac{\pi}{2}\right)\] | \[(0 ; \pi)\] |
| Чётность | Нечётная | Нечётная |
| Промежутки | Возрастающая | Убывающая |
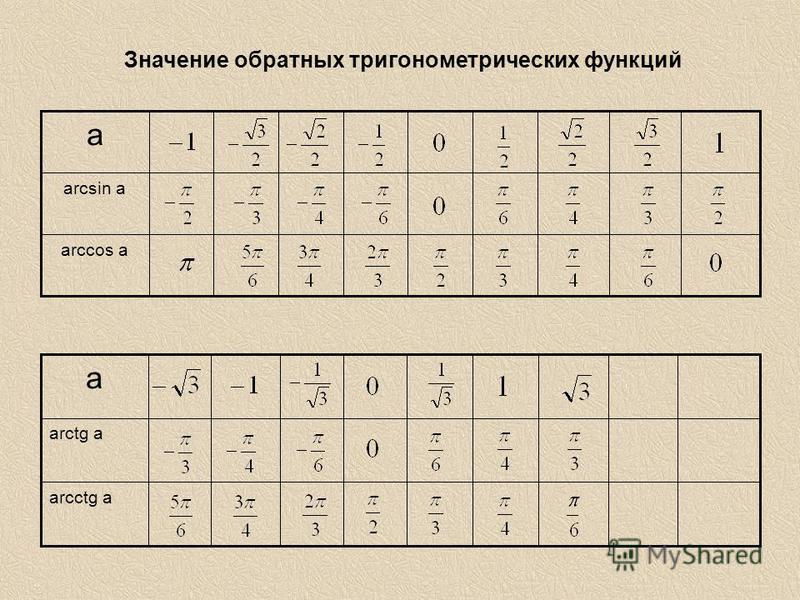
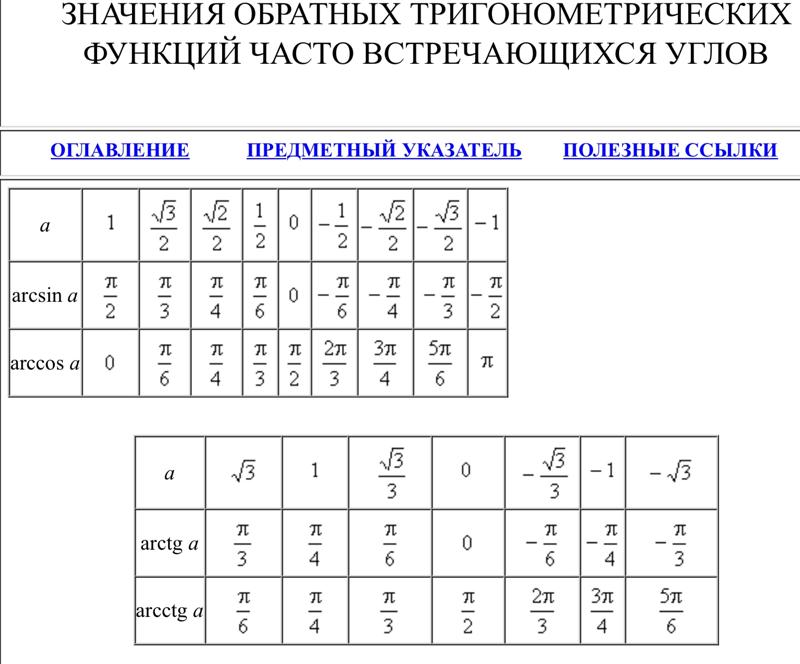
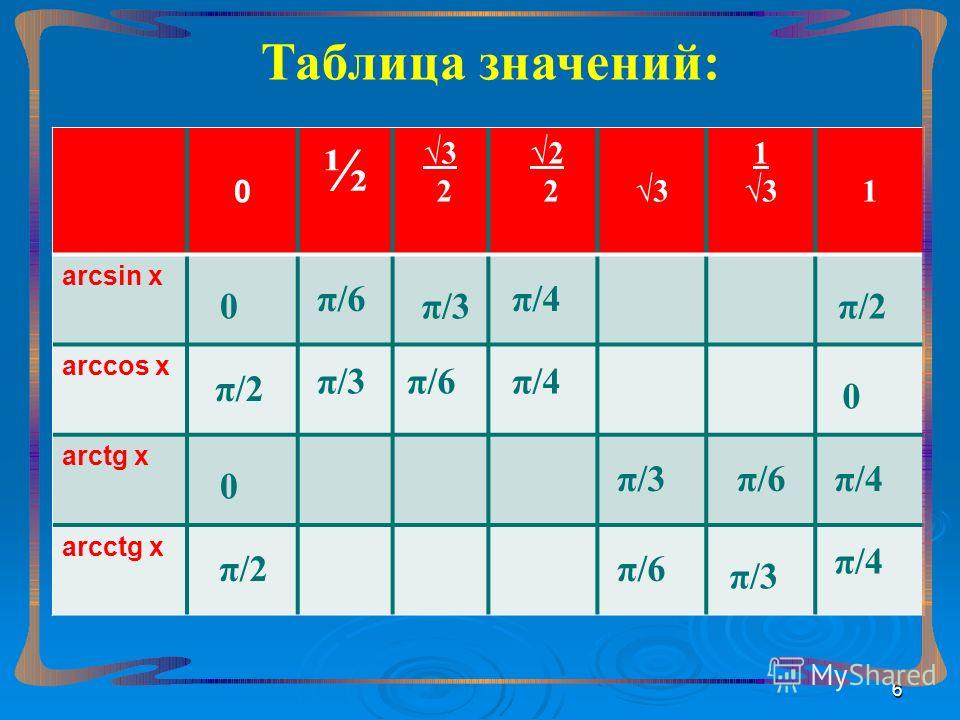
Главные значения: arcsin, arccos, arctg и arctg
Применяя таблицы определения значений прямых функций, мы имеем точные числовые значения для следующих углов. {\circ}=0..\]
{\circ}=0..\]
Учитывая данные вышеприведенной таблицы, можно вычислить необходимые для нас значения функций.
Для более практичного применения сведем все данные арксинуса в таблицу. Их необходимо запомнить, а лучше всего выучить наизусть. Так ка к ним придется возвращаться на постоянной основе.
| угол | -1 | \[-\frac{\sqrt{3}}{2}\] | \[-\frac{\sqrt{2}}{2}\] | \[-\frac{1}{2}\] | 0 | \[\frac{1}{2}\] | \[\frac{\sqrt{2}}{2}\] | \[\frac{\sqrt{3}}{2}\] |
| радианы | \[-\frac{\pi}{2}\] | \[-\frac{\pi}{3}\] | \[-\frac{\pi}{4}\] | \[-\frac{\pi}{6}\] | 0 | \[\frac{\pi}{6}\] | \[\frac{\pi}{4}\] | \[\frac{\pi}{3}\] |
| градусы | -90 | -60 | -45 | -30 | 0 | 30 | 45 | 60 |
| числовое значение | \[-\frac{\pi}{2}\] | \[-\frac{\pi}{3}\] | \[-\frac{\pi}{4}\] | \[-\frac{\pi}{6}\] | 0 | \[\frac{\pi}{6}\] | \[\frac{\pi}{4}\] | \[\frac{\pi}{3}\] |
Далее определимся с основными значения арккосинуса. {\circ}=1 . .\]
{\circ}=1 . .\]
Далее определяем нужные нам значения арккосинуса и сводим их в таблицу.
| угол | -1 | \[-\frac{\sqrt{3}}{2}\] | \[-\frac{\sqrt{2}}{2}\] | \[-\frac{1}{2}\] | 0 | \[\frac{1}{2}\] | \[\frac{\sqrt{2}}{2}\] | \[\frac{\sqrt{3}}{2}\] |
| радианы | \[\pi\] | \[-\frac{5\pi}{6}\] | \[-\frac{3\pi}{4}\] | \[-\frac{2\pi}{3}\] | \[\frac{\pi}{2}\] | \[\frac{\pi}{6}\] | \[\frac{\pi}{4}\] | \[\frac{\pi}{6}\] |
| градусы | 180 | 150 | 135 | 120 | 90 | 60 | 45 | 30 |
| числовое значение | \[\pi\] | \[-\frac{5\pi}{6}\] | \[-\frac{3\pi}{4}\] | \[-\frac{2\pi}{3}\] | \[\frac{\pi}{2}\] | \[\frac{\pi}{6}\] | \[\frac{\pi}{4}\] | \[\frac{\pi}{6}\] |
И напоследок остается вычислить значения арктангенса и арккотангенса. {\circ}=-\sqrt{3}…\]
{\circ}=-\sqrt{3}…\]
Далее все данные запишем в виде табличной формы.
Первая таблица для арктангенса
| угол | \[-\sqrt{3}\] | -1 | \[-\frac{\sqrt{3}}{2}\] | 0 | \[\frac{\sqrt{3}}{2}\] | 1 | \[\sqrt{3}\] |
| радианы | \[-\frac{\pi}{3}\] | \[-\frac{\pi}{4}\] | \[-\frac{\pi}{6}\] | 0 | \[\frac{\pi}{6}\] | \[\frac{\pi}{4}\] | \[\frac{\pi}{3}\] |
| градусы | -60 | -45 | -30 | 0 | 30 | 45 | 60 |
| числовое значение | \[-\frac{\pi}{3}\] | \[-\frac{\pi}{4}\] | \[-\frac{\pi}{6}\] | 0 | \[\frac{\pi}{6}\] | \[\frac{\pi}{4}\] | \[\frac{\pi}{3}\] |
Вторая таблица для арккотангенса
| угол | \[-\sqrt{3}\] | -1 | \[-\frac{\sqrt{3}}{2}\] | 0 | \[\frac{\sqrt{3}}{2}\] | 1 | \[\sqrt{3}\] |
| радианы | \[\frac{5\pi}{3}\] | \[\frac{3\pi}{4}\] | \[\frac{2\pi}{6}\] | \[\frac{\pi}{2}\] | \[\frac{\pi}{3}\] | \[\frac{\pi}{4}\] | \[\frac{\pi}{6}\] |
| градусы | 150 | 135 | 120 | 90 | 60 | 45 | 30 |
| числовое значение | \[\frac{5\pi}{3}\] | \[\frac{3\pi}{4}\] | \[\frac{2\pi}{6}\] | \[\frac{\pi}{2}\] | \[\frac{\pi}{3}\] | \[\frac{\pi}{4}\] | \[\frac{\pi}{6}\] |
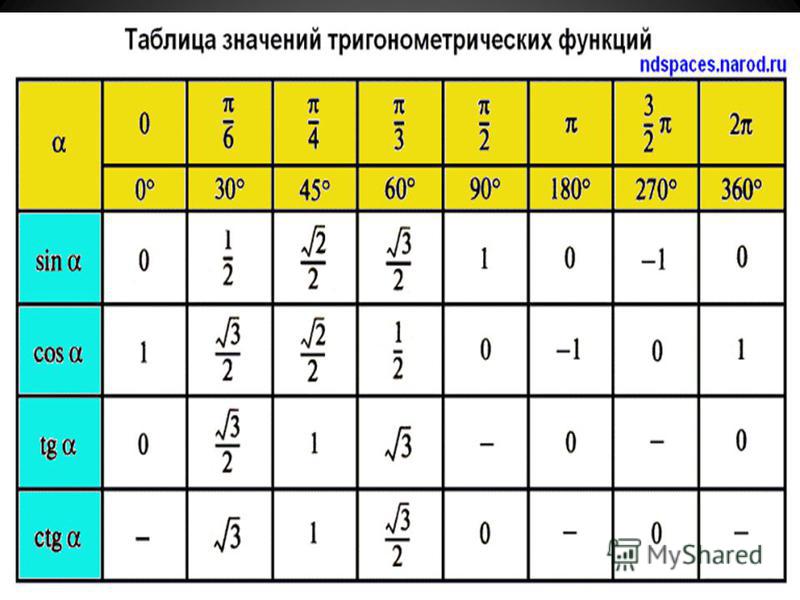
Рассмотрим, также значения для нестандартных угловых значений и сведем их в таблицу.
| угол | \[\pi / 12=15\] | \[\pi / 10=18\] | \[\pi/8 = 22,5 \] | \[\pi / 5=36\] | \[3 \pi / 10=54\] | \[3 \pi / 8=67,5\] | \[2 \pi / 5=72\] |
| sin | \[\sqrt{3}-1 / 2 \sqrt{2}\] | \[\sqrt{5}-1 / 4\] | \[\sqrt{2-\sqrt{2 / 2}} ;\] | \[\sqrt{5-\sqrt{5} / 2 \sqrt{2}}\] | \[\sqrt{5}+1 / 4\] | \[\sqrt{2+\sqrt{2 / 2}}\] | \[\sqrt{5+\sqrt{5} / 2 \sqrt{2}}\] |
| cos | \[\sqrt{3}-1 / 2 \sqrt{2}\] | \[\sqrt{5+\sqrt{5 / 2 \sqrt{2}}}\] | \[\sqrt{2+\sqrt{2 / 2}}\] | \[\sqrt{5}+1 / 4\] | \[\sqrt{5-\sqrt{5 / 2 \sqrt{2}}}\] | \[\sqrt{2-\sqrt{2 / 2}}\] | \[\sqrt{5}-1 / 4\] |
| tg | \[2-\sqrt{3}\] | \[\sqrt{1-\frac{2}{\sqrt{5}}}\] | \[\sqrt{\frac{\sqrt{2}-1}{\sqrt{2}+1}}\] | \[\sqrt{5-2 \sqrt{5}}\] | \[\sqrt{1+\frac{2}{\sqrt{5}}}\] | \[\sqrt{\frac{\sqrt{2}+1}{\sqrt{2}-1}}\] | \[\sqrt{5+2 \sqrt{5}}\] |
| ctg | \[2+\sqrt{3}\] | \[\sqrt{5+2 \sqrt{5}}\] | \[\sqrt{\frac{\sqrt{2}+1}{\sqrt{2}-1}}\] | \[\sqrt{1+\frac{2}{\sqrt{5}}}\] | \[\sqrt{5+-2 \sqrt{5}}\] | \[\sqrt{\frac{\sqrt{2}-1}{\sqrt{2}+1}}\] | \[\sqrt{1-\frac{2}{\sqrt{5}}}\] |
В данной таблице приведены значения углов. которые считаются нестандартными. также таблица необходима, чтобы облегчить жизнь, в первую очередь, школьной программе.
которые считаются нестандартными. также таблица необходима, чтобы облегчить жизнь, в первую очередь, школьной программе.
Все приведенные таблицы значений имеют очень большую роль в процессе решения. Их необходимо заучить наизусть и постоянно для проверки повторять.
Основные способы, которые помогут заполнить таблицу функций тригонометрии
Необходимо изобразить простую таблицу, где будет несколько столбцов и строк, необходимых для заполнения данных. Следующая задача, состоит в том, что нужно пустые графы заполнить. Записываем в первом столбике значение математических функций, ранее нами изученных.
В начальной строке, должны отображаться самые часто используемые значения углов: от нуля до девяноста градусов и так далее.
Оставшиеся ячейки нужно оставить незаполненными, для следующих действий. Чтобы понять тригонометрию, нужно изучать не только основные функции. Стоит уделить внимание и таким функциях как: косеканс (cosec) и секанс(sec).
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Нахождение значения arcsin через arccos, arctg, arcctg по таблицам Брадиса
Первое упоминание о таблице, датируется 20-ми годами прошлого века. Основоположником, является советский ученый математик, и талантливый педагог Владимир Брадис.
Основоположником, является советский ученый математик, и талантливый педагог Владимир Брадис.
Созданная Брадисом таблица, позволяет определить значения тригонометрических функций, с большой точностью, а именно до четырех знаков.
На практике решений, обычно требуется точность в три-четыре знака, после запятой, но не более. Для расчета, с такой точностью, значение синуса, в формуле достаточно трех известных слагаемых, а иногда и двух. Произвести простых четыре перемножения. Дважды разделить, умножить и отнять.
Если производить действия инженерным калькулятором, становится понятно, что все вышеперечисленные действия, уже запрограммированы в его микросхеме.
В таблице представлены следующие данные:
- число в квадратной и кубической степени;
- числа квадратных корней;
- логарифмические функции и значение;
- функции тригонометрии, представленный в градусах и радианах;
- обратные функции.
Таблица Брадиса, очень часто применяется в строительных целях. Она имеет большую популярность в инженерном проектировании. Проектирование зданий и сооружений тесно связано с таблицами Брадиса. При разработке проектов, ею пользуются при расчете подпорных стенок. Особенно это актуально при проектировании многоярусных набережных. Для проектирования и расчета сооружений. Например, для уточнения высоты или ширины. Создавая проект, не всегда есть доступ в интернет и поэтому обычный инженерный калькулятор в помощь строителям. Можно самому рассчитать обычный каркас, изобразить в виде чертежа. И самостоятельно создать простое, малых параметров сооружение.
Она имеет большую популярность в инженерном проектировании. Проектирование зданий и сооружений тесно связано с таблицами Брадиса. При разработке проектов, ею пользуются при расчете подпорных стенок. Особенно это актуально при проектировании многоярусных набережных. Для проектирования и расчета сооружений. Например, для уточнения высоты или ширины. Создавая проект, не всегда есть доступ в интернет и поэтому обычный инженерный калькулятор в помощь строителям. Можно самому рассчитать обычный каркас, изобразить в виде чертежа. И самостоятельно создать простое, малых параметров сооружение.
Можно определить точность углового значения до минуты. Существуют также таблицы, где есть семизначные значения.
Для того чтобы составить таблицы ученый пользовался методом: разложения функций (либо метод разложения на степень в ряд).
Краткие примеры таблиц Брадиса для определения значений тригонометрических функций
Мы показали , что представляет таблица, какие данные и значения отображает. {\prime}=4,102\]
{\prime}=4,102\]
Урок алгебры в 11-м классе «Обратные тригонометрические функции»
Тип урока: комбинированный, состоит из 7 учебно-воспитательных моментов: организационный момент, повторение изученного, подготовка к изучению материала, изучение и закрепление нового материала, тестовая работа, итог урока.
Цели урока:
- сформировать умение применять определения аркфункций для нахождения тригонометрических функций от аркфункций;
- развивать познавательный интерес учащихся к предмету через систему нестандартных задач;
- воспитывать нестандартно, логически мыслящую личность.
Оборудование: доска, таблицы, компьютер, мультимедийная установка, экран, учебник.
Ход урока
I. Организационный момент.
Ребята, сегодня мы проводим урок — обобщение по
теме: «Обратные тригонометрические функции». Материал этого параграфа в учебнике вынесен для
самостоятельного изучения, но поскольку задания
с аркфункциями стали включать в ЕГЭ, я решила не
только изучить новый материал на уроке, но
обобщить ваши знания по данной теме.
Материал этого параграфа в учебнике вынесен для
самостоятельного изучения, но поскольку задания
с аркфункциями стали включать в ЕГЭ, я решила не
только изучить новый материал на уроке, но
обобщить ваши знания по данной теме.
II. Актуализация опорных знаний:
1. Значения аркфункций:
Вспомните, для чего в 10 классе были введены понятия арксинуса, арккосинуса, арктангенса? (Для решения тригонометрических уравнений).
Давайте вспомним формулы, по которым решаются простейшие тригонометрические уравнения.
Слайд1:
вопросы к классу: -формула нахождения корней уравнения соs х=а;
-дать определение арккосинуса числа а ;
Слайд 2 :(вопросы аналогичные предыдущим)
Слайд 3
Слайд 4
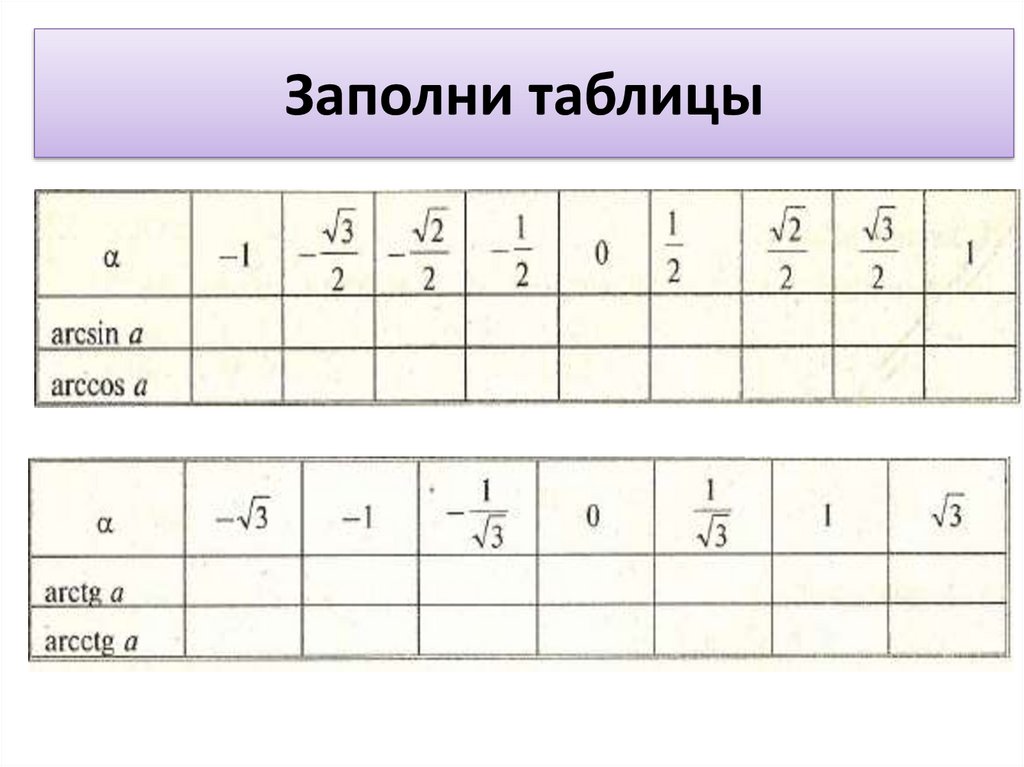
Заполним таблицу значений аркфункций: Слайд 5
Пользуясь ей решим следующие упражнения:
№655(из учебника)
2) arcsin(1/v2)-4 arcsin1=
4) arccos(-1)- arcsin(-1)=
6)4 arctg(-1)+3 arctg(v3)=
Из ЕГЭ:
1) arcsin(sin /3)+ arcsin (-v3/2)=
3)10cos(arctg(v3))=
Проверим получившиеся ответы: Слайд 6
2.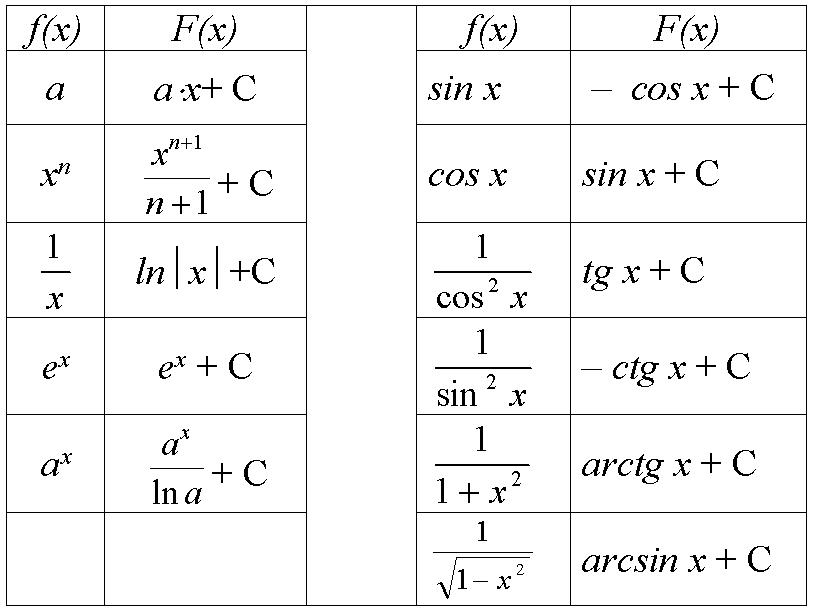 Вспомним формулы, связывающие аркфункции с
тригонометрическими функциями:
Вспомним формулы, связывающие аркфункции с
тригонометрическими функциями:
Слайд 7
С помощью них вычислим устно:
sin(arcsin(-1/5))=
sin(+ arcsin 3/4)=
(из ЕГЭ) 5 sin(+ arcsin (-3/5)=
cos(arccos(-2/3))=
sin(/2+ arccos 1/3)=
tg(arctg(-3))=
сtg(/2+ arctg 6)=
3. Нахождение значения тригонометрической функции от аркфункции.
1. Сильный ученик:
sin(arccos v3/4)=
2.(Из ЕГЭ) — сильный ученик
5v2 sin(/2- arctg(-1/7))=
б) Ребята, существует другой способ решения подобных заданий. Я буду рада, если кто-нибудь из вас его запомнит и будет его применять.
Посмотрите, во всех ранее решённых примерах — угол, лежащий в первой четверти, а это значит, что — угол острый. Вспомните, что называется синусом(косинусом, тангенсом и котангенсом) острого угла прямоугольного треугольника?
Решим следующий пример так:2v13 cos (arctg 2/3)=
tg 2/3-это значит, что отношение противолежащего катета к прилежащему равно 2:3
-А как найти гипотенузу?
-Гипотенуза по теореме Пифагора равна:
v4+9=v13
-Тогда cos =3/v13, а 2v13 cos (arctg 2/3)=
2v133/v13=6
в) Решим вторым способом следующие примеры:
1) tg(arccos (-1/3))=
2) 3v5 tg(arcsin(2/7)=
3) по вариантам:
а) сtg(arccos (2/5))=
б) v15 tg(arcsin(1/4))
4) Средний ученик:
sin(2 arctg 5)=
III. Изучение нового материала:
Изучение нового материала:
В материалах для подготовки к ЕГЭ есть задания, в которых необходимо знать свойства обратных тригонометрических функций. Обратные тригонометрические функции это математические функции, являющиеся обратными к тригонометрическим функциям. Название обратных тригонометрических функций образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (в переводе с латинского — дуга).
Пусть дана функция у=sin х. На всей области определения она являются кусочно-монотонной, и, значит, обратное соответствие у=arcsin х функцией не является.
Поэтому мы рассмотрим отрезок, на котором она возрастает и принимает все свои значения на [-|2;|2]. Так как для функции у=sin х на интервале
[-|2;|2] каждому значению аргумента
соответствует единственное значение функции, то
на этом отрезке существует обратная функция
у=arcsin х, график которой симметричен графику у=sin х
на отрезке [-1;1] относительно прямой у=х.
Пусть дана функция у=cos х. На всей области определения она являются кусочно-монотонной, и, значит, обратное соответствие у=arccos х функцией не является.
Поэтому мы рассмотрим отрезок, на котором она убывает и принимает все значения на [0;?]. Так как для функции у=cos х на интервале [0;?] каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция у=arccos х, график которой симметричен графику у=cos х на отрезке [-1;1] относительно прямой у=х.
2.Выполняем задания:
1. Найти число целых значений функции у= 12arccos х. (Объясняю сама)
0<arccos х<, тогда 0<12arccos х<12
12=123,14=37,8, значит, целых значений будет 38.
Ответ:38
2. Найти число целых значений функции у=5 arctg
х.
3. Самостоятельно:
у=1,7 arсctg х.
4. Найти наибольшее целое число, входящее в область значений функции у= 6 arcсtg(|sin х|).
5. Найти разность между наибольшим и наименьшим значениями функции:
у=24/ arcsin(sin хcos х)
IV. Дом.задание:
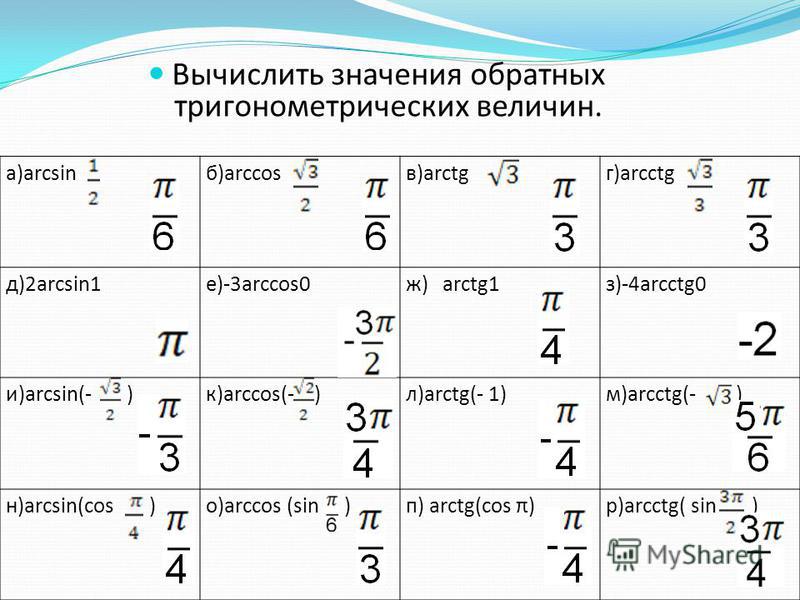
Вычислите:
- sin(2 arcsin 3/5)
- sin(arccos 1/3+arccos 2/3)
- sin( arccos 5/13)
2*.Постройте графики функций:
а) у=arccos|х|;
б) у=arccos х +arcsin х;
в) |у|=arctg х.
3.* Найдите разность между наибольшим и наименьшим значениями функции:
у=arccos (sin х cos х)
4*. Найдите наименьшее целое число, входящее в область значений функции:
у=40arcctg(cos х).
Приложение 1.
c — Эффективность вычисления арксинуса по таблице поиска синуса
спросил
Изменено 11 лет, 9 месяцев назад
Просмотрено 4к раз
Я реализовал таблицу поиска для вычисления значений синуса/косинуса в своей системе. Теперь мне нужны обратные тригонометрические функции (arcsin/arccos).
Мое приложение работает на встроенном устройстве, на котором я не могу добавить вторую таблицу поиска для arcsin, так как я ограничен в программной памяти. Таким образом, решение, которое я имел в виду, состояло в том, чтобы просмотреть таблицу поиска синуса, чтобы получить соответствующий индекс.
Мне интересно, будет ли это решение более эффективным, чем использование стандартной реализации из стандартной математической библиотеки.
Кто-нибудь уже экспериментировал с этим?
Текущая реализация LUT представляет собой массив значений синуса от 0 до PI/2. Значение, хранящееся в таблице, умножается на 409.6, чтобы оставаться с целочисленными значениями с достаточной точностью для моего приложения. Таблица поиска с разрешением 1/4096 дает нам массив из 6434 значений. Затем у меня есть две функции синуса и косинуса, которые принимают в качестве аргумента угол в радианах, умноженный на 4096. Эти функции преобразуют заданный угол в соответствующий угол в первом квадранте и считывают соответствующее значение из таблицы.
Мое приложение работает на dsPIC33F со скоростью 40 MIPS, и я использую компилятор C30.
- c
- производительность
- встроенная
- тригонометрия
- интерполяционные таблицы
3
Довольно сложно что-то сказать с уверенностью, так как вы не рассказали нам ни об оборудовании, ни о компиляторе, ни о своем коде.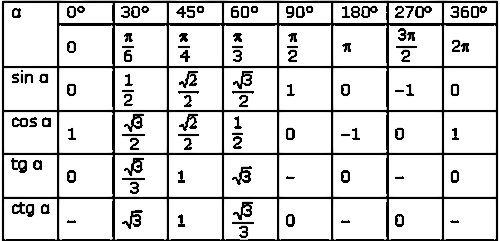 Однако априори я ожидаю, что стандартная библиотека вашего компилятора будет более эффективной, чем ваш код.
Однако априори я ожидаю, что стандартная библиотека вашего компилятора будет более эффективной, чем ваш код.
1
Возможно, к сожалению, вам приходится использовать компилятор C30, который не поддерживает C++, в противном случае я бы указал вам на Оптимизация приложений, интенсивно использующих математику, с помощью арифметики с фиксированной точкой и связанной с ней библиотекой.
Однако применяются общие принципы алгоритма CORDIC, и требуемый объем памяти будет намного меньше, чем ваша текущая реализация. В статье объясняется генерация arctan(), а arccos() и arcsin() могут быть рассчитаны из этого, как описано здесь.
Конечно, это предполагает также, что вам понадобятся квадратный корень и деление. Они могут быть дорогими, хотя PIC24/dsPIC имеют аппаратное целочисленное деление. В статье об ускорении математики также рассматривается квадратный корень. Вполне вероятно, что ваш подход к таблице поиска будет быстрее для прямого поиска, но, возможно, не для обратного поиска, но подходы, описанные в этой статье, являются более общими и точными (библиотека использует 64-битные целые числа как 36,28-битные числа). с фиксированной точкой, вы можете уйти с меньшей точностью и диапазоном в вашем приложении) и, безусловно, быстрее, чем стандартная библиотечная реализация, использующая программное обеспечение с плавающей запятой.
с фиксированной точкой, вы можете уйти с меньшей точностью и диапазоном в вашем приложении) и, безусловно, быстрее, чем стандартная библиотечная реализация, использующая программное обеспечение с плавающей запятой.
Вы можете использовать подход «на полпути», комбинируя укрупненную справочную таблицу для экономии памяти и числовую аппроксимацию для промежуточных значений (например, ряд Маклорена, который будет более точным, чем линейная интерполяция).
Несколько примеров здесь .
Этот вопрос также имеет несколько связанных ссылок.
Двоичный поиск 6434 потребует примерно 12 операций поиска, чтобы найти значение, за которым следует интерполяция, если требуется большая точность. Из-за характера кривой синусоиды вы получите гораздо большую точность на одном конце, чем на другом. Если вы можете сэкономить память, создание собственной обратной таблицы, равномерно распределенной по входным данным, вероятно, будет лучшим выбором для скорости и точности.
Что касается сравнения со встроенной версией, вам придется ее протестировать.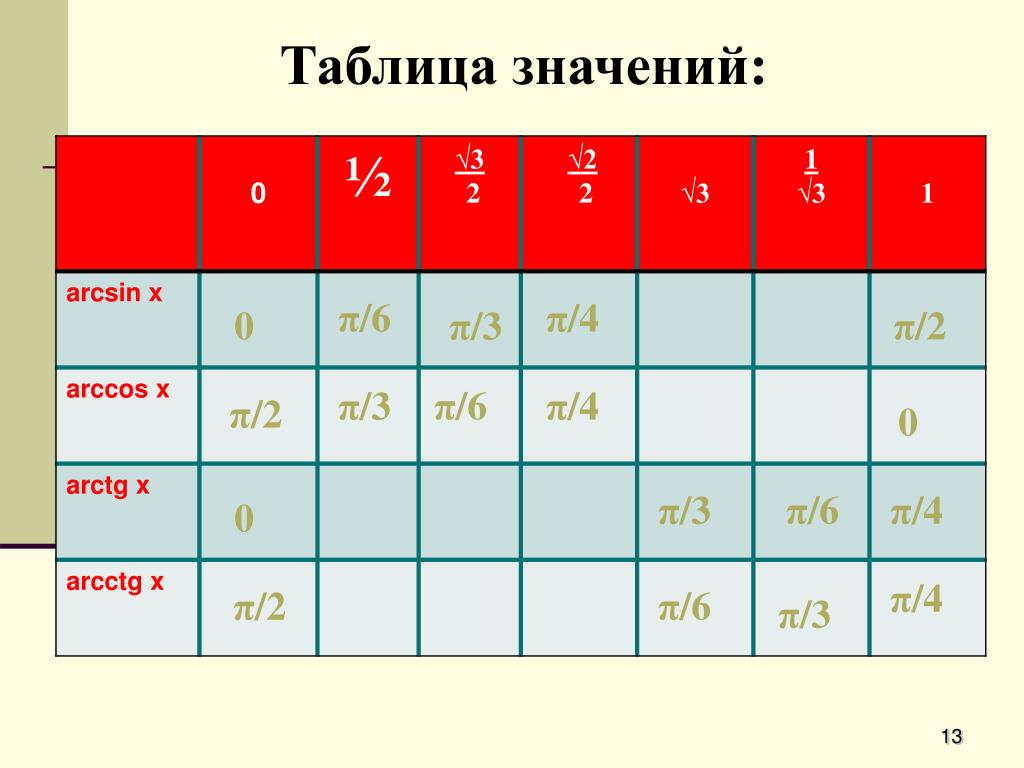 Когда вы это сделаете, обратите внимание на то, насколько увеличивается размер вашего изображения. В некоторых системах реализации стандартного ввода могут быть довольно громоздкими.
Когда вы это сделаете, обратите внимание на то, насколько увеличивается размер вашего изображения. В некоторых системах реализации стандартного ввода могут быть довольно громоздкими.
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Как использовать функцию Numpy Arctan
В этом уроке я покажу вам, как использовать функцию Numpy arctan для вычисления тригонометрического арктангенса в Python.
Я объясню синтаксис np.arctan, как работает функция и как ее использовать.
Если вам нужно что-то конкретное, просто нажмите на любую из следующих ссылок.
Содержание:
- Введение в Numpy Arctan
- Синтаксис np.arctan
- Примеры использования Numpy arctan
Хорошо. Давайте начнем.
Краткое введение в Numpy Arctan
Функция Numpy arctan вычисляет тригонометрический арктангенс в Python.
Как и многие другие тригонометрические функции в Numpy, такие как косинус и синус Numpy, вы можете использовать арктангенс Numpy для работы как с отдельными числами, так и с массивами Numpy.
Я покажу вам, как сделать и то, и другое, но сначала мы рассмотрим синтаксис.
Синтаксис np.arctan
Синтаксис функции arctan Numpy довольно прост:
Это, конечно, предполагает, что вы импортировали Numpy с псевдонимом np , что является общепринятым соглашением.
Допустимые форматы для ввода
Давайте кратко обсудим допустимые типы ввода для функции np.arctan.
На изображении синтаксиса, показанном выше, вы можете видеть, что ввод функции помечен как « ввод ».
Важно отметить, что этот ввод может принимать одну из нескольких различных форм:
- число (целое или с плавающей запятой)
- массив Numpy (целых или с плавающей запятой)
- список чисел Python или объект, подобный списку
np.arctan будет работать со всеми этими входными данными. Сказав это, эти разные входные данные будут давать немного разные выходные данные
Выходные данные np.arctan
Формат выходных данных немного зависит от входных данных:
- если вход представляет собой одно число, то выход будет одно число (арктангенс входа)
- , если ввод представляет собой массив Numpy, список Python или объект, подобный списку, то выход будет массивом Numpy арктангенсов
Дополнительные параметры
В дополнение к входному аргументу, np.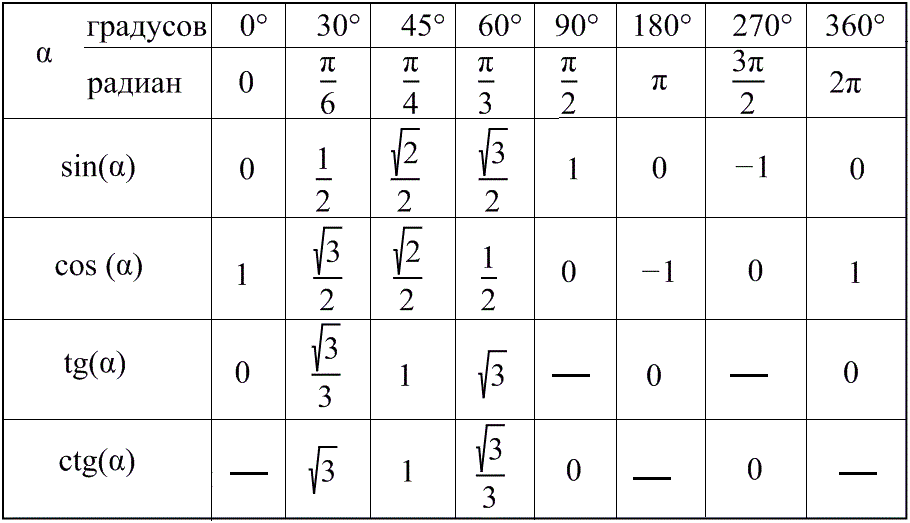 arctan функция имеет несколько необязательных параметров:
arctan функция имеет несколько необязательных параметров:
- out
- где
Они используются довольно редко, поэтому я не буду их здесь объяснять.
Примеры использования функции арктангенса Numpy
Теперь, когда мы рассмотрели синтаксис функции арктангенса Numpy, давайте рассмотрим несколько примеров.
Примеры:
- Вычислить Arctangent 0
- Вычислить Arctangent 1 000 000
- Использовать функцию Numpy Arctangent на массиве Numpy
- . Импортируйте Numpy и настройте Plotly
Прежде чем запускать примеры, вам потребуется запустить некоторый предварительный код.
В частности, вам нужно будет импортировать пакеты, которые мы собираемся использовать.
Вам также может понадобиться настроить рендеринг изображений для Plotly (если вы используете IDE).
Импорт пакетов
Во-первых, вы можете импортировать Numpy и Plotly с помощью этого кода.
импортировать numpy как np импортировать plotly.
 express как px
express как px
Очевидно, мы будем использовать Numpy для запуска функции np.arctan.
Но мы также будем использовать Plotly для построения графика функции арктангенса в примере 4.
Настройка рендеринга изображения
Далее, если вы используете IDE, такую как Spyder или PyCharm, вам может потребоваться настроить IDE так, чтобы он будет отображать выходные изображения из Plotly.
По умолчанию Plotly настроен на отправку выходных визуализаций в ваш браузер . Это нормально, если вы работаете в ноутбуке, но если вы используете IDE, это просто вызовет ошибку.
Итак, если вы используете IDE, вам нужно указать Plotly отображать выходные визуализации в виде изображений svg.
Вы можете сделать это с помощью следующего кода:
(Примечание: если вы используете Jupyter, , вы можете пропустить этот код !)
импортировать plotly.io как pio pio.renderers.default = 'svg'
После запуска кода установки вы должны быть готовы к запуску примеров.

ПРИМЕР 1: Вычисление арктангенса числа 0
Начнем с простого примера.
Здесь мы собираемся вычислить арктангенс 0.
np.арктан(0)
ВЫХОД:
0,0
Объяснение
Очевидно, это очень просто.
Мы использовали np.arctan для вычисления арктангенса 0, который равен 0,0.
(Обратите внимание, что np.arctan выводит числа с плавающей запятой.)
ПРИМЕР 2: Вычислить арктангенс числа 1 000 000
Теперь мы собираемся вычислить арктангенс числа 1 000 000.
нп.арктан(1000000)
ВЫХОД:
1,5707953267948966
Объяснение
Здесь мы вычислили арктангенс числа 1 000 000.
На самом деле я вычисляю арктангенс относительно большого числа.
Результат: 1,5707953267948966.
Возможно, вы этого не узнаете, но это примерно .
Это важно, поскольку , .
ПРИМЕР 3: Использование функции арктангенса Numpy для массива значений Numpy
Далее мы собираемся использовать функцию арктангенса Numpy для массива Numpy.

Помните, что np.arctan может работать с одним числом (как в примере 1 и примере 2), но также может работать с массивом чисел.
Создать массив Numpy
Во-первых, давайте просто создадим массив Numpy.
Мы будем использовать Numpy linspace для создания массива, содержащего 300 равномерно расположенных чисел от -10 до 10.
x_values = np.linspace (начало = -10, стоп = 10, число = 300)
Вычисление арктангенса с помощью Numpy
Далее мы собираемся вычислить арктангенс каждого числа в нашем массиве,
x_values .Для этого мы предоставляем
x_values в качестве входных данных для функции:arctan_values = np.arctan(x_values)
Давайте посмотрим на первые несколько значений
arctan_values , чтобы увидеть, что внутри:arctan_values[1:10]
ВЫХОД:
массив ([-1.47046099, -1.46978535, -1.46910058, -1.4684065, -1.46770291, -1,46698962, -1,46626643, -1,46553313, -1,46478951])Объяснение
Это довольно просто.

Здесь np.arctan вычислил арктангенс каждого элемента в
x_values .ПРИМЕР 4: Постройте график функции арктангенса с помощью Plotly
Наконец, давайте построим график функции арктангенса.
Для этого мы будем использовать Plotly для построения значений в
arctan_values , которые мы вычислили в примере 3.В частности, мы будем использовать функцию Plotly line, px.line, для построения данных:
px.line(x = x_values, y = arctan_values)
OUT:
Объяснение
Здесь мы построили функцию арктангенса с функцией Plotly line.
Мы отложили значения в
x_values по оси x.И мы отобразили значения в
arctan_values , которые мы вычислили с помощью np.arctan, по оси Y.Другие вопросы оставьте в комментариях ниже
У вас есть другие вопросы о том, как использовать np.arctan?
Если да, оставьте свои вопросы в разделе комментариев ниже.

Присоединяйтесь к нашему курсу, чтобы узнать больше о Numpy
В этом уроке я объяснил, как вычислить тригонометрический арктангенс в Python, используя Numpy arctan.
Это должно помочь вам с вычислением косинусов и выполнением тригонометрических операций, но если вы действительно хотите изучить Numpy, вам предстоит еще многому научиться.
Если вы серьезно относитесь к освоению Numpy и серьезно относитесь к науке о данных в Python, вам следует подумать о том, чтобы присоединиться к нашему премиальному курсу под названием Numpy Mastery .
Numpy Mastery научит вас всему, что вам нужно знать о Numpy, в том числе:
- Как создавать массивы Numpy
- Как изменять форму, разделять и комбинировать ваши массивы Numpy
- Что делает функция «случайное начальное число Numpy»
- Как использовать случайные функции Numpy
- Как выполнять математические операции с массивами Numpy
- и многое другое …
Кроме того, этот курс покажет вам систему практики, которая будет помочь вам освоить синтаксис в течение нескольких недель.


 express как px
express как px