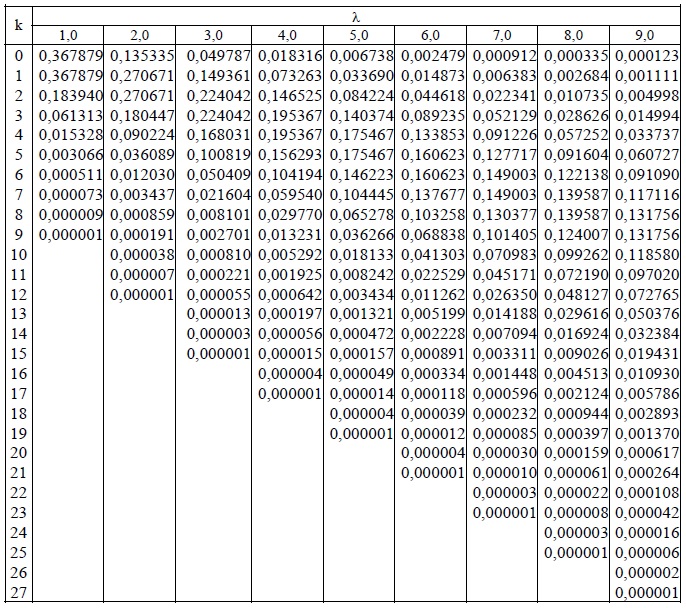
Таблица значений функции Лапласа —
Теория
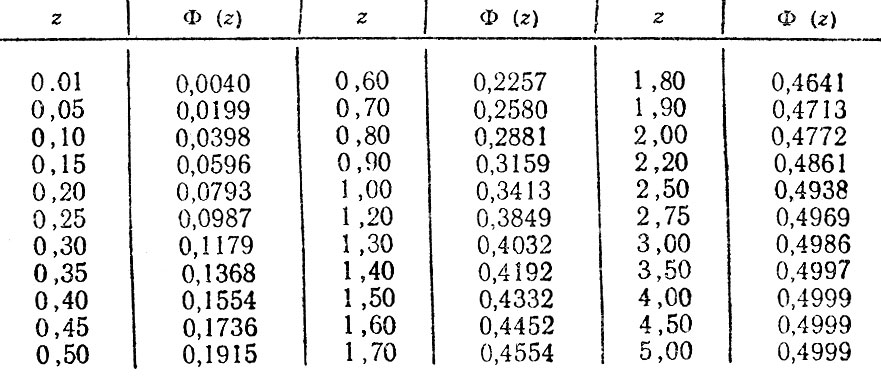
Таблица значений функции Лапласа
X | Ф(х)) | Ф(х) | X | Ф(х) | X | Ф(х) | |
0 | 0.0000 | 0.64 | 0.2389 | 1.28 | 0.3997 | 1.92 | 0.4726 |
0.02 | 0.0080 | 0.66 | 0.2454 | 1.30 | 0.4032 | 1.94 | 0. |
0.04 | 0.0160 | 0.68 | 0.2517 | 1.32 | 0.4066 | 1.96 | 0.4750 |
0.06 | 0.0239 | 0.70 | 0.2580 | 1.34 | 0.4099 | 1.98 | 0.4761 |
0.08 | 0.0319 | 0.72 | 0.2642 | 1.36 | 0.4131 | 2.00 | 0.4772 |
0.10 | 0.0398 | 0. | 0.2703 | 1.38 | 0.4162 | 2.05 | 0.4798 |
0.12 | 0.0478 | 0.76 | 0.2764 | 1.40 | 0.4192 | 2.10 | 0.4821 |
0.14 | 0.0557 | 0.78 | 0.2823 | 1.42 | 0.4222 | 2.15 | 0.4842 |
0.16 | 0.0636 | 0.80 | 0.2881 | 1.44 | 0. | 2.20 | 0.4861 |
0.18 | 0.0714 | 0.82 | 0.2939 | 1.46 | 0.4279 | 2.25 | 0.4878 |
0.20 | 0.0793 | 0.84 | 0.2995 | 1.48 | 0.4306 | 2.30 | 0.4893 |
0.22 | 0.0871 | 0.86 | 0.3051 | 1.50 | 0.4332 | 2.35 | 0.4907 |
0. | 0.0948 | 0.88 | 0.3106 | 1.52 | 0.4357 | 2.40 | 0.4918 |
0.26 | 0.1026 | 0.90 | 0.3159 | 1.54 | 0.4382 | 2.45 | 0.4929 |
0.28 | 0.1103 | 0.92 | 0.3212 | 1.56 | 0.4406 | 2.50 | 0.4938 |
0.30 | 0.1179 | 0.94 | 0. | 1.58 | 0.4429 | 2.55 | 0.4947 |
0.32 | 0.1255 | 0.96 | 0.3315 | 1.60 | 0.4452 | 2.60 | 0.4953 |
0.34 | 0.1331 | 0.98 | 0.3365 | 1.62 | 0.4474 | 2.65 | 0.4960 |
0.36 | 0.1406 | 1.00 | 0.3413 | 1.64 | 0.4495 | 2. | 0.4965 |
0.38 | 0.1480 | 1.02 | 0.3461 | 1.66 | 0.4515 | 2.75 | 0.4970 |
0.40 | 0.1554 | 1.04 | 0.3508 | 1.68 | 0.4535 | 2.80 | 0.4974 |
0.42 | 0.1628 | 1.06 | 0.3554 | 1.70 | 0.4554 | 2.85 | 0.4978 |
0.44 | 0. | 1.08 | 0.3599 | 1.72 | 0.4573 | 2.90 | 0.4981 |
0.46 | 0.1772 | 1.10 | 0.3643 | 1.74 | 0.4591 | 2.95 | 0.4985 |
0.48 | 0.1844 | 1.12 | 0.3686 | 1.76 | 0.4608 | 3.00 | 0.49865 |
0.50 | 0.1915 | 1.14 | 1. | 0.4625 | 3.20 | 0.49931 | |
0.52 | 0.1985 | 1.16 | 0.3770 | 1.80 | 0.4641 | 3.40 | 0.49966 |
0.54 | 0.2054 | 1.18 | 0.3810 | 1.82 | 0.4656 | 3.60 | 0.49984 |
0.56 | 0.2123 | 1.20 | 0.3849 | 1.84 | 0.4671 | 3.80 | 0. |
0.58 | 0.2190 | 1.22 | 0.3883 | 1.86 | 0.4686 | 4.00 | 0.499968 |
0.6 | 0.2257 | 1.24 | 0.3925 | 1.88 | 0.4699 | 4.50 | 0.499997 |
0.62 | 0.2324 | 1.26 | 0.3962 | 1.90 | 0.4713 | 5.00 | 0.499997 |
Приложение 2. Таблица значений функции Лапласа · Теория вероятностей и математическая статистика
Аннотация Содержание Введение
Раздел 1.
 Теория вероятностей
Теория вероятностей1.1. Комбинаторика 1.2. События 1.3. Beроятности сложных событий. Схема Бернулли 1.4. Дискретные случайные величины 1.5. Непрерывные случайные величины
Раздел 2. Математическая статистика
2.1. Выборочный метод
2. 2. Моделирование случайных величин
2. Моделирование случайных величин
Заключение Рекомендованный библиографический список
Приложение 1. Значения функции плотности стандартного нормального распределения Приложение 2. Таблица значений функции Лапласа Глоссарий
Таблица значений функции Лапласа
Если число свыше 5 (например, 7), то берется 5, т.е. значение будет 0.4999.
| 0.00 | 0. 0000 0000 | 0.32 | 0.1255 | 0.64 | 0.2389 | 0.96 | 0.3315 |
| 0.01 | 0.0040 | 0.33 | 0.1293 | 0.65 | 0.2422 | 0.97 | 0.3340 |
| 0.02 | 0.0080 | 0.34 | 0.1331 | 0.66 | 0.2454 | 0.98 | 0.3365 |
| 0.03 | 0.0120 | 0.35 | 0.1368 | 0.67 | 0.2486 | 0.99 | 0.3389 |
| 0.04 | 0.0160 | 0.36 | 0.1406 | 0.68 | 0.2517 | 1.00 | 0.3413 |
| 0.05 | 0.0199 | 0.37 | 0.1443 | 0.69 | 0.2549 | 1.01 | 0.3438 |
| 0.06 | 0.0239 | 0.38 | 0.1480 | 0.70 | 0.2580 | 1.02 | 0.3461 |
| 0.07 | 0.0279 | 0.39 | 0.1517 | 0.71 | 0.2611 | 1.03 | 0.3485 |
0. 08 08 | 0.0319 | 0.40 | 0.1554 | 0.72 | 0.2642 | 1.04 | 0.3508 |
| 0.09 | 0.0359 | 0.41 | 0.1591 | 0.73 | 0.2673 | 1.05 | 0.3531 |
| 0.10 | 0.0398 | 0.42 | 0.1628 | 0.74 | 0.2703 | 1.06 | 0.3554 |
| 0.11 | 0.0438 | 0.43 | 0.1664 | 0.75 | 0.2734 | 1.07 | 0.3577 |
| 0.12 | 0.0478 | 0.44 | 0.1700 | 0.76 | 0.2764 | 1.08 | 0.3599 |
| 0.13 | 0.0517 | 0.45 | 0.1736 | 0.77 | 0.2794 | 1.09 | 0.3621 |
| 0.14 | 0.0557 | 0.46 | 0.1772 | 0.78 | 0.2823 | 1.10 | 0.3643 |
| 0.15 | 0.0596 | 0.47 | 0.1808 | 0.79 | 0.2852 | 1.11 | 0. 3665 3665 |
| 0.16 | 0.0636 | 0.48 | 0.1844 | 0.80 | 0.2881 | 1.12 | 0.3686 |
| 0.17 | 0.0675 | 0.49 | 0.1879 | 0.81 | 0.2910 | 1.13 | 0.3708 |
| 0.18 | 0.0714 | 0.50 | 0.1915 | 0.82 | 0.2939 | 1.14 | 0.3729 |
| 0.19 | 0.0753 | 0.51 | 0.1950 | 0.83 | 0.2967 | 1.15 | 0.3749 |
| 0.20 | 0.0793 | 0.52 | 0.1985 | 0.84 | 0.2995 | 1.16 | 0.3770 |
| 0.21 | 0.0832 | 0.53 | 0.2019 | 0.85 | 0.3023 | 1.17 | 0.3790 |
| 0.22 | 0.0871 | 0.54 | 0.2054 | 0.86 | 0.3051 | 1.18 | 0.3810 |
| 0.23 | 0.0910 | 0.55 | 0.2088 | 0.87 | 0. 3078 3078 | 1.19 | 0.3830 |
| 0.24 | 0.0948 | 0.56 | 0.2123 | 0.88 | 0.3106 | 1.20 | 0.3849 |
| 0.25 | 0.0987 | 0.57 | 0.2157 | 0.89 | 0.3133 | 1.21 | 0.3869 |
| 0.26 | 0.1026 | 0.58 | 0.2190 | 0.90 | 0.3159 | 1.22 | 0.3883 |
| 0.27 | 0.1064 | 0.59 | 0.2224 | 0.91 | 0.3186 | 1.23 | 0.3907 |
| 0.28 | 0.1103 | 0.60 | 0.2257 | 0.92 | 0.3212 | 1.24 | 0.3925 |
| 0.29 | 0.1141 | 0.61 | 0.2291 | 0.93 | 0.3238 | 1.25 | 0.3944 |
| 0.30 | 0.1179 | 0.62 | 0.2324 | 0.94 | 0.3264 | ||
| 0.31 | 0.1217 | 0.63 | 0.2357 | 0.95 | 0. 3289 3289 |
| 1.26 | 0.3962 | 1.59 | 0.4441 | 1.92 | 0.4726 | 2.50 | 0.4938 |
| 1.27 | 0.3980 | 1.60 | 0.4452 | 1.93 | 0.4732 | 2.52 | 0.4941 |
| 1.28 | 0.3997 | 1.61 | 0.4463 | 1.94 | 0.4738 | 2.54 | 0.4945 |
| 1.29 | 0.4015 | 1.62 | 0.4474 | 1.95 | 0.4744 | 2.56 | 0.4948 |
| 1.30 | 0.4032 | 1.63 | 0.4484 | 1.96 | 0.4750 | 2.58 | 0.4951 |
| 1.31 | 0.4049 | 1.64 | 0.4495 | 1.97 | 0.4756 | 2.60 | 0.4953 |
| 1.32 | 0.4066 | 1.65 | 0.4505 | 1.98 | 0.4761 | 2. 62 62 | 0.4956 |
| 1.33 | 0.4082 | 1.66 | 0.4515 | 1.99 | 0.4767 | 2.64 | 0.4959 |
| 1.34 | 0.4099 | 1.67 | 0.4525 | 2.00 | 0.4772 | 2.66 | 0.4961 |
| 1.35 | 0.4115 | 1.68 | 0.4535 | 2.02 | 0.4783 | 2.68 | 0.4963 |
| 1.36 | 0.4131 | 1.69 | 0.4545 | 2.04 | 0.4793 | 2.70 | 0.4965 |
| 1.37 | 0.4147 | 1.70 | 0.4554 | 2.06 | 0.4803 | 2.72 | 0.4967 |
| 1.38 | 0.4162 | 1.71 | 0.4564 | 2.08 | 0.4812 | -2.74 | 0.4969 |
| 1.39 | 0.4177 | 1.72 | 0.4573 | 2.10 | 0.4821 | 2.76 | 0.4971 |
| 1.40 | 0.4192 | 1.73 | 0.4582 | 2. 12 12 | 0.4830 | 2.78 | 0.4973 |
| 1.41 | 0.4207 | 1.74 | 0.4591 | 2.14 | 0.4838 | 2.80 | 0.4974 |
| 1.42 | 0.4222 | 1.75 | 0.4599 | 2.16 | 0.4846 | 2.82 | 0.4976 |
| 1.43 | 0.4236 | 1.76 | 0.4608 | 2.18 | 0.4854 | 2.84 | 0.4977 |
| 1.44 | 0.4251 | 1.77 | 0.4616 | 2.20 | 0.4861 | 2.86 | 0.4979 |
| 1.45 | 0.4265 | 1.78 | 0.4625 | 2.22 | 0.4868 | 2.88 | 0.4980 |
| 1.46 | 0.4279 | 1.79 | 0.4633 | 2.24 | 0.4875 | 2.90 | 0.4981 |
| 1.47 | 0.4292 | 1.80 | 0.4641 | 2.26 | 0.4881 | 2.92 | 0.4982 |
| 1.48 | 0.4306 | 1. 81 81 | 0.4649 | 2.28 | 0.4887 | 2.94 | 0.4984 |
| 1.49 | 0.4319 | 1.82 | 0.4656 | 2.30 | 0.4893 | 2.96 | 0.4985 |
| 1.50 | 0.4332 | 1.83 | 0.4664 | 2.32 | 0.4898 | 2.98 | 0.4986 |
| 1.51 | 0.4345 | 1.84 | 0.4671 | 2.34 | 0.4904 | 3.00 | 0.49865 |
| 1.52 | 0.4357 | 1.85 | 0.4678 | 2.36 | 0.4909 | 3.20 | 0.49931 |
| 1.53 | 0.4370 | 1.86 | 0.4686 | 2.38 | 0.4913 | 3.40 | 0.49966 |
| 1.54 | 0.4382 | 1.87 | 0.4693 | 2.40 | 0.4918 | 3.60 | 0.49984 |
| 1.55 | 0.4394 | 1.88 | 0.4699 | 2.42 | 0.4922 | 3.80 | 0.49992 |
1. {- u} \ mathrm du = {\ sin (\ pi a) \ over \ pi} \ Gamma (1-a).
$$
Для упрощения мы применяем формулу отражения Эйлера для гамма-функции, чтобы приведенное выше выражение стало $1/\Gamma(a)$. Потому что $1/\Gamma(a)$ тоже целая функция. Мы видим, что соотношение $J(a,1)=1/\Gamma(a)$ выполняется везде. 9{a-1}$, что согласуется с таблицей. {- u} \ mathrm du = {\ sin (\ pi a) \ over \ pi} \ Gamma (1-a).
$$
Для упрощения мы применяем формулу отражения Эйлера для гамма-функции, чтобы приведенное выше выражение стало $1/\Gamma(a)$. Потому что $1/\Gamma(a)$ тоже целая функция. Мы видим, что соотношение $J(a,1)=1/\Gamma(a)$ выполняется везде. 9{a-1}$, что согласуется с таблицей.Таблицы обратного преобразования Лапласа функции [формула: см. текст]. 1990 г., июль-август; 95(4):433-467. doi: 10.6028/jres.095.036. Менахем Дишон 1 , Джон Т. Бендлер 2 , Джордж Х. Вайс 3 Принадлежности Принадлежности
Бесплатная статья ЧВК Менахем Дишон и др. J Res Natl Inst Stand Technol. 1990 июль-август. Бесплатная статья ЧВК . doi: 10.6028/jres.095.036. АвторыМенахем Дишон 1 , Джон Т. Бендлер 2 , Джордж Х. Вайс 3 Принадлежности
Абстрактный Обратное преобразование, [формула: см. текст], 0 < β < 1, представляет собой устойчивый закон, который возникает в ряде различных приложений в химической физике, физике полимеров, физике твердого тела и прикладной математике. Из-за его важных применений ряд исследователей предложил приближения к г ( т ). Однако до сих пор не было точно рассчитанных значений, доступных для проверки или других целей. Мы приводим здесь таблицы с точностью до шести цифр для г ( t ) для ряда значений β между 0,25 и 0,999. Кроме того, поскольку g ( t ), рассматриваемая как функция β , является унимодальной с пиком, приходящимся на t = t max , мы и табулируем, и строим график 9.0119 T MAX и 1/ G ( T MAX ) в зависимости от β , а также придает полиномиальные приближения к 1/ G ( T 414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414. Ключевые слова: численное обращение преобразований Лапласа; релаксационные процессы; стабильные законы; растянутые экспоненты. Цифры Рисунок 1а Кривые г ( т… Рисунок 1а Кривые г ( t ) как функция t в… Рисунок 1аКривые зависимости g ( t ) от t в окрестности пиковых значений для β = 0,25, 0,275 и 0,30. Рисунок 1b Кривые г ( т… Рисунок 1b Кривые г ( t ) как функция t в… Рисунок 1б Кривые г ( t ) как функция t в окрестности пиковых значений для β =0,35(0,1)0,95. Рисунок 1c Кривые г ( т… Рисунок 1c Кривые г ( t ) как функции плавника окрестности… Рисунок 1сКривые зависимости g ( t ) от fin окрестности пиковых значений для β =0,99, 0,995, 0,997, 0,998 и 0,999. Дельта-функция при β =1 показана вертикальной линией. Рисунок 2а Кривые т макс и… Рисунок 2а Кривые т макс и 1/ г ( т макс ) построены как… Рисунок 2а Кривые t max и 1/ g ( t max ), построенные как функция β. Рисунок 2b Кривая 1/ г (… Рисунок 2b Кривая 1/ г ( т макс ) построена как функция… Рисунок 2бКривая 1/ г ( т макс ) построена как функция т макс . Рисунок 3 Многочлен от второй до четвертой степени… Рисунок 3 Полиномиальные приближения от второй до четвертой степени до 1/ g ( t max )… Рисунок 3 Полиномиальные приближения от второй до четвертой степени до 1/ g ( t max ) в зависимости от β по сравнению с более точно рассчитанным значением этой величины. См. это изображение и информацию об авторских правах в PMC Похожие статьи
Посмотреть все похожие статьи Цитируется
Рекомендации
|


 74
74 4251
4251 24
24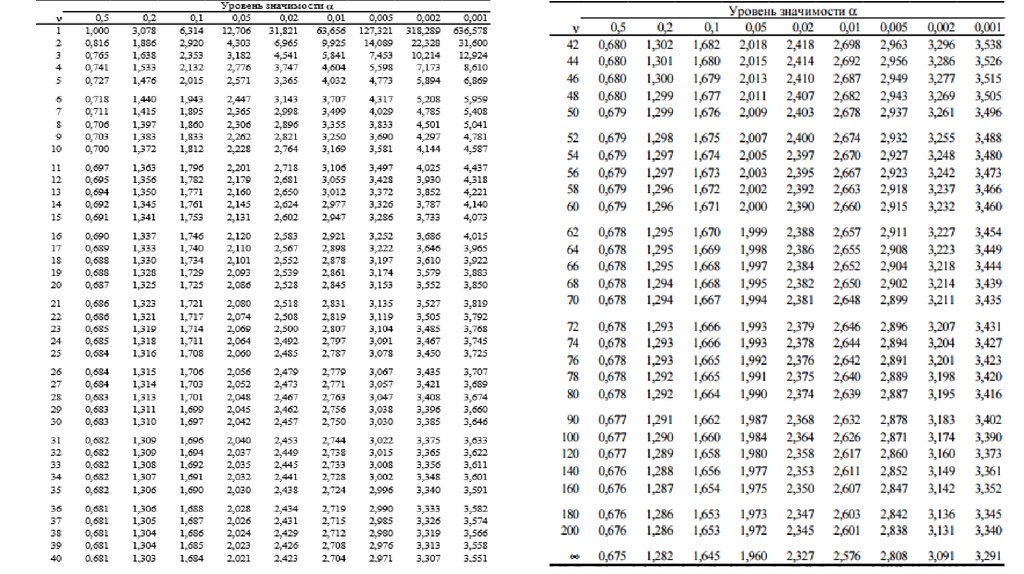 3264
3264 70
70
 78
78 499928
499928
 1990 г., июль-август; 95(4):433-467.
1990 г., июль-август; 95(4):433-467. 6028/jres.095.036
6028/jres.095.036