Значения синуса косинуса тангенса таблица: синуса, косинуса, тангенса, котангенса. Как пользоваться

Урок по геометрии «Значения синуса, косинуса и тангенса для углов 30, 45 и 60». | Презентация к уроку по геометрии (8 класс) на тему:

Урок по геометрии «Значения синуса, косинуса и тангенса

для углов 300, 450 и 600».

Комбинированный урок.

Продолжительность: 1 урок, 45 минут.

Цель урока:

Вывести значения синуса, косинуса и тангенса для углов 300, 450 и 600. Формировать навыки решения прямоугольных треугольников, используя синус, косинус и тангенс острого угла, в ходе решения задач.

Задачи урока:

1. повторить понятия синуса, косинуса, тангенса острого угла прямоугольного треугольника;
2. повторить теорему Пифагора;
3. вычислить значения синуса, косинуса и тангенса для углов 300, 450 и 600 в ходе решения задач;
4. составить таблицу значений синуса, косинуса и тангенса для углов 300, 450 и 600;
5. решать задачи на прямоугольный треугольник, используя понятия синус, косинус и тангенс острого угла;
6. развивать логическое мышление, взаимооценку, самооценку и самоконтроль   учащихся.

Оборудование: компьютер.

Демонстрации: презентация Microsoft PowerPoint.

Ход урока:

I. Организационный момент.

Учащиеся готовы к уроку. Начинаем наш урок с проверки домашнего задания.

II. Проверка домашнего задания.

     Учащимся задано на дом следующее задание: № 591 (в), тест, выучить определения синуса, косинуса и тангенса острого угла прямоугольного треугольника.

Учащиеся обмениваются своими тетрадями с соседями по парте и проверяют с помощью компьютера домашнее задание (слайды презентации № 4, 5), оценивают работу соседа, ставят оценку за работу.

III. Устная работа.

Учитель актуализирует знания учащихся в ходе устной работы по домашнему заданию (слайд  презентации № 6).

Учащиеся отвечают на предложенные вопросы и решают задачи на готовых чертежах (слайды  презентации № 7, 9). Если возникают трудности с решением предложенных заданий, то учащиеся устно разбирают решение задач с помощью компьютера (слайды  презентации № 8, 10).

IV. Сообщение темы и целей урока.

Учитель сообщает тему урока, ученики записывают ее в тетрадь. Учитель сообщает цели урока.

V. Введение нового материала.

Учитель:  «Сегодня на уроке мы вычислим значение синуса, косинуса и тангенса для углов 300, 450 и 600 в процессе решения задач». 

 

Учитель  предлагает учащимся решить первую задачу (слайд  презентации № 11).

 Ученики  делают  чертеж   в тетради, следуя за рекомендацией учителя принимают сторону  ВС за х, решают задачу.

Учащиеся сверяют своё решение с решением задачи № 1 (слайд презентации № 12).

Если учащиеся допустили ошибки, то исправляют их.

Учитель  предлагает учащимся решить вторую задачу самостоятельно (слайд  презентации № 13). Учащиеся решают задачу, сверяют своё решение с образцом (слайд презентации № 14).

Учащиеся заполняют таблицу значений синуса, косинуса и тангенса для углов 300, 450 и 600.

Выполнение учащимися физкультминутки  для улучшения мозгового кровообращения:

 Исходное положение (далее — и.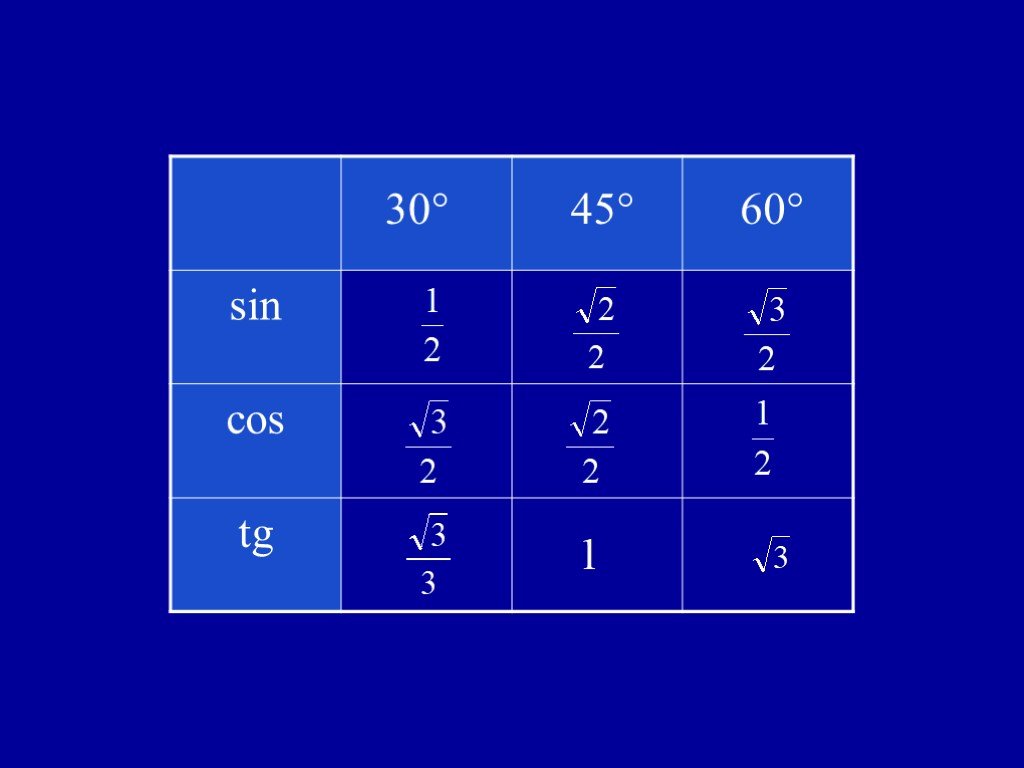 п.) — сидя на стуле. 1 — 2 — отвести голову назад и плавно наклонить назад, 3 — 4 — голову наклонить вперед, плечи не поднимать. Повторить 4 — 6 раз. Темп медленный.

И физкультминутки для глаз: Крепко зажмурить глаза (считать до 3, открыть их и посмотреть вдаль (считать до 5). Повторять 4 — 5 раз.

VI. Решение упражнений.

Учащиеся самостоятельно решают задачи 3 и 4. Решение и ответы к заданиям сверяют с образцом с помощью компьютера.

Задача № 3.

В прямоугольной трапеции основания равны 6  и 11, меньшая боковая сторона равна 4. Найдите синус, косинус и тангенс острого угла трапеции.

Задача № 4.

В прямоугольном треугольнике гипотенуза равна с, а один из острых углов равен α. Выразите второй острый угол и катеты через с и α и найдите их значения, если с=24, а α=600.

VII. Итоги урока.

Учитель в ходе устного опроса подводит итоги урока (слайды  презентации № 20, 21).

Учащиеся устно отвечают на вопросы.

Учитель задает учащимся следующие вопросы:

— С каким настроением Вы работали на уроке?

— Устали ли Вы?

— Какую бы отметку Вы бы поставили себе за этот урок?

VIII. Выставление оценок за урок с комментарием учителя.

IХ. Домашнее задание:  

          Выучить значения синуса, косинуса и тангенса для углов 300, 450 и 600;

№ 595; № 597; № 598(б)  (слайд  презентации № 22).

1.  

Таблица синусов углов от 0 до 90. Синус (sin x) и косинус (cos x) – свойства, графики, формулы

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Прежде всего напомню простой, но очень полезный вывод из урока «Что такое синус и косинус? Что такое тангенс и котангенс?»

Вот этот вывод:

Синус, косинус, тангенс и котангенс накрепко связаны со своими углами. Знаем одно — значит, знаем и другое.

Другими словами, у каждого угла есть свой неизменный синус и косинус. И почти у каждого — свой тангенс и котангенс. Почему почти? Об этом ниже.

Это знание здорово помогает в учёбе! Существует масса заданий, где требуется перейти от синусов к углам и наоборот.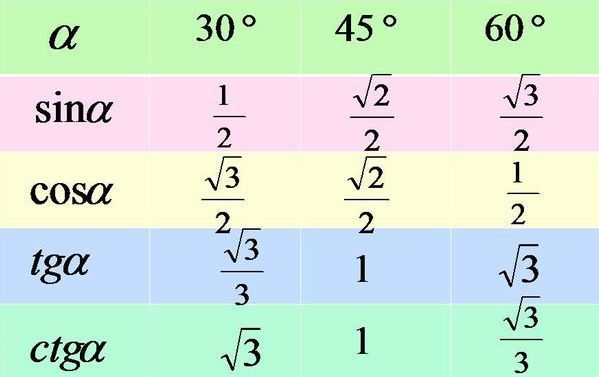 Для этого существует таблица синусов. Аналогично, для заданий с косинусом — таблица косинусов. И, как вы уже догадались, существует

таблица тангенсов и таблица котангенсов. )

Таблицы бывают разные. Длинные, где можно посмотреть, чему равен, скажем, sin37°6’. Раскрываем таблицы Брадиса, ищем угол тридцать семь градусов шесть минут и видим значение 0,6032. Понятное дело, запоминать это число (и тысячи других табличных значений) совершенно не требуется.

В сущности, в наше время длинные таблицы косинусов синусов тангенсов котангенсов не особо-то и нужны. Один хороший калькулятор заменяет их полностью. Но знать о существовании таких таблиц не мешает. Для общей эрудиции.)

И зачем тогда этот урок?! — спросите вы.

А вот зачем. Среди бесконечного количества углов существуют особые, о которых вы должны знать всё . На этих углах построена вся школьная геометрия и тригонометрия. Это, своего рода, «таблица умножения» тригонометрии. Если вы не знаете, чему равен, например, sin50°, никто вас не осудит.) Но если вы не знаете, чему равен sin30°, будьте готовы получить заслуженную двойку…

Таких особых углов тоже прилично набирается. Школьные учебники обычно любезно предлагают к запоминанию таблицу синусов и таблицу косинусов для семнадцати углов. Ну и, разумеется, таблицу тангенсов и таблицу котангенсов для тех же семнадцати углов… Т.е. предлагается запомнить 68 значений. Которые, между прочим, очень похожи между собой, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти — та ещё задачка…)

Мы пойдём другим путём. Заменим механическое запоминание на логику и смекалку. Тогда нам придётся зазубрить 3 (три!) значения для таблицы синусов и таблицы косинусов. И 3 (три!) значения для таблицы тангенсов и таблицы котангенсов. И всё. Шесть значений запомнить легче, чем 68, мне кажется…)

Все остальные необходимые значения мы будем получать из этих шести с помощью мощной законной шпаргалки

— тригонометрического круга. Если вы не изучали эту тему, сходите по ссылочке, не ленитесь. Этот круг не только для этого урока нужен. Он незаменим для всей тригонометрии сразу . Не пользоваться таким инструментом просто грех! Не хотите? Дело ваше. Заучивайте таблицу синусов. Таблицу косинусов. Таблицу тангенсов. Таблицу котангенсов. Все 68 значений для разнообразных углов.)

Итак, начнём. Для начала разобьём все эти особые углы на три группы.

Первая группа углов.

Рассмотрим первую группа углов из семнадцати особых . Это 5 углов: 0°, 90°, 180°, 270°, 360°.

Вот так выглядит таблица синусов косинусов тангенсов котангенсов для этих углов:

Угол х (в градусах)	0	90	180	270	360
Угол х (в радианах)	0
sin x	0	1	0	-1	0
cos x	1	0	-1	0	1
tg x	0	не сущ.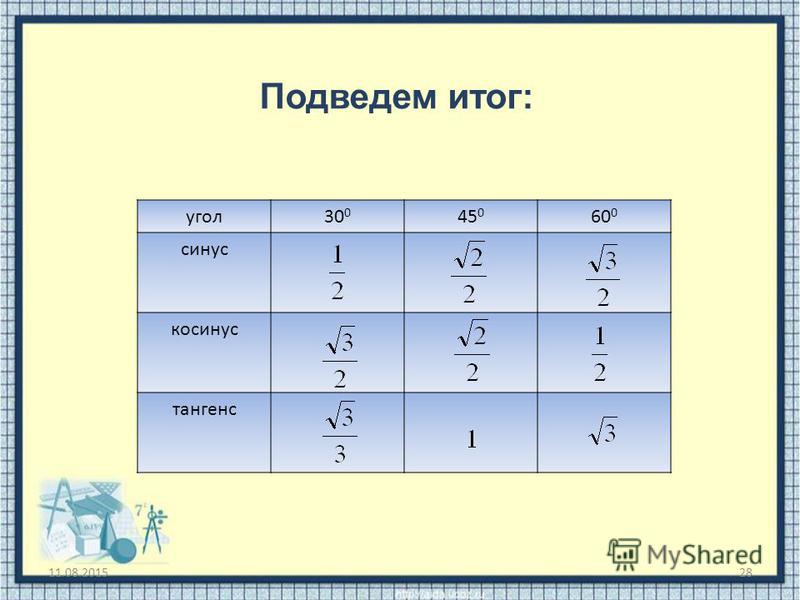	0	не сущ.	0
ctg x	не сущ.	0	не сущ.	0	не сущ.

Желающие запомнить — запоминайте. Но сразу скажу, что все эти единички и нолики очень путаются в голове. Гораздо сильнее, чем хочется.) Поэтому включаем логику и тригонометрический круг.

Рисуем круг и отмечаем на нём эти самые углы: 0°, 90°, 180°, 270°, 360°. Я эти углы отметил красными точками:

Сразу видно, в чём особенность этих углов. Да! Это углы, которые попадают точно на оси координат! Собственно, поэтому-то и путается народ… Но мы путаться не будем. Разберёмся, как находить тригонометрические функции этих углов без особого запоминания.

Кстати, положение угла в 0 градусов

полностью совпадает с положением угла в 360 градусов.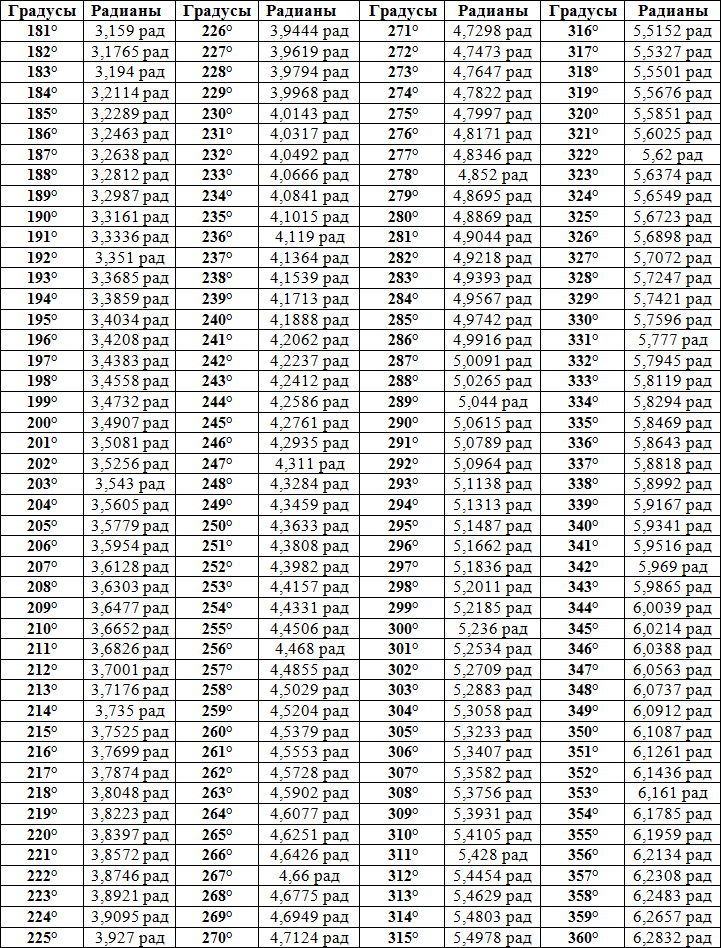 Это значит, что синусы, косинусы, тангенсы у этих углов совершенно одинаковы. Угол в 360 градусов я отметил, чтобы замкнуть круг.

Предположим, в сложной стрессовой обстановке ЕГЭ вы как-то засомневались… Чему равен синус 0 градусов? Вроде ноль… А вдруг единица?! Механическое запоминание такая штука. В суровых условиях сомнения грызть начинают…)

Спокойствие, только спокойствие!) Я подскажу вам практический приём, который выдаст стопроцентно правильный ответ и начисто уберёт все сомнения.

В качестве примера разберёмся, как чётко и надёжно определить, скажем, синус 0 градусов. А заодно, и косинус 0. Именно в этих значениях, как ни странно, частенько люди путаются.

Для этого на круге нарисуем произвольный угол х . В первой четверти, чтобы недалеко от 0 градусов было. Отметим на осях синус и косинус этого угла

х, всё чин-чинарём. Вот так:

А теперь — внимание! Уменьшим угол х , приблизим подвижную сторону к оси ОХ. Наведите курсор на картинку (или коснитесь картинки на планшете) и всё увидите.

Теперь включаем элементарную логику!. Смотрим и размышляем: как ведёт себя sinx при уменьшении угла х? При приближении угла к нулю? Он уменьшается! А cosx — увеличивается! Остаётся сообразить, что станет с синусом, когда угол схлопнется совсем? Когда подвижная сторона угла (точка А) уляжется на ось ОХ и угол станет равным нулю? Очевидно, и синус угла уйдёт в ноль. А косинус увеличится до… до… Чему равна длина подвижной стороны угла (радиус тригонометрического круга)? Единице!

Вот и ответ. Синус 0 градусов равен 0. Косинус 0 градусов равен 1. Совершенно железно и безо всяких сомнений!) Просто потому, что иначе

быть не может.

Совершенно аналогично можно узнать (или уточнить) синус 270 градусов, например. Или косинус 180. Нарисовать круг, произвольный угол в четверти рядышком с интересующей нас осью координат, мысленно подвигать сторону угла и уловить, чем станет синус и косинус, когда сторона угла уляжется на ось.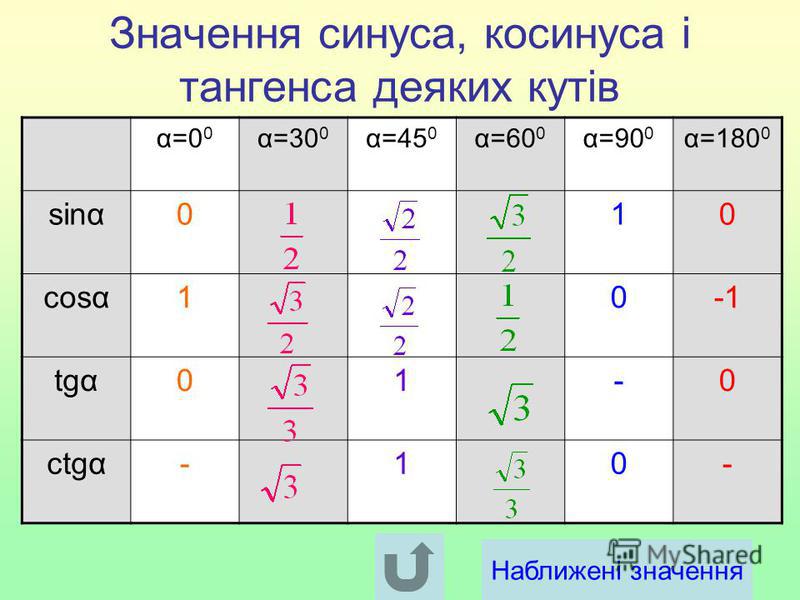 Вот и всё.

Как видите, для этой группы углов ничего заучивать не надо. Не нужна здесь таблица синусов… Да и таблица косинусов — тоже.) Кстати, после нескольких применений тригонометрического круга все эти значения запомнятся сами по себе. А если забудутся — нарисовал за 5 секунд круг и уточнил. Куда проще, чем звонить другу из туалета с риском для аттестата, правда?)

Что касается тангенса и котангенса — всё то же самое. Рисуем на круге линию тангенса (котангенса) — и всё сразу видно. Где они равны нулю, а где — не существуют. Что, не знаете про линии тангенса и котангенса? Это печально, но поправимо.) Посетили Раздел 555 Тангенс и котангенс на тригонометрическом круге — и нет проблем!

Если вы поняли, как чётко определить синус, косинус, тангенс и котангенс для этих пяти углов — я вас поздравляю! На всякий случай сообщаю, что вы теперь можете определять функции любых углов, попадающих на оси. А это и 450°, и 540°, и 1800°, и ещё бесконечное количество. ..) Отсчитал (правильно!) угол на круге — и нет проблем с функциями.

Но, как раз, с отсчётом углов и случаются проблемы да ошибки… Как их избежать, написано в уроке: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в градусах. Элементарно, но очень помогает в борьбе с ошибками.)

А вот урок: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в радианах — покруче будет. В смысле возможностей. Скажем, определить на какую из четырёх полуосей попадает угол

вы сможете за пару секунд. Я не шучу! Именно за пару секунд. Ну конечно, не только 345 «пи»…) И 121, и 16, и -1345. Любой целый коэффициент годится для мгновенного ответа.

А если угол

Подумаешь! Верный ответ получается секунд за 10. Для любого дробного значения радианов с двойкой в знаменателе.

Собственно, этим и хорош тригонометрический круг. Тем, что умение работать с некоторыми углами он автоматически расширяет на бесконечное множество углов.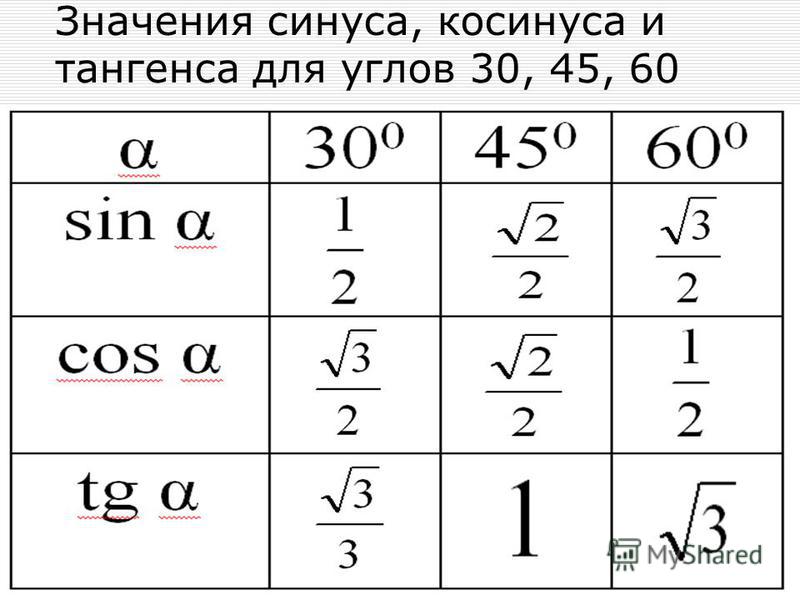

Итак, с пятью углами из семнадцати — разобрались.

Вторая группа углов.

Следующая группа углов — это углы 30°, 45° и 60°. Почему именно эти, а не, к примеру, 20, 50 и 80? Да как-то сложилось так… Исторически.) Дальше будет видно, чем хороши эти углы.

Таблица синусов косинусов тангенсов котангенсов для этих углов выглядит так:

Угол х (в градусах)	0	30	45	60	90
Угол х (в радианах)	0
sin x	0				1
cos x	1				0
tg x	0		1		не сущ.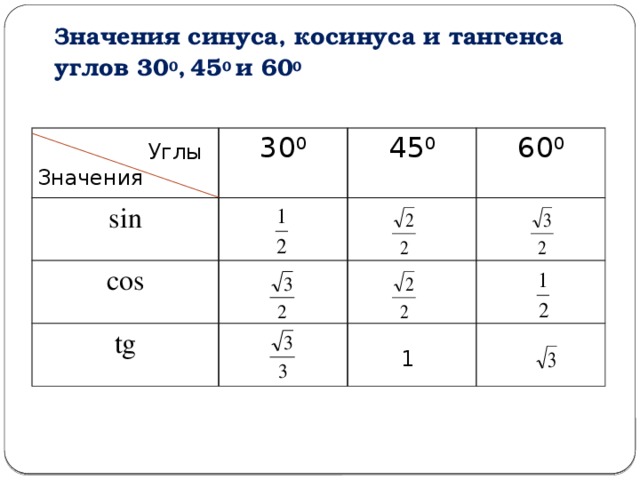
ctg x	не сущ.		1		0

Я оставил значения для 0° и 90° из предыдущей таблицы для завершённости картины.) Чтобы было видно, что эти углы лежат в первой четверти и возрастают. От 0 до 90. Это пригодится нам дальше.

Значения таблицы для углов 30°, 45° и 60° надо запомнить. Зазубрить, если хотите. Но и здесь есть возможность облегчить себе жизнь.) Обратите внимание на значения таблицы синусов этих углов. И сравните со значениями таблицы косинусов…

Да! Они одни и те же! Только расположены в обратном порядке. Углы возрастают (0, 30, 45, 60, 90) — и значения синуса возрастают от 0 до 1. Можете убедиться с калькулятором. А значения косинуса — убывают от 1 до нуля. Причём, сами значения одни и те же.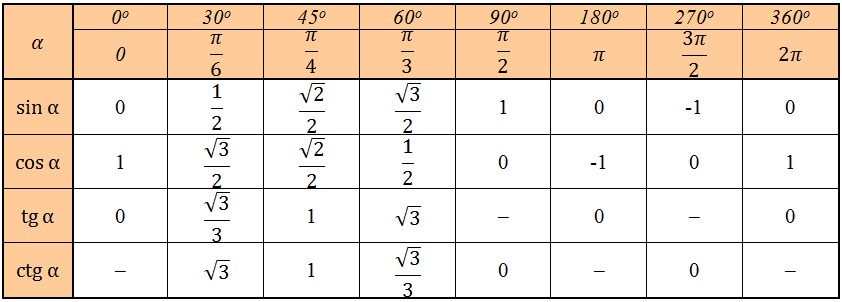 Для углов 20, 50, 80 так бы не получилось…

Отсюда полезный вывод. Достаточно выучить три значения для углов 30, 45, 60 градусов. И помнить, что у синуса они возрастают, а у косинуса — убывают. Навстречу синусу.) На половине пути (45°) они встречаются, т.е синус 45 градусов равен косинусу 45 градусов. А дальше опять расходятся… Три значения можно выучить, правда?

С тангенсами — котангенсами картина исключительно та же самая. Один в один. Только значения другие. Эти значения (ещё три!) тоже надо выучить.

Ну вот, практически всё запоминание и закончилось. Вы поняли (надеюсь), как определять значения для пяти углов попадающих на оси и выучили значения для углов 30, 45, 60 градусов. Всего 8.

Осталось разобраться с последней группой из 9 углов.

Вот эти углы:
120°; 135°; 150°; 210°; 225°; 240°; 300°; 315°; 330°. Для этих углов надо железно знать таблицу синусов, таблицу косинусов и т.д.

Кошмар, правда?)

А если добавить сюда углы, типа: 405°, 600°, или 3000° и много-много такого же красивого?)

Или углы в радианах? Например, про углы:

и многие другие, вы должны знать всё .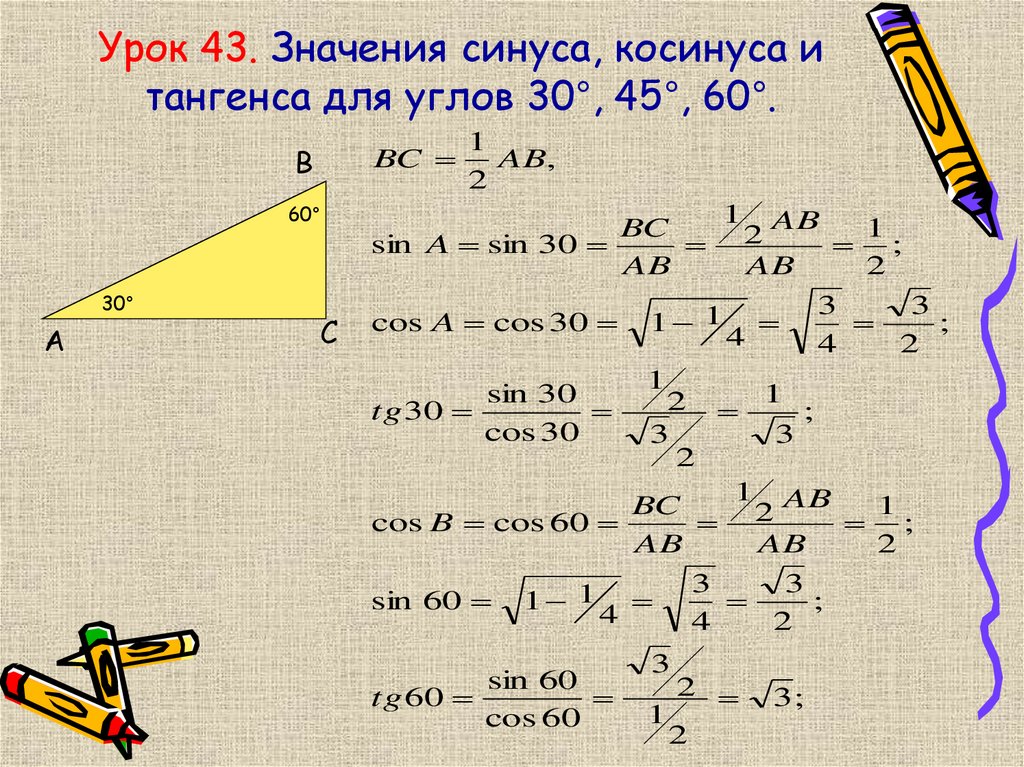

Самое забавное, что знать это всё — невозможно в принципе. Если использовать механическую память.

И очень легко, фактически элементарно — если использовать тригонометрический круг. Если вы освоите практическую работу с тригонометрическим кругом, все эти ужасные углы в градусах будут легко и элегантно сводиться к старым добрым:

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Примечание . В данной таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. Для обозначения дроби — символ «/».

См. также полезные материалы:

Для определения значения тригонометрической функции , найдите его на пересечении строки с указанием тригонометрической функции.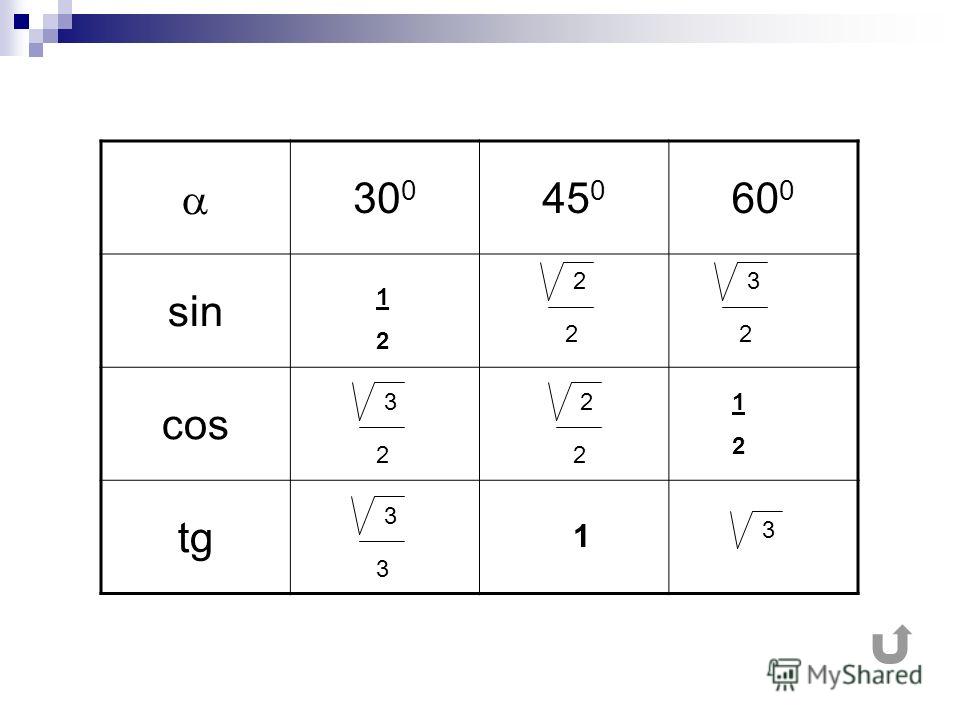 Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.

Синус пи, косинус пи, тангенс пи и других углов в радианах

Приведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах . Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан.

Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны 180 градусам.

Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180 .

Примеры :
1. Синус пи .
sin π = sin 180 = 0
таким образом, синус пи — это тоже самое, что синус 180 градусов и он равен нулю.

2. Косинус пи .
cos π = cos 180 = -1
таким образом, косинус пи — это тоже самое, что косинус 180 градусов и он равен минус единице.

3. Тангенс пи
tg π = tg 180 = 0
таким образом, тангенс пи — это тоже самое, что тангенс 180 градусов и он равен нулю.

Таблица значений синуса, косинуса, тангенса для углов 0 — 360 градусов (часто встречающиеся значения)

значение угла α (градусов)	значение угла α в радианах (через число пи)	sin (синус)	cos (косинус)	tg (тангенс)	ctg (котангенс)	sec (секанс)	cosec (косеканс)
0	0	0	1	0	—	1	—
15	π/12			2 — √3	2 + √3
30	π/6	1/2	√3/2	1/√3	√3	2/√3	2
45	π/4	√2/2	√2/2	1	1	√2	√2
60	π/3	√3/2	1/2	√3	1/√3	2	2/√3
75	5π/12			2 + √3	2 — √3
90	π/2	1	0	—	0	—	1
105	7π/12		—	— 2 — √3	√3 — 2
120	2π/3	√3/2	-1/2	-√3	-√3/3
135	3π/4	√2/2	-√2/2	-1	-1	-√2	√2
150	5π/6	1/2	-√3/2	-√3/3	-√3
180	π	0	-1	0	—	-1	—
210	7π/6	-1/2	-√3/2	√3/3	√3
240	4π/3	-√3/2	-1/2	√3	√3/3
270	3π/2	-1	0	—	0	—	-1
360	2π	0	1	0	—	1	—

Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения. Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.

Таблица значений тригонометрических функций sin, cos, tg для наиболее популярных углов

0, 15, 30, 45, 60, 90 … 360 градусов
(цифровые значения «как по таблицам Брадиса»)

значение угла α (градусов)	значение угла α в радианах	sin (синус)	cos (косинус)	tg (тангенс)	ctg (котангенс)
0	0
15		0,2588	0,9659	0,2679
30		0,5000		0,5774
45		0,7071
		0,7660
60		0,8660	0,5000	1,7321
	7π/18

Справочные данные по тригонометрическим функциям синус (sin x) и косинус (cos x). Геометрическое определение, свойства, графики, формулы. Таблица синусов и косинусов, производные, интегралы, разложения в ряды, секанс, косеканс. Выражения через комплексные переменные. Связь с гиперболическими функциями.

Геометрическое определение синуса и косинуса

|BD| — длина дуги окружности с центром в точке A .
α — угол, выраженный в радианах.

Определение
Синус (sin α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.

Косинус (cos α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.

Принятые обозначения

;
;
.

;
;
.

График функции синус, y = sin x

График функции косинус, y = cos x

Свойства синуса и косинуса

Периодичность

Функции y = sin x и y = cos x периодичны с периодом 2 π .

Четность

Функция синус — нечетная. Функция косинус — четная.

Область определения и значений, экстремумы, возрастание, убывание

Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).

	y = sin x	y = cos x
Область определения и непрерывность	— ∞	— ∞
Область значений	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Возрастание
Убывание
Максимумы, y = 1
Минимумы, y = -1
Нули, y = 0
Точки пересечения с осью ординат, x = 0	y = 0	y = 1

Основные формулы

Сумма квадратов синуса и косинуса

Формулы синуса и косинуса от суммы и разности

;
;

Формулы произведения синусов и косинусов

Формулы суммы и разности

Выражение синуса через косинус

;
;
;
.

Выражение косинуса через синус

;
;
;
.

Выражение через тангенс

; .

При , имеем:
; .

При :
; .

Таблица синусов и косинусов, тангенсов и котангенсов

В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.

Выражения через комплексные переменные

;

Формула Эйлера

{ -∞

Секанс, косеканс

Обратные функции

Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.

Арксинус, arcsin

Арккосинус, arccos

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Подсказка по запоминанию синуса, косинуса и тангенса специальных углов (тригонометрия)

ПОДСКАЗКА ПО ТРИГОНОМЕТРИИ

Существует простой способ запомнить значения синуса, косинуса и тангенса особых тригонометрических углов.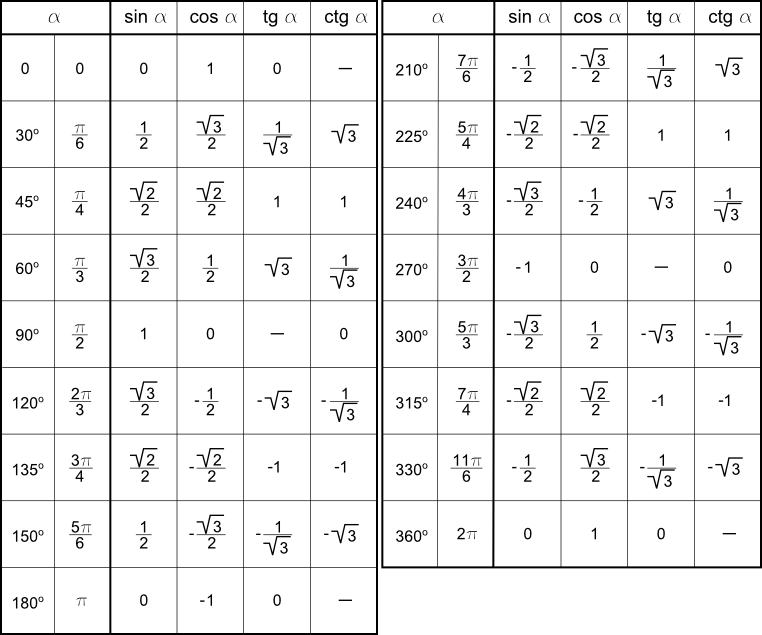

Специальные триггерные углы: 0º, 30º, 45º, 60º и 90º. Что делает эти углы особенными? Треугольник 30°-60°-90° составляет половину равностороннего треугольника, а треугольник 45°-45°-90° — половину квадрата. В обоих случаях триггерные функции (синус, косинус и тангенс) могут быть выражены в виде простых отношений.

Вот способ быстрого вычисления синуса, косинуса и тангенса углов 0°, 30°, 45°, 60° и 90°.

ШАГ 1: Специальные углы.

Запишите специальные углы по порядку.

ШАГ 2: Целые числа.

Запишите целые числа от 0 до 4 по порядку.

ШАГ 3: Квадратные корни.

Квадратный корень каждого числа.

ШАГ 4: Найдите синус тета.

Разделите каждое число на 2.

Это синус 0°, 30°, 45°, 60° и 9.0º.

Это так просто. Вот резюме:

• Напишите числа от 0 до 4.
• Квадратный корень каждого числа.
• Разделите каждое число на 2.

ШАГ 5: Найдите косинус тета.

Просто запишите предыдущие числа в обратном порядке.

Почему это работает? Потому что синус теты равен косинусу дополнения теты: sin( θ )=cos(90º– θ). То, что противоположно тэте, соседствует с ее дополнением.

ШАГ 6: Найдите тангенс тэты.

Разделите синус тета на косинус тета.

TRIG CHART

Эта диаграмма показывает все шаги вместе.

• Напишите специальные углы.
• Запишите целые числа от 0 до 4.
• Квадратный корень каждого числа.
• Разделите каждое число на 2. Это даст вам синус тета.
• Запишите числа в обратном порядке. Это дает вам косинус тета.
• Разделить две предыдущие строки (синус на косинус). Это дает вам касательную тета.

ПРИМЕЧАНИЕ

Существует два разных, но эквивалентных способа записи приведенной выше таблицы.

Это связано со следующими свойствами иррациональных чисел:

Так, например, существуют альтернативные способы выражения следующих значений триггера:

На диаграмме в этом блоге используется стандартная форма .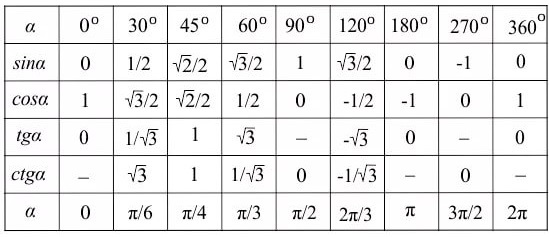 В большинстве математических курсов используется стандартная форма, что означает, что в знаменателе нет иррациональных чисел (например, корня 2).

Иногда вы найдете триггерную таблицу в другой нестандартной форме. В этой форме вы видите 1 над корнем 2 вместо корня 2 над 2, и вы видите 1 над корнем 3 вместо корня 3 над 3.

Важно понимать, что обе формы верны. Однако стандартная форма ожидается в большинстве математических курсов.

КРИС МАКМУЛЛЕН, PH.D.

Copyright © 2015 Chris McMullen, автор серии учебных пособий по математике Improve Your Math Fluency

• Практическое пособие по основам тригонометрии с ответами
• Изучите или повторите основные навыки тригонометрии
• Флэш-карты тригонометрии (для Kindle)
• Рабочая тетрадь по основам алгебры с ответами
• Системы уравнений: одновременные, замена, правило Крамера
• Другие тома охватывают обыкновенные дроби, деление в столбик, арифметику и т. д.
• Также ищите книги по четвертому измерению, астрономии, концептуальной химии и т. д.

Нравится:

Нравится Загрузка…

Таблица Sin Cos Tan — формулы, значения, примеры и часто задаваемые вопросы

Таблица Sin Cos Tan

Тригонометрические функции sin, cos и tan являются основными функциями, которые мы рассматриваем при решении тригонометрических задач. «Таблица sin cos tan» состоит из значений sin, cos и tan стандартных углов 0°, 30°, 45°, 60° и 90°, а иногда и других углов, таких как 180°, 270° и 360°.

Формула Sin Cos Tan

Три отношения sin, cos и tan имеют свои индивидуальные формулы. Предположим, что ABC — прямоугольный треугольник с прямым углом в точке B, как показано на рисунке ниже:

Три стороны прямоугольного треугольника приведены ниже:

AB = Сторона, прилежащая к углу θ

BC = Сторона, противоположная углу θ

CA = Гипотенуза к углу θ формулы cos и tan, имеем:

sin θ = Противоположная сторона / Гипотенуза = BC / CA

cos θ = Прилежащая сторона / Гипотенуза = AB / CA

tan θ = Противоположная сторона / Прилежащая сторона = CB / AB

Диаграмма Sin Cos Tan (таблица)

Посмотрим таблицу, в которой значения sin, cos и tan приведены для стандартных углов 0°, 30° (π/6), 45° (π/4), 60° (π/3) и 90° (π/2).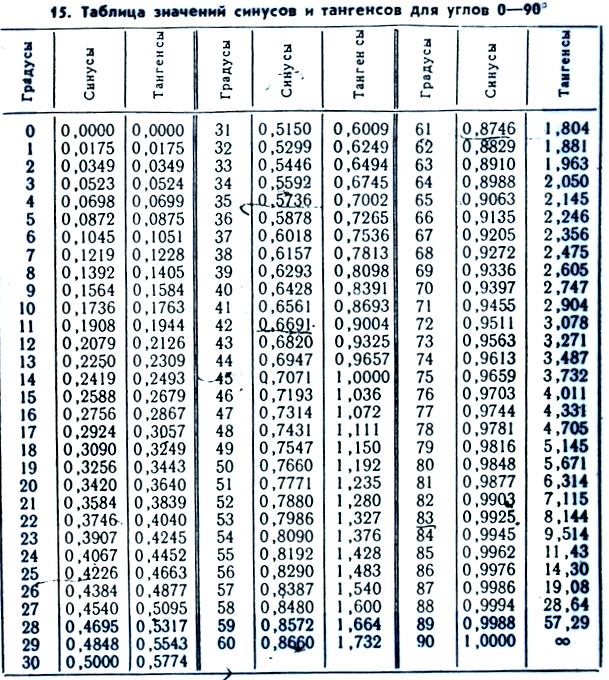

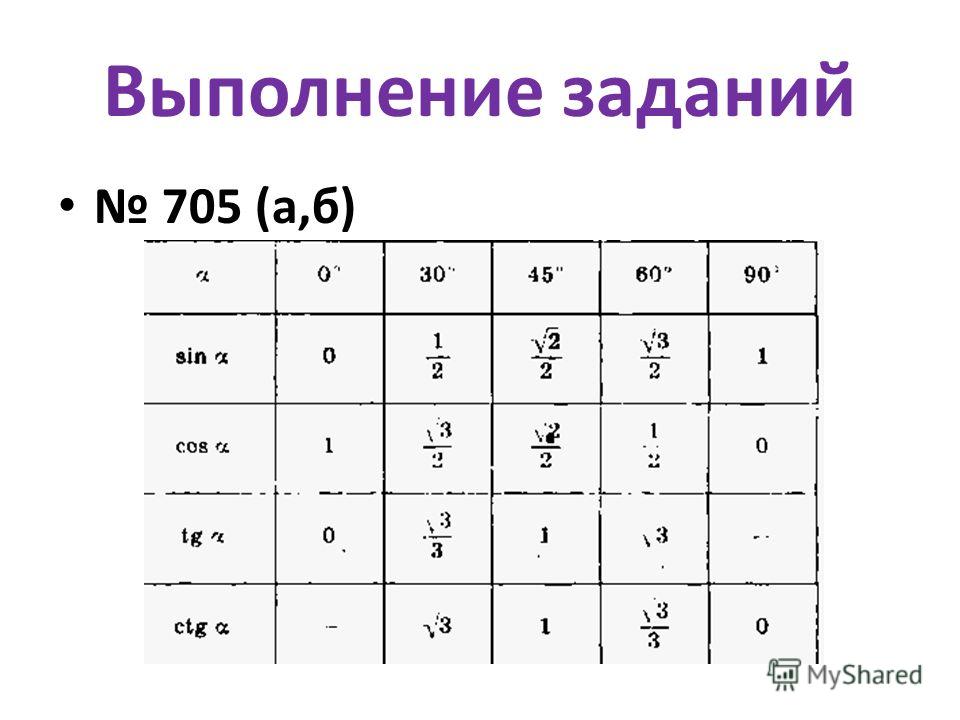
Как запомнить значения Sin Cos Tan?

Чтобы найти значения sin, cos, tan, выполните следующие действия:

• Создайте таблицу и укажите первую строку с углами 0°, 30°, 45°, 60°, 90° и напишите тригонометрическую функцию. имя в первом столбце, например грех.

• Теперь определим значения sin. Напишите числа 0, 1, 2, 3, 4 под углами 0°, 30°, 45°, 60°, 90° соответственно.

• Теперь разделите числа на 4 и найдите квадратный корень. Мы получим √(0/4), √(¼), √(2/4), √(¾) и √(4/4).

• Упростив это, мы получим значения синуса для этих 5 углов.

• Теперь для оставшихся трех углов используйте следующие формулы:

sin (180° − x) = sin x

sin (180° + x) = – (sin x)

sin (360° − x) = – (sin x)

Это означает,

sin 180° = sin (180° − 0°) = sin 0° = 0

sin 270° = sin (180° +90°) = – (sin 90°) = -1

Sin 360° = sin (360 ° − 0°) = – (sin 0°) = 0

• Теперь определим значения cos по формуле cos x = sin (90° – x).

  No related posts.