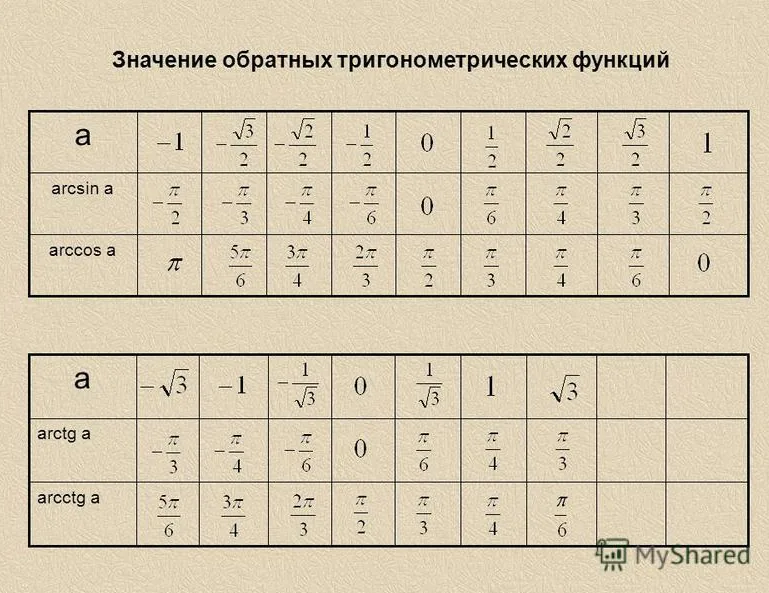
Таблицы тригонометрических функций, основные значения
Оглавление
Время чтения: 6 минут
1 887
Для начала определим понятие «тригонометрические функции».
Определение
С помощью тригонометрических функций выражается зависимость длин сторон треугольников от острых углов при гипотенузе. Употребление тригонометрических функций довольно широко. Астрономия, физика, медицина – это неполный перечень использования тригонометрических функций.
Из учебника геометрии нам известно, что к тригонометрическим функциям относятся синус (sin), косинус (cos), тангенс(tg), котангенс(ctg), секанс (sec) и косеканс (cosec). В данной статье мы разберем первые четыре.
Следуя тригонометрическим определениям функций sin, cos, tg и ctg можно найти их значения для углов 0 и 90 градусов:
sin 0⁰= 0, cos 0⁰=1, tg 0⁰=0, ctg 0⁰ — не определяется;
sin 90⁰=1, cos 90⁰=0, ctg 90⁰=0, tg 90° — не определяется.
На уроках геометрии изучая прямоугольные треугольники в основном вычисляют тригонометрические функции углов 0°, 30°, 45°, 60° и 90°.
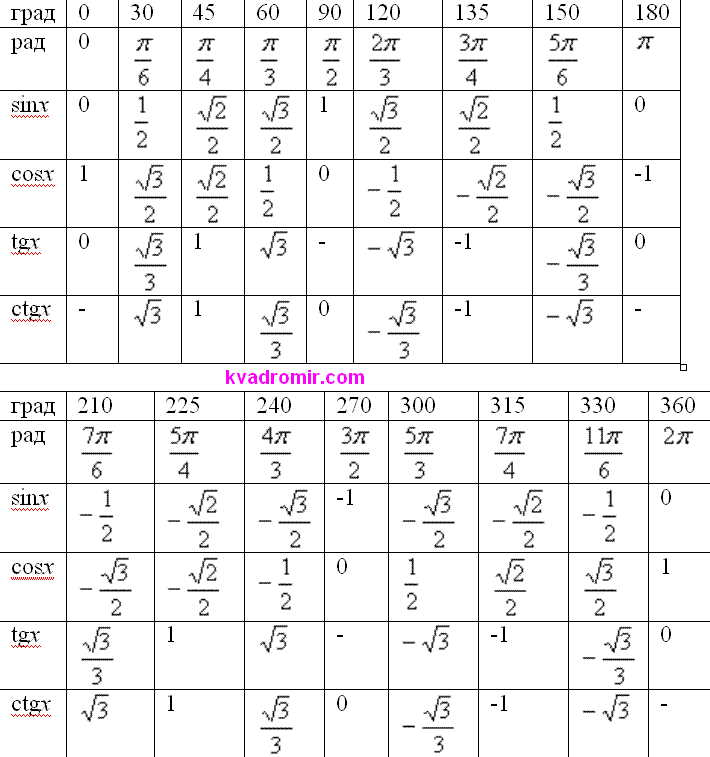
Извлеченные значения тригонометрических функций для углов были составлены в таблицу, которую называют таблица тригонометрических функций, таблица значений тригонометрических функций, таблицей тригонометрических функций углов и т.д
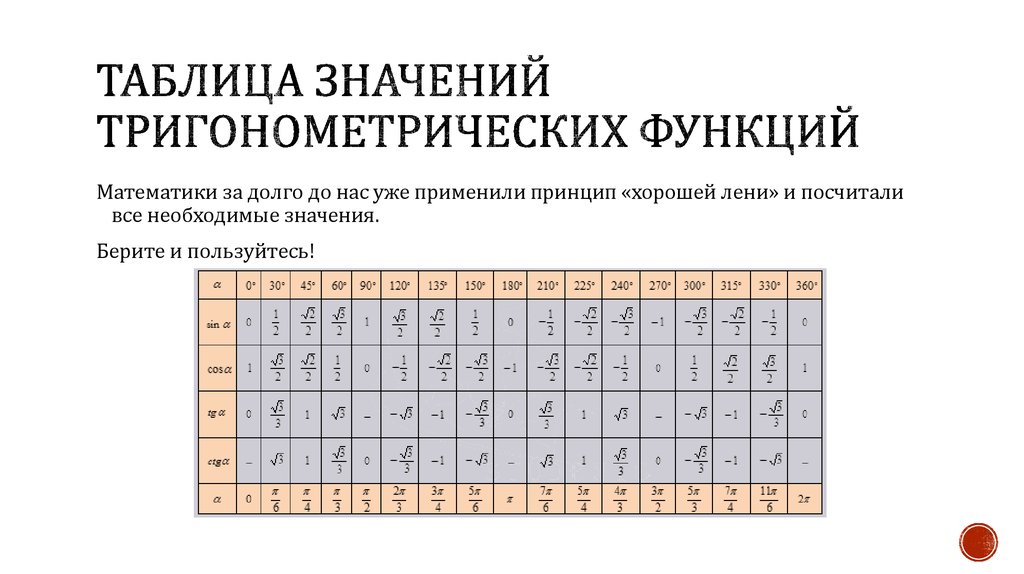
Используя формулы приведения, тригонометрическая таблица может быть увеличена до угла 360° и 2π радиан:
Используя особенности цикличности тригонометрических функций, любой угол, отличный от уже известного на 360°, может быть посчитан и занесен в таблицу. Например, тригонометрическая функция для угла 30° будет иметь такое же значение и для угла 30°+360°, и для угла 30°+2⋅360°, и для угла 30°+3⋅360° и т.д.
При помощи таблицы значений углов тригонометрических функций можно найти величину всех углов единичной окружности.
Как пользоваться таблицей тригонометрических функций
Для того чтобы посчитать тригонометрическую функцию, достаточно отыскать нужную тригонометрическую функцию и значение угла или радиан в таблице. Там где пересекаются строка с функцией и столбец со значением, будет необходимое значение тригонометрической функции.
Там где пересекаются строка с функцией и столбец со значением, будет необходимое значение тригонометрической функции.
На изображении, представленном ниже, можно проследить, каким образом определить значение тангенса 30⁰, которое равно:
Точно также используется расширенная тригонометрическая таблица. Главным достоинством ее использования является подсчет тригонометрической функции практически любого угла. Например, с легкостью мы можем найти значение
cos 1230° = cos (1230°−360°) = cos (870°−360°) = cos (510°−360°) = cos 150°:
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Таблица тригонометрических функций Брадиса
Если вам необходимо найти значение какого-то угла для его целого значения, целых градусов и целых минут, то можно воспользоваться таблицами Брадиса. Существует 2 вида таблицы: таблица для sin и cos и таблица для tg и ctg.
Таблицы Брадиса помогают найти максимально приближенное значение тригонометрических функций.
Как использовать таблицы Брадиса
Попробуем на практике как работать с таблицами Брадиса.
Пользуясь таблицей Брадиса для синусов, вычислим sin 24°36′. Для этого в столбце слева таблицы синусов и косинусов выбираем значение градусов – 24°, а в верхней строке обнаруживаем значение минут – 36′. На их пересечении получаем необходимое значение:
sin 24°36′. = 0,4163.
Для того чтобы найти значения sin 24°37′ необходимо обратиться к поправке в правой части таблицы. В нашем примере к значению 36′, которое есть в таблице, нужно прибавить поправку для 1′ , которая равна 0,0003. Получаем: sin24°37′=0,4163+0,0003=0,4166.
Чтобы посчитать значение sin24°40′ также воспользуемся поправкой в правой части таблицы. В этом случае от значения 42′, которое есть в таблице, отнимаем поправку для 2′, которая равна 0,0005. Получим: sin24°40′ = 0,4179 — 0,0005 = 0,4174.
Чтобы расчищать косинус, выполняем те же манипуляции, но градусы смотрим в правом столбце, а минуты – в нижней колонке таблицы. Например, cos 15°=0,9655. Для значений тангенса до 90° и котангенса малого угла поправок нет.
Для закрепления полученных знаний найдем tg 76°34′. Согласно таблице он 4,187.
Найдем ctg 12°36′=4,474.
Значения тригонометрических функций разных углов
Рассмотрим значения тригонометрических функций углов от 0° до 360°. Углы изобразим на единичной окружности с радиусом единица. Одна сторона угла всегда будет совпадать с положительным направлением оси абсцисс, а другая будет перемещаться при росте угла против часовой стрелки.
Синус
Синус угла — это высота, на которой оказалась точка пересечения второй стороны угла с единичной окружностью.
Для изображённого угла высота этой точки — 0,6. Значит синус этого угла равен 0,6.
При изменении угла от 0° до 360° синус изменяется. Когда угол равен нулю, его стороны схлопываются, как книжка, и совпадают с положительным направлением оси абсцисс, и вторая сторона пересекает единичную окружность на высоте 0, т.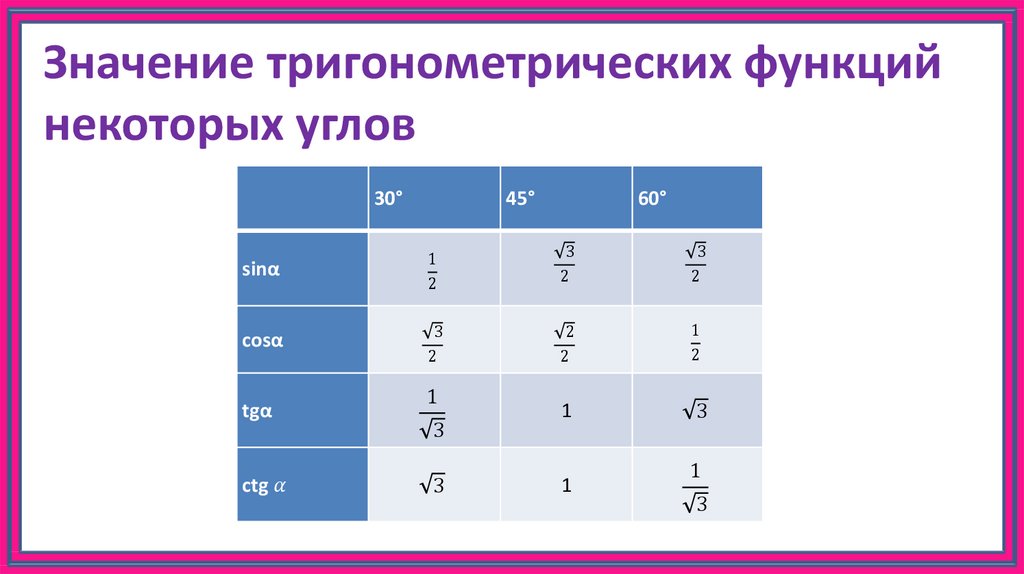 е. синус 0° равен 0. С увеличением угла синус возрастает, и синус 90° равен 1. Затем синус начинает уменьшаться, и синус 180° уже снова равен 0. Потом синус продолжает уменьшаться, и синус 270° уже равен –1. А после этого с дальнейшим увеличением угла синус обратно возрастает до нуля, и синус 360° уже равен 0.
е. синус 0° равен 0. С увеличением угла синус возрастает, и синус 90° равен 1. Затем синус начинает уменьшаться, и синус 180° уже снова равен 0. Потом синус продолжает уменьшаться, и синус 270° уже равен –1. А после этого с дальнейшим увеличением угла синус обратно возрастает до нуля, и синус 360° уже равен 0.
Косинус
Косинус угла — это абсцисса точки пересечения второй стороны с единичной окружностью.
Косинус изображённого угла равен 0,7.
При изменении угла от 0° до 360° значение косинуса изменяется. Если угол равен нулю, то обе его стороны совпадают с положительным направлением оси абсцисс и пересекает единичную окружность в самой правой точке, у которой абсцисса равна единице. Т.е. косинус 0° равен 1. При росте угла косинус уменьшается, и косинус 90° уже равен 0. Потом косинус уменьшается ещё дальше при увеличении угла, и косинус 180° равен –1. Затем косинус снова увеличивается, и косинус 270° уже равен 0. Косинус продолжает увеличиваться, и косинус 360° уже снова равен 1.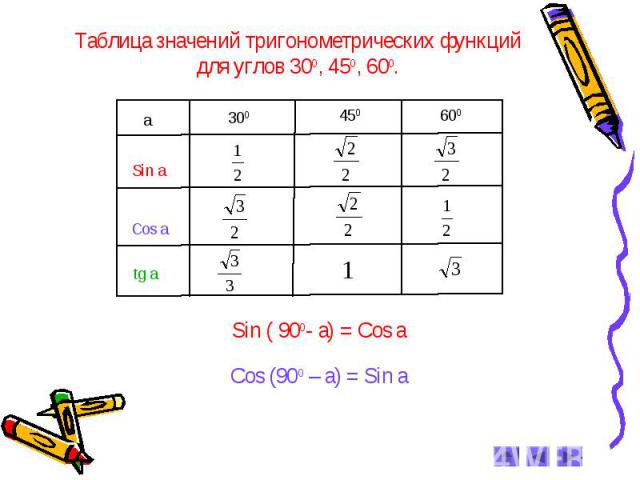 ## ТангенсТангенс — это синус делённый на косинус. Чтобы найти значение тангенса, нужно построить дополнительную прямую, которая называется ось тангенсов. И масштаб на этой прямой выбирается такой же, как и на оси синусов и косинусов, т.е. отрезок, равный радиусу окружности, принимается за 1. Так вот тангенс угла — это высота, на которой продолжение 2й стороны угла пересекает ось тангенсов.
## ТангенсТангенс — это синус делённый на косинус. Чтобы найти значение тангенса, нужно построить дополнительную прямую, которая называется ось тангенсов. И масштаб на этой прямой выбирается такой же, как и на оси синусов и косинусов, т.е. отрезок, равный радиусу окружности, принимается за 1. Так вот тангенс угла — это высота, на которой продолжение 2й стороны угла пересекает ось тангенсов.
Для изображённого угла тангенс равен примерно 1,4.
В отличие от синуса и косинуса тангенс не ограничен плюс и минус единицей, и может принимать любые значения от минус до плюс бесконечности. Посмотрим, как изменяется тангенс при изменении угла от 0° до 360°. Если угол равен нулю, то вторая сторона его так же, как и первая, пересекает ось тангенсов на высоте 0, и тангенс 0° равен 0. При увеличении угла тангенс всегда возрастает. И в первой четверти до 90° он возрастает от 0 до +∞. И наконец, тангенс 90° не определён, потому что продолжение стороны не пересекает ось тангенсов. А когда угол увеличивается снова, то сторону нужно продолжать в другом направлении. Тангенс продолжает возрастать уже от –∞ до 0, и наконец тангенс 180° равен 0. Снова возрастает угол и снова возрастает тангенс уже от 0 до +∞ и тангенс 270° опять не определён. И при увеличении угла тангенс снова возрастает от –∞ до 0, и тангенс 360° равен нулю.## КотангенсКотангенс — это косинус деленный на синус. Чтобы определить значение котангенса, нужно построить дополнительную прямую. Она называется ось котангенсов. И масштаб на этой прямой выбирается так же, как и на оси синусов и косинусов — отрезок, равный радиусу окружности, принимается за 1. Так вот котангенс угла это абсцисса, на которой продолжение 2й стороны пересекает ось котангенсов. И для изображённого угла котангенс равен примерно 1,3.
Тангенс продолжает возрастать уже от –∞ до 0, и наконец тангенс 180° равен 0. Снова возрастает угол и снова возрастает тангенс уже от 0 до +∞ и тангенс 270° опять не определён. И при увеличении угла тангенс снова возрастает от –∞ до 0, и тангенс 360° равен нулю.## КотангенсКотангенс — это косинус деленный на синус. Чтобы определить значение котангенса, нужно построить дополнительную прямую. Она называется ось котангенсов. И масштаб на этой прямой выбирается так же, как и на оси синусов и косинусов — отрезок, равный радиусу окружности, принимается за 1. Так вот котангенс угла это абсцисса, на которой продолжение 2й стороны пересекает ось котангенсов. И для изображённого угла котангенс равен примерно 1,3.
Посмотрим как меняется котангенс при изменении угла от 0° до 360°. И сразу возникает особенность — когда угол равен нулю, обе его стороны совпадают с положительным направлением оси абсцисс, и вторая сторона не пересекает ось котангенсов, и котангенс 0° не определён. При возрастании угла котангенс всё время убывает, и в первой четверти котангенс убывает от +∞ до 0.
← Предыдущий урок
Оглавление
Следующий урок →
\круг)\,.$ Все необходимые инструменты/идеи вкратце повторяются ниже.
Возникли проблемы с кратким обсуждением на этой странице?
Если да, просмотрите
ссылки выше (по порядку) — они предлагают гораздо более медленный и более мягкий подход.
| два специальных треугольника | взаимные отношения для триггерных функций | |
S ине О напротив H ипотенуза С озин А дальний H ипотенуза T агент O | Например: $\displaystyle\csc = \frac{1}{\sin}$ | |
| угол/номер | синус $\displaystyle\sin = \frac{\text{OPP}}{\text{HYP}}$ | косинус $\displaystyle\cos = \frac{\text{ADJ}}{\text{HYP}}$ | тангенс $\displaystyle\tan = \frac{\text{OPP}}{\text{ADJ}}$ | 9\circ = \frac{\pi}{2} \text{ рад}$$1$ | $0$ | не определено | $0$ ($\cot := \frac{\cos}{\sin}$) | не определено | $1$ |
Обратные числа сохраняют знак ($+/-$) исходного числа. Следовательно, во всех квадрантах:
|
Тригонометрические значения для произвольных специальных углов
В особых треугольниках и общих тригонометрических значениях
метод «Найти знаки уменьшения/размера»
был введен для нахождения
тригонометрические значения специальных углов.
Имея в наличии дополнительные инструменты и терминологию, это обсуждение
представлены здесь более широко и эффективно.
Методика RRQSS (Уменьшение ссылки/Размер квадранта/Знак)
| УМЕНЬШИТЬ: [Этот шаг необязателен. Как обсуждалось в разделе «Опорные углы», удалите все дополнительные вращения от $\,\theta\,$:
| |||
| ССЫЛКА/КВАДРАНТ: Отложить $\,\theta\,$ стандартным способом:
 $ $ Определить квадрант для $\,\theta\,.$ | |||
| РАЗМЕР/ЗНАК: Используйте эталонный угол/число, чтобы найти правильный РАЗМЕР нужного тригонометрического значения. |
ПРИМЕРЫ
В этом первом примере углы не равны 9\circ = -\frac{2}{\sqrt 3}\,$
ЗНАК: В квадранте IV котангенс отрицателен.
Таким образом: $\displaystyle\,\cot(-\frac{7\pi}{3}) = -\frac{1}{\sqrt 3}\,$
В этом последнем примере углы равны 9\циркуляр\,. $
$
$\displaystyle\frac{81\pi}{4} — 10\cdot 2\pi = \frac{81\pi}{4} — \frac{80\pi}{4} = \frac{\pi}4$
Работа с $\displaystyle\,\frac{\ pi}4\,$ вместо $\displaystyle\,\frac{81\pi}4\,.$
ЗНАК: В квадранте I косинус положителен.
Таким образом: $\displaystyle\,\cos\frac{81\pi}{4} = \frac{1}{\sqrt 2}\,$
Тригонометрические функции — формулы, графики, примеры, значения
Тригонометрические функции — это шесть основных функций, которые имеют входное значение домена в виде угла прямоугольного треугольника и числовой ответ в виде диапазона.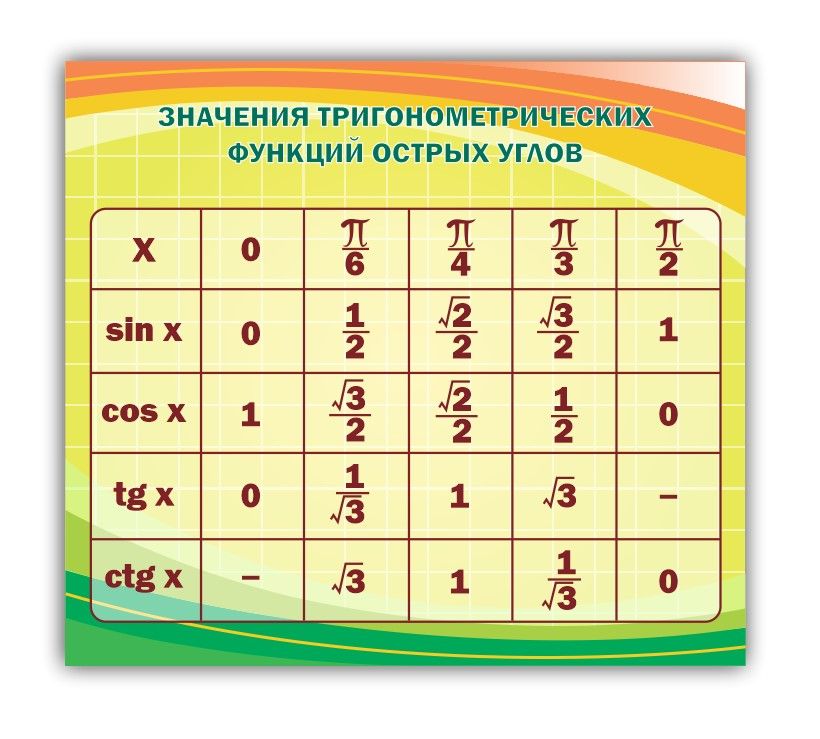 Тригонометрическая функция (также называемая «тригонометрической функцией») f(x) = sinθ имеет область определения, которая представляет собой угол θ, заданный в градусах или радианах, и диапазон [-1, 1]. Точно так же у нас есть домен и диапазон от всех других функций. Тригонометрические функции широко используются в исчислении, геометрии, алгебре.
Тригонометрическая функция (также называемая «тригонометрической функцией») f(x) = sinθ имеет область определения, которая представляет собой угол θ, заданный в градусах или радианах, и диапазон [-1, 1]. Точно так же у нас есть домен и диапазон от всех других функций. Тригонометрические функции широко используются в исчислении, геометрии, алгебре.
Здесь, в приведенном ниже содержании, мы будем стремиться понять тригонометрические функции в четырех квадрантах, их графики, область и диапазон, формулы и дифференцирование, интегрирование тригонометрических функций. Мы решим несколько примеров, используя эти шесть триггерных функций, чтобы лучше понять их и их приложения.
| 1. | Что такое тригонометрические функции? |
| 2. | Формулы тригонометрических функций |
| 3. | Значения тригонометрических функций |
| 3. | Триггерные функции в четырех квадрантах |
4. | График тригонометрических функций |
| 5. | Область и диапазон тригонометрических функций |
| 6. | Тождества тригонометрических функций |
| 7. | Обратные тригонометрические функции |
| 8. | Производные тригонометрических функций |
| 9. | Интегрирование тригонометрических функций |
| 10. | Часто задаваемые вопросы по тригонометрическим функциям |
Что такое тригонометрические функции?
В тригонометрии используются шесть основных тригонометрических функций. Эти функции являются тригонометрическими отношениями. Шесть основных тригонометрических функций — это функция синуса, функция косинуса, функция секанса, функция косеканса, функция тангенса и функция котангенса. Тригонометрические функции и тождества — отношения сторон прямоугольного треугольника. Сторонами прямоугольного треугольника являются перпендикулярная сторона, гипотенуза и основание, которые используются для вычисления значений синуса, косинуса, тангенса, секанса, косеканса и котангенса с использованием тригонометрических формул.
Формулы тригонометрических функций
У нас есть определенные формулы для нахождения значений триггерных функций с использованием сторон прямоугольного треугольника. Для записи этих формул мы используем сокращенную форму этих функций. Синус записывается как sin, косинус — как cos, тангенс — как tan, секанс — как sec, косеканс — как cosec, а котангенс — как cot. Основные формулы для нахождения тригонометрических функций следующие:
- sin θ = Перпендикуляр/Гипотенуза
- cos θ = Основание/Гипотенуза
- тангенс θ = Перпендикуляр/Основание
- с θ = гипотенуза/основание
- cosec θ = гипотенуза/перпендикуляр
- кроватка θ = основание/перпендикуляр
Как видно из приведенных выше формул, синус и косеканс обратны друг другу. Точно так же обратными парами являются косинус и секанс, тангенс и котангенс.
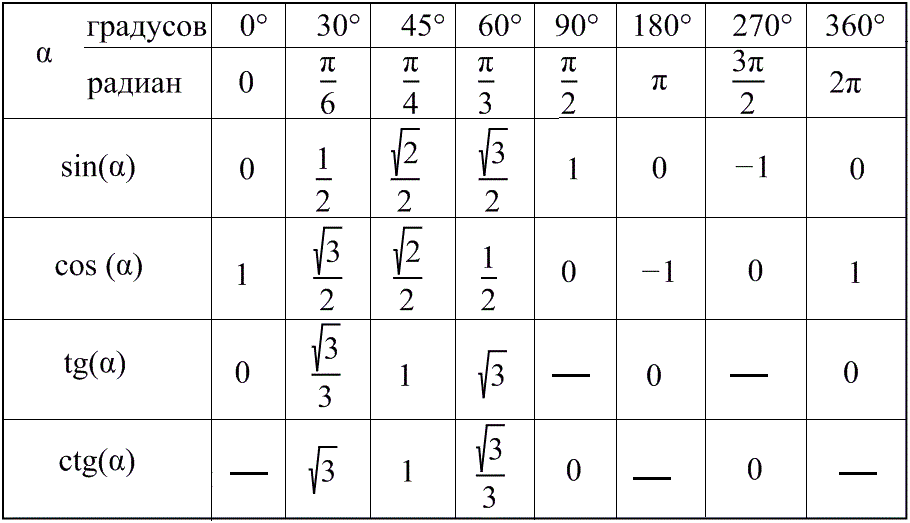
Значения тригонометрических функций
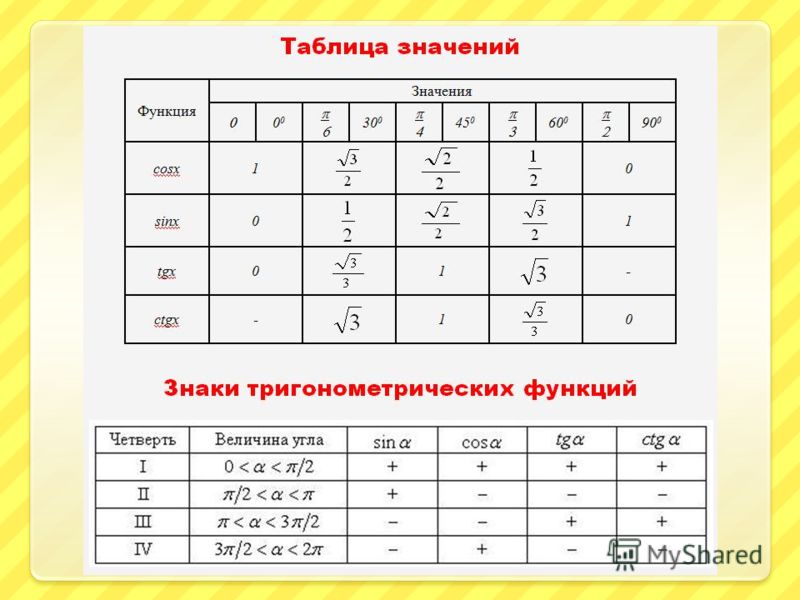
Тригонометрические функции имеют область определения θ, выраженную в градусах или радианах. Некоторые из главных значений θ для различных тригонометрических функций представлены ниже в таблице. Эти главные значения также называются стандартными значениями триггерных функций при определенных углах и часто используются в расчетах. Главные значения тригонометрических функций были получены из единичной окружности. Эти значения также удовлетворяют всем тригонометрическим формулам.
Некоторые из главных значений θ для различных тригонометрических функций представлены ниже в таблице. Эти главные значения также называются стандартными значениями триггерных функций при определенных углах и часто используются в расчетах. Главные значения тригонометрических функций были получены из единичной окружности. Эти значения также удовлетворяют всем тригонометрическим формулам.
Триггерные функции в четырех квадрантах
Угол θ является острым углом (θ < 90°) и измеряется относительно положительной оси x против часовой стрелки. Кроме того, эти триггерные функции имеют разные числовые знаки (+ или -) в разных квадрантах, которые основаны на положительной или отрицательной оси квадранта. Тригонометрические функции Sinθ, Cosecθ положительны в квадрантах I и II и отрицательны в квадрантах III и IV. Все тригонометрические функции имеют положительный диапазон в первом квадранте. Тригонометрические функции Tanθ, Cotθ положительны только в квадрантах I и III, а тригонометрические отношения Cosθ, Secθ положительны только в квадрантах I и IV.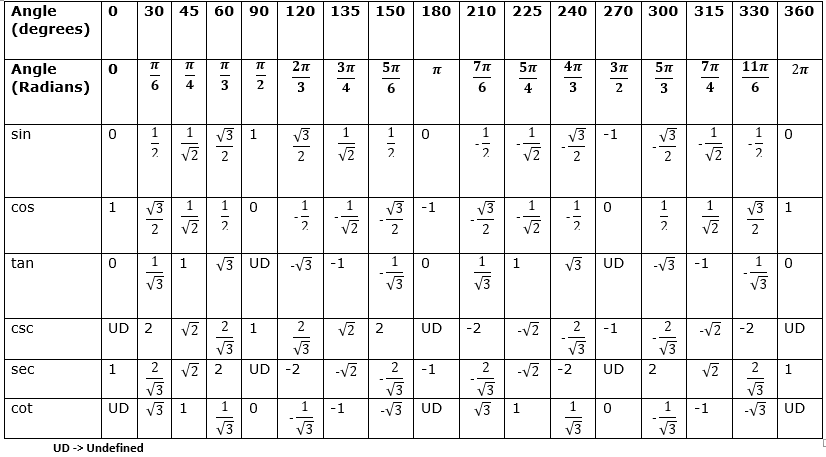
Тригонометрические функции имеют значения θ, (90° — θ) в первом квадранте. Тождества кофункций обеспечивают взаимосвязь между различными дополнительными тригонометрическими функциями для угла (90 ° — θ).
- sin(90°-θ) = cos θ
- cos(90°-θ) = sin θ
- тангенс (90°-θ) = раскладушка θ
- раскладушка (90°-θ) = тангенс θ
- сек (90°-θ) = cosec θ
- косек(90°-θ) = сек θ
Значение домена θ для различных тригонометрических функций во втором квадранте равно (π/2 + θ, π — θ), в третьем квадранте равно (π + θ, 3π/2 — θ), а в четвертом квадранте равно ( 3π/2 + θ, 2π — θ). Для π/2, 3π/2 тригонометрические величины изменяются как их дополнительные отношения, такие как Sinθ⇔Cosθ, Tanθ⇔Cotθ, Secθ⇔Cosecθ. Для π, 2π тригонометрические значения остаются прежними. Изменение тригонометрических отношений в разных квадрантах и углах можно понять из приведенной ниже таблицы.
| Тригонометрическое отношение | I — Квадрант | II — Квадрант | III квадрант | IV квадрант | |||
|---|---|---|---|---|---|---|---|
| θ | π/2 — θ | π/2 + θ | π — θ | π + θ | 3π/2 — θ | 3π/2 + θ | 2π — θ |
| Sinθ | Косθ | Косθ | Синθ | -Sinθ | -Косθ | -Косθ | -Sinθ |
| Cosθ | Синθ | -Sinθ | -Косθ | -Косθ | -Sinθ | Синθ | Косθ |
| Танθ | Котθ | — Кот θ | -Tanθ | Танθ | Котθ | — Кот θ | — Тан θ |
| Кот θ | Танθ | — Тан θ | — Кот θ | Котθ | Танθ | — Тан θ | — Кот θ |
| сек θ | Косекθ | -Косекθ | -сек | -сек | -Косекθ | Косекθ | сек θ |
| Cosecθ | сек θ | сек θ | Косекθ | -Косекθ | -сек | -сек | -Косекθ |
График тригонометрических функций
Графики тригонометрических функций имеют значение домена θ, представленное по горизонтальной оси x, и значение диапазона, представленное по вертикальной оси y. Графики Sinθ и Tanθ проходят через начало координат, а графики других тригонометрических функций через начало координат не проходят. Диапазон Sinθ и Cosθ ограничен [-1, 1]. Диапазон бесконечных значений представлен пунктирными линиями.
Графики Sinθ и Tanθ проходят через начало координат, а графики других тригонометрических функций через начало координат не проходят. Диапазон Sinθ и Cosθ ограничен [-1, 1]. Диапазон бесконечных значений представлен пунктирными линиями.
Область определения и диапазон тригонометрических функций
Значение θ представляет область определения тригонометрических функций, а результирующее значение представляет собой диапазон тригонометрической функции. Значения домена θ указаны в градусах или радианах, а диапазон представляет собой действительное числовое значение. Как правило, область определения тригонометрической функции представляет собой действительное числовое значение, но в некоторых случаях некоторые значения углов исключаются, поскольку это приводит к бесконечному значению диапазона. Тригонометрические функции являются периодическими функциями. В таблице ниже представлены область и диапазон шести тригонометрических функций.
| Тригонометрические функции | Домен | Диапазон |
|---|---|---|
| Sinθ | (-∞, + ∞) | [-1, +1] |
| Cosθ | (-∞ +∞) | [-1, +1] |
| Танθ | Р — (2n + 1)π/2 | (-∞, +∞) |
| Кот θ | Р — номер | (-∞, +∞) |
| сек θ | Р — (2n + 1)π/2 | (-∞, -1] U [+1, +∞) |
| Cosecθ | Р — номер | (-∞, -1] U [+1, +∞) |
Тождества тригонометрических функций
Тождества тригонометрических функций в широком смысле делятся на тождества взаимности, формулы Пифагора, тождества суммы и разности тригонометрических функций, формулы для кратных и дольных углов, тождеств суммы и произведения.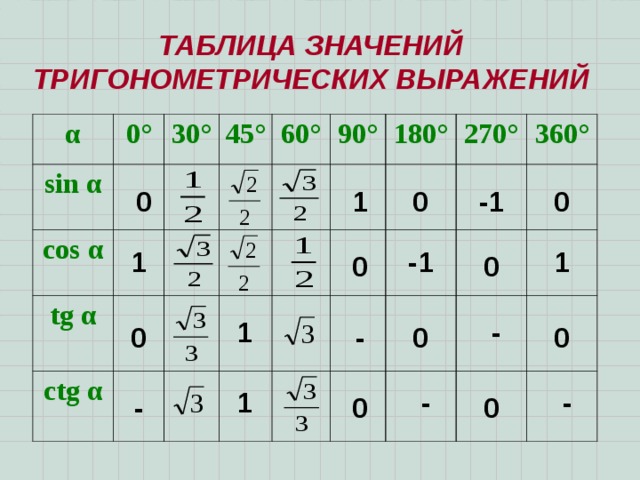 Все приведенные ниже формулы можно легко вывести, используя отношение сторон прямоугольного треугольника. Более высокие формулы могут быть получены с использованием основных формул тригонометрических функций. Взаимные тождества часто используются для упрощения тригонометрических задач.
Все приведенные ниже формулы можно легко вывести, используя отношение сторон прямоугольного треугольника. Более высокие формулы могут быть получены с использованием основных формул тригонометрических функций. Взаимные тождества часто используются для упрощения тригонометрических задач.
Взаимные тождества
- cosec θ = 1/sin θ
- сек θ = 1/cos θ
- раскладушка θ = 1/загар θ
- sin θ = 1/косек θ
- cos θ = 1/сек θ
- загар θ = 1/кот θ
Пифагорейские тождества
- Sin 2 θ + Cos 2 θ = 1
- 1 + Тан 2 θ = Секунда 2 θ
- 1 + Cot 2 θ = Cosec 2 θ
Тождества суммы и разности
- sin(x+y) = sin(x)cos(y) + cos(x)sin(y)
- cos(x+y) = cos(x)cos(y) – sin(x)sin(y)
- тангенс(х+у) = (тангенс х + тангенс у)/(1-тангенс х тангенс у)
- sin(x–y) = sin(x)cos(y) – cos(x)sin(y)
- cos(x–y) = cos(x)cos(y) + sin(x)sin(y)
- тангенс(х-у) = (тангенс х-тангенс у)/(1+тангенс х тангенс у)
Полуугольные тождества
- sin A/2 = ±√[(1 — cos A) / 2]
- cos A/2 = ±√[(1 + cos A) / 2]
- tan A/2 = ±√[(1 — cos A) / (1 + cos A)] (или) sin A / (1 + cos A) (или) (1 — cos A) / sin A
Тождества с двойным углом
- sin(2x) = 2sin(x) cos(x) = [2tan x/(1+tan 2 x)]
- cos(2x) = cos 2 (x)–sin 2 (x) = [(1-tan 2 x)/(1+tan 2 x)]
- cos(2x) = 2cos 2 (x)−1 = 1–2sin 2 (x)
- tan(2x) = [2tan(x)]/[1−tan 2 (x)]
- раскладушка(2x) = [раскладушка 2 (x) — 1]/[2раскладушка(x)]
- сек (2x) = сек 2 x/(2-сек 2 x)
- косек (2x) = (сек х косек х)/2
Трехугольные тождества
- Sin 3x = 3sin x – 4sin 3 x
- Cos 3x = 4cos 3 x — 3cos x
- Tan 3x = [3tanx-tan 3 x]/[1-3tan 2 х]
Идентификаторы продуктов
- 2sinx⋅cosy=sin(x+y)+sin(x−y)
- 2cosx⋅cosy=cos(x+y)+cos(x−y)
- 2sinx⋅siny=cos(x−y)−cos(x+y)
Сумма тождеств
- sinx+siny=2sin((x+y)/2) .
 cos((х-у)/2)
cos((х-у)/2) - sinx-siny=2cos((x+y)/2) . грех((х-у)/2)
- cosx+cosy=2cos((x+y)/2) . cos((х-у)/2)
- cosx-cosy=-2sin((x+y)/2 . sin((x-y)/2)
Обратные тригонометрические функции
Обратные тригонометрические функции являются обратными отношениями основных тригонометрических отношений. Здесь базовую тригонометрическую функцию Sin θ = x можно изменить на Sin -1 x = θ. Здесь x может иметь значения в целых числах, десятичных дробях, дробях или показателях степени. Для θ = 30° имеем θ = Sin -1 (1/2). Все тригонометрические формулы могут быть преобразованы в формулы обратной тригонометрической функции.
Произвольные значения: Формула обратной тригонометрической пропорции для произвольных значений применима ко всем шести тригонометрическим функциям. Для обратных тригонометрических функций синуса, тангенса, косеканса отрицательные значения переводятся как отрицательные значения функции.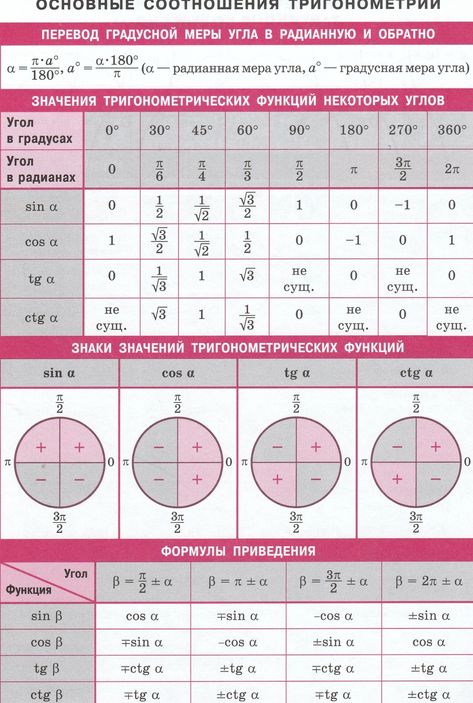 А для функций косеканса, секанса, котангенса минусы домена переводятся как вычитание функции из значения π.
А для функций косеканса, секанса, котангенса минусы домена переводятся как вычитание функции из значения π.
- Sin -1 (-x) = -Sin -1 x
- Тан -1 (-x) = -Tan -1 x
- Cosec -1 (-x) = -Cosec -1 x
- Cos -1 (-x) = π — Cos -1 x
- Секунда -1 (-x) = π — Секунда -1 x
- Детская кроватка -1 (-x) = π — Детская кроватка -1 x
Обратные тригонометрические функции обратных и дополнительных функций аналогичны основным тригонометрическим функциям. Взаимоотношения основных тригонометрических функций, синуса-косеканса, косеканса, тангенса-котангенса, можно интерпретировать для обратных тригонометрических функций. Также дополнительные функции, так как косинус, тангенс-котангенс и секанс-косеканс, можно интерпретировать как:
Обратные функции: Обратная тригонометрическая формула арксинуса, арккосинуса и арктангенса также может быть выражена в следующих формах.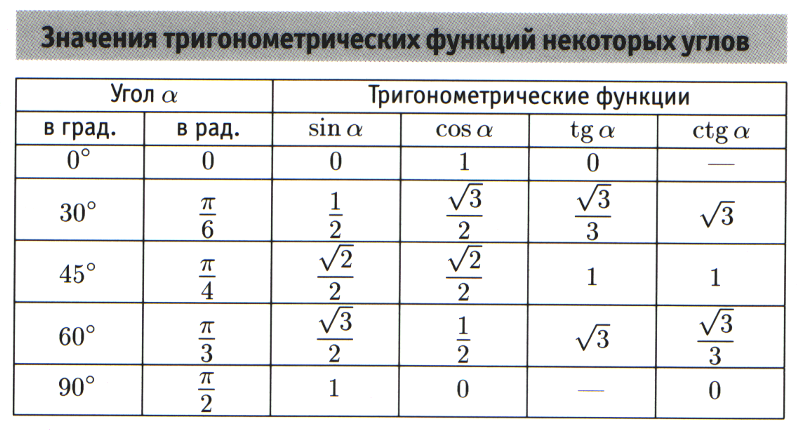
- Sin -1 x = Cosec -1 1/x
- Cos -1 x = сек -1 1/x
- Желто-коричневый -1 x = Детская кроватка -1 1/x
Дополнительные функции: Дополнительные функции синуса-косинуса, тангенса-котангенса, секанса-косеканса дают в сумме π/2.
- Sin -1 x + Cos -1 x = π/2
- Желто-коричневый -1 x + Детская кроватка -1 x = π/2
- сек -1 х + косек -1 х = π/2
Производные тригонометрических функций
Дифференцирование тригонометрических функций дает наклон касательной кривой. Дифференцирование Sinx есть Cosx, и здесь, применяя значение x в градусах для Cosx, мы можем получить наклон касательной кривой Sinx в конкретной точке. Формулы дифференцирования тригонометрических функций полезны для нахождения уравнения касательной, нормали, для нахождения погрешностей в вычислениях.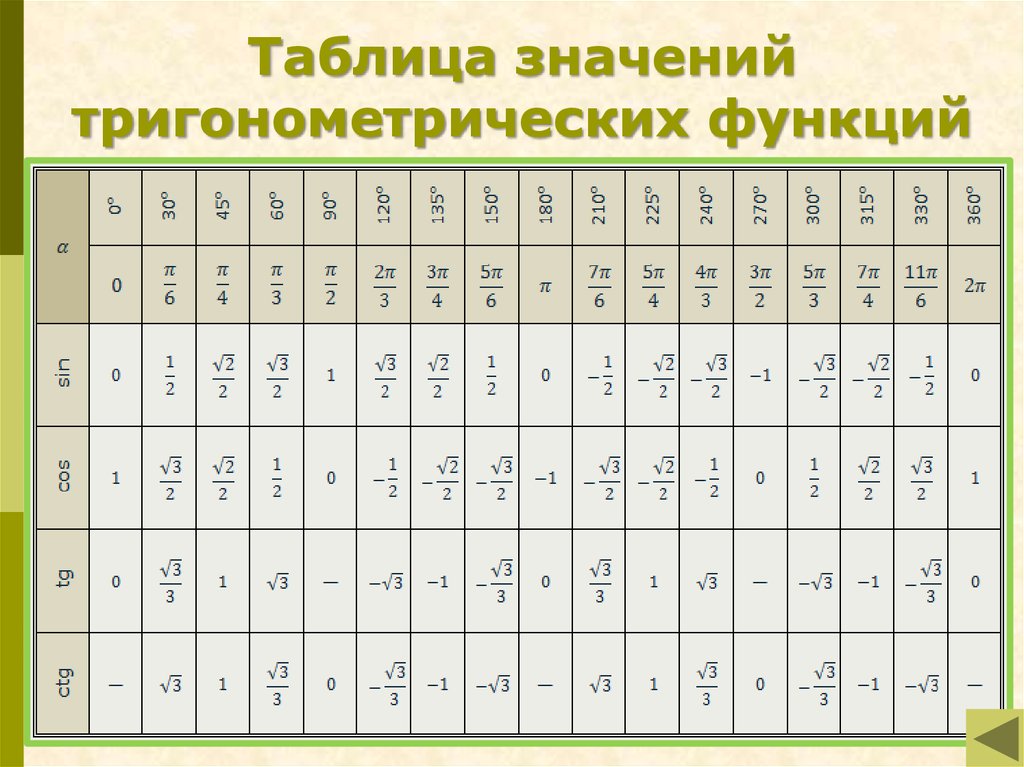
- д/дх. Sinx = Cosx
- д/дх. Cosx = -Sinx
- д/дх. Tanx = Секунда 2 x
- д/дх. Cotx = -Cosec 2 x
- d/dx.Secx = Secx.Tanx
- д/дх. Cosecx = — Cosecx.Cotx
Интегрирование тригонометрической функции
Интегрирование тригонометрических функций помогает найти площадь под графиком тригонометрической функции. Как правило, площадь под графиком тригонометрической функции может быть рассчитана относительно любой из осевых линий и в пределах определенного предельного значения. Интегрирование тригонометрических функций помогает найти площадь плоских поверхностей неправильной формы.
- ∫ cosx dx = sinx + C
- ∫ sinxdx = -cosx + C
- ∫ сек 2 х dx = tanx + C
- ∫ cosec 2 x dx = -cotx + C
- ∫ secx.tanx dx = secx + C
- ∫ cosecx.cotx dx = -cosecx + C
- ∫ tanx dx = log|secx| + С
- ∫ cotx.
 dx = log|sinx| + С
dx = log|sinx| + С - ∫ secx dx = log|secx + tanx| + С
- ∫ cosecx.dx = log|cosecx — cotx| + С
См. также
Следующие ссылки по теме помогают лучше понять тригонометрические тождества.
- Тригонометрия
- Суммировать формулы произведения
- Алгебраические тождества
Решенные примеры на тригонометрические функции
Пример 1: Найдите значение Sin75°.
Решение:
Цель состоит в том, чтобы найти значение Sin75°.
Здесь мы можем использовать формулу Sin(A + B) = SinA.CosB + CosA.SinB.
Здесь A = 30° и B = 45°
Sin 75° = Sin(30° + 45°)
= Sin30°.Cos45° + Cos30°.Sin45°
= (1/2) (1/√2) + (√3/2) (1/√2)
= 1/2√2 + √3/2√2
= (√3 + 1) / 2√2
Ответ: Sin75° = (√3 + 1) / 2√2
Пример 2: Найдите значение тригонометрических функций для заданного значения 12Tanθ = 5,
Решение:
Указано 12Tanθ = 5, и у нас есть Tanθ = 5/12
Tanθ = перпендикуляр/основа = 5/12
Применение теории Pythagorean.
 2 + Основание 2
2 + Основание 2 HYP 2 = 12 2 + 5 2
= 144 + 25
= 169
Hyp = 13
в округе.
Sinθ = Perp/Hyp = 5/13
Cosθ = базовый/Hyp = 12/13
Cotθ = базовый/Perp = 12/5
Secθ = Hyp/базовый = 13/12
Cosecθ = Hyp/Perp = 13/5
Пример 3: Найдите значение произведения шести тригонометрических функций.
Решение: Мы знаем, что cosec x является обратной величиной sin x, а sec x является обратной величиной cos x. Кроме того, tan x можно записать как отношение sin x и cos x, cot x можно записать как отношение cos x и sin x. Итак, у нас
sinx × cosx × tanx × cotx × secx × cosecx = sinx × cosx × (sinx/cosx) × (cosx/sinx) × (1/cosx) × (1/sinx)
= (sinx × cosx) / (sinx × cosx) × (sinx/cosx) × (cosx/sinx)
= 1 × 1
= 1
Ответ: Произведение шести тригонометрических функций равно 1.

перейти к слайду перейти к слайду перейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по тригонометрическим функциям
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о тригонометрических функциях
Что такое шесть тригонометрических функций?
Тригонометрические функции являются результатом отношения сторон прямоугольного треугольника. Для трех сторон треугольника, таких как гипотенуза, основание, высота, и для угла между гипотенузой и основанием, равного θ, значение шести тригонометрических отношений следующее.
- Sinθ = Высота/Гипотенуза
- Cosθ = Основание/Гипотенуза
- Tanθ = высота/база
- Cotθ = База/Высота
- секθ = гипотенуза/основание
- Cosecθ = Гипотенуза/Высота
Как найти тригонометрические функции?
Тригонометрические функции представляют собой отношение сторон прямоугольного треугольника. Далее также применим правило Пифагора Гипотенуза 2 = Высота 2 + база 2 . Кроме того, тригонометрические функции имеют разные значения для разных значений угла между гипотенузой и основанием прямоугольного треугольника.
Далее также применим правило Пифагора Гипотенуза 2 = Высота 2 + база 2 . Кроме того, тригонометрические функции имеют разные значения для разных значений угла между гипотенузой и основанием прямоугольного треугольника.
Что такое область определения и область значений тригонометрических функций?
Область определения тригонометрической функции — это значение θ в Sinθ, а диапазон — конечное числовое значение Sinθ. Это понятие можно аналогичным образом применить ко всем другим тригонометрическим функциям. Далее значения домена могут быть любыми угловыми значениями, но здесь мы имеем главные значения углов как 0°, 30°, 45°, 60°, 90°. И диапазоном являются самые высокие и самые низкие значения, которые получены. Это [-1, 1] для sinθ, cosθ и (-∞, +∞) для tanθ, cotθ.
Какой результат умножения шести тригонометрических функций?
Результат умножения шести тригонометрических функций выглядит следующим образом. Sinθ.Cosθ.Tanθ.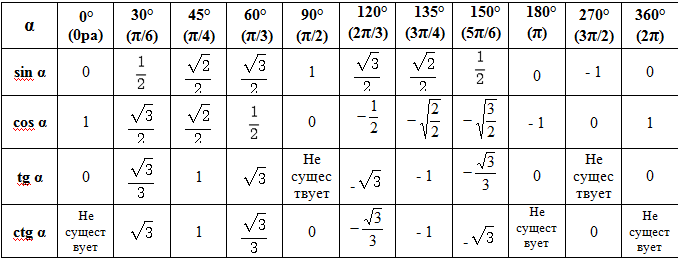 Cotθ.Secθ.Cosecθ = Sinθ.Cosθ.Sinθ/Cosθ.Cosθ/Sinθ.1/Cosθ.1/Sinθ = 1.
Cotθ.Secθ.Cosecθ = Sinθ.Cosθ.Sinθ/Cosθ.Cosθ/Sinθ.1/Cosθ.1/Sinθ = 1.
Каково общее решение тригонометрической функции Sinx?
Общее решение Sinx равно nπ + (-1) н х. Это представляет все более высокие значения угла Sinx. Для x = π/3 мы имеем более высокие значения x как 2π/3, 7π3, а общее решение x равно nπ +(-1) n π/3.
Каково общее решение тригонометрической функции Cosx?
Общее решение Cosx равно 2nπ + x. Это общее решение представляет все более высокие значения угла Cosx. Для x = π/4 высшие значения x равны 7π/4, 9π/4, а общее решение x равно 2nπ + π/4.
Каково общее решение триггерной функции Tanx?
Общее решение Tanx равно nπ + x. Общее решение представляет собой все более высокие значения углов Tanx. При x = π/6 более высокие значения x равны 7π/6, 13π/6, а общее решение x равно nπ + π/6.
Как дифференцировать тригонометрические функции?
Дифференцирование тригонометрической функции приводит к наклону касательной к кривой тригонометрической функции. Дифференцирование sinx приводит к cosx, который путем замены значения x в градусах дает значение наклона касательной к кривой sinx. Дифференциация рассчитывается с использованием первого принципа производных. Далее, у нас есть дифференцирование шести тригонометрических функций следующим образом.
Дифференцирование sinx приводит к cosx, который путем замены значения x в градусах дает значение наклона касательной к кривой sinx. Дифференциация рассчитывается с использованием первого принципа производных. Далее, у нас есть дифференцирование шести тригонометрических функций следующим образом.
- д/дх. Sinx = Cosx
- д/дх. Cosx = -Sinx
- д/дх. Tanx = Секунда 2 x
- д/дх. Cotx = -Cosec 2 x
- d/dx.Secx = Secx.Tanx
- д/дх. Cosecx = — Cosecx.Cotx
Каковы приложения тригонометрических функций?
Тригонометрические функции имеют множество приложений в исчислении алгебры координатной геометрии. Наклон линии, нормальная форма уравнения лжи, параметрические координаты параболы, эллипса, гиперболы вычисляются и представляются с помощью тригонометрических функций. Тригонометрические функции можно использовать для нахождения высоты дерева при заданном расстоянии дерева от точки наблюдения.

 cos((х-у)/2)
cos((х-у)/2) dx = log|sinx| + С
dx = log|sinx| + С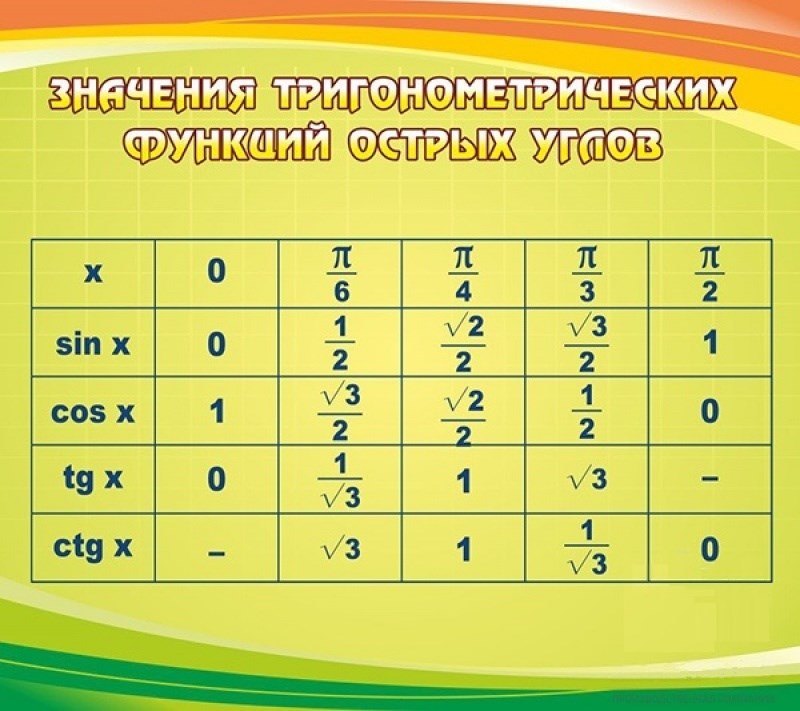 2 + Основание 2
2 + Основание 2