Значения выражения: Вычисление значения выражения — урок. Математика, 2 класс.

Страница 44 — ГДЗ Математика 3 класс. Моро, Бантова. Учебник часть 1

1. Главная
2. ГДЗ
3. 3 класс
4. Математика
5. Моро, Бантова. Учебник
6. Табличное умножение и деление
7. Страница 44. Часть 1

Вернуться к содержанию учебника

Табличное умножение и деление

Вопрос

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

1. 1) Увеличь в 6 раз числа: 3, 5, 7, 9, 10, 1.

2) Уменьши в 6 раз числа: 12, 24, 48, 42, 60, 6.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

2.

6 • 8	54 : 6	52 — 20 : 5	36 — 4 • 9	24 : 8
7 • 6	48 : 6	49 + 30 : 6	40 + 7 • 5	18 : 6
6 • 6	42 : 7	18 : 9 + 58	60 — 8 • 4	42 : 6

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

3. Запиши выражение. Найди знамение частного чисел 24 и с, если с = 3, с = 4, с = 24, с — 1.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

4. Найди ошибки и реши уравнения правильно.

21 — х = 14	х + 9 = 63	10 + х = 100
х = 21 + 14	х = 63 + 9	х = 100 — 10

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

5. Тетрадь в клетку стоит р., альбом на р. дороже, чем тетрадь, а ручка на р. дешев­ле, чем альбом.

Дополни условие задами и поставь вопрос так, чтобы задача решалась двумя действиями.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

В школьной столовой было 50 кг сахару. Его расходовали 6 дней, по 2 кг каждый день. Сколько килограммов сахару осталось?

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

Вычисли значение выражения 4 • b, если b = 3, b = 5, b = 6, b = 10.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

Занимательные рамки:

Ответ

Поделись с друзьями в социальных сетях:

Вернуться к содержанию учебника

---

Номер №342 — ГДЗ по Математике 6 класс: Мерзляк А.Г.

войтирегистрация

1. Ответкин
2. Решебники
3. 6 класс
4. Математика
5. Мерзляк
6. Номер №342

НАЗАД К СОДЕРЖАНИЮ

2014г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №342 по учебнику Математика. 6 класс. Учебник для учащихся общеобразовательных организаций / А. Г. Мерзляк, В.Б. Полонский, М.С. Якир. Вентана-Граф. 2014г.

2019г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №342 по учебнику Математика. 6 класс. Учебник / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, под редакцией В.Е. Подольского. Вентана-Граф. 4 издание, дополненное. 2019г.

Условие 20142019г.

Cменить на 2014 г.

Cменить на 2019 г.

Найдите значение выражения:
1) 15 4/9−4 4/9*3 3/8 ;
2) 81/88*(6−1 13/15*1 19/21) ;
3) (5 1/16−1 1/8)*( 5/6+ 3/14) ;
4) 5 1/16−1 1/8*( 5/6+ 3/14).

Найдите значение выражения:
1) 15 4/9−4 4/9*3 3/8 ;
2) 81/88*(6−1 13/15*1 19/21) ;
3) (5 1/16−1 1/8)*( 5/6+ 3/14) ;
4) 5 1/16−1 1/8*( 5/6+ 3/14).

Решение 1

Решение 1

Решение 2

Решение 2

Решение 3

Решение 3

Решение 4

Решение 4

Решение 5

Решение 5

ГДЗ по Математике 6 класс: Виленкин Н.Я.

Издатель: Виленкин Н.Я. Жохов В.И. Чесноков А.С. Шварцбурд С.И. 2013/2019г.

ГДЗ по Математике 6 класс: Мерзляк А.Г.

Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г. / 2019г.

ГДЗ по Математике 6 класс: Никольский С.М.

Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников, А.В. Шевкин. 2015-2018

ГДЗ по Математике 6 класс: Зубарева, Мордкович

Издатель: И.И. Зубарева, А.Г. Мордкович. 2014-2019г.

ГДЗ по Математике 6 класс: Дорофеев Г.В.

Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2016-2019г.

Сообщить об ошибке

Выберите тип ошибки:

Решено неверно

Опечатка

Плохое качество картинки

Опишите подробнее
в каком месте ошибка

Ваше сообщение отправлено
и скоро будет рассмотрено

ОК, СПАСИБО

[email protected]

© OTVETKIN.INFO

Классы

Предметы

Использование построителя выражений

Иногда написание выражения может быть сложной задачей. Но Expression Builder делает это намного проще. Выражения имеют много компонентов или «подвижных частей»: функции, операторы, константы, идентификаторы и значения. Используйте построитель выражений, чтобы быстро найти эти компоненты и точно вставить их. Существует два способа использования построителя выражений: используйте поле построителя выражений, которое может быть всем, что вам нужно, или используйте расширенный построитель выражений, если ваше выражение более сложное.

В этой статье

• Во-первых, как мне его найти?

• Посмотреть в действии

• Использование окна построителя выражений

• Использование расширенного построителя выражений

• Пошаговый пример

Прежде всего, как мне его найти?

Несмотря на то, что построитель выражений доступен во многих местах в Access, наиболее последовательный способ отобразить его — установить фокус на поле свойства, которое принимает выражение, например Источник управления или Значение по умолчанию , а затем щелкните Построитель выражений или нажмите CTRL+F2.

В макросе щелкните .

Совет     Если вы видите слово , выражение в меню, вы можете щелкнуть его, чтобы запустить построитель выражений.

Посмотреть в действии

В следующем видеоролике показано, как использовать построитель выражений для создания общего выражения для вычисляемого поля.

Использование блока Expression Builder

Конструктор выражений помогает быстрее и точнее создавать выражения с помощью интеллектуальных инструментов и контекстно-зависимой информации. Если вы видите расширенный построитель выражений, щелкните Меньше >> , чтобы просто отобразить окно построителя выражений.

IntelliSense и быстрые советы

1 IntelliSense (Access 2010 или более поздней версии) динамически отображает возможные функции и другие идентификаторы по мере ввода выражения.

Как только вы начнете вводить идентификатор или имя функции, IntelliSense отобразит раскрывающийся список возможных значений. Вы можете продолжить ввод или дважды щелкнуть правильное значение в списке, чтобы добавить его в выражение. Кроме того, вы можете использовать клавиши со стрелками вверх и вниз, чтобы выбрать нужное значение, а затем нажать клавишу TAB или ВВОД, чтобы добавить его в свое выражение. Например, если вы начнете вводить слово «Формат», в списке IntelliSense отобразятся все функции, названия которых начинаются с «Формат».

Совет     Чтобы скрыть раскрывающийся список IntelliSense, нажмите клавишу ESC. Чтобы показать его снова, нажмите CTRL+ПРОБЕЛ.

2 Быстрые подсказки отображают краткое описание выбранного элемента.

При отображении списка IntelliSense справа от выбранного элемента появляется краткое описание или краткий совет. По умолчанию выбран первый элемент в списке, но вы можете выбрать любой элемент в списке, чтобы просмотреть его краткую подсказку.

Быстрый совет может помочь вам определить назначение функции или тип элемента управления или свойства элемента.

Краткая информация и справка

1 Используйте краткую информацию, чтобы отобразить синтаксис функции, и щелкните имя функции, чтобы открыть раздел справки, посвященный этой функции.

Пока вы вводите функцию в выражение, функция «Краткая информация» отображает синтаксис функции, чтобы вы точно знали, какие аргументы требуются для функции.

2 Необязательные аргументы заключены в квадратные скобки ([]). Аргумент, который вы сейчас вводите, отображается жирным шрифтом. Не путайте квадратные скобки, обозначающие необязательные аргументы, с квадратными скобками, заключающими идентификаторы в фактическом выражении.

Верх страницы

Использование расширенного построителя выражений

Расширенный построитель выражений помогает искать и вставлять функции, операторы, константы и идентификаторы (например, имена полей, таблицы, формы и запросы), экономя время и уменьшая количество ошибок. Если вы видите только окно построителя выражений, нажмите Подробнее >> , чтобы увидеть расширенный построитель выражений, .

1 Используйте инструкции и ссылку «Справка», чтобы получить информацию о контексте, в котором вы вводите выражение.

2 В поле «Построитель выражений» введите свое выражение здесь или автоматически добавьте элементы выражения, дважды щелкнув элементы в списках ниже. Эти списки работают вместе как иерархия, чтобы помочь вам перейти к нужному компоненту выражения.

3 В списке Expression Elements щелкните тип элемента, чтобы просмотреть его категории в списке Expression Categories .

В списке Элементы выражения отображаются элементы верхнего уровня, доступные для построения выражения, такие как объекты базы данных, функции, константы, операторы и общие выражения.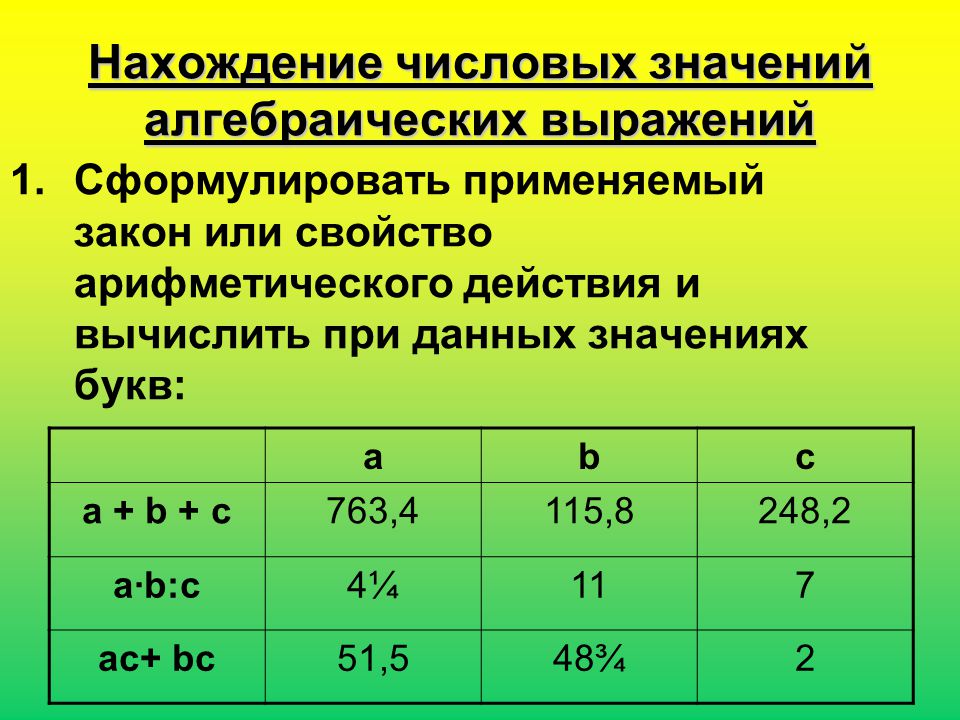 Содержимое этого списка зависит от контекста, в котором вы находитесь. Например, если вы вводите выражение в свойстве формы Control Source , список содержит элементы, отличные от тех, которые вы вводите в поле . Правило проверки свойство таблицы.

Совет    Чтобы использовать предварительно созданные выражения, включая отображение номеров страниц, текущей даты, а также текущей даты и времени, выберите Common Expressions .

4 В списке Категории выражений щелкните категорию, чтобы просмотреть ее значения в списке Значения выражений . Если в Expression Values ​​нет значений , дважды щелкните элемент категории, чтобы добавить его в окно построителя выражений.

Список Expression Categories содержит определенные элементы или категории элементов для выбора, который вы делаете в списке Expression Elements . Например, если щелкнуть Встроенные функции в списке Элементы выражений , список Категории выражений отобразит категории функций.

5 В списке Expression Values ​​ дважды щелкните значение, чтобы добавить его в поле Expression Builder.

В списке Значения выражений отображаются значения, если таковые имеются, для ранее выбранных элементов и категорий. Например, если вы щелкнули Встроенные функции в списке Элементы выражения , а затем щелкнули категорию функции в списке Категории выражений , Значения выражений 9Список 0032 отображает все встроенные функции для выбранной категории.

6 Чтобы просмотреть справку и информацию о выбранном значении выражения, если она доступна, щелкните ссылку.

Верх страницы

Пошаговый пример

В следующем примере показано, как использовать элементы выражения, категории и значения в расширенном построителе выражений для создания выражения.

1. Выберите элементы в списке Элементы выражения , например Функции , а затем Встроенные функции .

2. Выберите категорию в списке Категории выражений , например Program Flow .

3. Дважды щелкните элемент в списке Значения выражений 9Список 0032, например IIf , который добавляется в окно построителя выражений:

    IIf (<<выражение>>, <<истинная часть>>, <<ложная часть>>) 

   Текст-заполнитель заключен в угловые скобки (<< >>).

4. org/ListItem»>

   Замените любой текст-заполнитель допустимыми значениями аргументов. Вы можете ввести значения вручную или продолжить выбор элемента из трех списков.

5. Чтобы просмотреть раздел справки, содержащий дополнительные сведения о допустимых аргументах для функции, выберите функцию в списке Значения выражений , а затем щелкните ссылку в нижней части построителя выражений.

6. Если выражение содержит другие элементы, они могут быть разделены следующим заполнителем:

    <<Выражение>> 

   Замените этот заполнитель, чтобы сделать общее выражение действительным.

Верх страницы

Прогноз значения экспрессии генов на основе алгоритма XGBoost

Введение

Характеристика паттернов экспрессии генов в клетках в различных условиях является важной проблемой (Aigner et al.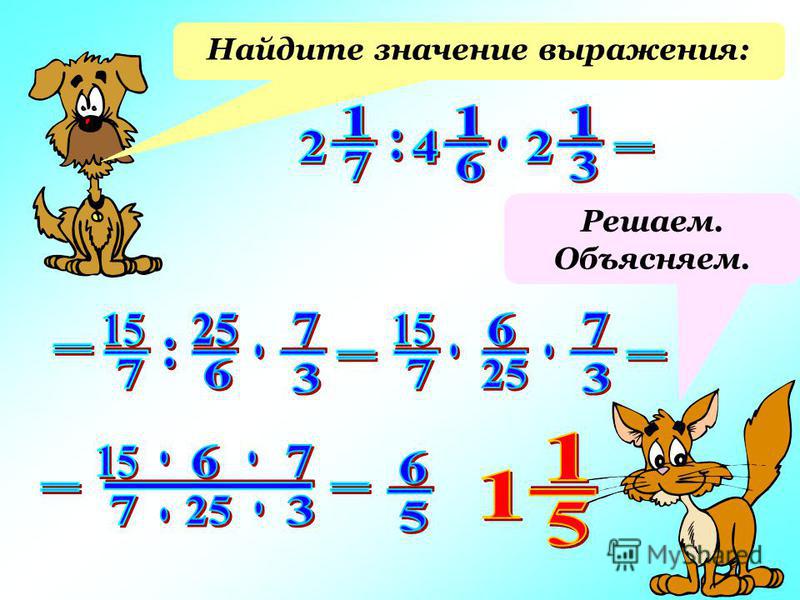 , 2010). Профилирование экспрессии генов является жизненно важным биологическим инструментом, обычно используемым для определения реакции клеток на заболевание или медикаментозное лечение (Celis et al., 2000; Mclachlan et al., 2005; Wang et al., 2006; Mallick et al., 2009).; Цзэн и др., 2016). Хотя стоимость профилирования экспрессии генов в последние годы неуклонно снижается, оно по-прежнему очень дорого, когда необходимо обрабатывать десятки или сотни образцов (Chen et al., 2016).

Экспрессия генов тесно связана, и некоторые методы коэкспрессии генов также широко изучались в последние годы для дальнейшего изучения взаимосвязи между экспрессией генов. (Озеров и др., 2016; Борисов и др., 2019). Учитывая, что экспрессия генов обычно сильно коррелирована, исследователи провели углубленный анализ профилей экспрессии генов и обнаружили, что около 1000 генов могут охватывать около 80% всего профиля экспрессии генов (Lamb et al., 2006). Эти гены называются генами-ориентирами, а остальные гены называются генами-мишенями (Penfold and Wild 2011). Вдохновленные этим, многие ученые предположили, что значение экспрессии гена-ориентира можно использовать для прогнозирования значения экспрессии гена-мишени, что значительно снизит стоимость профилирования экспрессии гена (Chen et al., 2016). Стоимость измерения профилей экспрессии, содержащих всего около 1000 ориентировочных генов, будет намного ниже по сравнению с профилями всего генома человека. Если исследователи хотят изучить экспрессию определенного гена-мишени, об этом можно судить по генам-ориентирам.

Однако эта задача очень сложна, потому что, в принципе, предсказание значения экспрессии гена представляет собой многозадачную регрессионную задачу. В 2016 году Ифей Чен и соавт. предложил алгоритм D-GEX на основе нейронной сети Back Propagation (Chen et al., 2016), в котором 943 гена-ориентира соответствуют 943 входным единицам, а 9520 генов-мишеней соответствуют 9520 выходным единицам. Тем не менее, точность прогнозирования этого алгоритма все еще имеет большие возможности для улучшения. Кроме того, глубокая сеть имеет плохую интерпретируемость, и для каждого гена-мишени мы не можем знать, какие гены-ориентиры оказывают гораздо большее влияние на его экспрессию. И последнее, но не менее важное: глубокая сеть должна считывать все данные в память во время обучения, и поэтому алгоритм склонен занимать чрезмерную память при фактическом использовании, а также имеет высокий спрос на GPU.

В дополнение к глубокой сети некоторые исследователи также использовали линейную регрессию, KNN и другие классические алгоритмы для прогнозирования экспрессии целевого гена (Chen, 2014), но результаты прогнозирования этих алгоритмов были менее точными.

Среди моделей Boosting Tree XGBoost (Chen and Guestrin, 2016) отличается очень сильным расширением и гибкостью. Он объединяет несколько древовидных моделей для создания более надежной модели учащегося. Кроме того, XGBoost характеризуется способностью автоматически использовать многопоточность ЦП для параллельных вычислений, что может ускорить вычисления.

Основываясь на вышеуказанном исследовательском опыте, мы предложили новый алгоритм прогнозирования значения экспрессии генов на основе XGBoost и создали модель прогнозирования регрессии для каждого целевого гена независимо. Результаты показали, что алгоритм XGBoost значительно улучшил точность предсказания, которая превосходит D-GEX, LR, KNN и другие алгоритмы. Он также обладал лучшей предсказательной способностью и способностью к обобщению. Наконец, алгоритм XGBoost обладал большей интерпретируемостью, чем другие алгоритмы.

Материалы и методы

В этом разделе мы впервые представили набор данных, который мы использовали для этой задачи. Затем мы представили алгоритм XGBoost и, наконец, показали три конкурирующих метода.

Набор данных

Набор данных, используемый в этой статье, совпадает с набором данных, использованным Yifei Chen et al. в предложенном алгоритме D-GEX в 2016 г., который представляет собой набор данных GEO (Gene Expression Omnibus, GEO), выбранный Институтом Броуда из опубликованной базы данных экспрессии генов (Edgar et al. , 2008), и данные экспрессии RNA-Seq, которые был получен из проекта Genotype-Tissue Expression (GTEx) (Lonsdale et al., 2013; GTEx Consortium, 2015). В обоих наборах данных каждая выборка имеет 943 гена-ориентира и 9520 генов-мишеней после предварительной обработки.

Набор данных GEO содержит в общей сложности 129 158 профилей экспрессии генов образцов клеточных линий, и следует отметить, что в этой статье мы называем каждый профиль образцом. Исходный набор данных GEO был сгенерирован платформой микрочипов Affymetrix, а значения выражения находятся в числовом диапазоне от 4 до 15. Поскольку некоторые образцы повторяются или очень похожи, мы сначала удалили повторяющиеся образцы из 129.,158 выборок, чтобы избежать лишних вычислений. Все выборки были сгруппированы в 100 классов с использованием алгоритма k-средних (Hartigan and Wong, 1979; Chen et al., 2016). В каждом классе рассчитывалось попарное евклидово расстояние между двумя выборками. Если попарное евклидово расстояние было меньше 1,0, одну из выборок удаляли. После удаления дубликатов образцов было получено 111 009 образцов, которые после случайного перемешивания были разделены на обучающую, проверочную и тестовую выборки в соотношении 8:1:1 (рис. 1). Таким образом, в обучающем наборе было 88 807 образцов, в проверочном наборе — 11 101 образец, а в тестовом наборе — 11 101 образец.

Рис. 1. Набор данных отдела генетической экспрессии (GEO). Во-первых, мы удалили повторяющиеся образцы из исходного набора данных GEO, а затем разделили его на обучающий набор, проверочный набор и тестовый набор в масштабе 8:1:1 после случайного перемешивания.

Мы использовали тренировочный набор для обучения моделей и скорректировали параметры в зависимости от производительности проверочного набора. Наконец, мы использовали результаты тестового набора для оценки модели.

Мы также провели эксперименты с данными экспрессии RNA-Seq для дальнейшей оценки надежности модели. Данные экспрессии RNA-Seq включают данные экспрессии GTEx и данные экспрессии 1000 геномов (1000G). Данные выражения GTEx состоят из 2921 профиль, которые были получены из различных образцов тканей (GTEx Consortium, 2015), и данные экспрессии 1000G содержат 462 профиля образцов лимфобластоидных клеточных линий (Lappalainen et al., 2013). Оба они были получены с платформы Illumina RNA-Seq и измерены на основе аннотаций Gencode V12 (Lappalainen et al., 2013; GTEx Consortium, 2015).

Аналогично Chen et al. разработанные ранее, мы по-прежнему использовали обучающий набор набора данных GEO в качестве обучающего набора, затем использовали данные 1000G в качестве проверочного набора и, наконец, использовали набор данных GTEx в качестве тестового набора для дальнейшей оценки способности моделей к обобщению, основанных на этом кроссе. -платформенный эксперимент (Chen et al., 2016).

Однако набор данных GEO и набор данных RNA-seq были получены с разных платформ, поэтому числовые масштабы также были разными. Поэтому мы выполнили квантильную нормализацию для всех наборов данных, что означает, что все наборы данных были стандартизированы путем вычитания среднего значения и последующего деления на стандартное отклонение каждого гена (Chen et al. , 2016).

Алгоритм XGBoost

XGBoost (Extreme Gradient Boosting) — это модель, которая была впервые предложена Тяньци Ченом и Карлосом Гестрином в 2011 году и постоянно оптимизировалась и совершенствовалась в ходе последующих исследований многих ученых (Chen and Guestrin, 2016) . Модель представляет собой структуру обучения, основанную на моделях Boosting Tree.

Традиционные модели Boosting Tree используют только информацию о первой производной. При обучении дерева n _th трудно реализовать распределенное обучение, поскольку используется остаток от прежних деревьев n-1 . XGBoost выполняет расширение Тейлора второго порядка для функции потерь и может автоматически использовать многопоточность ЦП для параллельных вычислений. Кроме того, XGBoost использует различные методы, чтобы избежать переобучения.

Алгоритм XGBoost кратко представлен следующим образом (Chen and Guestrin, 2016), а подробности приведены в дополнительных материалах. 9i,yi)+∑kΩ(fk)(2)

, где l — функция потерь, которая представляет собой ошибку между прогнозируемым значением и истинным значением; Ω — функция, используемая для регуляризации для предотвращения переобучения:

Ω(f)=γT+12λ∥w∥2(3)

, где T представляет количество листьев на дереве, а w представляет вес листья каждого дерева.

После разложения Тейлора второго порядка целевой функции и других вычислений, которые подробно описаны в дополнительных материалах, мы наконец можем получить информационный прирост целевой функции после каждого разделения:

Усиление=12[(∑i∈ILgi)2∑i∈ILhi+λ+(∑i∈IRgi)2∑i∈IRhi+λ+(∑i∈Igi)2∑i∈Ihi+λ]−γ (4)

Как видно из (4), для подавления роста дерева и предотвращения переобучения модели добавляется порог расщепления γ . Листовому узлу разрешается разделяться тогда и только тогда, когда прирост информации превышает γ . Это эквивалентно предварительной оценке дерева при оптимизации целевой функции.

Кроме того, мы также использовали следующие два превосходных метода XGBoost, чтобы избежать переобучения в эксперименте:

1. Если все веса выборки на листовых узлах меньше порогового значения, разделение останавливается. Это не позволяет модели изучать специальные обучающие образцы.

2. Произвольная выборка объектов при построении каждого дерева.

Все эти методы делают XGBoost более универсальным и повышают производительность в практических приложениях.

В ходе эксперимента регрессионная модель, основанная на XGBoost, обучалась независимо для каждого целевого гена, а количество входных ориентировочных генов составляло 943, что означает, что размерность входного объекта была 943, и эта размерность очень велика. Однако многие методы XGBoost для предотвращения переобучения могут помочь уменьшить степень переобучения и повысить точность прогнозирования регрессии.

Когда модель XGBoost фактически использовалась в эксперименте, были скорректированы следующие параметры, чтобы модель работала максимально эффективно:

1. n_estimators

n_estimators — количество итераций в обучении. слишком маленький n_estimators может привести к недообучению, из-за чего модель не в полной мере реализует свою способность к обучению. Однако слишком большое значение 90 285 n_estimators 90 288 обычно тоже не годится, потому что это приведет к переоснащению.

2. min_child_weight

Как мы упоминали ранее, min_child_weight определяет сумму выборочных весов наименьших листовых узлов для предотвращения переобучения.

3. max_depth

Максимальная глубина дерева. Чем больше глубина дерева, тем сложнее модель дерева и тем сильнее подгоночная способность, но в то же время модель намного легче подгонять.

4. подвыборка

Этот параметр означает частоту выборки всех обучающих выборок.

5. colsample_bytree

Последний параметр, который нам нужно настроить, это colsample_bytree . Это частота дискретизации признаков при построении каждого дерева. В данной задаче это эквивалентно частоте дискретизации гена-ориентира.

6. learning_rate

В большинстве алгоритмов скорость обучения — очень важный параметр, который нужно настраивать, как и в XGBoost. Это сильно влияет на производительность модели. Мы можем уменьшить вес каждого шага, чтобы сделать модель более надежной.

Подробная информация о конфигурации параметров была представлена ​​в Разделе 3.

Другие существующие методы

Существуют и другие методы, предложенные ранее исследователями, которые можно использовать в задаче прогнозирования значения экспрессии генов. В этом разделе мы кратко опишем эти методы, а в следующем разделе мы оценим производительность модели XGBoost, сравнив прогнозные результаты модели XGBoost с результатами этих существующих моделей.

D-GEX

D-GEX (Chen et al., 2016) — это алгоритм, предложенный Ифей Ченом и другими исследователями в 2016 году, в котором используется классическая модель нейронной сети BP. Количество генов-ориентиров – 9.43, а количество генов-мишеней равно 9520, поэтому теоретически количество входных и выходных нейронов сети составляет 943 и 9520 соответственно. Однако на реальных тренировках Yifei Chen et al. случайным образом разделил 9520 целевых генов на две группы из-за ограничения памяти графического процессора, и каждая группа содержала 4760 целевых генов. Поэтому сеть также была разделена на две независимые сети, соответствующие 943 входным нейронам и 4760 выходным нейронам, и обучалась независимо на двух графических процессорах.

Кроме того, сеть использовала среднеквадратичную ошибку в качестве функции потерь: 9i(t))2](5)

, где T — количество генов-мишеней, а N — количество обучающих выборок. Алгоритм D-GEX выбрал один, два или три скрытых слоя соответственно. Количество нейронов в каждом скрытом слое сети было одинаковым: 3000, 6000 или 9000 соответственно. Кроме того, они добавили в сеть Dropout Layer (Srivastava et al., 2014), чтобы уменьшить переоснащение, а метод Momentum (Sutskever et al. , 2013) использовался для ускорения обучения, благодаря чему модель приблизилась к оптимальной намного быстрее.

Линейная регрессия

Модель линейной регрессии была независимо установлена ​​для каждого целевого гена t следующим образом (Chen et al., 2016):

f(t)(x)=w(t)Tx+b(t)( 6)

, где w _(t) и b _t можно вычислить по следующей формуле:

(w(t),b(t))=argminw,b1N∑i=1N( yi(t)−w(t)Txi−b(t))2(7)

На основе (16), добавляя член регуляризации L1 или L2, модель LR-L1 и модель LR-L2 могут получить.

KNN

KNN — алгоритм непараметрического обучения. Для каждого гена-мишени обучающие выборки использовались для расчета евклидова расстояния этого целевого гена до всех генов-ориентиров во время обучения, а k генов-ориентиров с наименьшим евклидовым расстоянием определялись как k-ближайшие соседние гены-ориентиры целевого гена. ген (Hartigan, Wong, 1979; Chen et al. , 2016). В качестве прогностического значения будет использоваться среднее значение экспрессии k-ближайших соседних генов-ориентиров целевого гена.

Диапазон значения k, который мы пробовали в эксперименте, представлял собой целые числа от 2 до 20. Мы обнаружили, что при изменении значения k от 2 до 5 ошибка прогноза постепенно уменьшалась; а от 5 до 20 ошибка постепенно возрастала. Следовательно, оптимальное значение k, которое мы нашли в модели KNN, равно 5.

Результаты

В этом разделе мы впервые представили процесс настройки параметров алгоритма XGBoost и его высокую интерпретируемость. Затем мы показали результаты модели XGBoost как для данных GEO, так и для данных GTEx и сравнили их с предыдущими методами.

Настройка параметров модели

GridSearchCV , подмодуль модуля sklearn в Python (Pedregosa et al., 2011), использовался в эксперименте для проведения поиска по сетке по всем параметрам с целью поиска оптимальных параметров. Подробная информация о параметрах настройки представлена ​​в таблице 1:

Таблица 1 Подробная конфигурация параметров.

Возьмем, к примеру, целевой ген CHAD. Мы создали для него регрессионную модель XGBoost. Мы инициализировали все параметры модели, как показано в приведенной выше таблице 1, и настроили их по порядку.

Во-первых, мы скорректировали n_estimators , и абсолютная ошибка гена CHAD изменилась с n_estimators , как показано на рисунке 2 ниже:

Рисунок 2

Видно, что абсолютная ошибка проверочного набора не уменьшилась после 350 итераций, и для предотвращения переобучения оптимальное значение n_estimators было установлено равным 350.

Обновите значение n_estimators до 350 и отрегулируйте следующий параметр γ. В таблице 2 показана абсолютная ошибка проверочного набора, соответствующая различным значениям γ.

Таблица 2 Абсолютные ошибки проверочного набора, соответствующие различным γ.

Как видно из таблицы 2, 0,1 является оптимальным значением γ. Затем по очереди настраиваем остальные параметры, и в итоге можем получить оптимальные значения всех параметров, как показано в таблице 3.

Таблица 3 Оптимальные значения всех параметров.

Используя оптимальные параметры в таблице 3, абсолютная ошибка CHAD на проверочном наборе составляет 0,1513 и 0,1518 на тестовом наборе. Видно, что после настройки параметров производительность модели улучшилась. Таким образом, настройка параметров полезна для повышения точности.

Кроме того, XGBoost легко интерпретируется. После создания древовидной модели оценка важности для каждой функции может быть получена напрямую. Оценки важности рассчитываются и ранжируются для каждой функции в наборе данных. В модели с одним деревом оценка важности каждой функции рассчитывается по количеству улучшенных показателей производительности для точки разделения. Чем больше улучшение функции до точки разделения (ближе к корневому узлу), тем важнее эта функция.

Как правило, показатели важности измеряют ценность признаков при построении модели дерева. На рисунке 3 показаны 10 лучших ориентировочных генов с наивысшими баллами важности в задаче прогнозирования экспрессии генов CHAD и их конкретные баллы. Видно, что три знаковых гена: GATA3, PCMT1 и GNAS набрали самые высокие баллы в задаче прогнозирования, что также свидетельствует о том, что эти три гена являются ключевыми генами в прогнозировании значения экспрессии гена CHAD.

Рис. 3 10 основных ориентировочных генов с наивысшими баллами важности в задаче прогнозирования экспрессии генов CHAD и их конкретные баллы.

Сравнение производительности

Производительность на данных GEO

В ходе эксперимента мы обучили шесть моделей: LR, LR-L1, LR-L2, KNN, D-GEX и XGBoost соответственно на обучающем наборе и оптимизировали параметры в соответствии с производительности на проверочном наборе. Наконец, мы оценили способность прогнозирования различных моделей в зависимости от их производительности на тестовом наборе. i(t)|(8)

, где N — количество выборок.

Рисунок 4 представляет собой диаграмму MAE распределения прогностических значений всех 9520 целевых генов по шести алгоритмам в тестовом наборе. Как показано на рис. 4, алгоритм XGBoost значительно превосходит LR, LR-L1, LR-L2 и KNN и имеет лучшее распределение, чем D-GEX.

Рис. 4 Блок-диаграмма распределения средней абсолютной ошибки (MAE) шести алгоритмов в тестовом наборе.

Кроме того, мы дополнительно изучили показатель MAE на рисунке 5, чтобы подтвердить наш вывод. На рисунке 5 показана диаграмма рассеяния MAE XGBoost по сравнению с D-GEX на тестовом наборе. Точки над диагональю указывали на то, что модель XGBoost превзошла D-GEX по этим генам-мишеням, и мы обнаружили, что модель XGBoost имеет более низкий MAE, чем D-GEX на 9i(t)|](9)

, где N — количество образцов, а T — количество генов-мишеней.

В таблице 4 показаны общие ошибки шести алгоритмов на проверочном и тестовом наборах. Можно видеть, что результаты алгоритма XGBoost как на проверочном наборе, так и на тестовом наборе достигли более низкой общей ошибки, что указывает на то, что алгоритм XGBoost, используемый в этой статье, обладает хорошей способностью к прогнозированию и способности к обобщению для задачи прогнозирования значений экспрессии генов.

Таблица 4 Общая ошибка шести алгоритмов на проверочном и тестовом наборах.

Производительность на данных экспрессии RNA-Seq

Для дальнейшего изучения практичности модели XGBoost в этой задаче мы провели кросс-платформенный эксперимент, такой же, как у Chen et al. (Чен и др., 2016). Мы использовали обучающий набор данных GEO для обучения моделей, а данные выражения 1000G использовались в качестве проверочного набора для настройки параметров, и, наконец, мы оценили производительность данных выражения GTEx. Результаты всех пяти моделей показаны в таблице 5.

Таблица 5 Общая ошибка шести алгоритмов для данных 1000G и данных GTEx.

Общие ошибки в данных экспрессии RNA-seq также указывают на то, что модель XGBoost превзошла все другие модели обучения. Хотя для этой конкретной задачи обучающая выборка и тестовая выборка были сгенерированы с разных платформ. Это говорит о том, что модель XGBoost хорошо справляется с этой задачей и обладает хорошей способностью к обобщению.

Обсуждение

Алгоритм прогнозирования значений экспрессии генов на основе XGBoost превосходит алгоритм D-GEX и лучше, чем традиционные алгоритмы машинного обучения, такие как линейная регрессия и KNN.

В задаче прогнозирования значений экспрессии генов количество ориентировочных генов велико, что приводит к высокой размерности входных признаков. Это делает модель очень легкой для переоснащения. Для глубокой сети D-GEX очень высока не только входная размерность, но и выходная размерность. Поэтому обучить очень точную модель сложно, а обработка настройки параметров также чрезвычайно сложна. Кроме того, плохая интерпретируемость также является недостатком глубокой сети.

В алгоритме XGBoost добавлен контроль сложности модели. Случайная выборка выборок и признаков во время обучения снижает вероятность переобучения обученной модели, что улучшает способность модели к обобщению, и, в конечном итоге, ошибки прогнозирования для проверочного набора и тестового набора значительно уменьшаются. Кроме того, XGBoost больше ориентирован на интерпретируемость модели, поэтому мы можем узнать, какие гены-ориентиры оказывают большее влияние на значение экспрессии каждого целевого гена.

В то же время, хотя в алгоритме XGBoost существует последовательная связь между деревьями, узлы одного уровня могут быть распараллелены, а многопоточность ЦП автоматически используется для параллельных вычислений, что делает модель XGBoost быстрее, чем традиционные древовидные модели, а модель XGBoost имеет более высокую практическую ценность.

Заявление о доступности данных

Все наборы данных, сгенерированные и проанализированные для этого исследования, включены в статью/дополнительный материал.

Вклад автора

HZ задумал исследование. WL, YY, HZ и XQ разработали исследование. WL провел исследование. WL, HZ и YY написали рукопись. Все авторы прочитали и одобрили окончательный вариант рукописи.

Финансирование

Это исследование поддерживается Основной программой Национального фонда социальных наук Китая (грант № 18ZDA362).

Конфликт интересов

Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.

Дополнительный материал

Дополнительный материал к этой статье можно найти в Интернете по адресу: https://www.frontiersin.org/articles/10.3389/fgene.2019.01077/full#supplementary-material , Zien, A., Gehrsitz, A., Gebhard, P.M., McKenna, L. (2010). Анализ паттернов экспрессии анаболических и катаболических генов в нормальном хряще по сравнению с остеоартритом с использованием технологии комплементарного ДНК-чипа. Артрит Ревматизм 44 (12), 2777–2789. doi: 10.1002/1529-0131(200112)44:12<2777::aid-art465>3.0.co;2-h

CrossRef Полный текст | Google Scholar

Борисов Н., Шабалина И., Ткачев В., Сорокин М., Гаража А., Пулин А. и др. (2019). Shambhala: независимый от платформы гармонизатор данных для данных об экспрессии генов. BMC Биоинф. 20 (1), 66. doi: 10.1186/s12859-019-2641-8

CrossRef Full Text | Google Scholar

Селис Дж. Э., Крухёффер М., Громова И., Фредериксенб К., Остергаарда М., Тикьяэрб Т. и др. (2000). Профилирование экспрессии генов: мониторинг продуктов транскрипции и перехода с использованием ДНК-микрочипов и протеомики. ФЭБС лат. 480 (1), 2–16. doi: 10.1016/s0014-5793(00)01771-3

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Чен Т., Гестрин К. (2016). XGBoost: масштабируемая система повышения дерева . Материалы 22-й международной конференции acm sigkdd по открытию знаний и интеллектуальному анализу данных (стр. 785–794). АКМ. doi: 10.1145/2939672.2939785

Полный текст CrossRef | Google Scholar

Чен Ю., Ли Ю., Нараян Р., Субраманиан А., Се Х. (2016). Вывод экспрессии генов с помощью глубокого обучения. Биоинформатика. 32 (12), 1832–1839. doi: 10.1093/bioinformatics/btw074

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Чен Ю. (2014). Машинное обучение для крупномасштабной геномики: алгоритмы, модели и приложения. Диссертации и тезисы — Gradworks . Докторская диссертация: Калифорнийский университет в Ирвине.

Google Scholar

Эдгар Р., Домрачев М., Лаш А. Е. (2008). Сборник экспрессии генов . Экспрессия генов NCBI и хранилище данных массива гибридизации. Исследование нуклеиновых кислот , 30 (1), 207–210. doi: 10.1007/978-1-4020-6754-9_6552

CrossRef Полный текст | Google Scholar

Консорциум GTEx. (2015). Пилотный анализ экспрессии генотипа-ткани (GTEx): регуляция мультитканевого гена у людей. Наука 348 (6235), 648–660. doi: 10.1126/science.1262110

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Хартиган, Дж. А., Вонг, Массачусетс (1979). Алгоритм AS 136: алгоритм кластеризации K-средних. JR Stat. соц. 28 (1), 100–108. doi: 10.2307/2346830

Полный текст CrossRef | Google Scholar

Ламб Дж., Кроуфорд Э. Д., Пек Д., Моделл Дж. В., Блат И. К., Вробель М. Дж. и др. (2006). Карта связности: использование сигнатур экспрессии генов для соединения небольших молекул, генов и болезней. Наука 313 (5795), 1929–1935. doi: 10.1126/science.1132939

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Lappalainen, T., Sammeth, M., Friedländer, M.R., AC‘t Hoen, P., Monlong, J., Rivas, M.A., et al. (2013). Секвенирование транскриптома и генома раскрывает функциональные различия у людей. Природа 501 (7468), 506–511. doi: 10.1038/nature12531

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Лонсдейл Дж. , Томас Дж., Сальваторе М., Филлипс Р., Ло Э., Шад С. и др. (2013). Проект экспрессии генотипа ткани (GTEx). Нац. Жене. 45 (6), 580. doi: 10.1038/ng.2653

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Маллик Б.К., Голд Д.Л., Баладандаютхапани В. (2009). Байесовский анализ данных экспрессии генов (Mallick/Bayesian Analysis of Gene Expression Data). Биоинф. Эксперименты по экспрессии генов 131, 1–4. doi: 10.1002/9780470742785.ch2

CrossRef Full Text | Google Scholar

Маклахлан, Г.Дж., До, К.А., Амбруаз, К. (2005). Микрочипы в исследованиях экспрессии генов [M] // Анализ данных экспрессии генов на микрочипах . John Wiley & Sons, Inc. doi: 10.1002/047172842x.ch2

CrossRef Полный текст | Google Scholar

Озеров И.В., Лежнина К.В., Изумченко Е., Артемов А.В., Мединцев С., Ванхаэлен К. и др. (2016). Анализ декомпозиции сети активации путей in silico (iPANDA) как метод разработки биомаркеров. Нац. коммун. 7, 13427. doi: 10.1038/ncomms13427

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Педрегоса Ф., Вароко Г., Грэмфор А., Мишель В., Тирион Б., Гризель О. и др. (2011). Scikit-learn: машинное обучение на питоне. Дж. Маха. Учиться. Рез. 12, 2825–2830.

Google Scholar

Пенфолд, Калифорния, Уайлд, Д.Л. (2011). Повторный взгляд на то, как делать выводы о генных сетях из профилей экспрессии. Интерфейс Focus 1 (6), 857–870. дои: 10.1098/rsfs.2011.0053

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Шривастава Н., Хинтон Г., Крижевский А., Суцкевер И., Салахутдинов Р. (2014). Dropout: простой способ предотвратить переоснащение нейронных сетей. Дж. Маха. Учиться. Рез. 15 (1), 1929–1958. doi: 10.1093/cs/33.4.249

CrossRef Полный текст | Google Scholar

Суцкевер И., Мартенс Дж., Даль Г., Хинтон Г. (2013). О важности инициализации и импульса в глубоком обучении[C]//International Conference on International Conference on Machine Learning .