Знаки синуса, косинуса и тангенса угла
Вспомним, что синусом угла называется ордината точки , полученной поворотом точки вокруг начала координат на угол .
Косинусом угла называется абсцисса точки , полученной поворотом точки вокруг начала координат на угол .
Тангенсом угла называется отношение синуса угла к его косинусу.
Котангенсом угла называется отношение косинуса угла к его синусу.
Также напомним, что оси координат делят плоскость на четыре четверти.
А сейчас давайте выясним, какие знаки имеют синус и косинус в зависимости от того, в какой четверти единичной окружности располагается точка.
Пусть на координатной плоскости изображена единичная окружность с
центром в начале координат. Точка совершает поворот против часовой стрелки на угол и оказывается в точке , которая расположена в первой четверти. Для точек, расположенных
в первой четверти, абсцисса и ордината положительны, а значит, и будут иметь положительные значения.
Пусть точка совершает поворот против часовой стрелки и оказывается в точке , которая расположена во второй четверти. Для точек, которые расположены во второй четверти, абсциссы отрицательны, а ординаты положительны, а значит, будет принимать отрицательные значения, а – положительные значения. То есть и при .
Теперь пусть точка совершает поворот против часовой стрелки и оказывается в точке , которая расположена в третьей четверти. Для точек, которые расположены в третьей четверти, абсциссы и ординаты отрицательны, а значит, и будут принимать отрицательные значения. То есть и , если .
И пусть точка совершает поворот против часовой стрелки и оказывается в точке , которая расположена в четвёртой четверти. У точек, которые
расположены в четвёртой четверти, абсциссы положительны, а ординаты
отрицательны, а значит, будет принимать положительные значения, а – отрицательные значения. То есть и при .
При этом важно помнить, что при повороте точки против часовой стрелки на угол, больший , а также при повороте точки по часовой стрелке на любой угол, знаки синуса и косинуса определяются тем, в какой четверти окажется точка.
Давайте определим знаки синуса и косинуса углов: , , , .
Итак, . Тогда углу соответствует точка единичной окружности, расположенная в третьей четверти. Мы с вами выяснили, что в третьей четверти синус и косинус принимают отрицательные значения. Поэтому и .
. А значит, углу в соответствует точка единичной окружности, расположенная во второй четверти. Мы выяснили, что во второй четверти синус принимает положительные значения, а косинус – отрицательные. Следовательно, , а .
Углу соответствует точка единичной окружности, расположенная в четвёртой четверти. В четвёртой четверти синус принимает отрицательные значения, а косинус – положительные. Следовательно, , .
И последний угол – угол .
Запишем , . Тогда можем сказать, что повороту точки с координатами на угол д соответствует точка, расположенная в первой четверти. Поэтому и .
Давайте выясним, какие знаки имеет тангенс. Мы знаем, что .
Если и имеют одинаковые знаки, то . Если же и имеют разные знаки, то .
Итак, в первой четверти синус и косинус принимают положительные значения, то есть имеют одинаковые знаки, а значит, тангенс в первой четверти также принимает положительные значения.
Во второй четверти синус принимает положительные значения, а косинус – отрицательные, то есть они имеют разные знаки, а значит, тангенс принимает отрицательные значения во второй четверти.
В третьей четверти синус и косинус принимают отрицательные значения, то есть имеют одинаковые знаки. Следовательно, тангенс в третьей четверти принимает положительные значения.
В четвёртой четверти синус принимает отрицательные значения, а
косинус – положительные, они имеют разные знаки.
Следовательно, в четвёртой
четверти тангенс принимает отрицательные значения.
А какие знаки имеет котангенс? . А значит, если и имеют одинаковые знаки, то . Если и имеют разные знаки, то . Следовательно, значения котангенса имеют те же знаки, что и значения тангенса.
Давайте определим знаки тангенса и котангенса углов: и .
. Тогда углу соответствует точка единичной окружности, расположенная во второй четверти. Мы с вами выяснили, что во второй четверти тангенс и котангенс принимают отрицательные значения. Поэтому и .
. А значит, углу, равному единице, соответствует точка единичной окружности, расположенная в первой четверти. В первой четверти тангенс и котангенс принимают положительные значения. Следовательно, и .
А сейчас давайте выполним несколько заданий.
Задание первое. Определите знак числа , если равняется: , .
Решение.
Второе задание. Определите
знак числа , если равняется: , .
Решение.
И ещё одно задание. Определите знак числа , если равняется: , .
Решение.
Что такое тригонометрическая окружность? | О математике понятно
Итак, друзья, я вас поздравляю! Начальный этап знакомства с тригонометрией благополучно пройден. Подытожим его. Теперь мы с вами:
1. Знаем, что такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике.
2. Знаем, как устроена связь между тригонометрическими функциями одного и того же угла и умеем находить полный набор функций, если известна хотя бы одна из них. Кроме того, ещё мы умеем (надеюсь) пользоваться основными тригонометрическими формулами. А чего? Зря, что ли, примеры разбирали?)
Это — самые азы тригонометрии. Без этих элементарных знаний и навыков — дальше никуда. Так что, прошу прогуляться и почитать, пока не поздно. Тем более там всё очень просто и доступно.)
Идём дальше.
Как мы уже с вами знаем, у каждого острого угла в прямоугольном треугольнике имеется свой джентльменский набор тригонометрических функций.
Знаем длины катетов и гипотенузу, делим друг на друга и считаем себе. И так для любого острого угла. Всё элементарно.
Вопрос: а если угол сделать тупым? Скажем, вот таким:
Что делать? Развалился наш прямоугольный треугольник. Ни катетов больше нет, ни гипотенузы… А тригонометрические функции тоже ушли в небытие, да?
Если бы древние математики не нашли выход из этой ситуации, то, возможно, вы бы сейчас и не читали этот сайт. Ибо не было бы у нас тогда ни планшетов, ни компьютеров, ни смартфонов, ни многих других полезных штучек…
Так как можно определять любые тригонометрические функции любых углов без прямоугольного треугольника? Что ж, пришла пора взрослеть дальше. Знакомимся!
Тригонометрическая окружность. Единичная окружность. Числовая окружность. Что всё это значит?
Это очень простые понятия.
Более того, эти понятия — верный друг и надёжный помощник во всех разделах тригонометрии! От простой работы с углами в градусах или в радианах до тригонометрических уравнений и неравенств. Почему? А потому, что эта штука — своего рода шпаргалка! Причём совершенно законная! Обычно ведь что бывает: за шпоры выгоняют, двойки ставят… А тут нарисовал окружность, угол, функцию — и сразу увидел всё что тебя интересует.
Например, такое простое задание:
Что больше — sin200° или sin(-100°)?
Кто не в теме, тот отдыхает в сторонке. А кто в теме, тот нацарапает что-то типа вот такого наскального рисунка:
и сразу же увидит всю необходимую информацию!
И никто слова не скажет! Даже суровая комиссия в боевой обстановке ЕГЭ. Так зачем же такой шанс упускать, правда?
Чуть позже, в соответствующем уроке, мы разберём эту страшную задачку. И про злые углы типа -100 градусов тоже поговорим.
)
А пока начнём. Для начала нарисуем самый обычный привычный нам острый угол. Назовём его, как обычно, «альфа». Вот так:
Угол как угол, пока ничего выдающегося, но… Раз есть угол (пока что острый), то у него должны быть и свои тригонометрические функции! Косинус там или тангенс… А где их взять? Ни гипотенузы, ни катетов больше нет, только угол. Тупик?
Спокойствие! Сейчас всё увидите.)
Для начала нарисуем самые обычные и знакомые нам координатные оси. OX по горизонтали, OY — по вертикали, всё чин-чинарём… Нарисуем и… приколотим горизонтальную сторону угла к положительной полуоси OX. Приколотим покрепче, дабы не оторвать ненароком.) Вершину угла поместим в начало координат, точку О. А вот вторую сторону угла прибивать не будем и оставим подвижной. Зачем? А чтобы угол менять можно было. Хотим побольше, хотим поменьше. Хотим острый, хотим тупой — любой! Раздвижной у нас угол будет. Как угол раствора циркуля, только одна из его ножек будет прибитой.
) Конец подвижной стороны обозначим буквой А.
Получим вот такой незамысловатый рисунок:
Итак, угол у нас пристроен, это хорошо. А где же его синус и косинус — спросите вы? Потерпите минутку, торопыги, сейчас всё увидите! Я же только начал.)
Введём теперь координаты x и y конца подвижной стороны угла (точки А) и отметим их на осях. Это будут точки В и С соответственно. Ясное дело, что ОВ и ОС — какие-то числа. Длины отрезков. Или координаты точки А.
ОВ = х
ОС = у
Так вот, оказывается, иксовая координата точки А (отрезок ОВ) будет косинусом угла альфа, а игрековая координата (отрезок ОС) — его синусом!
Смотрим на рисунок:
Стоп-стоп! С какого такого перепугу-то? Ведь мы же чётко зарубили себе на носу из прошлых двух уроков, что синус и косинус — это отношения сторон в прямоугольном треугольнике! Которые от длин этих самых сторон никак не зависят.
А у нас тут координаты точки А присутствуют. Которые могут быть любыми!
Всё верно. Любыми. Но! Давайте посмотрим внимательнее на треугольник АВО. Прямоугольный, между прочим.) Ибо координаты точки, они обычно перпендикулярами отмечаются на осях, да… По нашему заклинанию косинус угла альфа — это отношение прилежащего катета к гипотенузе. Или ОВ/ОА. Синус альфа — соответственно ОС/ОА. Причём мы с вами помним, что синус/косинус никак не зависят от длин сторон. А это совсем прекрасно! Почему? А потому, что мы имеем полное право выбирать длины сторон как хотим. Как нам удобно, так и выберем. В частности, мы имеем полное право принять длину гипотенузы ОА за единичку (ОА=1)! Причём единицы измерения нас вообще не волнуют — миллиметр, километр, миля, дюйм… Синус и косинус от этого всё равно не изменятся.)
Почему именно гипотенуза (а не катеты) и именно единичка (а не 2, 10, 157 и т.д)? Потому, что так нам (и древним людям) очень удобно! Именно при таком выборе у нас достигаются максимальные упрощения.
Смотрите, что получается:
Вот и все дела.) Косинус — иксовая координата точки А, а синус — игрековая (если гипотенуза ОА — единичка). Да, ненаучно, да нестрого, но зато понятно. И запоминается проще. А запомнить очень важно. Причём, запомнить надёжно!
Запоминаем:
Косинус — по Х, синус — по Y.
Именно в таком порядке. Не путаемся!
Как видите, всё просто. Пока что всё идёт в рамках геометрии восьмого класса. С той лишь разницей, что катеты превратились у нас в координаты х и у точки А, а гипотенуза — та и вовсе превратилась в единичку. Очень удобное число.) Однако… Тема урока называется «Тригонометрическая окружность», не так ли? Пока ни слова про окружность не было!
Всё правильно. Но остались совсем пустяки. Сейчас мы с вами резко повзрослеем и колоссально расширим наши возможности всего одним движением руки! Как? Очень просто.
Берём подвижную сторону угла (т.е. ОА) и… проворачиваем её вокруг точки О на полный оборот! Как вы думаете, какую линию при этом опишет точка А? Ну, конечно! Окружность!
Вот так:
Вот и всё. Это и есть тригонометрическая окружность!
Это научное название. А на математическом сленге обычно говорят «тригонометрический круг». Или совсем коротко — просто «круг». Или — «радар» :).
Ну хорошо, окружность начертили. Но почему — тригонометрическая? Окружность как окружность… Вскрою тайну. Любой точке на окружности соответствуют два числа — координаты этой точки по X и координаты этой точки по Y. То есть, А(х; у). А икс и игрек у нас что? Только что разбирались… Да! Косинус и синус угла альфа. То есть, не что иное, как его тригонометрические функции. Вот и весь смысл.
А теперь, вспомнив, что ОА = 1 и что ОА — радиус окружности, можно сообразить, что это же самое понятие — и единичная окружность тоже.
А если вспомнить самый первый урок по тригонометрии (а чуть конкретнее — то, что синус и косинус — просто какие-то числа), то наша с вами тригонометрическая окружность будет ещё и числовой окружностью.
Вот так. Сразу три термина в одном. Очень удобно и практично.
Запоминаем:
Тригонометрическая, единичная и числовая окружности — это всё одно и то же понятие. В рамках тригонометрии.
Так, ну хорошо. Окружность изобразили. Угол у нас крутящийся, меняющийся. А раз крутящийся, то нам уже ничто не запрещает прокрутить подвижную сторону ОА куда угодно. Например, так, чтобы угол альфа стал каким-нибудь тупым!
Хотя бы вот так:
А как увидеть его синус и косинус? Не вопрос! Всё точно так же. Опускаем перпендикуляры из точки А на оси OX и OY и всё видим:
Самые глазастые, возможно, уже заметили, что синус угла альфа у нас положительный (точка С лежит на положительной полуоси OY).
А вот косинус альфа — отрицательный! Ибо точка В, иксовая координата точки А (т.е. не что иное, как косинус альфа!), лежит на отрицательной полуоси OХ. Значит, у любого тупого угла синус положительный, а косинус — отрицательный. Чего, кстати, принципиально не бывает в прямоугольном треугольнике: там все тригонометрические функции — синус, косинус, тангенс, котангенс — положительные.
А здесь — пожалуйста! Не зря же мы с вами расширили наши возможности!) Ну а коли так, раз уж мы столкнулись с отрицательным косинусом у тупого угла, то пришла пора разобраться и с такой важной штукой, как знаки синуса/косинуса по четвертям. До кучи и знаки тангенса/котангенса разберём сразу же.
Знаки синуса и косинуса, тангенса и котангенса по четвертям.
Всё проще простого. Для начала напомню, что координатные четверти (или по-другому квадранты) в тригонометрии нумеруются точно так же, как и при работе с обычными задачами на координаты точек — против часовой стрелки.
Вот так:
А что же со знаками синуса/косинуса по четвертям? Тоже всё элементарно, Ватсон.) С первой и второй четвертями мы уже разобрались выше. Незаметно для себя.) С первой четвертью вообще вопросов нет. Там только острые углы, у которых все функции (в том числе и синус с косинусом) — положительные. Со второй четвертью тоже всё ясно: синус положительный, а косинус — отрицательный. Это мы уже выяснили, когда тупой угол рисовали.
Осталось лишь разобраться с третьей и четвёртой четвертями. Как? Точно так же! Не зря же мы с вами тут углы мотать учимся потихоньку.)
Мы же знаем, что ОА — подвижная сторона нашего угла альфа. Вот и продолжим её крутить от положительной полуоси ОХ в нужную нам сторону! В третью четверть. Получим вот такую картинку:
Как видно из рисунка, для любого угла в третьей четверти уже станет отрицательным не только косинус, но и синус тоже:
Для четвёртой четверти тоже ничего хитрого.
Крутим и рисуем:
И видим, что синус в четвёртой четверти остаётся по-прежнему отрицательным. А косинус? Да! Косинус снова становится положительным:
Так, по всем четвертям пробежались. Как видите, всё просто. Для лучшего запоминания можно нарисовать знаки синуса/косинуса прямо на нашем круге.
Запоминаются обе картинки достаточно просто и быстро. Особенно если железно помнить наше секретное заклинание: «Косинус — по икс, синус — по игрек.» Кстати, сопоставьте заклинание с картинками! Очень полезно.)
Ну хорошо, с синусом/косинусом всё понятно. А тангенс и котангенс? Тоже никаких проблем. Если, конечно, помнить из второго урока, что тангенс — это синус поделить на косинус:
А котангенс — наоборот.
Вот теперь и прикинем. В первой четверти у нас всё шоколадно. Всё с плюсом — и синус и косинус. А плюс поделить на плюс — что будет? Конечно же, плюс! Во второй четверти знаки синуса и косинуса — разные.
Плюс и минус. А это значит, что их отношение (что синуса к косинусу, что наоборот) будет всегда отрицательным. Ибо в борьбе минуса с плюсом всегда выигрывает минус. Так уж повелось в математике.) В третьей четверти как синус, так и косинус имеют знак «минус». А их отношение? Минус на минус — будет… будет… плюс! А в четвёртой четверти знаки синуса/косинуса опять разные. Стало быть, их отношение (тангенс с котангенсом) снова будет с минусом! Вот и все дела.)
Получаем для тангенса/котангенса вот такую картинку:
Запомнить знаки тоже проще простого: плюс-минус-плюс-минус. Простое чередование знаков.)
И вот тут у некоторых назревает закономерный вопрос:
А можно ли увидеть тангенс и котангенс на круге? Синус — по игрек, косинус — по икс. Это понятно.) А тангенс и котангенс???
Ух, какие вы любопытные, оказывается! Все-то секреты вам раскрой сразу же! Да, можно! Можно увидеть тангенс и котангенс на числовой окружности! Любого угла.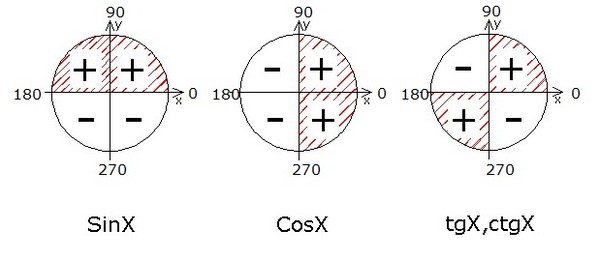
Только для этого на нашем рисунке необходим ещё один дополнительный взмах пера. Всего один. Какой именно — в спецтеме «Тангенс и котангенс на тригонометрической окружности».
Итак, полдела сделали. Нарисовали угол, с его помощью начертили окружность. Осталась вторая половина дела. А именно — научиться проделывать обратную операцию. По любой произвольной точке на окружности научиться определять сам угол! А вот эта задачка та ещё…
Об этом — в следующей теме: «Как отсчитывать углы на тригонометрической окружности?».
Синус и косинус
Я решил, что не будем слишком долго разжевывать теоретическую часть введения в тригонометрию так, как в любом случае мало кто ее будет читать и уж тем более маловероятно, что он там все поймет. Я считаю, что лучший способ изучения математики — это не зубрежка, а работа с конкретными примерами и чем больше тем лучше. Поэтому я решил опустить несколько скучных лекций и приступить сразу к главному.
Определение синуса и косинуса
Итак, в первую очередь, начнем с определения.
Во-первых построим числовую окружность и отметим на ней некоторые точки:
Если точка М числовой единичной окружности соответствует числу t, то абсциссу точки М называют косинусом числа и обозначают , а ординату точки М называют синусом числа и обозначают .
Итак, судя по нашему рисунку мы видим, что
если , то
Отсюда следует, что
Вспомним, что каждая точка числовой окружности имеет в системе свои координаты, причем для точек:
- первой четверти:
- второй четверти
- третьей четверти:
- четвертой четверти:
Это нам с вами поможет составить таблицу знаков синуса и косинуса по четвертям окружности:
| I | II | III | IV | |
| синус | + | + | – | – |
| косинус | + | – | – | + |
В дальнейшем эту таблицу мы с вами продолжим, а также разберемся в каких случаях она применяется.
Основное тригонометрическое тождество
Надеюсь, все вы помните, что уравнение числовой окружности имеет вид:
Тем самым фактически мы можем получить важнейшее равенство, связывающее синус и косинус между собой, а именно:
В дальнейшем мы будем называть это равенство основным тригонометрическим тождеством. А если оно «основное», то знать его нужно всем обязательно, в отличие от большинства других формул тригонометрии.
Ну и последнее, что я хочу сказать по теории, это, конечно, таблицы значений синусов и косинусов, с которыми вы, наверное, уже сталкивались, если изучали курс геометрии.
Но для тех, у кого их нет, я выложу основные из значений:
1 часть таблицы (значения от 0 до 180º):
| 0 | |||||||||
| 0º | 30º | 45º | 60º | 90º | 120º | 135º | 150º | 180º | |
| sin t | 0 | 1 | 0 | ||||||
| cos t | 1 | 0 | –1 |
2 часть таблицы (значения до 360º):
| 210º | 225º | 240º | 270º | 300º | 315º | 330º | 360º | |
| sin t | –1 | 0 | ||||||
| cos t | 0 | 1 |
С теорией покончено, давайте решим несколько примеров:
Решение уравнений и неравенств
ПРИМЕР 1 Вычислить и , если
а) ; б) ; в)
Решение
а) В первую очередь смотрим в таблицу значений синуса и косинуса и видим сразу, что такого значения t там нет, но, как вы должны знать, данная таблица составлена по числовой окружности, поэтому 0º = 360º.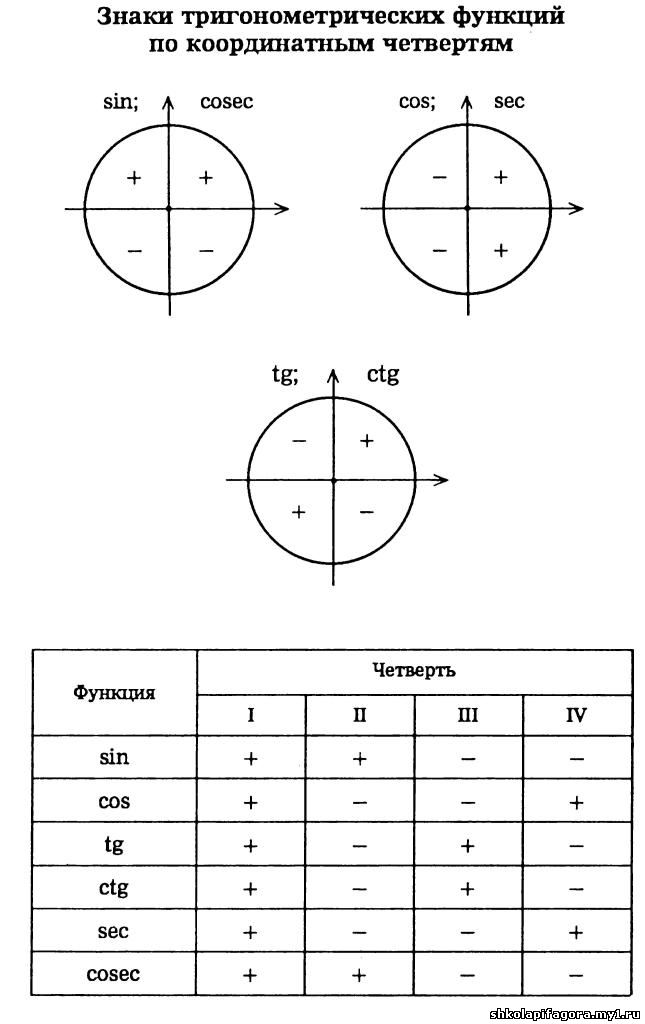
Т.е. все значения после будут повторяться. Остается лишь найти, в какой четверти находится .
Имеем,
Если, кому не понято, то вначале я неправильную дробь перевел в смешанное число, а дальше в принципе все понятно, если целая часть четная — то ее опускаем, т.к. будет (), а если нечетная — то в конце концов останется еще и его будем прибавлять к нашей обыкновенной дроби.
Отсюда следует, что числу соответствует та же точка числовой окружности, что и .
Теперь заглянем в таблицу и видим, что
, а
б) Также переписываем неправильную дробь в виде смешанного числа:
;
-12 — четное число, поэтому забываем про него и значения смотрим по второму слагаемому —. В итоге у нас вышло отрицательное число, а значит, отсчитывать значения мы будет по часовой стрелке, т.е. начиная с четвертой четверти, а не с первой. Отсчитав, видим, что соответствует , (чтобы было понятнее соответствует -60º, а 360º — 60º = 300º, поэтому и смотрим ответ у , значит,
,
в) Здесь все вообще супер — просто.
. Как видите, в значении целая часть и причем она четная, а это значит, она будет соответствовать значению . Как видим представленное значение t соответствует значению нуля, т.е.
.
ПРИМЕР 2 Решить уравнение:
Учтем, что sin t — это ордината точки M(t) числовой окружности. Значит, нам нужно найти на числовой окружности точки с ординатой и записать, каким числам t они соответствуют.
В нашем случае, если посмотреть в таблицу мы видим, что данной ординате соответствуют точки и
Следовательно,
Ответ: ;
Как вы, надеюсь, понимаете с косинусом все будет наоборот, вы будете искать значение абсциссы (т.е. в таблице смотреть значения косинуса).
С уравнениями, думаю, все понятно. Перейдем к неравенствам. С ними обстоят дела похоже, но кое-чем отличаются.
ПРИМЕР 3 Решить неравенство
Решение:
Учтем, что cos t — абсцисса точки M(t) числовой окружности.
Значит, нам нужно найти на числовой окружности точку с абсциссой и записать, каким числам t они соответствуют. Прямая пересекает числовую окружность в двух точках. Неравенству же соответствуют все точки открытой дуги (т.е. все что находится между этими точками пересечения). Согласно таблице, это точки и . Получается, решением неравенства будут все точки, входящие в данный интервал.
Ответ: .
Завершая в данном уроке разговор о синусе и косинусе хотел бы вам также представить еще несколько важных формул, которые справедливы для любого значения t.
1. sin (-t) = -sin t; cos (-t) = cos t
К примеру,
2. sin (t + 2πk) = sin t; cos (t + 2πk) = cos t
Это очевидно, так как 2π — это период функции, равный одному кругу, а k — это количество таких периодов. И вы, уже должны были понять, что, когда первый круг заканчивается 360º, то все начинается сначала, т.е. 390º будут соответствовать 30º
3. sin (t + π) = -sin t; cos (t + π) = -cos t
Это также очевидно, если вы внимательно изучали таблицу, то заметили, что значения после половины периода π соответствуют другому периоду, но с противоположным знаком.
4. sin (t + = cos t; cos (t + = -sin t
Также, если внимательно изучали таблицу, то и эту закономерность вы должны были заметить.
Ну вот с основными закономерностями таблицы синусов и косинусов мы ознакомились и на этом можно заканчивать.
Всем спасибо, если есть вопросы по теме пишите, обязательно отвечу!!!
2`. Тогда соотношения:
`sin θ = y/r` `cos θ = x/r` `tan θ = y/x` | `csc θ = r/y` `сек θ = r/x` `кроватка θ = x/y` |
Чем это отличается от определений, которые мы уже встречали в разделе 2 «Синус, косинус, тангенс и обратные отношения»? С той лишь разницей, что теперь х или и (или оба) могут быть отрицательными , потому что теперь наш угол может быть в любом квадранте. Отсюда следует, что тригонометрические отношения могут оказаться как отрицательными, так и положительными.
В предыдущем разделе задействованные углы всегда были меньше 90 °, поэтому все 6 отношений были положительными.
Обратите внимание, что r всегда положителен.
Пример 1
Давайте посмотрим, как определяются тригонометрические отношения используя конкретный пример. Пусть наш угол θ будет определяется точкой `(-2,3)` следующим образом: 92) `=sqrt(4+9)=sqrt13`
Для этого примера мы определяем тригонометрические отношения для θ в следующим образом:
`sin theta=y/r=3/sqrt13=0,83205`
`cos theta=x/r=(-2)/sqrt13=-0,55470`
`tan theta=y/x=3/-2=-1,5`
`csc theta=r/y=sqrt13/3=1.2019`
`sec theta=r/x=sqrt13/-2=-1,80278`
`cot theta=x/y=(-2)/3=-0,6667`
Четыре квадранта — позитив или негатив?
Обратите внимание на пример выше, что наш угол находился во втором квадранте.
Также обратите внимание, что во втором квадранте значение y положительное. Поскольку r всегда положительно, то y/r всегда будет положительным в квадранте II. Таким образом, мы заключаем, что «греховая тета» всегда будет положительной во втором квадранте.
Также обратите внимание на (в случае `cos theta`), что x было отрицательным. Во втором квадранте x всегда отрицательное. Так что «cos theta» тоже всегда будет отрицательным.
Для случая tan theta y положительно, а x отрицательно, поэтому y/x всегда будет отрицательным.
Рассматривая другие квадранты, мы видим закономерность.
В Квадранте II «sin theta» положительна, «cos theta» и «tan theta» отрицательны.
В квадранте III `tan тета` положительна (и x , и y отрицательны, поэтому `y/x` положительна), `sin theta` и `cos theta` отрицательны.
В Квадранте IV `cos theta` положителен, `sin theta` и `tan theta` отрицателен.
Конечно, обратные соотношения, «csc тета», «sec тета» и «кот тета» следуют одной и той же схеме:
В Квадранте II «csc theta» положительна, «sec theta» и «cot theta» отрицательны.
В квадранте III «cot theta» положительный, «csc theta» и «sec theta» отрицательный.
В Квадрант IV , «sec тета» положительный, «csc тета» и «кот тета» отрицательный.
Нам не нужно запоминать наизусть реципрокные, но рекомендуется запомнить, где `sin theta`, `cos theta` и `tan theta` положительны.
Мы используем эту диаграмму, чтобы запомнить, какие отношения положительны в каждый квадрант. Мы можем запомнить это, используя:
A ll S T o C ентр.
Это означает : В первом квадранте (I), все отношения являются положительными.
Во втором квадранте (II) синус (и cosec) равны
положительный.
В третьем квадранте (III) находятся тан (и котан). положительный.
В четвертом квадранте (IV) cos (и сек) положительный.
Они просто следуют из знака (+ или -) x или y для каждого квадранта, как мы видели выше.
Эти знаки важны, когда мы находим угол от заданное соотношение.
Интерактивный график
Вот интерактивный график, на котором вы можете изучить концепции тригонометрических соотношений.
Перетащите точку P по кривой во все 4 квадранта и наблюдайте за коэффициентами sin, cos и tan. этот результат. Обратите внимание, в частности, на положительные отношения в каждом квадранте.
Также обратите внимание, что `sin theta` определяется как как y/r, а `cos theta` определяется как `x/r`, а `tan theta` определяется как `y/x`. 90,(7pi)/6,(11pi)/4dot Если вы видите это сообщение, это означает, что JavaScript отключен в вашем браузере.
Включите JS , чтобы это приложение заработало.
Получение изображения
Пожалуйста, подождите…
Зарегистрируйтесь для получения специальных предложений
+91
Обновлено: 27-06-2022
ЗАГРУЗИТЕ ФОТО И ПОЛУЧИТЕ ОТВЕТ СЕЙЧАС!
Текст Решение
Решение : 
Стенограмма
показать заданный вопрос заключается в том, что мы должны оценить этот синус косинус тангенс следующих углов первый угол 300 градусов хорошо так что извините позвольте мне сделать это снова так что первый угол грех 300 градусов начните со знака и тогда, соответственно, грех 15 градусов, мы можем легко правильно подписать 300 градусов h грех 360 градусов минус 60 хорошо и понять это из графика, так что все вы должны быть семьей об этом после школы в колледж это ваш 0 это ваш 90 это ваш 180 это твой
70 на этом ваши 360 градусов завершены, поэтому все углы положительны в первом квадранте, во втором квадранте sin, а Cos sin противоположен sin, то есть ваш Kaushik положителен в третьем tan, а кроватка положителен, а ресторан отрицателен в четвертом.
ваши расходы и наоборот, конечно, цифры 1 или положительные и отрицательные, поэтому давайте поймем, что это грех 360 — 60 360 — 60 это означает, что это значение находится в четвертом квадранте ваше имя четвертое это ваш первый второй третий квадрант так что это значение лежит в четвертом квадранте и из этого делаем вывод что sin будет отрицательным он станет равным минусу ок еще что хочу прояснить это то что это значение если у вас 36887 производство и издание от 360
не приводит к изменению тригонометрических функций, поэтому знак останется таким, как минус 60 градусов, и вы все знаете, каково значение sin 60 градусов, поэтому долина равна минус корень 3 на 2, теперь нам нужно вычислить, что мы нужно вычислить косинус 300 градусов, поэтому, используя ту же формулу, которую мы можем написать, или мы можем легко использовать другую эту идентичность: sin квадратный тета + cos квадратный тета равен 1, хорошо, поэтому что нам нужно сделать, мы знаем значение греха 300 2 3 минус 2 на 2 минус корень 3 на 2 весь квадрат + потому что квадрат тета равен 1 показать значение
Кос в квадрате тета получается как 1 минус 3 на 4 это здесь, так что если я решу это для значения кос в квадрате тета получается равным единице по телефону, так что это означает, что значение кос в квадрате выходит как плюс минус один на два, теперь еще один вопрос, который у нас есть, но мы должны выбрать одно значение как его положительное или отрицательное.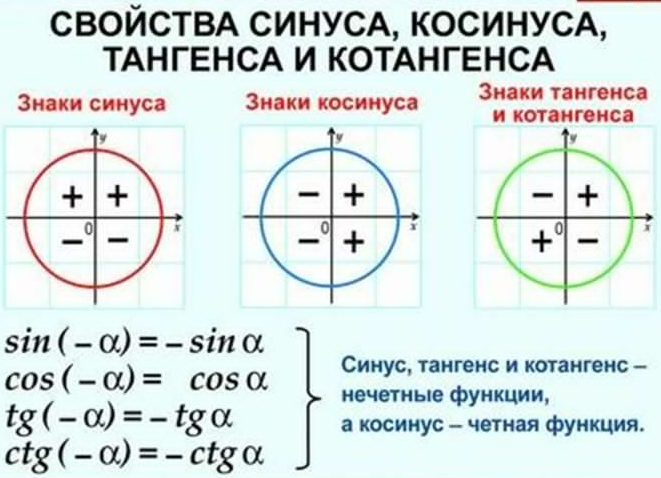
Один за двумя, поэтому мы вызвали 300 нет 311 LINE, какой квадрант он определенно выровняет четвертый квадрант, поэтому значение тетушки Cos в четвертом Квартал и плакат так что мы должны продать дорого и как один на два сейчас подходит к очереди часть 10
равно sin theta по cos 360 внутренняя стена ATI вычислила, что такое -2 разделить на 12, значение получается как минус корень 3 и также может проверить правильность долины или нет 302 309 четвертый квадрант и значение тангенса в четвертой четверти отрицательное, и мы получили соответствующий ответ, поэтому следующая часть — это ваше — 405 градусов Prime — 405 градусов знак минус указывает, что угол по часовой стрелке
позвольте мне показать это, так что минус sin в основном указывает, что угол направлен по часовой стрелке, так что у нас есть — 405 — 405 начнется отсюда, чтобы начать отсюда вот так и закончится где-то в 4-м квадранте, образуя терминал в этой точке, хорошо 405 — 360 получается из 45 ° таким образом, он будет составлять угол 45 градусов по часовой стрелке с этой осью x, и каково значение sin, а угол четвертого квадранта будет лежать в четвертой четверти, а значение sin в четвертой четверти отрицательно, так что мы должны сделать это мы должны ж обряд
грех 360 + материал качества 45 градусов, что означает этот символ минус, представляющий направление по часовой стрелке, поэтому, если я снова двигаюсь в течение 360 180 дней без изменений в тригонометрических функциях, получается грех 45 градусов и что такое значение греха 45 это 1 на корень, теперь мы должны использовать это тождество ваш квадрат квадрата тета равен 1 минус квадрат тета греха равен 1 минус один на два целых квадрата равен 1 минус 1 на 2 это создать в теперь у нас есть значение
потому что тета + 1 на 2 + 1 на 2 это означает, что значение вашей причины -405 выходит на ваш плюс минус 1 на 2, но прежде всего мы должны проверить -15 лежит в четвертом квадранте и Четвертая четверть значение функции cos sin положительное у нас есть ваша причина -405 выходит как одна на две буквы говорят о загаре tan -45 равно вашему знаку — 405 на cos — 405 значение вашего знака — 405
равно 1 на корень 2 извините, думаю, что есть какая-то ошибка, значение sin в четвертом квадранте отрицательное, чтобы я мог получить, это минус 1 на корень 2, извините за ошибку, поэтому минус 1 на 2 в 2 на выиграл, окончательный ответ будет как 2 на корень 2 и буквы проверяют значение загара в четвертом квадранте четвертый квадрант и значение времени здесь отрицательное ответ Сурья аур правильный, теперь у нас есть 756, поэтому начнем с него, мы должны вычислить значение 7
9756 давайте разберем это как sin 6 плюс до свидания 6 равно sin на + 5 на 6, пытаясь преобразовать каждое значение в терминах Pi и 25, потому что упомянутая функция поиска не изменяется в тригонометрических функциях, которые он не менялся с пайей покупать он становится как ваш грех пи + 5 на 6 и что первое то мы должны проверить квадрант пи + 5 на 6 это значит он лежит в третьей четверти а значение греха в третий квадрант отрицательный, поэтому ваш минус и нет знака изменения
пока-пока 61586 — это то, что ваш грех 30 градусов, поэтому значение получается минус 1, если предположить, что до сих пор ясно, что путь стоимости будет использовать ту же сущность, потому что квадрат тета — это ваш 1 минус квадрат синуса тета на 1 минус минус 1 на 2 целый квадрат 1 минус 1 на 4 и ответ 3 на 4 так каково значение cos тета это означает значение cos тета получается или плюс минус корень 3 на 2 это подразумевает ваши затраты 7566 равно
, ваш 756 лежит в третьем квадранте, а в третьем квадранте и в третьем квадранте вызывает отрицательное значение, поэтому мы должны взять отрицательное значение корня 3 на 2 части, поэтому загар 75 на 6 — это ваш знак 7566, потому что 7566 значение из sin 75 на 6 минус 1 на 2, а значение Cos A минус корень 3 на 2 показывает, что значение выходит из 1 при положительном корне 3, поэтому самое последнее проверьте значение тангенса
этот пост является ответом правильный теперь последний переход к четвертой части 11 по еде начиная со знака 11 пи на 4 мы можем написать синусоиду минус 5 на 4 потому что 12 — 11 на 4 грех 35 — 42 фестиваль последняя проверка где 35 35 кратно 5, так что тригонометрическая функция не изменится, поэтому получится ваш знак
пи на 4 9 самое последнее подумайте, какой знак мы должны поставить рядом с 35 — 54, завершив один круг, чтобы, завершив другой круг, завершить это становится вашим 35 35 — 54 лежит во втором квадранте здесь значение греха положительное, поэтому у нас будет положительный знак с ним, поэтому ваше значение греха пи на 4 — это ваши 45000, чтобы быть единицей по корню, чтобы знать, что мы рассчитаем значение cos cos 11 pi на 4 равно cos квадрат 1 минус квадрат sin 11541 минус 1 на корень 2 весь квадрат
1 минус 1 на 2 равно 1 на 2, но мы должны проверить стоимость для проверки, это лежит во второй четверти, см.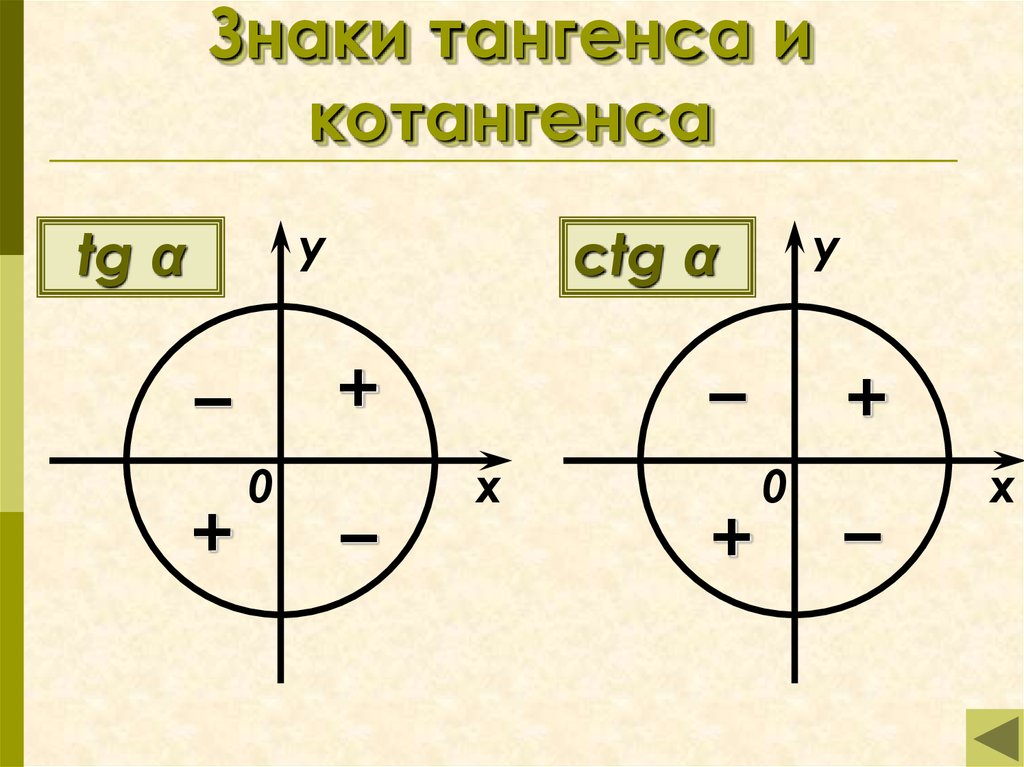
Это ваш второй квадрант, значение cos во втором квадранте отрицательное, хорошо, потому что 11 в квадрате, а потому что 11584 равно к вашему плюс минус 1 на 2 это означает причину 11 пи на 4 минус 1 на 2, потому что мы отклоним положительное значение в соответствии с этой таблицей, теперь мы должны вычислить значение тангенса
11 пи на 4 ваш знак 11 пи на 4 на cos 11 pi на 4 значение sin 11 на 4 — это то, что ограничивает 1 на 2 — это ваша последняя проверка с таблицей -2 правильное или не выполненное значение во втором квадранте — отрицательное значение VR обучения и отрицательное значение, поэтому наш ответ верно и вопроса
Формула приведения синуса и косинуса. Формулы приведения
Существует два правила использования формул приведения.
1. Если угол может быть представлен как (π/2 ±a) или (3*π/2 ±a), то имя функции изменяет sin на cos, cos на sin, tg на ctg, ctg на tg . Если угол можно представить как (π ±a) или (2*π ±a), то имя функции остается без изменений.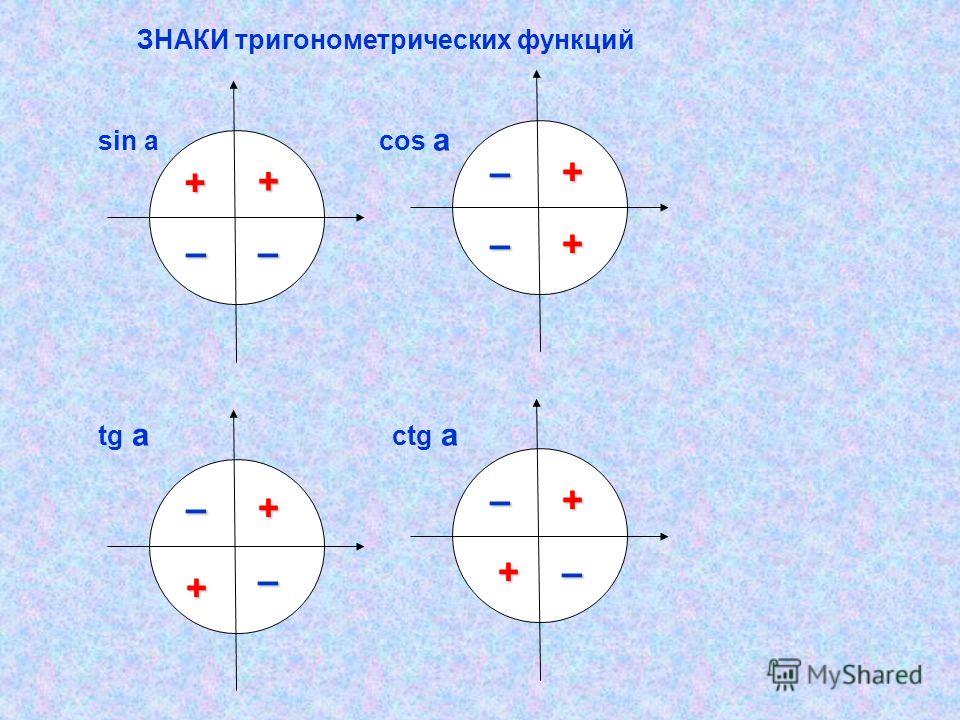
Посмотрите на рисунок ниже, на нем схематично показано, когда следует менять знак, а когда нет.
2. Правило «каким был, таким и остаешься».
Знак приведенной функции остается прежним. Если у исходной функции был знак плюс, то у редуцированной функции тоже есть знак плюс. Если исходная функция имела знак минус, то и редуцированная функция имеет знак минус.
На рисунке ниже показаны знаки основных тригонометрических функций в зависимости от четверти.
Рассчитать Sin(150˚)
Используем формулы приведения:
Sin(150˚) находится во второй четверти, из рисунка видно, что знак sin в этой четверти +. Это означает, что указанная выше функция также будет иметь знак плюс. Мы применили второе правило.
Теперь 150˚ = 90˚ +60˚. 90˚ это π/2. То есть мы имеем дело со случаем π/2+60, поэтому по первому правилу меняем функцию с sin на cos. В результате получаем Sin(150˚) = cos(60˚) = ½.
При желании все формулы приведения можно свести в одну таблицу.
Но запомнить эти два правила и пользоваться ими все же проще.
Тригонометрия. Формулы приведения.
Формулы литья не нужно учить, их нужно понимать. Поймите алгоритм их вывода. Это очень просто!
Возьмем единичный круг и разместим на нем все градусные меры (0°; 90°; 180°; 270°; 360°).
Проанализируем функции sin(a) и cos(a) в каждом квартале.
Помните, что мы рассматриваем функцию sin (a) по оси Y и функцию cos (a) по оси X.
В первой четверти видно, что функция sin(a)>0
И функция cos(a)>0
Первая четверть может быть описана через градусную меру, как (90 -α) или (360+α).
Во второй четверти видно, что функция sin(a)>0 , потому что ось Y положительна в этой четверти.
Функция cos(a), потому что ось X в этой четверти отрицательна.
Вторая четверть может быть описана через градусную меру, как (90+α) или (180-α).
В третьей четверти видно, что функции sin(a) Третья четверть может быть описана в градусах как (180+α) или (270-α).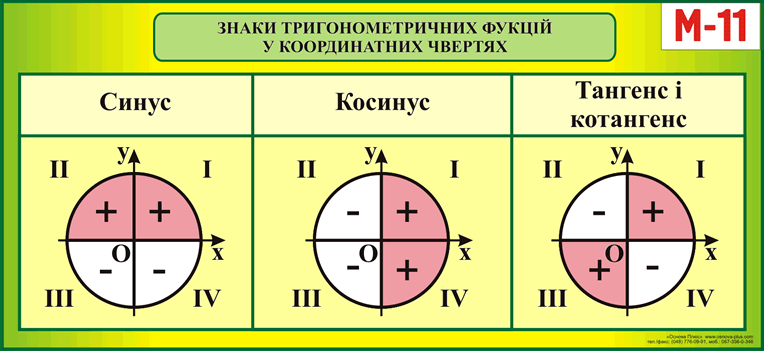
В четвертой четверти видно, что функция sin(a), потому что ось Y в этой четверти отрицательна.
Функция cos(a)>0 , потому что ось x положительна в этой четверти.
Четвертая четверть может быть описана в градусах как (270+α) или (360-α).
Теперь посмотрим на сами формулы приведения.
Вспомним простой алгоритм :
1. Квартал. (Всегда смотрите, в каком квартале вы находитесь).
2. Знак. (Для четверти см. функции положительного или отрицательного косинуса или синуса).
3. Если у вас в скобках (90° или π/2) и (270° или 3π/2), то функция заменяет .
И так начинаем разбирать этот алгоритм по четвертям.
Узнайте, чему будет равно выражение cos(90-α)
Расскажем об алгоритме:
1. Четверть первого.
Будет cos(90-α) = sin(α)
Узнаем, чему будет равно выражение sin(90-α)
Расскажем об алгоритме:
1.
Четверть первого.
Будет sin(90-α) = cos(α)
Узнаем чему будет равно выражение cos(360+α)
Расскажем об алгоритме:
1. Четверть первая.
2. В первой четверти знак функции косинуса положительный.
Будет cos(360+α) = cos(α)
Узнайте, чему будет равно
выражение sin(360 + α) Расскажем об алгоритме:
1. Четверть первого.
2. В первой четверти знак синуса положительный.
3. Если в скобках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(360+α) = sin(α)
Узнаем чему будет равно выражение cos(90+α)
Расскажем об алгоритме:
1. Четверть вторая.
3. В скобках стоит (90° или π/2), тогда функция меняется с косинуса на синус.
Будет cos(90+α) = -sin(α)
Узнаем, чему будет равно выражение sin(90+α)
Расскажем об алгоритме:
1. Четверть вторая.
3. В скобках стоит (90° или π/2), тогда функция меняется с синуса на косинус.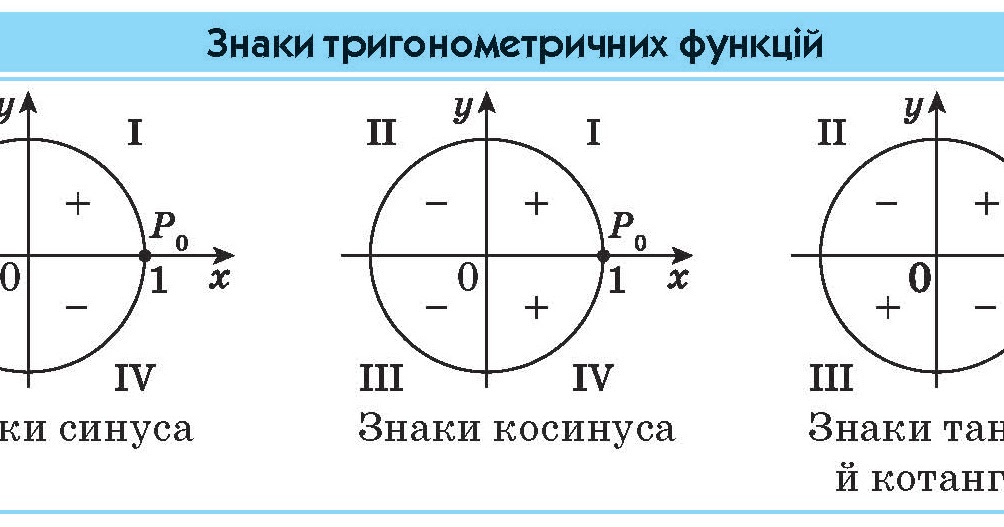
Будет ли sin(90+α) = cos(α)
Узнайте, чему будет равно 9 выражение cos(180-α)0011 Поговорим об алгоритме:
1. Четверть вторая.
2. Во второй четверти знак косинуса отрицательный.
3. Если в скобках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет cos(180-α) = cos(α)
Узнаем, чему будет равно выражение sin(180-α)
Расскажем об алгоритме:
1. Четверть вторая.
2. Во второй четверти знак синуса положительный.
3. Нет (90° или π/2) и (270° или 3π/2) в скобках, то функция не меняется.
Воля sin(180-α) = sin(α)
Я про третий и четвертый квартал аналогично, составим таблицу:
Подписывайтесь на канал на YOUTUBE и смотрите видео, готовьтесь к экзаменам по математике и геометрии вместе с нами.
Тема урока
- Изменение синуса, косинуса и тангенса при увеличении угла.
Цели урока
- Познакомиться с новыми определениями и вспомнить уже изученные.
- Ознакомиться с закономерностью изменения значений синуса, косинуса и тангенса при увеличении угла.
- Развивающая — развивать у учащихся внимание, усидчивость, усидчивость, логическое мышление, математическую речь.
- Воспитательная — через урок воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручку, самостоятельность.
Цели урока
- Проверка знаний учащихся.
План урока
- Повторение ранее изученного материала.
- Повторяющиеся задачи.
- Изменение синуса, косинуса и тангенса при увеличении угла.
- Практическое использование.
Повторение ранее изученного материала
Начнем с самого начала и вспомним, что будет полезно для освежения памяти. Что такое синус, косинус и тангенс и к какому разделу геометрии относятся эти понятия.
Тригонометрия — это такое сложное греческое слово: trigonon — треугольник, метро — мера.
Следовательно, по-гречески это означает: измерять треугольниками.
Предметы > Математика > Математика 8 класс
И еще одна задача В11 по этой же теме — из реальной ЕГЭ по математике.
Задача. Найдите значение выражения:
В этом коротком видеоуроке мы научимся применять формулы приведения к для решения реальных задач В11 из ЕГЭ по математике. Как видите, перед нами два тригонометрических выражения, каждое из которых содержит синусы и косинусы, а также довольно брутальные числовые аргументы.
Прежде чем решать эти задачи, вспомним, что такое формулы приведения. Итак, если у нас есть выражения типа:
, то мы можем избавиться от первого слагаемого (вида k π/2) по специальным правилам. Начертим тригонометрический круг, отметим на нем основные точки: 0, π/2; п; 3π/2 и 2π. Затем смотрим на первый член под знаком тригонометрической функции. У нас есть:
- Если интересующий нас член лежит на вертикальной оси тригонометрической окружности (например: 3π/2; π/2 и т. д.), то исходная функция заменяется кофункцией: синус равен заменяется косинусом, а косинус заменяется синусом.
- Если наш терм лежит на горизонтальной оси, то исходная функция не меняется. Просто убери первый член в выражении — и все.
д.), то исходная функция заменяется кофункцией: синус равен заменяется косинусом, а косинус заменяется синусом.Таким образом, мы получаем тригонометрическую функцию, не содержащую членов вида k · π/2. Однако на этом работа с формулами приведения не заканчивается. Дело в том, что перед нашей новой функцией, полученной после «отбрасывания» первого члена, может стоять знак плюс или минус. Как определить этот знак? Сейчас узнаем.
Представьте, что угол α, оставшийся внутри тригонометрической функции после преобразований, имеет очень малую градусную меру. Но что значит «малая мера»? Предположим, что α ∈ (0; 30°) — этого вполне достаточно. Возьмем в качестве примера функцию:
Тогда, следуя нашему предположению, что α ∈ (0; 30°), заключаем, что угол 3π/2 − α лежит в третьем координатном квадранте, т. е. 3π/2 − α ∈ (π; 3π/2).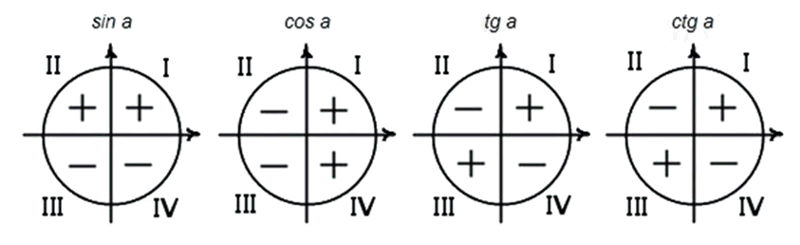
Напомним знак исходной функции, т. е. y = sin x на этом отрезке. Очевидно, синус в третьей координатной четверти отрицательный, потому что по определению синус — это ордината конца подвижного радиуса (короче, синус — это координата у). Ну, координата y в нижней полуплоскости всегда принимает отрицательные значения. Следовательно, в третьей четверти у также отрицательно.
Исходя из этих соображений, можно записать итоговое выражение:
Задача В11 - 1 вариант
Эти же приемы вполне подходят для решения задачи В11 из ЕГЭ по математике. Единственное отличие состоит в том, что во многих реальных задачах B11 вместо радианной меры (т. е. чисел π, π/2, 2π и т. д.) используется градусная мера (т. е. 90°, 180°, 270° и т. д.). так далее.). Давайте посмотрим на первую задачу:
Давайте сначала разберемся с числителем. cos 41° — это нетабличное значение, поэтому мы ничего не можем с ним сделать. Пока оставим это так.
Теперь посмотрим на знаменатель:
sin 131° = sin (90° + 41°) = cos 41°
Очевидно, перед нами формула приведения, поэтому синус заменили косинусом.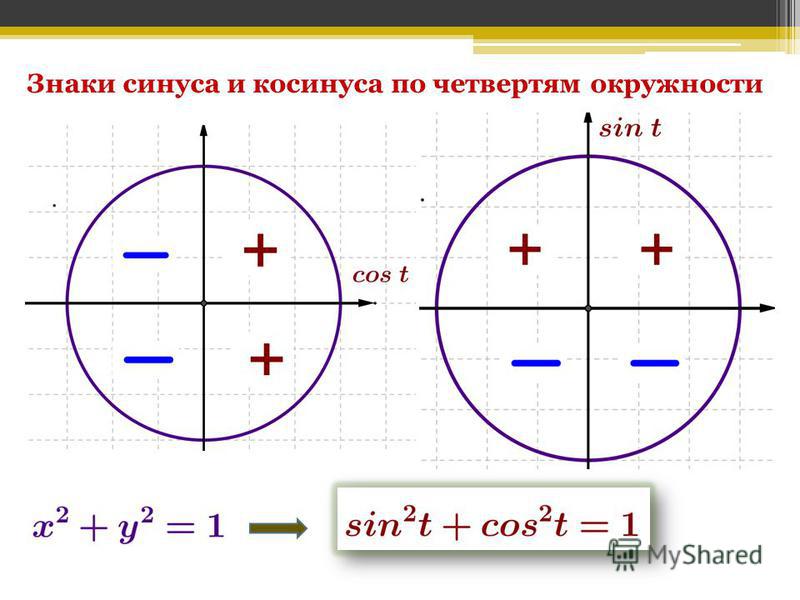
Кроме того, угол 41° лежит на отрезке (0°; 90°), т. е. в первой координатной четверти — именно так, как требуется для применения формул приведения. Но тогда 90° + 41° — вторая четверть координаты. Исходная функция y = sin x там положительна, поэтому перед косинусом на последнем шаге мы поставили плюсик (другими словами, ничего не ставили).
Осталось разобраться с последним элементом:
cos 240° = cos (180° + 60°) = -cos 60° = -0,5
Здесь мы видим, что 180° — это горизонтальная ось. Следовательно, и сама функция не изменится: был косинус — косинус тоже останется. Но опять возникает вопрос: будет ли перед полученным выражением cos 60° плюс или минус? Обратите внимание, что 180° — это третий квадрант координат. Косинус там отрицательный, поэтому в конце косинус будет со знаком минус. Итого получаем конструкцию -cos 60° = -0,5 — это табличное значение, так что все легко посчитать.
Теперь подставляем полученные числа в исходную формулу и получаем:
Как видите, число cos 41° в числителе и знаменателе дроби легко сокращается, и остается обычное выражение, равное − 10.
В этом случае минус можно либо вынести и поставить перед знаком дроби, либо «держать» рядом со вторым множителем до самого последнего шага вычислений. В любом случае, ответ -10. Вот и все, проблема B11 решена!
Задача B14 — 2-й вариант
Переходим ко второй задаче. Перед нами снова дробь:
Ну, у нас в первом координатном квадранте 27°, так что тут ничего менять не будем. А вот sin 117° нужно раскрасить (пока без всякого квадрата):
sin 117° = sin (90° + 27°) = cos 27°
Очевидно, перед нами снова формула приведения : 90° — вертикальная ось , поэтому синус изменится на косинус. Кроме того, угол α = 117° = 90° + 27° лежит во втором координатном квадранте. Исходная функция y = sin x там положительна, поэтому перед косинусом после всех преобразований все равно остается плюсик. Иными словами, ничего туда не добавляется — оставляем так: cos 27°.
Возвращаемся к исходному выражению, которое необходимо вычислить:
Как видим, после преобразований в знаменателе появился главный множитель.
тригонометрическое тождество: sin 2 27° + cos 2 27° = 1. Итого -4: 1 = -4 — вот мы и нашли ответ на вторую задачу B11.
Как видите, с помощью формул приведения такие задачи из ЕГЭ по математике решаются буквально в пару строчек. Нет синусов суммы и косинусов разности. Все, что нам нужно запомнить, это просто тригонометрический круг.
С центром в точке A .
α — это угол, выраженный в радианах.
Определение
Синус — Эта тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| на длину гипотенузы |AC|.
Косинус (cos α) — тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| на длину гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
График функции синуса, y = sin x
График функции косинуса, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y= sin x и y= cos x, периодические с a период 2 пи.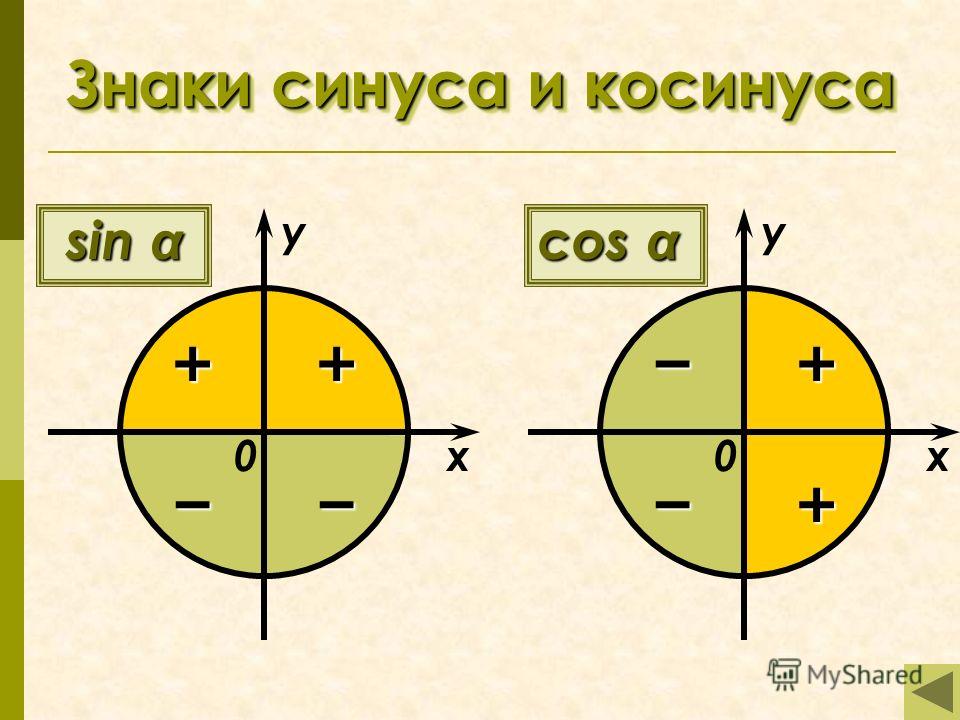
Четность
Функция синуса нечетная. Функция косинуса четная.
Область определения и значения, экстремумы, увеличение, уменьшение
Функции синуса и косинуса непрерывны в своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое число).
| у = грех х | у= cos х | |
| Объем и преемственность | — ∞ | — ∞ |
| Диапазон значений | -1 ≤ y ≤ 1 | -1 ≤ у ≤ 1 |
| По возрастанию | ||
| По убыванию | ||
| Максимумы, у= 1 | ||
| Минимум, у = — 1 | ||
| Нули, у= 0 | ||
| Точки пересечения с осью Y, x = 0 | у= 0 | у= 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса для суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы сумм и разностей
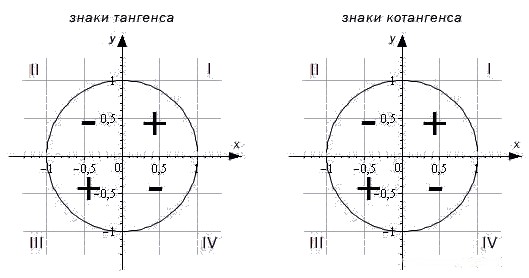
Выражение синуса через косинус
;
;
;
.