Знаки при умножении и делении: Умножение и деление отрицательных чисел

Умножение и деление отрицательных чисел

Умножение чисел

Когда требуется перемножить друг с другом числа с равными знаками, изначально перемножаются модули множителей, при этом полученный результат будет со знаком «+». 

Например

3 х 4 = 12

-3 х (-6) = +18 = 18

Когда требуется перемножить 2 числа с противоположными знаками, необходимо вычислить произведение модулей множителей, а перед итоговым результатом поставить знак «-».

Например

(-0,3) х 0,9 = -0,27

9 х (-8) =  -72

Правила знаков при умножении

Это правило совпадает с особенностями раскрытия скобок и его достаточно легко запомнить.  

Результатом умножения между собой двух отрицательных множителей станет число с положительным знаком.

Результатом умножения друг с другом двух множителей с противоположными знаками станет число с отрицательным знаком.

Это правило актуально для рациональных, целых и действительных чисел.

Если необходимо вычислить произведение длинного примера, знак результата определяется исходы из числа отрицательных множителей. 

Если их количество четное — ответ будет со знаком «+», а если нечетное — «-». 

Пример 

(-6) х (-3) х (-7) х (-1) х 14 х (-5) =

(в этом примере 5 множителей со знаком «-», следовательно результат вычисления получится отрицательным. Перемножаем модули чисел, при этом не обращая внимания на знаки)

= — 6 х 3 х 7 х 1 х 14 х 5 = — 8820

Умножение на ноль и единицу

При необходимости вычислить произведение числа с множителем ноль или единица, то умножение проходит по уже известным правилам.

0 х а = 0

0 х 0 = 0

а х 1 = а

Умножение на «-1»

При вычислении произведения числа с множителем «-1» знак результата меняется на противоположный.

а х (-1) = (-1) х а = -а

Деление чисел

При необходимости разделить между собой 2 числа с равными знаками, модуль делимого необходимо разделить на модуль делителя, при этом результат будет иметь знак «+».  

Пример 

(-6) : (-3) = +2 = 2

6 : 3 = 2

При необходимости разделить между собой 2 числа с противоположными знаками, делимое следует разделить на делитель, при этом результат станет отрицательным.

Пример 

(-6) : 3 = -2

26 : (-2) = -13

Правила знаков при делении

Это правило идентично правилу знаков при умножении.

Пример 

Найти значение выражения

(Обрати внимание — в числителе содержится 2 знака «-», которые при умножение дают плюс. В знаменателе присутствует 3 отрицательных числа, поэтому при умножении результат получается  со знаком минус. Далее сокращаем дроби и проводим вычисление уже известным способом)

= —  = -4.

Обрати внимание! При делении нуля на число, отличное от нуля, получается ноль:

0 : а = 0, а ≠ 0

Делить на ноль нельзя!

Деление на единицу

Все известные ранее правила деления на единицу действуют и на множество рациональных чисел.

а : 1 = а

а : (-1) = -а

а : а = 1

Знак минуса в дробях

Раздели число «-3» на 7, число 3 на «-7».

Записать частное каждого из этих действий в виде отрицательной дроби.                                                                                                                           

(-3) : 7 =  = —

3 : (-7) =  = —

Знак минуса в дроби может находиться:

•   непосредственно перед дробью,
•   в числителе,
•       в знаменателе. 

Обрати внимание! При записи отрицательной дроби знак «-» разрешено выносить перед дробью, передвигать из числителя в знаменатель или из знаменателя в числитель. 

Пример

Решить уравнение

— 25 х Х = -425

Требуется определить неизвестный множитель. Для этого необходимо разделить произведение на известный множитель.

Х = -425 : (-25)

Х = 17.

Пример

—  5826 : у = -3

Требуется вычислить неизвестный делитель.

Для этого необходимо делимое разделить на частное.

У = — 5826 : (-3)

У = 1942.

Поделиться статьей в соцсетях

Остались вопросы?
Наши репетиторы помогут

Остались вопросы?

Решение вирусных школьных задач | Школьная математика. Блог

Две однотипные задачи, которые в разное время взбудоражили интернет. Сталкиваются титанические плиты мнений, летят волосы, брызжет слюна, ломаются карандаши и ручки, рушатся семьи… Последнее не точно, но всё может быть.

Проблема вирусных школьных задач

Я рассмотрю здесь последнюю нашумевшую вирусную задачу, а именно:

\(8\div 2(2+2)=?\)

Алгоритм чтения математических выражений такой:

• в первую очередь мы определяем порядок действий;
• после этого читаем и выполняем их, начиная с последнего.

Но тут появляется первый камень преткновения – это отсутствие знака умножения между числом 2 и открывающейся скобкой. Этот камень успешно преодолевают все: и те, кто из школьной математики помнят только, что знак умножения можно опускать, и те, которые знают, в каких случаях допускается пропуск знака умножения, а именно, пункт 3.

Правило опускания знака умножения в выражениях.
Знак умножения при записи математических выражений можно опустить в таких случаях:
1. между буквенными множителями; 
2. между числовым и буквенным множителем; 
3. между множителем и скобкой; 
4. между выражениями в скобках.

Каждой ваше пожертвование увеличивает количество полезной и интересной информации на сайте Easy-Math.ru!

То есть, нашу задачу мы можем записать так:

\(8\div 2\times (2+2)\).

Вторым камнем преткновения является определение порядка действия. Здесь царит настоящая чехарда! Одни представляют это выражение в виде произведения дроби \(\frac{8}{2}\) и суммы \(2+2\), что в итоге приводит их к результату 16. Другие, вспоминая школьное правило порядка действий, сперва находят сумму, заключенную в скобки, а потом выполняют действия одинаковой ступени (умножение и деление).

Вторые также делятся на два лагеря: на тех, которые помнят со школьной скамьи, что действия одной ступени выполняются по порядку слева направо, и получают \(8\div 2=4\), \(4\times 4=16\), и тех, которые утверждают, что действие умножения имеет приоритет над действием деления, поэтому \(8\div 8=1\).

Кто же из них прав?

Решение вирусных школьных математических задач с опущенным знаком умножения

Я не буду рассматривать все варианты, предложенные в интернете, а просто покажу, какими правилами необходимо руководствоваться при решении подобных вирусных математических задач.

Первым действием, с чем никто не спорит, находится выражение в скобках. Получаем:

1) \(2+2=4\).

А вот дальше начинается самое интересное. Загвоздка подобных задач, приводящая к их неоднозначному толкованию, заключается в опущенном знаке умножения.

Столкновение мнений происходит из-за того, что кто-то забыл, что означает пропущенный знак умножения между числом и скобкой, кто-то не понял это в свое время, а у кого-то это вообще прошло мимо.

Пункт 3 в списке случаев, когда возможно опустить знак умножений, нам говорит, что это допускается между множителем и скобкой. А если есть явное указание на существование одного из множителей, значит существует, как минимум, ещё один множитель, а именно: выражение в скобках.

Предположим, что в данной задаче главное – это последовательность совершения действий, на чем настаивают некоторые комментаторы задачи, и после вычисления суммы в скобках нужно выполнить действия второй ступени: сперва деление 8 на 2, потом умножение 4 на 4. Но тогда получается, что в записи \(8\div 2(2+2)\) знак умножения пропущен между делителем

2 и скобкой (2+2), что является нарушением правил опускания знака умножения, и такая трактовка условия некорректная. Для корректного представления частного \(8\div 2\), оно должно было быть заключено в скобки следующим образом: \((8\div 2)(2+2)\).

Следовательно, мы можем рассматривать 2 перед скобкой только как множитель, 8 – это, безусловно, делимое, а делителем выступает выражение, представленное произведением \(2 \times (2+2)\). Само выражение \(8\div 2\times (2+2)\) при этом – это деление числа на произведение, где 2 – это первый множитель, а \((2+2)\) – это второй множитель.

Получается, полностью понятная запись этой задачи, тождественная исходной и не вызывающая разночтений, выглядит так:

\(8\div [2 \times (2+2)]\).

Корректность начального условия задачи и преобразования его при помощи скобок в такой вид я покажу чуть ниже.

А найти результат деления числа на произведение можно двумя способами:
1) делимое число разделить на результат произведения;
2) делимое разделить на первый множитель произведения, результат разделить на второй множитель и т.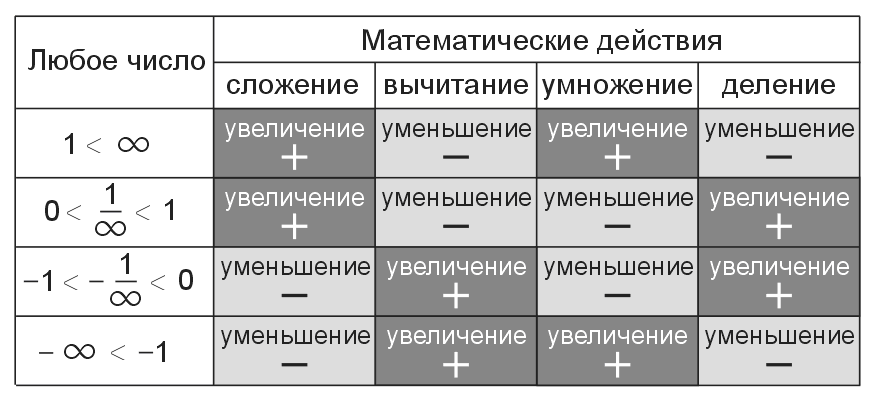 д.

Поэтому, второе действие решения этой задачи – нахождение произведения первого множителя 2 и второго, представляющего собой сумму выражения в скобках:

2) \(2\times 4=8\).

Остается только выполнить третье действие – найти частное от деления 8 на 8:

3) \(8\div 8=1\)

.

Итак, результат решения задачи:

\(8\div 2\times (2+2)=1\).

Подтверждением правильности исходной записи задачи и ее преобразования в полностью понятный вид является практика правописания алгебраических выражений: при записи деления числа на произведение, в котором были опущены знаки умножения, скобки, заключающие в делителе число, выраженное произведением, также обычно опускаются. То есть:
\(a\div ( k\times l\times m)=a\div (klm)=a\div klm\).

А в нашем случае мы имеем результат этой записи, то есть, в делителе, который выражен произведением с опущенным знаком умножения, были опущены скобки. И нам следует выполнить обратные действия, то есть: восстановить опущенные скобки и знак умножения. Тогда наш изначальный пример приобретет такой вид, тождественный начальному:

\(8\div [2\times (2+2)]\).

Да, вирусные примеры с опущенным знаком умножения специально записываются таким образом, который предполагает возникновение разночтения у людей с разной математической подготовкой. И без знания правил и четкого их понимания выпутаться практически невозможно.

Проверка решения вирусных математических задач с опущенным знаком умножения

Получив результат выполнения действий, его нужно проверить.

Проверкой данной вирусной математической задачи с опущенным знаком умножения, а также еще одним способом ее решения, служат тождественные преобразования исходного выражения.

Итак, мы имеем выражение \(8\div 2(2+2)\). Можем ли мы его упростить, просто заменив выражение в скобках его суммой? Ответ: нет. Потому что в этом случае у нас получается опущен знак умножения между двумя числами, что противоречит правилу, рассмотренному выше.

Упростить выражение, не нарушив правило опущения знака умножения, мы можем, представив выражение в скобке в виде буквы:

пусть \(x=(2+2)\),

тогда выражение приобретает вид:

\(8\div 2x\),

что не противоречит правилу опущения знака умножения. Идем далее:

\(8\div 2x=4\div x=4\div (2+2)= 4\div 4=1\).

Как видите, проверка показала правильность решения этой вирусной математической задачи.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 3.7 / 5. Количество оценок: 127

Оценок пока нет. Поставьте оценку первым.

Вам также пригодится:

Откройте для себя происхождение деления и умножения

В сегодняшней статье мы объясним происхождение математических символов деления и умножения.

Символ деления:

Существует множество способов обозначения деления, и мы собираемся объяснить происхождение некоторых наиболее часто используемых и известных всем символов.

Горизонтальная черта дробей, введенная арабами, была впервые использована в Европе математиком Фибоначчи в тринадцатом веке, хотя ее использование не получило распространения до шестнадцатого века.

Наклонная черта, вариант горизонтальной, была введена Де Морганом в 1845 году. Это был типографский ресурс в печатных книгах, позволяющий писать дробь одной строкой. Символ, который сегодня широко используется для обозначения деления:
Другим одним из знаков была скобка, хотя в настоящее время она используется мало. Чтобы выразить 21, разделенное на 3, мы напишем 21) 3 и поместим результат деления справа после еще одной скобки: 21) 3 (7,
9).0005 Этот знак встречается в произведении Arithmetica integra (1544) немецкого математика Михаэля Штифеля.

Этот же математик также использовал заглавные буквы M и D для обозначения умножения и деления в своей работе Deutsche Arithmetica (1545). Другие авторы также использовали D, в том числе использование в качестве перевернутой D, например, французы, Ж. Э. Галлимар (1685-1771), и другие авторы, упавшие d, такие как португальцы, Ж. А. да Кухна (1744-1787).

Один из до сих пор используемых символов деления — полоса с точками вверху и внизу. Он был введен швейцарским математиком Иоганном Генрихом Раном в его работе 9.0016 Немецкая алгебра (1659). Этот знак деления очень нагляден, вплоть до того, что черта дроби является общей нормой.

Этот символ не имел большого успеха ни в Швейцарии, ни в Европе. Впрочем, так было и в Великобритании, и в США. В частности, этот символ до сих пор используется в калькуляторах для деления.

Немецкий математик Готфрид В. Лейбниц ввел две точки ( : ), и в настоящее время это наиболее широко используемый символ. Согласно Лейбницу, одно из преимуществ использования этого символа состоит в том, что деление может быть проведено вдоль той же линии и сохраняется связь деления с умножением, для чего Лейбниц использовал точку.

Что касается гномона или угла, который мы используем для разделения факторов деления (делимое, делитель и частное), информации немного.

Но Бойер в своей History of Mathematics , стр. 282, говорит: «Арабы, а через них позже и европейцы, переняли большую часть своих арифметических ухищрений от индусов, и поэтому весьма вероятно, что метод «длинное деление», известное как «метод галеры» по своему сходству с кораблем с развернутыми парусами, также происходит из Индии». Судя по всему, в «методе галеры» использовался угол, аналогичный используемому в настоящее время.

Символ умножения:

Во времена вавилонян использовали идеограмму: «а-ду». В манускрипте Бахшиили , старейшем манускрипте по индийской математике, они помещают рядом один фактор и ничего больше. Индийский математик Бхаскара Ачария (1114–1185) использовал слово «бхавита» или «бха» сразу после факторов.

Другие математики использовали букву М для умножения и букву D для деления, как мы уже говорили ранее.
В старые времена арифметики многие алгоритмы использовали крест Сан-Андрес для решения продуктов деления и умножения и пропорций. Возможно, по этой причине в 1631 году Утред выбрал этот крест как символ умножения.

Он получил широкое признание, за исключением математиков Готфрида В. Лейбница и Исаака Ньютона, которые не чувствовали себя полностью комфортно с этим символом. Лейбниц в 1698 году в одном из своих писем к математику Иоганну Бернулли пишет: «Мне не нравится символ × как символ умножения, так как его можно принять за х; … Я часто просто связываю две величины точкой, а умножение обозначаю RS · PQ».

По этой причине Лейбниц ввел точку как символ умножения.

Были и другие символы для умножения. Например, швейцарский математик Иоганн Ран (1622–1676) использовал звездочку * в своей работе Teutsche Algebra (1659). А также Лейбниц, который ранее использовал упавшую C открытой стороной вниз в своей Dissertatio комбинаторного искусства (1666).

Я надеюсь, что этот пост о делении и умножении и символах, которые мы используем для их выражения, был интересен.

Если вы хотите узнать больше о делении и умножении, зарегистрируйтесь в Smartick и попробуйте его бесплатно.

Подробнее:

• Автор
• Последние сообщения

Smartick

Команда создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.

Последние сообщения от Smartick (посмотреть все)

Как вставить символ умножения и знак деления в Word

Знак умножения × (также известный как знак умножения или знак измерения для математической операции умножения) . Есть несколько популярных представлений для операции умножения: крест ( × ), точка ( ⋅ ) или звездочка ( ∗ 9).0044).

См. также как поставить х в ворде.

Знак дивизии ÷ является математическим символом в форме толстой кишки ( ∶ ), Obelus ( ÷ ), или Slash или Solidus ( /444 /, или Solidus ( / /44 /9004).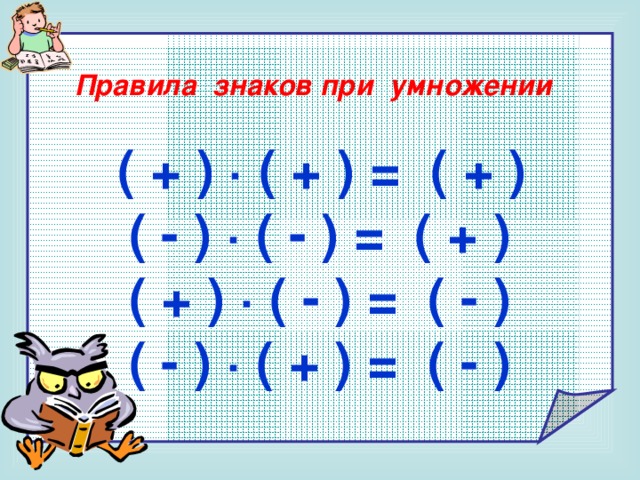

обозначают оператор деления. В большинстве стандартов косая черта ( / ) используется в качестве знака деления для линейного представления или дробной черты для структурированного представления. Символы ÷ и ∶ могут определять диапазон данных.

Мы настоятельно рекомендуем использовать инструменты Equation для вставки любого типа уравнений или математических, финансовых или даже логических формул и выражений.

Строчная Латинская буква X часто заменяет знак умножения , но это ошибка, которой нужно избегать.

Чтобы создать идеальный документ, используйте один из следующих способов вставки умножения 9Символ 0044 или знак деления :

Стандартный способ : с помощью диалогового окна Символ:

Чтобы открыть диалоговое окно Символ , выполните следующие действия:

   1.   На вкладке Вставить в группе Символы нажмите кнопку

Символ и нажмите Дополнительные символы. .. :

   2.   В диалоговом окне Symbol :

С помощью сочетания клавиш:

В Microsoft Word можно использовать Unicode для вставки любого из используемых символов:

	Горячая клавиша	Символ
Знак умножения	Введите 00d7 или 00D7 (не важно, прописные или строчные) и сразу нажмите Alt+X	×
Умножение Х	Введите 2715 и сразу же нажмите Alt+X	✕
Вектор или перекрестное произведение символ	Введите 2a2f или 2A2F и сразу нажмите Alt+X	⨯
Средняя точка	Тип 00b7 или 00B7 и сразу нажмите Alt+X	·
Точка символ	Введите 22c5 или 22C5 и сразу нажмите Alt+X	⋅
Знак раздела	Введите 00f7 или 00F7 и сразу нажмите Alt+X	÷

Более быстрый способ : использование автозамены по математике:

Когда вы работаете с большим количеством документов и часто нужно вставить один специальный символ, вам не нужно каждый раз вставлять уравнение.

No related posts.