Когда косинус отрицательный
Свойства синуса, косинуса, тангенса и котангенса
В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.
Первое свойство — знак функции в зависимости от того, какой четверти единичной окружности приналдежит угол α . Второе свойство — периодичность. Согласно этому свойству, тигонометрическая функция не меняет значения при изменении угла на целое число оборотов. Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах α и — α .
Знаки тригонометрических функций по четвертям
Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?
Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A 0 ( 1 , 0 ) и, поворачивая ее вокруг точки O на угол α , попадем в точку A 1 ( x , y ) . В зависимости от того, в какой четверти будет лежать точка A 1 ( x , y ) , угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно.
В зависимости от того, в какой четверти будет лежать точка A 1 ( x , y ) , угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно.
Для наглядности приведем иллюстрацию.
Угол α = 30 ° лежит в первой четверти. Угол — 210 ° является углом второй четверти. Угол 585 ° — угол третьей четверти. Угол — 45 ° — это угол четвертой четверти.
При этом углы ± 90 ° , ± 180 ° , ± 270 ° , ± 360 ° не принадлежат ни одной четверти, так как лежат на координатных осях.
Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.
Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус — это ордината точки A 1 ( x , y ) . Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной — отрицательна.
Косинус — это абсцисса точки A 1 ( x , y ) . В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.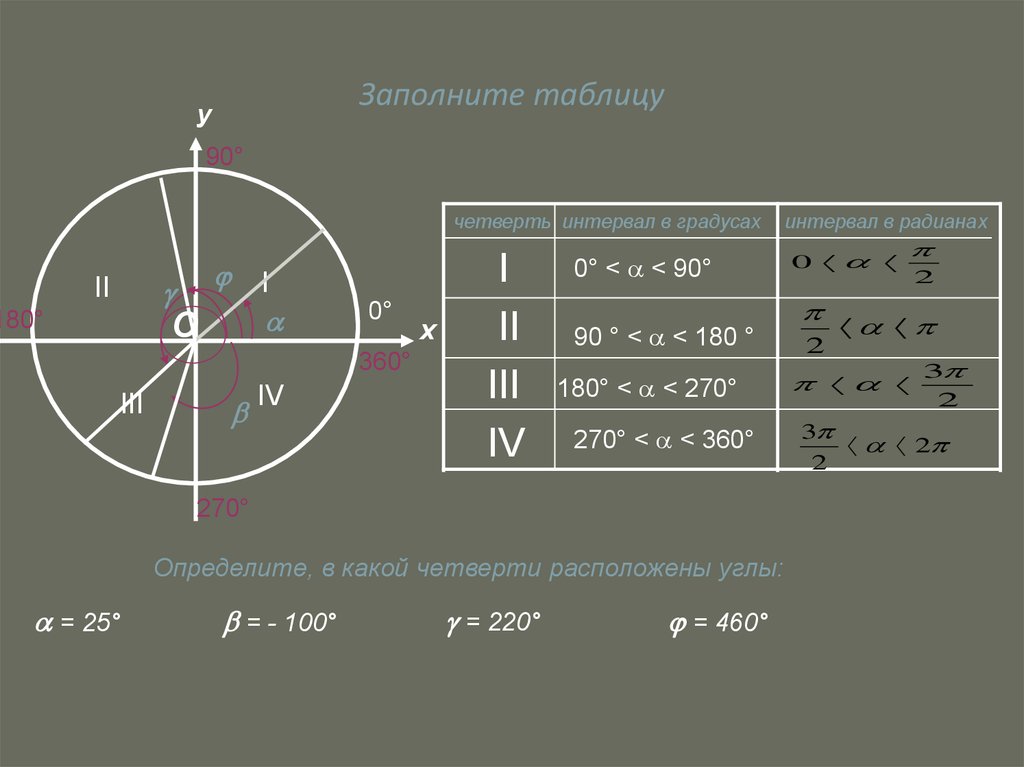
Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций. Тангенс — отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки — отрицательным. Аналогично определяются знаки котангенса по четвертям.
- Синус угла α имеет знак плюс в 1 и 2 четвертях, знак минус — в 3 и 4 четвертях.
- Косинус угла α имеет знак плюс в 1 и 4 четвертях, знак минус — в 2 и 3 четвертях.
- Тангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
- Котангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
Свойство периодичности
Свойство периодичности — одно из самых очевидных свойств тригонометрических функций.
При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.
Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A 1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса.
Математически данное свойство записывается так:
sin α + 2 π · z = sin α cos α + 2 π · z = cos α t g α + 2 π · z = t g α c t g α + 2 π · z = c t g α
Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов.
sin 13 π 5 = sin 3 π 5 + 2 π = sin 3 π 5
t g ( — 689 ° ) = t g ( 31 ° + 360 ° · ( — 2 ) ) = t g 31 ° t g ( — 689 ° ) = t g ( — 329 ° + 360 ° · ( — 1 ) ) = t g ( — 329 ° )
Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов
Вновь обратимся к единичной окружности.
Точка A 1 ( x , y ) — результат поворота начальной точки A 0 ( 1 , 0 ) вокруг центра окружности на угол α .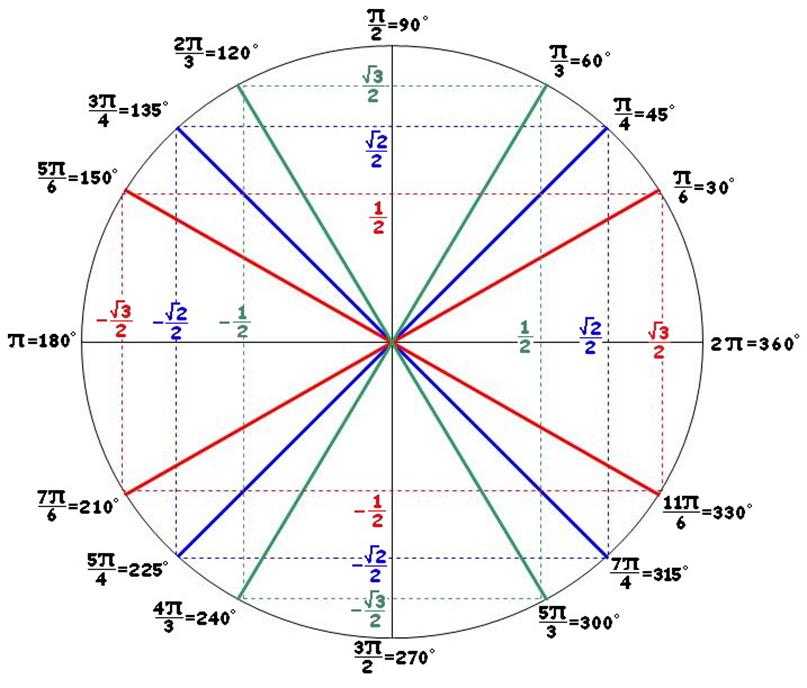 Точка A 2 ( x , — y ) — результат поворота начальной точки на угол — α .
Точка A 2 ( x , — y ) — результат поворота начальной точки на угол — α .
Точки A 1 и A 2 симметричны относительно оси абсцисс. В случае, когда α = 0 ° , ± 180 ° , ± 360 ° точки A 1 и A 2 совпадают. Пусть одна точка имеет координаты ( x , y ) , а вторая — ( x , — y ) . Вспомним определения синуса, косинуса, тангенса, котангенса и запишем:
sin α = y , cos α = x , t g α = y x , c t g α = x y sin — α = — y , cos — α = x , t g — α = — y x , c t g — α = x — y
Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов.
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов
sin — α = — sin α cos — α = cos α t g — α = — t g α c t g — α = — c t g α
Согласно этому свойству, справедливы равенства
sin — 48 ° = — sin 48 ° , c t g π 9 = — c t g — π 9 , cos 18 ° = cos — 18 °
Рассмотренное свойство часто используется при решении практических задач в случаях, когда нужно избавиться от отрицательных знаков углов в агрументах тригонометрических функций.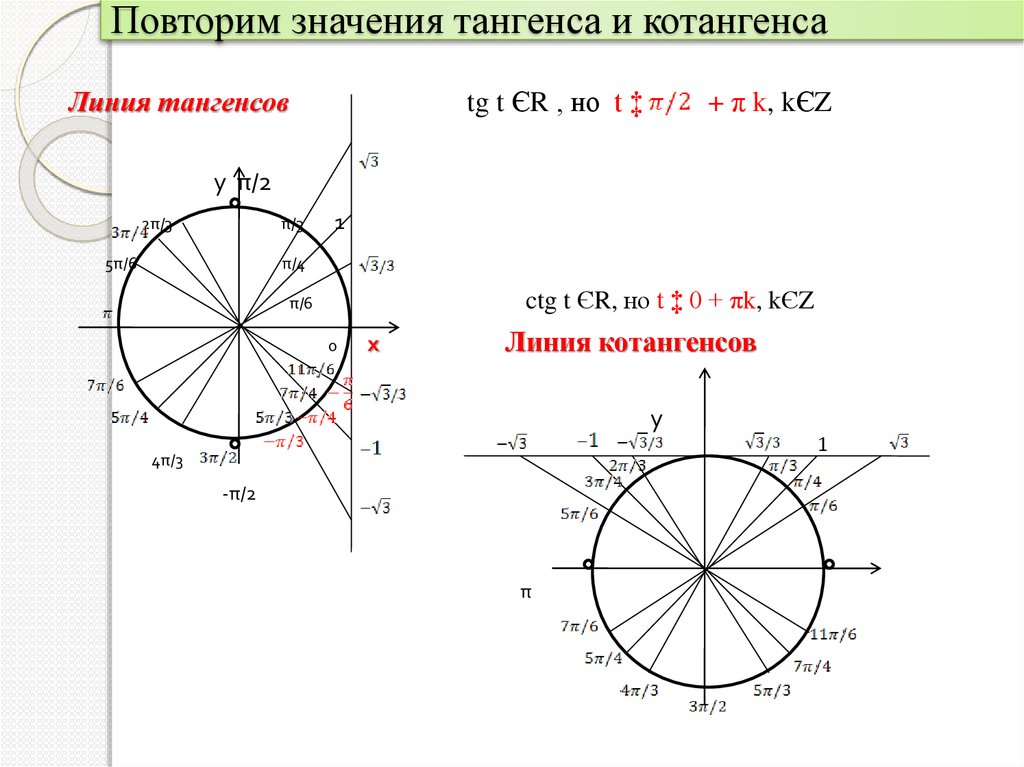
Косинус
1) Пусть дан угол и нужно определить косинус этого угла.
2) Достроим на этом угле любой прямоугольный треугольник.
3) Измерив, нужные стороны, можем вычислить косинус.
Косинус острого угла больше \(0\) и меньше \(1\)
Если при решении задачи косинус острого угла получился больше 1 или отрицательным, то значит где-то в решении есть ошибка.
Косинус числа
Косинус числа можно определить с помощью числовой окружности – косинус числа равен абсциссе соответствующей точки на ней.Числовая окружность позволяет определить косинус любого числа, но обычно находят косинус чисел как-то связанных с Пи : \(\frac\) , \(\frac\) , \(-2π\).
Например, для числа \(\frac\) — косинус будет равен \(\frac>\) . А для числа \(-\) \(\frac\) он будет равен \(-\) \(\frac>\) (приблизительно \(-0,71\)).
Косинус для других часто встречающихся в практике чисел смотри в тригонометрической таблице .
Значение косинуса всегда лежит в пределах от \(-1\) до \(1\). При этом вычислен косинус может быть для абсолютно любого угла и числа.
Косинус любого угла
Благодаря числовой окружности можно определять косинус не только острого угла, но и тупого, отрицательного, и даже большего, чем \(360°\) (полный оборот). Как это делать — проще один раз увидеть, чем \(100\) раз услышать, поэтому смотрите картинку.
Теперь пояснение: пусть нужно определить косинус угла КОА с градусной мерой в \(150°\). Совмещаем точку О с центром окружности, а сторону ОК – с осью \(x\). После этого откладываем \(150°\) против часовой стрелки. Тогда ордината точки А покажет нам косинус этого угла.
Если же нас интересует угол с градусной мерой, например, в \(-60°\) (угол КОВ), делаем также, но \(60°\) откладываем по часовой стрелке.
И, наконец, угол больше \(360°\) (угол КОС) — всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов».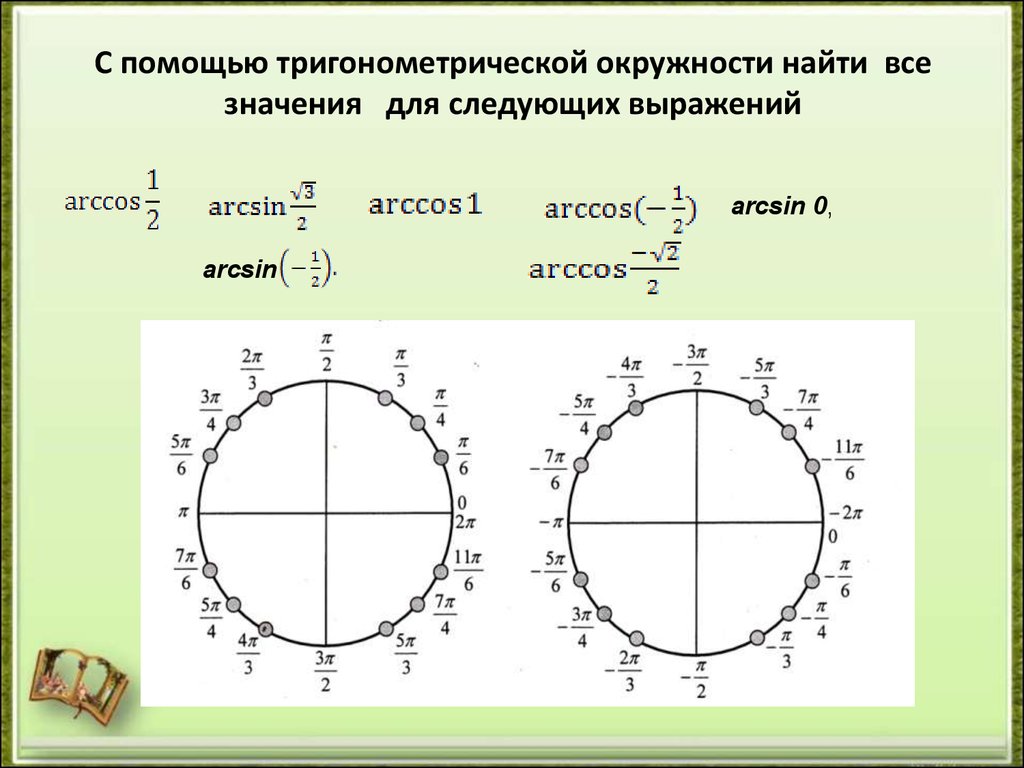 Конкретно в нашем случае угол \(405°\) отложен как \(360° + 45°\).
Конкретно в нашем случае угол \(405°\) отложен как \(360° + 45°\).
Несложно догадаться, что для откладывания угла, например, в \(960°\), надо сделать уже два оборота (\(360°+360°+240°\)), а для угла в \(2640°\) — целых семь.
Стоит запомнить, что:
Косинус прямого угла равен нулю. Косинус тупого угла — отрицателен.
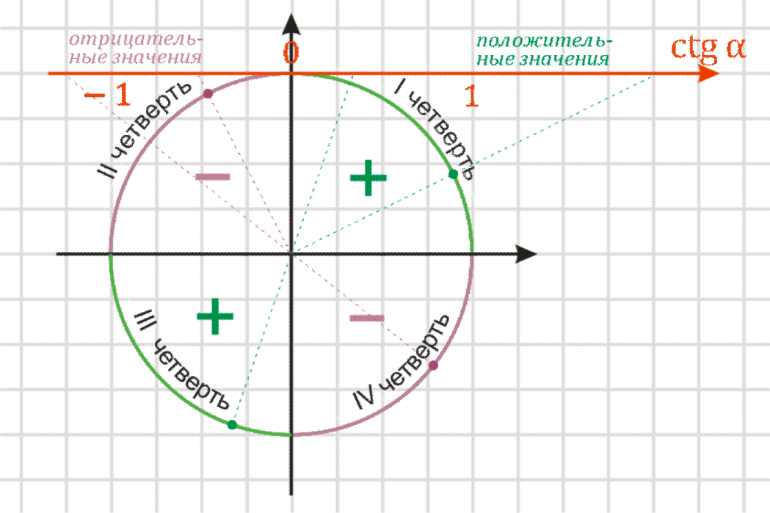
Знаки косинуса по четвертям
С помощью оси косинусов (то есть, оси абсцисс, выделенной на рисунке красным цветом) легко определить знаки косинусов по четвертям числовой (тригонометрической) окружности:
— там, где значения на оси от \(0\) до \(1\), косинус будет иметь знак плюс (I и IV четверти – зеленая область),
— там, где значения на оси от \(0\) до \(-1\), косинус будет иметь знак минус (II и III четверти – фиолетовая область).
Пример. Определите знак \(\cos 1\).
Решение: Найдем \(1\) на тригонометрическом круге. Будем отталкиваться от того, что \(π=3,14\). Значит единица, примерно, в три раза ближе к нулю (точке «старта»). 2x=\) \(\frac\)
2x=\) \(\frac\)
— котангенсом и синусом того же угла (или числа): формулой \(ctgx=\) \(\frac>\)
Другие наиболее часто применяемые формулы смотри здесь .
Функция \(y=\cos\)
Если отложить по оси \(x\) углы в радианах, а по оси \(y\) — соответствующие этим углам значения косинуса, мы получим следующий график:
График данной функции называется косинусоида и обладает следующими свойствами:
— область определения – любое значение икса: \(D(\cos )=R\)
— область значений – от \(-1\) до \(1\) включительно: \(E(\cos )=[-1;1]\)
— четная: \(\cos(-x)=\cos\)
— периодическая с периодом \(2π\): \(\cos(x+2π)=\cos\)
— точки пересечения с осями координат:
ось абсцисс: \((\) \(\frac\) \(+πn\),\(;0)\), где \(n ϵ Z\)
ось ординат: \((0;1)\)
— промежутки знакопостоянства:
функция положительна на интервалах: \((-\) \(\frac\) \(+2πn;\) \(\frac\) \(+2πn)\), где \(n ϵ Z\)
функция отрицательна на интервалах: \((\) \(\frac\) \(+2πn;\) \(\frac\) \(+2πn)\), где \(n ϵ Z\)
— промежутки возрастания и убывания:
функция возрастает на интервалах: \((π+2πn;2π+2πn)\), где \(n ϵ Z\)
функция убывает на интервалах: \((2πn;π+2πn)\), где \(n ϵ Z\)
— максимумы и минимумы функции:
функция имеет максимальное значение \(y=1\) в точках \(x=2πn\), где \(n ϵ Z\)
функция имеет минимальное значение \(y=-1\) в точках \(x=π+2πn\), где \(n ϵ Z\).
Геометрия. Урок 1. Тригонометрия
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:
sin ∠ A = C B A B
cos ∠ A = A C A B
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
sin ∠ B = A C A B
cos ∠ B = B C A B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике.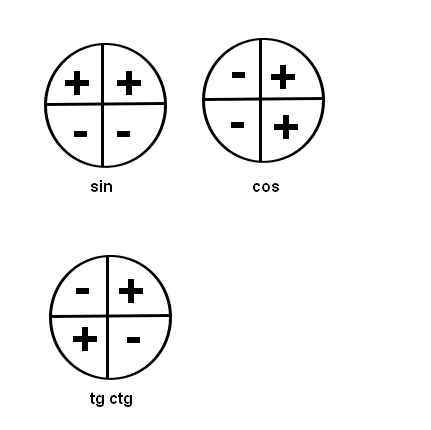 Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )
На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .
Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .
Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Поскольку O C A B – прямоугольник, A B = C O .
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .
(Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .
Координата по оси x – косинус угла , координата по оси y – синус угла .
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
Границы тангенса. Тригонометрические функции
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Yandex.RTB R-A-339285-1
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла (sin α) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла (cos α) — отношение прилежащего катета к гипотенузе.
Тангенс угла (t g α) — отношение противолежащего катета к прилежащему.
Котангенс угла (c t g α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Приведем иллюстрацию.
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Важно помнить!
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами (1 , 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 (x , y).
Определение дается через координаты точки A 1 (x , y).
Синус (sin) угла поворота
Синус угла поворота α — это ордината точки A 1 (x , y). sin α = y
Косинус (cos) угла поворота
Косинус угла поворота α — это абсцисса точки A 1 (x , y). cos α = х
Тангенс (tg) угла поворота
Тангенс угла поворота α — это отношение ординаты точки A 1 (x , y) к ее абсциссе. t g α = y x
Котангенс (ctg) угла поворота
Котангенс угла поворота α — это отношение абсциссы точки A 1 (x , y) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0 , 1) и (0 , — 1). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Важно помнить!
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z)Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z)
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами (1 , 0).
Положительному числу t
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус (cos) числа t
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс (tg) числа t
Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t.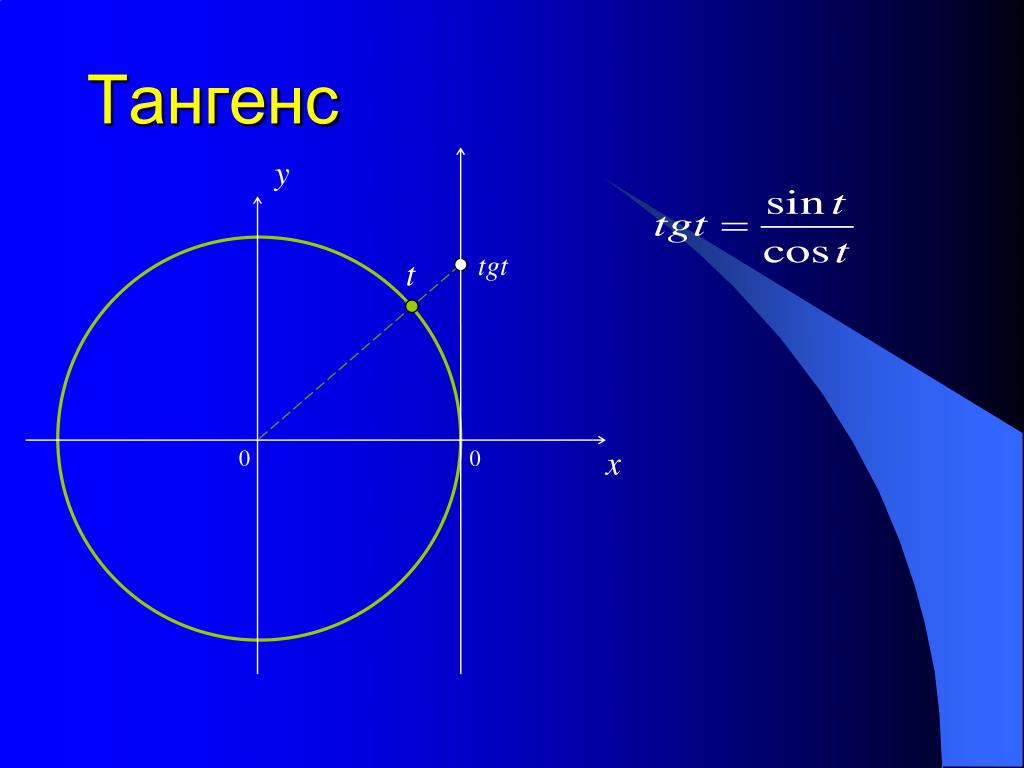 t g t = y x = sin t cos t
t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t , совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z).
Можно сказать, что sin α , cos α , t g α , c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу 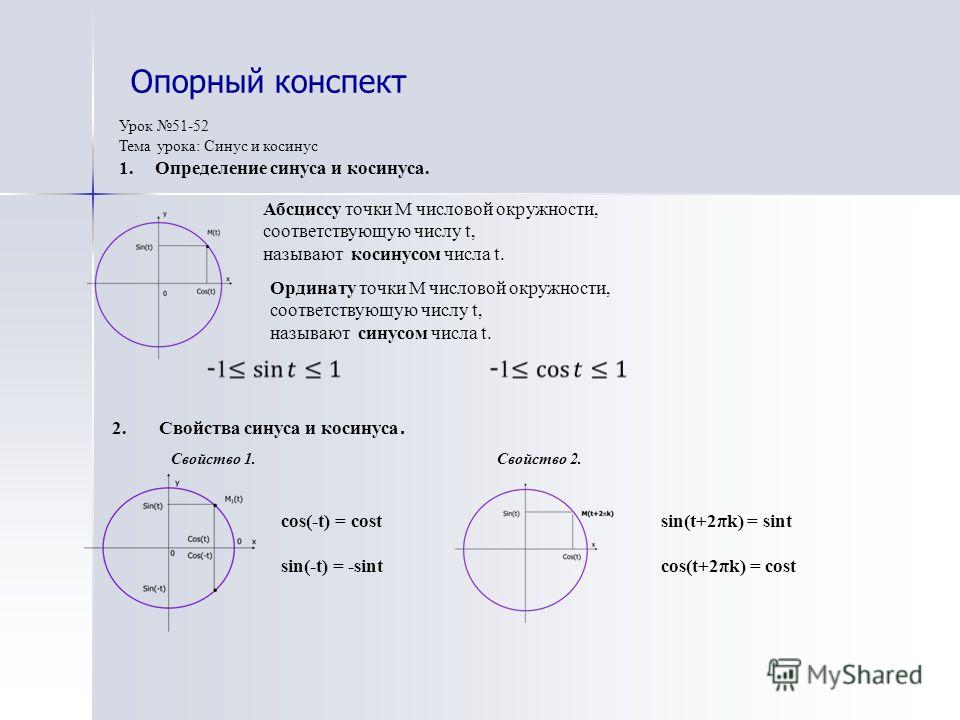 Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A (1 , 0) на угол величиной до 90 градусов и проведем из полученной точки A 1 (x , y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 (x , y) .
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Одним из разделов математики, с которыми школьники справляются с наибольшими трудностями, является тригонометрия. Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи.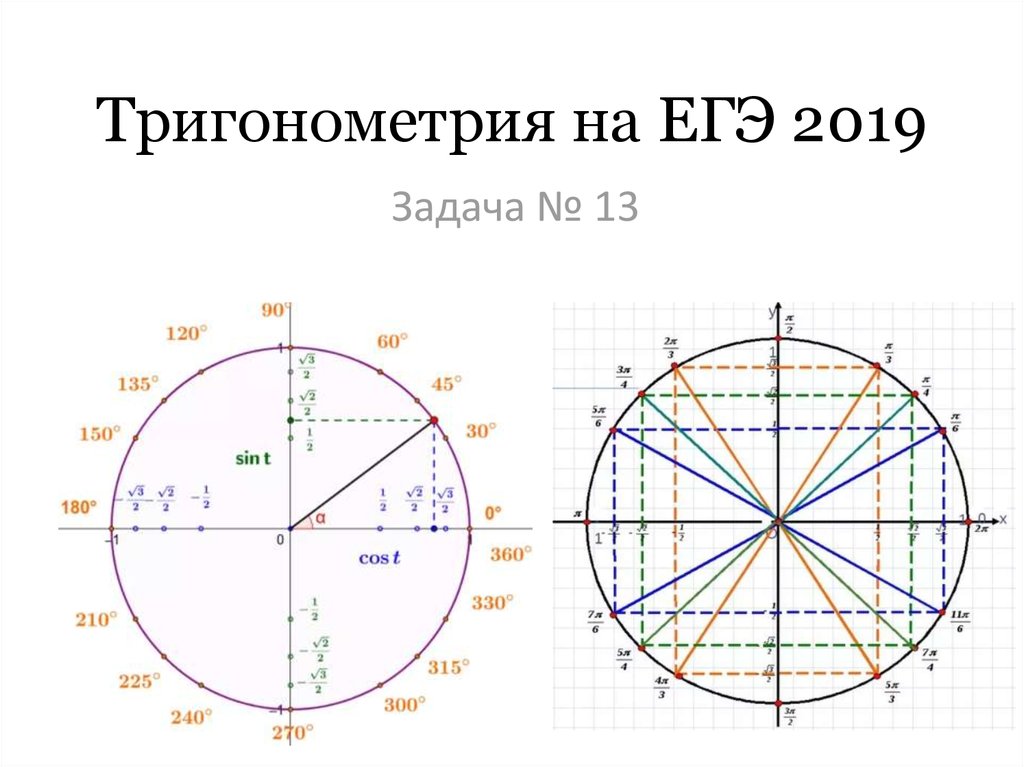 Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.
Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.
Истоки тригонометрии
Знакомство с данной наукой следует начать с определения синуса, косинуса и тангенса угла, однако прежде необходимо разобраться, чем вообще занимается тригонометрия.
Исторически главным объектом исследования данного раздела математической науки были прямоугольные треугольники. Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.
Начальный этап
Первоначально люди рассуждали о взаимоотношении углов и сторон исключительно на примере прямоугольных треугольников. Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.
Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.
Изучение тригонометрии в школе сегодня начинается с прямоугольных треугольников, после чего полученные знания используются учениками в физике и решении абстрактных тригонометрических уравнений, работа с которыми начинается в старших классах.
Сферическая тригонометрия
Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют иные правила, а сумма углов в треугольнике всегда больше 180 градусов. Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».
Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой. Обратите внимание — она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.
Обратите внимание — она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.
Прямоугольный треугольник
Немного узнав про способы применения тригонометрии, вернемся к базовой тригонометрии, чтобы в дальнейшем разобраться, что такое синус, косинус, тангенс, какие расчёты можно с их помощью выполнять и какие формулы при этом использовать.
Первым делом необходимо уяснить понятия, относящиеся к прямоугольному треугольнику. Во-первых, гипотенуза — это сторона, лежащая напротив угла в 90 градусов. Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.
Например, если две стороны равны 3 и 4 сантиметрам соответственно, длина гипотенузы составит 5 сантиметров. Кстати, об этом знали ещё древние египтяне около четырех с половиной тысяч лет назад.
Две оставшиеся стороны, которые образуют прямой угол, носят название катетов.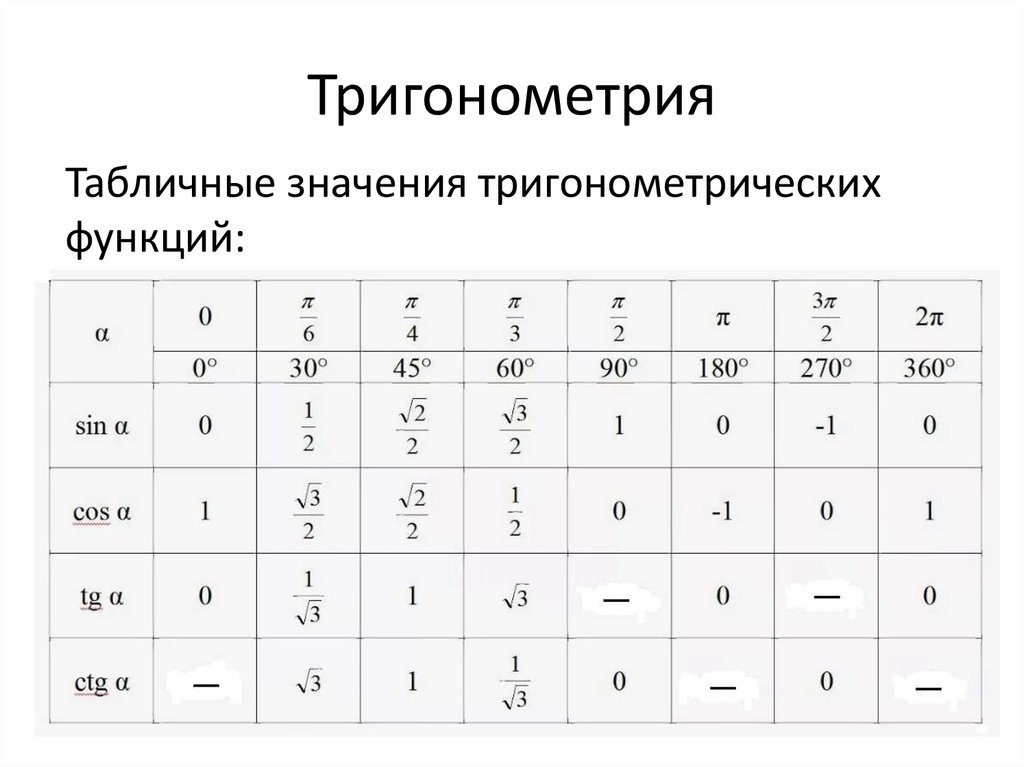 Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.
Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.
Определение
Наконец, твердо понимая геометрическую базу, можно обратиться к определению синуса, косинуса и тангенса угла.
Синусом угла называется отношение противолежащего катета (т. е. стороны, располагающейся напротив нужного угла) к гипотенузе. Косинусом угла называется отношение прилежащего катета к гипотенузе.
Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза — это по умолчанию самая длинная Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы. Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.
Наконец, тангенсом угла называется отношение противолежащей стороны к прилежащей. Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Котангенс, соответственно, представляет собой отношение прилежащей к углу стороны к противолежащей. Тот же результат мы получим, разделив единицу на тангенс.
Итак, мы рассмотрели определения, что такое синус, косинус, тангенс и котангенс, и можем заняться формулами.
Простейшие формулы
В тригонометрии не обойтись без формул — как найти синус, косинус, тангенс, котангенс без них? А ведь именно это требуется при решении задач.
Первая формула, которую необходимо знать, начиная изучать тригонометрию, говорит о том, что сумма квадратов синуса и косинуса угла равна единице. Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.
Многие учащиеся не могут запомнить вторую формулу, также очень популярную при решении школьных задач: сумма единицы и квадрата тангенса угла равна единице, деленной на квадрат косинуса угла. Присмотритесь: ведь это то же самое утверждение, что и в первой формуле, только обе стороны тождества были поделены на квадрат косинуса. Выходит, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько базовых формул вы в любой момент сможете сами вывести требуемые более сложные формулы на листе бумаги.
Присмотритесь: ведь это то же самое утверждение, что и в первой формуле, только обе стороны тождества были поделены на квадрат косинуса. Выходит, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько базовых формул вы в любой момент сможете сами вывести требуемые более сложные формулы на листе бумаги.
Формулы двойного угла и сложения аргументов
Ещё две формулы, которые требуется выучить, связаны со значениями синуса и косинуса при сумме и разности углов. Они представлены на рисунке ниже. Обратите внимание, что в первом случае оба раза перемножается синус и косинус, а во втором складывается попарное произведение синуса и косинуса.
Также существуют формулы, связанные с аргументами в виде двойного угла. Они полностью выводятся из предыдущих — в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.
Наконец, обратите внимание, что формулы двойного угла можно преобразовать так, чтобы понизить степень синуса, косинуса, тангенса альфа.
Теоремы
Двумя основными теоремами в базовой тригонометрии являются теорема синусов и теорема косинусов. С помощью этих теорем вы легко сможете понять, как найти синус, косинус и тангенс, а значит, и площадь фигуры, и величину каждой стороны и т. д.
Теорема синусов утверждает, что в результате деления длины каждой из сторон треугольника на величину противолежащего угла мы получим одинаковое число. Более того, это число будет равно двум радиусам описанной окружности, т. е. окружности, содержащей все точки данного треугольника.
Теорема косинусов обобщает теорему Пифагора, проецируя её на любые треугольники. Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны. Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Ошибки по невнимательности
Даже зная, что такое синус, косинус и тангенс, легко совершить ошибку из-за рассеянности внимания или ошибки в простейших расчётах. Чтобы избежать таких ошибок, ознакомимся с наиболее популярными из них.
Во-первых, не следует преобразовывать обыкновенные дроби в десятичные до получения окончательного результата — можно и ответ оставить в виде обыкновенной дроби, если в условии не оговорено обратное. Такое преобразование нельзя назвать ошибкой, однако следует помнить, что на каждом этапе задачи могут появиться новые корни, которые по задумке автора должны сократиться. В этом случае вы напрасно потратите время на излишние математические операции. Особенно это актуально для таких значений, как корень из трёх или из двух, ведь они встречаются в задачах на каждом шагу. То же касается округлений «некрасивых» чисел.
Далее, обратите внимание, что к любому треугольнику применима теорема косинусов, но не теорема Пифагора! Если вы по ошибке забудете вычесть удвоенное произведение сторон, умноженное на косинус угла между ними, вы не только получите совершенно неверный результат, но и продемонстрируете полное непонимание предмета. Это хуже, чем ошибка по невнимательности.
Это хуже, чем ошибка по невнимательности.
В-третьих, не путайте значения для углов в 30 и 60 градусов для синусов, косинусов, тангенсов, котангенсов. Запомните эти значения, ведь синус 30 градусов равен косинусу 60, и наоборот. Их легко перепутать, вследствие чего вы неизбежно получите ошибочный результат.
Применение
Многие ученики не спешат приступать к изучению тригонометрии, поскольку не понимают её прикладного смысла. Что такое синус, косинус, тангенс для инженера или астронома? Это понятия, благодаря которым можно вычислить расстояние до далёких звёзд, предсказать падение метеорита, отправить исследовательский зонд на другую планету. Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.
В заключение
Итак, вы синус, косинус, тангенс. Вы можете использовать их в расчётах и успешно решать школьные задачи.
Вся суть тригонометрии сводится к тому, что по известным параметрам треугольника нужно вычислить неизвестные. Всего этих параметров шесть: длины трёх сторон и величины трёх углов. Всё различие в задачах заключается в том, что даются неодинаковые входные данные.
Как найти синус, косинус, тангенс исходя из известных длин катетов или гипотенузы, вы теперь знаете. Поскольку эти термины обозначают не что иное, как отношение, а отношение — это дробь, главной целью тригонометрической задачи становится нахождение корней обычного уравнения либо же системы уравнений. И здесь вам поможет обычная школьная математика.
В этой статье собраны таблицы синусов, косинусов, тангенсов и котангенсов . Сначала мы приведем таблицу основных значений тригонометрических функций, то есть, таблицу синусов, косинусов, тангенсов и котангенсов углов 0, 30, 45, 60, 90, …, 360
градусов (0, π/6, π/4, π/3, π/2, …, 2π
радиан). После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В.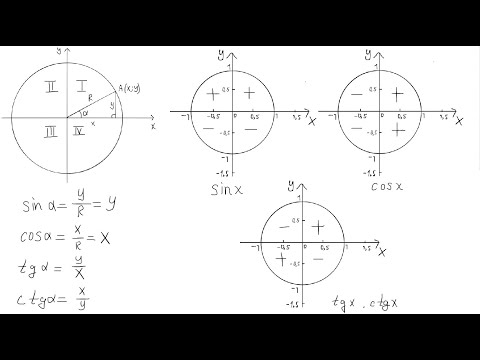
Навигация по странице.
Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с.
 , ил.
, ил. - Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2
Позволяют установить ряд характерных результатов – свойств синуса, косинуса, тангенса и котангенса . В этой статье мы рассмотрим три основных свойства. Первое из них указывает знаки синуса, косинуса, тангенса и котангенса угла α в зависимости от того, углом какой координатной четверти является α . Дальше мы рассмотрим свойство периодичности, устанавливающее неизменность значений синуса, косинуса, тангенса и котангенса угла α при изменении этого угла на целое число оборотов. Третье свойство выражает зависимость между значениями синуса, косинуса, тангенса и котангенса противоположных углов α и −α .
Если же Вас интересуют свойства функций синуса, косинуса, тангенса и котангенса, то их можно изучить в соответствующем разделе статьи .
Навигация по странице.
Знаки синуса, косинуса, тангенса и котангенса по четвертям
Ниже в этом пункте будет встречаться фраза «угол I
, II
, III
и IV
координатной четверти».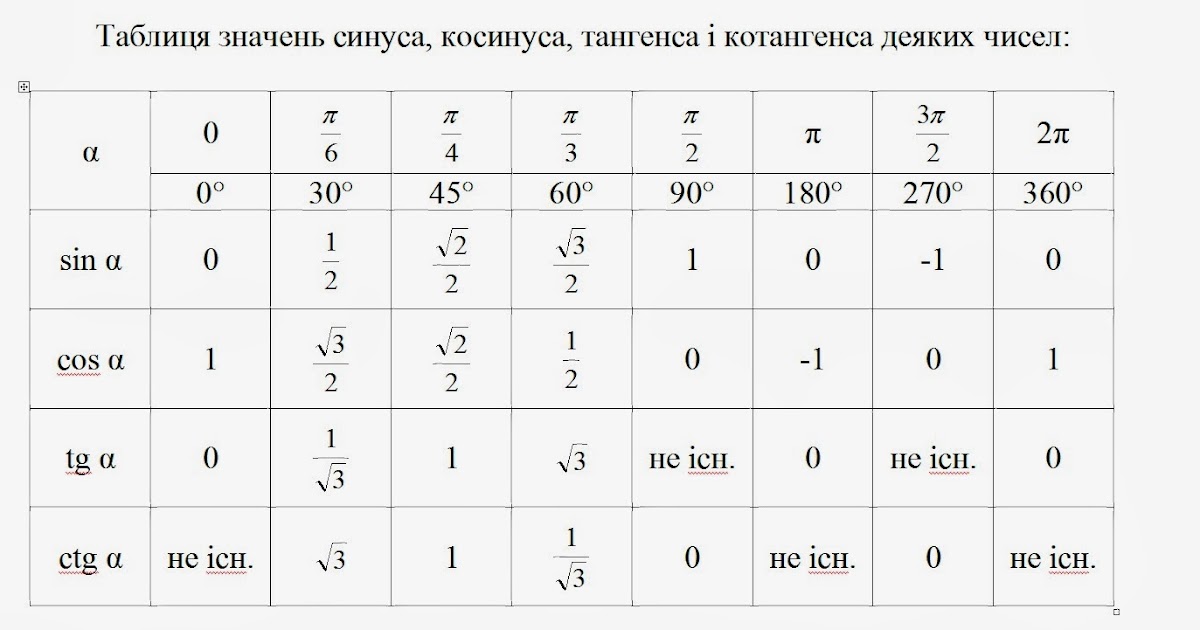 Объясним, что же это за углы.
Объясним, что же это за углы.
Возьмем единичную окружность , отметим на ней начальную точку А(1, 0) , и повернем ее вокруг точки O на угол α , при этом будем считать, что мы попадем в точку A 1 (x, y) .
Говорят, что угол α является углом I , II , III , IV координатной четверти , если точка А 1 лежит в I , II , III , IV четверти соответственно; если же угол α таков, что точка A 1 лежит на любой из координатных прямых Ox или Oy , то этот угол не принадлежит ни одной из четырех четвертей.
Для наглядности приведем графическую иллюстрацию. На чертежах ниже изображены углы поворота 30 , −210 , 585 и −45 градусов, которые являются углами I , II , III и IV координатных четвертей соответственно.
Углы 0, ±90, ±180, ±270, ±360, … градусов не принадлежат ни одной из координатных четвертей.
Теперь разберемся, какие знаки имеют значения синуса, косинуса, тангенса и котангенса угла поворота α в зависимости от того, углом какой четверти является α .
Для синуса и косинуса это сделать просто.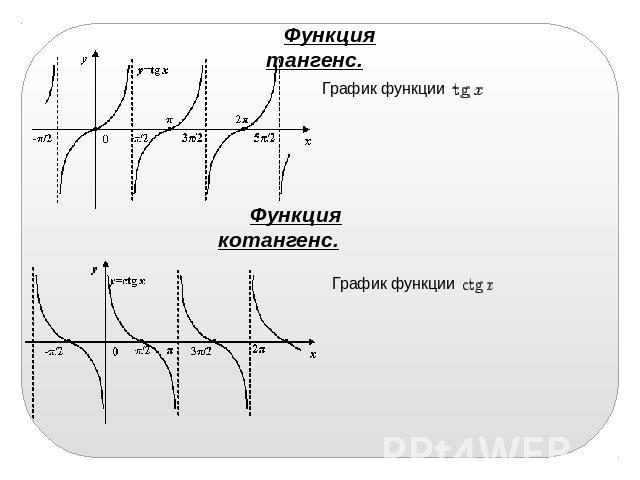
По определению синус угла α — это ордината точки А 1 . Очевидно, что в I и II координатных четвертях она положительна, а в III и IV четвертях – отрицательна. Таким образом, синус угла α имеет знак плюс в I и II четвертях, а знак минус – в III и VI четвертях.
В свою очередь косинус угла α — это абсцисса точки A 1 . В I и IV четвертях она положительна, а во II и III четвертях – отрицательна. Следовательно, значения косинуса угла α в I и IV четвертях положительны, а во II и III четвертях – отрицательны.
Чтобы определить знаки по четвертям тангенса и котангенса нужно вспомнить их определения: тангенс – это отношение ординаты точки A 1
к абсциссе, а котангенс – отношение абсциссы точки A 1
к ординате. Тогда из правил деления чисел с одинаковыми и разными знаками следует, что тангенс и котангенс имеют знак плюс, когда знаки абсциссы и ординаты точки A 1
одинаковые, и имеют знак минус – когда знаки абсциссы и ординаты точки A 1
различны. Следовательно, тангенс и котангенс угла имеют знак +
в I
и III
координатных четвертях, и знак минус – во II
и IV
четвертях.
Следовательно, тангенс и котангенс угла имеют знак +
в I
и III
координатных четвертях, и знак минус – во II
и IV
четвертях.
Действительно, например, в первой четверти и абсцисса x , и ордината y точки A 1 положительны, тогда и частное x/y , и частное y/x – положительно, следовательно, тангенс и котангенс имеют знаки + . А во второй четверти абсцисса x – отрицательна, а ордината y – положительна, поэтому и x/y , и y/x – отрицательны, откуда тангенс и котангенс имеют знак минус.
Переходим к следующему свойству синуса, косинуса, тангенса и котангенса.
Свойство периодичности
Сейчас мы разберем, пожалуй, самое очевидное свойство синуса, косинуса, тангенса и котангенса угла. Оно состоит в следующем: при изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса этого угла не изменяются.
Это и понятно: при изменении угла на целое число оборотов мы из начальной точки А
всегда будем попадать в точку А 1
на единичной окружности, следовательно, значения синуса, косинуса, тангенса и котангенса остаются неизменными, так как неизменны координаты точки A 1
.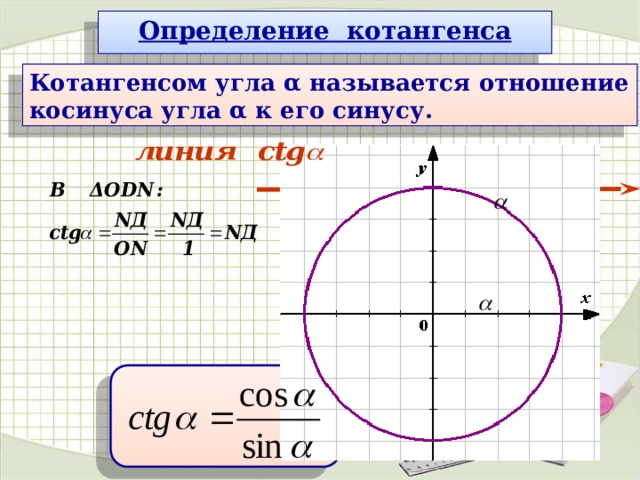
С помощью формул рассматриваемое свойство синуса, косинуса, тангенса и котангенса можно записать так: sin(α+2·π·z)=sinα , cos(α+2·π·z)=cosα , tg(α+2·π·z)=tgα , ctg(α+2·π·z)=ctgα , где α — угол поворота в радианах, z – любое , абсолютная величина которого указывает количество полных оборотов, на которые изменяется угол α , а знак числа z указывает направление поворота.
Если же угол поворота α задан в градусах, то указанные формулы перепишутся в виде sin(α+360°·z)=sinα , cos(α+360°·z)=cosα , tg(α+360°·z)=tgα , ctg(α+360°·z)=ctgα .
Приведем примеры использования этого свойства. Например, , так как , а . Вот еще пример: или .
Это свойство вместе с формулами приведения очень часто используется при вычислении значений синуса, косинуса, тангенса и котангенса «больших» углов.
Рассмотренное свойство синуса, косинуса, тангенса и котангенса иногда называют свойством периодичности.
Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов
Пусть А 1
– точка, полученная в результате поворота начальной точки А(1, 0)
вокруг точки O
на угол α
, а точка А 2
– это результат поворота точки А
на угол −α
, противоположный углу α
.
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов базируется на достаточно очевидном факте: упомянутые выше точки А 1
и А 2
либо совпадают (при ), либо располагаются симметрично относительно оси Ox
. То есть, если точка A 1
имеет координаты (x, y)
, то точка А 2
будет иметь координаты (x, −y)
. Отсюда по определениям синуса, косинуса, тангенса и котангенса записываем равенства и .
Сопоставляя их, приходим к соотношениям между синусами, косинусами, тангенсами и котангенсами противоположных углов α
и −α
вида .
Это и есть рассматриваемое свойство в виде формул.
Приведем примеры использования этого свойства. Например, справедливы равенства и .
Остается лишь заметить, что свойство синусов, косинусов, тангенсов и котангенсов противоположных углов, как и предыдущее свойство, часто используется при вычислении значений синуса, косинуса, тангенса и котангенса, и позволяет полностью уйти от отрицательных углов.
Список литературы.
- Алгебра: Учеб.
 для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7 - Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Введение в тригонометрию. Тангенс и котангенс любого числа
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Введение в тригонометрию.
Тангенс и котангенс любого числа.
1) Повторение.
2) Определение тангенса и котангенса любого числа.
3) Знаки тангенса и котангенса по четвертям окружности.
4) Задача №1. Определяем значения тангенса и котангенса чисел
двух макетов.
5) Линия тангенсов и линия котангенсов.
6) Задача №2. Решить уравнение tg t (ctg t)=a.
7) Задача №3. Решить неравенство tg t (ctg t)˅a.
A
Тангенсом острого угла прямоугольного
треугольника называется отношение
противолежащего катета к прилежащему
AC
tgB
BC
С
В
Котангенсом острого угла прямоугольного
треугольника называется отношение
прилежащего катета к противолежащему
BC
сtgB
AC
Таким образом, тангенс и котангенс – взаимно
обратные числа
содержание
sin t
tgt
cos t
t ϵ единичной
окружности
cos t 0
Для любого ли числа определен
(k Z )
2
тангенс не определен
тангенс?для чисел t
k
У
2
sin t
cos t
ctgt
sin t
t
0
cos t
sin t 0
Х
Для любого
ли числа определен
котангенс
не определен
для чисел t k
котангенс?
(k Z )
содержание
1 sin t Какие
1
значения
может
тангенс
и котангенс могут
принимать
тангенс
и котангенс?
принимать
любые значения
1 cos t 1
У
sin t
tgt
cos t
cos t
ctgt
sin t
II
I
Из определения следует, что
Определи знаки тангенса и
тангенс и котангенс положительны
котангенса по четвертям
в тех четвертях, в которых знаки
числовой окружности?
синуса и косинуса совпадают
Х
III
IV
У
II
У
III
II
Х
IV
хt cos t
содержание
I
III
yt sin t
I
Х
IV
Будем определять значения тангенса и учтем, что
У котангенс – число обратное тангенсу.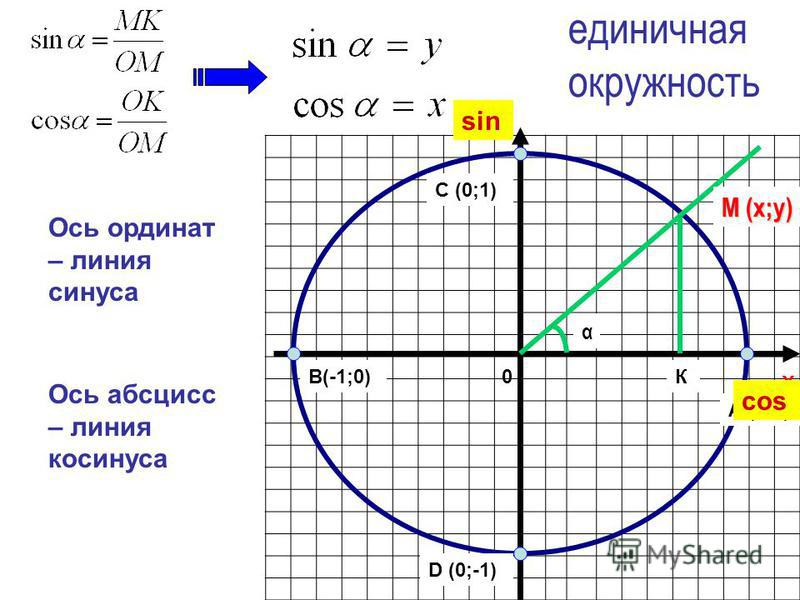
2
3 3
4
2
3
5
74511
7 5 3
sin
sin
sin
sin
sin
6711
45 75 3
4
1 321 3 21 13321 26 1
6
3
6
3
4
4
2
tg
tgtgtg 523
: : : нет
3131
745sin
11
7 5sin
3 0 222002 0 22222 0 3Х
sin
6346342tgcos
sin
sin
sin
0cos
323
3 103102 2 1 1
cos
cos
523 tg cos
1
1
2
1
663443
22 0 :: 1: 1
нет
321 31
636434cos
tgtg
tgtg cos
:
523 22220 2 22222 11
3643 2cos
3 3
7 64
cos
cos
cos
634643 2
6 5
7 6
4 4
3
3
2
5
3
4
0
6
4
3
0
1
3
1
3
3
1
1
3
2
2 3 5
3 4 6
3 1
0
1
3
1
1 3
3
7 5 4 3 5 7 11
6
4
3 2 3 4 6
1
1
1
3 3 1
0
3
3
1
1
1 3
3 1
0
3
3
содержание
значения синуса и косинуса
tgt ?
Геометрическая интерпретация тангенса.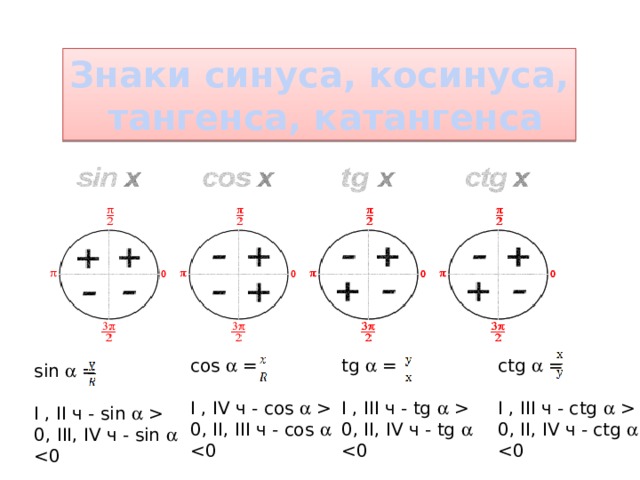
Или «Как его увидеть?»
Y
Как «увидеть»
синус и косинус
мы уже знаем
sin t
t
cos t
содержание
X
Проведем
касательную
через конец
радиуса
окружности,
параллельную
оси Оу
tgt ?
tgt
sin t
AB
cos t
BC
Используем
геометрические
соображения
Треугольник АВС
подобен
треугольнику А1В1С
содержание
A1 B1
B1C
B1C 1
Y
A1
sin t
С
t
A
cos
Bt
AB A1 B1
BC
1
tgt A1 B1
B1
Таким образом, tgt
это ордината
X
точки А1 на
нашем чертеже
Линия
тангенсов.
Линия тангенсов поможет нам определять значения
Найдите значение тангенса.
тангенсов чисел двух макетов без вычислений.
Y
Значения
тангенсов чисел
двух макетов:
3 1,7
3
0 ,6
3
1
3
1
3
3
3
4
2
3
?
4
4
0
0
3
3
1
tg
X
3
содержание
1
Линия
тангенсов.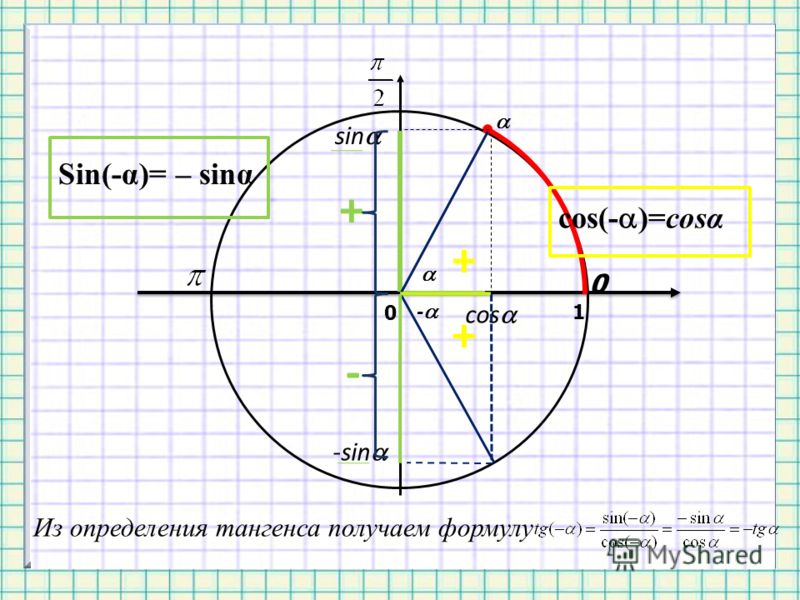
Найдите значение тангенса.
Y
Значения
тангенсов чисел
двух макетов:
5
tg
?
6
3 1,7
3
0 ,6
3
1
3
3
0
содержание
5
6 2
3
2
6
3
X
Линия
тангенсов.
Найдите значение тангенса.
Y
Значения
тангенсов чисел
двух макетов:
3 1,7
3
0 ,6
3
1
7
6
4
3
0
5
6
6
содержание
4
tg
?
3
2
3
2
3
3
X
Линия
тангенсов.
Аналогичные рассуждения приводят к
геометрической интерпретации котангенса.
сtgt ?
Проведем
касательную
через конец
радиуса
окружности,
параллельную
оси Ох
содержание
Y
A
t
Линия
котангенсов.
X
Абсцисса точки А – значение
котангенса числа t на нашем
чертеже
Найдите значение котангенса.
Y
Значения
котангенсов чисел
двух макетов:
5
сtg
?
6
3 1,7
3
0 ,6
3
1
0
6
5
6
содержание
Линия
котангенсов.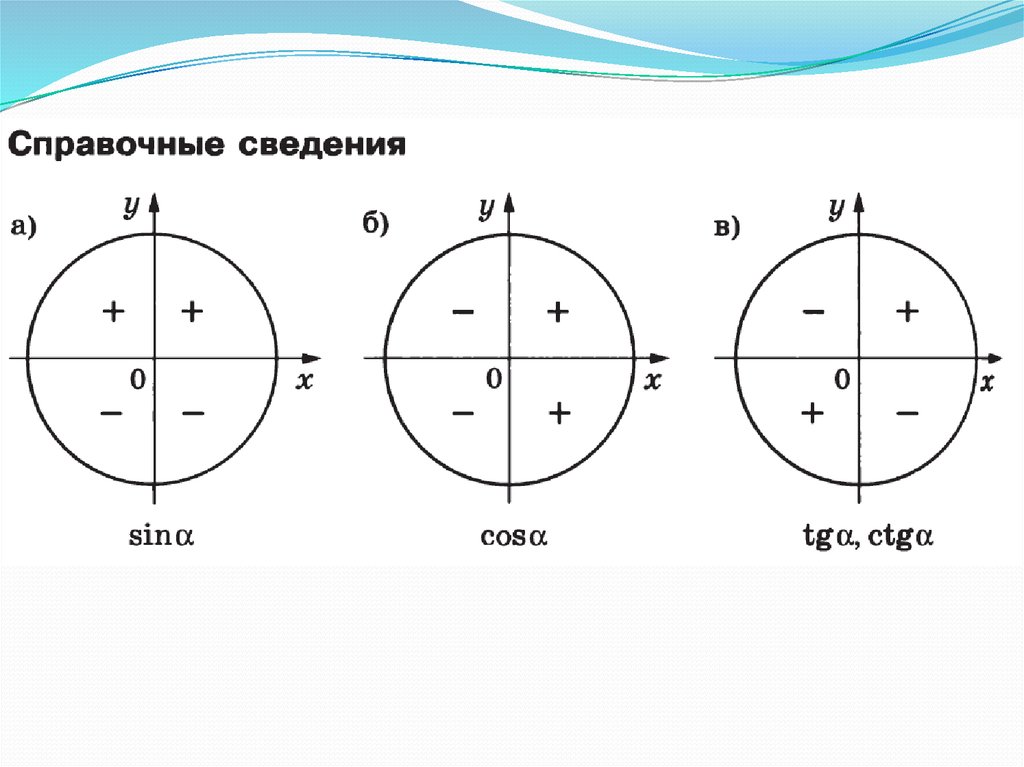
2
3
2
3
3 X
tgt 3
Y
3 1,7
3
?
3
Ответ:
t
2 k
3
или
t 43 k
2 k
t
3
k Z
содержание
Каждой точке
окружности
соответствует
бесконечно
много чисел
X
4 ?
3
сtgt 1
Y
Каждой точке
окружности
соответствует
бесконечно
много чисел
Ответ:
3
t
2 k
34
или
t 74 k
2 k
t
4
k Z
содержание
1
3?
4
X
7
?
4
сtgt 3
Y
Первый способ
3 1,7
Ответ:
t
2 k
6
или
t 76 k
2 k
t
6
k Z
содержание
?
6
7
?
6
Каждой точке
окружности
соответствует
бесконечно
много чисел
3 X
3
сtgt 3 tgt
3
Второй способ
Y
3
0 ,6
3
Ответ:
t
2 k
6
или
t 76 k
2 k
t
6
k Z
содержание
3
3
?
6
Каждой точке
окружности
соответствует
бесконечно
много чисел
X
7
?
6
tgt
3
3
3
0 ,6
3
Каждой точке
красного луча
поставим в
соответствие
точку числовой
окружности
Полученные дуги
симметричны
относительно начала
координат
Y
?
2
3
3
?
6
Таким образом,
достаточно рассмотреть правую
полуокружность.
содержание
X
Ответ:
t k ; k
2
6
k Z
tgt 1
Y
Каждой точке
красного луча
поставим в
соответствие
точку числовой
окружности
1
?
4
X
?
2
Ответ:
t k ; k
4
2
k Z
содержание
ctgt 3
Y
Каждой точке
красного луча
поставим в
соответствие
точку числовой
окружности
Достаточно рассмотреть
верхнюю полуокружность.
?
6
?
3 X
Ответ:
t k ; k
6
k Z
содержание
English Русский Правила
Графики функций тангенса и котангенса
Определения тангенса и котангенса
Напомним, что функции тангенса и котангенса определяются через синус и косинус:
\[\tan t = \frac{{\sin t}}{{\cos t}},\;\;\cot t = \frac{{\cos t}}{{\sin t}},\ ]
, где \(t\) — угол между радиус-вектором точки на единичной окружности и положительной осью x (измеряется против часовой стрелки).
Мы видим из определений, что котангенс есть величина, обратная тангенсу, то есть
\[\cot t = \frac{1}{{\tan t}}.\]
Рассмотрим свойства этих двух функций более подробно.
График и свойства касательной функции
Домен и кодовый домен касательной функции
Касательная функция не определена в точках \(t = \frac{\pi }{2} + \pi n,\) \(n \in \mathbb{Z}\), в которых \(\cos t = 0.\) Диапазон \(\tan t\) — все действительные числа. Формально мы можем написать
\[\text{dom}(\tan t) = \left\{ {t \in \mathbb{R} \left|\, t \ne \frac{\pi }{2} + \pi n \right .,\,n \in \mathbb{Z}} \right\},\;\text{codom}(\tan t) = \mathbb{R},\]
, где dom обозначает домен, а codom обозначает кодовый домен или диапазон функции.
Монотонность касательной функции
Показать, что функция тангенса возрастает на открытом интервале \(\left( { — \frac{\pi }{2},\frac{\pi }{2}} \right).\) Выберите две произвольные точки \ (t_1, t_2\) из этого интервала такое, что \(t_1 \gt t_2.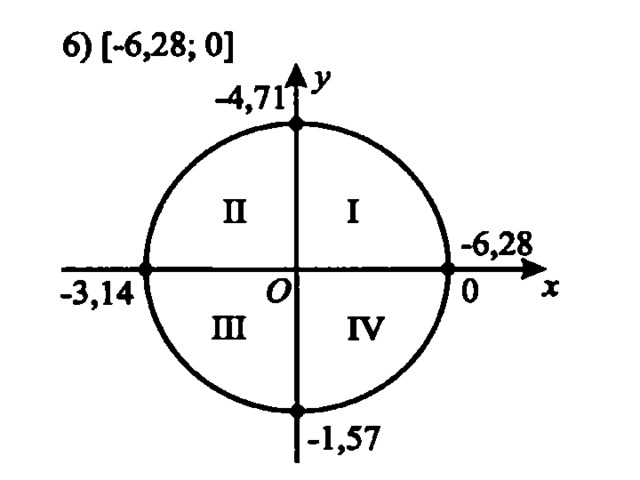 \) Для определения знака разности \(\tan {t_1} — \tan {t_2},\) представим ее в виде
\) Для определения знака разности \(\tan {t_1} — \tan {t_2},\) представим ее в виде
\[\tan {t_1} — \tan {t_2} = \frac{{\sin {t_1}}}{{\cos {t_1}}} — \frac{{\sin {t_2}}}{{\ cos {t_2}}} = \frac{{\sin {t_1}\cos {t_2} — \sin {t_2}\cos {t_1}}}{{\cos {t_1}\cos {t_2}}} = \ frac{{\sin\left({{t_1} — {t_2}} \right)}}{{\cos {t_1}\cos {t_2}}}.\]
Углы \(t_1\) и \(t_2\) лежат в квадранте \(1\text{st}\) или в квадранте \(4\text{th}\), где косинус положительный. Следовательно, \(\cos {t_1} \gt 0\) и \(\cos {t_2} \gt 0.\) Очевидно, что
\[0 \lt {t_1} — {t_2} \lt \pi , \стрелка вправо \sin \left( {{t_1} — {t_2}} \right) \gt 0.\]
Мы видим, что если \(t_1 \gt t_2,\), то
\[\tan {t_1} — \tan {t_2} = \frac{{\sin \left( {{t_1} — {t_2}} \right)}}{{\cos {t_1}\cos {t_2} }} \gt 0,\]
, что означает, что функция тангенса строго возрастает на данном интервале.
Четность касательной функции
Легко доказать, что функция тангенса нечетна:
\[\tan \left( { — t} \right) = \frac{{\sin \left( { — t} \right)}}{{\cos \left({ — t} \right)}} = \frac{{ — \sin t}}{{\cos t}} = — \frac{{\sin t}}{{\cos t}} = — \tan t.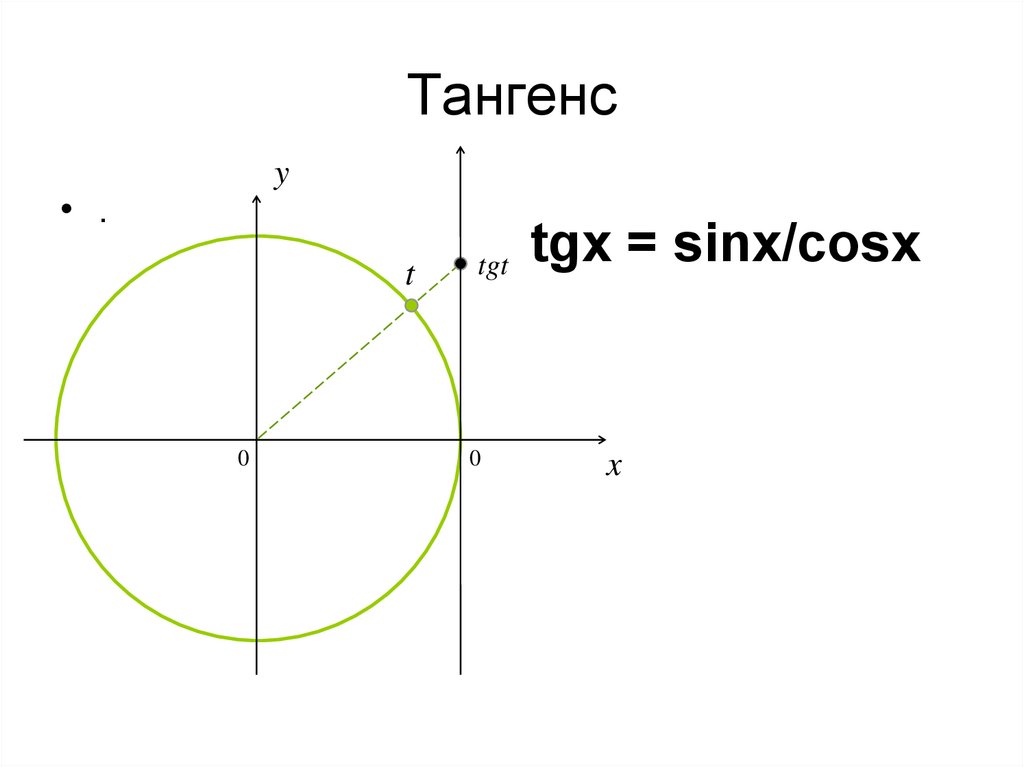 \]
\]
Как и любая другая нечетная функция, график касательной функции симметричен относительно начала координат.
Периодичность касательной функции
Касательная функция является периодической с наименьшим периодом \(\pi:\)
\[\tan \left( {t + \pi n} \right) = \tan t,\]
, где \(n \in \mathbb{Z}.\)
Нули функции касательной
Тангенс будет равен нулю, если его числитель (синус) равен нулю. Следовательно, корни уравнения \(\tan t = 0\) равны
\[t = \pi n,\;n \in \mathbb{Z}.\]
График касательной функции \(y = \tan t\)
Поскольку \(\tan t\) не определено, когда \(\cos t = 0,\), функция тангенса имеет вертикальные асимптоты в точках \(t = \frac{\pi }{2} + \pi n,\ ) \(n \in \mathbb{Z}.\) График касательной состоит из бесконечного числа кривых, которые могут быть получены друг из друга сдвигом вдоль оси \(x-\) над \(n\pi\ ), где \(n\) — целое число.
Рис. 1.График и свойства функции котангенса
Домен и кодовый домен функции котангенса
Функция \(\cot t = \frac{{\cos t}}{{\sin t}}\) не определена в \(t = \pi n,\) \(n \in \mathbb{Z }\) где \(\sin t = 0. \) Кодовая область (или диапазон) \(\cot t\) представляет собой набор всех действительных чисел. Таким образом, у нас есть
\) Кодовая область (или диапазон) \(\cot t\) представляет собой набор всех действительных чисел. Таким образом, у нас есть
\[\text{dom}(\cot t) = \left\{ {t \in \mathbb{R} \left|\, t \ne \pi n \right.,\,n \in \mathbb{ Z}} \right\},\;\text{codom}(\cot t) = \mathbb{R}.\]
Монотонность функции котангенса
Котангенс является убывающей функцией между любыми двумя соседними точками разрыва. Докажем это следующим образом. Пусть точки \(t_1\) и \(t_2\) принадлежат открытому интервалу \(\left( {0,\pi } \right).\) Предположим, что \(t_1 \gt t_2.\) Определите знак разница \(\cot {t_1} — \cot {t_2}.\) Используя тождество суммы и произведения, мы можем написать
\[\кроватка {t_1} — \кроватка {t_2} = — \frac{{\sin \left( {{t_1} — {t_2}} \right)}}{{\sin {t_1}\sin {t_2 }}}.\]
Углы \(t_1\) и \(t_2\) находятся в квадранте \(1\text{st}\) или в квадранте \(2\text{nd}\), где синус положительный, поэтому как \(\sin {t_1} \gt 0\), так и \(\sin {t_2} \gt 0.\) Кроме того,
\[0 \lt {t_1} — {t_2} \lt \pi , \стрелка вправо \sin \left( {{t_1} — {t_2}} \right) \gt 0. \]
\]
Таким образом, дробь в правой части вышеприведенной формулы положительна. Учитывая знак минус перед дробью, мы заключаем, что \(\cot {t_1} — \cot {t_2} \lt 0\), когда \(t_1 — t_2 \gt 0.\)
Следовательно, функция котангенса строго убывает в интервале \(\left( {0,\pi } \right).\)
Четность функции котангенса
Функция \(\cot t\) нечетная:
\[\cot \left( { — t} \right) = \frac{{\cos \left( { — t} \right)}}{{\sin \left({ — t} \right)}} = \frac{{\cos t}}{{ — \sin t}} = — \frac{{\cos t}}{{\sin t}} = — \cot t.\]
График функции котангенса симметричен относительно начала координат.
Периодичность функции котангенса
Как и тангенс, функция котангенса периодична с наименьшим периодом \(\pi:\)
\[\cot \left( {t + \pi n} \right) = \cot t,\]
, где \(n \in \mathbb{Z}.\)
Нули функции котангенса
Котангенс будет иметь нули в точках, где косинус равен нулю. Следовательно, решение уравнения \(\cot t = 0\) равно
\[t = \frac{\pi }{2} + \pi n,\;n \in \mathbb{Z}.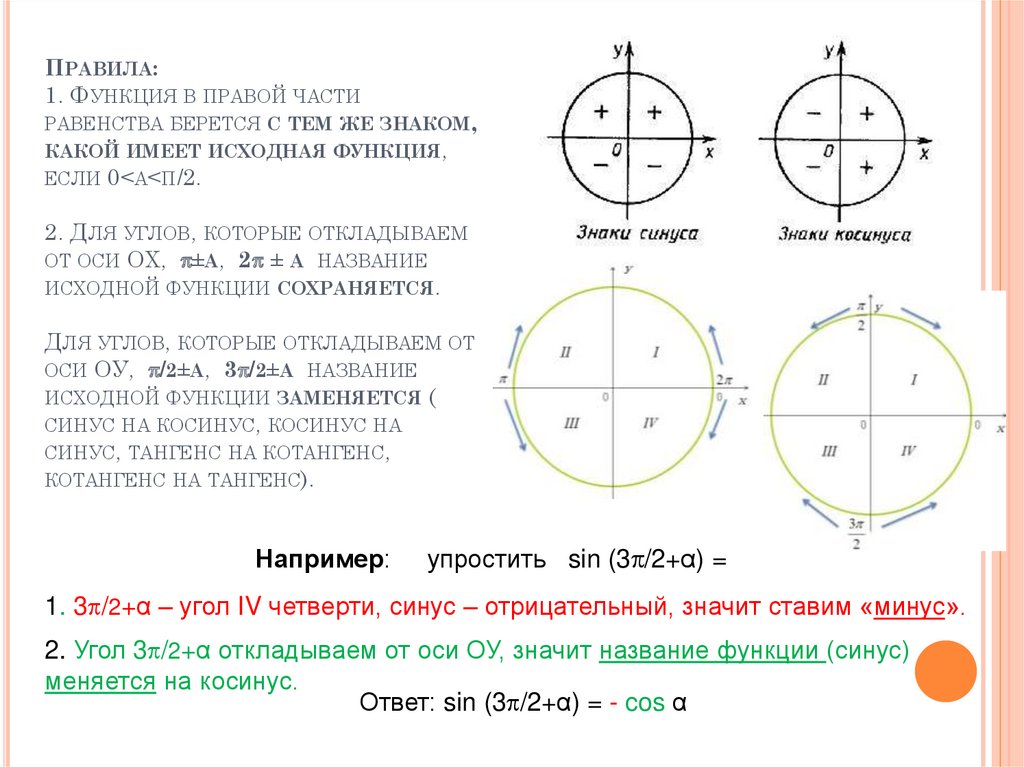 \]
\]
График функции котангенса \(y = \cot t\)
График котангенса имеет вертикальные асимптоты в точках \(t = \pi n,\) \(n \in \mathbb{Z}.\) Он всегда убывает между точками разрыва. Функция котангенса \(\pi\) периодична, поэтому отдельные кривые могут быть получены друг из друга с помощью переноса на \(n\pi\) единиц, где \(n \in \mathbb{Z}.\)
Рис. 2.См. решенные проблемы на стр. 2.
Другие тригонометрические функции | Предварительное исчисление
Результаты обучения
- Найдите точные значения тригонометрических функций секанса, косеканса, тангенса и котангенса 30° (π/6), 45° (π/4) и 60° (π/3).
- Используйте опорные углы для вычисления тригонометрических функций секанса, косеканса, тангенса и котангенса.
- Использовать свойства четных и нечетных тригонометрических функций.
- Распознавать и использовать фундаментальные тождества.
- Вычисление тригонометрических функций с помощью калькулятора.

Найдите точные значения тригонометрических функций секанса, косеканса, тангенса и котангенса
Чтобы определить оставшиеся функции, мы еще раз нарисуем единичный круг с точкой [латекс]\влево(х,у\вправо)[/ латекс], соответствующий углу [латекс]t[/латекс], как показано на рисунке 1. Как и в случае с синусом и косинусом, мы можем использовать координаты [латекс]\влево(х,у\вправо)[/латекс] чтобы найти другие функции.
Рисунок 1
Первая функция, которую мы определим, это тангенс. Тангенс угла представляет собой отношение значения y к значению x соответствующей точки на единичной окружности. На рисунке 1 тангенс угла [latex]t[/latex] равен [latex]\frac{y}{x},x\ne 0[/latex]. Поскольку значение y равно синусу [latex]t[/latex], а значение x равно косинусу [latex]t[/latex], тангенс угла [latex ]t[/латекс] также можно определить как [латекс]\фракция{\sin t}{\cos t},\cos t\ne 0[/латекс].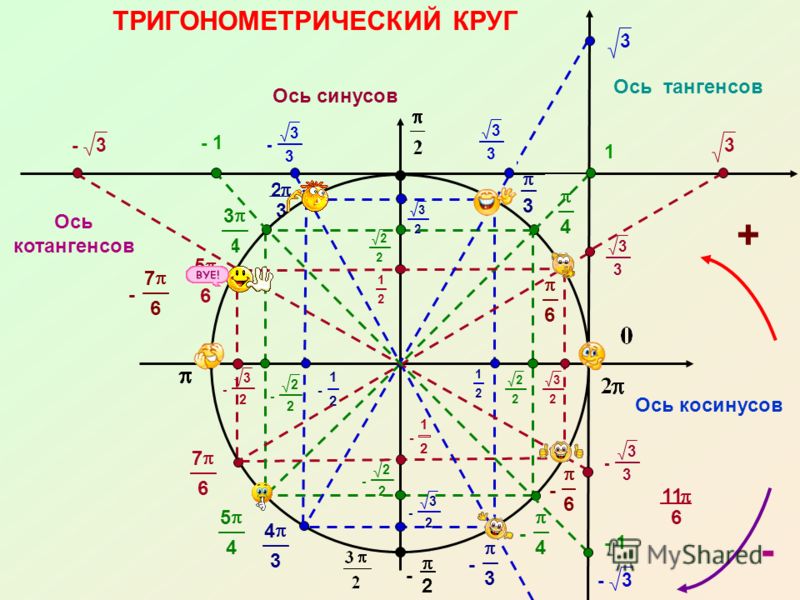 Функция тангенса обозначается аббревиатурой [латекс]\тангенс[/латекс]. Остальные три функции могут быть выражены как обратные функции, которые мы уже определили.
Функция тангенса обозначается аббревиатурой [латекс]\тангенс[/латекс]. Остальные три функции могут быть выражены как обратные функции, которые мы уже определили.
- Функция секанса является обратной функцией косинуса. На рисунке 1 секанс угла [latex]t[/latex] равен [latex]\frac{1}{\cos t}=\frac{1}{x},x\ne 0[/latex] . Функция секущей обозначается аббревиатурой [латекс]\сек[/латекс].
- Функция котангенса является обратной величиной функции тангенса. На рисунке 1 котангенс угла [latex]t[/latex] равен [latex]\frac{\cos t}{\sin t}=\frac{x}{y},y\ne 0[/ латекс]. Функция котангенса обозначается как [латекс]\кот[/латекс].
- Функция косеканса является обратной функцией синуса. На рисунке 1 косеканс угла [latex]t[/latex] равен [latex]\frac{1}{\sin t}=\frac{1}{y},y\ne 0[/latex] . Функция косеканса обозначается аббревиатурой [латекс]\csc[/латекс].
Общее примечание: функции тангенса, секанса, косеканса и котангенса
Если [latex]t[/latex] — действительное число, а [latex]\left(x,y\right)[/latex] — точка где конечная сторона угла [latex]t[/latex] радиан пересекает единичную окружность, тогда
[латекс]\begin{gathered}\tan t=\frac{y}{x},x\ne 0\\ \sec t=\frac{1}{x},x\ne 0\\ \csc t=\frac{1}{y},y\ne 0\\ \cot t=\frac{x}{y},y\ne 0\end{gathered}[/latex]
Пример 1.
 Тригонометрический поиск Функции из точки на единичной окружности
Тригонометрический поиск Функции из точки на единичной окружностиТочка [latex]\left(-\frac{\sqrt{3}}{2},\frac{1}{2}\right)[/latex] находится на единичный круг, как показано на рис. 2. Найдите [латекс]\sin t,\cos t,\tan t,\sec t,\csc t[/latex] и [латекс]\cot t[/латекс].
Рисунок 2
Показать решение
Попробуй
единичный круг, как показано на рис. 3. Найдите [латекс]\sin t,\cos t,\tan t,\sec t,\csc t[/latex] и [латекс]\cot t[/латекс].
Рисунок 3
Показать решение
Пример 2: нахождение тригонометрических функций угла /латекс], когда [латекс]t=\frac{\pi }{6}[/латекс].
Показать решение
Попробуйте
Найдите [латекс]\sin t,\cos t,\tan t,\sec t,\csc t[/latex] и [латекс]\cot t[/латекс], когда [латекс]t =\frac{\pi }{3}[/латекс].
Показать решение
Попробуйте
Поскольку мы знаем значения синуса и косинуса для общих углов первого квадранта, мы можем найти и другие значения функций для этих углов, установив [latex]x[/latex] равным косинусу и [ латекс]y[/латекс] равный синусу, а затем с использованием определений тангенса, секанса, косеканса и котангенса.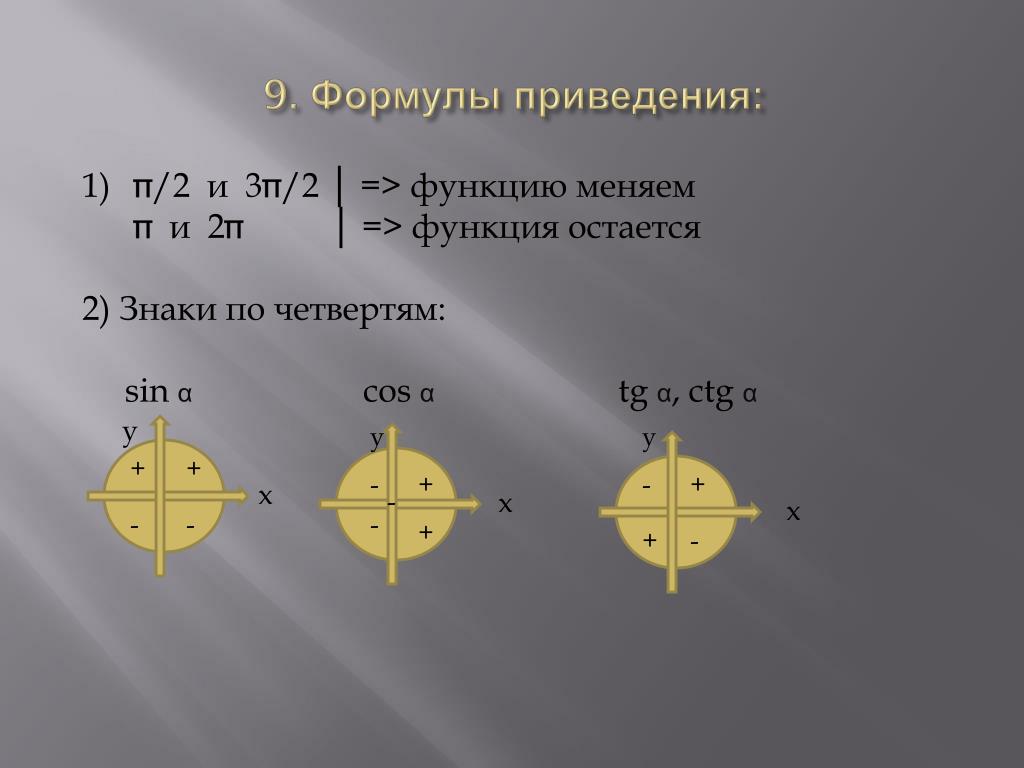 Результаты представлены в таблице ниже. 9{\ circ} [/латекс]
Результаты представлены в таблице ниже. 9{\ circ} [/латекс]
Использование опорных углов для вычисления тангенса, секанса, косеканса и котангенса
Мы можем вычислять тригонометрические функции углов вне первого квадранта, используя опорные углы, как мы уже сделали с функциями синуса и косинуса. Процедура та же: Найдите опорный угол образован конечной стороной данного угла с горизонтальной осью. Значения тригонометрической функции для исходного угла будут такими же, как и для эталонного угла, за исключением положительного или отрицательного знака, который определяется значениями x – и y в исходном квадранте. На рис. 4 показано, какие функции в каком квадранте положительны.
Процедура та же: Найдите опорный угол образован конечной стороной данного угла с горизонтальной осью. Значения тригонометрической функции для исходного угла будут такими же, как и для эталонного угла, за исключением положительного или отрицательного знака, который определяется значениями x – и y в исходном квадранте. На рис. 4 показано, какие функции в каком квадранте положительны.
Чтобы помочь нам вспомнить, какие из шести тригонометрических функций положительны в каждом квадранте, мы можем использовать мнемоническую фразу «Умный класс триггеров». Каждое из четырех слов во фразе соответствует одному из четырех квадрантов, начиная с квадранта I и вращаясь против часовой стрелки. В квадранте I, то есть « A », a Все шесть тригонометрических функций положительны. В квадранте II, « S mart», только s ine и его обратная функция, косеканс, положительны. В квадранте III « T установка» только t тангенс и его обратная функция, котангенс, положительны. Наконец, в квадранте IV, « C девушка», только c озин и его обратная функция, секанс, положительны.
В квадранте III « T установка» только t тангенс и его обратная функция, котангенс, положительны. Наконец, в квадранте IV, « C девушка», только c озин и его обратная функция, секанс, положительны.
Рисунок 4
Как: Дан угол не в первом квадранте, используя опорные углы, чтобы найти все шесть тригонометрических функций.
- Измерьте угол, образованный конечной стороной данного угла и горизонтальной осью. Это опорный угол.
- Оцените функцию по эталонному углу.
- Обратите внимание на квадрант, в котором находится конечная сторона исходного угла. На основе квадранта определите, является ли выход положительным или отрицательным.
Пример 3. Использование опорных углов для нахождения тригонометрических функций
Использование опорных углов для нахождения всех шести тригонометрических функций [латекс]-\frac{5\pi }{6}[/latex].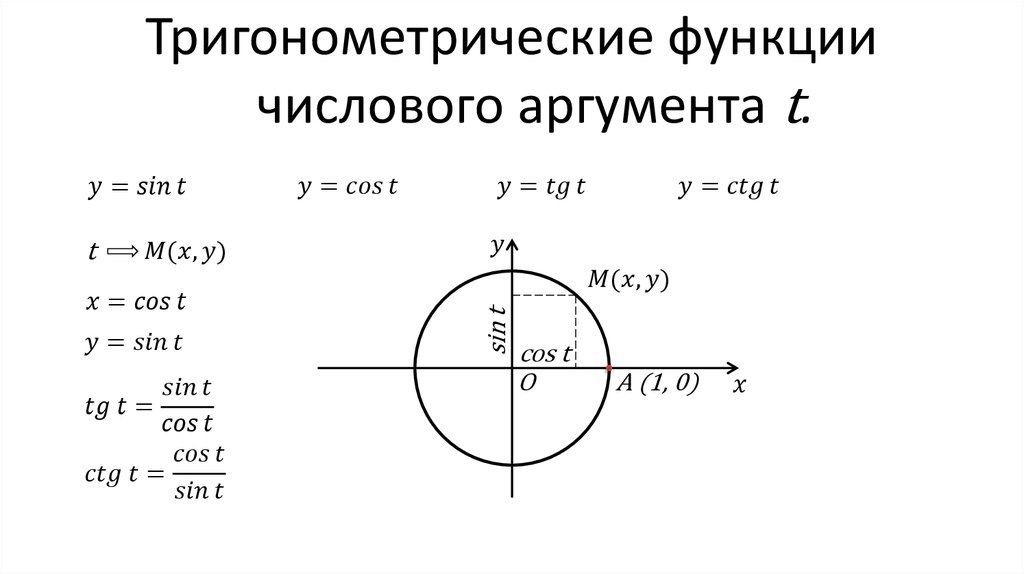
Показать решение
Попробуйте
Используйте опорные углы, чтобы найти все шесть тригонометрических функций [латекс]-\frac{7\pi }{4}[/latex].
Показать решение
Попробуйте
Использование четных и нечетных тригонометрических функций
Чтобы иметь возможность свободно использовать наши шесть тригонометрических функций как с положительными, так и с отрицательными угловыми входными данными, мы должны изучить, как каждая функция обрабатывает отрицательные входные данные. Как оказалось, между функциями в этом отношении есть важное различие. 9{3}[/latex] – нечетная функция.
Мы можем проверить, является ли тригонометрическая функция четной или нечетной, нарисовав единичную окружность с положительным и отрицательным углами, как показано на рисунке 7. Синус положительного угла равен [latex]y[/latex]. Синус отрицательного угла равен − y . Таким образом, синусоидальная функция является нечетной функцией. Таким образом мы можем проверить каждую из шести тригонометрических функций. Результаты представлены в таблице ниже.
Таким образом, синусоидальная функция является нечетной функцией. Таким образом мы можем проверить каждую из шести тригонометрических функций. Результаты представлены в таблице ниже.
Рисунок 7
| [латекс]\begin{array}{l}\sin t=y\hfill \\ \sin \left(-t\right)=-y\hfill \\ \sin t\ne \sin \left(-t\right)\hfill \end{массив}[/latex] | [латекс]\begin{array}{l}\text{cos}t=x\hfill \\ \cos\left(-t\right)=x\hfill\\ \cos t=\cos\left(- t\right)\hfill \end{массив}[/latex] | [латекс]\begin{array}{l}\text{tan}\left(t\right)=\frac{y}{x}\hfill \\ \tan \left(-t\right)=-\ frac{y}{x}\hfill \\ \tan t\ne \tan \left(-t\right)\hfill \end{массив}[/latex] |
| [латекс]\begin{array}{l}\sec t=\frac{1}{x}\hfill \\ \sec \left(-t\right)=\frac{1}{x}\ hfill \\ \sec t=\sec \left(-t\right)\hfill \end{массив}[/latex] | [латекс]\begin{array}{l}\csc t=\frac{1}{y}\hfill \\ \csc \left(-t\right)=\frac{1}{-y}\hfill \\ \csc t\ne \csc \left(-t\right)\hfill \end{массив}[/latex] | [латекс]\begin{array}{l}\cot t=\frac{x}{y}\hfill \\ \cot \left(-t\right)=\frac{x}{-y}\hfill \\ \cot t\ne кроватка\left(-t\right)\hfill \end{массив}[/latex] |
Общее примечание: четные и нечетные тригонометрические функции
Четная функция — это функция, в которой [латекс]f\left(-x\right)=f\left(x\right)[/latex].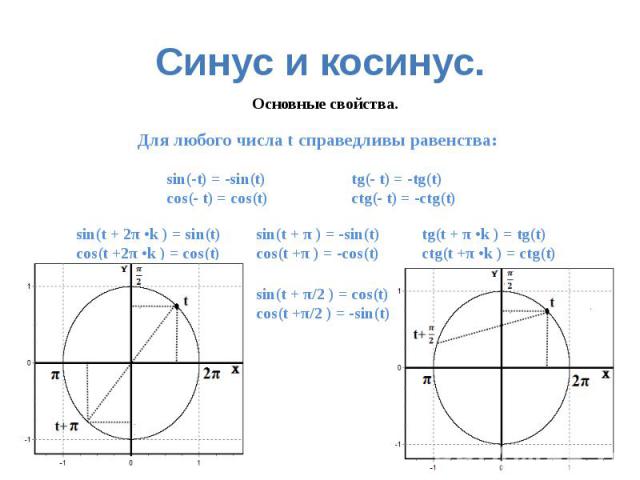
Нечетная функция — это функция, в которой [латекс]f\left(-x\right)=-f\left(x\right)[/latex].
Косинус и секанс четные:
[латекс]\begin{gathered}\cos \left(-t\right)=\cos t \\ \sec \left(-t\right)=\sec t \end {gathered}[/latex]
Синус, тангенс, косеканс и котангенс нечетны:
[латекс]\начало{собрано}\sin\left(-t\right)=-\sin t \\ \tan \left(-t\right)=-\tan t \\\csc \left(- t\right)=-\csc t \\ \cot \left(-t\right)=-\cot t \end{gathered}[/latex]
Пример 4. Использование четных и нечетных свойств тригонометрических функций
Если [латекс]\сек t=2[/латекс], что такое [латекс]\сек (-t)[/латекс]?
Показать решение
Попробуйте
Если [латекс]\cot t=\sqrt{3}[/латекс], что такое [латекс]\кот (-t)[/латекс]?
Показать решение
Распознавание и использование фундаментальных тождеств
Мы исследовали ряд свойств тригонометрических функций. Теперь мы можем пойти дальше и вывести некоторые фундаментальные тождества. Идентичности — это утверждения, истинные для всех значений входных данных, для которых они определены. Обычно тождества можно вывести из уже известных нам определений и отношений. Например, тождество Пифагора, которое мы узнали ранее, было получено из теоремы Пифагора и определений синуса и косинуса.
Теперь мы можем пойти дальше и вывести некоторые фундаментальные тождества. Идентичности — это утверждения, истинные для всех значений входных данных, для которых они определены. Обычно тождества можно вывести из уже известных нам определений и отношений. Например, тождество Пифагора, которое мы узнали ранее, было получено из теоремы Пифагора и определений синуса и косинуса.
Общее примечание: фундаментальные тождества
Мы можем вывести некоторые полезные тождества из шести тригонометрических функций. Остальные четыре тригонометрические функции можно связать обратно с функциями синуса и косинуса, используя следующие основные соотношения: \sec t=\frac{1}{\cos t}[/latex]
[латекс]\csc t=\frac{1}{\sin t}[/latex]
[латекс]\cot t= \frac{1}{\tan t}=\frac{\cos t}{\sin t}[/latex] 9\circ \right)[/латекс].
Показать решение
Попробуйте
Оценить [латекс]\csc\left(\frac{7\pi }{6}\right)[/latex].
Показать решение
Пример 6. Использование тождеств для упрощения тригонометрических выражений
Simplify [latex]\frac{\sec t}{\tan t}[/latex]. 9{2}t[/latex]
Пример 7. Использование тождеств для связи тригонометрических функций
If [latex]\text{cos}\left(t\right)=\frac{12}{13}[/latex] и [latex]t[/latex] находится в квадранте IV, как показано на рисунке 8, найдите значения остальных пяти тригонометрических функций.
Рисунок 8
Показать решение
Попробуйте
Если [latex]\sec \left(t\right)=-\frac{17}{8}[/latex] и [latex]0 Показать решение Как мы обсуждали в начале главы, функция, которая повторяет свои значения через равные промежутки времени, известна как периодическая функция . Другие функции также могут быть периодическими. Например, длина месяцев повторяется каждые четыре года. Если [latex]x[/latex] представляет продолжительность времени, измеренную в годах, а [latex]f\left(x\right)[/latex] представляет количество дней в феврале, тогда [latex]f\left( x+4\right)=f\left(x\right)[/латекс]. Этот шаблон повторяется снова и снова во времени. Другими словами, каждые четыре года в феврале гарантированно будет такое же количество дней, как и четыре года назад. Положительное число 4 является наименьшим положительным числом, удовлетворяющим этому условию, и называется периодом. А период — это кратчайший интервал, за который функция завершает один полный цикл — в этом примере период равен 4 и представляет собой время, которое требуется нам, чтобы убедиться, что в феврале одинаковое количество дней. Период [latex]P[/latex] повторяющейся функции [latex]f[/latex] — это число, представляющее интервал, такой что [latex]f\left (x+P\right)=f\left(x\right)[/latex] для любого значения [latex]x[/latex]. Период функций косинуса, синуса, секанса и косеканса равен [latex]2\pi [/latex]. Период функций тангенса и котангенса равен [латекс]\пи [/латекс]. Найдите значения шести тригонометрических функций угла [latex]t[/latex] на основе рисунка 9 . Рисунок 9 Показать решение Найдите значения шести тригонометрических функций угла [latex]t[/latex] на основе рисунка 10. Рисунок 10 Показать решение Если [латекс]\sin \left(t\right)=-\frac{\sqrt{3}}{2}[/latex]\text {cos}\left(t\right)=\frac{1}{2}[/latex], найти [латекс]\text{sec}\left(t\right),\text{csc}\left(t \right),\text{tan}\left(t\right),\text{кроватка}\left(t\right)[/latex]. Показать решение Если [латекс]\sin \left(t\right)=\frac{\sqrt{2}}{2}[/latex] и [латекс]\cos \left(t\right)= \frac{\sqrt{2}}{2}[/latex], найти [латекс]\text{sec}\left(t\right),\text{csc}\left(t\right),\text{ tan}\left(t\right),\text{ и кроватка}\left(t\right)[/latex]. Показать решение Мы научились вычислять шесть тригонометрических функций для общих углов первого квадранта и использовать их в качестве справочных углов для углов в других квадрантах. Чтобы оценить тригонометрические функции других углов, мы используем научный или графический калькулятор или компьютерную программу. Если калькулятор имеет режим градусов и режим радиан, убедитесь, что выбран правильный режим, прежде чем выполнять вычисления. [латекс]\текст{(для научного калькулятора):}\frac{1}{30\times \frac{\pi }{180}}\text{COS}[/latex] или [ латекс]\текст{(для графического калькулятора):}\frac{1}{\cos \left(\frac{30\pi }{180}\right)}[/latex] Вычисление косеканса [latex]\frac{5\pi }{7}[/latex]. Показать решение Вычислите котангенс [латекс]-\frac{\pi }{8}[/латекс]. Показать решение Какие другие \(3\) тригонометрические функции и как они связаны с функциями косинуса, синуса и тангенса? Как ведут себя графики функций секанса, косеканса и котангенса и как эти графики соотносятся с графиками функций косинуса, синуса и тангенса? Что такое тригонометрическое тождество и почему тождества важны? Функции синуса и косинуса, первоначально определенные в контексте точки, пересекающей единичную окружность, также являются центральными в тригонометрии прямоугольного треугольника. Одним из мощных аспектов тригонометрии является то, что предмет дает нам возможность рассмотреть одну и ту же идею с разных точек зрения. Например, мы заметили, что функции \(f(t) = \cos(t)\) и \(g(t) = \sin(t+\frac{\pi}{2})\) на самом деле та же функция; в качестве другого, для значений \(t\) в области \((-\frac{\pi}{2}, \frac{\pi}{2})\text{,}\) мы знаем, что запись \( y = \tan(t)\) равносильно написанию \(t = \arctan(y)\text{. Хотя почти на каждый вопрос, связанный с тригонометрией, можно ответить, используя функции синуса, косинуса и тангенса, иногда бывает удобно использовать три связанные функции, которые связаны с тремя другими возможными сочетаниями отношений сторон в прямоугольных треугольниках. Для любого действительного числа \(t\), для которого \(\cos(t) \ne 0\text{,}\) мы определяем секанс числа \(t\text{,}\), обозначаемый \(\sec( t)\text{,}\) по правилу \begin{уравнение*}
\sec(t) = \frac{1}{\cos(t)}\text{.}
\end{уравнение*} Для любого действительного числа \(t\), для которого \(\sin(t) \ne 0\text{,}\) мы определяем косеканс числа \(t\text{,}\), обозначаемый \(\csc( t)\text{,}\) по правилу \begin{уравнение*}
\csc(t) = \frac{1}{\sin(t)}\text{.}
\end{уравнение*} Для любого действительного числа \(t\), для которого \(\sin(t) \ne 0\text{,}\) мы определяем котангенс числа \(t\text{,}\), обозначаемый \(\cot( t)\text{,}\) по правилу \begin{уравнение*}
\cot(t) = \frac{\cos(t)}{\sin(t)}\text{. В частности, обратите внимание, что, как и функция тангенса, секанс, косеканс и котангенс также полностью определяются в терминах функций синуса и косинуса. В контексте прямоугольного треугольника с углом \(\theta\text{,}\) мы знаем, как думать о \(\sin(\theta)\text{,}\) \(\cos(\theta) \text{,}\) и \(\tan(\theta)\) как отношения сторон треугольника. Теперь мы можем сделать то же самое с другими тригонометрическими функциями: \начать{выровнять*}
\ sec (\ theta) & = \ frac {1} {\ cos (\ theta)} = \ frac {1} {\ frac {\ text {adj}} {\ text {hyp}}} = \ frac {\ текст {гип}}{\текст {прил.}}\\
\csc(\theta) &= \frac{1}{\sin(\theta)} = \frac{1}{\frac{\text{opp}}{\text{hyp}}} = \frac{\ текст{hyp}}{\текст{opp}}\\
\ cot (\ theta) & = \ frac {\ cos (\ theta)} {\ sin (\ theta)} = \ frac {\ frac {\ text {adj}} {\ text {hyp}}} {\ frac {\ text {opp}} {\ text {hyp}}} = \ frac {\ text {adj}} {\ text {opp}}
\end{align*} Благодаря этим трем дополнительным тригонометрическим функциям у нас теперь есть выражения, учитывающие все шесть возможных комбинаций двух сторон прямоугольного треугольника в отношении. Рассмотрим прямоугольный треугольник с гипотенузой длины \(61\) и катетом длиной \(11\text{.}\). Пусть \(\alpha\) будет углом, противоположным стороне длины \(11\text{ .}\) Найдите точную длину другой стороны, а затем определите значение каждой из шести тригонометрических функций, вычисляемых в \(\alpha\text{.}\) Кроме того, каковы точные и приблизительные измерения двух непрямые углы в треугольнике? Поскольку функции синуса и косинуса используются для определения каждой из остальных четырех тригонометрических функций, отсюда следует, что мы можем преобразовать информацию, известную о других функциях, обратно в информацию о функциях синуса и косинуса. Например, если мы знаем, что в некотором треугольнике \(\csc(\alpha) = \frac{5}{3}\text{,}\) следует, что \(\sin(\alpha) = \frac{ 3}{5}\text{. Также часто можно просмотреть данную информацию в контексте единичного круга. С ранее предоставленной информацией о том, что \(\csc(\alpha) = \frac{5}{3}\text{,}\), естественно рассматривать \(\alpha\) как угол в прямоугольном треугольнике, лежащий напротив катета длины \(3\) с гипотенузой, равной \(5\text{,}\), поскольку \(\csc(\alpha) = \frac{\text{hyp}}{\text{opp}} \text{.}\) Теорема Пифагора затем говорит нам, что сторона, примыкающая к \(\alpha\), имеет длину \(4\text{,}\), как показано в \(\треугольнике OPQ\) на рисунке 4.5.3. . Но мы могли бы также рассматривать \(\sin(\alpha) = \frac{3}{5}\) как \(\sin(\alpha) = \frac{\frac{3}{5}}{1} \text{,}\) и, таким образом, представьте, что прямоугольный треугольник имеет гипотенузу \(1\) и вертикальный катет \(\frac{3}{5}\text{.}\) Этот треугольник похож на первоначально рассмотренный \(3\)-\(4\)-\(5\) прямоугольный треугольник, но его можно рассматривать как лежащий внутри единичного круга. Предположим, что \(\beta\) является углом в стандартном положении с его конечной стороной в квадранте II, и вы знаете, что \(\sec(\beta) = -2\text{.}\) Без использования вычислительного устройства в в любом случае определите точные значения остальных пяти тригонометрических функций, вычисляемых в \(\beta\text{.}\) Как и функция тангенса, функции секанса, косеканса и котангенса определяются через функции синуса и косинуса, поэтому мы можем определить точные значения этих функций в каждой из специальных точек на единичной окружности. Кроме того, мы можем использовать наше понимание единичного круга и свойств функций синуса и косинуса, чтобы определить ключевые свойства этих других тригонометрических функций. Используя тот факт, что \(\sec(t) = \frac{1}{\cos(t)}\text{,}\), заметим, что везде \(\cos(t) = 0\text{,} \) значение \(\sec(t)\) не определено. Мы обозначаем такие случаи в следующей таблице как «u». Во всех остальных точках значение функции секущей является просто обратной величиной функции косинуса. Так как \(|\cos(t)| \le 1\) для всех \(t\text{,}\), то \(|\sec(t)| \ge 1\) для всех \(t\ ) (для которого определено значение секанса). Попробуйте
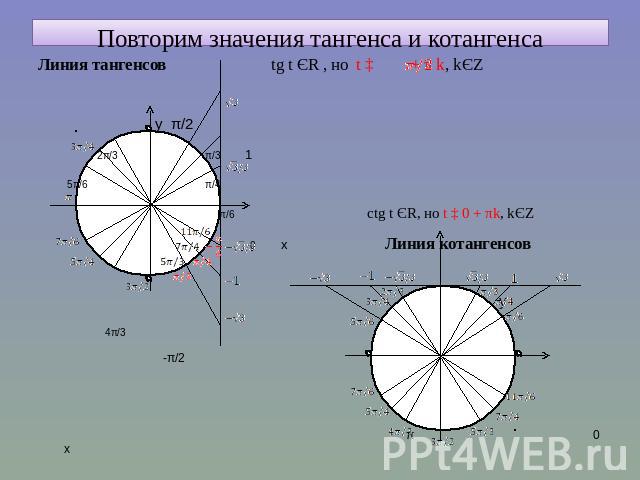 Тригонометрические функции являются периодическими. Для четырех тригонометрических функций, синуса, косинуса, косеканса и секанса, оборот одного круга или [латекс]2\пи [/латекс] даст одинаковые результаты для этих функций. А для тангенса и котангенса только половина оборота даст одинаковые результаты.
Тригонометрические функции являются периодическими. Для четырех тригонометрических функций, синуса, косинуса, косеканса и секанса, оборот одного круга или [латекс]2\пи [/латекс] даст одинаковые результаты для этих функций. А для тангенса и котангенса только половина оборота даст одинаковые результаты.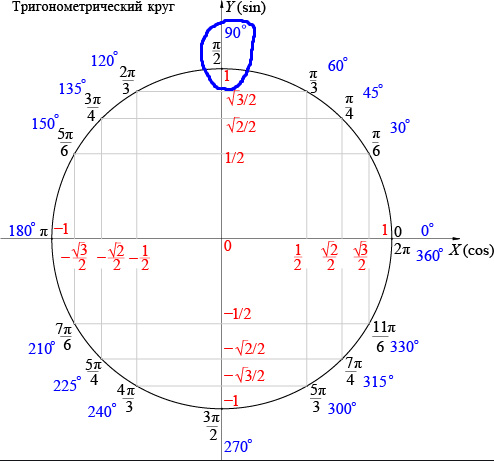
Общее примечание: период функции
Пример 8. Нахождение значений тригонометрических функций
Попробуйте
Пример 9. Нахождение значения тригонометрических функций
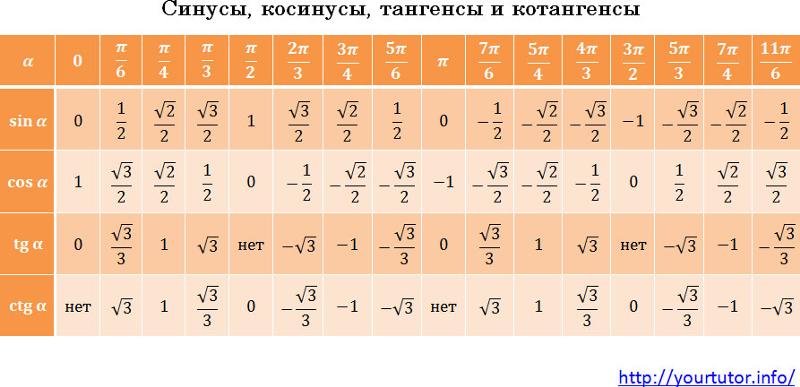
Попробуйте
Вычисление тригонометрических функций с помощью калькулятора
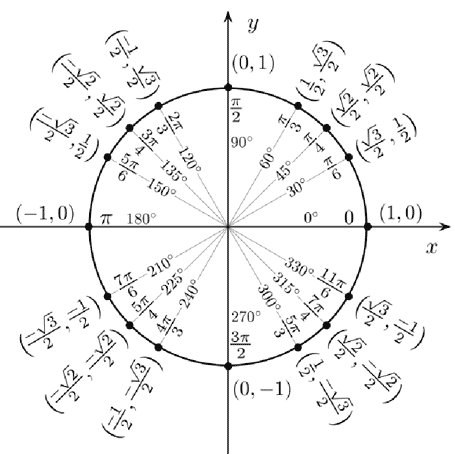 \circ [/latex], мы могли бы нажать
\circ [/latex], мы могли бы нажать Как: Дан угол измеряйте в радианах, используйте научный калькулятор, чтобы найти косеканс.
Как: Для измерения угла в радианах используйте графическую утилиту/калькулятор, чтобы найти косеканс.

Пример 10. Оценка секанса с помощью технологии
Попробуйте
Попробуйте
Ключевые уравнения
Касательная функция [латекс]\tan t=\frac{\sin t}{\cos t}[/латекс] Функция секанса [латекс]\sec t=\frac{1}{\cos t}[/латекс] Функция косеканса [латекс]\csc t=\frac{1}{\sin t}[/латекс] Функция котангенса [латекс]\cot t=\frac{1}{\tan t}=\frac{\cos t}{\sin t}[/latex] Ключевые понятия

Глоссарий
повторяющейся функции [латекс]f[/латекс] такой, что [латекс]f\left(x+P\right)=f\left(x\right)[ /латекс] APC Другие тригонометрические функции и тождества
Мотивирующие вопросы
 Они позволяют нам найти недостающую информацию в прямоугольных треугольниках простым способом, когда мы знаем один из непрямых углов и одну из трех сторон треугольника или две стороны, где одна является гипотенузой. Кроме того, мы определили функцию тангенса в терминах функций синуса и косинуса, а функция тангенса предлагает дополнительные возможности для поиска недостающей информации в прямоугольных треугольниках. Мы также видели, как обратные функции ограниченного синуса, косинуса и тангенса позволяют нам находить недостающие углы в самых разных условиях, включая прямоугольные треугольники.
Они позволяют нам найти недостающую информацию в прямоугольных треугольниках простым способом, когда мы знаем один из непрямых углов и одну из трех сторон треугольника или две стороны, где одна является гипотенузой. Кроме того, мы определили функцию тангенса в терминах функций синуса и косинуса, а функция тангенса предлагает дополнительные возможности для поиска недостающей информации в прямоугольных треугольниках. Мы также видели, как обратные функции ограниченного синуса, косинуса и тангенса позволяют нам находить недостающие углы в самых разных условиях, включая прямоугольные треугольники. }\). Какую перспективу мы выбираем, часто зависит от контекста и предоставленной информации.
}\). Какую перспективу мы выбираем, часто зависит от контекста и предоставленной информации. Определение 4.5.1. Функции секанса, косеканса и котангенса.
 }
\end{уравнение*}
}
\end{уравнение*} }\)
}\) Предварительный просмотр 4.5.1.
Подраздел 4.5.1 Соотношения в прямоугольных треугольниках
 }\) Отсюда мы можем обычным способом определить недостающую информацию в заданном треугольнике.
}\) Отсюда мы можем обычным способом определить недостающую информацию в заданном треугольнике. Перспектива единичного круга особенно ценна, когда используются такие соотношения, как \(\frac{\sqrt{3}}{2}\text{,}\) \(\frac{\sqrt{2}}{2}\text {,}\) и \(\frac{1}{2}\) возникают в прямоугольных треугольниках.
Перспектива единичного круга особенно ценна, когда используются такие соотношения, как \(\frac{\sqrt{3}}{2}\text{,}\) \(\frac{\sqrt{2}}{2}\text {,}\) и \(\frac{1}{2}\) возникают в прямоугольных треугольниках. Мероприятие 4.5.2.
Подраздел 4.5.2 Свойства функций секанса, косеканса и котангенса
 Начнем с исследования секущей функции.
Начнем с исследования секущей функции. \(т\) \(0\) \(\ гидроразрыва {\pi}{6}\) \(\ гидроразрыва {\pi}{4}\) \(\ гидроразрыва {\pi}{3}\) \(\ гидроразрыва {\pi}{2}\) \(\frac{2\pi}{3}\) \(\frac{3\pi}{4}\) \(\frac{5\pi}{6}\) \(\пи\) \(\cos(t)\) \(1\) \(\ гидроразрыва {\ sqrt {3}} {2} \) \(\ гидроразрыва {\ sqrt {2}} {2} \) \(\ гидроразрыва{1}{2}\) \(0\) \(-\frac{1}{2}\) \(-\frac{\sqrt{2}}{2}\) \(-\frac{\sqrt{3}}{2}\) \(-1\) \(\сек(т)\) \(1\) \(\frac{2}{\sqrt{3}}\) \(\sqrt{2}\) \(2\) и \(-2\) \(-\sqrt{2}\) \(-\frac{2}{\sqrt{3}}\) \(-1\)
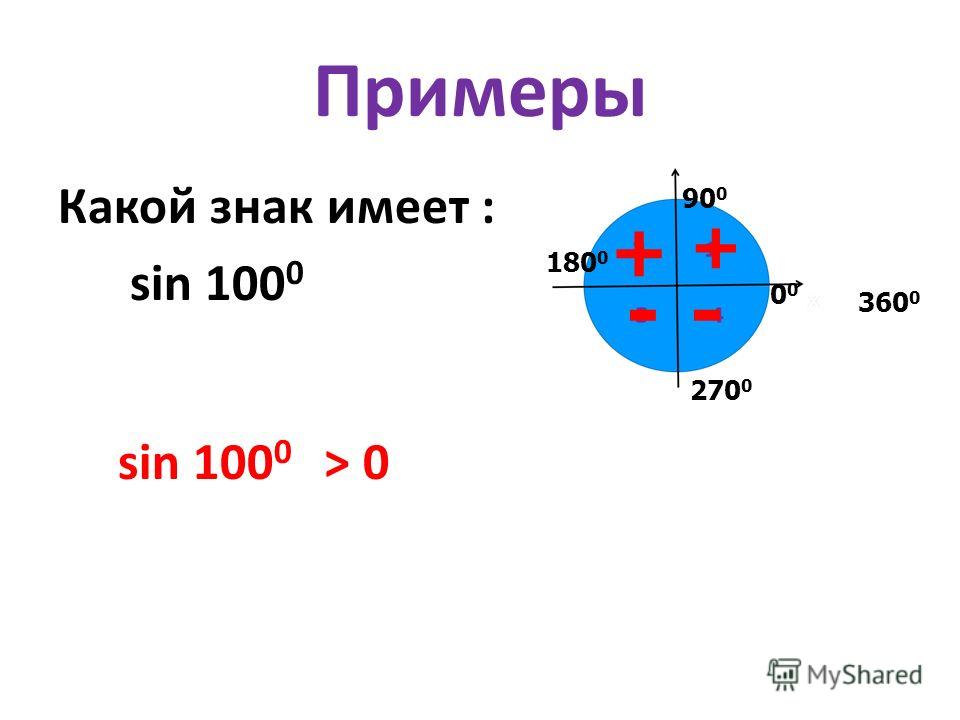 5.5.
5.5.| \(т\) | \(\frac{7\pi}{6}\) | \(\frac{5\pi}{4}\) | \(\frac{4\pi}{3}\) | \(\frac{3\pi}{2}\) | \(\frac{5\pi}{3}\) | \(\frac{7\pi}{4}\) | \(\frac{11\pi}{6}\) | \(2\пи\) |
| \(\cos(t)\) | \(-\frac{\sqrt{3}}{2}\) | \(-\frac{\sqrt{2}}{2}\) | \(-\frac{1}{2}\) | \(0\) | \(\ гидроразрыва{1}{2}\) | \(\ гидроразрыва {\ sqrt {2}} {2} \) | \(\ гидроразрыва {\ sqrt {3}} {2} \) | \(0\) |
| \(\сек(т)\) | \(-\frac{2}{\sqrt{3}}\) | \(-\sqrt{2}\) | \(-2\) | и | \(2\) | \(\sqrt{2}\) | \(\frac{2}{\sqrt{3}}\) | \(1\) |
Таблица 4.5.4 и Таблица 4.5.5 помогают нам определить тренды функции секущей. Знак \(\sec(t)\) соответствует знаку \(\cos(t)\) и, таким образом, положителен в квадранте I, отрицателен в квадранте II, отрицателен в квадранте III и положителен в квадранте IV.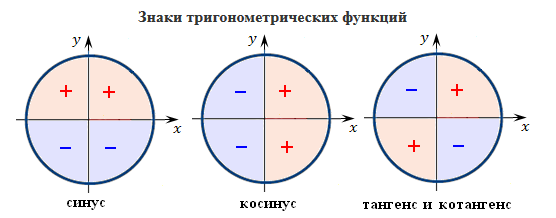
Кроме того, мы наблюдаем, что по мере приближения \(t\)-значений в первом квадранте к \(\frac{\pi}{2}\text{,}\) \(\cos(t)\) становится ближе к \(0\) (при этом он всегда положителен). Поскольку числитель функции секущей всегда равен \(1\text{,}\), а его знаменатель приближается к \(0\) (в то время как знаменатель остается положительным), это означает, что \(\sec(t)\) неограниченно возрастает как \(t\) приближается к \(\frac{\pi}{2}\) с левой стороны. Как только \(t\) немного больше, чем \(\frac{\pi}{2}\) в квадранте II, значение \(\cos(t)\) становится отрицательным (и близким к нулю). Это заставляет значение \(\sec(t)\) уменьшаться без ограничений (отрицательно и все дальше от \(0\)) при \(t\), приближающемся к \(\frac{\pi}{2}\) с правой стороны. Таким образом, мы видим, что \(p(t) = \sec(t)\) имеет вертикальную асимптоту в точке \(t = \frac{\pi}{2}\text{;}\) периодичность и знаковое поведение \ (\cos(t)\) означает, что это асимптотическое поведение функции секущей будет повторяться.
Нанеся данные в таблицу вместе с ожидаемыми асимптотами и интуитивно соединив точки, мы увидим график функции секущей на рисунке 4.5.6.
Рисунок 4.5.6. График функции секущей со специальными точками, исходящими из единичного круга, плюс функция косинуса (пунктирная, голубого цвета).Как из таблицы, так и из графика видно, что функция секущей имеет период \(P = 2\pi\text{.}\) Подведем итог нашей недавней работы следующим образом.
Свойства функции секущей.
Для функции \(p(t) = \sec(t)\text{,}\)
его областью определения является множество всех действительных чисел, кроме \(t = \frac{\pi}{2} \pm k\pi\), где \(k\) — любое целое число;
его диапазоном является множество всех действительных чисел \(y\) таких, что \(|y| \ge 1\text{;}\)
его период равен \(P = 2\pi\text{.}\)
Мероприятие 4.5.3.
В этом упражнении мы развиваем стандартные свойства функции косеканса, \(q(t) = \csc(t)\text{.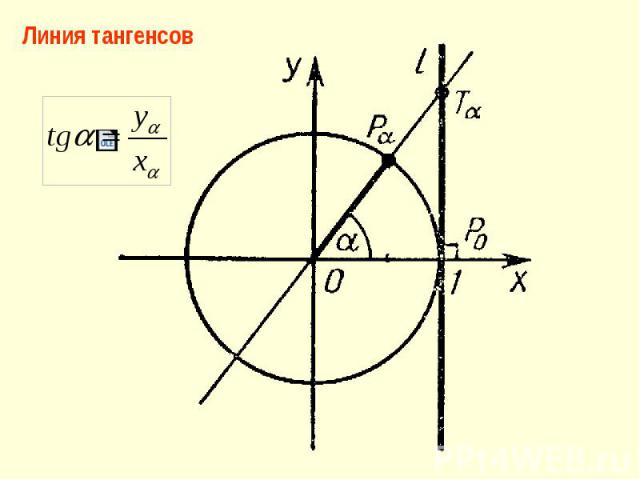 }\)
}\)
Заполните таблицы 4.5.8 и 4.5.9, чтобы определить точные значения функции косеканса в особых точках на единичной окружности. Введите «\(u\)» для любого значения, при котором \(q(t) = \csc(t)\) не определено.
Таблица 4.5.8.
Таблица 4.\(т\) \(0\) \(\ гидроразрыва {\pi}{6}\) \(\ гидроразрыва {\pi}{4}\) \(\ гидроразрыва {\pi}{3}\) \(\ гидроразрыва {\pi}{2}\) \(\frac{2\pi}{3}\) \(\frac{3\pi}{4}\) \(\frac{5\pi}{6}\) \(\пи\) \(\sin(t)\) \(0\) \(\ гидроразрыва{1}{2}\) \(\ гидроразрыва {\ sqrt {2}} {2} \) \(\ гидроразрыва {\ sqrt {3}} {2} \) \(1\) \(\ гидроразрыва {\ sqrt {3}} {2} \) \(\ гидроразрыва {\ sqrt {2}} {2} \) \(\ гидроразрыва{1}{2}\) \(0\) \(\csc(t)\) \(\) \(\) \(\) \(\) \(\) \(\) \(\) \(\) \(\)  5.9.
5.9.\(т\) \(\frac{7\pi}{6}\) \(\frac{5\pi}{4}\) \(\frac{4\pi}{3}\) \(\frac{3\pi}{2}\) \(\frac{5\pi}{3}\) \(\frac{7\pi}{4}\) \(\frac{11\pi}{6}\) \(2\пи\) \(\sin(t)\) \(-\frac{1}{2}\) \(-\frac{\sqrt{2}}{2}\) \(-\frac{\sqrt{3}}{2}\) \(-1\) \(-\frac{\sqrt{3}}{2}\) \(-\frac{\sqrt{2}}{2}\) \(-\frac{1}{2}\) \(0\) \(\csc(t)\) \(\) \(\) \(\) \(\) \(\) \(\) \(\) \(\) В каких квадрантах \(q(t) = \csc(t)\) положительно? отрицательный?
При каких значениях \(t\) \(q(t) = \csc(t)\) имеет вертикальную асимптоту? Почему?
Какова область определения косеканса? Каков его диапазон?
Нарисуйте точный помеченный график \(q(t) = \csc(t)\) на осях, показанных на рисунке 4.
 5.7, включая особые точки, исходящие из единичной окружности.
5.7, включая особые точки, исходящие из единичной окружности.Каков период функции косеканса?
Мероприятие 4.5.4.
В этом упражнении мы развиваем стандартные свойства функции котангенса, \(r(t) = \cot(t)\text{.}\)
Заполните таблицы 4.5.10 и 4.5.11, чтобы определить точные значения функции котангенса в особых точках на единичной окружности. Введите «u» для любого значения, при котором \(r(t) = \cot(t)\) не определено.
Таблица 4.5.10.
Таблица 4.\(т\) \(0\) \(\ гидроразрыва {\pi}{6}\) \(\ гидроразрыва {\pi}{4}\) \(\ гидроразрыва {\pi}{3}\) \(\ гидроразрыва {\pi}{2}\) \(\frac{2\pi}{3}\) \(\frac{3\pi}{4}\) \(\frac{5\pi}{6}\) \(\пи\) \(\sin(t)\) \(0\) \(\ гидроразрыва{1}{2}\) \(\ гидроразрыва {\ sqrt {2}} {2} \) \(\ гидроразрыва {\ sqrt {3}} {2} \) \(1\) \(\ гидроразрыва {\ sqrt {3}} {2} \) \(\ гидроразрыва {\ sqrt {2}} {2} \) \(\ гидроразрыва{1}{2}\) \(0\) \(\cos(t)\) \(1\) \(\ гидроразрыва {\ sqrt {3}} {2} \) \(\ гидроразрыва {\ sqrt {2}} {2} \) \(\ гидроразрыва{1}{2}\) \(0\) \(-\frac{1}{2}\) \(-\frac{\sqrt{2}}{2}\) \(-\frac{\sqrt{3}}{2}\) \(-1\) \(\загар(т)\) \(0\) \(\frac{1}{\sqrt{3}}\) \(1\) \(\frac{3}{\sqrt{3}}\) и \(-\frac{3}{\sqrt{3}}\) \(-1\) \(-\frac{1}{\sqrt{3}}\) \(0\) \(\кроватка(т)\)  5.11.
5.11.\(т\) \(\frac{7\pi}{6}\) \(\frac{5\pi}{4}\) \(\frac{4\pi}{3}\) \(\frac{3\pi}{2}\) \(\frac{5\pi}{3}\) \(\frac{7\pi}{4}\) \(\frac{11\pi}{6}\) \(2\пи\) \(\sin(t)\) \(-\frac{1}{2}\) \(-\frac{\sqrt{2}}{2}\) \(-\frac{\sqrt{3}}{2}\) \(-1\) \(-\frac{\sqrt{3}}{2}\) \(-\frac{\sqrt{2}}{2}\) \(-\frac{1}{2}\) \(0\) \(\cos(t)\) \(-\frac{\sqrt{3}}{2}\) \(-\frac{\sqrt{2}}{2}\) \(-\frac{1}{2}\) \(0\) \(\frac{1}{2}\) \(\ гидроразрыва {\ sqrt {2}} {2} \) \(\ гидроразрыва {\ sqrt {3}} {2} \) \(1\) \(\загар(т)\) \(\frac{1}{\sqrt{3}}\) \(1\) \(\frac{3}{\sqrt{3}}\) и \(-\frac{3}{\sqrt{3}}\) \(-1\) \(-\frac{1}{\sqrt{3}}\) \(0\) \(\кроватка(т)\) В каких квадрантах \(r(t) = \cot(t)\) положительно? отрицательный?
При каких значениях \(t\) \(r(t) = \cot(t)\) имеет вертикальную асимптоту? Почему?
Какова область определения функции котангенса? Каков его диапазон?
Нарисуйте точный помеченный график \(r(t) = \cot(t)\) на осях, показанных на рисунке 4.
Рисунок 4.5.12. Оси построения \(r(t) = \cot(t)\text{.}\) 5.12, включая особые точки, исходящие из единичной окружности.
5.12, включая особые точки, исходящие из единичной окружности.На интервалах, где функция определена в каждой точке интервала, всегда ли \(r(t) = \cot(t)\) возрастает, всегда убывает или ни то, ни другое?
Каков период функции котангенса?
Как бы вы описали связь между графиками функций тангенса и котангенса?
Подраздел 4.5.3 Несколько важных тождеств
Тождество — это уравнение, истинное для всех возможных значений \(x\), для которых определены соответствующие величины. Примером нетригонометрического тождества является число 9.2 + 2x + 1\текст{,} \end{уравнение*}
, так как это уравнение истинно для любого значения \(x\text{,}\), а левая и правая части уравнения представляют собой просто два разных, но полностью эквивалентных выражения.
Тригонометрические тождества — это просто тождества, включающие тригонометрические функции.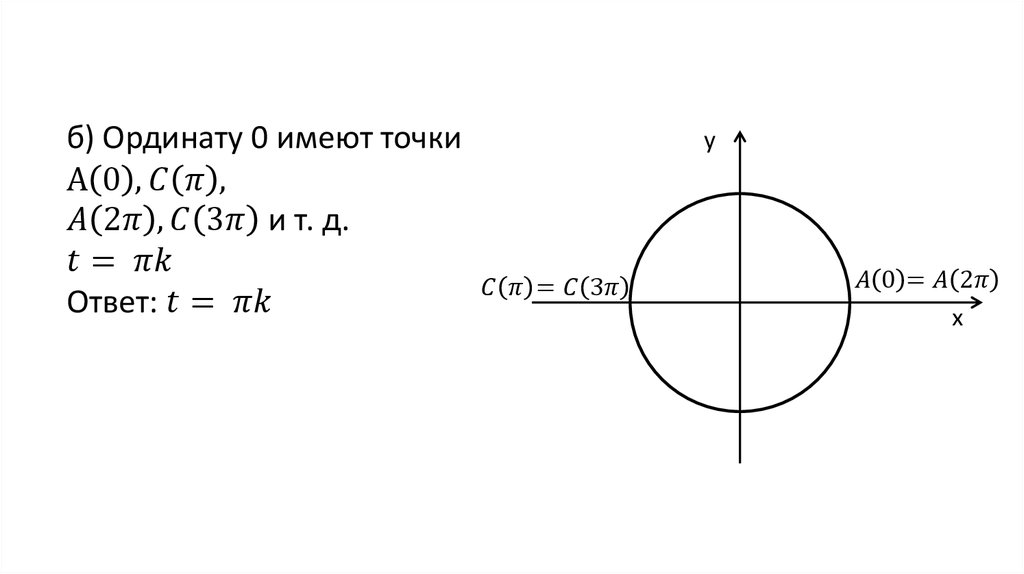 Хотя существует большое количество таких тождеств, которые можно изучить, мы решили сосредоточиться на тех из них, которые оказываются наиболее полезными при изучении исчисления. Наиболее важным тригонометрическим тождеством является фундаментальное тригонометрическое тождество, которое является тригонометрическим переформулированием теоремы Пифагора. 92(\ тета) \текст{.}
\end{уравнение*}
Хотя существует большое количество таких тождеств, которые можно изучить, мы решили сосредоточиться на тех из них, которые оказываются наиболее полезными при изучении исчисления. Наиболее важным тригонометрическим тождеством является фундаментальное тригонометрическое тождество, которое является тригонометрическим переформулированием теоремы Пифагора. 92(\ тета) \текст{.}
\end{уравнение*}
Эти тождества оказываются полезными в исчислении, когда мы разрабатываем формулы для производных функций тангенса и котангенса.
В исчислении также полезно знать пару других стандартных тождеств для сумм углов или двойных углов. Мы просто констатируем эти тождества без каких-либо оснований. Для получения дополнительной информации о них см. Раздел 10.4 в Тригонометрии Колледжа 1 Стица и Зегера 2 . 92(\тета)\текст{.}\)
Для любого действительного числа \(\theta\text{,}\) \(\sin(2\theta) = 2\sin(\theta)\cos(\theta)\text{.}\)
Мероприятие 4.
 5.5.
5.5.В этом упражнении мы исследуем, как идентичность суммы двух углов для синусоидальной функции помогает нам по-другому взглянуть на среднюю скорость изменения синусоидальной функции.
Напомним, что для любой функции \(f\) на интервале \([a,a+h]\text{,}\) ее средняя скорость изменения равна
\begin{уравнение*} AV_{[a,a+h]} = \frac{f(a+h)-f(a)}{h}\text{.} \end{уравнение*}
Пусть \(f(x) = \sin(x)\text{.}\) Используйте определение \(AV_{[a,a+h]}\) для записи выражения для средней скорости изменение функции синуса на интервале \([a+h,a]\text{.}\)
Применить идентичность суммы двух углов для функции синуса, \(\sin(\alpha + \beta) = \sin(\alpha) \cos(\beta) + \cos(\alpha) \sin(\beta) )\text{,}\) в выражение \(\sin(a+h)\text{.}\)
Объясните, почему ваша работа в пунктах (а) и (б) вместе с алгеброй показывает, что
\begin{уравнение*} AV_{[a,a+h]} = \sin(a) \cdot \frac{\cos(h)-1}{h} — \cos(a) \frac{\sin(h)}{h} \текст{.
 }
\end{уравнение*}
}
\end{уравнение*}В исчислении мы переходим от средней скорости изменения к мгновенной скорости изменения, приближая \(h\) к \(0\) в выражении для средней скорости изменения. Используя вычислительное устройство в радианном режиме, исследуйте поведение
\begin{уравнение*} \ гидроразрыва {\ соз (ч) -1} {ч} \end{уравнение*}
, когда \(h\) приближается к \(0\text{.}\) Что происходит? Точно так же, как \(\frac{\sin(h)}{h}\) ведет себя при малых значениях \(h\text{?}\) Что это говорит нам о \(AV_{[a,a+ h]}\) для функции синуса, когда \(h\) приближается к \(0\text{?}\)
Подраздел 4.5.4 Резюме
Функции секанса, косеканса и котангенса определяются соответственно как обратные функции косинуса, синуса и тангенса. то есть
\begin{уравнение*} \sec(t) = \frac{1}{\cos(t)}, \csc(t) = \frac{1}{\sin(t)}, \text{и} \cot(t) = \ frac{1}{\tan(t)}\text{.} \end{уравнение*}
График функции котангенса аналогичен графику функции тангенса, за исключением того, что он убывает на каждом интервале, на котором он определен, в каждой точке интервала и имеет вертикальные асимптоты везде, где \(\tan(t) = 0 \) и равен нулю везде, где \(\tan(t)\) имеет вертикальную асимптоту.

Графики функций секанса и косеканса отличаются от графиков функций косинуса и синуса несколькими способами, в том числе тем, что их областью значений является множество всех действительных чисел \(y\), таких что \(y \ge 1\) и они имеют вертикальные асимптоты везде, где функция косинуса и синуса соответственно равна нулю. 92(t)\) совпадает (во всех точках, где определено \(f\)) как функция, значение которой всегда равно \(1\text{.}\)
Упражнения 4.5.5 Упражнения
1.
Вопросы 8-16:
Найдите точное значение каждого без использования калькулятора:
а) \(\tan{ \left( \frac{7 \pi}{4} \right) }\) =
б) \(\tan{ \left( \frac{5 \pi}{4} \right) }\) =
c) \(\cot{ \left( \frac{5 \pi}{3} \ справа) }\) =
d) \(\sec{ \left( \frac{3 \pi}{4} \right) }\) =
e) \(\csc{ \left( \frac{\pi}{3} \right) }\) =
2.
Предположим, что угол \(\theta\) находится в первом квадранте, \(0 \leq \theta \leq \pi /2\text{,}\) и \(\displaystyle \cos(\theta) = \frac {1}{8}\text{. }\) Найдите точные значения (в виде дробей, а не десятичных приближений) для следующего.
}\) Найдите точные значения (в виде дробей, а не десятичных приближений) для следующего.
(a) \(\csc(\theta)\) =
(b) \(\cot(\theta)\) =
3.
Предположим, что угол \(\theta\) находится в четвертом квадранте, \(\frac{3\pi}{2} \leq \theta \leq 2\pi\text{,}\) и \(\displaystyle \ tan(\theta) = \frac{-2}{3}.\) Найдите точные значения (в виде дробей, а не десятичных приближений) для следующего.
(a) \(\sec(\theta)\) =
(b) \(\sin(\theta)\) =
4.
Пусть \(\beta\) угол в квадранте II, удовлетворяющий условию \(\cos(\beta) = -\frac{12}{13}\text{.}\) Определите значения остальных пяти тригонометрических функций оценивается в \(\бета\) точно и без оценки какой-либо тригонометрической функции на вычислительном устройстве.
Как изменятся ваши ответы, если \(\бета\) находится в квадранте III?
5.
Для каждого из следующих преобразований стандартных тригонометрических функций используйте свое понимание преобразований, чтобы определить область определения, диапазон, асимптоты и период функции с тщательным обоснованием. Затем проверьте свои результаты, используя Desmos или другая графическая утилита.
Затем проверьте свои результаты, используя Desmos или другая графическая утилита.
\(\displaystyle f(t) = 5\sec(t-\frac{\pi}{2}) + 3\)
\(\displaystyle g(t) = -\frac{1}{3}\csc(2t) — 4\)
\(\displaystyle h(t) = -7\tan(t+\frac{\pi}{4}) + 1\)
\(\displaystyle j(t) = \frac{1}{2}\cot(4t) — 2\)
6.
В прямоугольном треугольнике с гипотенузой 1 и вертикальным катетом \(x\text{,}\) с углом \(\theta\) напротив \(x\text{,}\) определите простейшее выражение, которое вы можете для каждого из следующие величины через \(x\text{.}\)
\(\displaystyle \sin(\theta)\)
\(\displaystyle \sec(\theta)\)
\(\displaystyle\csc(\theta)\)
\(\displaystyle \tan(\theta)\)
\(\displaystyle \cos(\arcsin(x))\)
\(\displaystyle \cot(\arcsin(x))\)
stitz-zeager.

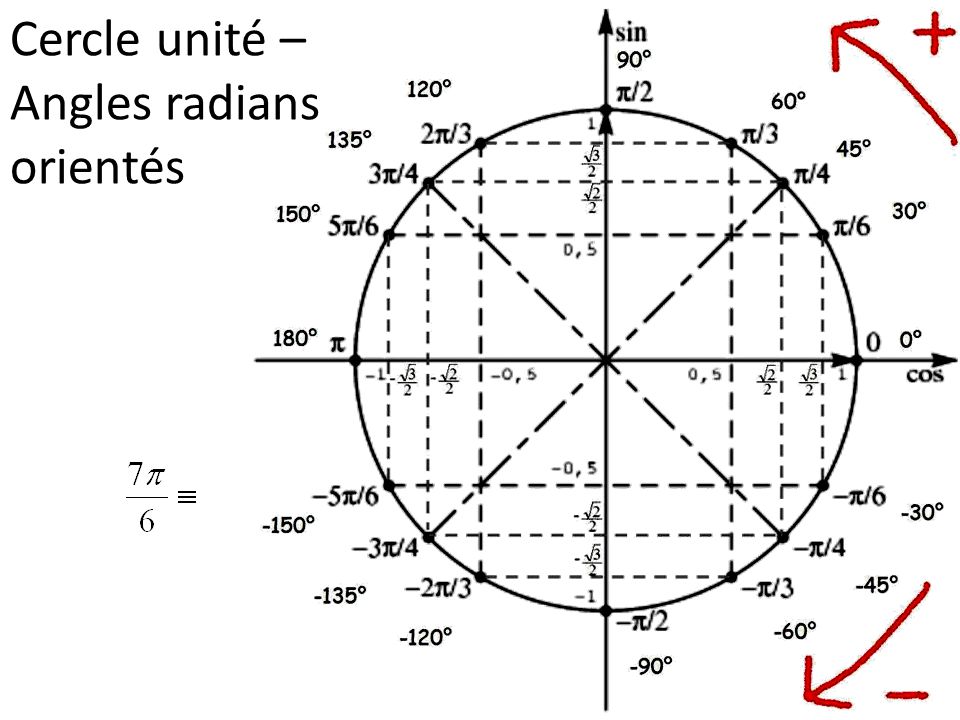 , ил.
, ил.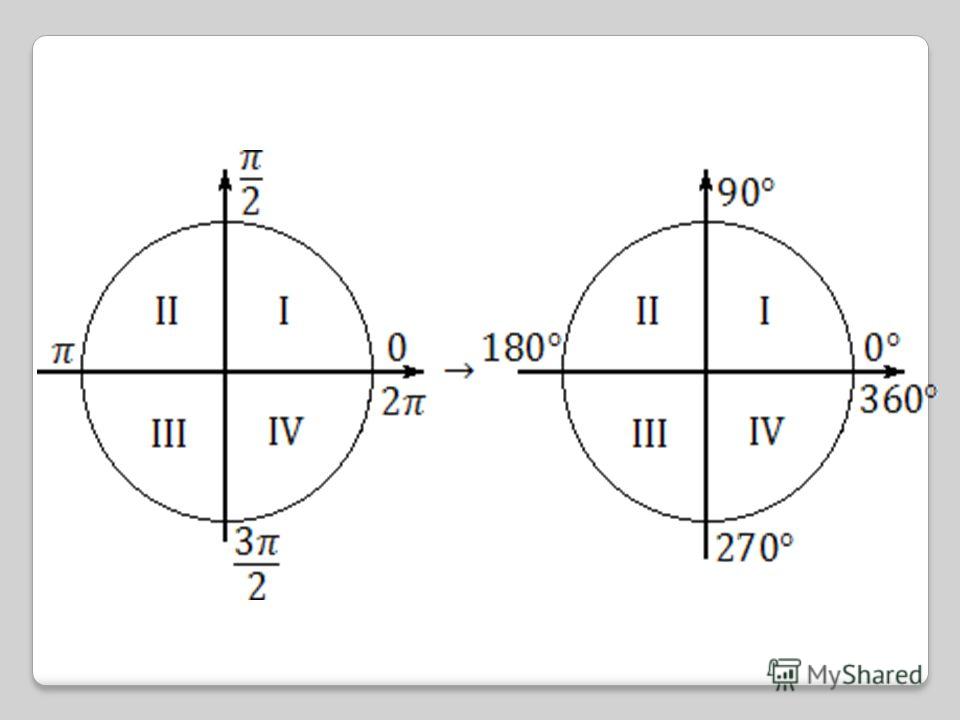 для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
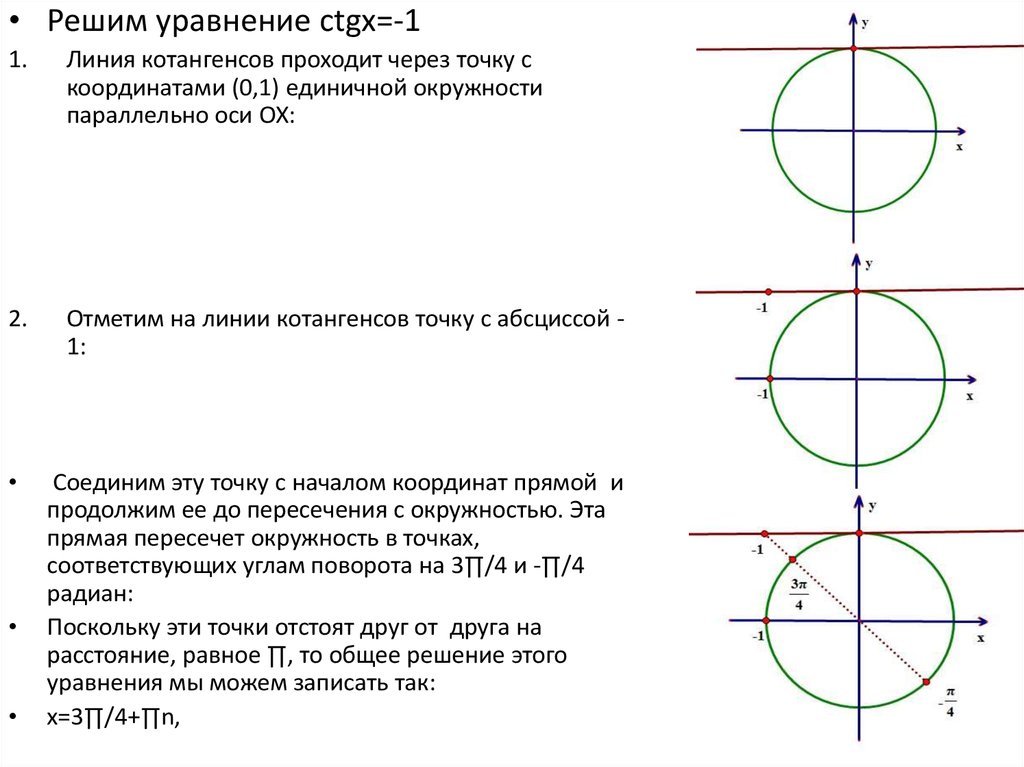 5.9.
5.9. 5.7, включая особые точки, исходящие из единичной окружности.
5.7, включая особые точки, исходящие из единичной окружности.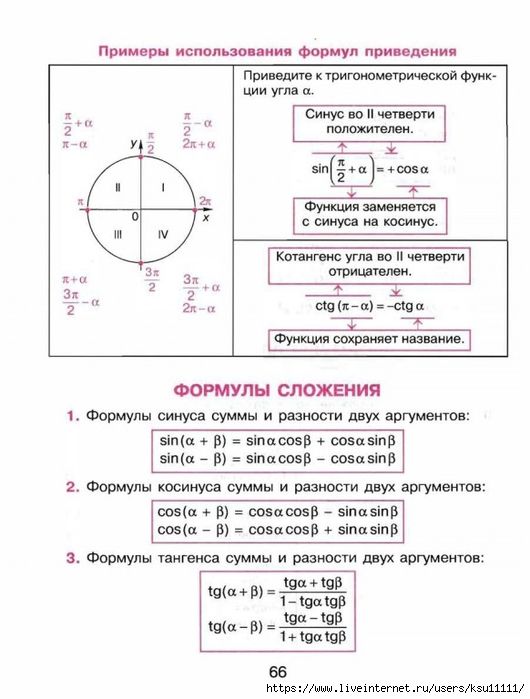 5.11.
5.11. 5.12, включая особые точки, исходящие из единичной окружности.
5.12, включая особые точки, исходящие из единичной окружности.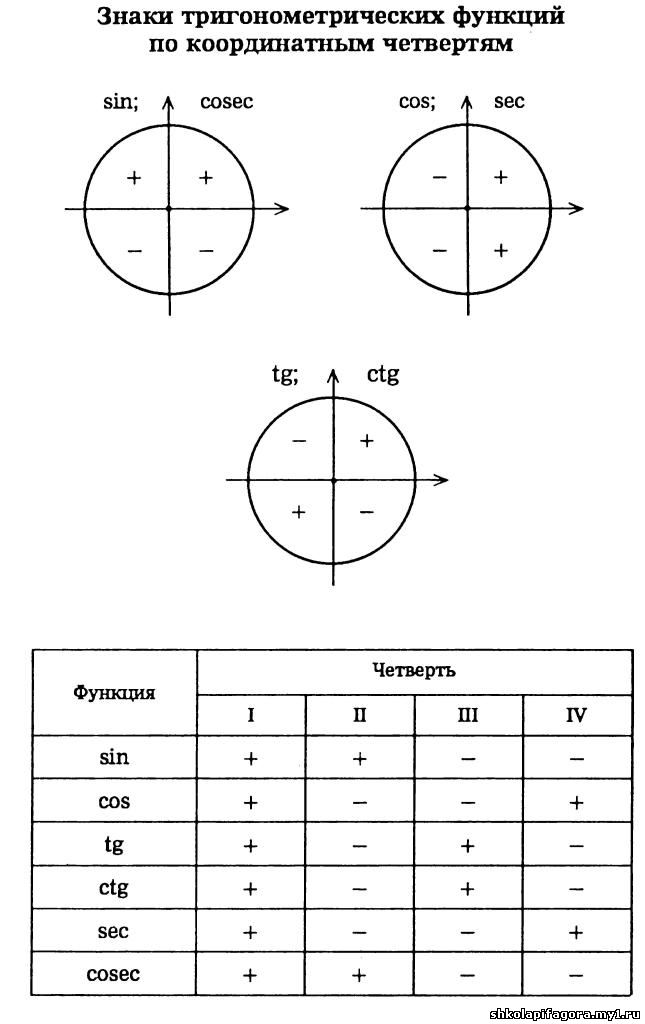 }
\end{уравнение*}
}
\end{уравнение*}