Что сначала подключать плюс или минус?
Для того чтобы сложить два отрицательных числа надо сложить два числа и поставить знак минус. Минус на минус дает плюс. Существуют определенные правила для знаков при сложении и вычитании.
Содержание
Основные операции в математике
Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).
Операции действия:
- сложение (+)
- вычитание (-)
- умножение (*)
- деление (:)
Операции отношения:
- равно (=)
- больше (>)
- меньше (<)
- больше или равно (≥)
- меньше или равно (≤)
- не равно (≠)
Сложение — операция, которая позволяет объединить два слагаемых.
- Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.

Вычитание — действие, обратное сложению.
- Запись вычитания: 10 – 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.
Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 – 1 = 9.
Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.
- Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.
- 3 * 4 = 3 + 3 + 3 + 3
В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 * 2 = 5 + 5 = 10.
Поэтому и множитель, и множимое называют сомножителями.
Деление — арифметическое действие обратное умножению.
- Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.
В этом случае произведение делителя 6 и частного 5, в качестве проверки, дает делимое 30. 4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
При знаке квадратного корня показатель корня принято опускать: √16 = 4.
3√8 = 2 — корень третьей степени называется — кубическим.
Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно представляют обратные друг другу действия. Далее узнаем порядок выполнения арифметических действий.
Источник: http://skysmart.ru/articles/mathematic/poryadok-dejstvij-v-matematike
Снятие аккумуляторной батареи
Перед началом проведения работ необходимо подготовить инструмент. Для ослабления зажимов потребуется рожковый ключ, а чтобы снять крепления АКБ, нужен ключ с воротком. Крайне важно во время снятия и при последующей установке аккумулятора на автомобиль соблюдать правила техники безопасности. Чтобы защитить руки от повреждений, следует надеть матерчатые перчатки. Одновременно можно провести техническое обслуживание батареи, и для этого потребуются резиновые перчатки с очками. Также следует подготовить пищевую соду, необходимую для нейтрализации содержащихся в электролите кислот.
Одновременно можно провести техническое обслуживание батареи, и для этого потребуются резиновые перчатки с очками. Также следует подготовить пищевую соду, необходимую для нейтрализации содержащихся в электролите кислот.
Рекомендуем: В какой последовательности подключать аккумулятор к машине
Процесс демонтажа аккумулятора не вызовет проблем даже у начинающего автомобилиста:
Особое внимание следует обратить на то, что первым снимается зажим «минус». Если начинать с положительного контакта, то при случайном касании кузова ключом возникнет короткое замыкание. Владельцам машин с подушками безопасности необходимо сначала изучить инструкцию. В некоторых моделях после выключения зажигания система удержания защитных устройств остается активной еще несколько минут. В такой ситуации снимать батарею можно через 3−5 минут.
Современные иномарки оснащены большим количеством электронных устройств, и при отключении питания может произойти сбой бортового компьютера.
Если же АКБ вышла из строя, и ее необходимо менять, то придется воспользоваться портативной батареей, которая будет подавать напряжение в бортовую сеть во время замены основного источника питания.
Источник: http://xn—-7sbbbsdlxdyr8aax.xn--p1ai/obzory/chto-reshaetsya-pervym-plyus-ili-minus.html
Решение уравнений
- – Индивидуальные занятия
- – В любое удобное для вас время
- – Бесплатное вводное занятие
Источник: http://MyAlfaSchool.ru/articles/slozhenie-i-vychitanie-otricatelnyx-chisel
Что такое сложение плюс или минус?
При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс. То есть, если стоят рядом два минуса, в сумме получается плюс.
Источник: http://orto-ryukzak.ru/chto-pervoe-plius-ili-minus
Где находится масса на аккумуляторе?
Масса аккумулятора как правило представлена минусовой клеммой. Если быть технически корректным, то у аккумулятора массы нет, масса есть у автомобиля. У современных автомобилей масса крепится к минусовому выводу аккумулятора.
Если быть технически корректным, то у аккумулятора массы нет, масса есть у автомобиля. У современных автомобилей масса крепится к минусовому выводу аккумулятора.
Источник: http://kr-professional.ru/pri-ustanovki-akkumulyatora-chto-snachala-plyus-ili-minus/
Что такое двойные скобки?
Двойные скобки избегаются: нужно изменить предложение, чтобы двойных скобок не было, или использовать скобки разного рисунка. … Лопатина, круглые скобки используются для внешнего выделения, квадратные — для внутреннего, например: Виргинские острова, группа мелких о-вов в Вест-Индии.
Источник: http://avtograf70.ru/vaz/vy-sprashivali-chto-delat-snachala-plyus-ili-minus.html
Рекомендации профессионалов
Производите работы в условиях открытого пространства, поскольку на улице газы не скапливаются. Желательно снять ювелирные украшения, включая кольца и браслеты для рук. Используйте индивидуальные средства защиты – перчатки диэлектрические и защитные очки.
Заметим, что после отсоединения провода с положительной клеммы остаточный ток может навредить работе электрики автомобиля, если произойдет касание провода с металлической поверхностью кузова. Также это может послужить причиной короткого замыкания.
Помните о том, что стандартные аккумуляторы для авто способны генерировать ток силой до сотен ампер, что эквивалентно заряду сварочного аппарата.
Аккумуляторы в гибридных автомобилях могут производить 300 вольт энергии, а это говорит об опасной для жизни и здоровья человека силе тока. Проводка зачастую дифференцируются по цвету. Вам удастся снизить вероятность удара током, если вы воспользуйтесь перчатками, а также инструментом с изоляцией.
Источник: http://TrueScooters.ru/motor-avto/posledovatelnost-podklyucheniya-akkumulyatora. html
html
Какие клеммы на аккумулятор лучше купить?
Медная Медные клеммы для аккумулятора на первый взгляд – самый лучший выбор. Лучшая из возможных электропроводимость, не так сильно окисляется, имеет большее пятно соприкосновения. Плавится при температуре выше 1050 градусов.
Источник: http://kr-professional.ru/pri-ustanovki-akkumulyatora-chto-snachala-plyus-ili-minus/
Математика. Сложение и вычитание | Сайт Леонида Некина
«Вот смотри, я написал на бумаге
$6 + 2$
Это называется шесть плюс два. Это значит, что ты вначале берешь у папы шесть конфет, а потом еще две. Сколько всего конфет тебе достанется? Раз ты пока этого не знаешь, то давай сначала потренируемся на счетах. Мы откладываем на счетах шесть бусинок и затем добавляем к ним еще две. Сколько всего бусинок получилось? Правильно, восемь. Записываем ответ:
$6 + 2 = \underline{\,8\,}$
Шесть плюс два равно восемь. Мы решили пример на сложение: мы сложили числа $6$ и $2$ и в результате получили $8$. Вот, держи восемь конфет. (Разумеется, речь идет о крошечных конфетах-горошинах.)
Вот, держи восемь конфет. (Разумеется, речь идет о крошечных конфетах-горошинах.)
А теперь, смотри, я написал
$5 — 3$
Это называется пять минус три. Это значит, что у нас на двоих пять конфет. Три из них я отдаю тебе. Сколько же тогда конфет остается у меня? Давай отложим на счетах вначале пять бусинок, а потом из них в обратную сторону переложим три. Что получается в результате? Правильно, пять минус три равно два:
$5 — 3 = \underline{\,2\,}$
Мы решили пример на вычитание. Из числа $5$ вычли число $3$ и получили $2$».
После такого объяснения ребенок уже способен самостоятельно делать упражнения на сложение и вычитание. Взрослый вручает ему листок бумаги, на котором написано, например, следующее:
$7 + 3 =$
$7 — 3 =$
$10 + 2 =$
$10 — 2 =$
и так далее.
В задачу ребенка входит выполнить на счетах указанные действия и записать ответ. После того как все ответы будут записаны, он показывает их взрослому. Взрослый восхищается правильными ответами, обводит их в кружочек, а неправильные просит пересчитать еще раз. Если один и тот же неправильный ответ появляется снова и снова, взрослый разбирается вместе с ребенком, где источник ошибки. Постепенно числа в примерах становятся всё больше и больше, однако второе число нет смысла делать больше тридцати, пока ребенку приходится пересчитывать его по бусинкам от начала до конца. Важно, чтобы ребенок не просто понял принцип сложения и вычитания, но и выработал соответствующий навык, то есть почти никогда не ошибался. Движения руки должны стать уверенными, — чтобы, откладывая одну бусинку, не задевать соседние. И еще один принцип: если сбился со счета, то не надо продолжать наобум — начинай всё сначала.
Взрослый восхищается правильными ответами, обводит их в кружочек, а неправильные просит пересчитать еще раз. Если один и тот же неправильный ответ появляется снова и снова, взрослый разбирается вместе с ребенком, где источник ошибки. Постепенно числа в примерах становятся всё больше и больше, однако второе число нет смысла делать больше тридцати, пока ребенку приходится пересчитывать его по бусинкам от начала до конца. Важно, чтобы ребенок не просто понял принцип сложения и вычитания, но и выработал соответствующий навык, то есть почти никогда не ошибался. Движения руки должны стать уверенными, — чтобы, откладывая одну бусинку, не задевать соседние. И еще один принцип: если сбился со счета, то не надо продолжать наобум — начинай всё сначала.
После того как ребенок начнет обращаться со счетами более или менее уверенно, ему можно подсказать одну «хитрость» (если он сам до нее не додумается): второе число, точно так же, как и первое, необязательно пересчитывать по бусинкам от начала до конца: можно вначале отложить десятки (пусть даже десяток получится «рваный» — часть бусинок с одного ряда, часть — со следующего) и только потом продолжать считать по отдельным бусинкам.
Еще на одно открытие можно натолкнуть ребенка, давая ему примеры такими парами:
$1 + 26 =$
$26 + 1 =$
Оказывается, удобнее вначале отложить большее число, а потом прибавлять к нему меньшее. Результат всё равно остается один и тот же.
Необязательное дополнение 1: «уравнения»
Постепенно можно переходить к более сложным заданиям. В следующем примере вместо многоточия надо поставить такое число, чтобы получился правильный ответ:
$\ldots + 3 = 9$
Подобного рода задачи решаются методом обращения времени вспять. Допустим, мы только что решили обычный пример «какое-то число плюс $3$» и в результате получили $9$. Откладываем на счетах $9$ бусинок. Теперь как бы движемся по времени назад, воспроизводя решение примера в обратном порядке. Перекладываем бусинки обратно и считаем: три-бусинка, два-бусинка, раз-бусинка. Остается $6$ бусинок. Значит, вместо многоточия надо поставить шестерку:
$\underline{\,6\,} + 3 = 9$
Впрочем, очень скоро становится ясно, что перекладываемые бусинки можно считать и обычным образом: раз-бусинка, два-бусинка, три-бусинка. Результат от этого не изменится. Интересно отметить, что мы выполняем в точности такие же действия, как если бы решали пример «${9 — 3}$».
Результат от этого не изменится. Интересно отметить, что мы выполняем в точности такие же действия, как если бы решали пример «${9 — 3}$».
Подобным же образом можно найти, какое число должно стоять вместо многоточия в таком примере:
$\ldots — 2 = 5$
Снова обращаем время вспять, и обнаруживается, что мы выполняем такие действия, как будто решаем пример «${5 + 2}$». В итоге получаем:
$\underline{\,7\,} — 2 = 5$
Но вот еще один пример с многоточием:
$9 + \ldots = 12$
Здесь многоточие стоит не на первом месте, а на втором, поэтому вспять обратить время не получится. Давайте, для начала, решим этот пример методом подбора. Попробуем вместо многоточия поставить единицу. Откладываем сперва девять бусинок, потом добавляем еще одну. Получился правильный ответ? Нет. Выходит, маловато добавили. Добавляем вторую бусинку. Снова маловато. Добавляем третью — теперь в самый раз. Всего добавили три бусинки. Значит, мы можем написать:
$9 + \underline{\,3\,} = 12$
Тут можно ввести небольшое усовершенствование. Давайте, после того как мы отложили $9$ бусинок, пометим еще как-нибудь бусинку номер двенадцать. Например, сдвинем ее чуть-чуть влево — не до конца, а так, чтобы сразу после нее в ряду бусинок образовался небольшой разрыв. Теперь мы сразу видим, какие именно бусинки надо добавить к первым девяти, чтобы всего получилось двенадцать. Остается их только пересчитать: раз, два, три — ответ готов. Но посмотрим внимательно на счеты. Здесь у нас отмечено $12$ бусинок, поскольку именно после $12$-ой бусинки идет разрыв. Из них $9$ стоят особняком — сдвинуты до упора влево, — а остальные нам надо было пересчитать. То есть получается, что мы на самом-то деле отвечали на вопрос, сколько будет «${12 — 9}$».
Давайте, после того как мы отложили $9$ бусинок, пометим еще как-нибудь бусинку номер двенадцать. Например, сдвинем ее чуть-чуть влево — не до конца, а так, чтобы сразу после нее в ряду бусинок образовался небольшой разрыв. Теперь мы сразу видим, какие именно бусинки надо добавить к первым девяти, чтобы всего получилось двенадцать. Остается их только пересчитать: раз, два, три — ответ готов. Но посмотрим внимательно на счеты. Здесь у нас отмечено $12$ бусинок, поскольку именно после $12$-ой бусинки идет разрыв. Из них $9$ стоят особняком — сдвинуты до упора влево, — а остальные нам надо было пересчитать. То есть получается, что мы на самом-то деле отвечали на вопрос, сколько будет «${12 — 9}$».
Теперь мы так же легко можем справиться и с таким примером:
$14 — \ldots = 8$
Откладываем $14$ бусинок, помечаем бусинку номер $8$ — например, сдвигая ее немножко вправо — и сразу видим, какие бусинки надо отнять от четырнадцати, чтобы получить восемь. Простым пересчетом находим, что их ровно $6$.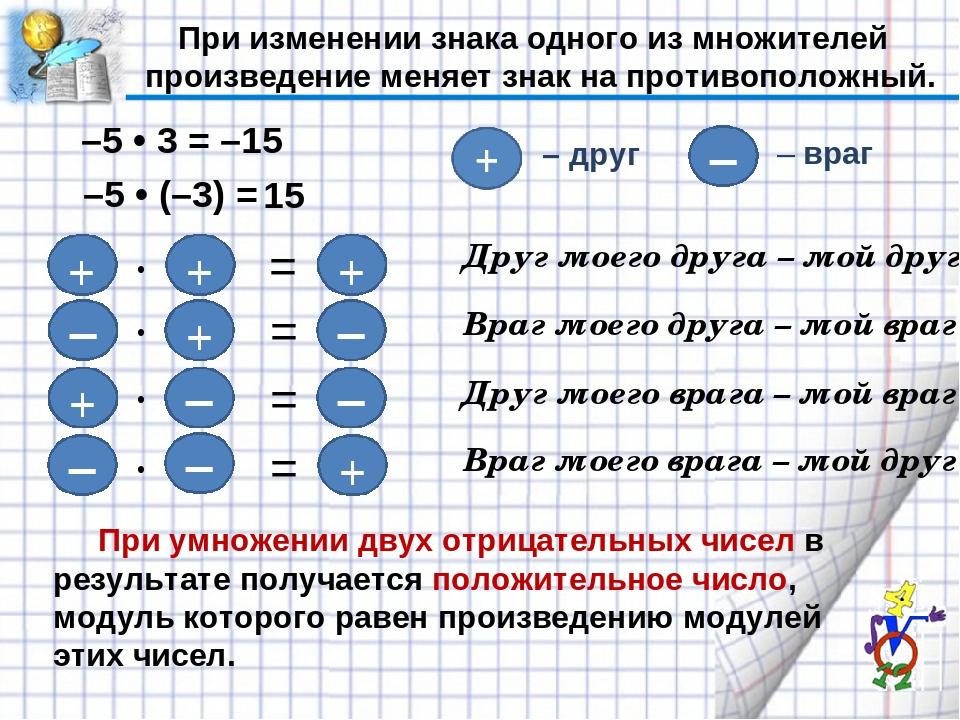 Таким образом, многоточие надо заменить на шестерку:
Таким образом, многоточие надо заменить на шестерку:
$14 — \underline{\,6\,} = 8$
И снова приглядимся к счетам. По расположению бусинок мы видим, что фактически решали пример «${14 — 8}$».
Необязательное дополнение 2: «отрицательные числа»
Пусть теперь дано:
$3 — 3 =$
Тут всё просто: откладываем сначала три бусинки, а потом те же три бусинки отправляем обратно. В результате получается «ничто» — ноль. А как быть, если встретится такое задание?
$3 — 5 =$
Мы привычным движением откладываем справа налево три бусинки, затем начинаем перекладывать по бусинке обратно: раз-бусинка, два-бусинка, три-бусинка — мы еще не успели переложить столько бусинок, сколько требуется, а они уже кончились. Что делать? Берем и разворачиваем счеты обратной стороной. Теперь все бусинки у нас оказались слева, и мы можем продолжить наше перекладывание: четыре-бусинка, пять-бусинка. С правой стороны у нас оказалось две бусинки. Вот это мы и напишем в качестве ответа. Только мы должны честно сознаться, что немножко схитрили, развернув счеты другой стороной Поэтому мы напишем не просто двойку, а еще поставим перед ней черточку — знак минус:
Только мы должны честно сознаться, что немножко схитрили, развернув счеты другой стороной Поэтому мы напишем не просто двойку, а еще поставим перед ней черточку — знак минус:
$3 — 5 = \underline{-2\,}$
Такие числа со знаком минус впереди, полученные хитрым способом, называются отрицательными. Нам еще предстоит много иметь с ними дело в будущем. Заметим, что мы всего переложили слева направо $5$ бусинок, из них $3$ на лицевой стороне счет, а остальные на обратной. Поэтому мы с тем же успехом могли бы решить пример «${5 — 3}$» и приписать к ответу знак минус.
Но вот еще один пример с многоточием:
$7 — \ldots = -3$
Откладываем $7$ бусинок и начинаем действовать методом подбора. Отнимаем для начала одну бусинку. Мало. Еще одну. Опять мало. Впрочем, ясно, что даже если сразу отнять все $7$ бусинок, это всё равно будет мало. Поэтому единым махом перекладываем назад все оставшиеся бусинки и говорим «семь». Переворачиваем счеты обратной стороной. Тут нам надо переложить еще $3$ бусинки. Так сразу и делаем. А теперь, поочередно касаясь их пальцем, продолжаем счет: «восемь», «девять», «десять». Это и есть ответ, который мы ищем:
Так сразу и делаем. А теперь, поочередно касаясь их пальцем, продолжаем счет: «восемь», «девять», «десять». Это и есть ответ, который мы ищем:
$7 — \underline{\,10\,} = -3$
Поучается, что с лицевой стороны мы насчитали $7$ бусинок, а с обратной стороны — еще $3$ бусинки. Значит, мы фактически решили пример «$7 + 3$».
Конспект
1. Сложение. Пусть у нас в одной кучке шесть конфет, а в другой — две. Смешаем эти кучки в одну. Сколько в ней оказалось конфет? Ответ на эту задачу записывается в виде ${6 + 2 = 8}$ (шесть плюс два равно восемь). Мы выполнили пример на сложение: сложили шесть и два и получили восемь. Для решения этого примера на счетах откладываем вначале шесть бусинок, потом две и пересчитываем отложенные бусинки.
2. Вычитание. Пусть у нас есть кучка из пяти конфет. Мы взяли из нее три конфеты. Сколько осталось? Ответ записывается в виде ${5 — 3 = 2}$ (пять минус три равно два). Это пример на вычитание: мы вычли из пяти три и получили два. Для решения этого примера на счетах откладываем пять бусинок, возвращаем обратно три и пересчитываем оставшиеся.
Для решения этого примера на счетах откладываем пять бусинок, возвращаем обратно три и пересчитываем оставшиеся.
3. Уравнения. Допустим в решенном примере на сложение «потерялось» первое число: ${\ldots + 3 = 9}$. Какое число потерялось? Представляем себе, что мы решили этот пример на счетах, и после этого «обращаем время вспять», фактически выполняя те же действия, которые мы совершаем при решении примера ${9 — 3 = 6}$. Подобным же образом, обращая время вспять, можно найти «потерянное» число в примере на вычитание: ${\ldots — 2 = 5}$, а именно: ${5 + 2 = 7}$. Глядя на бусинки, нетрудно также установить, что в примере ${9 + \ldots = 12}$ потерялось число ${12 — 9 = 3}$, а в примере ${14 — \ldots = 8}$ потерянным оказалось число ${14 — 8 = 6}$.
4. Отрицательные числа. Решая на счетах пример ${3 — 5}$, обнаруживаем, что из трех отложенных бусинок можно в обратную сторону переложить только три. Оставшиеся две бусинки перекладываем, развернув счеты обратной стороной. Ответ записываем в виде: ${3 — 5 = -2}$ (три минус пять равно минус два). С тем же успехом мы могли бы вычесть из пяти три и приписать перед результатом знак минус.
Ответ записываем в виде: ${3 — 5 = -2}$ (три минус пять равно минус два). С тем же успехом мы могли бы вычесть из пяти три и приписать перед результатом знак минус.
Задачи
1.2.1. «Мама дала Денису $7$ конфет, а папа $5$ конфет. Сколько конфет стало у Дениса?» Такого рода задач можно придумать множество, и хорошо, если они поначалу будут полностью соответствовать реальности. Главное действующее лицо — сам ребенок, и речь идет о приятных вещах. Мама в самом деле дает ему вкусные конфеты и спрашивает: «Сколько конфет я тебе дала?» Ребенок отвечает: «Семь». Потом он получает конфеты от папы, пересчитывает их и говорит: «Пять». Теперь он готов с радостью подумать над вопросом: «А сколько у тебя всего конфет?». Опять-таки, имеются в виду маленькие конфетки, не больше горошины.
1.2.2. Задачи на вычитание придумывать несколько труднее. Не следует повторять ошибку Мальвины, взявшуюся обучать арифметике Буратино. Если ребенок не любит делиться конфетами с младшим братиком, то это неподходящая тема для первых занятий по математике. Не слишком хорошо начинать и с таких задачек: «У Дениса было $10$ конфет. $4$ из них он съел. Сколько конфет осталось?» Здесь недостает наглядности: съеденных конфет-то не видно! Пожалуй, лучше так: «У папы было $10$ конфет. $4$ из них он оставил себе, а остальные дал Денису. Сколько конфет папа дал Денису?»
Не слишком хорошо начинать и с таких задачек: «У Дениса было $10$ конфет. $4$ из них он съел. Сколько конфет осталось?» Здесь недостает наглядности: съеденных конфет-то не видно! Пожалуй, лучше так: «У папы было $10$ конфет. $4$ из них он оставил себе, а остальные дал Денису. Сколько конфет папа дал Денису?»
1.2.3. К вычитанию можно подойти еще и с другой стороны.
— Денис, сколько тебе дать конфет, — спрашивает папа.
— Двенадцать, — отвечает Денис.
— Хорошо, — говорит папа и дает Денису девять конфет. — Сколько конфет я должен тебе еще дать, чтобы получилось двенадцать?
Примеры из «динамических» прописей
Сложение и вычитание в пределах 20-ти («серый» шрифт для обводки)
То же с «уравнениями» (т.е. пробелами для вставки чисел)
Сложение и вычитание в пределах 20-ти (разность может быть отрицательной)
То же с «уравнениями»
Последовательность выполнения математических действий без скобок — Dudom
Числовые,буквенные выражения и выражения с переменными в своей записи могут содержать знаки различных арифметических действий. При преобразовании выражений и вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий.
При преобразовании выражений и вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий.
В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.
Навигация по странице.
Сначала умножение и деление, затем сложение и вычитание
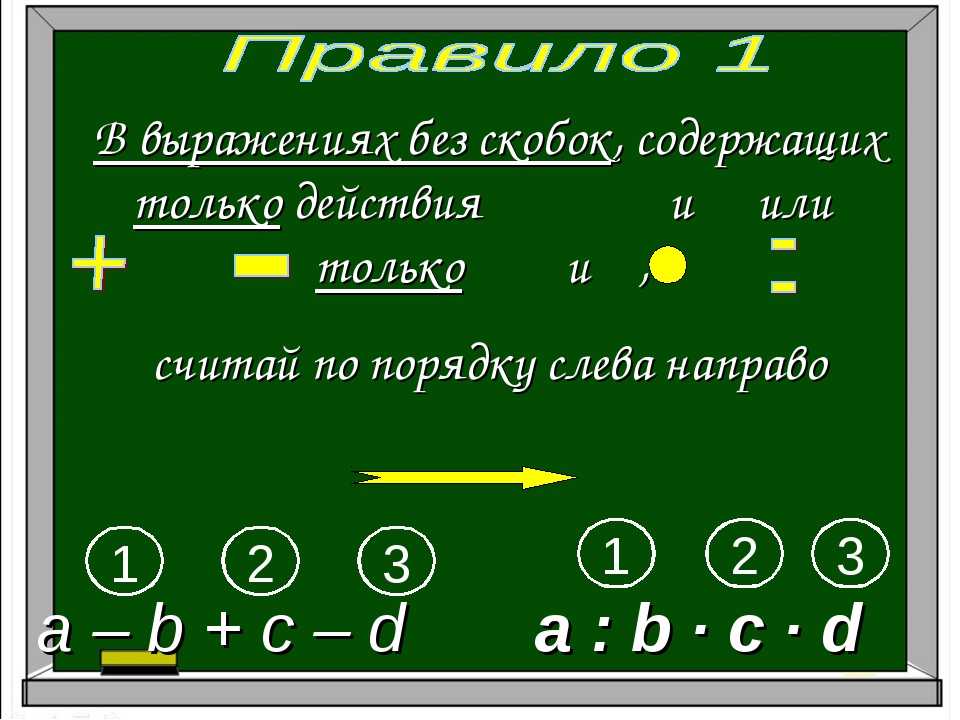
В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок:
- действия выполняются по порядку слева направо,
- причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Выполните действия 7−3+6 .
Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .
Кратко решение можно записать так: 7−3+6=4+6=10 .
Укажите порядок выполнения действий в выражении 6:2·8:3 .
Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.
Вычислите значение выражения 17−5·6:3−2+4:2 .
Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .
В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .
На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так:
Для предыдущего примера это выглядело бы так:
.
Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.
Действия первой и второй ступени
В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.
Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени.
В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат скобки, указывающие порядок выполнения действий. В этом случае правило, задающее порядок выполнения действий в выражениях со скобками, формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
В этом случае правило, задающее порядок выполнения действий в выражениях со скобками, формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Выполните указанные действия 5+(7−2·3)·(6−4):2 .
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .
Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .
На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .
Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Выполните действия в выражении 4+(3+1+4·(2+3)) .
Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .
Порядок выполнения действий в выражениях с корнями, степенями, логарифмами и другими функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции, то их значения вычисляются до выполнения остальных действий, при этом также учитываются правила из предыдущих пунктов, задающие порядок выполнения действий. Иными словами, перечисленные вещи, грубо говоря, можно считать заключенными в скобки, а мы знаем, что сначала выполняются действия в скобках.
Рассмотрим решения примеров.
Выполните действия в выражении (3+1)·2+6 2 :3−7 .
В этом выражении содержится степень 6 2 , ее значение нужно вычислить до выполнения остальных действий. Итак, выполняем возведение в степень: 6 2 =36 . Подставляем это значение в исходное выражение, оно примет вид (3+1)·2+36:3−7 .
Дальше все понятно: выполняем действия в скобках, после чего остается выражение без скобок, в котором по порядку слева направо сначала выполняем умножение и деление, а затем – сложение и вычитание. Имеем (3+1)·2+36:3−7=4·2+36:3−7= 8+12−7=13 .
Другие, в том числе и более сложные примеры выполнения действий в выражениях с корнями, степенями и т.п., Вы можете посмотреть в статье вычисление значений выражений.
В данном разделе мы познакомимся с порядком действий, с выражениями со скобками и без них.
1) Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо.
Например,
В числовом выражении 3 арифметических действия: сложение, вычитание и вычитание.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо:
Полностью пример записываем так:
10 + 15 — 6 — 8 = 25 — 6 — 8 = 19 — 8 = 11
Например,
В числовом выражении 3 арифметических действия: деление, умножение и деление.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни сложения ни вычитания, действия выполняют по порядку слева направо:
Полностью пример записываем так:
15 : 5 • 4 : 6 = 3 • 4 : 6 = 12 : 6 = 2
2) Если тебе нужно выполнить несколько арифметических действий (сложение, вычитание, умножение и деление), то сначала выполняют умножение и деление по порядку слева направо, а затем сложение и вычитание по порядку слева направо.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим деление, потом умножение, затем вычитание и сложение.
Полностью пример записываем так:
10 — 15 : 3 + 6 • 8 = 10 — 5 + 6 • 8 = 10 — 5 + 48 = 5 + 48 = 53
3) Если в выражении есть скобки, то сначала выполняют действия в скобках, но обязательно учитывать первое и второе правила.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим вычитание в скобках, затем деление, потом умножение и сложение.
Полностью пример записываем так:
(25 — 10) : 3 + 6 • 8 = 15 : 3 + 6 • 8 = 5 + 6 • 8 = 5 + 48 = 53
Например,
В числовом выражении 4 арифметических действия: сложение, деление, сложение и деление.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим действия в скобках (деление, затем сложение), затем деление, потом сложение.
Полностью пример записываем так:
42 + 18 : (6 + 12 : 4) = 42 + 18 : (6 + 3) = 42 + 18 : 9 = 42 + 2 = 44
Вывод:Поделись с друзьями в социальных сетях:
Порядок действий в выражениях без скобок
Для правильного вычисления выражений, в которых нужно произвести более одного действия, нужно знать порядок выполнения арифметических действий. Арифметические действия в выражении без скобок условились выполнять в следующем порядке:
- Если в выражении присутствует возведение в степень, то сначала выполняется это действие в порядке следования, т. е. слева направо.
- Затем (при наличии в выражении) выполняются действия умножения и деления в порядке их следования.
- Последними (при наличии в выражении) выполняются действия сложения и вычитания в порядке их следования.
В качестве примера рассмотрим следующее выражение:
| 3 | 1 | 5 | 2 | 4 | 6 | |||
|---|---|---|---|---|---|---|---|---|
| 3 | · | 4 2 | — | 2 3 | : | 2 | + | 20 |
Сначала необходимо выполнить возведение в степень (число 4 возвести в квадрат и число 2 в куб):
3 · 16 — 8 : 2 + 20
Затем выполняются умножение и деление (3 умножить на 16 и 8 разделить на 2):
И в самом конце, выполняются вычитание и сложение (из 48 вычесть 4 и к результату прибавить 20):
48 — 4 + 20 = 44 + 20 = 64
Действия первой и второй ступени
Арифметические действия делятся на действия первой и второй ступени. Сложение и вычитание называются действиями первой ступени, умножение и деление – действиями второй ступени.
Сложение и вычитание называются действиями первой ступени, умножение и деление – действиями второй ступени.
Если выражение содержит действия только одной ступени и в нём нет скобок, то действия выполняются в порядке их следования слева направо.
Пример 1. Вычислить значение выражения:
15 + 17 — 20 + 8 — 12
Решение. Данное выражение содержит действия только одной ступени – первой (сложение и вычитание). Надо определить порядок действий и выполнить их.
| 1 | 2 | 3 | 4 | |||||
|---|---|---|---|---|---|---|---|---|
| 15 | + | 17 | — | 20 | + | 8 | — | 12 |
Пример 2. Вычислить значение выражения:
60 : 15 · 7 : 2 · 3
Решение. Данное выражение содержит действия только одной ступени – второй (умножение и деление). Надо определить порядок действий и выполнить их.
| 1 | 2 | 3 | 4 | |||||
|---|---|---|---|---|---|---|---|---|
| 60 | : | 15 | · | 7 | : | 2 | · | 3 |
Если выражение содержит действия обеих ступеней, то первыми выполняются действия второй ступени, в порядке их следования (слева направо), а затем действия первой ступени.
Пример. Вычислить значение выражения:
24 : 3 + 5 · 2 — 17
Решение. Данное выражение содержит четыре действия: два первой ступени и два второй. Определим порядок их выполнения: согласно правилу первым действием будет деление, вторым – умножение, третьим – сложение, а четвёртым – вычитание.
поставьте знаки плюс/минус между цифрами
Начните с последовательности ненулевых цифр 123456789. Задача состоит в том, чтобы поставить плюс или минус знаки между ними так, что результатом описанной арифметической операции будет 100.
Мы получили один ответ
12 + 3 — 4 + 5 + 67 + 8 + 9 = 100
и предположил, что существует как минимум еще один. Я не утверждаю, что провел исчерпывающий поиск, но кажется, что есть больше, чем просто два ответа. Один из них
123 + 4 — 5 + 67 — 89 = 100
Я уверен, что там как минимум еще один. Хотите найти?
Есть острое наблюдение, что в двух приведенных выше примерах по крайней мере одна из операций — вычитание. И это также верно для всех добавочных (тех, в которых разрешены только операции сложения и вычитания) примеров ниже. На самом деле невозможно избежать вычитания, даже если цифры идут в произвольном порядке. Чтобы понять почему, полезно вспомнить понятие цифровых корней.
И это также верно для всех добавочных (тех, в которых разрешены только операции сложения и вычитания) примеров ниже. На самом деле невозможно избежать вычитания, даже если цифры идут в произвольном порядке. Чтобы понять почему, полезно вспомнить понятие цифровых корней.
Вы можете разрешить любые операции, кроме сложения и вычитания. Это приводит к совершенно новому набору проблем с числами, имеющими дробные части. Варианты включают установку целей, отличных от 100. Вот, например, представление единицы, в которой используются все десять цифр:
. 1 = 148/296 + 35/70
Есть много способов весело провести время, решая арифметические задачи. Один из способов — попытаться представить числа ограниченными средствами. Например, я могу представить 100 пятью тройками как 100 = 33×3 + 3/3. Удивительно, как много чисел можно представить таким образом.
В 1960-х годах очень популярным стал другой вид числовых головоломок. Криптарифмы — это головоломки, полученные
когда цифры в числовых расчетах заменены буквами. Обычно различаются
буквы обозначают разные цифры. Звезды заменяют любую цифру и не связаны друг с другом.
Обычно различаются
буквы обозначают разные цифры. Звезды заменяют любую цифру и не связаны друг с другом.
Я получил следующее письмо из Бельгии:
От: Gui et Nicole RULMONT
Дата: вторник, 22 апреля 1997 г., 17:02:44 +0200
Уважаемый Cut-the-Knot,
Сначала извините за мой английский. Я бельгиец, и меня очень заинтересовал ваш сайт!
Вы писали в «Веселье с цифрами»: Начните с последовательности ненулевых цифр 123456789. Задача состоит в том, чтобы расставить между ними знаки плюс или минус так, чтобы результатом описанной арифметической операции было 100.
Несколько лет назад я нашел во французском журнале Science et Vie 11 решений:
1 + 2 + 34 — 5 + 67 — 8 + 9 = 100
12 + 3 — 4 + 5 + 67 + 8 + 9= 100
123 — 4 — 5 — 6 — 7 + 8 — 9 = 100
123 + 4 — 5 + 67 — 89 = 100
123 + 45 — 67 + 8 — 9 = 100
123 — 45 — 67 + 89 = 100
12 — 3 — 4 + 5 — 6 + 7 + 89 = 100
12 + 3 + 4 + 5 — 6 — 7 + 89 = 100
1 + 23 — 4 + 5 + 6 + 78 — 9 = 100
1 + 23 — 4 + 56 + 7 + 8 + 9 = 100
1 + 2 + 3 — 4 + 5 + 6 + 78 + 9 = 100
Если мы поставим «-» перед 1, у нас будет еще одно решение:
-1 + 2-3 + 4 + 5 + 6 + 78 + 9 = 100
Использование «. » десятичное разделение Я нашел другое решение:
» десятичное разделение Я нашел другое решение:
1 + 2,3 — 4 + 5 + 6,7 + 89 = 100 (моё решение)
А как насчет 987654321? Есть 15 решений, сказал Science et Vie :
98 — 76 + 54 + 3 + 21 = 100
9 — 8 + 76 + 54 — 32 + 1 = 100
98 + 7 + 6 — 5 — 4 — 3 + 2 — 1 = 100
98 — 7 — 6 — 5 — 4 + 3 + 21 = 100
9 — 8 + 76 — 5 + 4 + 3 + 21 = 100
98 — 7 + 6 + 5 + 4 — 3 — 2 — 1 = 100
98 + 7 — 6 + 5 — 4 + 3 — 2 — 1 = 100
98 + 7 — 6 + 5 — 4 — 3 + 2 + 1 = 100
98 — 7 + 6 + 5 — 4 + 3 — 2 + 1 = 100
98 — 7 + 6 — 5 + 4 + 3 + 2 — 1 = 100
98 + 7 — 6 — 5 + 4 + 3 — 2 + 1 = 100
98 — 7 — 6 + 5 + 4 + 3 + 2 + 1 = 100
9 + 8 + 76 + 5 + 4 — 3 + 2 — 1 = 100
9 + 8 + 76 + 5 — 4 + 3 + 2 + 1 = 100
9 — 8 + 7 + 65 — 4 + 32 — 1 = 100
Напишите знак «-«, три решения:
-9 + 8 + 76 + 5-4 + 3 + 21 = 100
-9 + 8 + 7 + 65 — 4 + 32 + 1 = 100
-9-8 + 76 — 5 + 43 + 2 + 1 = 100
С десятичной точкой:>
9 + 87,6 + 5,4 — 3 + 2 — 1 = 100 (моё решение)
Если «перетасовать» цифры, то есть много решений. Я нашел некоторые, когда
Я был молод, например:
Я нашел некоторые, когда
Я был молод, например:
91 + 7,68 + 5,32 — 4 = 100
98,3 + 6,4 — 5,7 + 2 — 1 = 100
538 + 7 — 429 — 13 = 100
(8×9,125) + 37 — 6 — 4 = 100 и т.д. и т.п.. ..
очень интересуюсь криптарифмами и собираю их. Вы хотите получить французские криптарифмы? Знаете ли вы неанглийские криптарифмы? Спасибо!
Gui et Nicole Rulmont
Энтони Лезар отмечает, что решение 1 + 2 + 3 — 4 + 5 + 6 + 78 + 9 = 100 можно немного изменить без изменения результата: 1! + 2! + 3 — 4 + 5 + 6 + 78 + 9 = 100.
Примечание : Существует целая куча страниц, предлагающих практические задачи такого рода. Кроме того, Inder Jeet Taneja собрал фантастическую коллекцию различных последовательных представлений чисел от 1 до 11111.
|Контакты| |Главная страница| |Содержание| |Ты знал?| |Алгебра|
Copyright © 1996-2018 Александр Богомольный
Ключевые слова для математических операций
Первым шагом в решении текстовой задачи всегда является чтение задачи. Вы должны уметь переводить слов в математические символы, ориентируясь на ключевых слов , которые указывают на математические процедуры, необходимые для решения задачи — как на операцию, так и на порядок выражения. Точно так же, как вы можете перевести испанский язык на английский, вы можете перевести английские слова в символы, язык математики. Многие (если не все) ключевые слова, обозначающие математические операции, являются знакомыми словами.
Вы должны уметь переводить слов в математические символы, ориентируясь на ключевых слов , которые указывают на математические процедуры, необходимые для решения задачи — как на операцию, так и на порядок выражения. Точно так же, как вы можете перевести испанский язык на английский, вы можете перевести английские слова в символы, язык математики. Многие (если не все) ключевые слова, обозначающие математические операции, являются знакомыми словами.Для начала вы переводите английские фразы в алгебраических выражений. Алгебраическое выражение представляет собой набор чисел, переменных , операций и символов группировки. Вы переведете неизвестное число как переменную x или n . Символы группировки обычно представляют собой набор круглых скобок, но они также могут быть наборами скобок или фигурных скобок.
При переводе выражений необходимо хорошо знать основные ключевые слова, которые преобразуются в математические операции: ключевые слова сложения, ключевые слова вычитания, ключевые слова умножения и ключевые слова деления, которые рассматриваются в следующих четырех разделах.
Добавление ключевых слов
Вот некоторые распространенные примеры дополнительных ключевых слов:
- СУММА _____ И _____
- ВСЕГО _____ И _____
- _____ ПЛЮС _____
- _____ УВЕЛИЧИЛСЯ НА _____
- УСИЛЕНИЕ
- ПОДЪЕМ
- ДОПОЛНИТЕЛЬНО
- УВЕЛИЧЕНИЕ НА
Первые два ключевых слова (СУММА и ИТОГО) называются ведущие ключевые слова потому что они ведут выражение. Вторые два ключевых слова (ПЛЮС и УВЕЛИЧЕНИЕ НА) — это ключевые слова, которые указывают точное размещение знака плюс. Последние четыре ключевых слова встречаются в текстовых задачах и могут указывать на сложение.
Если выражение начинается с ведущих ключевых слов СУММА или ИТОГО, ведущее ключевое слово определяет соответствующее И. Затем знак плюс физически заменяет И в выражении.
Пример 1: Переведите следующее: сумма пяти и числа
Следующие шаги помогут вам перевести эту проблему:
1. Подчеркните слова до и после И, если они соответствуют ведущему ключевому слову СУММА ИЗ.
Подчеркните слова до и после И, если они соответствуют ведущему ключевому слову СУММА ИЗ.
- сумма пяти и числа
2. Обведите ведущее ключевое слово и укажите соответствующее И, которое оно определяет.
3. Переведите каждое подчеркнутое выражение и замените AND знаком плюс.
- Выражение переводится как 5 + x .
Пример 2: Переведите следующее: сумма числа и минус три
Используйте следующие шаги для перевода этой проблемы:
1. Ключевое слово ВСЕГО ИЗ является ведущим ключевым словом, определяющим И, поэтому подчеркните слова до и после И: «число» и «минус три».
- сумма числа и отрицательной тройки
2. Обведите ведущее ключевое слово и укажите соответствующее И, которое оно определяет.
3. Переведите каждое подчеркнутое выражение и замените AND знаком плюс.
- Выражение переводится как x + −3.
Пример 3: Переведите следующее: сумма семи и отрицательных четырех
Переведите этот пример следующим образом:
1. Слово СУММА является ведущим ключевым словом, определяющим И, поэтому подчеркните слова до и после И: «семь» и «минус четыре».
- сумма семи и отрицательных четырех
2. Обведите ведущее ключевое слово и укажите соответствующее И, которое оно определяет.
3. Переведите каждое подчеркнутое выражение и замените AND знаком плюс.
- Выражение переводится как 7 + −4.
Напоминание: Ключевое слово AND переводится как «плюс», потому что ведущее ключевое слово SUM OF. С другими ведущими ключевыми словами (обсуждаемыми в следующих разделах) И может означать другие вещи. Также обратите внимание, что вы не упрощаете выражение и получаете «3» за ответ, потому что вы просто переводите слова в символы, а не выполняете математические операции.
Также обратите внимание, что вы не упрощаете выражение и получаете «3» за ответ, потому что вы просто переводите слова в символы, а не выполняете математические операции.
Два других ключевых слова в списке дополнительных ключевых слов, PLUS и INCREASED BY, могут быть правильно переведены с помощью стратегии прямого перевода . В стратегии прямого перевода вы переводите каждое слово в соответствующий ему алгебраический символ, по одному, в том же порядке, как написано, как показано в примере 4.
Пример 4: Переведите следующее: число, увеличенное на двадцать четыре
- Выражение переводится как x + 24,
Некоторые дополнительные ключевые слова, такие как ПРИБЫЛЬ, БОЛЬШЕ, УВЕЛИЧЕНИЕ и ПОВЫШЕНИЕ, обычно встречаются в задачах-рассказах, как в примере 5.
Пример 5: Переведите следующую сюжетную задачу в математическое выражение о весе полузащитника: Защитный полузащитник весил двести двадцать два фунта в начале весенней тренировки. Он набрал семнадцать фунтов после четырех недель тренировок с командой.
Он набрал семнадцать фунтов после четырех недель тренировок с командой.
- Выражение переводится как 222 + 17.
Примечание: Не все числа, упомянутые в словесной задаче, должны быть включены в математическое выражение. Число «четыре» — это просто интересный факт, а не информация, необходимая для написания выражения о весе полузащитника.
Вам также может быть интересно, почему ответ не 239 фунтов. Это потому, что вопрос просит вас перевести проблему истории в математическое выражение, а не оценивать выражение.
Пример 6: Переведите следующую текстовую задачу в математическое выражение о текущей почасовой оплате кассира: Кассир в бакалейной лавке зарабатывал 6,25 доллара в час. Он получил прибавку в размере 25 центов в час.
- Выражение переводится как 6,25 + 0,25.
Примечание: Почасовая оплата указана в долларах, а надбавка — в центах. Каждый раз, когда вы добавляете два числа, которые имеют единиц , убедитесь, что оба числа измеряются в одних и тех же единицах; если это не так, преобразуйте одно из чисел в те же единицы, что и другое. Измерение обоих чисел в одних и тех же единицах называется 9.0130 однородных единиц. В этом примере вы конвертируете его надбавку, 25 центов, в 0,25 доллара, поскольку его почасовая оплата измеряется в долларах, а не в центах, поэтому надбавка также должна быть в долларах.
Измерение обоих чисел в одних и тех же единицах называется 9.0130 однородных единиц. В этом примере вы конвертируете его надбавку, 25 центов, в 0,25 доллара, поскольку его почасовая оплата измеряется в долларах, а не в центах, поэтому надбавка также должна быть в долларах.
Вычитание ключевых слов
Ключевые слова на вычитание также включают ведущие ключевые слова, ключевые слова, которые можно переводить по одному слову за раз, и ключевые слова, встречающиеся в задачах-рассказах. Посмотрите на следующий список ключевых слов вычитания:
- РАЗНИЦА МЕЖДУ _____ И _____
- _____ МИНУС _____
- _____ УМЕНЬШИЛСЯ НА _____
- ПОТЕРЯ
- МЕНЬШЕ
- МЕНЬШЕ
- ЗАБЕРИТЕ
Одно ключевое слово вычитания (РАЗНИЦА МЕЖДУ) представляет собой выражение, состоящее из двух частей, которое начинается с ведущего ключевого слова, определяющего соответствующее И. Вы можете использовать те же методы подчеркивания и обведения ключевых слов, которые показаны в предыдущем разделе, для перевода этих выражений.
Вы можете использовать те же методы подчеркивания и обведения ключевых слов, которые показаны в предыдущем разделе, для перевода этих выражений.
Пример 7: Переведите следующее: разница между четырьмя и шестью
Вот как вы переводите Пример 7:
1. Поскольку ключевое слово РАЗНИЦА МЕЖДУ является ведущим ключевым словом, которое определяет соответствующее И, подчеркните слова до и после И: «четыре» и «шесть».
- разница между четырьмя и шестью
2. Обведите ведущее ключевое слово и укажите соответствующее И, которое оно определяет.
3. Переведите каждое подчеркнутое выражение и замените И знаком минус.
- Выражение переводится как 4 – 6.
Примечание: И не всегда переводится как сложение. Здесь РАЗНИЦА МЕЖДУ — это ведущее ключевое слово, которое определяет, что И означает вычитание.
Другие ключевые слова вычитания, такие как MINUS и DECREASED BY, используют стратегию прямого перевода. Пример 8 представляет собой задачу на вычитание слов, которая переводится по одному ключевому слову за раз в точном порядке выражения.
Пример 8: Переведите следующее: двадцать четыре уменьшить на число
- Выражение переводится как 24 – x .
В задаче на вычитание вы можете найти ключевые слова на вычитание LOSS, LESS, FEWER и TAKE AWAY, как показано в примере 9.
Пример 9: Переведите следующую текстовую задачу в математическое выражение о текущей стоимости материалов на стройплощадке: Строительная компания хранила на строительной площадке материалы на сумму 1253 доллара. Компания понесла убытки в размере 300 долларов из-за ущерба, нанесенного ураганом.
- Выражение переводится как 1 253 – 300.
Умножение ключевых слов
Вот некоторые распространенные примеры ключевых слов умножения:
- УМНОЖИТЬ _____ НА _____
- ПРОДУКТ _____ И _____
- _____ РАЗ _____
- ДВОЙНОЙ _____
- ДВАЖДЫ _____
- ТРОЙНОЙ _____
- ПРОЦЕНТ _____
- ДОЛЯ _____
Для двух ключевых слов умножения, MULTIPLY и PRODUCT OF, ведущее ключевое слово определяет соответствующее BY или AND, как показано в примере 10.
Пример 10: Переведите следующее: произведение семи и числа
Переведите этот пример следующим образом:
1. Поскольку ПРОИЗВЕД ИЗ является ведущим ключевым словом, которое соответствует И, подчеркните слова до и после И: «семь» и «число».
- произведение семи и числа
2. Обведите ведущее ключевое слово и укажите соответствующее И, которое оно определяет.
3. Переведите каждое подчеркнутое выражение и замените AND знаком времени.
- Выражение переводится как 7 × x .
Примечание: Имейте в виду, что И не всегда означает сложение. Ключевое слово PRODUCT OF определяет, что И в этом выражении означает умножение.
Выражение умножения, переведенное методом прямого перевода, показано в примере 11.
Пример 11: Переведите следующее: число, умноженное на пятнадцать
Выражение переводится как x x 15.
Некоторые ключевые слова умножения, такие как DOUBLE, TWICE и TRIPLE, преобразуются в число и операцию умножения, как показано в примерах 12 и 13.
Пример 12: Переведите следующее: дважды число
Выражение преобразуется в 2 × x .
Пример 13: Переведите следующую текстовую задачу в математическое выражение: У Дженнифер в банке было 15 долларов. За следующие две недели она удвоила свои деньги.
Выражение преобразуется в 2 × 15.
Одним из ключевых слов, указывающих на умножение, является OF. Однако в текстовых задачах вы можете увидеть более одного употребления слова «из». Единственная OF, которая указывает на умножение, — это та, которая следует за ключевым словом PERCENT, знаком процента, ключевым словом FRACTION или дробью. См. примеры 14 и 15.
Пример 14: Переведите следующее: двадцать пять процентов от четырехсот долларов
Выражение переводится как 0,25 × 400.
Примечание: Помните, что перед умножением процент заменяется десятичной дробью.
Пример 15: Переведите следующее: одна треть от двадцати семи
Выражение переводится как .
Ключевые слова раздела
Некоторые распространенные примеры ключевых слов разделения:
- ЧАСТЬ _____ И _____
- РАЗДЕЛИТЬ _____ НА _____
- _____ ДЕЛИТСЯ НА _____
- ДЕЛИМ НА ПОЛОВИНУ
- ПО
Некоторым людям трудно различить ключевые слова ПРОИЗВЕДЕНИЕ ИЗ и ЧАСТНОЕ ИЗ. Вот подсказка, которая поможет вам запомнить, какое из них указывает на деление, а какое на умножение: ЧАСТНОЕ — более сложное слово, чем «ПРОИЗВЕД», а деление — более сложная операция, чем умножение.
Помните: Ведущие ключевые слова определяют соответствующие И или BY для обозначения деления, обычно обозначаемого символом ÷.
Пример 16: Переведите следующее: частное семи и числа
1. Поскольку ключевое слово ЧАСТНОЕ ИЗ является ведущим ключевым словом, которое определяет И, подчеркните слова до и после И: «семь» и «число».
Поскольку ключевое слово ЧАСТНОЕ ИЗ является ведущим ключевым словом, которое определяет И, подчеркните слова до и после И: «семь» и «число».
- частное семи и числа
2. Обведите ведущее ключевое слово и укажите соответствующее И, которое оно определяет.
3. Переведите каждое подчеркнутое выражение и замените И знаком деления.
- Выражение переводится как 7 ÷ n .
Примечание: Здесь ключевое слово ЧАСТНОЕ определяет И для обозначения деления.
Пример 17: Переведите следующее: разделите минус тридцать шесть на девять
1. Поскольку слово DIVIDE является ведущим ключевым словом, определяющим BY, подчеркните слова до и после BY: «минус тридцать шесть» и «девять».
- минус тридцать шесть разделить на девять
2. Обведите ведущее ключевое слово и укажите соответствующий BY, который оно определяет.
Обведите ведущее ключевое слово и укажите соответствующий BY, который оно определяет.
3. Переведите каждое подчеркнутое выражение и замените BY знаком деления.
- Выражение переводится как .
Примечание: Первое число идет в числителе при использовании дроби для обозначения деления. Число в числителе (-36) помещается внутри «дома» при использовании длинного символа деления.
Некоторые ключевые слова раздела можно переводить по одному слову. Вместо этого вы просто следуете предложению и заменяете его алгебраическими обозначениями по ходу дела.
Пример 18: Переведите следующее: число, деленное на 16
Выражение переводится как .
Часто в сюжетных задачах ключевым словом, указывающим на деление, является PER. Когда в сюжетной задаче требуется указать скорость транспортного средства в милях в час, настройте выражение, чтобы разделить количество миль на количество часов. Вы не только напрямую переводите «мили» ÷ «часы», но также определяете количество миль и количество часов, находя их в другом месте задачи. См. пример 19.
Вы не только напрямую переводите «мили» ÷ «часы», но также определяете количество миль и количество часов, находя их в другом месте задачи. См. пример 19.
Пример 19: Переведите следующую текстовую задачу в математическое выражение о скорости: Требуется три часа, чтобы проехать 150 миль до дома бабушки. Как найти среднюю скорость в милях в час?
В вопросе вы найдете «мили» ÷ «часы». В первой части задачи вы найдете количество миль, 150 миль, и количество часов, три часа.
Выражение переводится как 150 ÷ 3.
Math Kids — Add, Subtract, Count в App Store
Описание
Увлекательный бесплатный способ для дошкольников научиться сложению, вычитанию, счету и математике!
Начать обучение вашего ребенка никогда не рано. Дошкольники, детсадовцы, малыши и дети постарше стремятся выучить азбуку, счет, сложение, вычитание и многое другое! Лучший способ поощрять это — ежедневно делиться с ними умными, хорошо сделанными образовательными приложениями и играми.
Math Kids — идеальное введение в основы счета, сложения и вычитания. Он научит вашего малыша, дошкольника, первоклассника сортировке и логическим навыкам наряду с начальной математикой, давая им идеальную основу для обучения на протяжении всей жизни.
Math Kids — это бесплатная обучающая игра, предназначенная для обучения маленьких детей числам и математике. В нем есть несколько мини-игр, в которые полюбят малыши и дети дошкольного возраста, и чем больше они будут играть, тем лучше станут их математические навыки! Math Kids поможет дошкольникам, детсадовцам, первоклассникам научиться определять числа и начать обучение с ребусов на сложение и вычитание. Они отлично проведут время, выполняя игры и зарабатывая наклейки, а вы прекрасно проведете время, наблюдая, как они растут и учатся.
Math Kids предлагает ряд головоломок, которые обучают вашего ребенка, пока он играет, в том числе:
• Счет. Научитесь считать предметы в этой простой игре на сложение.
• Сравнить. Дети могут развивать свои навыки счета и сравнения, чтобы видеть, какая группа предметов больше или меньше.
Дети могут развивать свои навыки счета и сравнения, чтобы видеть, какая группа предметов больше или меньше.
• Добавление головоломки — забавная мини-игра, в которой дети решают математические задачи, перетаскивая числа на экране.
• Добавление удовольствия — Сосчитайте объекты и нажмите на недостающее число.
• Тест на добавление. Проверьте математические и математические способности вашего ребенка.
• Головоломка с вычитанием. Заполните пропущенные символы в математической задаче.
• Веселье с вычитанием: посчитайте предметы, чтобы решить головоломку!
• Викторина по вычитанию. Узнайте, насколько ваш ребенок улучшил свои математические навыки вычитания.
Когда дети могут играть во время обучения, они лучше запоминают информацию. Это также заставляет их хотеть учиться чаще, что даст им огромный импульс, когда они пойдут в детский сад.
Math Kids также имеет ряд функций, которые помогают взрослым отслеживать и управлять успеваемостью своего ребенка. Настраивайте игровые режимы, увеличивая или уменьшая сложность, или проверяйте табели успеваемости, чтобы увидеть результаты предыдущих раундов.
Настраивайте игровые режимы, увеличивая или уменьшая сложность, или проверяйте табели успеваемости, чтобы увидеть результаты предыдущих раундов.
Math Kids — идеальное введение в основы счета, сложения и вычитания. Он научит вашего малыша сортировке и логическим навыкам наряду с ранней математикой, что даст им идеальную основу для обучения на протяжении всей жизни.
Примечание для родителей:
Создавая Math Kids, мы сосредоточились на создании наилучших условий обучения для детей всех возрастов. Мы сами родители, поэтому точно знаем, что делает образовательную игру хорошей, а что нет. Мы выпустили Kids Math как совершенно бесплатную игру без встроенных покупок и сторонней рекламы. Math Kids — это полнофункциональная программа, не требующая разочарований и готовая к работе. Это именно то образовательное приложение, которое мы хотим для наших детей, и мы думаем, что оно понравится и вашей семье!
— С наилучшими пожеланиями от родителей в RV AppStudios
000Z» aria-label=»October 7, 2022″> 7 октября 2022 г.
Версия 1.3.8
Помогите своему ребенку освоить математические навыки с помощью лучших обучающих мини-игр! Math Kids предлагает множество красочных головоломок и игр, предназначенных для обучения сложению, вычитанию и многому другому, с забавным интерфейсом, разработанным специально для детей.
Новое в этом обновлении:
— Улучшения графики и интерфейса
— Новые награды и анимация
— Повышение производительности
Рейтинги и обзоры
1,2 тыс. оценок
Лучшие приложения для обучения детей!
Не буду врать, я искал ОТЛИЧНЫЕ приложения, которые не содержат рекламы и действительно образовательны… когда я нашел их, я удалил ВСЕ другие приложения для своего дошкольника и загрузил все детские приложения RV AppStudios а также приложения Duck Duck Moose, потому что они оба предлагают очень образовательные и хорошо продуманные приложения, а также все без рекламы (больше никаких рекламных роликов или неуместной рекламы для моего ребенка!) Тот факт, что они оба предлагают БЕСПЛАТНЫЕ приложения, Удивительно, но я бы не стал возражаю платить небольшую сумму за приложения, если я знаю, что они помогают разработчикам.
Я делюсь этими приложениями с каждым родителем, которого знаю, а также с родителями онлайн!
Просто идея, хотя мне очень нравятся эти приложения, так что можете ли вы также попробовать приложение для шаблонов, простой детский поиск слов (помогает читать/просматривать слова), визуальный таймер с секундами/минутами/часами (похожий на MouseTimer), приложение Find It (как Waldo, но для детей) и дроби (например, игровое приложение Food Circle). Я искал и искал приложения с ними и, похоже, не нашел ничего хорошего!
Отличное приложение для детей
У меня есть братья и сестры, и нам так весело играть в это обучающее приложение. Я думаю, что это приложение должно привлечь так много детей, чтобы играть в него, потому что это потрясающая игра, и мои братья и сестры любят ее, и я очень люблю ее, и я очень люблю ее. очень весело, и это помогает ему учиться, и так весело играть в нее мои братья и сестры, моя старшая, моей сестре пять лет, а моему младшему брату четыре года, и они ходят в дошкольное учреждение, и я предлагаю вам, ребята, получить эту игру для своих детей, братьев и сестер, если ты старшая сестра или твоя мама или папа эта игра потрясающая или старший брат такая веселая и крутая и лучшая игра на свете.
Эта игра веселая 🤩
Итак, я только что получил эту игру, но она мне так нравится, что я могу иметь наклейки, которые я так люблю, и делать разные вещи, если вы хотите поиграть в другую ☝️ как некоторые игры, если я знаю, поэтому я перехожу к другой, которая кажется круто 😎 поэтому я думаю, что вы должны получить эту игру, она говорит восхитительно, когда вы получаете правильный ответ или хорошая работа или хорошая работа, ведь я так люблю, что могу играть в эту игру весь день, и я хочу стать лучше в математике и во всем остальном те стоят денег и тому подобное, так что я счастлив, что у меня есть эта игра😀так что я думаю, что вы должны получить эту игру до свидания ✌️
Разработчик, RV AppStudios LLC, указал, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см.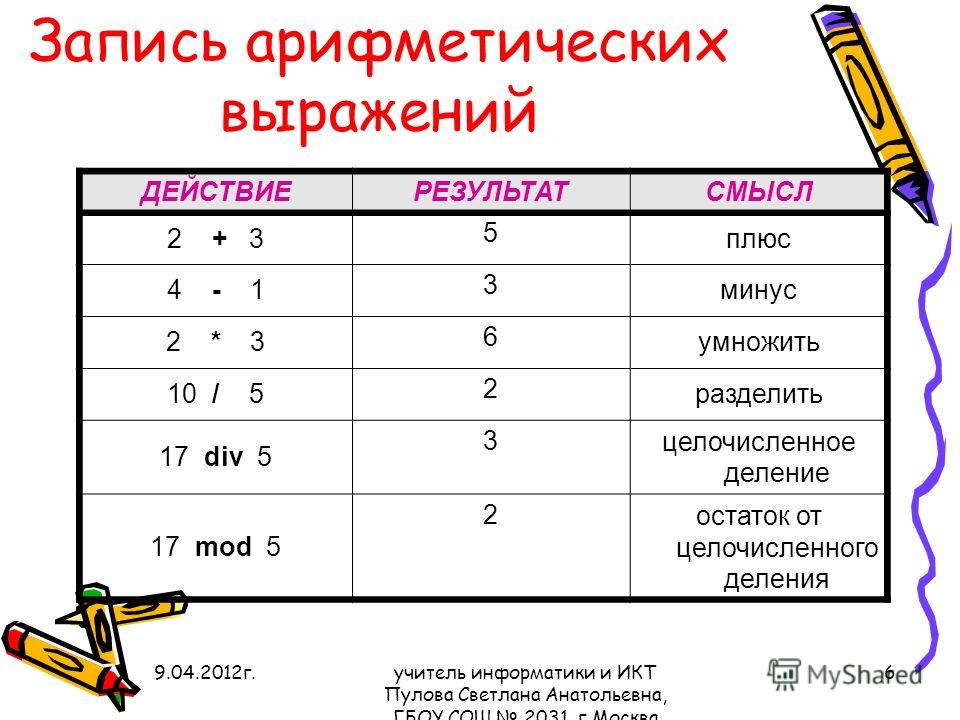



 Я делюсь этими приложениями с каждым родителем, которого знаю, а также с родителями онлайн!
Я делюсь этими приложениями с каждым родителем, которого знаю, а также с родителями онлайн!