Знаки в логике: Логические знаки в логике — Домострой

Содержание

Список логических символов — frwiki.wiki

В логике для выражения логического представления обычно используется набор символов . В следующей таблице перечислены многие символы с их именами, возможные способы их чтения и связанные области математики . Кроме того, третий столбец содержит неформальное определение, четвертый столбец дает краткий пример, пятый дает их код Unicode, а шестой и седьмой — числовые или текстовые ссылки, используемые в документах HTML (см. Сущность HTML ). Последний столбец содержит символ LaTeX .

Резюме

1 Основные логические символы
2 Продвинутые и редко используемые логические символы
3 Статьи по теме
4 Примечания и ссылки
- 4.1 Примечания
- 4.2 Ссылки

Основные логические символы

Символ	Фамилия	Объяснение	Примеры	Юникод (шестнадцатеричный)	HTML (десятичный)	HTML (текст)	Латекс
	Чтение
	Категория
	Участие	A ⇒ B истинно, только если либо A ложно, либо B истинно. → означает то же, что и ⇒ (этот символ также может указывать на домен и ко-домен функции ; см. Таблицу математических символов ). Означает то же, что и ⇒ (этот символ также может относиться к включению ).	Пусть x будет действительным числом: x = 2 ⇒ x ² = 4 истинно, но x ² = 4 ⇒ x = 2 обычно ложно (потому что x также может быть −2).	U + 21D2 U + 2192 U + 2283	& # 8658; & # 8594; & # 8835;	& rArr; & rarr; & Как дела;	⇒{\ displaystyle \ Rightarrow} \ Правая стрелка →{\ displaystyle \ to} \ к ⊃{\ displaystyle \ supset} \ supset ⟹{\ displaystyle \ implies} \ подразумевает
	вовлеченный если так является достаточным условием для
	Логика высказываний , алгебра Гейтинга
	Логическая эквивалентность	A ⇔ B истинно, если A и B ложны или если A и B истинны.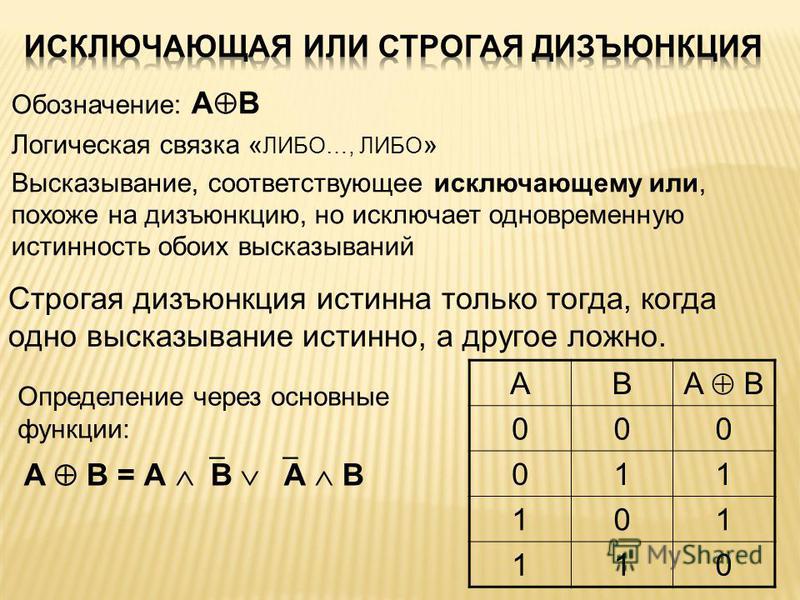	х + 5 знак равно у + 2 ⇔ х + 3 = у	U + 21D4 U + 2261 U + 2194	& # 8660; & # 8801; & # 8596;	& hArr; & Equiv; & harr;	⇔{\ displaystyle \ Leftrightarrow} \ Leftrightarrow ≡{\ Displaystyle \ Equiv} \ Equiv ↔{\ displaystyle \ leftrightarrow} \ leftrightarrow ⟺{\ Displaystyle \ iff} \ iff
	если и только если равно означает то же, что и
	Логика высказываний
	Отрицание	Утверждение ¬ A истинно тогда и только тогда, когда A ложно.	¬ (¬ А ) ⇔ А х ≠ у ⇔ ¬ ( х = у )	U + 00AC U + 02DC U + 0021	& # 172; & # 732; & # 33;	& нет; & тильда; & искл;	¬{\ displaystyle \ neg}\ lnot или \ neg ∼{\ displaystyle \ sim} \ sim
	Не Нет
	Логика высказываний
	Соединение	Утверждение A ∧ B истинно, если истинны A и B ; в противном случае это ложь.	n <4 ∧ n > 2 ⇔ n = 3, когда n — целое число .	U + 2227 U + 00B7 U + 0026	& # 8743; & # 183; & # 38;	& а также; & middot; & amp;	∧{\ Displaystyle \ клин}\ клин или \ земля &{\ Displaystyle \ &} \ &
	а также
	Логика высказываний , булева алгебра
	Инклюзивная дизъюнкция	Утверждение A ∨ B истинно, если истинны A или B , или оба; если оба ложны, утверждение ложно.	n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3, когда n — целое число .	U + 2228 U + 002B U + 2225	& # 8744; & # 43; & # 8741;	&золото;	∨{\ displaystyle \ lor}\ lor или \ vee
	или же
	Логика высказываний , булева алгебра
⊕ ⊻	Исключительная дизъюнкция	Утверждение A ⊕ B истинно, когда истинно либо A, либо B, только одно или другое. A ∨ B не означает одно и то же, потому что включает случай, когда оба истинны.	(¬ A ) ⊕ A всегда верно, A ⊕ A всегда ложно.	U + 2295 U + 22BB	& # 8853; & # 8891;	& oplus;	⊕{\ displaystyle \ oplus} \ oplus ⊻{\ displaystyle \ veebar} \ veebar
	xor
	Логика высказываний , булева алгебра
	Тавтология	Утверждение ⊤ безусловно верно.	A ⇒ ⊤ всегда верно.	U + 22A4	& # 8868;		⊤{\ displaystyle \ top} \вершина
	Высокая Правда
	Логика высказываний , булева алгебра
	Противоречие	Утверждение ⊥ безусловно ложно. (Символ ⊥ также может относиться к перпендикулярным линиям .)	⊥ ⇒ A всегда верно.	U + 22A5	& # 8869;	& perp;	⊥{\ displaystyle \ bot} \ бот
	Низкий Ложь
	Логика высказываний , булева алгебра
	Универсальный квантификатор	∀ x : P ( x ) или ( x ) P ( x ) означает, что P ( x ) истинно для всех x .	∀ n ∈ ℕ: n ² ≥ n .	U + 2200	& # 8704;	& для всех;	∀{\ displaystyle \ forall} \ для всех
	За все Для всех Для каждого
	вычисление предикатов
∃	Экзистенциальный квантификатор	∃ x : P ( x ) означает, что существует хотя бы один x такой, что P ( x ) истинно.	∃ n ∈ ℕ: n положительно.	U + 2203	& # 8707;	&существовать;	∃{\ Displaystyle \ существует} \ существуют
	Это существует
	вычисление предикатов
∃!	Уникальный экзистенциальный квантификатор	∃! x : P ( x ) означает, что существует ровно один x такой, что P ( x ) истинно.	∃! n ∈ ℕ: n + 5 = 2 n .	U + 2203 U + 0021	& # 8707; & # 33;		∃!{\ displaystyle \ существует!} \ существуют!
	Есть ровно один
	вычисление предикатов
≔ ≡ : ⇔	Определение	x ≔ y или x ≡ y означает, что x определяется как другое имя для y, но обратите внимание, что ≡ также может означать что-то еще, например конгруэнтность . Р : ⇔ Q означает , что Р определяется как логически эквивалентны с Q .	cosh x ≔ (ехр х + ехр (- х )) / 2 Исключающее ИЛИ Б : ⇔ ( ∨ B ) ∧ ¬ ( ∧ B )	U + 2254 (U + 003A; U + 003D) U + 2261 U + 003A; U + 229C	& # 8788; (& # 58; & # 61;) & # 8801; & # 8860;	& Equiv; & hArr;	знак равно{\ displaystyle: =} знак равно ≡{\ Displaystyle \ Equiv} \ Equiv : ⇔{\ displaystyle: \ Leftrightarrow} : \ Leftrightarrow
	определяется как
	Всюду
()	Порядок операций	Операции в круглых скобках имеют приоритет.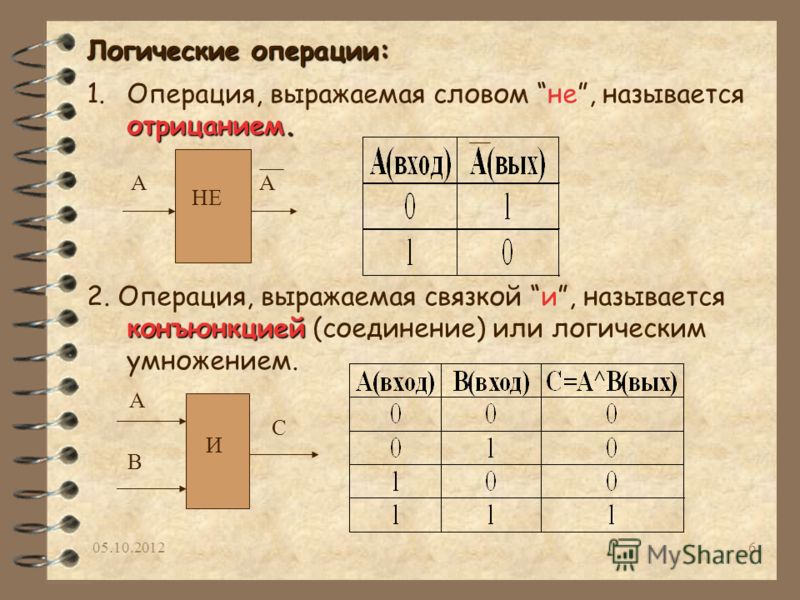	(8 ÷ 4) ÷ 2 = 2 ÷ 2 = 1, но 8 ÷ (4 ÷ 2) = 8 ÷ 2 = 4.	U + 0028 U + 0029	& # 40; & # 41;		( ){\ Displaystyle (~)} ()
	круглые скобки, скобки
	Всюду
⊢	Удержание	x ⊢ y означает, что y доказуемо относительно x (в определенной формальной системе ).	A → B ⊢ ¬ B → ¬ A	U + 22A2	& # 8866;		⊢{\ displaystyle \ vdash} \ vdash
	доказуемо ( стопор )
	Логика высказываний , исчисление предикатов
⊨	Моделирование	x ⊨ y означает, что x семантически влечет y .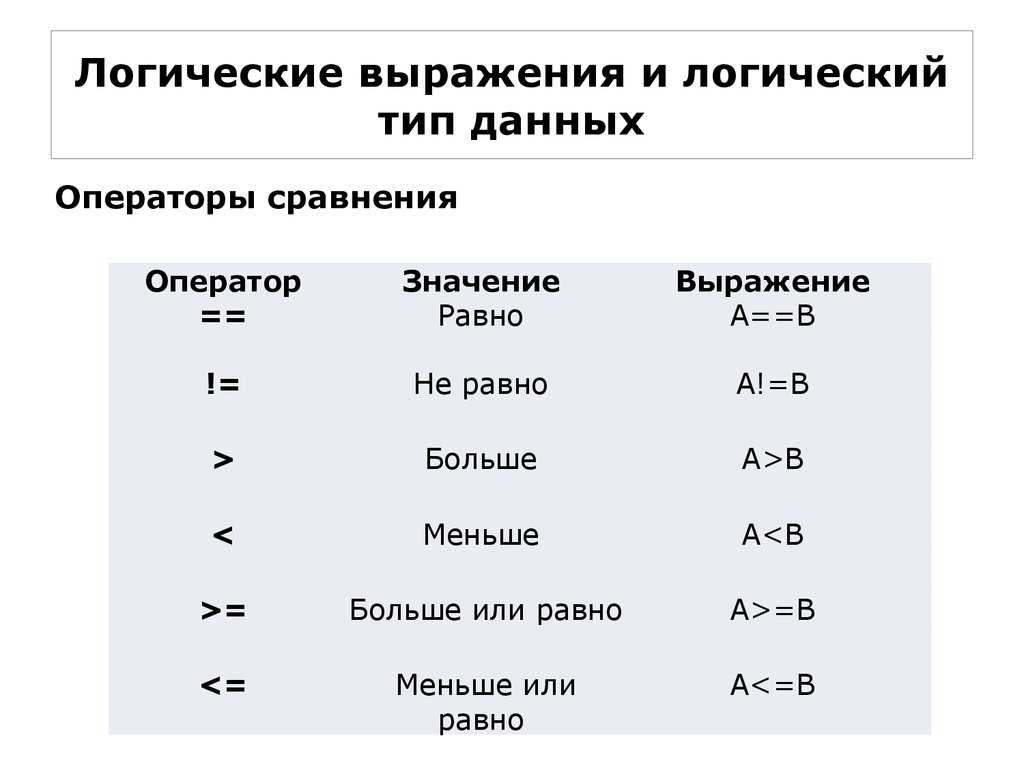	A → B ⊨ ¬ B → ¬ A	U + 22A8	& # 8872;		⊨{\ displaystyle \ vDash} \ vDash
	Включает
	Логика высказываний , исчисление предикатов

Продвинутые и редко используемые логические символы

Монеты Куайна

Статьи по Теме

Юзеф Мария Бохенский
Таблица математических символов
Логический разъем
Инфиксные, префиксные, польские и постфиксные обозначения
Таблица истинности
Логический квадрат
Логический шестиугольник

Примечания и ссылки

Заметки

(ru) Эта статья частично или полностью взята из статьи в англоязычной Википедии под названием « Список логических символов » ( см. список авторов ) .

Типографские символы
Пунктуация	Скобы ({}) · Круглые скобки (()) · шевроны (<> или <> или ⟨⟩) · Крючки ([]) · Половина крючки (⸢ ⸣ ⸤ ⸥) · кавычки ( «» или «» или » или «» или » или » » или ») · Апостроф (‘ или ‘) · запятая (,) · косая черта (/) · обратная косая черта (\) · косое пропускание (⸍ ⸌) · Пробел () · Точка () . · многоточие (… или …) · запятой (;) · двоеточие (:) · восклицательный знак ! () · восклицательный знак переворачивается (¡) · Точка Вопросительный знак ? () · Выброс знак вопроса (¿ ) · Восклицательный знак (‽) · Знак иронии (moins) · Коммерческий знак минус (⁒) · Дефис (- или -) · Дефис (- или — или -) · Другая пунктуация
Диакритический знак (от латинского алфавита )	Акут (◌) · Двойной ударения (◌̋) · апостроф (◌) · Двойной апостроф (◌̏) · Каре (◌) · Caret подписался (◌̭) · Бар включен (◌̶) · Краткая (◌ ̆) · Обратный бриф (◌̑) · Подписанный бриф (◌̮) · Подписанный обратный бриф (◌̯) · Caron (◌̌) · Cédille (◌̧) · Рог (◌ ̛) · Крючок в голове (◌̉) · вертикальная линия (◌̍) · вертикальная линия , на которые подписан (◌̩) · Macron (◌̄) · Macron подписался (◌) · Огонек (◌̨) · Огонек suscrit (◌᷎) · Точка подписки (◌̣) · Точка suscrit (◌̇) · Главный раунд (◌̊) · Круглый подписался (◌̥) · Тильда (◌) · Тильда подписался (◌̰) · линия suscrit (◌̅) · Двойной Overline (◌̿) · черта подписываемый (◌) · Двойной функция подписываемый (◌̳) · Умляут (◌̈) · Умляут подписался (◌̤) · Умляут (◌̈) · разделенные по подписчикам (◌̦) · запятой верхний индекс (◌̓)
Типографский символ	Ampersand (&) · В знаке (@) · Звездочка (*) · Астеризм (⁂) · Вертикальная черта (\| или \|) · Пунктирного круг (◌) · Copyright (©) · Фонографические авторские права (℗) · Товарный знак (® или ?) · Товарный знак (™ или ?) · знак обслуживания (℠) · Флажок (✓) · Паук (#) · Пунктирные крест (⁜) · Референтная метка (※) · Степень (°) · Цельсия (° C) · Фаренгейта (° F) · Количество ( Et ) · и Tironian (icule) · Manicule (☞) · Obele († и ‡) · Prime: минута, второй и третий ( » » ‘) · Пункт (§) · Поэтому (∴ ) · из (∵) · пестрой-де-Муш (¶) · Midpoint (·) · Чип (•) · Подчеркивание (_) · Ведущий дефис (~) · Конец знак статьи (◼) · х бюллетеней для голосования (✘ ) · Пояснительный символ (ɔ 🙂
Математический символ	Больше (+) · Меньше (-) · Плюс или минус (±) · Крест (x) или точка (⋅) умножения · Двоеточие (:) или Obelus (÷) деления · Равно (=) · Отличается от (≠ ) · Меньше или больше (<, ≤,>, ≥, ≮ и ≯) · приближение (≈) · дробная черта (/ или /) · процент (%) · до тысячи (‰) · Через десять миль (‱ ) · Квадрат , куб и экспонирование ( ²³ .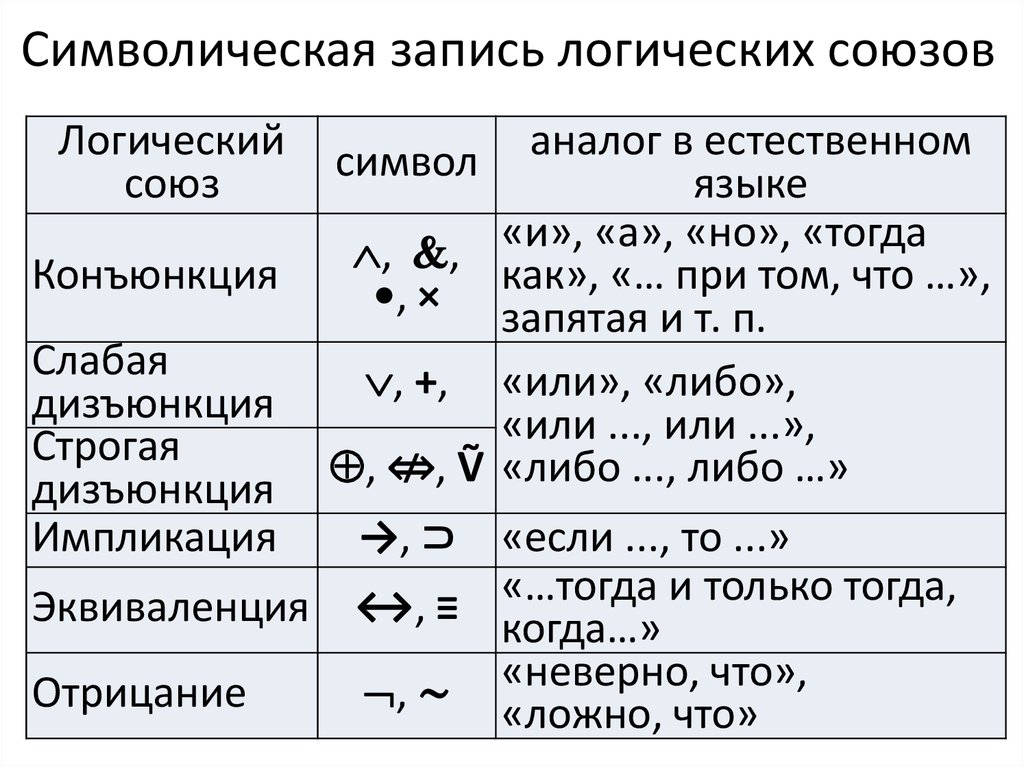 .. ⁿ ) · Радикал (√) · Интеграл (∫) · Сумма (Σ) · индексированный продукт (Π) · Микро (μ) · Вся партия (⌊ ⌋ ⌈ ⌉)
Логический символ	И и или логическое (∧ ∨) · Экзистенциальные и универсальные кванторы (∃ ∀) · Отрицание (¬) · Пустое множество (∅) · Пересечение и объединение (∩ ∪) · Подмножество и надмножество (⊆ ⊇) · Принадлежность (∈ ∋) · Дополнительные (∁) · Монеты Куайн (⌜ ⌝ ⌞ ⌟)
Символ валюты	Валюта (¤) · Бат (฿) · Биткойн (₿) · Седи (₵) · Цент (¢) · Двоеточие (₡) · Доллар ($) · Донг (₫) · Драм (֏) · Евро (€) · Гуарани (₲) · гривна (₴) · Кип (₭) · Фунт стерлингов (£) · Турецкая лира (₺) · Азербайджанский манат (₼) · Найра (₦) · Филиппинское песо (₱) · Риель (៛) · Рубль Русский (₽) · Индийская рупия (₹) · Шекель (₪) · тенге (₸) · Тугрик (₮) · Вон (₩) · Йена или юань (¥)

ЯЗЫК КАК ЗНАКОВАЯ СИСТЕМА Логика

Сразу хочу сказать, что здесь никакой воды про язык как знаковая сис , и только нужная информация. Для того чтобы лучше понимать что такое язык как знаковая сис , настоятельно рекомендую прочитать все из категории Логика.

Мы отмечали, что предметом логики является абстрактное мышление и что любая абстрактная мысль (идея) нечувственна. В силу нечувственности идеи возникает проблема ее фиксации в сознании. Эта проблема решается с помощью языка: идея находит свое выражение в слове или словосочетании. Хотя слова языка сами по себе чувственны, это, как правило, абстрактная чувственность по отношению к обозначенным ими предметам: слово и стоящий за ним предмет обычно не имеют непосредственной чувственной связи. Абстрактность словесной (вербальной) чувственности и делает язык незаменимым помощником сознания при абстрактном мышлении — настолько незаменимым, что последнее можно именовать вербальным.

Будучи знанием об абстрактном мышлении, логика не может не интересоваться языками. Она рассматривает их как знаковые системы. Устойчивый интерес логики (и не только логики) к языкам в конце XIX века привел к созданию семиотики — науки о знаках. У нее три основных раздела:

*Раздел семиотики*	*Коротко о предмете исследования*	*Подробно о предмете исследования*
Синтактика	отношения между знаками	правила построения выражений языка из отдельных знаков
Семантика	отношение между знаком и его значением	связь знака с тем, что он обозначает
Прагматика	отношение человека к знакам	влияние человека на использование знаков и знаков — на поведение человека

Ключевым понятием семиотики является понятие знака. Знак — это материальный предмет, репрезентирующий (заменяющий в процессе познания и общения) другой предмет. В данном определении следует обратить внимание на то, что знак всегда материален, а вот репрезентировать (обозначать) он может что угодно: как материальное, так и нематериальное. Например, слово «стол» обозначает материальную вещь, а слово «мышление» — нематериальный процесс.

По характеру отношения репрезентации различают три типа знаков:

*Тип знака*	*Отношение репрезентации*	*Примеры*
Индикатор	Каузальное (причинно-следственное)	Дым (по отношению к огню), улыбка (по отношению к хорошему настроению)
Образ	Отношение подобия (внешнего сходства)	Фотография (по отношению к тому, что сфотографировано)
Символ	Неопределенное	Буква алфавита, арабская цифра

Любой знак имеет смысловое и предметное значения (часто для краткости используют слова «смысл» и «значение», имея в виду два указанных вида значений) . Об этом говорит сайт https://intellect.icu . Смысловое значение — это мысль о предмете, зафиксированная в знаке. Предметным же значением является сам репрезентируемый (обозначаемый) знаком предмет.

Возьмем, например, слово «лес». Чтобы указать смысловое значение, дают описание мысли, заключенной в знаке. Для слова «лес» смысл можно передать словосочетанием «множество деревьев». Это неточное указание смыслового значения. Точнее нужно выразиться так: «массив дикорастущих деревьев». Что касается предметного значения слова «лес», то в этом качестве выступает произвольный элемент множества, обозначенного данным словом.

В учебниках логики можно встретить заявление, будто бы бывают знаки без смыслового или предметного значения. Например, Ю.В. Ивлев в качестве примера знака, не имеющего смысла, приводит математическое число, а ярким примером знака без предметного значения он считает выражение «вечный двигатель». Все примеры отсутствия у знака того или иного значения не выдерживают серьезной критики.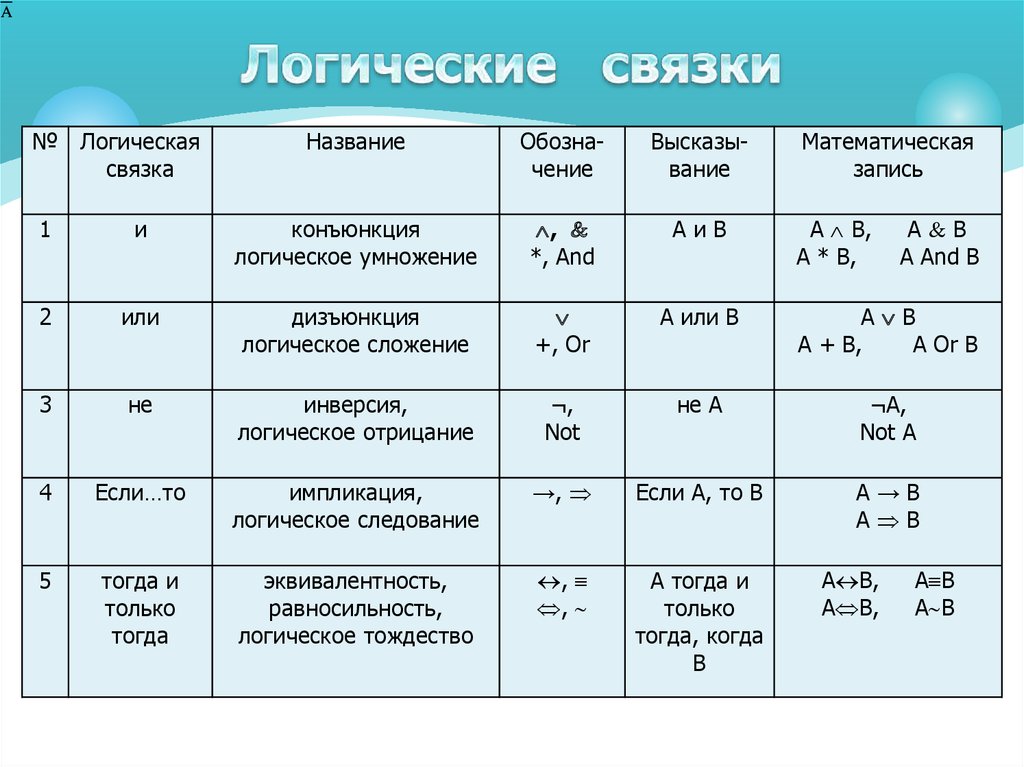 Возьмем математическое число «один». Его смысл — минимальное количество при натуральном счете. Что касается «вечного двигателя», «кентавра», «русалки» и т. п., то здесь утверждение об отсутствии у таких знаков предметного значения основано на слишком узком понимании предмета: последний, считают сторонники этой точки зрения, может быть лишь материальным.

Всякое выражение языка относится к той или иной семантической категории — к группе терминов, выполняющих одну и ту же семантическую функцию, т. е. одинаковым образом репрезентирующих предметы.

Семантических категории бывают двух типов: дескриптивные и логические. Дескриптивная категория репрезентирует конкретный предмет, т. е. предмет, неразрывно связанный с другими предметами, а логическая — абстрактный предмет, т. е. такой, который взят сам по себе, в отрыве от других предметов. Например, слово «лес» обычно представляет собой дескриптивную категорию, так как соответствующий ему предмет не рассматривают, как правило, вне связи с другими предметами — небом, землей, животными и т. д. А вот соединительный союз «и» — типичный представитель логической категории, или логический термин, так как он обозначает абстрактное соединение, т. е. соединение чего угодно, без привязки к каким-то определенным предметам. Какие еще логические термины часто встречаются в языке, будет указано в следующей лекции, а пока оставим логические категории в стороне.

Среди дескриптивных категорий основной является предложение — выражение законченной мысли. По цели высказывания выделяют три вида предложений: повествовательное, вопросительное, восклицательное. Главный из этих видов — первый.

В составе любого предложения имеются, как минимум, две дескриптивных категории: имя и признак. Имя — это выражение языка, называющее предмет, признак — знак наличия свойства. Например, в предложении «Земля круглая» слово «Земля» — имя, а слово «круглая» — признак. Две указанные категории присутствуют в предложении всегда, даже тогда, когда оно состоит из единственного слова. Так, в предложении «Темнеет» помимо высказанного признака «темнеет» имеется невысказанное имя «пространство».

Имена делят на единичные и общие. Единичное имя обозначает какой-то единичный, т.е. единственный и неповторимый, предмет, а общее — произвольный элемент какого-то множества. Например, имя «Земля» — единичное, а имя «планета» — общее. Впрочем, одно и то же выражение языка в одних случаях можно рассматривать как единичное имя, в других — как общее. Все зависит от того, что имеется в виду. Сравним две фразы: «Человек живет на Земле десятки тысяч лет» и «Человек рождается и умирает». Слово «человек» в первом случае использовано как единичное имя, обозначающее уникальный род живых существ, а во втором — как общее имя, которое указывает на произвольного представителя множества людей.

Что касается признака, то следует учитывать, что стандартно его выражают не менее чем двумя словами, причем первое из них — глагол-связка «быть». В приведенных выше предложениях этот глагол не высказан, а лишь подразумевается. Во многих западноевропейских языках такое построение предложений запрещено, а в русском встречается сплошь и рядом.

Русский глагол-связка «быть» в настоящем времени имеет две формы: «есть» (единственное число) и «суть» (множественное число третьего лица). Вторая форма — устаревшая, сейчас обычно используется лишь первая — и для единственного, и для множественного числа, но в логике для большей строгости высказываний сохранили обе формы. Например, предложение «Земля круглая» стандартно должно быть представлено как «Земля есть круглая», а предложение «Эти часы отстают» — как «Эти часы суть отстающие». Подробнее особенности стандартного выражения суждений освещены в рамках седьмой лекции.

Иногда помимо имен и признаков в составе предложений выделяют знаки свойств и отношений, причем под свойством понимается отличие предмета от других однородных предметов, а под отношением — отличие, присущее паре, тройке и т.д. разнородных предметов. Возьмем для примера такое вот предложение: «Лекция по логике идет в 225-й аудитории». Переведем в стандартную форму: «Лекция по логике есть идущая в 225-й аудитории». Все слова этого предложения можно распределить всего по двум категориям: имя «лекция по логике» и признак «есть идущая в 225-й аудитории». Но можно провести и другой, более детальный семантический анализ, согласно которому «лекция» и «аудитории» — имена, «по логике» и «225-й» — знаки свойств, а «… есть идущая в …» — знак отношения.

При записи последнего знака троеточиями обозначены два свободных места данного отношения, которые должны быть заняты какими-то разнородными предметами (в примере этими предметами являются лекция и аудитория). Такое отношение называется двухместным. Но бывают отношения и с большим количеством мест. Например, в предложении «Орел находится между Тулой и Курском» отношение «… находится между … и …» трехместное. Однако любое многоместное отношение можно свести к комбинации двухместных. Для последнего примера сделаем это так: «Тула находится с северной стороны от Орла, а Курск — с южной».

Статью про язык как знаковая сис я написал специально для тебя. Если ты хотел бы внести свой вклад в развии теории и практики, ты можешь написать коммент или статью отправив на мою почту в разделе контакты. Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое язык как знаковая сис и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Логика

Семантика | Понятия и категории

СЕМАНТИКА – дисциплина, изучающая знаки и знаковые системы с точки зрения их смысла; как правило, рассматривается в рамках семиотики (науки о знаковых системах) совместно с двумя другими ее разделами: синтактикой и прагматикой. Первая из них изучает отношения знаков между собой (синтаксис), вторая – отношения между знаками и производящими и интерпретирующими их субъектами, тогда как семантика рассматривает знаки в их отношении к обозначаемым (не имеющими знаковой природы) объектам. Наиболее важным предметом изучения для семантики является язык, а потому она входит в качестве составной части в лингвистику (как семантика естественного языка) и в логику (как семантика формальных языков). Возникающая и в логике, и в лингвистике семантическая проблематика является выражением общей философской проблемы связи мышления и бытия. Вопрос о том, в какой мере язык способен выразить неязыковую реальность, тесно коррелирован с вопросом о способности мысли понять внешний для нее предмет. Из основных взглядов на природу знака, лежащих в основе семантических построений, нужно выделить те, которые были сформулированы на рубеже 19 и 20 вв. в работах Г. Фреге и Ф. де Соссюра. Их концепции (в значительной мере противостоящие друг другу) и до сих пор определяют методы исследования и терминологию в лингвистике и логике. Фреге принадлежит теория тройственной природы языкового знака. Сам знак (единичный объект), во-первых, указывает на другой объект (значение знака), а во-вторых, на соответствующее означаемому объекту понятие (смысл знака).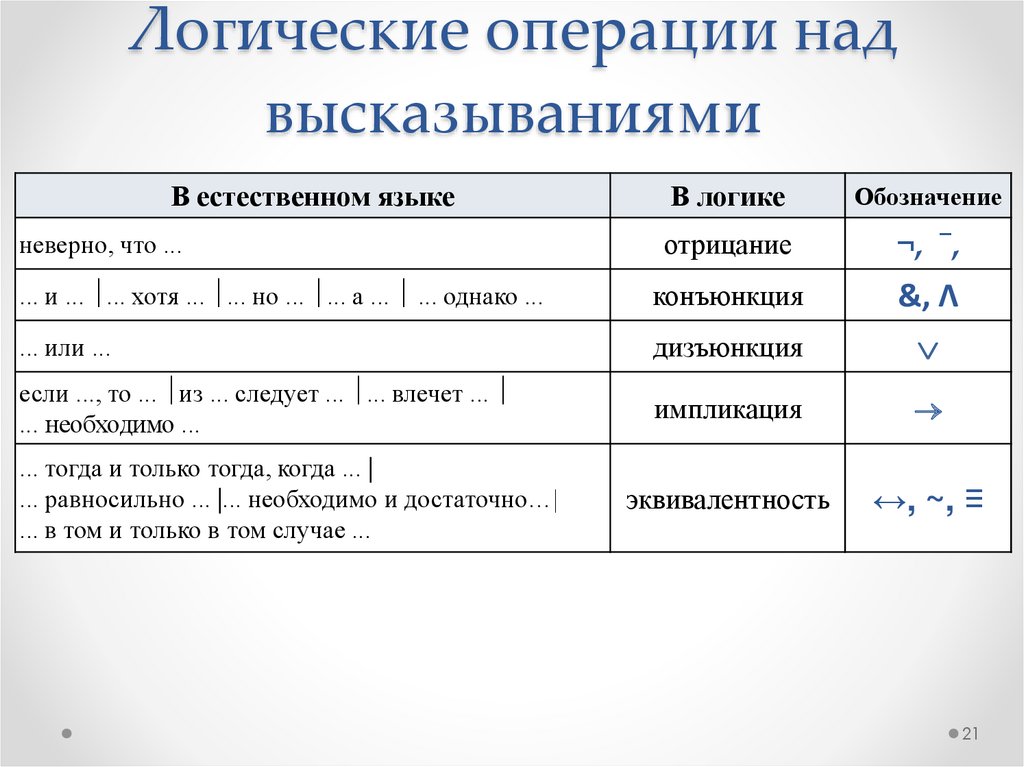 Введенное таким образом различение между смыслом и значением стало впоследствии ключевым для многих логических и лингвистических теорий, в которых, впрочем, была принята иная, нежели у Фреге, терминология. Для означаемого объекта используют термины «референт», «денотат», «десигнат». То, что Фреге назвал «смыслом», иногда называют «сигнификатом». Впрочем, интерпретация разными исследователями приведенных терминов сильно варьируется. Часто употребляемой для выражения введенного Фреге семантического различения является также пара «экстенсионал» – «интенсионал». Различение между смыслом и значением Фреге ввел также для предложений языка, утверждая, что для широкого класса предложений значением являются истинность или ложность. Он указал также на существование таких языковых конструкций, которые имеют смысл, но не имеют значения (напр., утверждения о вымышленных объектах).

Согласно Фреге, в основе любого мыслительного акта лежит стремление выразить сущность, самостоятельно существующий предмет, который обозначается в языке своим именем и о котором сказывает его понятие. Соссюр рассматривает природу знака как двойственную, называя знак единством означающего и означаемого. Под последним понимается именно то, что Фреге называл смыслом, но подход Соссюра в принципе иной. Семантические свойства языка определяются тем, что он представляет собой систему. Знаки существуют только в отношении друг к другу, и именно эти отношения, а не связь с внеязыковыми сущностями определяют смысл знака. Поэтому референциальная семантика вообще отсутствует у Соссюра. Эта позиция разделяется и до сих пор многими лингвистами (главным образом французскими). Греймас и Курте называют «исключение референта необходимым условием развития лингвистики».

Подход Соссюра является лингвистическим коррелятом той философской установки, которая стремится исключить из рассмотрения категорию сущности. Она была разработана, напр., в Марбургской школе, для философов которой критерием объективности знания является не отношение знания к «реально существующему» объекту (которое совершенно невозможно установить), а внутренняя согласованность самого знания.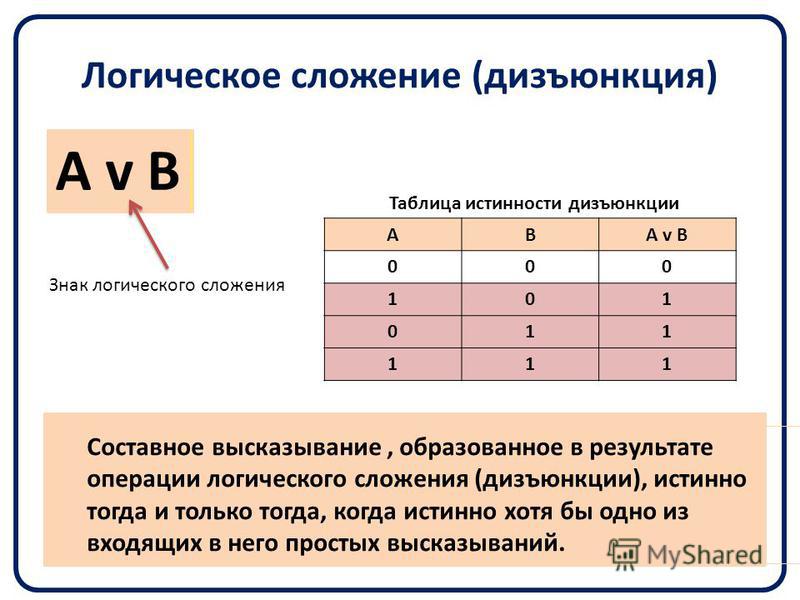 Последнее рассматривается как структура, т.е. совокупность отношений элементов, определяемых (подобно единицам языка у Соссюра) лишь своим местом в системе и отношениями друг с другом.

В логике и математике разработан аналитический аппарат, позволяющий описывать семантику формальных языков. В основе этого аппарата лежит понятие интерпретации. Последняя есть функция, которая сопоставляет каждому имени (индивидной константе) языка некоторый объект из заданного множества, а каждому выражению языка (предикатной константе) некоторое отношение объектов этого же множества. Важнейшим элементом семантики формальных языков является понятие истинности, которая рассматривается как формальное свойство правильно построенного выражения языка. Существенной в этом случае является необходимость введения метаязыка. Только с его помощью можно описать область объектов, задать интерпретирующую функцию и делать выводы относительно истинности языковых выражений. Формальные основания для различения объектного языка и метаязыка были получены А. Тарским. Последующее развитие логики (С. Крипке, Р.Мартин, П.Вудруфф) привело, однако, к построению «семантически замкнутых» языков, т.е. таких, которые сами содержат в себе возможности делать выводы о семантических свойствах (в частности, об истинности) языковых выражений. Однако общей особенностью любого формального подхода является необходимость выражать неязыковые объекты средствами языка (пусть даже метаязыка). Исследование семантики свойств оказывается поэтому исследованием отношений между знаками, а не отношений между знаком и объектом, не имеющим природы знака. Таким образом семантика обращается в синтактику.

При описании семантики естественного языка лингвисты также прибегают к понятию функциональной зависимости, реализуя схему, очень похожую на схему интерпретации формальных языков. При этом используется аппарат семантических категорий, введенный К.Айдукевичем (см. Семантических категорий теория). Простейшими категориями являются имя и предложение. Первое имеет в качестве экстенсионала объект, второе – значение истины или лжи.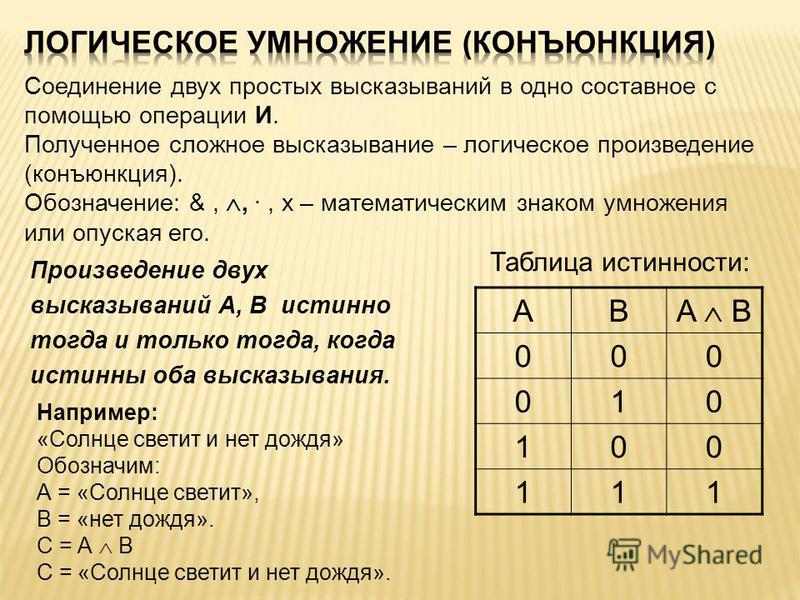 Интенсионал языкового знака, принадлежащего к этим категориям, есть функция (в строгом, теоретико-множественном смысле – Д.Льюис, а еще раньше Р.Карнап), ставящая ему в соответствие его экстенсионал. Более сложные категории получаются из простейших согласно правилам синтаксиса и должны включать все возможные грамматические формы. Их семантика определяется построением интенсионалов, которые также являются функциями, но уже более сложными. Природа интенсионала часто определяется по-разному. Н.Хомский, напр., видит в них врожденные схемы действия, присущие человеческой психике. Р.Монтегю представляет их объективными идеальными сущностями, которые схватываются сознанием.

По существу в логике, описывающей формальные языки, и в лингвистике, изучающей естественный язык, вводятся одни и те же процедуры: установление функциональной связи между выражениями языка и «реальными» объектами и отношениями. Однако логика (а в еще большей мере математика) требует явного описания (опять же с помощью языка) как функций, так и областей интерпретации. В лингвистике же, когда речь идет об интерпретирующей функции (интенсионале), может подразумеваться некоторая когнитивная операция (вовсе не описанная явно), совершаемая носителем языка, который производит и интерпретирует знаки. Поэтому если логика сближает семантику с синтактикой, то лингвистика обращает ее в прагматику. Эта «потеря» семантики возникает в тех теориях, которые разделяют существенный элемент учения Фреге: язык рассматривается как средство для выражения неязыковых сущностей, т.е. для представления объективной реальности. В таких теориях пытаются установить связь мысли с немыслимым, что порождает естественные трудности. Альтернативой фрегевского понимания семантики (помимо школы Соссюра, о которой сказано выше) является теория семантических примитивов (А. Вержбицка). Она прямо связана с учением Р. Декарта, о том, что всякая сложная идея сводима к простым, понятным интуитивно и не нуждающимся ни в каком прояснении. Еще большая зависимость обнаруживает теория семантических примитивов от философии Г. Лейбница, поскольку может быть представлена как развитие его попытки создания универсальной характеристики. По мысли Вержбицкой, всякий дискурс есть конструкция, построенная из достаточно простых элементов по известным правилам. Смысл любого языкового построения ясен в той мере, в какой прояснена процедура построения, а также смысл этих элементов. Последние же, называемые семантическими примитивами, ясны интуитивно. Их описание не требует прибегать к особым приемам (напр., к введению интенсионалов и экстенсионалов), поскольку их смысл абсолютно прозрачен и не нуждается в каком-либо выражении. Важно, что число этих примитивов невелико и их нумерация легко достижима.

Г.Б. Гутнер

Новая философская энциклопедия. В четырех томах. / Ин-т философии РАН. Научно-ред. совет: В.С. Степин, А.А. Гусейнов, Г.Ю. Семигин. М., Мысль, 2010, т. III, Н – С, с. 514-515.

Литература:

Шрейдер Ю.А. Логика знаковых систем. М., 1974;

Семиотика (сборник трудов; ред. Ю.С.Степанов). М., 1983;

Смирнова Е.Д. Логика и философия. М., 1996;

Соссюр Ф. Труды по языкознанию. М., 1977, с. 31–288;

Тондл Л. Проблемы семантики. М., 1975;

Фреге Г. Избранные работы. М., 1997, с. 25–49;

Wierzbicka A. Semantic Primitives. Fr./M., 1972.

Полный список логических символов

В философии и математике логика играет ключевую роль в формализации действительных дедуктивных выводов и других форм рассуждений. Ниже приводится полный список наиболее известных символов в логике, включающий символы из логики высказываний, логики предикатов, булевой логики и модальной логики.

Для удобства чтения эти символы разделены по функциям на таблицы . Другие полные списки символов — с разбивкой по темам и типам — также можно найти на соответствующих страницах ниже (или на панели навигации).

Содержание

Предпочитаете версию в формате PDF?

Получите основную сводку математических символов в форме электронной книги — вместе с использованием каждого символа и кодом LaTeX.

Да. Это было бы полезно.

Константы

В логике константы часто используются для обозначения определенных объектов в логической системе. В следующей таблице представлены наиболее примечательные из них, а также их соответствующий пример и значение.

‘ложь \land \lnot Q \equiv \bot$

Название символа	Объяснение	Пример
$ A, B, C $	General Constants (в пределах логической системы)	$ B \ GE_1 + A_1 + A_1 + A_1 + A_1 + A_1 + A_1 + A_1 + A_1 + A_1 + A_1 + A_1 + A_104444403 9003 9003 9003 9003 9004 4004 4003 9003 9003.	$\mathbb{B}$	Логическая область	В булевой логике $\mathbb{B} = \{ 0 ,1\}$.
$\top$ (или $1$ в булевой логике)	Тавтология , Значение истинности «истина»	$P \lor \lnot P \equiv \top$
$\bot$ (или $0$ в булевой логике)	Противоречие , $30 Значение истинности’

Переменные

Как и в других областях математики, переменных используются в качестве символов-заполнителей для различных объектов в логике. В следующей таблице представлены наиболее примечательные из них, а также их соответствующий пример и значение.

\gamta, alpha,mabe, \alpha, 9,009 , \phi, \psi$

Symbol Name	Explanation	Example
$x, y, w, z$	Quantification variables	$x_1 + x_2 = y$
$\mathbf {x}, \mathbf{y}, \mathbf{w}, \mathbf{z}$	Метапеременные для количественных переменных	Для всех переменных $\mathbf{x}_1$ и $\mathbf{x} _2$, ‘$\mathbf{x}_1 = \mathbf{x}_2$’ — это формула.
$f, g, h$	Функциональные символы	$h\left( f_1(x), g(x, y) \right)$
$\mathbf{s}, \mathbf{ t}$	Метапеременные для термов	Для всех термов $\mathbf{t}_1$ и $\mathbf{t}_2$, ‘$f(\mathbf{t}_1, \mathbf{t}_2 )$’ является термином.
$P, Q, R$	Пропозициональные / Предикатные символы	$P(x, a) \land Q_1(z)$
Метапеременные для формул	Для всех формул $\alpha$ и $\beta$, $\alpha \land \beta \equiv \beta \land \alpha$.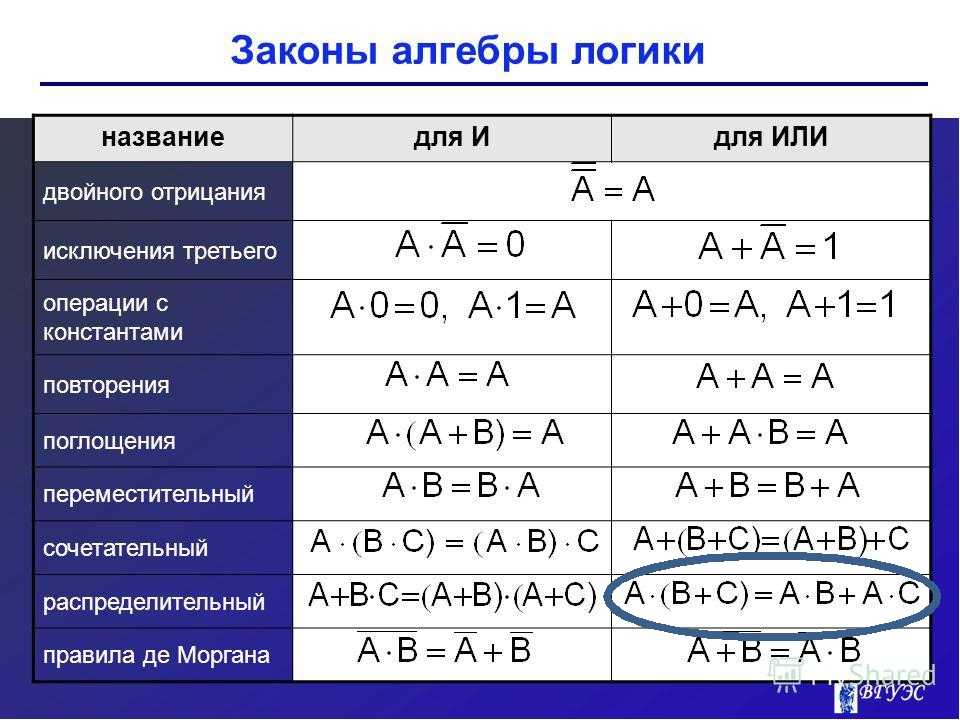
$\Sigma, \Phi, \Psi$	Метапеременные для наборов предложений	Если $\Sigma$ противоречива, то $\Sigma \cup \Phi$ несовместима.
$\mathcal{L}$	Метапеременная для формальных языков	формула в $\mathcal{L}$.

Операторы

Операторы — это символы, используемые для обозначения математических операций, которые служат для преобразования одного или нескольких входных данных в аналогичный выходной. В логике к этим операторам относятся логические связки из пропозициональной/модальной логики, кванторы из логики предикатов, а также другие операторы, связанные с синтаксической подстановкой и семантическим оцениванием.

Унарные логические связки

Имя символа	Пояснение	Пример
$\lnot P$, $\sim\!\!P$, $\overline{P}$	Отрицание $P$ (не $P$)	$\lnot \lnot P \equiv P$
$\Diamond P$	Возможно $P$	Если $\Diamond P$, то $\Diamond \Diamond P$.
$\Box P$	Обязательно $P$	Если $\Box P$, то $\neg \Diamond \neg P$.

двоичная логическая соединительная связь

. P \equiv P$ $P 92)$

Название символа	Объяснение	Пример
$ P \ LAND Q $	CONCUNCTION ($ P $	($ P $ Q $
$P \lor Q$	Дизъюнкция ($P$ или $Q$)	$\neg (P \lor Q) \equiv$ $\neg P \ земля \neg Q$
$P \veebar Q$, $P \oplus Q$	Эксклюзивная дизъюнкция ($P$ xor $Q$)	$P \oplus Q \equiv$ $(P \lor Q) \land \neg(P \land Q)$
$P \uparrow Q$	Отрицание конъюнкции ($P$ nand $Q$)	$P \uparrow Q \equiv \neg (P \land Q)$
$P \downarrow Q$	Отрицание дизъюнкция ($P$ или $Q$)	$P \downarrow Q \equiv \\ (\neg P \land \neg Q)$
$P \to Q$	Условное (Если $P$, то $Q$)	Для всех $P$, $P\to P$ является тавтологией.
$P \not\to Q$	Безусловный (Не ‘если $P$, то $Q$’)	$P \not\to Q \equiv P \land \neg Q$
$P \leftarrow Q$	Обратное условное (Если $Q$, то $P$)	$Q \leftarrow (P \land Q)$
not\leftarrow Q$	Обратное безусловное (Не ‘если $Q$, то $P$’)	$(P \to Q) \land \\ (P \not\leftarrow Q)$
$P \leftrightarrow Q$	Бикондиционал ($P$ тогда и только тогда, когда $Q$)	$P \leftrightarrow Q \equiv$ $(P \to Q) \land (P \leftarrow Q)$
$P \not \leftrightarrow Q$	Безусловный (Не ‘$P$ тогда и только тогда, когда $Q$’)	Если $P \not\to Q$, то $P \not\leftrightarrow Q$.
$\существует ! \mathbf{x}$	Квантификация уникальности (Существует единственный $\mathbf{x}$)	$\exists !\, q, r \in \mathbb{Z}\,$ $( n=dq+r \, \land$ $0 \le\|r\|
$\mathrm{N} \mathbf{x}$, $\nexists \mathbf{x}$	Квантификация несуществования ($\mathbf{x}$ не существует)	$\mathrm{N}x P(x) \equiv \\ \forall x \, \neg P(x)$
$\exists_n\mathbf{x}$	Численная квантификация (имеется ровно $n$ $\mathbf{x}$)	$\exists_3 x \in \mathbb{Z}\, (5 < x < 9)$
$ \exists_{\ge n} \mathbf{x}$	Числовая квантификация (Существует не менее $n$ $\mathbf{x}$)	$\exists_{\ge 2} x \, Q (x) \equiv$ $\exists x \exists y \, (Q(x) \land$ $Q(y) \land x \ne y)$
$\exists_{\le n} \mathbf{x}$	Численный количественный анализ 92 + 5$
$\mathbf{\alpha}[\mathbf{x}/\mathbf{t_0}]$	Формула подстановки (формула $\mathbf{\alpha}$ со свободными вхождениями $\mathbf{x}$ заменяется термином $\mathbf{t_0}$)	$(\forall x (x = y)) [x/a] =$ $\forall x (x = y)$

Операторы на основе оценки

$tigma ^

Символ Название	Объяснение	Пример
{\ сигма (х / и)} = \ топ $.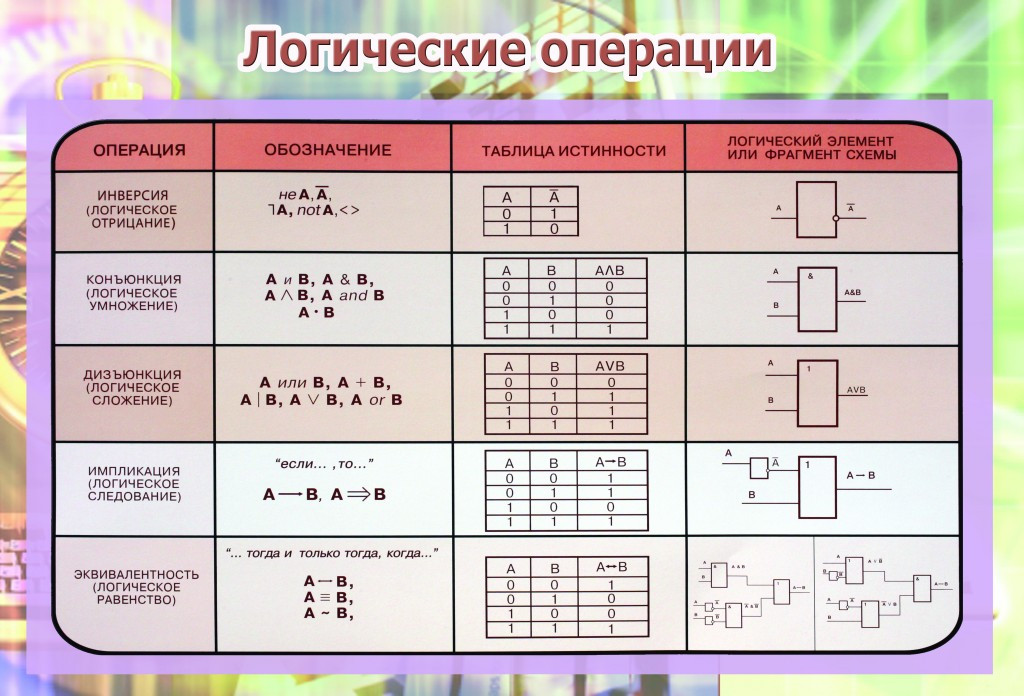

Реляционные символы

В логике реляционные символы играют ключевую роль в превращении одной или нескольких математических единиц в формулы и предложения и могут встречаться как внутри логической системы, так и вне ее (как металогические символы). В следующей таблице представлены наиболее примечательные из этих символов, а также их соответствующее значение и пример.

9{\sigma} = \top$, затем $\sigma\models\phi$.

Символ Название	Пояснение	Пример
$\mathbf{t}_1 = \mathbf{t}_2$	Идентификационный символ в логической системе с равенством	‘1($\neg \left ) \right)$’ — формула языка арифметики первого порядка.
$\альфа\! \ подразумевает \! \beta$	Предложение $\alpha$ подразумевает предложение $\beta$	$\forall x \, (x \ge 1) \! \подразумевает 1 \ge 1$
$\альфа \! \подразумевается\! \бета$	Предложение $\alpha$ следует из предложения $\beta$	$5 \mid x \! \подразумевается\! 5 \mid 7x$
$\alpha \equiv \beta$, $\alpha \Leftrightarrow \beta$, $\alpha \! \ифф\! \beta$	Предложения $\alpha$ и $\beta$ логически эквивалентны	$\neg (P \to Q) \equiv \\ P \land \neg Q$
$\sigma \ модели \alpha$	Оценка $\sigma$ удовлетворяет формуле $\alpha$
$\Phi \models \phi$	Множество предложений $\Phi$ влечет за собой предложения $\phi$ ($\phi$ является логическим следствием $\Phi$)	Если $\ Phi\models\phi$, затем $\Phi\cup\Psi\models\phi$.
$\Phi \nvDash \phi$	Набор предложений $\Phi$ не влечет за собой предложение $\phi$	$\{P \to Q, Q \to R \} \nvDash R $
$\модели\фи$	Предложение $\phi$ является тавтологией	$\models \forall x \, (x = x)$
$\Phi \vdash \phi$	Набор предложений $\Phi$ доказывает предложения $\phi$	$\forall x \, P(x,a) \vdash \\ P(a,a)$
$\Phi \nvdash \phi$	Набор предложений $ \Phi$ не доказывает предложения $\phi$	$\exists x \, R(x) \nvdash R(a)$
$\vdash \phi$	{\circ}$
$\Phi \следовательно \phi$	$\Phi$, следовательно $\phi$	$P \lor Q, \neg P \\ \следовательно Q$

Основной список символов см.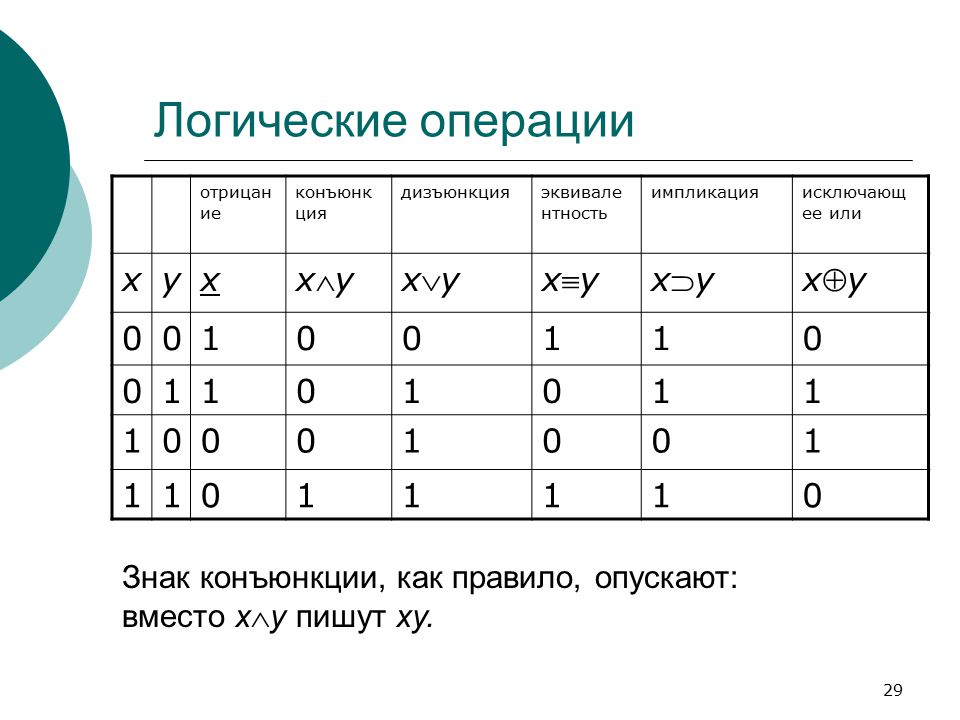 в разделе математические символы. Списки символов, классифицированных по типу и предмету , см. на соответствующих страницах ниже.

Предпочитаете версию в формате PDF?

Получите основную сводку математических символов в электронной книге , форма — вместе с использованием каждого символа и кодом LaTeX.

Да. Это было бы полезно.

Дополнительные ресурсы

Полное руководство по изучению высшей математики : Автономная система из 10 принципов для эффективного обучения математике, мышления и решения задач
Ultimate LaTeX Reference Guide : Полное справочное руководство для создания процесс более упорядоченный, более эффективный и менее болезненный
Введение в логику первого порядка — синтаксис и семантика : 8-страничный учебник о том, как формулы первого порядка строятся из примитивных символов и как они интерпретируются в результате
Расчет высказываний Bell & Machover — ключевые понятия & Structural Rules : 9-страничное введение в систему аксиоматического линейного доказательства в логике высказываний, а также ее 3 схемы аксиом и 12 правил структурного вывода

Логические символы — Citizendium

Содержание этой страницы создано в Википедии и еще не было значительно улучшено. Авторам предлагается заменить и добавить материал, чтобы сделать эту статью оригинальной.

В логике базовый набор логических символов используется как сокращение для логических конструкций. Поскольку эти символы часто считаются знакомыми, они не всегда объясняются. Для удобства в следующей таблице перечислены некоторые распространенные символы вместе с их названиями, произношением и соответствующими областями математики. Кроме того, в третьем столбце содержится неформальное определение, а в четвертом столбце приведен краткий пример.

Имейте в виду, что вне логики разные символы имеют одно и то же значение, а один и тот же символ имеет, в зависимости от контекста, разные значения.

Примечание : Эта статья содержит логические символы. Без надлежащей поддержки рендеринга вы можете увидеть вопросительные знаки, прямоугольники или другие символы вместо логических символов.

908:30

Символ	Имя	Пояснение	примеров	Юникод Значение	HTML Сущность	LaTeX символ
	Следует читать как
	Категория
	материальное значение	A ⇒ B означает, что если A верно, то B также верно; если A ложно, то о B ничего не говорится. → может означать то же, что и ⇒ (символ может также указывать домен и домен функции; см. таблицу математических символов). ⊃ может означать то же, что и ⇒ (символ может также означать надмножество).	x = 2 ⇒ x ² = 4 верно, но x ² = 4 ⇒ x = 2 в общем случае может быть 0 x	.	U+21D2 U+2192 U+2283	⇒ → &up;	⇒ {\ displaystyle \ Rightarrow} \ Rightarrow → {\ displaystyle \ to} \ to ⊃ {\ Displaystyle \ расстроен} \ расстроен
	подразумевает; если .. то
	логика высказываний, алгебра Гейтинга
	эквивалент материала	A ⇔ B означает, что A истинно тогда и только тогда, когда B истинно.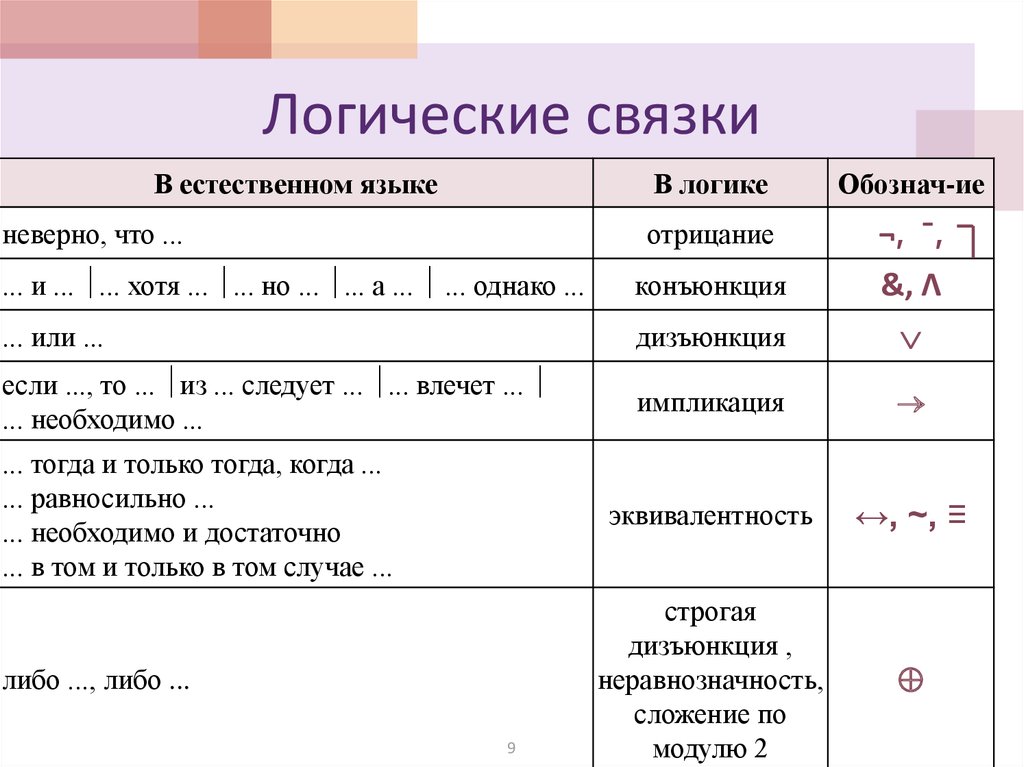	x + 5 = y +2 ⇔ x + 3 = y	U+21D4 U+2261 U+2194	⇔ &эквивалент; ↔	⇔ {\ Displaystyle \ Leftrightarrow} \ Leftrightarrow ≡ {\ Displaystyle \ эквив} \ эквив ↔ {\ Displaystyle \ Leftrightarrow} \ Leftrightarrow
	тогда и только тогда, когда; если
	пропозициональная логика
	отрицание	Утверждение ¬ A истинно тогда и только тогда, когда A ложно. Косая черта, помещенная через другой оператор, аналогична «¬», помещенной впереди.	¬(¬ A ) ⇔ A x ≠ y ⇔ ¬( x = y )	U+00AC U+02DC	&нет; &тильда; ~	¬{\ displaystyle \ lnot} \ lnot ∼ {\ displaystyle \ sim} \ sim
	нет
	пропозициональная логика
	логическое соединение	Заявление A ∧ B верно, если A и B оба верны; иначе это ложь.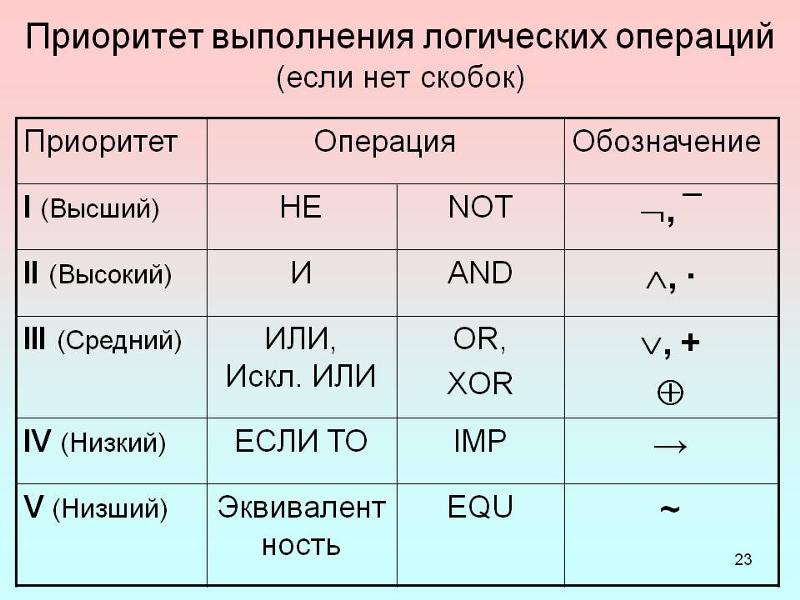	n < 4 ∧ n >2 ⇔ n = 3, когда n является натуральным числом.	и+2227 и+0026	&и; &ампер;	∧ {\ Displaystyle \ клин} \ клин или \ земля \ & ^[1]
	и
	пропозициональная логика
	логическая дизъюнкция	Утверждение A ∨ B истинно, если A или B (или оба) верны; если оба ложны, утверждение ложно.	n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3, когда n — натуральное число.	U+2228	&или;	∨{\ Displaystyle \ лор} \ лор
	или
	пропозициональная логика
	исключительная дизъюнкция	Утверждение A ⊕ B истинно, когда истинны либо A, либо B, но не оба. A ⊻ B означает то же самое.	(¬ A ) ⊕ A всегда верно, A ⊕ A всегда ложно.	У+2295 У+22ББ	+	⊕ {\ displaystyle \ oplus} \ oplus ⊻ {\ displaystyle \ veebar} \ veebar
	хор
	логика высказываний, булева алгебра
	Тавтология	Утверждение ⊤ безусловно истинно.	A ⇒ ⊤ всегда верно.	У+22А4	т	⊤{\ displaystyle \ top} \ top
	верх
	логика высказываний, булева алгебра
	Противоречие	Утверждение ⊥ безусловно ложно.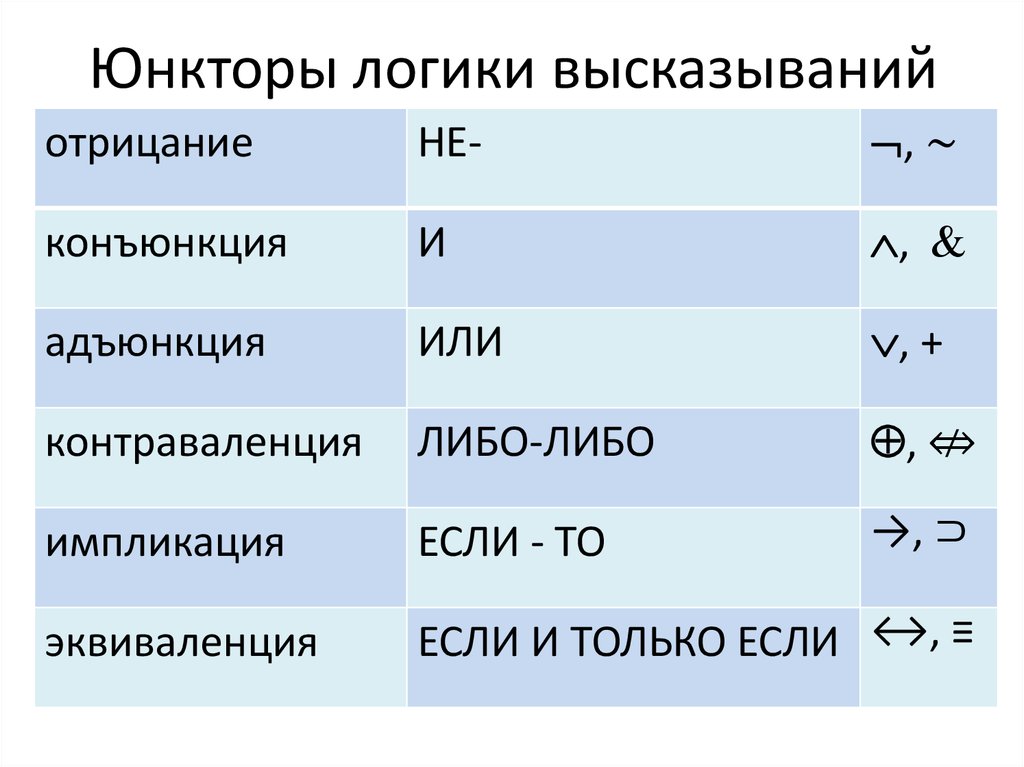	⊥ ⇒ всегда верно.	У+22А5	% Ф	⊥{\ Displaystyle \ бот} \ бот
	дно
	логика высказываний, булева алгебра
∀	универсальный количественный анализ	∀ x : P ( x ) означает P ( x ) верно для всех х .	∀ n ∈ N : n ² ≥ n .	У+2200	∀	∀{\ displaystyle \ forall} \ forall
	для всех; для любого; для каждого
	логика предикатов
∃	экзистенциальная квантификация	∃ x : P ( x ) означает наличие хотя бы одного x , так что P ( x ) истинно.	∃ n ∈ N : n четно.	U+2203	&существовать;	∃ {\ Displaystyle \ существует} \ существует
	существует
	логика первого порядка
∃!	количественная оценка уникальности	∃! x : P ( x ) означает ровно одну x , так что P ( x ) верно.	∃! n ∈ N : n + 5 = 2 n .	U+2203 U+0021	&существовать; !	∃! {\ Displaystyle \ существует!} \ существует!
	существует ровно один
	логика первого порядка
	определение	x := y или x ≡ y означает, что x определяется как другое имя для y (но обратите внимание, что ≡ может также означать другие вещи, такие как конгруэнтность). P :⇔ Q означает, что P определяется как логически эквивалентный Q .	COSH x : = (1/2) (exp x + exp ( — x )) A XOR B : ⇔ ( A ∨ B ) ⇔ A ∨ B ) ( A ∨ B ) ( A ∨ B ). ∧ Б )	U+2254 (U+003A U+003D) U+2261 U+003A U+229C	:= : &экв; ⇔	: = {\ Displaystyle: =}: = ≡ {\ Displaystyle \ эквив} \ эквив ⇔ {\ Displaystyle \ Leftrightarrow} \ Leftrightarrow
	определяется как
	везде
( )	группировка по приоритету	Сначала выполните операции внутри скобок.	(8/4)/2 = 2/2 = 1, но 8/(4/2) = 8/2 = 4.	U+0028 U+0029	( )	( ) {\ Displaystyle (~)} ( )

	везде
⊢	вывод	x ⊢ y означает, что y получено из x .	А → В ⊢ ¬ В → ¬ А	У+22А2	⊢{\ Displaystyle \ vdash} \ vdash
	предполагает или является производным от
	логика высказываний, логика первого порядка

↑ Хотя этот символ доступен в LaTeX, система Mediawiki TeX не поддерживает этот символ.

Таблица логических математических символов | Justfreetools

Чтение логических символов пугает многих людей больше, чем следовало бы. Сам термин «символическая логика» звучит устрашающе, и наличие даже небольшой доли символизма может отпугнуть многих читателей от текстов, которые в противном случае были бы вполне понятны. Следующее объяснение знакомит с символикой, используемой в этой работе, и перечисляет некоторые вариации, которые могут встречаться в других работах. Следует отметить, что технические термины, используемые в этом приложении, также объясняются под их собственными заголовками в основной части словаря, и там, где это уместно, даны перекрестные ссылки.

Строчные курсивные буквы из этой части алфавита: p , q , r …, используются как пропозициональные переменные. Это означает, что они обозначают предложения или утверждения. Некоторым логикам не нравятся эти категории, и они предпочитают называть их буквами предложения или сентенциальными переменными. В любом случае они возникают там, где можно заменить предложение, так же как x и y в алгебре стоят там, где можно заменить выражение для числа. Утверждение типа «Если кто-то считает, что p и q тогда он считает, что p ‘ говорит, что в любом случае, в котором кто-то верит соединению (например, «Идет дождь и ветрено», то этот человек верит его отдельным частям (что это встречаются заглавные буквы (P, Q,…) или курсивные прописные P , Q ,…

Строчные курсивные буквы с конца алфавита: x , y , z … используются как объектные переменные. Это означает, что они стоят там, где может иметь место ссылка на человека, вещь или число. Используя такую переменную, приведенный выше пример можно было бы сформулировать так: «Если x считает, что p и q , тогда x считает, что p ’, где x обозначает любого человека. Это обозначение является практически универсальным, хотя типографский вид переменных различается.

Как и в обычной математике, строчные латинские буквы, особенно n, k, j…, используются в контексте для обозначения определенных чисел. С самого начала алфавита a, b, c… также являются отдельными константами или терминами, используемыми в контексте для обозначения определенных вещей или людей. Фа означает, что некоторая конкретная вещь, а, есть F и, следовательно, является самостоятельным предложением, истинным или ложным, в зависимости от обстоятельств. Ф x – нет, потому что переменная 90 799 x ничего не выделяет.

Заглавные латинские буквы F, G, R обозначают предикаты и выражения отношений. Конкретные их примеры являются стандартными: например, тождество (=), неидентичность (≠), больше и меньше (>, <) и другие математические отношения. По обычному соглашению сказуемые буквы стоят перед терминами, к которым они применяются. Fn означает, что n равно F; Rab означает, что a имеет отношение R к b. В некоторых работах это будет написано aRb.

Наиболее простыми отношениями между предложениями, изучаемыми в логике, являются функции истинности. К ним относятся:

Не . Не- р является отрицанием р. В классическом понимании ложным является утверждение, когда p истинно, и наоборот. В этой работе написано не- p в неформальном контексте, а ¬ p в более формальном контексте. Это означает то же самое. Встречающиеся варианты включают — p и ~ стр.

А. p и q – это соединение двух предложений. Это истинно тогда и только тогда, когда они оба истинны. В этой работе написано p и q . Встречающиеся варианты включают p · q и, чаще, p ∧ q .

Или . p или q — это дизъюнкция двух предложений. Оно истинно тогда и только тогда, когда истинно хотя бы одно из них. В этой работе написано p ∨ q , и это стандарт. Иногда встречается исключительная дизъюнкция, означающая, что одно из p , q , но не оба оба, пишется p ⊻ q.

Значение . Логика изучает различные виды следствий. Самый простой из них называется материальной импликацией. Здесь написано p → q . Наиболее распространенный вариант – 90 799 p 90 800 ⊃ q 90 800 .

Эквивалентность 908:00 . Если p → q и q → p , то p и q называются эквивалентными (у них одинаковое истинностное значение). Неофициально это часто выражается как p iff q . Написано p ↔ q . Наиболее распространенная альтернатива: p ≡ q .

Это основной набор функций истинности, в терминах которых обычно определяются другие. В исчислении предикатов изучается внутренняя структура предложений, а также отношения между ними. Ключевыми понятиями являются два квантификатора:

Универсальный квантификатор . В этой работе это написано ∀. (∀ x )F x означает, что все является F. Возможные варианты включают (A x )F x и ( x )F x .

Квантор существования . В данной работе это написано ∃. (∃ x )F x означает, что что-то является F. Основное изменение, которое может встречаться, это (E x )F x .

В исчислении предикатов могут быть определены числовые кванторы, например (∃n x )(F x ) означает, что существует n x таких, что F x. Основная вариация (∃! x )F x (называется E-sriek x), что означает, что существует ровно одно x такое, что x является F.

Термины могут быть определены из определенных описаний . Основные встречающиеся примеры: (1 x )F x (уникальное x такое, что x является F) и (µ x )F x (наименьшее x 90 800 такое, что 90 799 x 90 800 равно F).

Модальная логика изучает понятие необходимости или возможности предложений. Основные обозначения:

Обязательно p . Написано □ р . Основная вариация — N p .

Возможно стр . Написано ⋄ стр . Основная вариация М р .

В *метатеории или теории логических систем предметом обсуждения становятся формулы и их отношения. В этой работе заглавные буквы A, B являются переменными для формул, где A1…An относится к последовательности формул. В других произведениях может встречаться греческий язык в различных формах (α, β…). Основные отношения, которые имеют значение:

Существует доказательство B из A. Стандартно это записывается как A ⊦ B.

B истинно во всех интерпретациях, в которых A истинно. Обычно это записывается A ⊧ B.

В традиционной или аристотелевской логике не существует такого же набора понятий. Предполагается, что предложения состоят из терминов, таких как подлежащее и сказуемое, или среднего термина силлогизма. В этой работе для них используются заглавные латинские буквы (S, P, M). Теория множеств вводит небольшой новый набор фундаментальных терминов:

{ x : F x } относится к набору объектов x , которые соответствуют условию F. Теперь это стандарт. На множество также можно ссылаться, перечисляя его элементы («расширенно»): {a, b, c} — это множество, элементами которого являются a, b и c.

Набор без элементов или нулевой набор записывается как ∅. Более старая вариация — ∧.

Сами наборы обозначаются заглавными буквами S, T и т. д. Возможны различные типографские варианты.

∈ обозначает принадлежность к множеству. x ∈ S означает, что x является элементом множества S.

x ∈ { y : G y } означает, что x элементов, являющихся элементом множества G .

<…> относится к упорядоченному n-кортежу.

Основные понятия, используемые для построения множеств, включают:

Пересечение . S Союз . S ∪ R — это множество вещей, принадлежащих либо S, либо R. Это тоже стандартно.

Дополнение 908:00 . S̄ — это множество вещей, не принадлежащих S.

Декартово произведение . S×R — это множество упорядоченных пар, первый член которых принадлежит S, а второй — R.

Отношения между множествами включают: что S ⊆ S).

Собственное подмножество : S ⊂ R означает, что S включено в R (это подмножество, но не идентичное R).

Основные нестандартные обозначения, с которыми можно столкнуться, – это польские обозначения, которые объясняются в основной части словаря, а также подстановочная квантификация и ее обозначения.

В настоящее время у нас есть около 5611 калькуляторов, таблиц преобразования и полезных онлайн-инструментов и программных функций для студентов, преподавателей и преподавателей, дизайнеров и просто для всех.

Вы можете найти на этой странице финансовые калькуляторы, ипотечные калькуляторы, калькуляторы для кредитов, калькуляторы автокредита и калькуляторы лизинга, калькуляторы процентов, калькуляторы выплат, пенсионные калькуляторы, калькуляторы амортизации, инвестиционные калькуляторы, калькуляторы инфляции, калькуляторы финансов, калькуляторы подоходного налога , калькуляторы сложных процентов, калькулятор зарплаты, калькулятор процентной ставки, калькулятор налога с продаж, калькуляторы фитнеса и здоровья, калькулятор ИМТ, калькуляторы калорий, калькулятор жировых отложений, калькулятор BMR, калькулятор идеального веса, калькулятор темпа, калькулятор беременности, калькулятор зачатия беременности, срок родов калькулятор, математические калькуляторы, научный калькулятор, калькулятор дробей, калькулятор процентов, генератор случайных чисел, калькулятор треугольника, калькулятор стандартного отклонения, другие калькуляторы, калькулятор возраста, калькулятор даты, калькулятор времени, калькулятор часов, калькулятор среднего балла, калькулятор оценок, конкретный калькулятор, подсеть калькулятор, генератор паролей калькулятор преобразования tor и многие другие инструменты, а также для редактирования и форматирования текста, загрузки видео с Facebook (мы создали один из самых известных онлайн-инструментов для загрузки видео с Facebook). Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других сайтов социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все видео, которые вы загружаете, загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, ALT-кодах для Mac, Windows и Linux и других полезных советах и инструментах (как написать смайлики онлайн и т. д.)

Есть много очень полезных бесплатных онлайн-инструментов, и мы будем рады, если вы поделитесь нашей страницей с другими или пришлете нам какие-либо предложения по другим инструментам, которые придут вам на ум. Также, если вы обнаружите, что какой-либо из наших инструментов не работает должным образом или нуждается в лучшем переводе, сообщите нам об этом. Наши инструменты сделают вашу жизнь проще или просто помогут вам выполнять свою работу или обязанности быстрее и эффективнее.

Ниже приведены наиболее часто используемые многими пользователями по всему миру.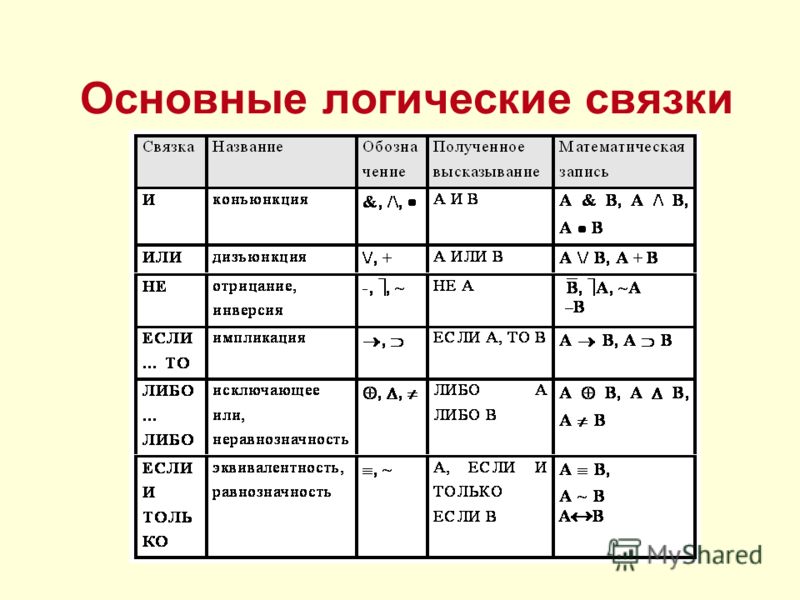

Бесплатные онлайн калькуляторы и инструменты
Калькуляторы часовых поясов/часов/дат
Бесплатные онлайн калькуляторы перевода единиц
Бесплатные онлайн инструменты для веб-дизайна
Бесплатные онлайн инструменты для электричества и электроники

Инструменты PDF
Код
Экология
Другое
Бесплатные онлайн-загрузчики для социальных сетей
Числа
Алгебра
Trigonometry
Probability & Statistics
Calculus & analysis
Mathematical symbols
Algebra symbols
Asterisk sign
Basic math symbols
Calculus symbols
Division sign
Equals sign
Geometry symbols
Greek alphabet
Символ бесконечности
Символ бесконечности ALT-код
Символ бесконечности в MS Word
Символ бесконечности на Facebook
Infinity symbol on keyboard
Infinity symbol on mac
Is infinity a real number
Logic symbols
Minus sign
Multiplication dot
Number symbols
Plus sign
Roman numerals
Set theory symbols
Статистические символы
Знак времени

И мы продолжаем развивать дальше.