1 n 2 сумма ряда – Как найти сумму ряда: примеры решений, определение

Как найти сумму ряда: примеры решений, определение

Общий член ряда представляе собой рациональную дробь. Выполним разложение дроби на простейшие с помощью метода неопределенных коэффициентов:

$$ \frac{1}{(2n+1)(2n+3)} = \frac{A}{2n+1} + \frac{B}{2n+3} = \frac{A(2n+3)+B(2n+1)}{(2n+1)(2n+3)} $$

Приравниваем числитель последней дроби к числителю первой дроби:

$$ A(2n+3)+B(2n+1) = 1 $$

Раскрываем скобки:

$$ 2An + 3A + 2Bn + B = 1 $$

Теперь определяем находим неизвестные коэффициенты:

$$ \begin{cases} n^0: &2A+2B=0 \\ n^1: &3A+B=1 \end{cases}\Rightarrow \begin{cases} A=\frac{1}{2} \\ B=-\frac{1}{2} \end{cases} $$

После разложения общий член ряда записывается следующим образом:

$$ a_n =\frac{1}{(2n+1)(2n+3)}=\frac{1}{2} \frac{1}{2n+1} — \frac{1}{2} \frac{1}{2n+3} $$

Далее составим частичную сумму ряда: $$ S_n = a_1 + a_2 + a_3 + a_4 + … + a_n $$

$$ a_1 = \frac{1}{2} \bigg (\frac{1}{3}-\frac{1}{5}\bigg ) $$

$$ a_2 = \frac{1}{2} \bigg (\frac{1}{5}-\frac{1}{7}\bigg ) $$

$$ a_3 = \frac{1}{2} \bigg (\frac{1}{7}-\frac{1}{9}\bigg ) $$

$$ …………………………………. $$

$$ a_{n-1}=\frac{1}{2} \bigg (\frac{1}{2n-1}-\frac{1}{2n+1} \bigg ) $$

$$ a_n = \frac{1}{2} \bigg (\frac{1}{2n+1}-\frac{1}{2n+3} \bigg ) $$

Замечание

Достаточно часто читатели нам присылают просьбы найти суммы своих рядов по причине того, что они не понимают, откуда получается $ a_{n-1} $. Обратите внимание, чтобы составить $ a_{n-1} $ необходимо подставить в $ a_n $ вместо буковки $ n $ выражение $ n-1 $. После выполнить раскрытие скобок.

Итого, получаем:

$$ S_n = \frac{1}{2} \bigg (\frac{1}{3}-\frac{1}{5}\bigg ) + \frac{1}{2} \bigg (\frac{1}{5}-\frac{1}{7}\bigg ) + \frac{1}{2} \bigg (\frac{1}{7}-\frac{1}{9}\bigg ) + … $$

$$ … + \frac{1}{2} \bigg (\frac{1}{2n-1}-\frac{1}{2n+1} \bigg ) + \frac{1}{2} \bigg (\frac{1}{2n+1}-\frac{1}{2n+3} \bigg ) = $$

Выносим дробь одну вторую $ \frac{1}{2} $ за скобки:

$$ = \frac{1}{2} \bigg (\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-\frac{1}{9} … + $$

$$ + … \frac{1}{2n-1} — \frac{1}{2n+1} + \frac{1}{2n+1} — \frac{1}{2n+3} \bigg) = $$

Замечаем, что в скобках есть подобные слагаемые, которые взаимно уничтожаются. Остаются только лишь два из них:

$$ S_n = \frac{1}{2}\bigg (\frac{1}{3}-\frac{1}{2n+3} \bigg ) $$

Теперь осталось вычислить предел частичной суммы $ S_n $. Если он существует и конечен, то он является суммой ряда, а сам ряд сходится:

$$ S=\lim_{n\to\infty} S_n = \lim_{n\to\infty} \frac{1}{2}\bigg (\frac{1}{3}-\frac{1}{2n+3} \bigg ) = $$

$$ = \frac{1}{2} \lim_{n\to\infty} \bigg (\frac{1}{3}-\frac{1}{2n+3} \bigg ) = \frac{1}{2} \cdot \frac{1}{3} = \frac{1}{6} $$

xn--24-6kcaa2awqnc8dd.xn--p1ai

Сумма числового ряда. Сходимость ряда. Решение рядов

Онлайн сервис Math34.biz поможет найти сумму ряда онлайн как числовой последовательности, так и функционального ряда.                                                     Сумма ряда для математиков есть нечто особое в понимании анализа числовых величин и предельного перехода. Про общее решение рядов сказано и написано очень много полезных трудов за прошедшие несколько столетий. Лично для каждого преподавателя служит важным долгом донести свои накопленные знания в математике до конечного слушателя, то есть студента. Искать проще простого такую сумму ряда 1/n. Будет вам сумма ряда 1/n^2 представлена в краткой записи. И искомая сумма конечного ряда найдется сразу на сайте Math34.biz. Наряду с определением суммы ряда онлайн последовательности числовой, сайт в онлайн режиме может найти так называемую частичную сумму ряда. Однозначно это поможет для аналитических представлений, когда сумму ряда онлайн нужно выразить и найти как решение лимита числовой последовательности частичных сумм ряда. По свое сути сумма ряда есть не что иное, как обратная операция разложения функции в ряд. Операции практически взаимные по природе. Так уж сложилось, что сходимость ряда изучается после прохождения курса лекции в математическом анализе после пределов. Найденное решение рядов означает результат исследования его на сходимость или расходимость. Этот результат определяется однозначно. В сравнении с аналогами, Math34.biz имеет свои неоспоримые преимущества, потому что умеет найти сумму ряда онлайн как числового, так и функционального ряда, что позволяет однозначно определять область сходимости начального исходного ряда, применяя практически все известные науке методологии. Опираясь на теорию рядов, необходимым во все времена условием сходимости последовательности числовой будет равенство нулю лимита общего члена числового ряда на бесконечности. Но это условие является не достаточным при установлении сходимости числового ряда онлайн. Немного отвлечемся от насущной проблемы и порассуждаем с другой философской позиции по поводу рядов в математике. Для вас это решение рядов онлайн позволит стать наилучшим калькулятором и помощником на каждый день. Совсем не охота просиживать прекрасные зимние деньки за уроками, когда сумма ряда находится в два счета прямо на ваших глазах. Если понадобится кому-то определить ту самую ходимость ряда, то потребуется несколько секунд после предварительного ввода правильных данных. В то время, как аналогичные сайты требуют вознаграждения за свои услуги, мы стараемся быть полезными каждому желающему попробовать научиться самому решать примеры, используя наш простой сервис. На ваше усмотрение мы можем представить решение рядов в онлайн режиме на любом современном устройстве, то есть в любом браузере. В случае расхождения ряда онлайн, сайт Math34.biz покажет соответствующее этому факту сообщение. Так вот найти и доказать, что сумма ряда 1/n на бесконечности расходится — будет простым заданием. Навсегда запомните, как сумма ряда 1/n^2 сходится и имеет в математике огромное смысловое значение. А вот сумма конечного ряда обычно определяется после использования, например, интегрального признака или признака Раабе, о котором мало кто знает в рядовых вузах. По определению сходимости рядов онлайн учеными выведены разные достаточные признаки сходимости или расходимости ряда. Более известны и часто применяемы из этим методов — это признаки Д’Аламбера, признак сходимости Коши, признак сходимости Раабе, признак сравнения числовых рядов, а также интегральный признак сходимости числового ряда. Заслуживают особого внимания такие числовые ряды, у которых знаки слагаемых обязательно строго чередуются друг за другом с минуса на плюс и обратно, а абсолютные величины этих числовых рядов убывают монотонно, то есть равномерно. На практике изучения рядов оказалось, что для таких числовых рядов необходимый признак сходимости знакопеременного ряда онлайн является достаточным, то есть равенство нулю лимита общего члена числового ряда на бесконечности. Найденная сумма ряда таким способом оказывается равносильно другим применяемым методам. Сходимость ряда занимает колоссальную трату времени, так как сам процесс предполагает полное исследование функции. Решение рядов онлайн на сайте Math34.biz обеспечивает максимальную точность в расчетах. Есть много разных сайтов, которые представляют сервисы вычисления суммы ряда онлайн, а также разложения функций в ряд в режиме онлайн в любой точке из области определения исследуемой функции. Разложить функцию в ряд онлайн в этих сервисах можно без труда, так как используется функционал вычисления производной, а вот обратная операция — найти сумму функционального онлайн ряда, членами которого являются не числа, а функции, не редко бывает невозможным на практике в силу трудностей, возникающих на почве отсутствия необходимых вычислительных ресурсов. Для пользователей сайта Math34.biz таких сложностей просто не существует. Используйте наш ресурс для вычислений суммы рядов онлайн, проверки и закрепления своих знаний. Если же сумма ряда расходится, то мы не получим ожидаемого результата для дальнейших действий в какой-то общей задачей. Этого можно заранее избежать, применяя свои знания как специалиста. Напоследок нельзя не упомянуть как сумма ряда 1/n самая простая в выражении и ее часто приводят в пример. Даже когда хотят показать некоторый признак сходимости в деле, то доказывают это для суммы ряда 1/n^2, потому что прозрачно для учеников такое представление и не путаются студенты. Поскольку имеем выражение для сложного общего члена ряда, то сумма конечного ряда была бы полезна, если будет доказано для мажорирующего ряда (относительно исходного) его сходимость. С другой стороны сходимость ряда будет происходить независимо от начальных условий задачи. Лучшее решение рядов может предложить только наш сервис Math34.biz, потому что только мы гарантируем экономию вашего времени, соотнеся траты на вычисление с полезность и точностью результата. Поскольку искомая сумма ряда представима в большинстве случаев мажорирующим рядом, то как раз целесообразнее исследовать именно его. Отсюда сходимость ряда от мажорирующего общего члена однозначно укажет на сходимость основного выражения, и задача решится сама собой сразу же. Наверняка каждый студент мечтал о том, чтобы иметь под рукой великолепный бесплатный калькулятор, такой как Math34.biz, и применять его повсеместно при необходимости. Преподаватели высших учебных заведений также могут использовать наше решение рядов онлайн и проверять работы своих подопечных курсантов. Для некоторого случая сумма ряда может быть вычислена в задаче для физики, химии или прикладной дисциплины, не застревая в рутинных вычислениях, чтобы не сбиться с основного направления при исследовании некоторого природного процесса. Для начала обычно записывают самое что не наесть упрощённое выражение в виде суммы ряда 1/n и оправдан такой подход. Число Пи присутствует во многих вычислительных операциях, но сумма ряда 1/n^2 можно сказать является классическим пример сходимости гармонического ряда на бесконечности. Что же все-таки означает выражение «сумма конечного ряда»? А это означает как раз, что он сходится и предел его частичных сумм имеет конкретное числовое значение. Если же подтвердится сходимость ряда и это повлияет на конечную устойчивость системы, то тогда возможно изменить входные параметры задачи и попробовать сделать заново. Напоследок хотим вам дать неявный на первый взгляд, но очень полезный на практике совет. Даже если вы имеет достаточный опыт в решении рядов и не нуждаетесь в подобных сервисах по решению рядов онлайн, приступить к нахождению суммы ряда мы предлагаем вам с определения сходимости ряда. Потратьте всего минуту на это действие, используя Math34.biz, чтобы на протяжении всего вычисления суммы ряда просто держать этот факт в голове. Лишним не будет! О сумме ряда онлайн много написано на сайтах по математике, приложено много иллюстраций как в прошлом веке ученые обозначали символами выражения суммы ряда. По большому счету мало что изменилось, но интересные моменты есть. Если сходимость ряда в онлайне представляется невозможным, то просто проверьте введенные данные и спокойно повторите запрос. Лучше все-таки сначала перепроверить общий член ряда. И всякое решение рядов онлайн покажется сразу на сайте, вам не придется нажимать дополнительные ссылки для того, чтобы получить ответ на поставленную задачу. Лучшее, по мнению экспертов, заставляет студентов более требовательно подходить к выбору калькулятора решения рядов. В сумму ряда как онлайн сервиса вкладывают понятие сходимости ряда, то есть существование конечной суммы. Наряду с этим разделом представлены такие базовые темы как интегралы и производная, поскольку все они тесно связаны. Давайте вместе с нами поговорим как сумма ряда 1/n расходится при стремлении переменной к бесконечности. Однако другая сумма такого ряда как 1/n^2 будет наоборот сходиться и примет конечное числовое выражение. Интересно изучать случаи, когда сумма конечного ряда представляется постепенно в виде промежуточных частичных сумм ряда при пошаговом увеличении переменной на единицу, а может и несколько единиц сразу. Проверку на сходимость ряда в онлайне рекомендуем делать после собственных решений заданий. Это позволит вам детально разобраться в теме и повысить свой уровень знаний. Не забывайте про это никогда, мы стараемся только для вас. Как-то на уроке учитель показал решение рядов онлайн с помощью вычислительной техники. Нужно сказать, что это всем понравилось изрядно. После этого случая калькулятор был востребован на всем курсе изучения математики. Лишним не будет проверить, как сумма ряда вычисляется калькулятором онлайн за несколько секунд после того, как вы запросите показать результат. Сразу станет понятно, в каком направлении стоит держать ход решения задачи. Поскольку о сходимости ряда в некоторых дорогих учебниках написано не много, то лучше скачать из Интернета несколько хороших докладов выдающихся ученых и пройти курс обучения по их методике. Результат будет хорошим. При решении рядов нельзя исключать самый первый признак сходимости, а именно стремление к нулю предела общего его члена. Хоть и не достаточное это условие, но необходимое всегда. Целостность решенного примера производит приятное ощущение на ученика, когда он понимает, что сумма ряда вычислена не прибегая к подсказкам. Учебники предназначены как пособие к применению на практике своих навыков. По мере забывания пройденного материала, нужно каждый четверг уделять хотя бы пять минут на беглый просмотр лекций, иначе к началу сессии вы все позабудете, а как вычисляется сходимость ряда вы тем более позабудете. Начните с одного раза и в дальнейшем переборите свою лень. Не зря заставляют преподаватели доказывать, как сумма ряда 1/n будет расходится. А вот если все-таки сумма ряда 1/n^2 будет представлена как знакопеременный ряд, то ничего страшного не случится — ведь абсолютный ряд то сходится! Ну и конечно сумма конечного ряда для вас может представлять особый интерес, когда вы изучаете эту дисциплину самостоятельно. Львиную долю примеров решают с помощью метода Даламбера и решение рядов при этом сводится к вычислению пределов, как отношение его соседних членов, а именно последующего на предыдущий. Поэтому желаем вам удачи в решении математики и пусть вы никогда не будете ошибаться! Возьмем за базовую основу так называемое решение рядов онлайн по направлению исследовательского разногласия причастности основополагающих принципов и научных межотраслевых направлений. Позвольте нам для вас найти ответ и рассказать утвердительно, что сумма ряда решается несколькими принципиально разными методами, но в конце концов результат один и тот же. Подсказка про сходимость ряда не всегда очевидна для студентов, даже если им заранее сказать ответ, хотя конечно это безусловно подталкивает их к правильному ходу решения. Абстракция в математике хоть и выступает на первое местною, однако она подкреплена теорией и доказывает некоторые неоспоримые факты в два счета. Нельзя пропустить такой аспект при решении рядов онлайн, как применимость или неприменимость базовых теоретических принципом сходимости числового ряда и представления сложной суммы ряда в некотором упрощенном варианте для более приятного глазу вида. Но известны случаи, когда сумма ряда 1/n будет сходиться и мы не станем вас напрягать этим казусом, потому что всего на просто нужно вместо символа бесконечности подставить некоторое целое число и тогда вся сумма сведется к обычному арифметическому ряду. Гармоничный ряд это сумма ряда 1/n^2, то сеть в любой возведенной степени. Сумма конечного ряда вычисляется за несколько секунд на сайте Math34.biz

math24.biz

ряды / Сумма ряда / Математика

Пусть $%x$% — число из условия, то есть $%|x| < 1$%. Рассмотрим некоторое $%q\in(0,1)$%, для которого $%|x| < q$%. На отрезке $%[-q,q]$% ряды будет сходиться абсолютно и равномерно, и тогда их члены можно произвольным образом переставлять. Используем то, что $%\frac1{1+x^{2^k}}=1-x^{2^k}+x^{2^{k+1}}-x^{3\cdot2^k}+\cdots$%. Получится сумма следующих рядов:

$%x-x^2+x^3-x^4+\cdots$%;

$%2x^2-2x^4+2x^6-\cdots$%;

$%4x^4-4x^8+4x^{12}-\cdots$%;

и так далее.

Из свойств двоичного разложения чисел можно увидеть, что коэффициент при любой степени окажется равен 1 после приведения подобных членов, то есть получается $%x+x^2+x^3+\cdots=\frac{x}{1-x}$%.

Можно, скорее всего, и какое-то более простое рассуждение найти.

Добавление. Вот более простое рассуждение, основанное на знании ответа. Оно не требует применения соображений о перестановке членов рядов (кстати, про равномерную сходимость можно было не упоминать — достаточно абсолютной сходимости при фиксированном $%x$%).

Будем из $%\frac{x}{1-x}$% последовательно вычитать члены ряда — тогда легко будет увидеть закономерность. На первом шаге будет $%\frac{x}{1-x}-\frac{x}{1+x}=\frac{2x^2}{1-x^2}$%. После вычитания второго члена суммы из того, что получилось, будет $%\frac{2x^2}{1-x^2}-\frac{2x^2}{1+x^2}=\frac{4x^4}{1-x^4}$%, и так далее. По индукции отсюда следует, что разность между $%\frac{x}{1-x}$% и $%n$%-й частичной суммой ряда из условия будет равна $%\dfrac{2^nx^{2^n}}{1-x^{2^n}}$%, где $%x^{2^n}$% стремится к нулю, и знаменатель стремится к 1. Числитель можно представить в виде $%n$%-й степени числа $%2x^{2^n/n}$%. Эта величина также стремится к нулю, так как $%|x| < 1$%, а показатель $%2^n/n$% стремится к бесконечности. При возведении в $%n$%-ю степень стремление к нулю тем более сохранится. Значит, частичные суммы сходятся к $%\frac{x}{1-x}$%.

math.hashcode.ru

Гармонический ряд — Юнциклопедия

Гармонический ряд — числовой ряд 1 + 1/2 + 1/3 + 1/4 + … + 1/n + … .

Называется он так потому, что каждый член гармонического ряда, начиная со второго, равен среднему гармоническому двух соседних (см. Средние значения). Члены гармонического ряда с возрастанием номера убывают и стремятся к нулю, однако частичные суммы S_n = 1 + 1/2 + 1/3 + … + 1/n неограниченно возрастают. Чтобы в этом убедиться, достаточно заметить, что

S₁ = 1, S₂ = 1 + 1/2, S₄ = S₂ + (1/3 + 1/4) > S₂ + (1/4 + 1/4) = 1 + 2/2, S₈ = S₄ + (1/5 + 1/6 + 1/7 + 1/8) > S₄ + (1/8 + 1/8 + 1/8 + 1/8) > 1 + 3/2.

Продолжая эти рассуждения, приходим к выводу, что сумма 2^k членов гармонического ряда больше, чем 1 + k/2. Отсюда следует, что частичные суммы гармонического ряда неограниченно возрастают, т. е. гармонический ряд является расходящимся (см. Ряд). Однако этот рост идет очень медленно. Л. Эйлер, изучавший свойства гармонического ряда, нашел, что

S_{1 000} ≈ 7,48, а S_{1 000 000} ≈ 14,39.

Более того, Эйлер установил замечательную зависимость для частичных сумм гармонического ряда, показав, что существует предел разности S_n — ln n, т. е. lim_n→∞ (S_n — ln n) = C.

Число C в его честь называется постоянной Эйлера, она приближенно равна 0,5772 (сам Эйлер, исходя из других соображений, вычислил C с точностью до 15 знаков).

Представим себе «лесенку», сложенную из n одинаковых кирпичей, следующим образом: второй кирпич подложен под первый так, что центр тяжести первого приходится на правый край второго, затем под эти два кирпича подложен третий так, что общий центр тяжести первых двух приходится на правый край третьего и т.д. (рис. 1). У такой «лесенки» центр тяжести проецируется в точку А, следовательно, «лесенка» не упадет. Если длина кирпича l, то 1-й окажется сдвинутым относительно 2-го на l/2, 2-й окажется сдвинутым относительно 3-го на l/4, (k+1)-й относительно k-го на l/2k, и вся «лесенка» будет сдвинута вправо на

∆_n= = 1/2 • (1 + 1/2 + 1/3 + … + 1/(n-1)).

Выражение в скобках есть частичная сумма гармонического ряда. Следовательно, указанным способом можно сложить «лесенку», сдвинутую сколь угодно далеко вправо. Однако, как было замечено, ∆_n растет очень медленно. Например, если сложить 1000 кирпичей, то ∆_{1 000} составит всего лишь 3,8 длины кирпича.

yunc.org

Сумма ряда Википедия

Числовой ряд — одно из центральных понятий математического анализа. Ряд записывается как бесконечная сумма^[1]:

a1+a2+a3+…+an+…{\displaystyle a_{1}+a_{2}+a_{3}+\ldots +a_{n}+\ldots }; краткая запись: ∑n=1∞an{\displaystyle \sum _{n=1}^{\infty }a_{n}}

Здесь a1,a2,a3…{\displaystyle a_{1},a_{2},a_{3}\dots } — последовательность вещественных или комплексных чисел; эти числа называются членами ряда.

Чтобы присвоить такому ряду числовое значение, рассмотрим последовательность «частичных сумм», которые получаются, если оборвать бесконечную сумму на каком-то члене:

S1=a1{\displaystyle S_{1}=a_{1}}

S2=a1+a2{\displaystyle S_{2}=a_{1}+a_{2}}

S3=a1+a2+a3{\displaystyle S_{3}=a_{1}+a_{2}+a_{3}}

⋯{\displaystyle \cdots }

Sn=a1+a2+a3+⋯+an{\displaystyle S_{n}=a_{1}+a_{2}+a_{3}+\dots +a_{n}}

⋯{\displaystyle \cdots }

Если последовательность частичных сумм имеет предел S{\displaystyle S} (конечный или бесконечный), то говорят, что сумма ряда равна S.{\displaystyle S.} При этом, если предел конечен, то говорят, что ряд сходится. Если предел не существует или бесконечен, то говорят, что ряд расходится^[1].

Ряды широко применяются в математике и других науках для вычислений, для анализа поведения разнообразных функций и т. п.

Примеры

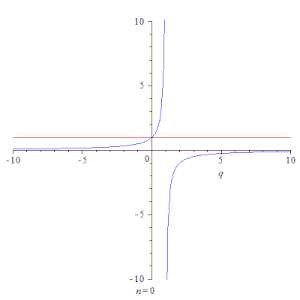Анимация, показывающая сходимость частичных сумм геометрической прогрессии ∑k=0nqk{\displaystyle \sum \limits _{k=0}^{n}q^{k}} (красная линия) к её сумме 11−q{\displaystyle {1 \over 1-q}} (синия линия) при |q|<1{\displaystyle |q|<1}.

Простейшим примером сходящегося ряда является сумма членов бесконечной геометрической прогрессии^[2] со знаменателем q<1{\displaystyle q<1}:

a+aq+aq2+aq3+…{\displaystyle a+aq+aq^{2}+aq^{3}+\dots }

Частичная сумма Sn=a1−qn1−q.{\displaystyle S_{n}=a{\frac {1-q^{n}}{1-q}}.} Предел этого выражения limn→∞Sn=a1−q,{\displaystyle \lim _{n\to \infty }S_{n}={\frac {a}{1-q}},} это и есть сумма бесконечной геометрической прогрессии^[1]. Например, при a=1,q=12{\displaystyle a=1,q={\frac {1}{2}}} получается ряд, сумма которого равна 2:

1+12+14+18+…{\displaystyle 1+{\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+\dots }

Десятичную дробь с бесконечной дробной частью можно рассматривать как сумму ряда^[2]; например, число π=3,1415926…{\displaystyle \pi =3{,}1415926\dots } есть сумма следующего ряда:

3+1101+4102+1103+5104+9105+…{\displaystyle 3+{\frac {1}{10^{1}}}+{\frac {4}{10^{2}}}+{\frac {1}{10^{3}}}+{\frac {5}{10^{4}}}+{\frac {9}{10^{5}}}+\dots }

Более сложным примером является ряд обратных квадратов, сумму которого лучшие математики Европы не могли найти более 100 лет:

∑n=1∞1n2=π26{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {\pi ^{2}}{6}}}

Ряд 1+1+1+…{\displaystyle 1+1+1+\dots } расходится, сумма его бесконечна. Расходится и гармонический ряд:∑n=1∞1n=∞.{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}={\infty }.} «Ряд Гранди» 1−1+1−1+1−1…{\displaystyle 1-1+1-1+1-1\dots } расходится, его частичные суммы колеблются от 1 до 0, поэтому предела частичных сумм не существует, суммы у этого ряда нет.

Классификация рядов

Положительный ряд — ряд, все члены которого неотрицательны. У положительных рядов сумма всегда существует, но может быть бесконечна.

Знакочередующийся ряд — ряд, в котором знаки членов чередуются: плюс, минус, плюс, минус и т. д. Для таких рядов существует простой признак сходимости Лейбница. Знакочередующийся вариант приведенного выше гармонического ряда, в отличие от последнего, сходится:

1−12+13−14+15−⋯=ln⁡(2){\displaystyle 1-{1 \over 2}+{1 \over 3}-{1 \over 4}+{1 \over 5}-\cdots =\ln(2)}

Говорят, что числовой ряд сходится абсолютно, если сходится ряд из абсолютных величин его членов:

∑n=1∞|an|{\displaystyle \sum _{n=1}^{\infty }|a_{n}|}

Абсолютно сходящийся ряд сходится и в обычном смысле этого понятия. При этом всякий такой ряд обладает важным свойством переместительности: при любой перестановке членов абсолютно сходящегося ряда получается сходящийся ряд с той же суммой^[3].

Критерий абсолютной сходимости: ряд из вещественных чисел сходится абсолютно тогда и только тогда, когда сходятся как ряд из положительных его членов, так и ряд из отрицательных членов.

Операции над рядами

Пусть заданы сходящиеся ряды ∑n=1∞an{\displaystyle \sum _{n=1}^{\infty }a_{n}} и ∑n=1∞bn{\displaystyle \sum _{n=1}^{\infty }b_{n}}. Тогда:

• Их суммой называется ряд ∑n=1∞(an+bn),{\displaystyle \sum _{n=1}^{\infty }(a_{n}+b_{n}),} разностью — ряд ∑n=1∞(an−bn).{\displaystyle \sum _{n=1}^{\infty }(a_{n}-b_{n}).}
• Их произведением Коши^[en] называется ряд ∑n=1∞cn{\displaystyle \sum _{n=1}^{\infty }c_{n}}, где:

cn=∑k=1nakbn−k+1=a1b1+(a1b2+a2b1)+(a1b3+a2b2+a3b1)+⋯+(a1bn+a2bn−1+⋯+anb1){\displaystyle c_{n}=\sum _{k=1}^{n}a_{k}b_{n-k+1}=a_{1}b_{1}+(a_{1}b_{2}+a_{2}b_{1})+(a_{1}b_{3}+a_{2}b_{2}+a_{3}b_{1})+\dots +(a_{1}b_{n}+a_{2}b_{n-1}+\dots +a_{n}b_{1})}

Если оба ряда сходятся, то их сумма и разность также сходятся. Если оба ряда сходятся абсолютно, то их сумма сходится абсолютно. Если хотя бы один из исходных рядов сходится абсолютно, то произведение рядов сходится.

Необходимый признак сходимости ряда

Ряд a1+a2+a3+…+an+…{\displaystyle {a}_{1}+{a}_{2}+{a}_{3}+\ldots +{a}_{n}+\ldots } может сходиться лишь в том случае, когда член an{\displaystyle {a}_{n}} (общий член ряда) с возрастанием его номера стремится к нулю:

limn→∞an=0.{\displaystyle \lim _{n\rightarrow \infty }{a}_{n}=0.}

Это необходимый признак сходимости ряда, но он не является достаточным — у гармонического ряда общий член с ростом номера неограниченно уменьшается, тем не менее ряд расходится. Если же общий член ряда не стремится к нулю, то ряд заведомо расходится.

Сходимость числовых рядов

Свойство 1. Если ряд

∑n=1∞an=a1+a2+a3+a4+…{\displaystyle \sum _{n=1}^{\infty }{a}_{n}={a}_{1}+{a}_{2}+{a}_{3}+{a}_{4}+\ldots }   (1.1)

сходится и его сумма равна S, то ряд

∑n=1∞can=ca1+ca2+ca3+ca4+…{\displaystyle \sum _{n=1}^{\infty }c{a}_{n}=c{a}_{1}+c{a}_{2}+c{a}_{3}+c{a}_{4}+\ldots }  (1.2)

где c — произвольное число, также сходится и его сумма равна cS. Если же ряд (1.1) расходится и с ≠ 0, то ряд (1.2) расходится.

Свойство 2. Если сходится ряд (1.1) и сходится ряд

∑n=1∞bn{\displaystyle \sum _{n=1}^{\infty }{b}_{n}},

а их суммы равны S1{\displaystyle {S}_{1}} и S2{\displaystyle {S}_{2}} соответственно, то сходятся и ряды

∑n=1∞(an±bn){\displaystyle \sum _{n=1}^{\infty }({a}_{n}\pm {b}_{n})},

причём сумма каждого равна соответственно S1±S2{\displaystyle {S}_{1}\pm {S}_{2}}.

Для выяснения ключевого в анализе вопроса, сходится или нет заданный ряд, предложены многочисленные признаки сходимости (см. список).

Нерешённые проблемы

До сих пор неизвестно, сходится ли «ряд Флинт Хиллз» (Flint Hills Series)^[4]:

∑n=1∞cosec2⁡(n)n3{\displaystyle \sum _{n=1}^{\infty }{\frac {\operatorname {cosec} ^{2}(n)}{n^{3}}}}

Если удастся доказать, что этот ряд сходится, то как следствие получится важный факт: мера иррациональности числа π{\displaystyle \pi } меньше, чем 2,5.

Известно, что сумма ряда обратных квадратов и суммы других рядов с обратными чётными степенями выражаются через степени числа π,{\displaystyle \pi ,} но мало что известно про сумму обратных кубов («константу Апери»):

113+123+133+143+⋯≈1,2020569{\displaystyle {\frac {1}{1^{3}}}+{\frac {1}{2^{3}}}+{\frac {1}{3^{3}}}+{\frac {1}{4^{3}}}+\dots \approx 1{,}2020569}.

Никто пока не сумел связать это значение с классическими константами или элементарными функциями^[5].

Вариации и обобщения

Обобщением понятия ряда является понятие двойного ряда.

Обобщением понятия суммы ряда является понятие суммирующей функции ряда, выбор которой делает понятие суммы расходящегося (в классическом смысле) ряда приемлемым. Предложено множество вариантов такого обобщения: сходимость по Пуассону — Абелю, Борелю, Чезаро, Эйлеру, Ламберту и другие.

В анализе исследуются ряды не только из чисел, но и из функций: степенные ряды, функциональные ряды, ряды Фурье, ряды Лорана и др.

Примечания

Литература

• Выгодский М. Я. Справочник по высшей математике. — 12-е изд.. — М.: Наука, 1977. — 872 с.
• Зорич В. А.. Глава III. Предел. § 1. Предел последовательности // Математический анализ, часть I. — М.: Наука, 1981. — С. 104—114. — 544 с.
• Письменный Д. Т. Часть 2 // Конспект лекций по высшей математике. — 6-е изд. — М.: Айрис-пресс, 2008.
• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, в трёх томах. — 6-е изд.. — М.: Наука, 1966. — Т. 2. — 680 с.

Ссылки

wikiredia.ru

Сумма ряда Вики

Числовой ряд — одно из центральных понятий математического анализа. Ряд записывается как бесконечная сумма^[1]:

a1+a2+a3+…+an+…{\displaystyle a_{1}+a_{2}+a_{3}+\ldots +a_{n}+\ldots }; краткая запись: ∑n=1∞an{\displaystyle \sum _{n=1}^{\infty }a_{n}}

Здесь a1,a2,a3…{\displaystyle a_{1},a_{2},a_{3}\dots } — последовательность вещественных или комплексных чисел; эти числа называются членами ряда.

Чтобы присвоить такому ряду числовое значение, рассмотрим последовательность «частичных сумм», которые получаются, если оборвать бесконечную сумму на каком-то члене:

S1=a1{\displaystyle S_{1}=a_{1}}

S2=a1+a2{\displaystyle S_{2}=a_{1}+a_{2}}

S3=a1+a2+a3{\displaystyle S_{3}=a_{1}+a_{2}+a_{3}}

⋯{\displaystyle \cdots }

Sn=a1+a2+a3+⋯+an{\displaystyle S_{n}=a_{1}+a_{2}+a_{3}+\dots +a_{n}}

⋯{\displaystyle \cdots }

Если последовательность частичных сумм имеет предел S{\displaystyle S} (конечный или бесконечный), то говорят, что сумма ряда равна S.{\displaystyle S.} При этом, если предел конечен, то говорят, что ряд сходится. Если предел не существует или бесконечен, то говорят, что ряд расходится^[1].

Ряды широко применяются в математике и других науках для вычислений, для анализа поведения разнообразных функций и т. п.

Примеры[ | код]

Анимация, показывающая сходимость частичных сумм геометрической прогрессии ∑k=0nqk{\displaystyle \sum \limits _{k=0}^{n}q^{k}} (красная линия) к её сумме 11−q{\displaystyle {1 \over 1-q}} (синия линия) при |q|<1{\displaystyle |q|<1}.

Простейшим примером сходящегося ряда является сумма членов бесконечной геометрической прогрессии^[2] со знаменателем q<1{\displaystyle q<1}:

a+aq+aq2+aq3+…{\displaystyle a+aq+aq^{2}+aq^{3}+\dots }

Частичная сумма Sn=a1−qn1−q.{\displaystyle S_{n}=a{\frac {1-q^{n}}{1-q}}.} Предел этого выражения limn→∞Sn=a1−q,{\displaystyle \lim _{n\to \infty }S_{n}={\frac {a}{1-q}},} это и есть сумма бесконечной геометрической прогрессии^[1]. Например, при a=1,q=12{\displaystyle a=1,q={\frac {1}{2}}} получается ряд, сумма которого равна 2:

1+12+14+18+…{\displaystyle 1+{\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+\dots }

Десятичную дробь с бесконечной дробной частью можно рассматривать как сумму ряда^[2]; например, число π=3,1415926…{\displaystyle \pi =3{,}1415926\dots } есть сумма следующего ряда:

3+1101+4102+1103+5104+9105+…{\displaystyle 3+{\frac {1}{10^{1}}}+{\frac {4}{10^{2}}}+{\frac {1}{10^{3}}}+{\frac {5}{10^{4}}}+{\frac {9}{10^{5}}}+\dots }

Более сложным примером является ряд обратных квадратов, сумму которого лучшие математики Европы не могли найти более 100 лет:

∑n=1∞1n2=π26{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {\pi ^{2}}{6}}}

Ряд 1+1+1+…{\displaystyle 1+1+1+\dots } расходится, сумма его бесконечна. Расходится и гармонический ряд:∑n=1∞1n=∞.{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}={\infty }.} «Ряд Гранди» 1−1+1−1+1−1…{\displaystyle 1-1+1-1+1-1\dots } расходится, его частичные суммы колеблются от 1 до 0, поэтому предела частичных сумм не существует, суммы у этого ряда нет.

Классификация рядов[ | код]

Положительный ряд — ряд, все члены которого неотрицательны. У положительных рядов сумма всегда существует, но может быть бесконечна.

Знакочередующийся ряд — ряд, в котором знаки членов чередуются: плюс, минус, плюс, минус и т. д. Для таких рядов существует простой признак сходимости Лейбница. Знакочередующийся вариант приведенного выше гармонического ряда, в отличие от последнего, сходится:

1−12+13−14+15−⋯=ln⁡(2){\displaystyle 1-{1 \over 2}+{1 \over 3}-{1 \over 4}+{1 \over 5}-\cdots =\ln(2)}

Говорят, что числовой ряд сходится абсолютно, если сходится ряд из абсолютных величин его членов:

∑n=1∞|an|{\displaystyle \sum _{n=1}^{\infty }|a_{n}|}

Абсолютно сходящийся ряд сходится и в обычном смысле этого понятия. При этом всякий такой ряд обладает важным свойством переместительности: при любой перестановке членов абсолютно сходящегося ряда получается сходящийся ряд с той же суммой^[3].

Критерий абсолютной сходимости: ряд из вещественных чисел сходится абсолютно тогда и только тогда, когда сходятся как ряд из положительных его членов, так и ряд из отрицательных членов.

Операции над рядами[ | код]

Пусть заданы сходящиеся ряды ∑n=1∞an{\displaystyle \sum _{n=1}^{\infty }a_{n}} и ∑n=1∞bn{\displaystyle \sum _{n=1}^{\infty }b_{n}}. Тогда:

• Их суммой называется ряд ∑n=1∞(an+bn),{\displaystyle \sum _{n=1}^{\infty }(a_{n}+b_{n}),} разностью — ряд ∑n=1∞(an−bn).{\displaystyle \sum _{n=1}^{\infty }(a_{n}-b_{n}).}
• Их произведением Коши^[en] называется ряд ∑n=1∞cn{\displaystyle \sum _{n=1}^{\infty }c_{n}}, где:

cn=∑k=1nakbn−k+1=a1b1+(a1b2+a2b1)+(a1b3+a2b2+a3b1)+⋯+(a1bn+a2bn−1+⋯+anb1){\displaystyle c_{n}=\sum _{k=1}^{n}a_{k}b_{n-k+1}=a_{1}b_{1}+(a_{1}b_{2}+a_{2}b_{1})+(a_{1}b_{3}+a_{2}b_{2}+a_{3}b_{1})+\dots +(a_{1}b_{n}+a_{2}b_{n-1}+\dots +a_{n}b_{1})}

Если оба ряда сходятся, то их сумма и разность также сходятся. Если оба ряда сходятся абсолютно, то их сумма сходится абсолютно. Если хотя бы один из исходных рядов сходится абсолютно, то произведение рядов сходится.

Необходимый признак сходимости ряда[ | код]

Ряд a1+a2+a3+…+an+…{\displaystyle {a}_{1}+{a}_{2}+{a}_{3}+\ldots +{a}_{n}+\ldots } может сходиться лишь в том случае, когда член an{\displaystyle {a}_{n}} (общий член ряда) с возрастанием его номера стремится к нулю:

limn→∞an=0.{\displaystyle \lim _{n\rightarrow \infty }{a}_{n}=0.}

Это необходимый признак сходимости ряда, но он не является достаточным — у гармонического ряда общий член с ростом номера неограниченно уменьшается, тем не менее ряд расходится. Если же общий член ряда не стремится к нулю, то ряд заведомо расходится.

Сходимость числовых рядов[ | код]

Свойство 1. Если ряд

∑n=1∞an=a1+a2+a3+a4+…{\displaystyle \sum _{n=1}^{\infty }{a}_{n}={a}_{1}+{a}_{2}+{a}_{3}+{a}_{4}+\ldots }   (1.1)

сходится и его сумма равна S, то ряд

∑n=1∞can=ca1+ca2+ca3+ca4+…{\displaystyle \sum _{n=1}^{\infty }c{a}_{n}=c{a}_{1}+c{a}_{2}+c{a}_{3}+c{a}_{4}+\ldots }  (1.2)

где c — произвольное число, также сходится и его сумма равна cS. Если же ряд (1.1) расходится и с ≠ 0, то ряд (1.2) расходится.

Свойство 2. Если сходится ряд (1.1) и сходится ряд

∑n=1∞bn{\displaystyle \sum _{n=1}^{\infty }{b}_{n}},

а их суммы равны S1{\displaystyle {S}_{1}} и S2{\displaystyle {S}_{2}} соответственно, то сходятся и ряды

∑n=1∞(an±bn){\displaystyle \sum _{n=1}^{\infty }({a}_{n}\pm {b}_{n})},

причём сумма каждого равна соответственно S1±S2{\displaystyle {S}_{1}\pm {S}_{2}}.

Для выяснения ключевого в анализе вопроса, сходится или нет заданный ряд, предложены многочисленные признаки сходимости (см. список).

Нерешённые проблемы[ | код]

До сих пор неизвестно, сходится ли «ряд Флинт Хиллз» (Flint Hills Series)^[4]:

∑n=1∞cosec2⁡(n)n3{\displaystyle \sum _{n=1}^{\infty }{\frac {\operatorname {cosec} ^{2}(n)}{n^{3}}}}

Если удастся доказать, что этот ряд сходится, то как следствие получится важный факт: мера иррациональности числа π{\displaystyle \pi } меньше, чем 2,5.

Известно, что сумма ряда обратных квадратов и суммы других рядов с обратными чётными степенями выражаются через степени числа π,{\displaystyle \pi ,} но мало что известно про сумму обратных кубов («константу Апери»):

113+123+133+143+⋯≈1,2020569{\displaystyle {\frac {1}{1^{3}}}+{\frac {1}{2^{3}}}+{\frac {1}{3^{3}}}+{\frac {1}{4^{3}}}+\dots \approx 1{,}2020569}.

Никто пока не сумел связать это значение с классическими константами или элементарными функциями^[5].

Вариации и обобщения[ | код]

Обобщением понятия ряда является понятие двойного ряда.

Обобщением понятия суммы ряда является понятие суммирующей функции ряда, выбор которой делает понятие суммы расходящегося (в классическом смысле) ряда приемлемым. Предложено множество вариантов такого обобщения: сходимость по Пуассону — Абелю, Борелю, Чезаро, Эйлеру, Ламберту и другие.

В анализе исследуются ряды не только из чисел, но и из функций: степенные ряды, функциональные ряды, ряды Фурье, ряды Лорана и др.

Примечания[ | код]

Литература[ | код]

• Выгодский М. Я. Справочник по высшей математике. — 12-е изд.. — М.: Наука, 1977. — 872 с.
• Зорич В. А.. Глава III. Предел. § 1. Предел последовательности // Математический анализ, часть I. — М.: Наука, 1981. — С. 104—114. — 544 с.
• Письменный Д. Т. Часть 2 // Конспект лекций по высшей математике. — 6-е изд. — М.: Айрис-пресс, 2008.
• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, в трёх томах. — 6-е изд.. — М.: Наука, 1966. — Т. 2. — 680 с.

Ссылки[ | код]

ru.wikibedia.ru

Сумма ряда — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

Сумма числового ряда <math>a_1+a_2+\ldots +a_n+\ldots\ </math> определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится^[1]. Элементы ряда <math>a_n</math> представляют собой комплексные числа (в частности, вещественные).

Определение

Пусть <math>\sum_{i=1}^\infty a_i=a_1+a_2+\ldots</math> — числовой ряд. Число <math>S_n=a_1+a_2+\ldots+a_n</math> называется n-ой частичной суммой ряда <math>\sum_{i=1}^\infty a_i</math>.

Сумма (числового) ряда — это предел частичных сумм <math>S_n</math>, если он существует и конечен. Таким образом, если существует число <math> S=\lim_{n\to\infty}\sum_{i=1}^{n}a_i</math>, то в этом случае пишут <math>\sum_{i=1}^{\infty}a_i=S</math>. Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то ряд называется расходящимся.

Дальнейшим обобщением понятия суммы ряда является понятие суммирующей функции ряда.

Сходимость числовых рядов

Свойство 1. Если ряд

<math>\sum_{n=1}^{\infty} {u}_{n} = {u}_{1} + {u}_{2} + {u}_{3} + {u}_{4} + …</math>   (1.1)

сходится и его сумма равна S, то ряд

<math>\sum_{n=1}^{\infty} c{u}_{n} = c{u}_{1} + c{u}_{2} + c{u}_{3} + c{u}_{4} + …</math>  (1.2)

где c — произвольное число, также сходится и его сумма равна cS. Если же ряд (1.1) расходится и с ≠ 0, то ряд (1.2) расходится.

Свойство 2. Если сходится ряд (1.1) и сходится ряд

<math>\sum_{n=1}^{\infty } {v}_{n}</math>,

а их суммы равны <math>{S}_{1}</math> и <math>{S}_{2}</math> соответственно, то сходятся и ряды

<math>\sum_{n=1}^{\infty } ({u}_{n} \pm {v}_{n})</math>,

причём сумма каждого равна соответственно <math>{S}_{1} \pm {S}_{2}</math>.

Необходимый признак сходимости ряда

Ряд <math>{u}_{1} + {u}_{2} + {u}_{3} + … + {u}_{n} + …</math>   может сходиться лишь в том случае, когда член <math>{u}_{n}</math> (общий член ряда) стремится к нулю:

<math>\lim_{n\rightarrow \infty} {u}_{n} = 0.</math>

Это необходимый признак сходимости ряда (но не достаточный!). Если же общий член ряда не стремится к нулю — это достаточный признак расходимости.

Примеры

• <math>\sum_{n=0}^{\infty}q^n=\frac{1}{1-q},</math> где <math>|q|<1,</math> — сумма геометрической прогрессии, в частности
  • <math>\sum_{i=0}^\infin \frac{1}{2^i} = 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \ldots = 2</math>
• <math>\sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}</math>.
• <math>\sum_{n=1}^{\infty}\frac{1}{n}={\infty}</math> — гармонический ряд расходится.
• <math>\sum_{n=1}^\infty\frac{1}{n (n+1)}=\sum_{n=1}^\infty\left(\frac{1}{n}-\frac{1}{n+1}\right)=1</math> — телескопический ряд.

См. также

Обобщения числовых рядов

Признаки сходимости

Напишите отзыв о статье «Сумма ряда»

Литература

• Выгодский М. Я. [eqworld.ipmnet.ru/ru/library/books/Vygodskij1977ru.djvu Справочник по высшей математике]. — 12-е изд. — М.: Наука, 1977.
• Письменный Д. Т. Часть 2 // Конспект лекций по высшей математике. — 6-е изд. — М.: Айрис-пресс, 2008.
• Савельева Р. Ю. [festival.1september.ru/articles/507571/ Высшая математика. Теория рядов].
• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: ФИЗМАТЛИТ, 1960. — Т. 2. — 680 с. — ISBN 5-9221-0155-2.

Примечания

Отрывок, характеризующий Сумма ряда

Те же счастливые, восторженные лица обратились на мохнатую фигуру Денисова и окружили его.
– Голубчик, Денисов! – визгнула Наташа, не помнившая себя от восторга, подскочила к нему, обняла и поцеловала его. Все смутились поступком Наташи. Денисов тоже покраснел, но улыбнулся и взяв руку Наташи, поцеловал ее.
Денисова отвели в приготовленную для него комнату, а Ростовы все собрались в диванную около Николушки.
Старая графиня, не выпуская его руки, которую она всякую минуту целовала, сидела с ним рядом; остальные, столпившись вокруг них, ловили каждое его движенье, слово, взгляд, и не спускали с него восторженно влюбленных глаз. Брат и сестры спорили и перехватывали места друг у друга поближе к нему, и дрались за то, кому принести ему чай, платок, трубку.
Ростов был очень счастлив любовью, которую ему выказывали; но первая минута его встречи была так блаженна, что теперешнего его счастия ему казалось мало, и он всё ждал чего то еще, и еще, и еще.
На другое утро приезжие спали с дороги до 10 го часа.
В предшествующей комнате валялись сабли, сумки, ташки, раскрытые чемоданы, грязные сапоги. Вычищенные две пары со шпорами были только что поставлены у стенки. Слуги приносили умывальники, горячую воду для бритья и вычищенные платья. Пахло табаком и мужчинами.
– Гей, Г’ишка, т’убку! – крикнул хриплый голос Васьки Денисова. – Ростов, вставай!
Ростов, протирая слипавшиеся глаза, поднял спутанную голову с жаркой подушки.
– А что поздно? – Поздно, 10 й час, – отвечал Наташин голос, и в соседней комнате послышалось шуршанье крахмаленных платьев, шопот и смех девичьих голосов, и в чуть растворенную дверь мелькнуло что то голубое, ленты, черные волоса и веселые лица. Это была Наташа с Соней и Петей, которые пришли наведаться, не встал ли.
– Николенька, вставай! – опять послышался голос Наташи у двери.
– Сейчас!
В это время Петя, в первой комнате, увидав и схватив сабли, и испытывая тот восторг, который испытывают мальчики, при виде воинственного старшего брата, и забыв, что сестрам неприлично видеть раздетых мужчин, отворил дверь.
– Это твоя сабля? – кричал он. Девочки отскочили. Денисов с испуганными глазами спрятал свои мохнатые ноги в одеяло, оглядываясь за помощью на товарища. Дверь пропустила Петю и опять затворилась. За дверью послышался смех.
– Николенька, выходи в халате, – проговорил голос Наташи.
– Это твоя сабля? – спросил Петя, – или это ваша? – с подобострастным уважением обратился он к усатому, черному Денисову.
Ростов поспешно обулся, надел халат и вышел. Наташа надела один сапог с шпорой и влезала в другой. Соня кружилась и только что хотела раздуть платье и присесть, когда он вышел. Обе были в одинаковых, новеньких, голубых платьях – свежие, румяные, веселые. Соня убежала, а Наташа, взяв брата под руку, повела его в диванную, и у них начался разговор. Они не успевали спрашивать друг друга и отвечать на вопросы о тысячах мелочей, которые могли интересовать только их одних. Наташа смеялась при всяком слове, которое он говорил и которое она говорила, не потому, чтобы было смешно то, что они говорили, но потому, что ей было весело и она не в силах была удерживать своей радости, выражавшейся смехом.
– Ах, как хорошо, отлично! – приговаривала она ко всему. Ростов почувствовал, как под влиянием жарких лучей любви, в первый раз через полтора года, на душе его и на лице распускалась та детская улыбка, которою он ни разу не улыбался с тех пор, как выехал из дома.

wiki-org.ru