Рациональные числа: определение и примеры
Важное понятие из базового курса математики — это рациональные числа. Тему изучают еще в шестом классе средней школы, поскольку без нее невозможно продвинуться в дальнейшее изучение предмета. Математическое понятие является очень простым по смыслу, признаки таких чисел улавливаются без труда.
Каким определением можно характеризовать рациональные числа?
Рациональное число – это любое число, которое реально записать в виде дроби «a/c», и при этом «а» будет являться целым числом, а «с» — относиться к разряду натуральных. Дробь может быть как положительной, так и отрицательной — в последнем случае число не перестает быть рациональным.
Например, -3 можно уверенно записывать, как -3/1 — в ответе мы все равно получаем -3. При этом верхняя часть дроби представляет собой целое число, нижняя часть относится к натуральным — пример полностью удовлетворяет условиям из определения.
Если суммировать, то к разряду рациональных можно относить:
- Любые обыкновенные дроби — как со знаком «плюс», так и со знаком «минус».
- Любые смешанные числа с любым знаком — поскольку они с легкостью переводятся в вид обыкновенной дроби.
- Все целые числа — каждое из них можно разделить на 1 и получить то же самое целое число, то есть удовлетворить условиям определения.
- Число ноль — для него действуют те же правила, что и в предыдущем пункте.
- Десятичные дроби — например, 0,5 можно записать в виде 5/10 или 1/2, иными словами, получить обыкновенную дробь. Правда, здесь нужно сделать оговорку — это относится лишь к конечным дробям, даже если после запятой у них очень много знаков. А вот если дробь является бесконечной, то есть знаки после запятой могут продолжаться сколько угодно и никогда не заканчиваться — о рациональности речи уже не пойдет.
Разумеется, два таких числа, прибавленных друг к другу, в результате тоже дадут рациональное число. То же относится к умножению и вычитанию.
Для чего нужны рациональные числа?
Многих интересует вопрос, в чем смысл этого понятия. Термин «рациональные числа» служит для облегчения восприятия, поскольку объединяет в себе широкую группу чисел — целых и дробей.
Если усвоить это математическое понятие, то постигать науку дальше будет проще — при изучении новых параграфов учебника уже не придется долго и старательно перечислять, к каким именно числам относится то или иное правило. Достаточно будет воспользоваться названием группы — «рациональные».
Похожие статьи
infoogle.ru
1.2. Рациональные числа
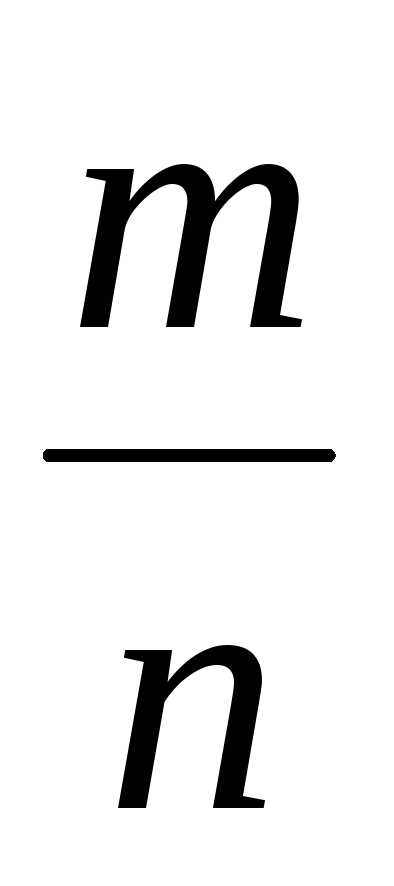 ,
где
,
где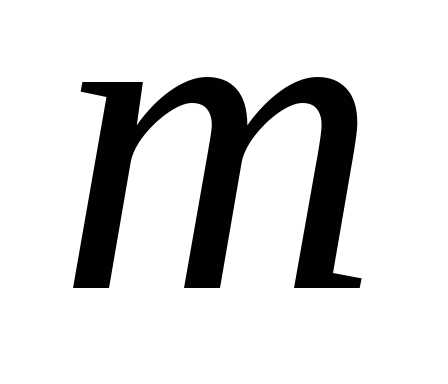 – целое число, а
– целое число, а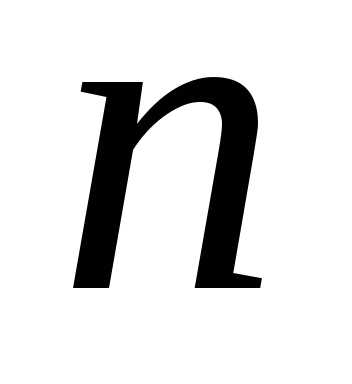 – натуральное. Множество рациональных
чисел обозначают буквой
– натуральное. Множество рациональных
чисел обозначают буквой .
При этом выполняется соотношение
.
При этом выполняется соотношение ,
так как любое целое число
,
так как любое целое число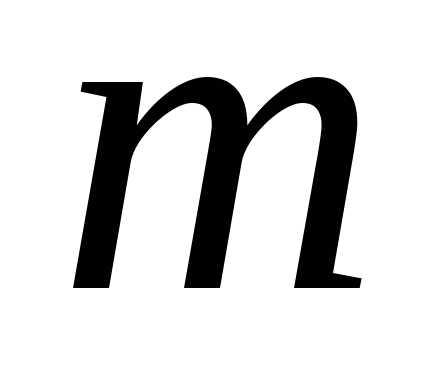 можно представить в виде
можно представить в виде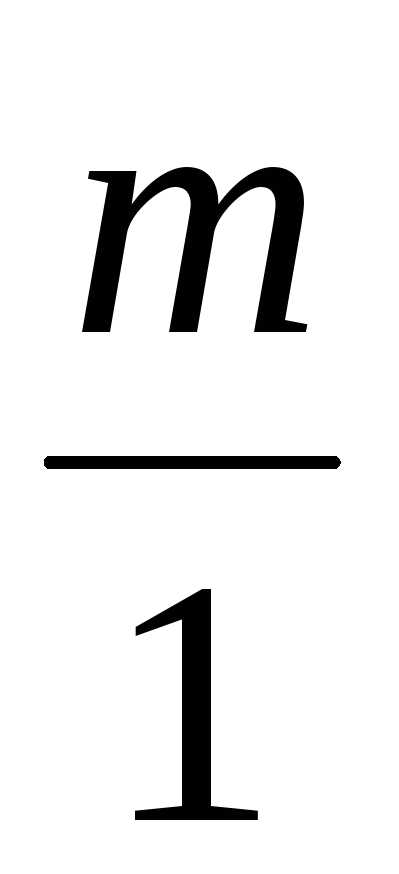 .
Таким образом, можно сказать, что
рациональные числа – это все целые
числа, а также положительные и отрицательные
обыкновенные дроби.
.
Таким образом, можно сказать, что
рациональные числа – это все целые
числа, а также положительные и отрицательные
обыкновенные дроби.Десятичные дроби – это такие обыкновенные дроби, у которых знаменатель – единица с нулями, то есть 10; 100; 1000 и т.д. Десятичные дроби записывают без знаменателей. Сначала пишется целая часть числа, справа от нее ставится запятая; первая цифра после запятой означает число десятых, вторая – сотых, третья – тысячных и т.д. Цифры, стоящие после запятой, называются десятичными знаками.
Бесконечной называется десятичная дробь, у которой после запятой бесконечно много цифр.
Каждое рациональное
число 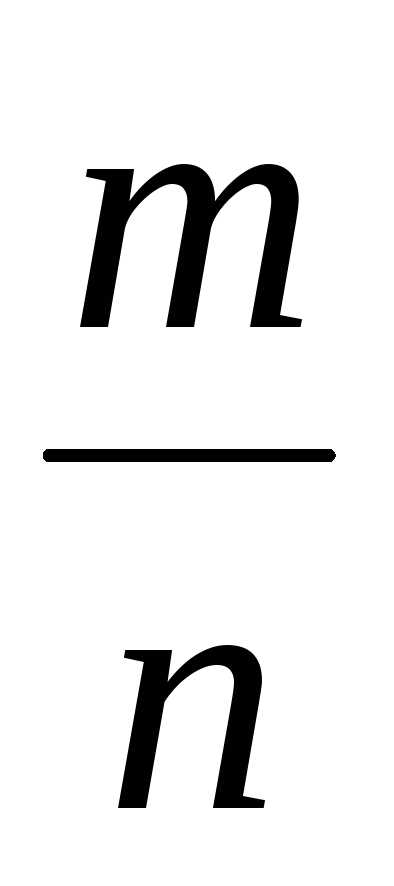 может быть представлено в виде конечной
или бесконечной десятичной дроби. Это
достигается делением числителя на
знаменатель.
может быть представлено в виде конечной
или бесконечной десятичной дроби. Это
достигается делением числителя на
знаменатель.
Бесконечную десятичную дробь называют периодической, если у нее, начиная с некоторого места, одна цифра или группа цифр повторяется, непосредственно следуя одна за другой. Повторяющуюся цифру или группу цифр называют периодом и записывают в скобках. Например, .
Верно и обратное утверждение: любую бесконечную десятичную периодическую дробь можно представить в виде обыкновенной дроби.
Перечислим некоторые сведения о периодических дробях.
1. Если период дроби начинается сразу после запятой, то дробь называется чисто-периодической, если не сразу после запятой – смешанно-периодической.
Например, 1,(58) – чисто-периодическая дробь, а 2,4(67) – смешанно-периодическая.
2. Если несократимая
дробь 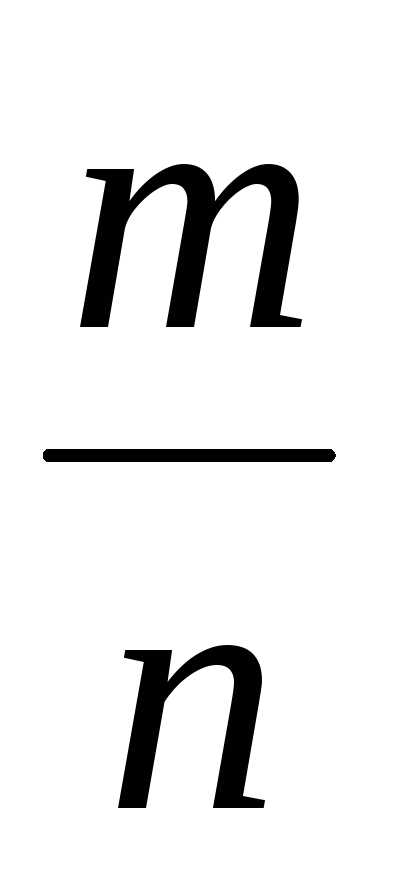 такова, что в разложении ее знаменателя
на простые множители содержатся лишь
числа 2 и 5, то запись числа
такова, что в разложении ее знаменателя
на простые множители содержатся лишь
числа 2 и 5, то запись числа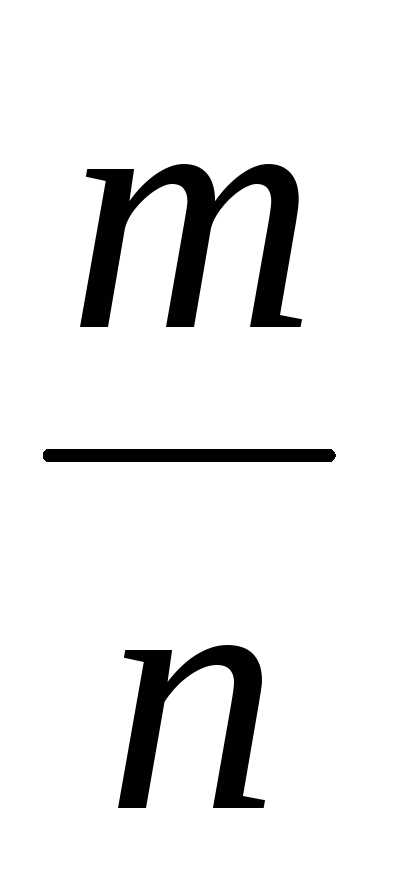 в виде десятичной дроби представляет
собой конечную десятичную дробь; если
в указанном разложении есть другие
простые множители, то получится
бесконечная десятичная периодическая
дробь.
в виде десятичной дроби представляет
собой конечную десятичную дробь; если
в указанном разложении есть другие
простые множители, то получится
бесконечная десятичная периодическая
дробь.
3. Если несократимая
дробь 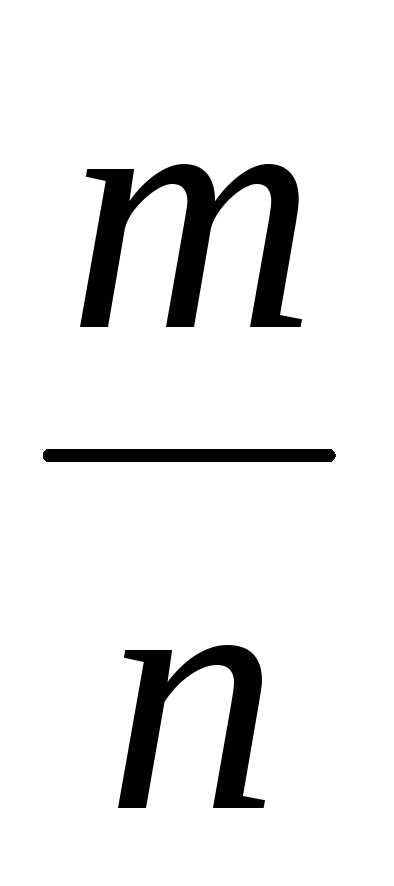
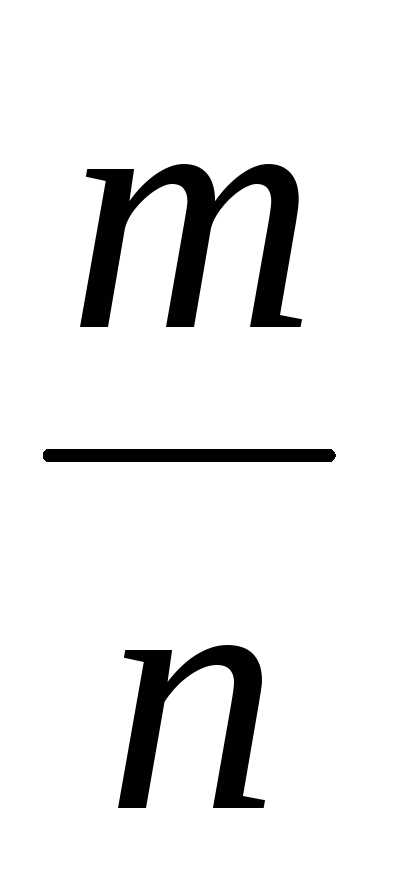 в виде десятичной дроби представляет
собой чисто-периодическую десятичную
дробь; если в указанном разложении,
наряду с другими простыми множителями,
есть 2 или 5, то получится смешанно-периодическая
десятичная дробь.
в виде десятичной дроби представляет
собой чисто-периодическую десятичную
дробь; если в указанном разложении,
наряду с другими простыми множителями,
есть 2 или 5, то получится смешанно-периодическая
десятичная дробь.4. У периодической дроби период может быть любой длины, то есть содержать любое количество цифр.
1.3. Иррациональные числа
Иррациональным числом называется бесконечная десятичная непериодическая дробь.
Примерами
иррациональных чисел служат корни из
натуральных чисел, не являющихся
квадратами натуральных чисел. Например, 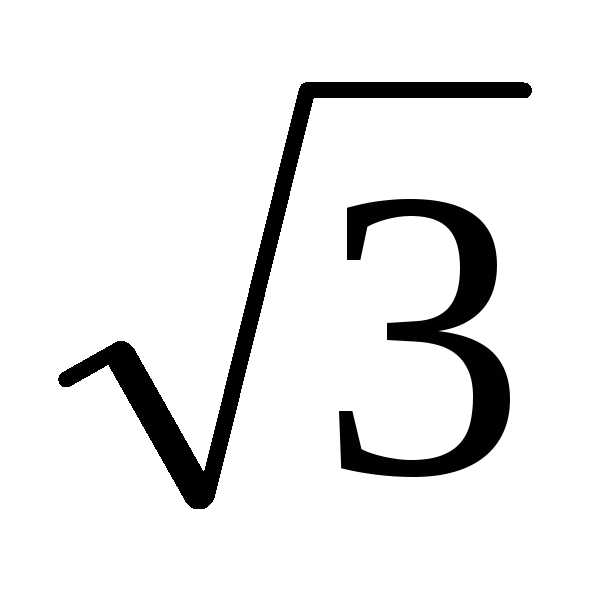 ,
, .
Иррациональными являются числа;.
Множество иррациональных чисел обозначают
буквой
.
Иррациональными являются числа;.
Множество иррациональных чисел обозначают
буквой
Пример 1.10. Доказать,
что 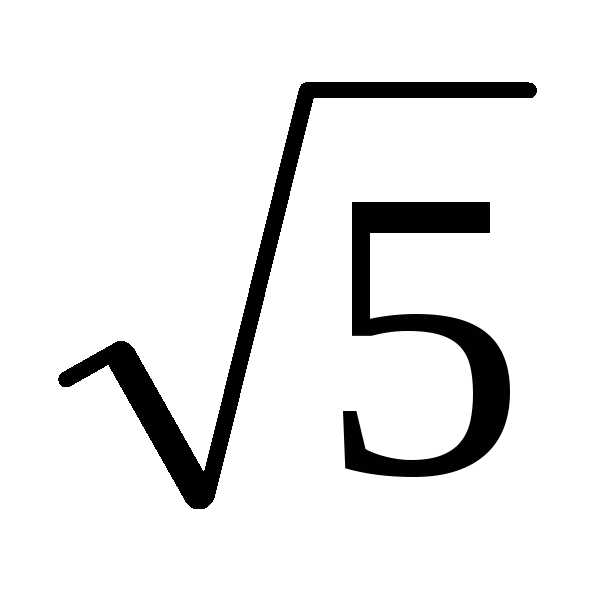 – иррационально число.
– иррационально число.
Решение. Предположим,
что 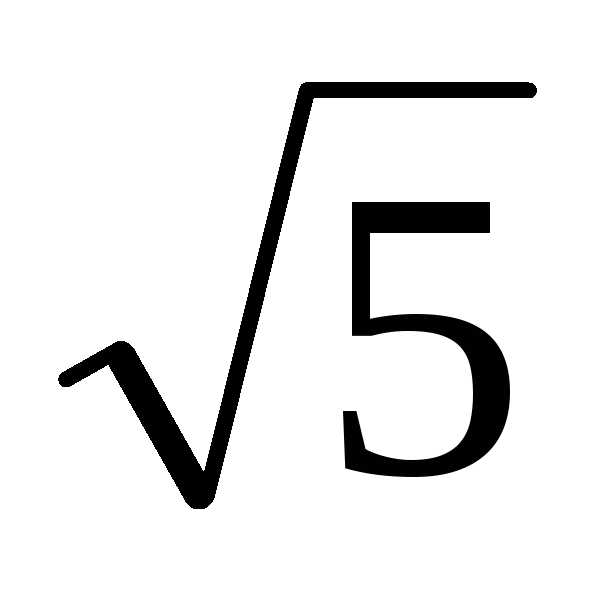 – рациональное число. Очевидно, оно не
является целым, а поэтому
– рациональное число. Очевидно, оно не
является целым, а поэтому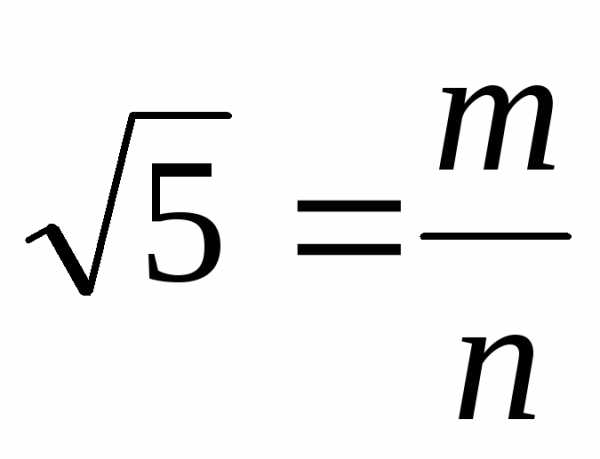 ,
где
,
где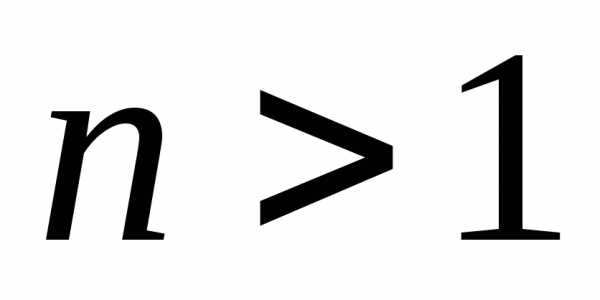 и
и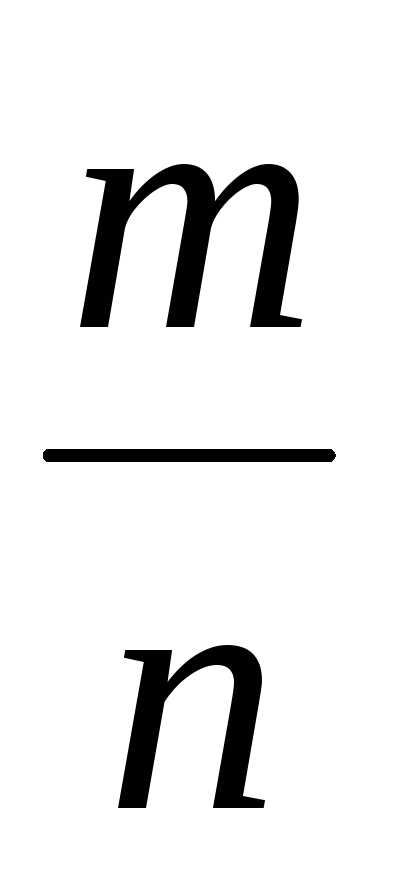 – несократимая дробь; значит, числа
– несократимая дробь; значит, числа и
и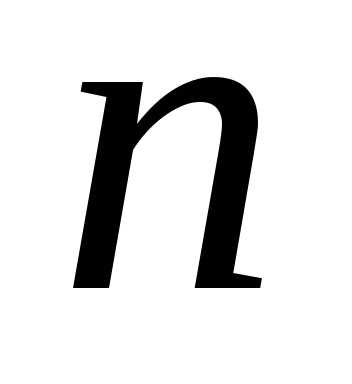 взаимно простые. Так как
взаимно простые. Так как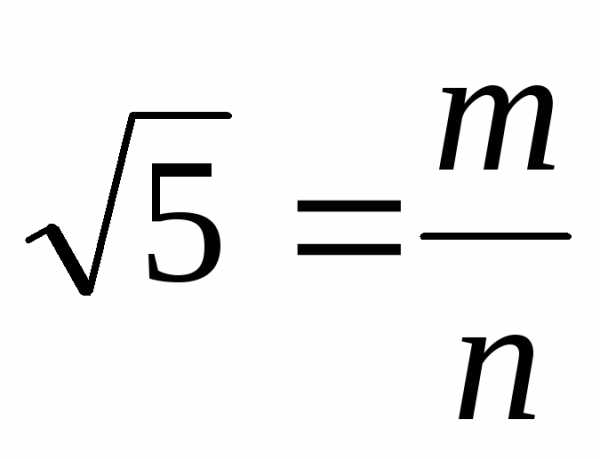 ,
то
,
то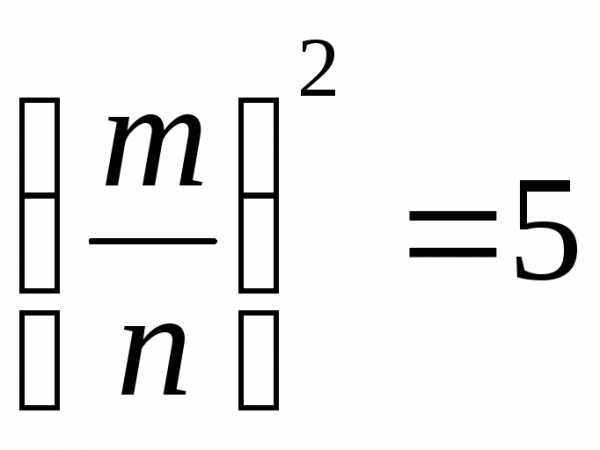 ,
то есть.
,
то есть.
Последнее равенство
означает, что 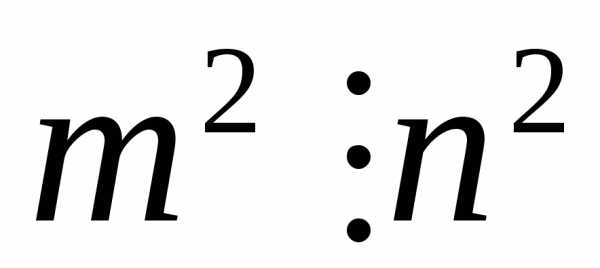
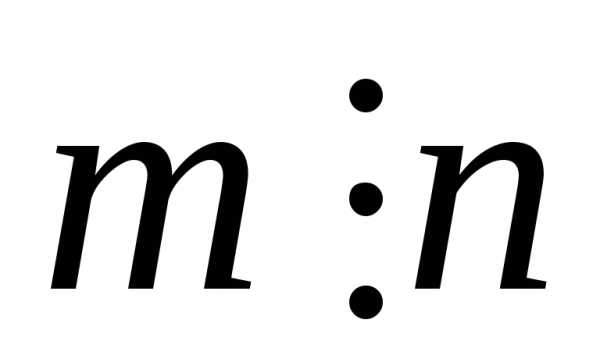 ,
то есть
,
то есть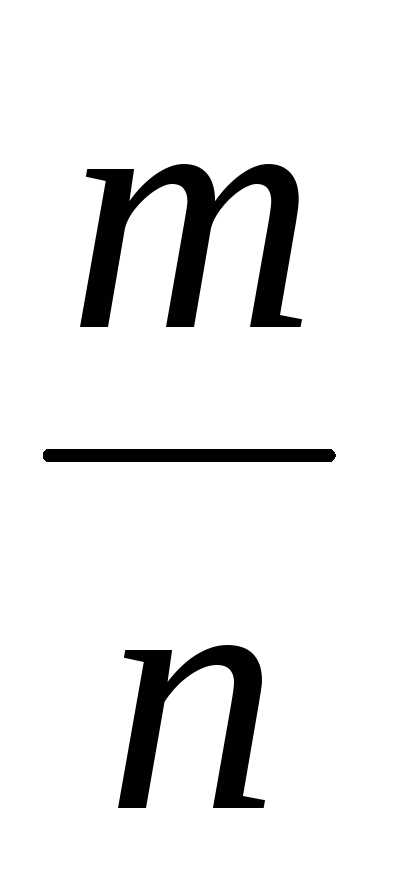 – сократимая дробь, что противоречит
условию. Следовательно, сделанное
предположение о рациональности числа
– сократимая дробь, что противоречит
условию. Следовательно, сделанное
предположение о рациональности числа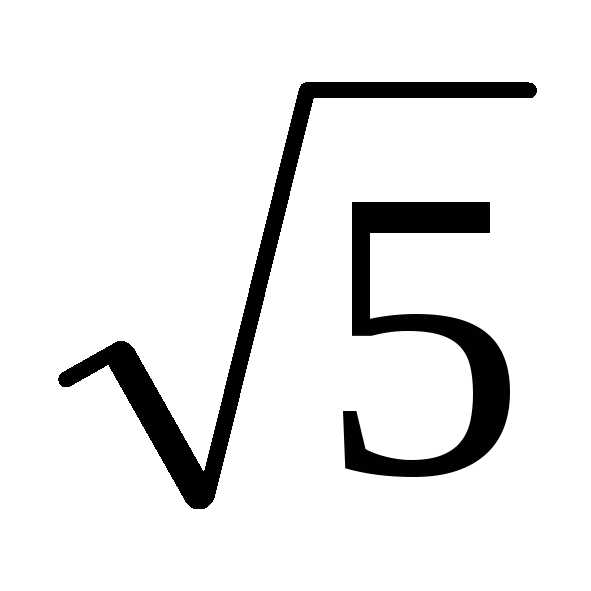 неверно и
неверно и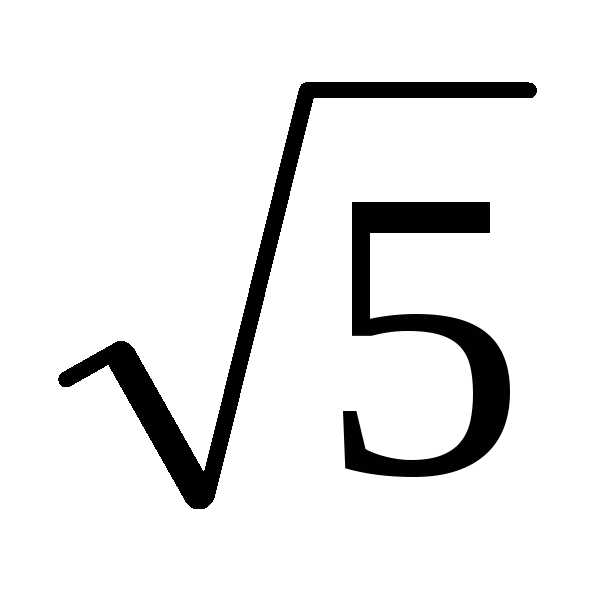 является иррациональным числом.
является иррациональным числом.studfiles.net
Рациональное число — Википедия
Материал из Википедии — свободной энциклопедии

Рациональное число (лат. ratio — отношение, деление, дробь) — число, которое можно представить обыкновенной дробью mn{\displaystyle {\frac {m}{n}}}, числитель m{\displaystyle m} — целое число, а знаменатель n{\displaystyle n} — натуральное число, к примеру 2/3. Понятие дроби возникло несколько тысяч лет назад, когда, сталкиваясь с необходимостью измерять некоторые вещи (длину, вес, площадь и т. п.), люди поняли, что не удаётся обойтись целыми числами и необходимо ввести понятие доли: половины, трети и т. п. Дробями и операциями над ними пользовались, например, шумеры, древние египтяне и греки.
Множество рациональных чисел[ | ]
Множество рациональных чисел обозначается Q{\displaystyle \mathbb {Q} } (от лат. quotient, «частное») и может быть записано в таком виде:
- Q={mn∣m∈Z, n∈N}.{\displaystyle \mathbb {Q} =\left\{{\frac {m}{n}}\mid m\in \mathbb {Z} ,\ n\in \mathbb {N} \right\}.}
Другими словами, числитель (m) может иметь знак, а знаменатель (n) должен быть положительным целым числом.
При этом оказывается, что разные записи могут представлять одну и ту же дробь, например, 34{\displaystyle {\frac {3}{4}}} и 912{\displaystyle {\frac {9}{12}}}, (все дроби, которые можно получить друг из друга умножением или делением числителя и знаменателя на одно и то же натуральное число, представляют одно и то же рациональное число). Поскольку делением числителя и знаменателя дроби на их наибольший общий делитель можно получить единственное несократимое представление рационального числа, то можно говорить об их множестве как о множестве несократимых дробей со взаимно простыми целым числителем и натуральным знаменателем:
- Q={mn∣m∈Z, n∈N, gcd(m,n)=1}.{\displaystyle \mathbb {Q} =\left\{{\frac {m}{n}}\mid m\in \mathbb {Z} ,\ n\in \mathbb {N} ,\ \gcd(m,n)=1\right\}.}
Здесь gcd(m,n){\displaystyle \gcd(m,n)}
encyclopaedia.bid
определение, сумма, разность, умножение, деление
Произвольное целочисленное число b называется рациональным числом, если его возможно написать в виде b/1. Число, которое возможно написать в виде дроби b / m , где b является целым числом, а m натуральным числом, называется рациональной дробью.
Например
-3 = -3 / 1 ; 5 = 5/1 ; 2 = 2/1 ; 0 = 0/1 ; 48 = 48 /1
Какие числа можно назвать рациональными
Рациональным числом может быть также и любая отрицательная дробь, если её опять же можно записать в виде, например :
— (2/4) = -2 / 4 ; -(4/8) = -4 / 8 ; -(3/1) = -3/1
Такие числа как 0,47 ; 2(2/7) — так мы будем обозначать смешанную дробь, -3,51367, ; -7,823321 , -4* (2/5).
Теперь покажем что все эти числа являются рациональными числами :
0,47 = 47 / 100 ; 2*(2/7) = 16/7 ; -3,51367 = -351367 / 100000 ; -7,823321 = — 7823321 / 1000000 ;
-4* (2/5) = — 22/ 5
Сумма, разность, произведение, частное рац. чисел
Также рациональными числами является сумма, разность и прозведение рациональных чисел:
Как всегда покажем на примере : — 3/7 + 4/7 = 1/7 5/8 3/4 = 5/8 6/8 = -1/8
3/10 + 5/10 = 8/10 = 0.8
(3/6) * 3(3/4) = (3/6) * (15/4) = (45/24)
Если делителем является любое число отличное от нуля, то частное двух рациональных чисел является также рациональным числом .
Например:
-0.5 / (3/7) = — (5*7) / (10*3) = -35 / 30 = — 7/6
Любое рациональное число в виде дроби
Вы уже научились представлять некоторые обыкновенные дроби в виде десятичных дробей. К примеру :
7/ 25 = 0,28 Потому что 7 делить на 25 получается 0,28
Но не все обыкновенные дроби получается представить как десятичную дробь
Например, если нам придётся делить 2 на 3, то мы получим сначала нуль целых, а позже множество шестёрок после запятой, которые никогда не закончатся, в таких случаях обычно округляют Например : 2/3 = 0,66667…
Деление в этом случае просто бесконечно, оно никогда не закончится, тогда мы можем записать 1/3 = 0,333333…
При делении 5 на 11, можно получить 5/11 = 0,4545454545 , а при делении 1 на 15, можно получить, что 1/15 = 0.066666666…
В записях 0,333…, 0,4545… и 0,0666… несколько или одна цифра начинает бесконечно повторяться много много раз. Такие записи называются периодическими дробями
Вместо записи 0,333… обычно пишут 0,(3), вместо 0,4545… пишут 0,(45), а вместо 0,0666… пишут 0,0(6).
Примечание : другими словами, после того как заканчивается часть где цифры не повторяются, и начинается так называемая периодическая часть, в скобках пишут ту часть, которая в дальнейшем повторяется множество раз.
Получается, что абсолютно любое рациональное число можно представить в виде десятичной дроби (частный случай это когда дробь является целым числом, например: 3/1 = 3 ), либо если мы имеем дело с бесконечной частью дроби, тогда мы записываем в виде периодической дроби.
Примеры таких дробей описаны выше.
Для дроби 2/3 число 0,6 будет являться значением, приближенном к одной трети, которое округлено до десятых с недостатком, но 0.3 < 1/3
Число 0,4 будет являться значением, приближенным к этой дроби округлённом до десятых с избытком:
0,4 > 1/3 .
Мы можем это записать в виде двойного неравенства : 0,3 < 1/3 < 0,4
Если число 5/11 = 0,454545… округлить до десятых, то получим 5/11 приблизительно равное 0,5, если это число округлить до сотых, то получим 5/11 = 0,45 , а если округлить до тысячных, то получим 5/11 = 0,455
Нужна помощь в учебе?
Предыдущая тема: Функция y = k/x: ее график и свойства при k0
Следующая тема:   Иррациональные числа: понятие и особенности
Все неприличные комментарии будут удаляться.
www.nado5.ru
Рациональные числа, зачем нужны рациональные числа, в чем их особенность
Рациональным числом называют число, которое можно записать в виде отношения mn, где m — целое число, a n — натуральное число. Чтобы понимать значение рационального числа, необходимо знать, что такое натуральные числа, целые числа, дроби (правильные \(\frac{2}{3}\), неправильные \(\frac{3}{2}\), бесконечные периодические 0,(4) и смешанные \(4 \frac{2}{3}\),). Натуральные числа представляют собой числа, которые мы используем при счете (1, 2, 3…). В свою очередь целые числа – это натуральные числа, а также противоположные им и ноль (1, 2, -1, -2…). Дробью называется число, записанное в виде отношения mn (\(\frac{2}{3}\)), где m – целое, а n – натуральное число. Понятие дроби берет свое начало еще с древних времен, когда людям в торговых делах и бытовых нуждах требовалось определить часть какого-либо целого.
История рациональных чисел началась с возникновением финансово-кредитных отношений между людьми. Чтобы в численном виде представить задолженность человека, нужно было записывать числа, противоположные натуральным. Так появились отрицательные числа (-3, -167). А для того, чтобы записывать часть целого (например, возвращение долга частями), стали использовать дроби. Именно поэтому математикам необходимо было как-то объединить такие характерные числа, дать им общее название. Так появились рациональные числа (от латинского ratio – «отношение»).
Для усвоения материала приведем пример задания на определение рациональных чисел из ряда чисел.
Задача. Даны числа: -34, 480, 0,11, \(\frac{1}{2}\), 8. Какие из них рациональные?
Решение.
Рассмотрим отдельно каждое из заданных чисел:
- Число -34 – целое число;
- Число 480 – натуральное число;
- Число 0,11 = \(\frac{11}{100} \) – десятичная дробь;
- Число \(\frac{1}{2}\) — правильная дробь;
- Число 8 – натуральное число.
Каждое из заданных чисел можно представить в виде дроби с целым и натуральным знаменателем. Значит, все 5 чисел являются рациональными числами.
Ответ: все числа являются рациональными.
Чтобы хорошо понимать специфику рациональных чисел, нужно усвоить два правила:
- Сумма рациональных чисел является рациональным числом.
- Произведение рациональных чисел является рациональным числом.
Теория в математике очень важна. Умение отличать натуральные числа от целых, рациональные от иррациональных поможет Вам не запутаться и не ошибиться в практике. Удачи!
myalfaschool.ru
