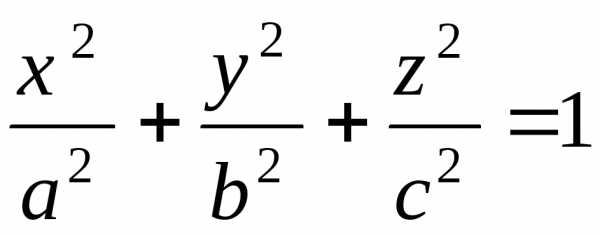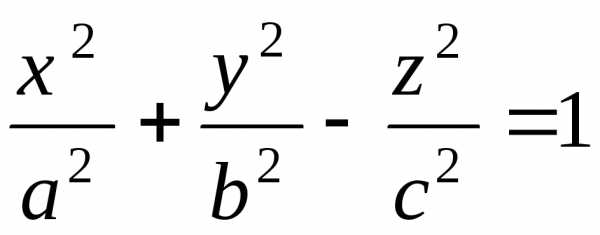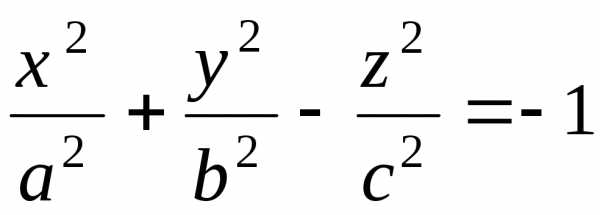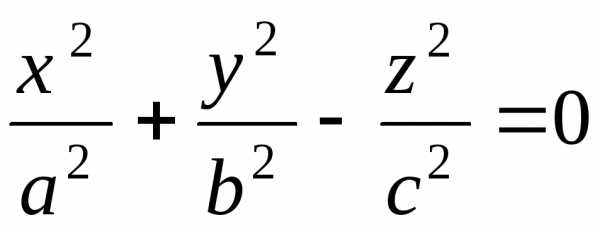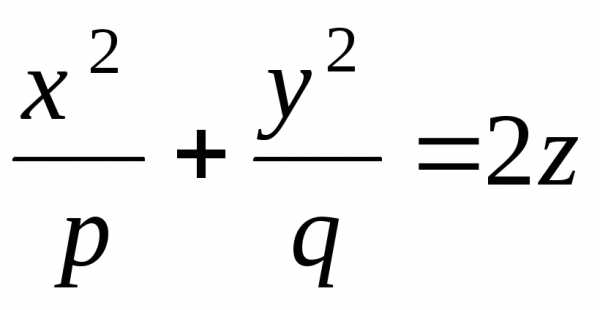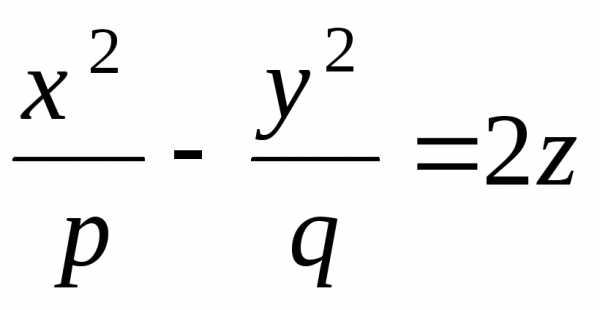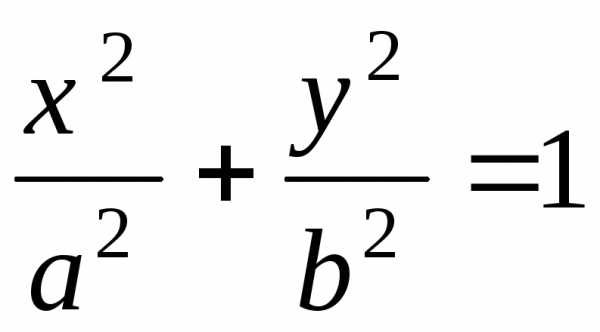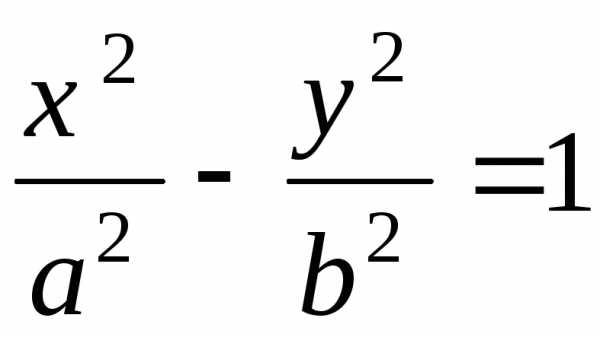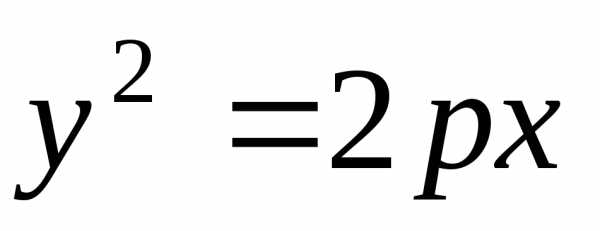Поверхности второго порядка
§ 7. Цилиндрические и конические поверхности. Поверхности вращения
Основные теоретические сведения
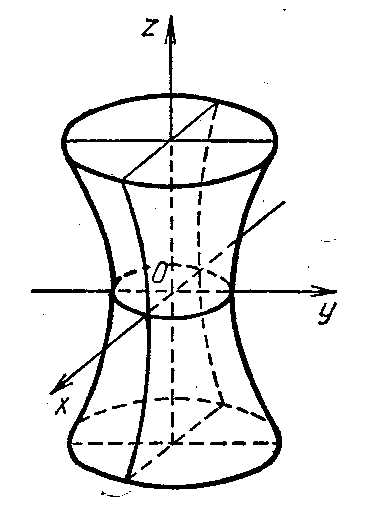
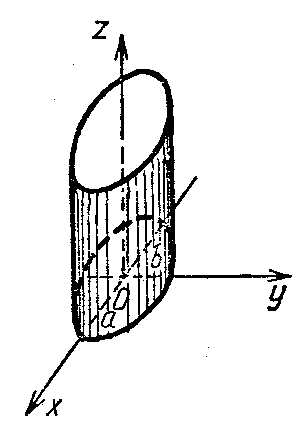
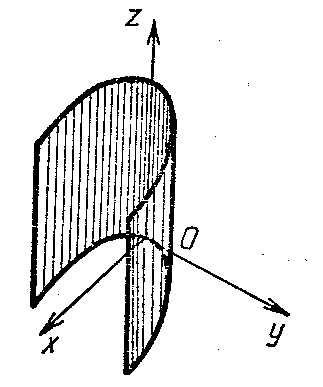
Цилиндрической поверхностью или просто цилиндром называется всякая поверхность, которую можно получить движением прямой, перемещающийся параллельно некоторому вектору и все время пересекающей данную линию, которая носит название направляющей. Движущаяся прямая называется образующей.
Конической поверхностью или просто конусом называется поверхность, образованная движением прямой, проходящей через данную точку, называемую вершиной конуса, и скользящей по данной кривой. Движущаяся прямая называется образующей конуса, а кривая, по которой скользит образующая, — направляющей.
Вращением фигуры 
 описывает
окружность с центром на оси вращения,
лежащую в плоскости, перпендикулярной
к оси вращения.
описывает
окружность с центром на оси вращения,
лежащую в плоскости, перпендикулярной
к оси вращения.Поверхность, образованная вращением линии вокруг оси, называется поверхностью вращения.
Канонические уравнения поверхностей второго порядка
Поверхность второго порядка задается в прямоугольных координатах уравнением второй степени
(7.1)
Путем преобразования
координат (поворотом осей и параллельным
переносом) уравнение (7.1) приводится к
каноническому виду. В случае, когда в
уравнении (7.1) отсутствуют члены с
произведением координат
,
это уравнение выделением полных квадратов
по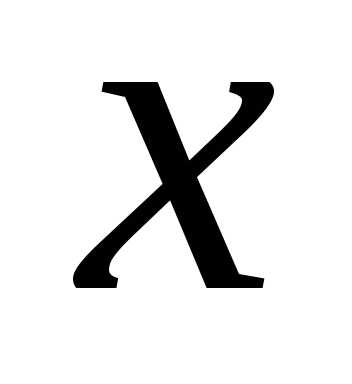 ,
, ,
,
Форму и расположение поверхностей второго порядка обычно изучают методом параллельных сечений. Сущность метода заключается в том, что поверхность пересекается несколькими плоскостями, параллельными координатным плоскостям. Форма и параметры полученных сечений позволяют выяснить форму самой поверхности.
Таблица 3
Поверхность второго порядка, каноническое уравнение | Вид |
1 | 2 |
Эллипсоид
| |
1 | 2 |
Гиперболоид: однополостный,
двуполостный,
| |
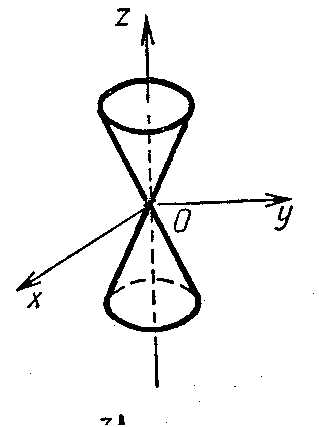
| Конус,
| |
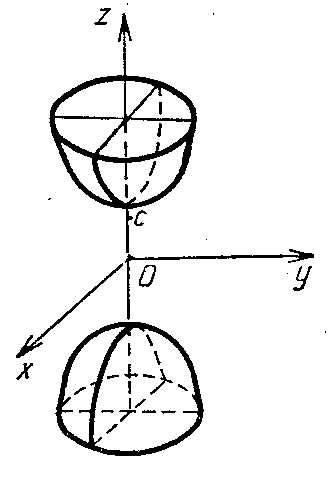
Параболоид: эллиптический, гиперболический, | |
1 | 2 |
Цилиндр: эллиптический, гиперболический, параболический, | |
Примеры решения задач
Задача 7.1. Составить
уравнение сферы, радиус которой  ,
а центр находится в точке.
,
а центр находится в точке.
Решение. Сфера – это множество точек, отстоящих
от центра на одном и том же расстоянии.
Следовательно, обозначив через 
 сферы и выразив через них равенство
сферы и выразив через них равенство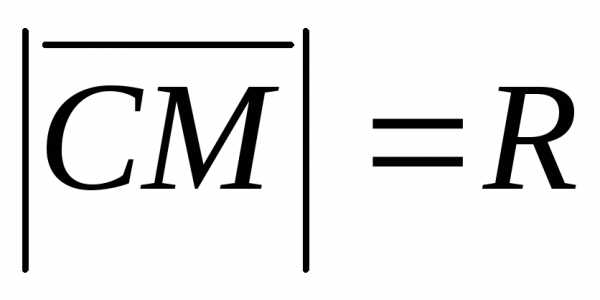 ,
будем иметь
,
будем иметь.
Возведя обе части равенства в квадрат, получим искомое каноническое уравнение сферы:
.
Если центр сферы поместить в начало координат, то уравнение сферы имеет более простой вид:
.
Ответ. .
Задача 7.2. Составить уравнение конической поверхности с вершиной в начале координат и направляющей
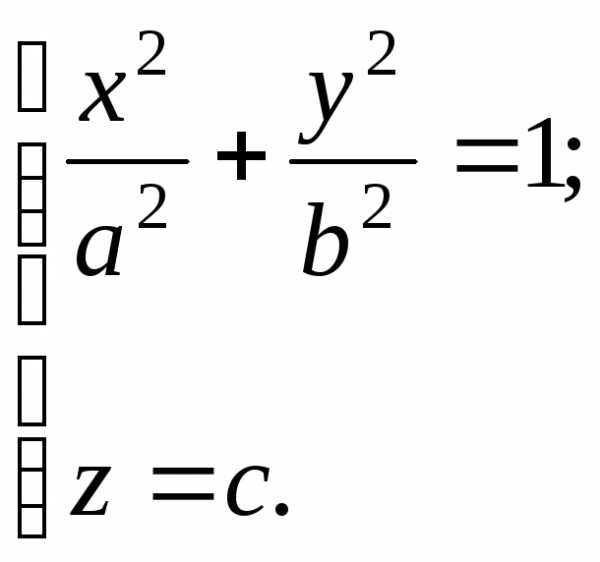 (7.1)
(7.1)
Решение. Канонические уравнения образующих
через точку 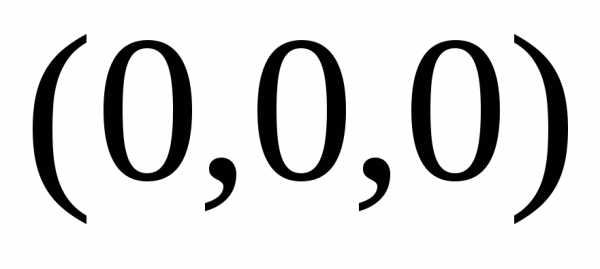 и точку
и точку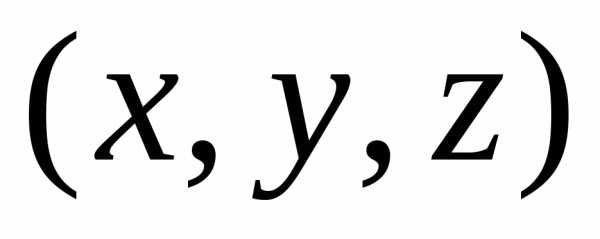
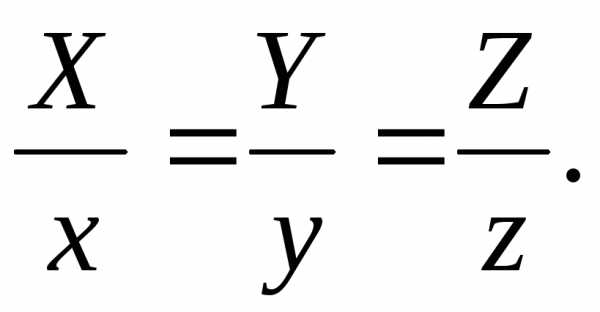 (7.2)
(7.2)
Исключим  ,
, ,
, из уравнений (7.1) и (7.2). Для этого в
уравнениях (7.2) заменим
из уравнений (7.1) и (7.2). Для этого в
уравнениях (7.2) заменим на
на и определим
и определим и
и :
:
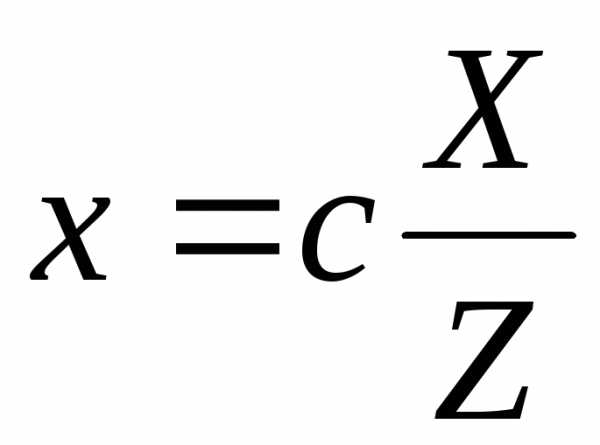 ;
; 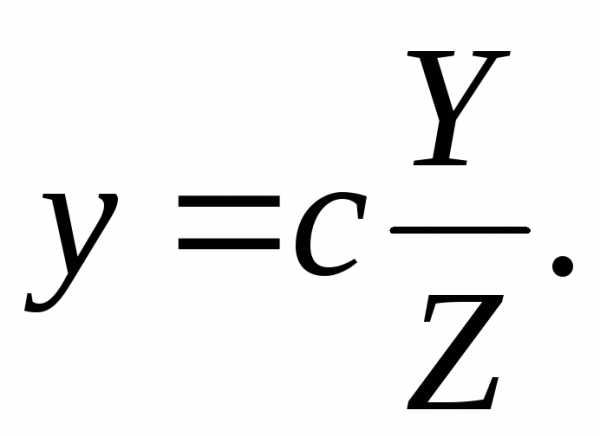
Подставив эти
значения 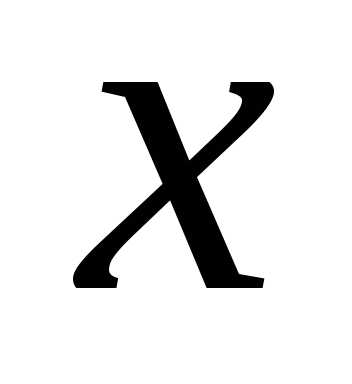
 в первое уравнение системы (7.1), будем
иметь:
в первое уравнение системы (7.1), будем
иметь: 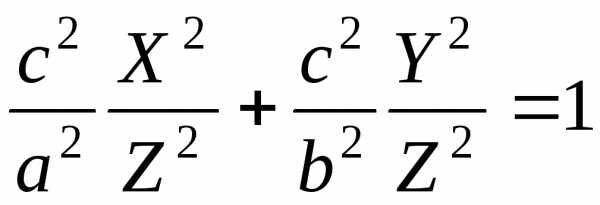 или
или 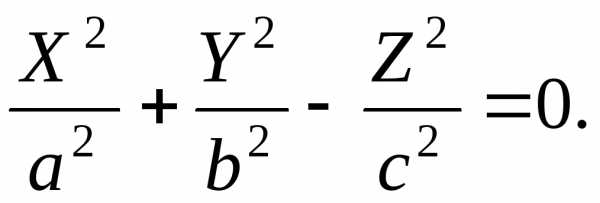
Полученное уравнение определяет конус второго порядка (см. табл. 3)
Задача 7.3. Какую поверхность определяет уравнение
Решение. Эта поверхность есть гиперболический
цилиндр с образующими, параллельными
оси 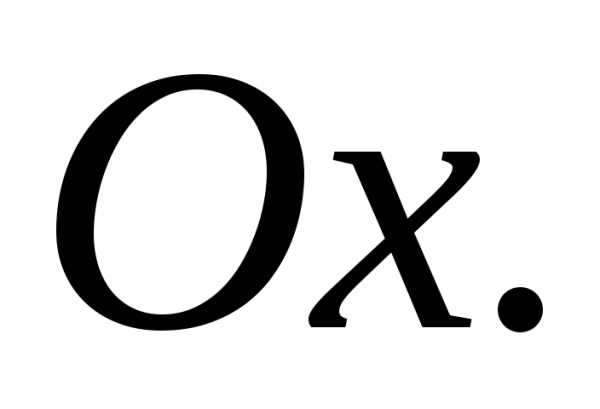 Действительно, данное уравнение не
содержит
Действительно, данное уравнение не
содержит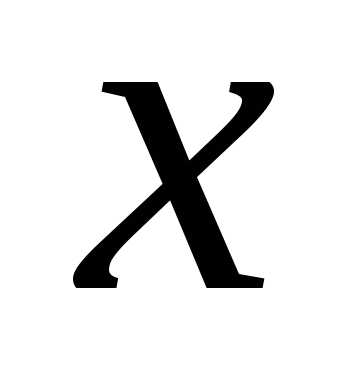 ,
а направляющая цилиндра есть гипербола
,
а направляющая цилиндра есть гипербола
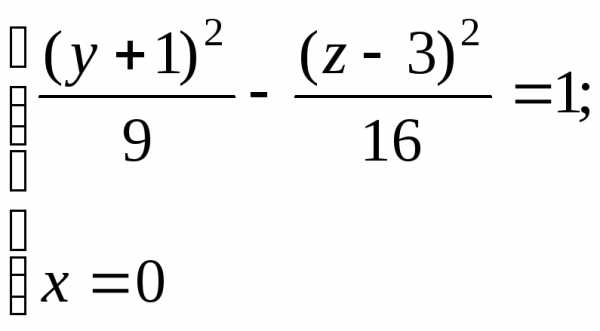
с центром симметрии
в точке 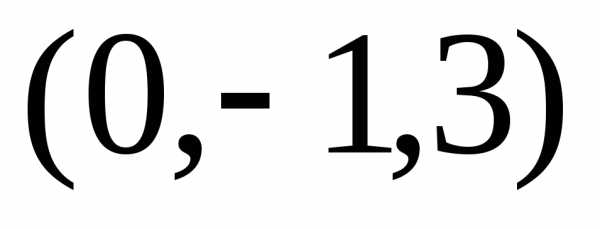 и действительной осью, параллельной
оси
и действительной осью, параллельной
оси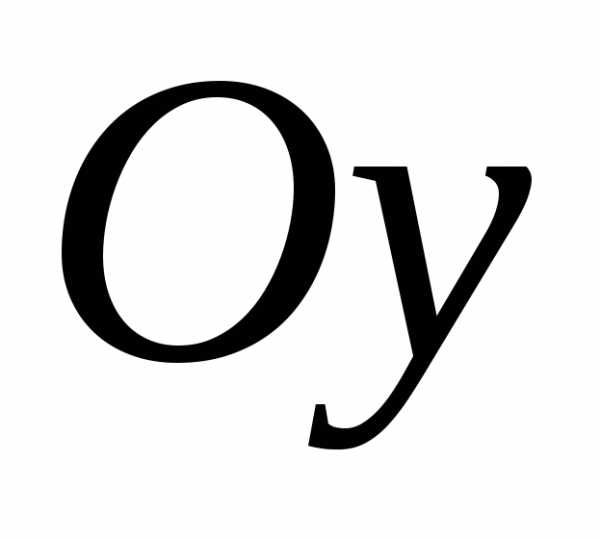 .
.
Задача 7.4. Исследовать и построить поверхность, заданную уравнением
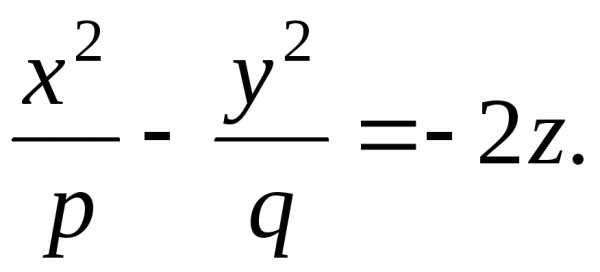
Решение. Пересечем поверхность плоскостью 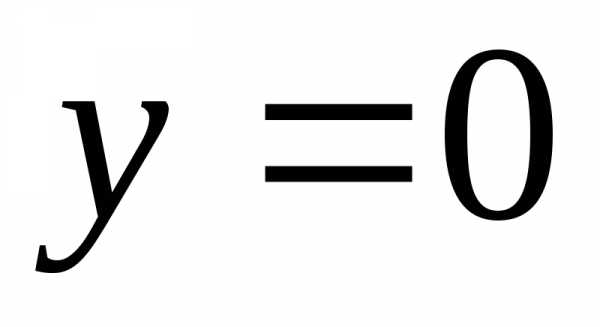 .
В результате имеем
.
В результате имеем
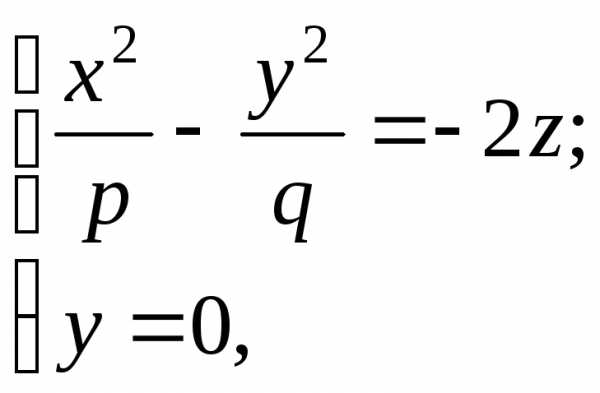
откуда 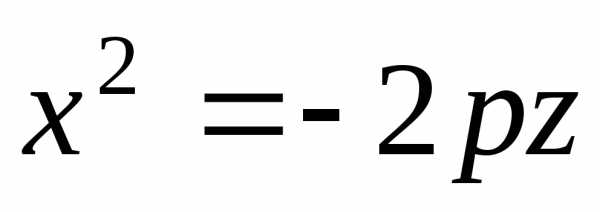 .
Это уравнение параболы в плоскости
.
Это уравнение параболы в плоскости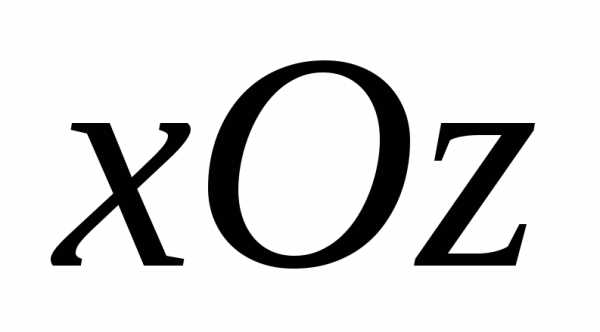
Сечение заданной
поверхности плоскостью 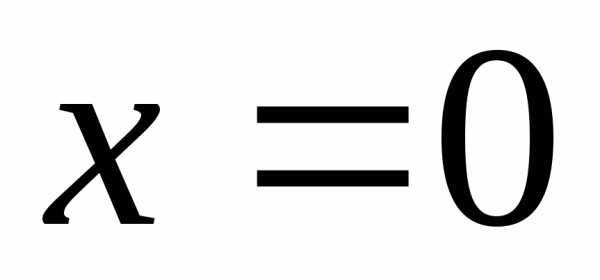
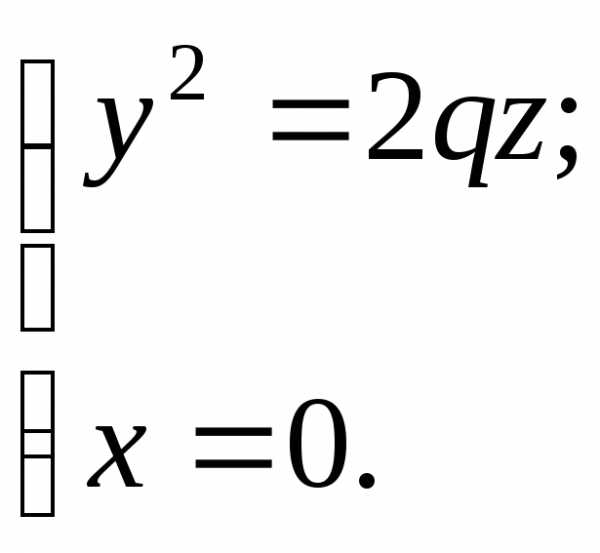
Сечение плоскостью 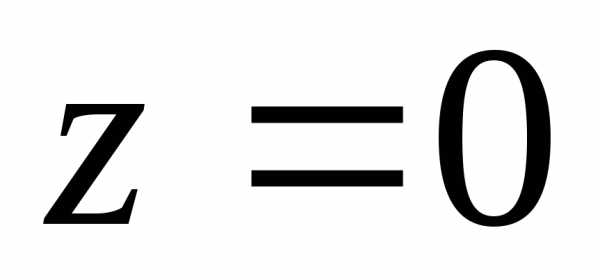 есть пара пересекающихся прямых:
есть пара пересекающихся прямых:
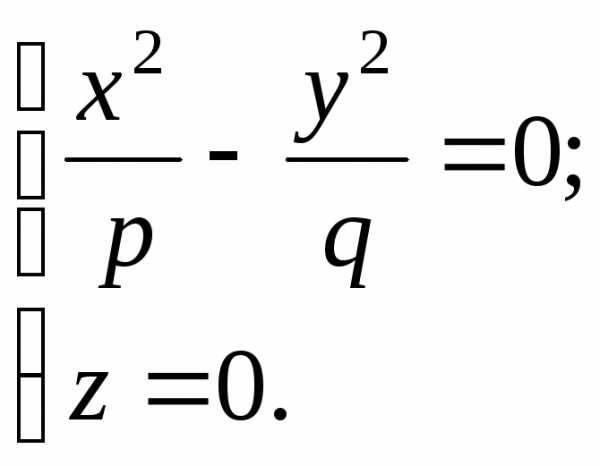
Сечение плоскостями,
параллельными плоскости  ,
есть гиперболы:
,
есть гиперболы:
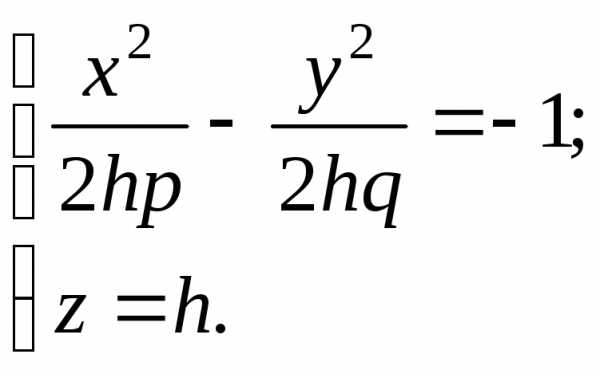
При  действительная ось гиперболы параллельна
оси
действительная ось гиперболы параллельна
оси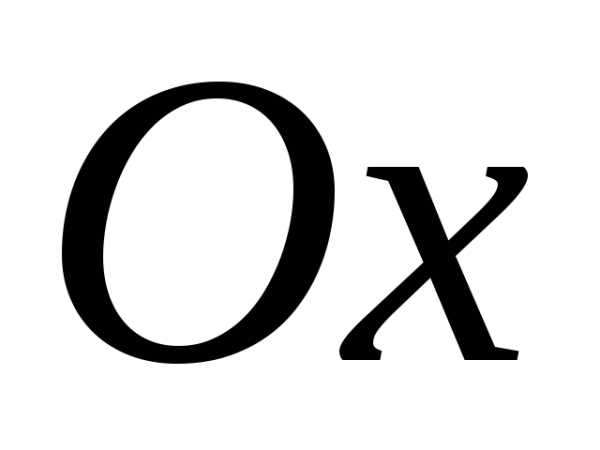 ,
при
,
при оси
оси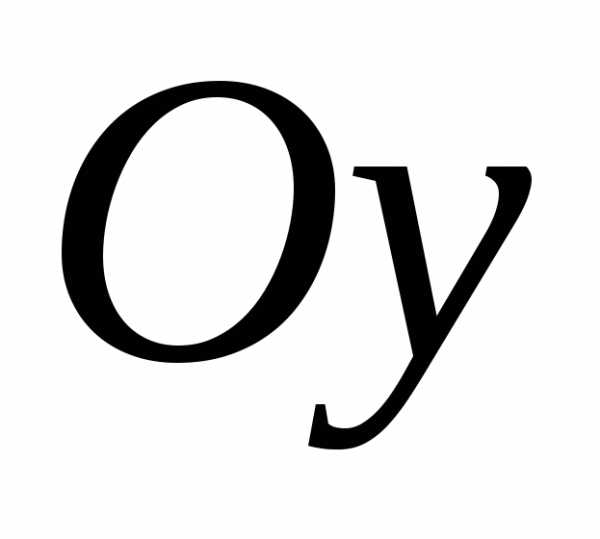
Замечание. Интересным свойством гиперболического параболоида является наличие прямых линий, лежащих всеми своими точками на его поверхности. Такие прямые называются прямолинейными образующими гиперболического параболоида. Через каждую точку гиперболического параболоида проходят две прямолинейные образующие.
Задача 7.5. Какую поверхность определяет уравнение
Решение. Чтобы привести данное уравнение к
каноническому виду, выделим полные
квадраты переменных 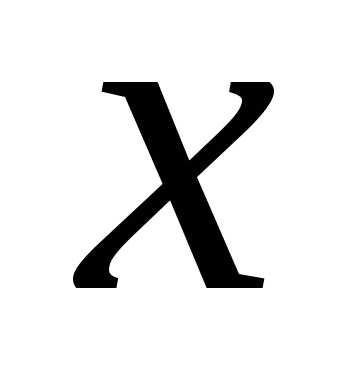 ,
, ,
, :
:
Отсюда
Сравнивая полученное уравнение с табличными (см. табл. 3), видим, что это уравнение однополостного гиперболоида, центр которого смещен в точку Путем параллельного переноса системы координат по формулам
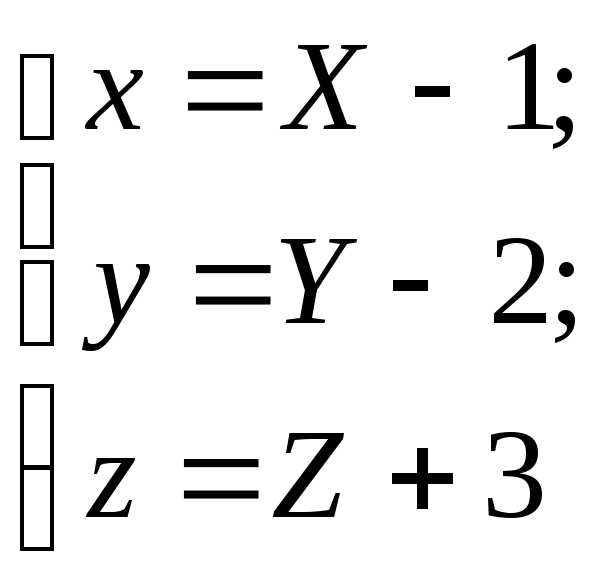
приведем уравнение к каноническому виду:
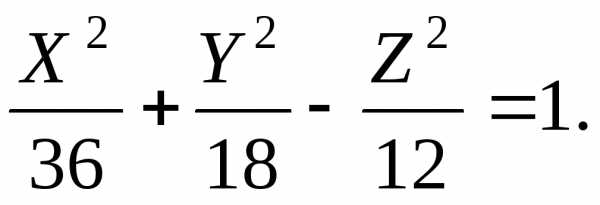
Замечание. Однополостный гиперболоид, как и гиперболический, имеет два семейства прямолинейных образующих.
studfiles.net
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА • Большая российская энциклопедия
ПОВЕ́РХНОСТИ ВТОРО́ГО ПОРЯ́ДКА, множества точек 3-мерного пространства, координаты которых в декартовой системе координат удовлетворяют алгебраическому уравнению 2-й степени $$a_{11}x^2+a_{22}y^2+a_{33}z^2+ 2a_{12}xy+ 2a_{13}xz+\\ + 2a_{23}yz+ 2a_{14}x+ 2a_{24}y+ 2a_{34}z+a_{44}= 0.\tag{*}$$ Это уравнение может и не определять действительного геометрич. образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую П. в. п. Существует прямоугольная система координат, в которой уравнение (*) приводится к одному из следующих канонич. видов, каждому из которых соответствует определённый класс поверхности второго порядка.
Нераспадающиеся поверхности
Невырождающиеся:
эллиптические
1. $\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$ – эллипсоид,
2. $\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=-1$ – мнимый эллипсоид;
гиперболические
3. $\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$ – однополостный гиперболоид,
4. $\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=-1$ – двуполостный гиперболоид;
параболические ($p\gt 0, q\gt 0$)
5. $\frac{x^2}{p}+\frac{y^2}{q}=2z$ – эллиптич. параболоид,
6. $\frac{x^2}{p}-\frac{y^2}{q}=2z$ – гиперболич. параболоид.
Вырождающиеся:
цилиндрические
7. $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ – эллиптич. цилиндр,
8. $\frac{x^2}{a^2}+\frac{y^2}{b^2}=-1$ – мнимый эллиптич. цилиндр,
9. $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ – гиперболич. цилиндр,
10. $y^2=2px$ – параболич. цилиндр;
конические
11. $\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=0$ – конус,
12. $\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=0$ – мнимый конус.
Распадающиеся вырождающиеся поверхности
13. $\frac{x^2}{a^2}-\frac{y^2}{b^2}=0$ – пара пересекающихся плоскостей,
14. $\frac{x^2}{a^2}+\frac{y^2}{b^2}=0$ – пара мнимых пересекающихся плоскостей,
15. $x^2=a^2$ – пара параллельных плоскостей,
16. $x^2=–a^2$ – пара мнимых параллельных плоскостей,
17. $x^2=0$ – пара совпадающих плоскостей.
П. в. п., имеющая единственный центр симметрии (центр П. в. п.), называется центральной П. в. п.; без центра симметрии или с неопределённым центром – нецентральной поверхностью второго порядка.
Среди П. в. п., содержащих хотя бы одну точку, ограниченными являются лишь эллиптические, все остальные неограниченные. Пересечения П. в. п. с плоскостью являются линиями второго порядка.
Исследование вида П. в. п. может быть проведено (таблицы 1 и 2) без приведения уравнения (*) к канонич. виду с помощью т. н. инвариантов П. в. п., составленных из коэффициентов этого уравнения. Основные инварианты: $$S=a_{11}+a_{22}+a_{33}, \\ T=\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix} + \begin{vmatrix} a_{11} & a_{13} \\ a_{31} & a_{33} \end{vmatrix} + \begin{vmatrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{vmatrix}, \\ \delta=\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{12} & a_{22} & a_{23} \\ a_{13} & a_{23} & a_{33} \end{vmatrix}, \Delta=\begin{vmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{12} & a_{22} & a_{23} & a_{24} \\ a_{13} & a_{23} & a_{33} & a_{34} \\ a_{14} & a_{24} & a_{34} & a_{44} \end{vmatrix}.$$
| Таблица 1. Классификация поверхностей второго порядка по инвариантам | ||||
| Невырождающиеся поверхности | Вырождающиеся поверхности | |||
| $\Delta \gt 0$ | $\Delta \lt 0$ | $\Delta = 0$ | ||
| Центральные поверхности $\delta \neq 0$ | $\delta S\gt 0, T\gt 0$ | Мнимый эллипсоид | Эллипсоид | Мнимый конус |
| $\delta S \leq 0$ и(или) $T \leq 0$ | Однополостный гиперболоид | Двуполостный гиперболоид | Действительный конус | |
| Нецентральные поверхности $\delta = 0$ | Гиперболический параболоид | Эллиптический параболоид | Цилиндрические и распадающиеся поверхности (см. табл. 2) | |
| Таблица 2. Цилиндрические и распадающиеся поверхности второго порядка ($\Delta=0, \delta=0$) | ||||
| $T\gt 0$ | Цилиндрические поверхности $\Delta’ \neq 0$ | Распадающиеся поверхности $\Delta’ = 0$ | ||
| Эллиптический цилиндр | Пара мнимых пересекающихся плоскостей | |||
| Мнимый $\Delta’S \gt 0$ | Действительный $\Delta’S \lt 0$ | |||
| $T\lt 0$ | Гиперболический цилиндр | Пара пересекающихся плоскостей | ||
| $T = 0$ | Параболический цилиндр | Пара мнимых параллельных плоскостей $\Delta» \gt 0$ | Пара совпадающих плоскостей $\Delta» = 0$ | |
| Пара параллельных плоской $\Delta» \lt 0$ | ||||
Их значения не меняются при параллельном переносе и повороте системы координат. Используются также семиинварианты (полуинварианты) $Δ′$ и $\Delta″$, которые являются инвариантами относительно поворота системы координат:$$Δ′=Δ_{11}+Δ_{22}+Δ_{33},$$ где $Δ_{ij}$ – алгебраич. дополнение элемента $a_{ij}$ в $Δ$; $$\Delta»=\begin{vmatrix} a_{11} & a_{14} \\ a_{14} & a_{44} \end{vmatrix} + \begin{vmatrix} a_{22} & a_{24} \\ a_{24} & a_{44} \end{vmatrix} + \begin{vmatrix} a_{33} & a_{34} \\ a_{34} & a_{44} \end{vmatrix}.$$Их значения не меняются при повороте осей координат. Инварианты П. в. п. определяют П. в. п. с точностью до движений евклидова пространства. Любые две нераспадающиеся П. в. п., инварианты которых соответственно равны, эквивалентны по отношению к группе движения пространства, т. е. могут быть совмещены движением.
По отношению к более широкой, чем группа движений, группе аффинных преобразований эквивалентными являются П. в. п., канонич. уравнения которых совпадают; имеется 17 аффинно эквивалентных классов, канонич. уравнения которых получаются из уравнений 1–17 при $a=b=c=1$ и $2p=2q=1$.
В проективной геометрии эквивалентными являются П. в. п., которые могут быть переведены друг в друга при проективных преобразованиях (группа которых шире, чем группа аффинных преобразований). Имеется 8 проективно эквивалентных классов, т. е. между некоторыми аффинными классами имеется проективная общность. Это связано с тем, что при проективных преобразованиях исчезает особая роль бесконечно удалённых элементов пространства. Напр., эллипсоид и двуполостный гиперболоид, различные с аффинной точки зрения, принадлежат одному проективному классу поверхностей второго порядка.
П. в. п. впервые представлены уравнениями 2-й степени у Л. Эйлера (1748), совр. названия невырожденных П. в. п. даны Г. Монжем (1801).
bigenc.ru
Понятие поверхности второго порядка
Поверхностью называется непрерывное двупараметрическое множество точек.
Поверхность второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
в котором по крайней мере один из коэффициентов отличен от нуля.
Уравнение мы будем называть общим уравнением поверхности второго порядка.
Очевидно, поверхность второго порядка, рассматриваемая как геометрический объект, не меняется, если от данной декартовой прямоугольной системы координат перейти к другой декартовой системе координат. Отметим, что исходное уравнение и уравнение, полученное после преобразования координат, алгебраически эквивалентны.
Инварианты уравнения поверхности второго порядка.
Справедливо следующее утверждение.
являются инвариантами уравнения (1) поверхности второго порядка относительно преобразований декартовой системы координат.
Классификация поверхностей второго порядка
Теорема: Для произвольной поверхности , заданной общим уравнением существует такая декартова прямоугольная система координат, что в этой системе поверхностьимеет уравнение одного из следующих семнадцати канонических видов.
1) — эллипсоид,
2) — мнимый эллипсоид,
3) — однополостный гиперболоид,
4) — двуполостный гиперболоид,
5) — конус,
6) — мнимый конус (точка),
7) — эллиптический параболоид,
8) — гиперболический параболоид,
9) — эллиптический цилиндр,
10) — мнимый эллиптический цилиндр,
11) — две мнимые пересекающиеся плоскости (ось),
12) — гиперболический цилиндр,
13) — две пересекающиеся плоскости,
14) — параболический цилиндр,
15) — две параллельные плоскости,
16) — две мнимые параллельные плоскости,
17) — две совпадающие плоскости (плоскость).
В выше перечисленных уравнениях — положительные параметры. Систему координат называют канонической.
Классификация центральных поверхностей.
Пусть S — центральная поверхность второго порядка. Перенесем начало координат в центр этой поверхности, а затем произведем стандартное упрощение уравнения этой поверхности. В результате указанных операций уравнение поверхности примет вид:
Так как инвариант для центральной поверхности отличен от ноля и его значение, вычисленное для уравнения , равно, то коэффициенты удовлетворяют условию:
Возможны следующие случаи:
1. Коэффициенты одного знака, а коэффициентотличен от нуля. В этом случае поверхностьS называется эллипсоидом.
Если коэффициенты одного знака, то левая часть ни при каких значенияхне обращается в нуль, т.е. уравнению поверхностине удовлетворяют координаты никакой точки. В этом случае поверхностьназываетсямнимым эллипсоидом.
Если знак коэффициентов противоположен знаку коэффициента , то поверхностьназываетсявещественным эллипсоидом. В дальнейшем термином «эллипсоид» мы будем называть лишь вещественный эллипсоид.
Обычно уравнение эллипсоида записывают в канонической форме. Очевидно, числа
положительны. Обозначим эти числа соответственно . После несложных преобразований уравнение эллипсоидаможно записать в следующей форме:
Уравнение называетсяканоническим уравнением эллипсоида.
Если эллипсоид задан своим каноническим уравнением то оси,иназываются его главными осями.
2. Из четырех коэффициентов , два – одного знака, а два других – противоположного. В этом случае поверхность называетсяоднополостным гиперболоидом.
Обычно уравнение однополостного гиперболоида записывают в канонической форме. Пусть, ради определенности,
Тогда числа:
положительны. Обозначим эти числа соответственно . После несложных преобразований уравнениеоднополостного гиперболоида можно записать в следующей форме:
Уравнение называетсяканоническим уравнением однополостного гиперболоида.
Если однополостный гиперболоид задан своим каноническим уравнением то оси,иназываются его главными осями.
3. Знак одного из первых трех коэффициентов , противоположен знаку остальных коэффициентов. В этом случае поверхность называетсядвуполостным гиперболоидом.
Запишем уравнение двуполостного гиперболоида в канонической форме. Пусть, ради определенности,
Тогда:
Обозначим эти числа соответственно через . После несложных преобразований уравнениедвуполостного гиперболоида можно записать в следующей форме:
Уравнение называетсяканоническим уравнением двуполостного гиперболоида.
Если двуполостный гиперболоид задан своим каноническим уравнением, то оси ,иназываются его главными осями.
4. Коэффициент равен нулю. В этом случае поверхностьназываетсяконусом второго порядка.
Если коэффициенты — одного знака, то левая часть обращается в нульлишь для, т.е. уравнению поверхностиудовлетворяют координаты только одной точки. В этом случае поверхностьназываетсямнимым конусом второго порядка. Если коэффициенты имеют разные знаки, то поверхностьявляетсявещественным конусом второго порядка.
Обычно уравнение вещественного конуса второго порядка записывают в канонической форме. Пусть, ради определенности,
Обозначим
соответственно через . Тогда уравнениеможно записать в виде
Уравнение называетсяканоническим уравнением вещественного конуса второго порядка.
Классификация нецентральных поверхностей второго порядка.
Пусть — нецентральная поверхность второго порядка, т.е. поверхность, для которой инвариантравен нулю. Произведем стандартное упрощение уравнения этой поверхности. В результате уравнение поверхности примет вид
для системы координат
Так как инвариант и его значение, вычисленное для уравнения, равно, то один или два из коэффициентовравны нулю. В соответствии с этим рассмотрим следующие возможные случаи.
1. Один из коэффициентов равен нулю. Ради определенности будем считать, что(если равен нулю какой-либо другой из указанных коэффициентов, то можно перейти к рассматриваемому случаю путем
переименования осей координат). Перейдем от координат к новым координатампо формулам.
Подставляя , найденные изв левую частьи заменяя затем
на ,на,наи на , получим следующее уравнение поверхностив новой системе координат:
1) Пусть ,. Поверхностьраспадается на пару плоскостей.
При этом, очевидно, эти плоскости будут мнимыми, если знаки и — одинаковы, и вещественными, если знаки и различны.
2) Пусть . Уравнениепринимает вид:
Известно, что уравнение является уравнением цилиндра с образующими, параллельными оси. При этом, еслиимеют одинаковый знак, то левая часть отлична от нуля для любыхи, т.е. цилиндр будетмнимым. Если же среди коэффициентов имеются коэффициенты разных знаков, то цилиндр будетвещественным. Отметим, что в случае, когда иимеют одинаковые знаки, a — противоположный, то величины положительны.
Обозначая их соответственно через и, мы приведем уравнениек виду:
Таким образом, в отмеченном случае мы имеем эллиптический цилиндр. В случае, и имеют различные знаки, мы получимгиперболический цилиндр. Легко убедиться, что уравнение гиперболического цилиндра может быть приведено к виду:
3) Пусть . Произведем параллельный перенос системы координат, выбирая новое начало в точке с координатами:
При этом оставим старые обозначения координат . Очевидно, для того чтобы получить уравнение поверхностив новой системе координат, достаточно заменить в уравнениина . Получим следующее уравнение:
Уравнение определяет так называемыепараболоиды. Причем если и имеют одинаковый знак, то параболоид называетсяэллиптическим. Обычно уравнение эллиптического параболоида записывают в канонической форме:
Уравнение легко получается из. Еслии имеют разные знаки, то параболоид называетсягиперболическим. Каноническое уравнение гиперболического параболоида имеет вид:
Это уравнение также легко может быть получено из .
2. Два из коэффициентов , , равны нулю. Ради определенности будем считать, что и . Перейдем отк новым координатам по формулам:
Подставляя , найденные изв левую частьи заменяя затемна , на , на и на , получим следующее уравнение поверхностив новой системе координат:
1) Пусть . Поверхностьраспадается напару параллельных плоскостей.
При этом, очевидно, эти плоскости будут мнимыми, если знаки иодинаковы, ивещественными, если знаки и — различны, причем при эти плоскости сливаются в одну.
2) Хотя бы один из коэффициентов илиотличен от нуля. В этом случае повернем систему координат вокруг оситак, чтобы новая ось абсцисс стала параллельной плоскости. Легко убедиться, что при таком выборе системы координат, при условии сохранения обозначениядля новых координат точек, уравнениепримет вид:
которое является уравнением параболического цилиндра с образующими, параллельными новой оси .
studfiles.net
| Номер | Название формулы | Запись формулы | ||||||
| (1) | Эллипсоид |
| ||||||
| (2) | Мнимый эллипсоид |
| ||||||
| (3) | Мнимая коническая поверхность |
| ||||||
| (4) | Однополостной гиперболоид |
| ||||||
| (5) | Двуполостной гиперболоид |
| ||||||
| (6) | Коническая поверхность |
| ||||||
| (7) | Эллиптический параболоид |
| ||||||
| (8) | Эллиптический цилиндр |
| ||||||
| (9) | Мнимый эллиптический цилиндр |
| ||||||
| (10) | Пара совпадающих прямых |
| ||||||
| (11) | Гиперболический параболоид |
| ||||||
| (12) | Гиперболический цилиндр |
| ||||||
| (13) | Пара пересекающихся плоскостей |
| ||||||
| (14) | Параболический цилиндр | y2 = 2px | ||||||
| (15) | Параллельные плоскости | |||||||
| (16) | Мнимые параллельные плоскости |
| ||||||
| (17) | Пара совпадающих плоскостей | x2 = 0 |
scolaire.ru
Поверхности второго порядка
Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.
1. Эллипсоид.
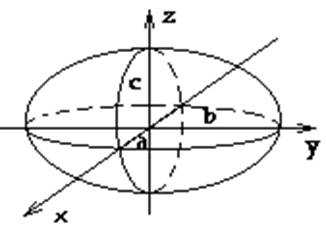 Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением :
Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением :(1)
Уравнение (1) называется каноническим уравнением эллипсоида.
Установим геометрический вид эллипсоида. Для этого рассмотрим сечения данного эллипсоида плоскостями, параллельными плоскости Oxy. Каждая из таких плоскостей определяется уравнением вида z=h , где h – любое число, а линия, которая получается в сечении, определяется двумя уравнениями
(2)Исследуем уравнения (2) при различных значениях h .
1) Если
> c (c>0), то и уравнения (2) определяют мнимый эллипс, т. е. точек пересечения плоскости z=h с данным эллипсоидом не существует.2) Если
, то и линия (2) вырождается в точки (0; 0; + c ) и (0; 0; — c ) (плоскости касаются эллипсоида).3) Если
, то уравнения (2) можно представить в видеоткуда следует, что плоскость z=h пересекает эллипсоид по эллипсу с полуосями
и . При уменьшении значения и увеличиваются и достигают своих наибольших значений при , т. е. в сечении эллипсоида координатной плоскостью Oxy получается самый большой эллипс с полуосями и .Аналогичная картина получается и при пересечении данной поверхности плоскостями, параллельными координатным плоскостям Oxz и Oyz .
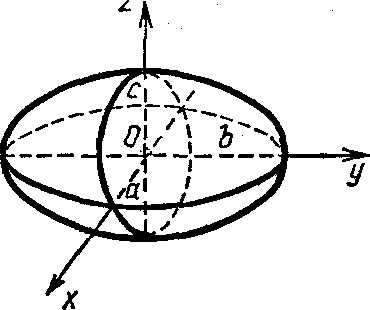
Таким образом, рассмотренные сечения позволяют изобразить эллипсоид как замкнутую овальную поверхность (рис. 156). Величины a, b, c называются полуосями эллипсоида. В случае a=b=c эллипсоид является сферо й .
2. Однополосный гиперболоид.
Однополосным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением (3)Уравнение (3) называется каноническим уравнением однополосного гиперболоида.
Установим вид поверхности (3). Для этого рассмотрим сечение ее координатными плоскостями Oxy ( y=0) и Oyx (x=0). Получаем соответственно уравнения
ииз которых следует, что в сечениях получаются гиперболы.
Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy . Линия, получающаяся в сечении, определяется уравнениями
или (4)из которых следует, что плоскость z=h пересекает гиперболоид по эллипсу с полуосями
и ,достигающими своих наименьших значений при h=0, т.е. в сечении данного гиперболоида координатной осью Oxy получается самый маленький эллипс с полуосями a*=a и b*=b. При бесконечном возрастании
величины a* и b* возрастают бесконечно.Таким образом, рассмотренные сечения позволяют изобразить однополосный гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления (по обе стороны) от плоскости Oxy.
Величины a, b, c называются полуосями однополосного гиперболоида.
3. Двуполостный гиперболоид.
Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
(5)
Уравнение (5) называется каноническим уравнением двуполостного гиперболоида.
Установим геометрический вид поверхности (5). Для этого рассмотрим его сечения координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения
ииз которых следует, что в сечениях получаются гиперболы.
Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, полученная в сечении, определяется уравнениями
или (6)из которых следует, что при
>c (c>0) плоскость z=h пересекает гиперболоид по эллипсу с полуосями и . При увеличении величины a* и b* тоже увеличиваются.При
уравнениям (6) удовлетворяют координаты только двух точек: (0;0;+с) и (0;0;-с) (плоскости касаются данной поверхности).При
уравнения (6) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом не существует.Величина a, b и c называются полуосями двуполостного гиперболоида.
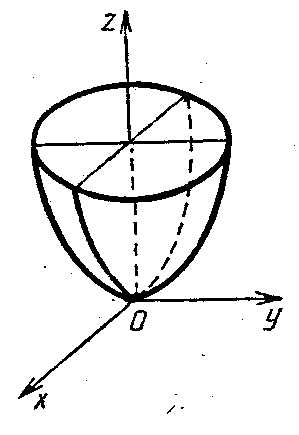
4. Эллиптический параболоид.
Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
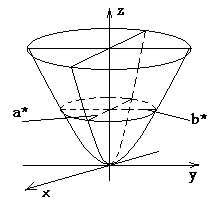 (7)
(7)где p>0 и q>0.
Уравнение (7) называется каноническим уравнением эллиптического параболоида.
Рассмотрим сечения данной поверхности координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения
ииз которых следует, что в сечениях получаются параболы, симметричные относительно оси Oz, с вершинами в начале координат.
Теперь рассмотрим сечения данного параболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями
или (8)из которых следует, что при
плоскость z=h пересекает эллиптический параболоид по эллипсу с полуосями и . При увеличении h величины a и b тоже увеличиваются; при h=0 эллипс вырождается в точку (плоскостьz=0 касается данного гиперболоида). При hТаким образом, рассмотренные сечения позволяют изобразить эллиптический параболоид в виде бесконечно выпуклой чаши.
Точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами.
В случае p=q уравнение (8) определяет окружность с центром на оси Oz, т.е. эллиптический параболоид можно рассматривать как поверхность, образованную вращением параболы вокруг её оси (параболоид вращения).
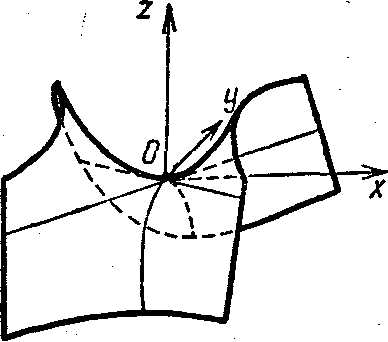
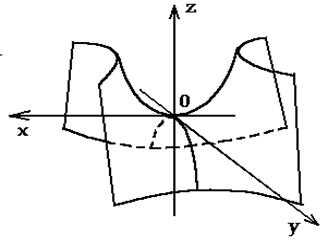
5. Гиперболический параболоид.
Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат, определяется уравнением
(9)
mirznanii.com
Поверхности второго порядка. Канонические уравнения поверхностей второго порядка
б) ;
в) ;
г) ;
д) ;
е) .
§ 8.5. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Геометрическое место точек 3 – мерного пространства, координаты которых в некоторой прямоугольной системе координат удовлетворяют уравнению
(8.5.1)
где хотя бы один из коэффициентов не равен нулю, называется поверхностью второго порядка.
Для любой поверхности второго порядка существует прямоугольная система координат , в которой уравнение этой поверхности имеет один из следующих 17 видов:
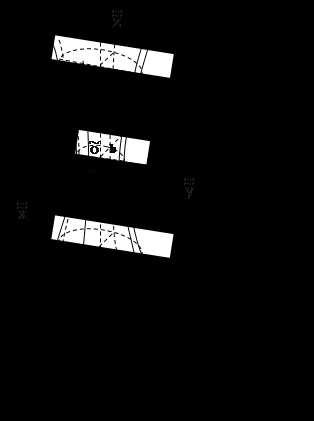
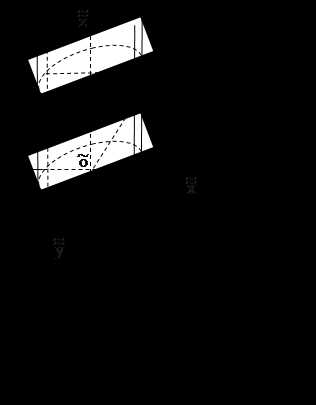
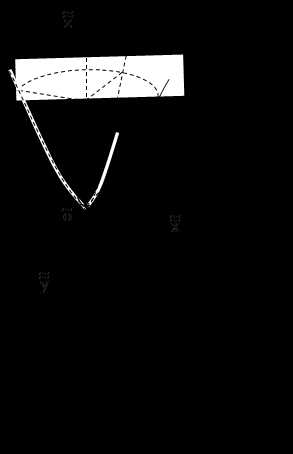
1) эллипсоид (рис. 8.4);
2) мнимый эллипсоид ;
3) однополостный гиперболоид (рис. 8.5);
4) двуполостный гиперболоид (рис. 8.6);
5) конус (рис. 8.7);
6) мнимый конус ;
7) эллиптический параболоид (рис. 8.8);
8) гиперболический параболоид (рис. 8.9);
9) эллиптический цилиндр (рис. 8.10);
10) мнимый эллиптический цилиндр ;
11) гиперболический цилиндр (рис. 8.11);
12) параболический цилиндр (рис. 8.12);
13) пара пересекающихся плоскостей ;
14) пара мнимых пересекающихся плоскостей ;
15) пара параллельных плоскостей ;
16) пара мнимых параллельных плоскостей ;
17) пара совпадающих плоскостей .
Уравнения 1) – 17) называются каноническими уравнениями поверхностей второго порядка.
 | |||
 | |||
Рис. 8.4 Рис. 8.5
 |
Рис. 8.6 Рис. 8.7
 | |||
 | |||
 |
Рис. 8.8 Рис. 8.10
Рис. 8.9
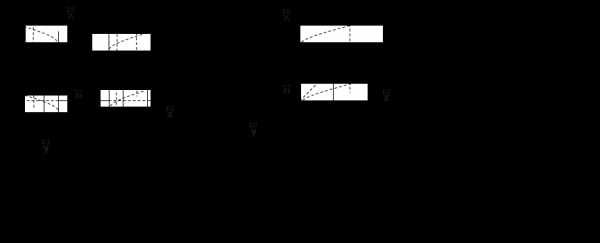 |
Рис. 8.11 Рис. 8.12
При преобразовании уравнения поверхности второго порядка (8.5.1) можно, как и в случае кривой второго порядка, использовать инварианты. Инвариантами поверхностей второго порядка являются
,
,
,
.
Их значения не меняются при повороте и параллельном переносе осей координат.
Пример 1. Поверхность задана уравнением в прямоугольной системе координат
.
Найдите каноническую систему координат и каноническое уравнение этой поверхности. Определите тип поверхности.
Решение. Найдем сначала ортогональное преобразование переменных, приводящее матрицу А квадратичной формы к диагональному виду.
.
Ее характеристический многочлен
.
Следовательно, матрица А имеет собственные значения .
Для нахождения собственных векторов матрицы А решаем однородные системы линейных уравнений с матрицами соответственно и выделяем по одному ненулевому решению:
,
;
,
;
,
.
Векторы ортогональны друг другу как собственные векторы симметричной матрицы, соответствующие различным собственным значениям. Нормируя их, получаем
,
,
и матрицу перехода Р к новому ортонормированному базису
.
Проверим правильность нахождения матрицы Р:
Матрица Р найдена верно.
Применяя к исходному уравнению ортогональное преобразование координат
,
получаем новое уравнение поверхности в прямоугольной системе координат со старым центром О и направляющими векторами :
.
Выполняя параллельный перенос системы координат по формулам
приходим к уравнению
или
.
Это – каноническое уравнение двуполостного гиперболоида в прямоугольной системе координат .
Вычислим координаты начала канонической системы координат в старой прямоугольной системе координат. Поскольку
 ,
,
.
Пример 2. Исследуйте поверхность второго порядка, заданную в прямоугольной системе координат уравнением
.
Решение. Начнем с приведения квадратичной формы к каноническому виду. Матрицей этой квадратичной формы является матрица
vunivere.ru
Поверхности второго порядка
Поверхности второго порядка.
Если в пространстве R3 ввести прямоугольную систему координат Oxyz, то каждая поверхность определяется некоторым уравнением F(x,y,z)=0,
(x,y,z) – координаты любой точки поверхности. Если F(x,y,z) – многочлены не выше второй степени относительно совокупности переменных x,y,z, то уравнение F(x,y,z)=0 называется уравнением второго порядка, а поверхность изображаемая этим уравнением называется поверхностью второго порядка.
Если поверхность имеет специфическое расположение относительно системы координат ( например, симметрична относительно некоторых координатных плоскостей, или имеет вершину в начале координат и пр.), то её уравнение имеет достаточно простой вид, который называется каноническим.
Канонический вид уравнений поверхностей второго порядка. Геометрическое изображение.
1). Сфера радиуса R с центром в начале координат (рис.56)
x2+y2+z2=R2.
Уравнение (x—x0)2+(y—y0)2+(z—z0)2=R2 изображает сферу радиуса R с центром в точке M0(x0,y0,z0).
2). Эллипсоид с полуосями a,b,c и центром в начале координат (рис. 57)
+ + =1.
При a=b=c=R эллипсоид превращается в сферу радиуса R.
3). Однополостный гиперболоид с полуосями a, b, c и осью Oz (рис. 58)
+ — =1.
Сечения гиперболоида горизонтальными плоскостями z=h являются эллипсами
+ =1+
Сечения гиперболоида вертикальными плоскостями x=h или y=h являются гиперболами.
— =1- или — =1-
4). Двуполостсный гиперболоид с полуосями a,b,c и осью Oz (рис.59)
+ — = -1.
Сечение гиперболоида горизонтальными плоскостями z=h, c являются эллипсами
+ = – 1.
Сечения гиперболоида вертикальными плоскостями x=h или y=h являются гиперболами.
— = — -1 или — =- -1.
5). Параболоид эллиптический с параметрами a,b,p и вершиной в начале координат ( рис.60)
+ = 2pz.
Сечение параболоида горизонтальными плоскостями z=h (h>0 при h< 0 при
P<0) есть эллипсы
+ = 2ph.
Сечение параболоида вертикальными плоскостями x=h или y=h являются параболами.
= 2pz — или = 2pz — .
6). Параболоид гиперболический с параметрами a, b, p и вершиной начале координат (рис.61)
— = 2pz.
Сечение параболоида горизонтальными плоскостями z=h представляют собой гиперболы
— = 1
Сечение вертикальными плоскостями x=h и y=h являются параболами
=-2pz + и = 2pz+ .
7). Конус эллиптический с вершиной в начале координат и осью Oz (рис.62)
+ — =1.
Если a=b, то конус круглый или круговой. Пересечение конуса горизонтальными плоскостями являются эллипсами
+ =
(при h=0 эллипс вырождается в точку).
Сечение конуса вертикальными плоскостями x=h и y=h являются гиперболами
— = — — =- . при h0
Или парой пересекающих прямых
— =0 — =0 при h=0
К поверхностям второго порядка относятся цилиндры направляющие которых – линии второго порядка. Мы ограничимся пересечением цилиндров, направляющие – прямые , параллельные оси Oz.
8) Цилиндры:
(1) Эллиптический (рис.63)
+ =1.
Если a=b=R, то цилиндр – круговой x2+y2=R.
(2) Гиперболический (рис.64)
— =1.
(3) Параболический (рис.65)
y2=2px.
Примечание . Если в каждом из приведённых канонических уравнений заменить x=x1—x0, y=y1—y0, z=z1—z0, где (x0,y0,z0) – фиксированные числа, то новые уравнения представляют те же поверхности и они занимают в системе координат O1x1y1z1 такое же положение относительно плоскостей x1=x0, y1=y0, z1=z0 как поверхности, заданные канонически относительно координатных плоскостей x=0, y=0, z=0. Другими словами, приведённые формулы представляют параллельный сдвиг поверхности на вектор OM=(x0,y0,z0).
Метод параллельных сечений
Если задано уравнение той или иной поверхности, то возникает задача исследования её формы и расположения относительно координатных осей. Для решения этой задачи обычно применяют метод параллельных сечений: поверхность пересекается несколькими плоскостями, параллельными плоскостями координат. Форма и размер полученных сечений позволяют выяснить геометрическую форму самой поверхности.
Пересечение поверхности с плоскостью
Линию в пространстве R3 можно определить как пересечение двух плоскостей. Таким образом уравнение линии можно записать в виде системы
Для исследования этой линии удобно воспользоваться цилиндром, проектирующем её на ту или иную координатную плоскость. Если, например, проектируем линию на плоскость Oxy, то исключим z из системы и получим уравнение (x,y)=0.Оно изображает направляющую проектирующего цилиндра на плоскость Oxy. В зависимости от того, будет ли (x,y)=0 эллипсом, гиперболой, параболой, парой прямых – изучаемая линия сохранит соответствующее название.
5.5.1. Сохранить уравнение сферы с центром в точке М0(-5;3;2) и касающейся плоскости 2x-2y+z-4=0.
Для составления уравнения сферы нужен её радиус. В данном случае R – расстояние от М0 до плоскости:
R= =6.
Искомое уравнение : (x+5)2+(y-3)2+(z-2)2=36.
5.5.2. Составить уравнение сферы, касающейся двух параллельных плоскостей 6x-3y-2z-35=0 и 6x-3y-2z+63 =0, если её центр расположен на прямой = = .
1) Определим точки М1 и М2 пересечения прямой с плоскостями (заметим что прямая перпендикулярна плоскостям ). Для этого параметрическое уравнение прямой x = 11+6t, y=-4-3t, z=-3-2t подставляем в уравнения плоскостей, находим t и возвращаемся к этим уравнениям.
6(11+6t) – 3(-4-3t) – 2(-3-2t)-35=0,
t=-1, M1 (5,-1,-1).
Аналогично находим М2(-7,5,3).
2) Центр сферы М0 — середина отрезка М1М2:М0(-1,2,1).
Радиус сферы R = М0М1==7.
3) Уравнение сферы (x+1)2+(y-2)2+(z-1)2=49.
5.5.4. Составим уравнение сферы ,проходящей через четыре точки О(0;0;0), А(2;0;0), В(1;1;0), С(1;0;-1).
Уравнение сферы ищем в виде
(x—a)2+(y—b)2+(z—c)2=R2.
Где (a, b, c) – координаты центра и – координаты центра и R – радиус неизвестные. Координаты данных точек превращают уравнение сферы в верные равенства, т.е.
После возведения в квадрат, приведения подобных слагаемых получается система, из которой a=1, b=0, c=0, R2=1.
Ответ. (x-1)2+y2+z2=1.
5.5.6. Найти точки пересечения поверхности + – =1 и прямой = = .
Параметрические уравнения прямой x=4t, y=-3t, z=-2+4t подставим в уравнение однополосного гиперболоида и определим значение t: + – =1, (t-1)2=0, t1,2=1. Следовательно, x=4, y=-3, z=-2. Прямая имеет с гиперболоидом две совпадающие точки пересечения, т. е. прямая касается поверхности гиперболоида в точке М1(4;-3;2).
5.5.7. При каких значениях параметра p плоскость 2x-2y—z=p касается сферы x2+y2+z2=81?
Если плоскость касается сферы, то расстояние от её центра до плоскости равно радиусу сферы, т. е . =9.
Отсюда =27, т.е. p=27.
5.5.10. Методом параллельных сечений исследовать поверхность, определяемую уравнением + – = -1.
1) Перепишем уравнение в виде + = -1. И пересекаем поверхность плоскостями z=h параллельными координатной плоскости Oxy.
В сечениях получаются линии с уравнениями + = -1.
При 2 эти уравнения имеют изображения ( мнимые эллипсы) при h = 2 они изображают точки (0;0;2) и (0;0;-2), а при 2 получаются эллипсы
+ = 1, где c=.
С увеличением увеличиваются и полуоси эллипсов 4с и 3с, т. е. эллипсы расширяются (рис.66). Поверхность симметрична относительно плоскости Oxy.
2) Перепишем уравнение поверхности в виде – = — -1 и пересечём её вертикальными плоскостями y=l. При каждом l (- ; + ) соответствующие уравнения описывают гиперболы. В частности, при l=0 получаем гиперболу – = -1, расположенную в плоскости Oxz.
3) Сечение поверхности плоскостями x=r также гиперболы
– =-1- .
Но из пп. 1) и 2) уже можно сделать вывод о строении поверхности : она состоит из эллипсов , <<нанизанных>> на гиперболу – =-1 ( =0). Поскольку два сечения, параллельных Oxz и Oyz – гиперболы, а одно – параллельное Oxy –эллипс, то поверхность называется гиперболоидом эллиптическим; для уточнения – двуполостный, ибо состоит из двух отдельных частей ( над и под плоскостью Oxy).
5.5.12. Определить линию пересечения поверхностей
(x-4)2+(y-7)2+(z+1)2=36 и 3x+y-z-9=0.
Первая поверхность это сфера, вторая- плоскость. Они пересекаются или по окружности, или в одной точке , или вовсе не пересекаются .
Найдём расстояние d от центра сферы М0(4;7;-1) до плоскости 3x+y—z-9=0.
d= = = .
Поскольку d <R (R=6- радиус сферы ), то плоскость пересекает эту сферу по окружности.
Центр O(x1;y1;z1) этой окружности расположен на перпендикуляре М0О, опущенным из центра сферы М0 на заданную плоскость (рис.67).
Уравнение перпендикуляра М0О в параметрической форме имеет вид
x = 4+3t, y=7+t, z=-1-y.
Подставим эти равенства в уравнение плоскости и находим t.
3(4+3t) + (7+t)- (-1-t)-9 =0, t=-1.
Подставим t= -1 в параметрические уравнения перпендикуляра М0О.
Находим : x=1, y=6 , z=0, т. е. О(1;6;0) – центр окружности пересечения сферы и плоскости.
Из ОМ0А (рис.67) находим r2=R2—d2, r2=36-11=25, r=5.
Таким образом получено, что кривая
Представляя собой окружность радиуса 5 с центром в точке О(1;6:0).
5.5.13. Составить уравнения касательных плоскостей к сфере
(x-2)2+ (y+1)2 + (z-3)2=6 в точках её пересечения с прямой = = .
Точки пересечения прямой со сферой получаются подстановкой равенств
x=1+t, y= —t, z=1+2t в уравнение сферы, определением t и подстановкой обратно в уравнение прямой .
Имеем (1+t-2)2 + (-t+1)2 + (1+2t-3)2=6 , 6(t-1)2=6, t1=0, t2=2. Далее x1=1, y1=0, z1=1, x2=3, y2=-2, z2=5. Итак, М1(1;0;1), М2(3;-2;5) – точки пересечения прямой и сферы.
Составим уравнение первой касательной плоскости, проходящей через
М1(1;0;1). Её нормальный вектор , где М0(2;-1;3) центр сферы:
= (-1;+1;-2) , а уравнение плоскости: — (x-1) + y-2(z-1)=0 или x=y+2z-15=0.
Уравнение второй плоскости по аналогии: x—y+2z-15=0.
Полученные плоскости параллельны потому, что данная прямая проходит через центр сферы М0(2;-1;3) (получается при t=1).
5.5.14. Установить, что плоскость y-2=0 пересекает эллипсоид
+ + =1 по эллипсу. Найти его полуоси и вершины.
Пересечение двух поверхностей в пространстве представляет некоторую линию, принадлежащую как одной так и другой поверхности. Уравнение этой линии в нашем случае имеет вид
Подставим y=2 в первое уравнение и получаем + =.
Это уравнение эллипса, расположенного в плоскости y-2=0.
Поско4льку каноническое уравнение полученного эллипса имеет вид + =1, то полуоси равны a= и b=, а вершины эллипса расположены в точках А1(0;2;-) и А2(8;2;0) — на большом диаметре,
В1(0;2;-) и В2(0;2;) – на меньшем диаметре.
5.5.15. Исследовать линию пересечения гиперболоида + — z2=1 с плоскостью 4x-3y-12z-6=0, пользуясь её проекциями на координатные плоскости.
Линия пересечения гиперболоида с плоскостью определяется системой
Выражаем из второго уравнения
Z= и z2=
И подставляем в первое уравнение. Получаем
9y2+8xy+16x-12y-60=0.
Это уравнение проекции на плоскость Oxy линии пересечения гиперболоида с плоскостью. Вместе с тем это уравнение цилиндрической поверхности с образующей, параллельной оси Oz, направляющая которой есть исследуемая линия. Уравнение этой линии следует привести к каноническому виду известными формулами преобразования координат (поворот осей и сдвиг). В данном случае методом разложения на множители можно получить ( y+2)(9y+8x-30)=0, т.е. наша линия представляет пару прямых y+2=0 и 8x+9y-30=0, которые пересекаются в точке
Т.е. М1(6;-2).
По аналогии с этим, проектируем искомую линию на плоскость Oxz. Получаем пару прямых x-3z=0 и 5x-9z-12=0, которые пересекаются в точке М2(6;2).
Наконец, на плоскость Oyz искомая линия проектируется в прямые y+2=0 и 5y+8z-6=0, которые пересекаются в точке М3(-2;2).
Если проекции на координатные плоскости данной линии являются пересекающимися прямыми, то сама линия представляет пару пересекающихся в точке М(6;-2;2) прямых. Координаты М получаются из координат её проекции М1, М2,М3.
5.5.17. Дан гиперболический параболоид x2- =z и одна из его касательных плоскостей: 10x-2y—z-21=0. Найти уравнение каждой из тех двух прямых, по которой плоскость касается с параболоидом.
Уравнение искомых прямых задаются системой уравнений, которую последовательно преобразуем.
studfiles.net