18 формула – Автошкола в Ижевске «Формула»

Результаты вычислений отображаются как в числовом виде, так и прописью. Суммы прописью удобно копировать из специальных полей.

Результаты вычислений можно сохранить, используя кнопку «Сохранить».
Таблицу сохраненных результатов можно редактировать, удаляя не нужные расчеты.
Кликнув по строке в таблице сохраненных результатов, можно перенести данные в основные расчеты.

Скопировав «Ссылку на результат», можно отправить ссылку на произведенные расчеты по e-mail или мессенджер.

Формула расчета НДС

Для выделения НДС из суммы нужно Цену с НДС умножить на 20 и разделить на 120.
Попробуем посчитать НДС, выделим НДС из 550: 550х18/120=83.90. НДС равен 83.90, сумма без НДС — 550-83.90 = 466.10.

Начислять НДС тоже не сложно. Необходимо Цену без НДС умножить на 0.20 (получаем сумму НДС) и к получившемуся результату прибавить Цену без НДС.

Из истории возникновения НДС

В России НДС (Налог на Добавленную Стоимость) впервые был введен в 1992 году. Первоначально правила и порядок начисления НДС регулировались отдельным законом «О налоге на добавленную стоимость», позже НДС стал регулироваться 21 главой Налогового кодекса.
Изначально ставка НДС доходила до 28%, но позже была снижена до 20%.
Сейчас основная ставка НДС, действующая на территории России — 20%. Пониженная ставка НДС 10% действует на медицинские и детские товары, печатные издания, книжную продукцию.

calculator888.ru

Формула как выделить ндс 18 от суммы

Понятие налога на добавленную стоимость

Прежде чем рассмотреть вопрос, как выделить НДС 18 от суммы, следует рассмотреть само понятие налога на добавленную стоимость (НДС).

Данный налог чаще всего составляет 18 % от стоимости продукции и вносится в бюджет страны по мере ее продажи.

Используя такой налог, как НДС, конечные потребители продукции  уплачивают производителям (продавцам) налоги со всей стоимости покупаемых благ.

По положениям Налогового Кодекса (статья 164) на территории Российской Федерации действуют три ставки НДС – нулевая, в размере 10 и 18%.

Формула как выделить НДС 18 от суммы помогает рассчитать размер данного налога при соответствующей налоговой ставке в 18 процентов.

Порядок действий при расчете НДС

В процессе расчета по формулеНДС, важно выполнить три основных действия:

1. Определить налоговую ставку, которая в нашем случае будет равняться 18 (нами рассматривается формула, как выделить НДС 18 от суммы). Все указания по ставкам делаются с упором на статью 164 Налогового Кодекса РФ.
2. Рассчитать налоговую базу,включающую исходную стоимость реализуемой продукции (товара или услуг), которая увеличена на размер акциза (в тех ситуациях, когда расчет осуществляется по подакцизной продукции).
3. Применить формулу НДС (выделить 18 % от суммы).

Величину налога, получаемую при проведении математических расчетов,  обязательно необходимо внести в счет-фактуру, которая должна передаваться заказчикам (покупателям) в соответствии со способом реализации товара (оказания услуг).

Формула как выделить НДС 18% от суммы

По действующемузаконодательству (ст. 168 Налогового Кодекса РФ) налог на добавленную стоимость предъявляетсяконтрагентам в качестве дополненияк ценамреализации продукции.

Для того, что бы определить общую сумму по счету,выставленному покупателю, необходимо использовать следующую формулу НДС:

НДС = Стоимость продукции (без НДС) * Ставка НДС/100%

НДС = Ст * 18 / 100

Если же у бухгалтера нет необходимости рассчитывать размер налога, то цена товара,предъявляемая клиенту, рассчитывается следующим образом:

Окончательная сумма (при ставке 18 %) = Начальная цена продукции  *1,18

Формула (как выделить НДС 18 % от суммы) может быть рассчитана на калькуляторе, в таблицах Excel, а также в специальном онлайн приложении, предназначенном для автоматизации бухгалтерской работы.

Значение НДС

Все коммерческие предприятия, работающие на общей системе налогообложения, должны правильно рассчитывать налог на добавленную стоимость, при этом своевременно отчисляя его в государственный бюджет.

Вопрос (формула), как выделить НДС 18 % от суммы, является актуальным для специалистов различных областей деятельности:

• Бухгалтер,
• экономист,
• менеджер по продажам,
• руководитель предприятия и др.

Ошибки, допущенные при расчете НДС, могут явиться основанием нарушения действующих Законов, что может привести к наложению штрафных санкций.

Примеры решения задач

ru.solverbook.com

18. Формула Ньютона-Лейбница.

Пусть функция y = f(x) непрерывна на отрезке [a; b] и F(x) — одна из первообразных функции на этом отрезке, тогда справедлива формула Ньютона-Лейбница: .

Формулу Ньютона-Лейбница называют основной формулой интегрального исчисления.

Для доказательства формулы Ньютона-Лейбница нам потребуется понятие интеграла с переменным верхним пределом.

Если функция y = f(x) непрерывна на отрезке [a; b], то для аргумента интеграл видаявляется функцией верхнего предела. Обозначим эту функцию, причем эта функция непрерывная и справедливо равенство.

Действительно, запишем приращение функции , соответствующее приращению аргументаи воспользуемся пятымсвойством определенного интегралаи следствием из десятого свойства:где.

Перепишем это равенство в виде . Если вспомнитьопределение производной функциии перейти к пределу при, то получим. То есть,- это одна из первообразных функцииy = f(x) на отрезке [a; b]. Таким образом, множество всех первообразных F(x) можно записать как , гдеС – произвольная постоянная.

Вычислим F(a), используя первое свойство определенного интеграла: , следовательно,. Воспользуемся этим результатом при вычисленииF(b): , то есть. Это равенство дает доказываемую формулу Ньютона-Лейбница.

Приращение функции принято обозначать как . Пользуясь этим обозначением, формула Ньютона-Лейбница примет вид.

Для применения формулы Ньютона-Лейбница нам достаточно знать одну из первообразныхy=F(x) подынтегральной функции y=f(x) на отрезке [a; b] и вычислить приращение этой первообразной на этом отрезке. В статье методы интегрированияразобраны основные способы нахождения первообразной. Приведем несколько примеров вычисления определенных интегралов по формуле Ньютона-Лейбница для разъяснения.

Пример.

Вычислить значение определенного интеграла по формуле Ньютона-Лейбница.

Решение.

Для начала отметим, что подынтегральная функция непрерывна на отрезке[1;3], следовательно, интегрируема на нем. (Об интегрируемых функциях мы говорили в разделе функции, для которых существует определенный интеграл).

Из таблицы неопределенных интеграловвидно, что для функциимножество первообразных для всех действительных значений аргумента (следовательно, и для) записывается как. Возьмем первообразную приC = 0: .

Теперь осталось воспользоваться формулой Ньютона-Лейбница для вычисления определенного интеграла: .

Пример.

По формуле Ньютона-Лейбница вычислите определенный интеграл .

Решение.

Подынтегральная функция непрерывна на отрезке [-1;2], поэтому, интегрируема на нем.

Найдем неопределенный интеграл методом подведения под знак дифференциала:. Так мы получили множество всех первообразных функциидля всех действительныхx, следовательно, и для .

Возьмем первообразную при С=0 и применим формулу Ньютона-Лейбница:

19. Несобственные интегралы первого рода

        Определение 4.1   Предположим, что функция задана на бесконечном промежутке видаи интегрируема на любом конечном отрезке, где. Таким образом, мы можем рассмотреть функцию

Если эта функция имеет предел то числоназываетсязначением несобственного интеграла первого рода

а сам интеграл называетсясходящимся (иными словами, интеграл сходится).

Если же предела не существует (например, еслипри), то интегралназываетсярасходящимся (то есть расходится) и не имеет никакого числового значения.     

Геометрически, в случае , величина несобственного интегралаозначает, по определению, площадь бесконечно длинной области, лежащей в координатной плоскости между лучомна оси, графикоми вертикальным отрезком(см. рис.).

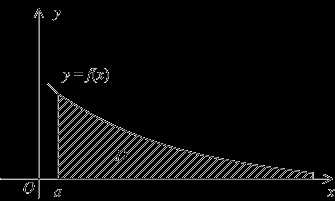
Рис.4.1.

Сходящиеся интегралы соответствуют таким областям , площадь которых конечна (хотя сама областьнеограничена), а расходящиеся (в случае) — неограниченным областям с бесконечной площадью. В случае, когдапри, часто пишут формально:

однако нужно ясно понимать, что эта запись означает расходимость интеграла и отсутствие у него числового значения.

Само определение значения интеграла через предел интегралов по конечным, но увеличивающимся отрезкам означает исчерпание площади путем учёта все большей её частиправый вертикальный отрезок, проведённый при, отодвигается всё дальше и дальше в бесконечность; в пределе будет учтена вся площадь под графиком(см. рис.).

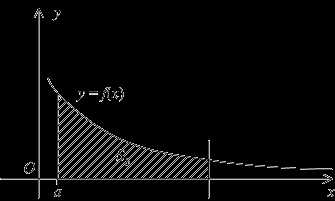
Рис.4.2.

studfiles.net

§18. Барометрическая формула. Распределение молекул в потенциальном силовом поле (распределение Больцмана)

При выводе основного уравнения молекулярно-кинетической теории и закона распределения Максвелла предполагалось, что на молекулы не действуют никакие внешние силы. Поэтому можно было считать, что молекулы равномерно распределены по объему сосуда.

Фактически же молекулы любого газа всегда находятся в поле тяготения Земли. Если бы не было теплового движения молекул атмосферного воздуха, то все они упали бы на Землю. Если бы не было тяготения, то атмосферный воздух рассеялся бы по всей Вселенной. Таким образом, тяготение и тепловое движение приводят газ в состояние, при котором его давление и концентрация молекул зависят от высоты.

Формула зависимости атмосферного давления от высоты над уровнем Земли получила название барометрической формулы. Для вывода барометрической формулы введем некоторые допущения:

— будем считать воздух идеальным газом, так как даже у поверхности Земли давление воздуха сравнительно невелико;

— ускорение свободного падения считаем практически постоянным и не зависящим от высоты, так как атмосферное давление становится пренебрежительно малым уже на высоте 100-200 км, гораздо меньшей по сравнению с радиусом Земли;

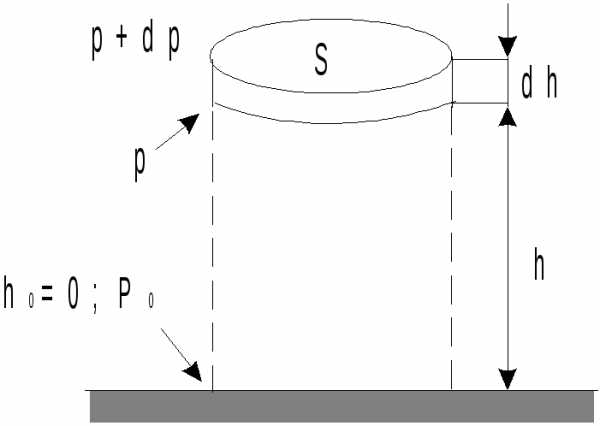
Рис.18.1

Атмосферное давление обусловлено весом вышележащих слоев газа. Выделим мысленно вертикальный столб воздуха (рис. 18.1) с площадью основания S.

Пусть на высоте h давление газа равно p, а на высоте (h+dh) давление равно (p+dp). Так как давление с увеличением высоты падает, то его приращение будет отрицательным (dp< 0).

Разность давлений p и (p+dp) равна весу газа, заключенного в столбе высотой dh, деленной на площадь S, то есть

или

, (18.1)

где  — плотность воздуха на высота h.

Заменив в этом уравнении плотность  по формуле, полученной с помощью уравнения Клапейрона-Менделеева (14.1):

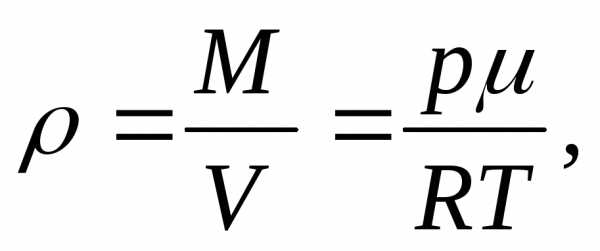
запишем выражение (18.1) в виде

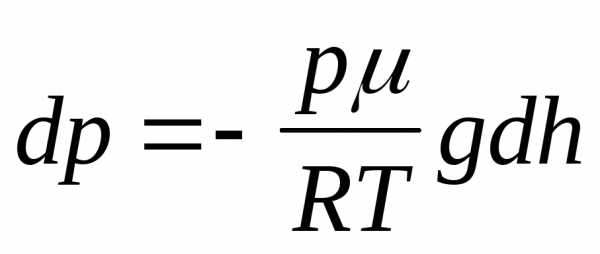
или

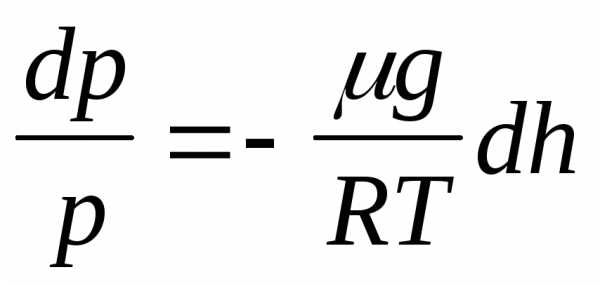^. (18.2)

Полагая T=const (в соответствии с принятыми допущениями) и интегрируя уравнение (18.2) по высоте от 0 до h, получим

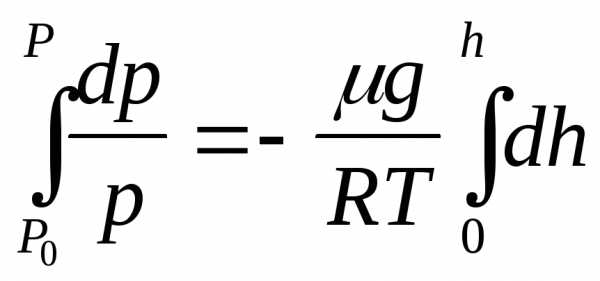
или

^,

откуда находим

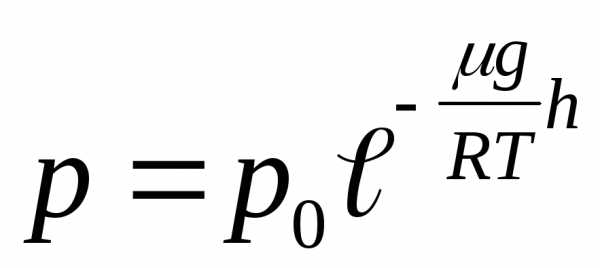, (18.3)

где p₀ — давление на высоте h = 0.

Выражение (18.3) носит название барометрической формулы. Из нее следует, что давление газа убывает с ростом высоты тем быстрее, чем тяжелее газ (чем больше ) и чем ниже температура. На рис.18.2 изображены две зависимости вида (18.3), соответствующие двум газам с разными молярными массами ₁ и ₂ при T=const (давление p₀ для h=0 у обоих газов принято условно одинаковым).

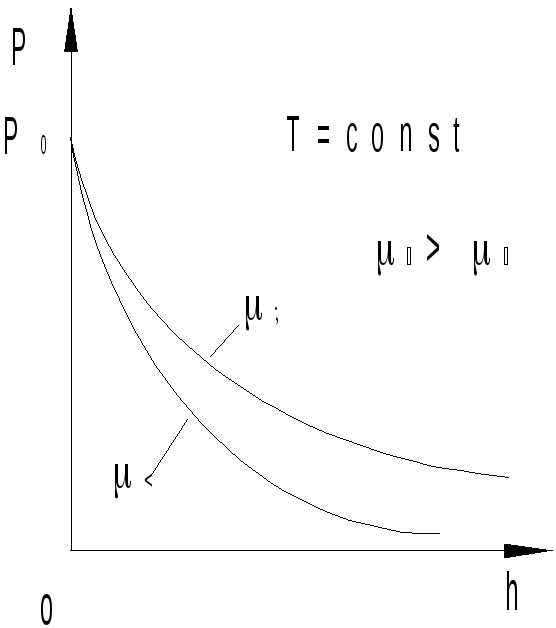
Рис.18.2

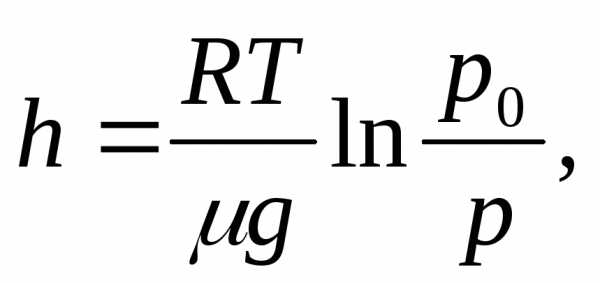(18.4)

лежит в основе принципа работы авиационных высотомеров (альтиметров): измеряя с помощью барометра давление, эти приборы показывают значение высоты над уровнем моря.

Из формулы (18.3) можно получить соотношение между концентрациями газа на различной высоте, подставив в нее уравнение состояния газа в форме (15.26):

^. (18.5)

Заменив отношение /R для однородного газа на отношение m/k (m — масса молекулы) и сократив обе части равенства на kТ, получим

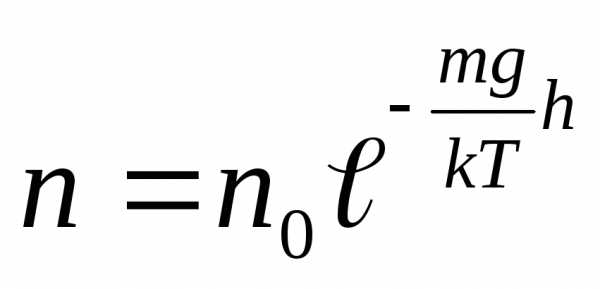^, (18.6)

где n₀ — концентрация молекул газа при h =0.

Из выражения (18.6) следует, что чем тяжелее газ (больше m) и чем меньше его температура Т, тем больше концентрация молекул у поверхности Земли по сравнению с концентрацией на некоторой высоте (преобладание тяготения Земли над тепловым движением молекул). И наоборот, чем легче газ и больше его температура, тем более тепловое движение молекул преобладает над тяготением и концентрация медленно убывает с ростом высоты.

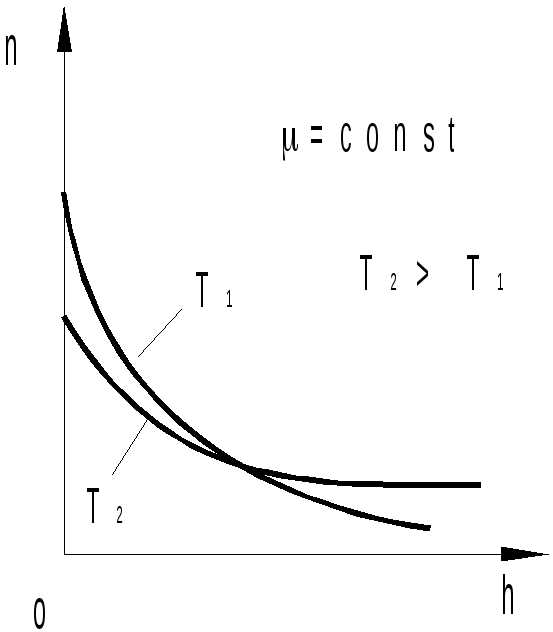
Рис.18.3

Сравнение этих зависимостей показывает, что чем меньше температура газа, тем большая неоднородность наблюдается в распределении концентрации молекул газа по высоте.

Произведение mgh в уравнении (18.6) представляет собой потенциальную энергию W_n одной молекулы в поле тяготения Земли. Следовательно, распределение молекул по высоте является вместе с тем и распределением их по значениям

потенциальной энергии:

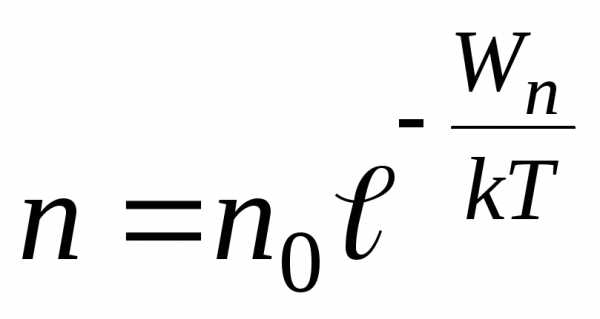^. (18.7)

Австрийский физик Л. Больцман доказал, что формула (18.7) справедлива для любой совокупности одинаковых частиц, находящихся в состоянии хаотического теплового движения в потенциальном поле любой природы. В связи с этим функцию (18.7) называют распределением Больцмана. Таким образом, распределение (18.6) является частным случаем более общего распределения (18.7). Между распределением Максвелла (17.6) и Больцмана (18.7) имеется большое сходство: и в том и в другом распределении в показателе степени экспоненты стоит отношение энергии молекулы (в одном случае потенциальной, а в другом кинетической) к величине кТ, определяющей среднюю кинетическую энергию теплового хаотического движения.

Распределения (17.6) и (18.7) могут быть объединены в одно распределение Максвелла-Больцмана, согласно которому число молекул, компоненты скоростей которых лежат в предел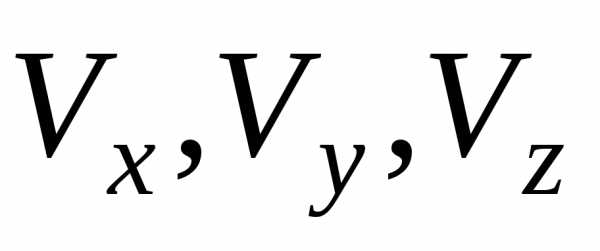ах от до ,а координаты в пределах от 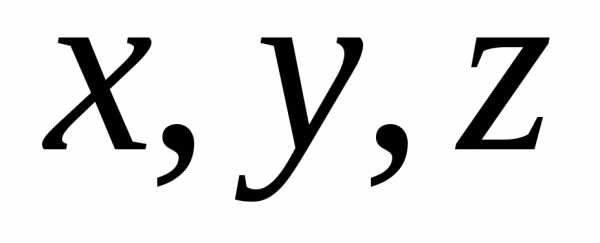до равно

, (18.8)

где .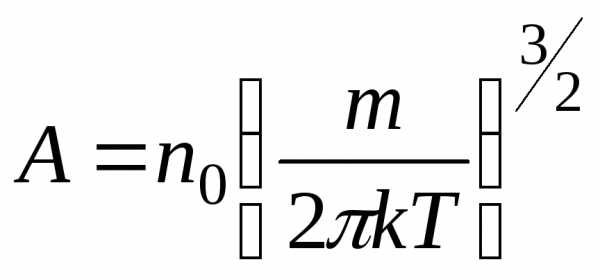

Из формулы (18.8) следует, что 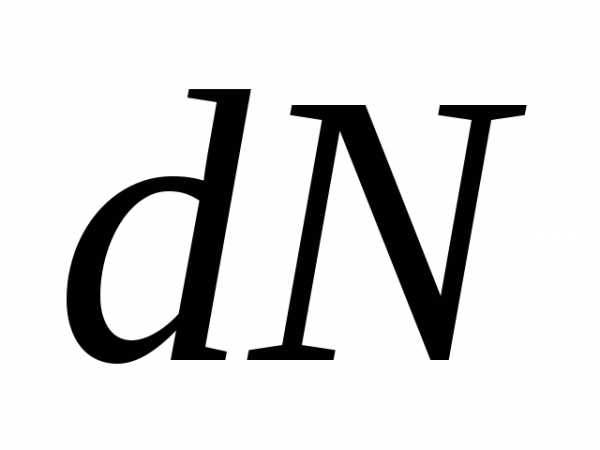определяется полной энергий молекулы.

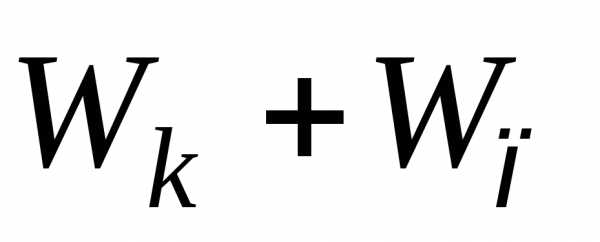Таким образом, в состоянии с постоянной температурой скорости молекул в каждой точке пространства распределены по закону Максвелла. Влияние силового поля сказывается только на изменении концентрации молекул от точки к точке.

studfiles.net

18. Формула обращения.

Формула обращения:

Формула обращения устанавливает связь между изображением и оригиналом.

Теория.

Оригинал f(t) в точках непрерывности определяется равенством:

(1)

F(s) – изображение по Лапласу оригиналаf(t), а интеграл в правой части этого равенства понимается в смысле главного значения, то есть:

И берется вдоль прямой, параллельной оси и расположенной в полуплоскости .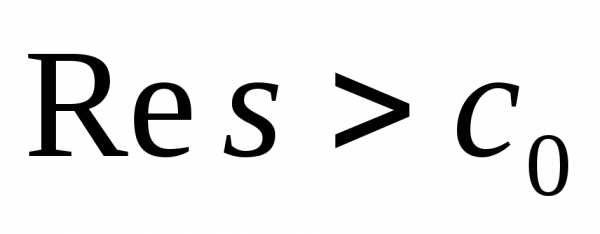

Доказательство

Теорема будет доказана, если удастся установить:

При 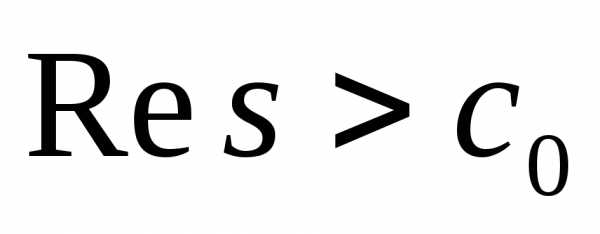сходится равномерно. Поэтому можно заменить порядок интегрирования:

Теперь вычисляем:

Введем новую переменную и обозначим ее значение:

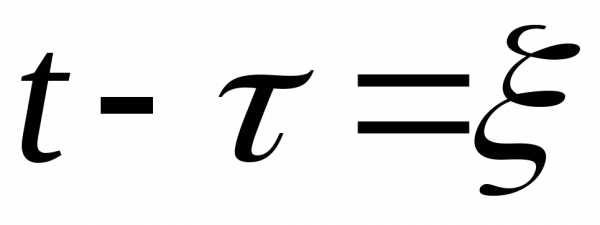
Тогда

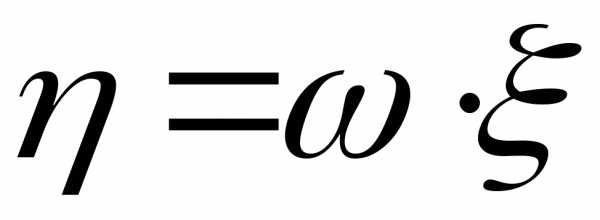
А теперь рассмотрим каждый из интегралов:

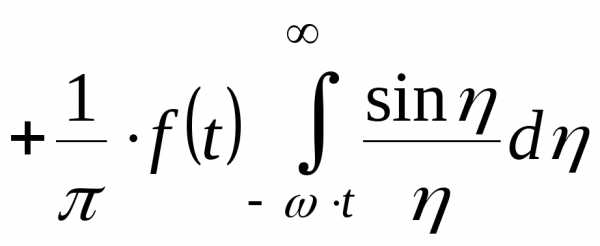
(2)

Устремим и обозначим.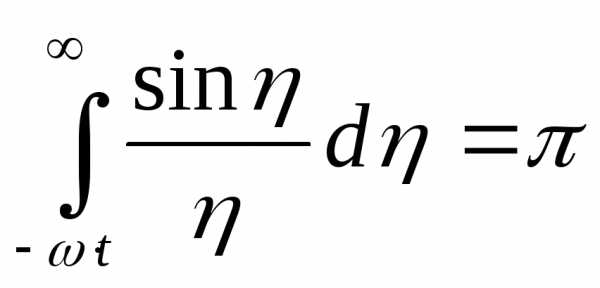

(3)

Функция f(t) – оригинал,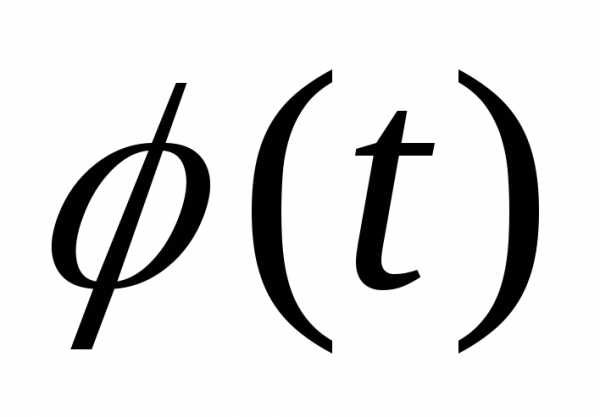ограничена. Все интегралы правой части последнего равенства являются сходящимися. Значит, что интервал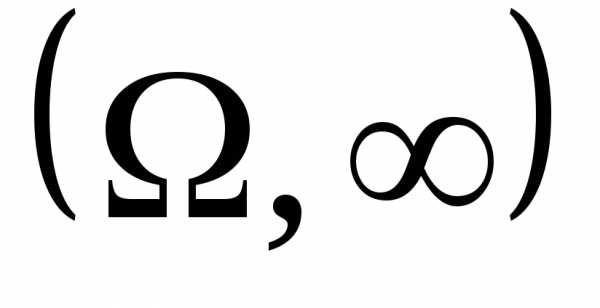будет меньше малого положительного числа. Значенияtхарактеризуют собой точки функцииf(t), то есть при фиксированном значении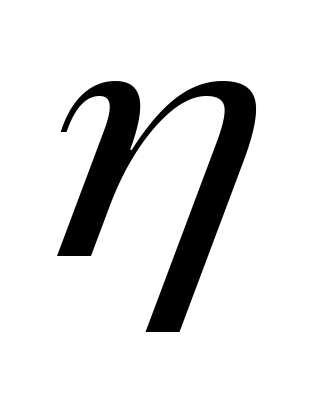выполняется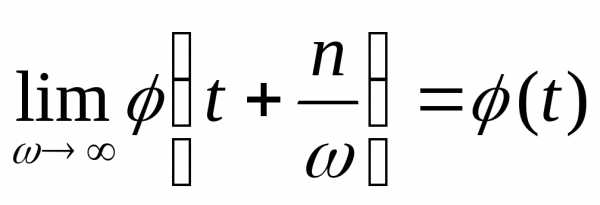, поэтому модуль интервала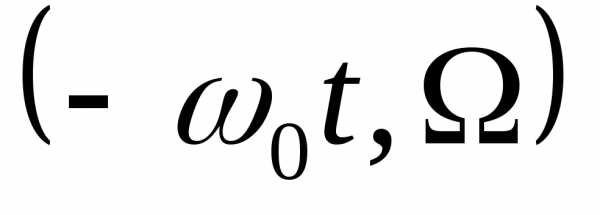стремится к нулю.

Окончательно получаем:

Теорема доказана.

Формула (1) называется формулой обращения. С ее помощью устанавливается связь между F(s) и соответствующего ему оригиналаf(t). Процесс получения оригинала по заданному изображению представляет собой обратное преобразование Лапласа:

, при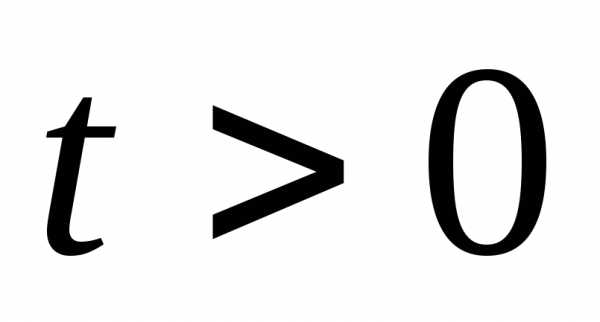(4)

Это обстоятельство показывает, что f(t) = оригинал.

Следует отметить, что формула (1) определяет оригинал только в точках его непрерывности. Как и доказательство (3) в точках разрыва функцииf(t) справедливо равенство функции:

(5)

Оригиналам всегда соответствует единственное изображение, которое определяется по формуле (1).

19. Свойства преобразования Лапласа.

1. Свойство линейности.

Если являются оригиналами и их изображения . И если— величины, которые не зависят отtиs, то справедливы следующие равенства:

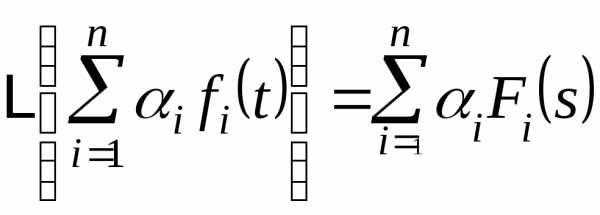(1)

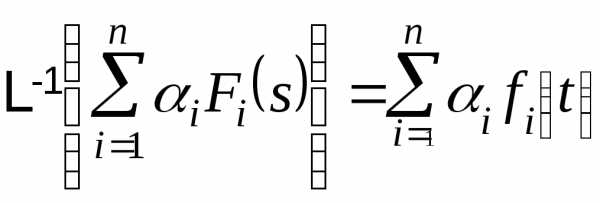(2)

Доказательство

По формуле преобразования Лапласа

Теперь находим

Так как интеграл суммы равен сумме интегралов, а множитель 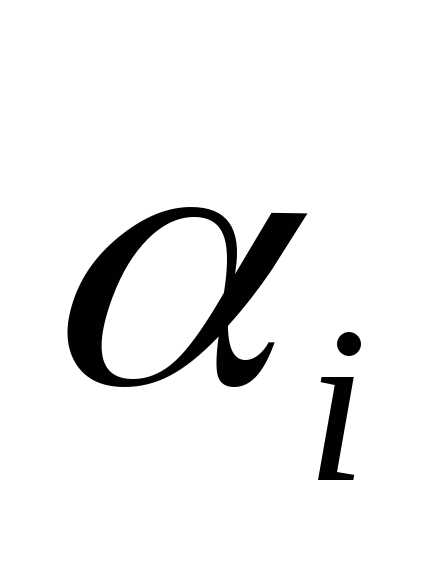не зависит от переменной интегрированияt, то можно записать:

Аналогично показываем справедливость формулы (2):

Теперь берем обратное преобразование Лапласа и по аналогии:

Теорема доказана.

2) Дифференцирование в области оригиналов.

Еслиf(t) является оригиналом и ее производная также является оригиналом, и ее изображение по ЛапласуF(s), то справедливо равенство:

(3)

Плюс означает, что значение функции – это значение ее предела при 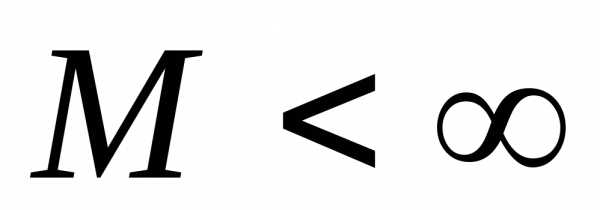справа, то есть(правосторонний предел).

Доказательство

Воспользуемся равенствами:

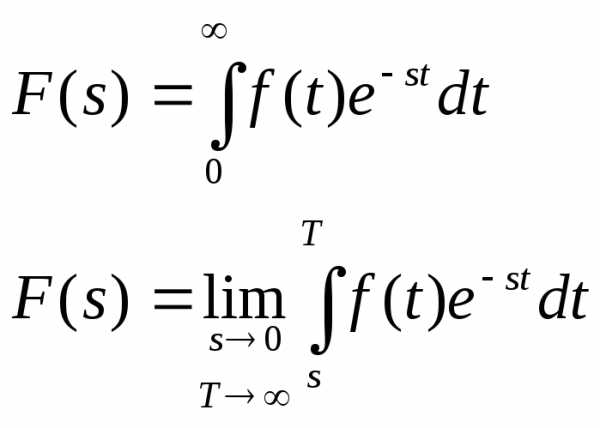
Найдем изображение по Лапласу:

Так как f(t) – оригинал, то для всехсправедливоили, тогда это справедливо для всех случаем, когда.

Справедливо следующее соотношение

Учтем равенства:

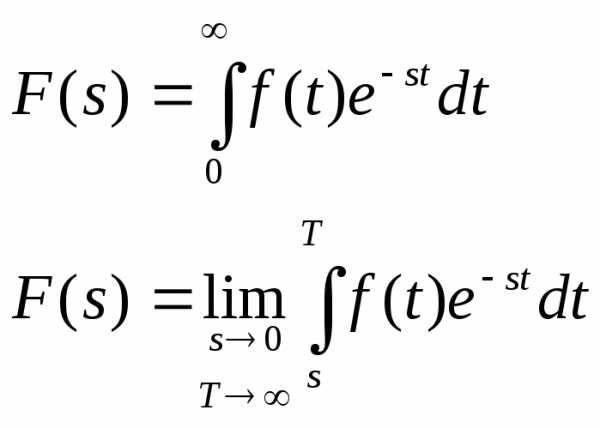
И получим формулу (3).

Если начальное значение функции , то формула (3) принимает вид:

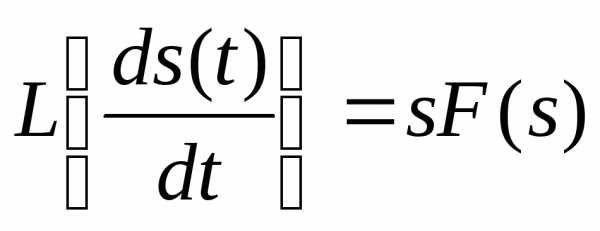
Для второй производной:

Для третьей производной:

И для n– ой производной:

(4)

3) Интегрирование оригинала.

Если f(t) является оригиналом, ее изображение F(s), то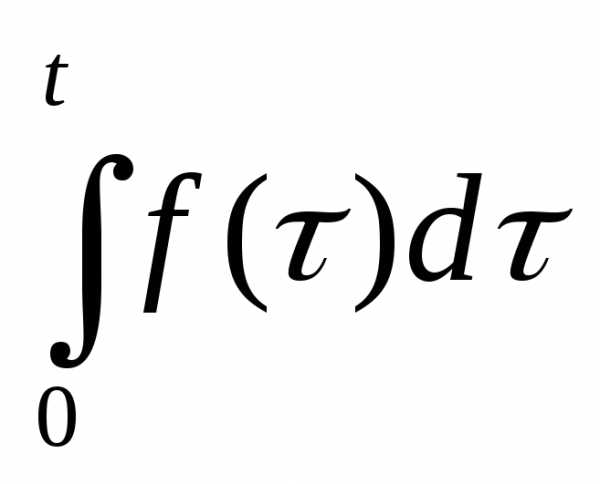также является оригиналом, а ее изображение по Лапласу:

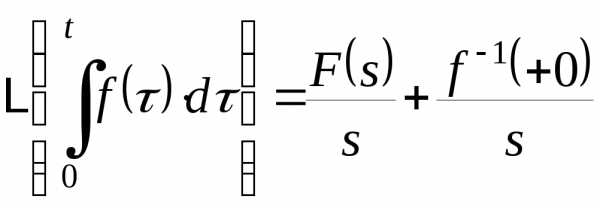(5)

Где 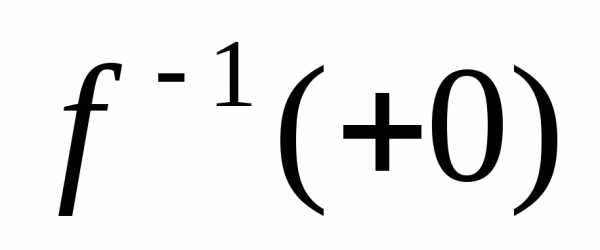— постоянная интегрирования.

Доказательство

Прежде всего покажем, что интеграл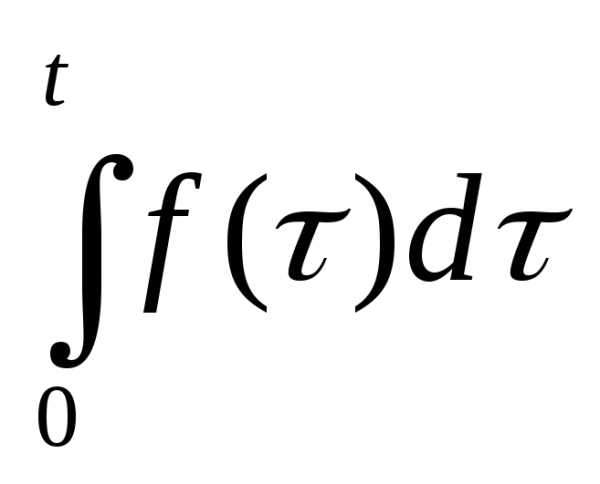является оригиналом. Условия (1) и (2) существования оригинала очевидны, так как они выполняются для функцииf(t). А теперь проверил выполнение условия (3). Оценим абсолютную величину заданного интеграла:

Следовательно, условие (3) также выполняется. Убедимся теперь в справедливости (5):

Интегрируя последнее равенство по частям, получим:

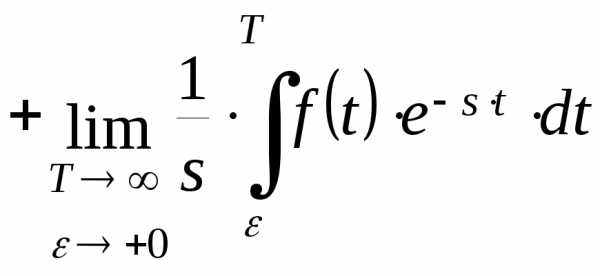
М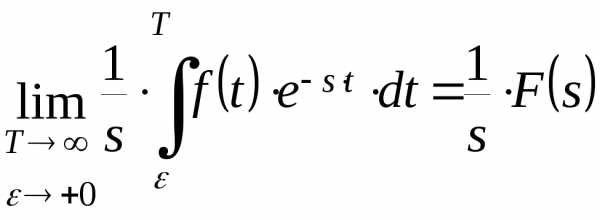одуль выражения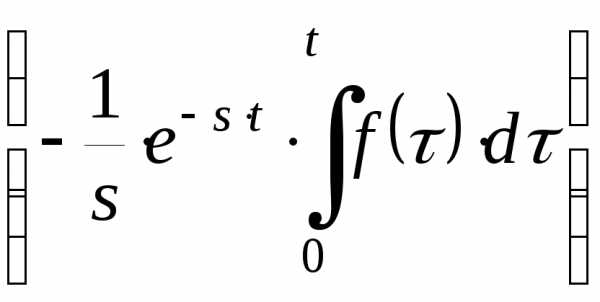для всех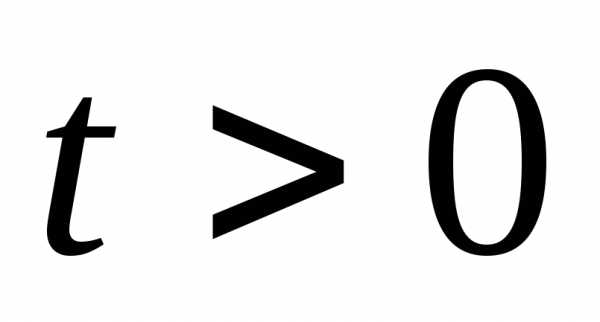меньше или равен, где, то предел первого слагаемого равен нулю.

(6)

И на основании свойств линейности получим формулу (5).

Теорема доказана.

4) Смещение в области оригинала.

Если f(t) – оригинал иF(s) – его изображение, то изображение смещенного оригинала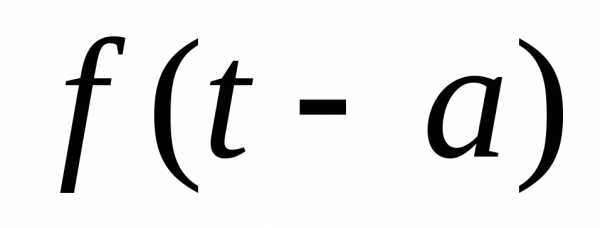, гдеa– положительное число, определяемое равенством:

(7)

Доказательство

При доказательстве используется:

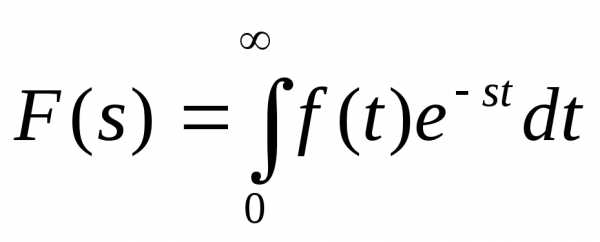
Введем новую переменную . Тогда будем иметь:

Умножим это равенство слева и справа на 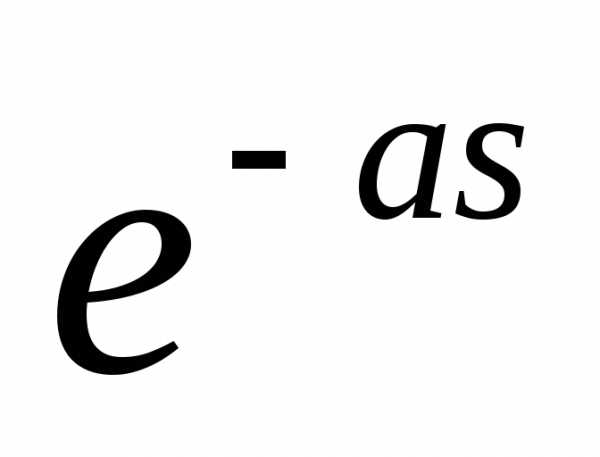. Будем считать, чтоaне зависит отt. Тогда получим:

Вносим под знак интеграла и получаем:

Теорема доказана.

5) Смещение в области изображений.

Если f(t) – оригинал иF(s) – его изображение, а – любое число, включая и комплексное, то справедливо:

(8)

Доказательство

Воспользуемся формулой прямого преобразования Лапласа:

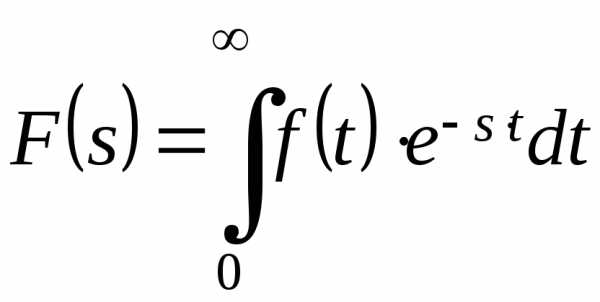
Инайдем:

Теорема доказана.

studfiles.net

18. Квадратурные формулы Гаусса

Опр. Говорят, что квадратурная формула

(1)

имеет алгебраическую степень точности m, если она является точной для любого многочлена степени m и существует многочлен степени , для которого квадратурная формула не является точной.

Квадратурные формулы наивысшей алгебраической степени точности называют квадратурными формулами Гаусса (при этом n считается фиксированным). Квадратурное правило имеет алгебраическую степень точности не ниже n тогда и только тогда, когда оно является интерполяционным. Следовательно, коэффициенты квадратурных правил Гаусса определяются формулой

. (2)

Таким образом, остается найти оптимальный набор узлов, при котором интерполяционная квадратурная формула будет иметь наивысшую алгебраическую степень точности. Последняя, как будет доказано, равна .

Лемма 1. Если квадратурное правило (1) имеет алгебраическую степень точности , то многочленстепениортогонален с весомна отрезкелюбому многочлену меньшей степени.

Д-во. Так как квадратурное правило (1) является точным для любого многочлена степени и,то приимеем, что док-ет лемму.

Из леммы 1 следует, что для построения квадратурного правила алгебраической степени точности необходимо найти многочлен степени, который был бы ортогонален любому многочлену меньшей степени.

Лемма 2. Если почти всюду на, то приведенный многочлен степени, ортогональный нас весомлюбому многочлену меньшей степени, существует и является единственным. При этом все его корни простые и находятся на отрезке.

Д-во. Для искомого приведенного многочлена степениусловия ортогональности любому многочлену меньшей степени дают систему линейных алгебраических уравнений(3)

относительно неизвестных коэффициентов . Системе (3) соответствует однородная система(4). Уравнения системы (4) умножим на соответствующие коэффициенты и сложим. Из полученного при этом выраженияи условия леммывытекает, что, т.е.. Поскольку однородная система (4) имеет только тривиальное решение, то соответствующая неоднородная система (3) имеет единственное решение.

Пусть — корни нечетной кратности многочлена, лежащие на отрезке. Требуется доказать, что. Допустим противное:. Тогда, в силу ортогональности, выполняется. С другой стороны, так какипочти всюду наимеем. Полученное противоречие доказывает, что. Лемма доказана.

Лемма 3. Если узлами интерполяционной квадратурной формулы (1) являются нули ортогонального многочлена , то квадратурная формула точна для любого мн-на степени.

Д-во. Пусть — произвольный многочлен степени. Представим его в виде,гдеи-многочлены степениn. Имеем

Здесь в силу ортогональностии, так как квадратурное правило интерполяционное, то

. Лемма доказана.

Теорема. Если почти всюду на, то существует квадратурное правило (1) наивысшей алгебраической степени точности.

Д-во. Существование квадратурного правила (1) алгебр-кой степени точности непосредственно следует из доказанных лемм. Остается доказать, что нельзя построить квадратурное правило (1), точное для любого многочлена степени. Для многочленастепениимеем значение интегралаи значение квадратурной суммы

.Т-ма док-на.

19. Квадр-ные формулы Гаусса с постоянной весовой ф-ей. Рассмотрим интеграл , (1) где- достаточно гладкая функция. Любой конечный отрезок интегрированиялинейным преобразованием приводится к отрезку. Поскольку в данном случае весовая функция, то квадратурное правило наивысшей алгебраической степени точности (2) существует. Его узлами явл-ся корни мн-на , ортогонального мн-нам меньшей степени с весом 1 на отрезке [-1;1].

_{Обозначим} . Очевидно, и. Возьмем произвольный многочленстепени. Используя условия ортогональности и проводя интегрирование по частям, получим

.

Продолжая процесс интегрирования по частям получим

Отсюда для , следует, что. Используя произвольность многочлена, последовательно получаем далее.

Таким образом, многочлен степени, производные которого определяются формулойимеет корни, каждый кратностиn. Следовательно, этот многочлен представляется в виде . Для искомого ортогонального многочлена в результате

получим выражение . (3)

Ортогональные многочлены, определяемые формулой (3) называют многочленами Лежандра. В случае выбора константы по правилу будут получаться приведенные многочлены. В практике вычислений для многочленов Лежандра используется формула Родрига.(4)

При этом получается квадрат нормы и рекуррентная формула.(5)

По формуле (3) находим . По формуле (4) находим. Отсюда определяем последовательно

и . Построим несколько квадратурных формул Гаусса вида (2).

При из уравненияполучаем один корень,и один коэффициент. Приходим к квадратурной формуле, имеющей наивысшую алгебраическую степень точности 1.

При из уравненияполучаем два корня,и два коэффициентаи. Приходим к квадратурной формуле, имеющей наивысшую алгебр-скую степень точности 3.

Формула для вычисления коэффициентов квадратурной формулы (2) может быть преобразована к виду(6)

При из уравненияполучаем три корняи три коэффициентаи. Приходим к квадратурной формуле, имеющей наивысшую алгебраическую степень точности 5.

studfiles.net