Координатная плоскость. Терминология (В. А. Тарасов). Видеоурок. Алгебра 7 Класс
Координатная ось и координатная плоскость нужны для того, чтобы связать местность, точку пространства с числом или упорядоченной парой чисел. Такая связь используется давно. Например, на дороге ставят указатель расстояния до какого-либо объекта, месторасположение которого характеризуется одним числом. Математики разработали модель, удобную для описания любой прямолинейной дороги – это координатная ось. Чтобы из любой прямой получить координатную ось, необходимо отметить на прямой начало отсчёта, масштаб и направление отсчёта (на прямой отмечаем точку 0 и точку 1 (см. Рис. 1)). Этим мы добились взаимооднозначного соответствия между точками и числами (например, числу 3 сопоставляется единственная точка A на координатной прямой, точке B сопоставляется единственное число -2 – координата этой точки).
Рис. 1. Координатная ось
Математиками также была разработана модель, которая, в частности, позволяет описать любой зрительный зал (расположение мест в зале), так как известно, что в билете указывается номер ряда и номер места, то есть пара чисел, в которой номера упорядочены. Такая модель получила название координатная плоскость. На данном уроке, тема которого: «Координатная плоскость. Терминология», мы рассмотрим координатную плоскость с прямоугольной системой координат.
Чтобы из обычной плоскости получить координатную с прямоугольной системой координат, необходимо провести две координатные оси, пересекающиеся в точках начала отсчёта. Горизонтальная ось называется ось абсцисс (направление отсчёта – слева направо), вертикальная – ось ординат (направление отсчёта – снизу вверх) (см. Рис. 2).
Любой точке M координатной плоскости сопоставляются два числа (две координаты): . Для получения этих координат необходимо через точку M провести две прямые, параллельные координатным осям. Одна прямая пересечёт ось абсцисс (ось X) в точке с координатами , вторая прямая пересечёт ось ординат (ось Y) в точке с координатами (см. Рис. 2).
Четыре прямых угла, образованных координатными осями, называются координатными углами.
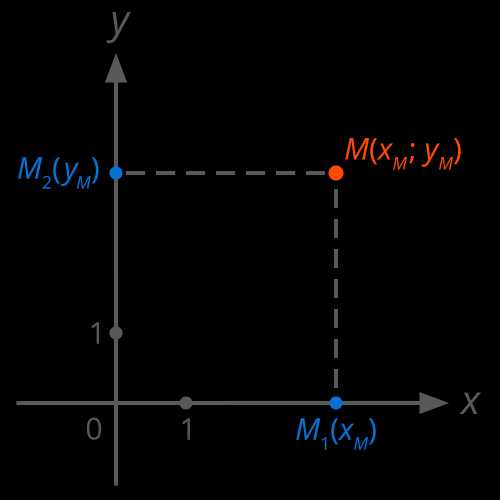
Рис. 2. Координатная плоскость
Построить точки по заданным координатам , .
Решение
Для построения точки M необходимо отложить единицу на оси X и провести перпендикулярную прямую; на оси Y откладываем число 3 и проводим перпендикулярную оси Y прямую. На пересечении перпендикуляров получим точку M с координатами
Для построения точки N необходимо отложить на оси X число 3 и провести перпендикулярную оси X прямую; на оси Y откладываем число 1 и проводим перпендикулярную оси Y прямую. На пересечении перпендикуляров получим точку N с координатами (см. Рис. 3).

Рис. 3. Иллюстрация к задаче
Задача 2
По знакам координат определить, в каком координатном углу находится точка.
а) причём .
Решение
Построим координатную плоскость и обозначим на ней точку M (см. Рис. 4а).
Рис. 4а. Иллюстрация к задаче
Ответ: точка Mлежит во втором координатном углу (ΙΙ).
б) причём
Решение
Построим координатную плоскость и обозначим на ней точку N (см. Рис. 4б).

Рис. 4б. Иллюстрация к задаче
Ответ: точка N лежит в третьем координатном углу (ΙΙΙ).
в) причём
Решение
Построим координатную плоскость и обозначим на ней точку P (см. Рис. 4в).
Ответ: точка P лежит в четвёртом координатном углу (ΙV).
Рис. 4в. Иллюстрация к задаче
Задача 3
В каких координатных углах находятся точки?
а) С положительной ординатой –
Решение
Построим координатную плоскость. Так как ордината точки больше нуля, а знак абсциссы не задан, то такая точка может лежать в первом (точка M) или втором (точка N) координатном углу (см. Рис. 5а).
Рис. 5а. Иллюстрация к задаче
Ответ: Ι, ΙΙ.
б) С отрицательной ординатой –
Решение
Построим координатную плоскость. Так как ордината точки меньше нуля, а знак абсциссы не задан, то такая точка может лежать в третьем (точка M) или четвёртом (точка N) координатном углу (см. Рис. 5б).
Ответ: ΙΙΙ, ΙV.

Рис. 5б. Иллюстрация к задаче
в) С положительной абсциссой – .
Решение
Построим координатную плоскость. Так как абсцисса точки больше нуля, а знак ординаты не задан, то такая точка может лежать в первом (точка M) или четвёртом (точка N) координатном углу (см. Рис. 5в).
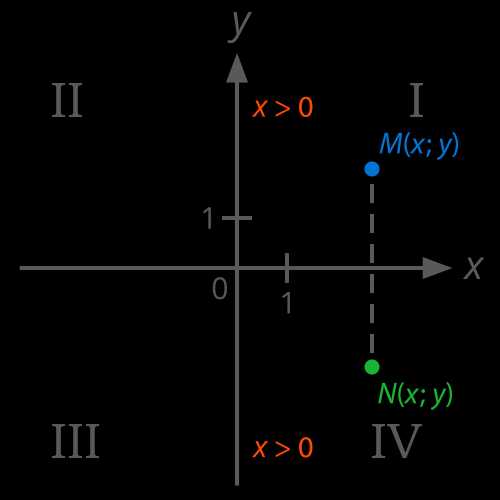
Рис. 5в. Иллюстрация к задаче
Ответ: Ι, ΙV.
г) С отрицательной абсциссой – .
Решение
Построим координатную плоскость. Так как абсцисса точки меньше нуля, а знак ординаты не задан, то такая точка может лежать во втором (точка M) или третьем (точка N) координатном углу (см. Рис. 5г).
Ответ: ΙΙ, ΙΙΙ.
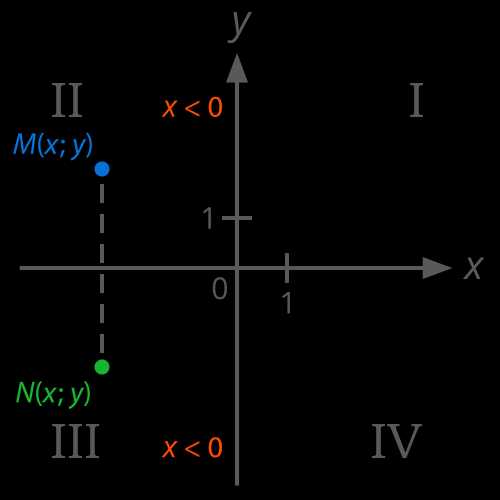
Рис. 5г. Иллюстрация к задаче
Задача 4
Постройте точки , , , , определите, на какой прямой они лежат.
Решение
Построим координатную плоскость и обозначим на ней заданные точки. У всех этих точек абсцисса одинаковая и равна 4, следовательно, они лежат на одной (вертикальной) прямой (см. Рис. 6), уравнение которой .
Рис. 6. Иллюстрация к задаче
Ответ: все заданные точки лежат на прямой .
Задача 5
Постройте точки , , , определите, на какой прямой они лежат.
Решение
Построим координатную плоскость и обозначим на ней заданные точки. У всех этих точек ордината одинаковая и равна 3, следовательно, они лежат на одной (горизонтальной) прямой (см. Рис. 7), уравнение которой .

Рис. 7. Иллюстрация к задаче
Ответ: все заданные точки лежат на прямой .
Задача 6
По данным рисунка 8 напишите уравнения прямых и координаты точек их пересечения.
Решение
На рисунке видим, что абсцисса точки
Уравнение прямой MK , так как ордината у любых точек этой прямой равна 4. Уравнение прямой NP , так как ордината у всех точек этой прямой равна -3. Уравнение прямой MN , так как абсцисса у всех точек этой прямой равна 5. Уравнение прямой KP , так как абс
interneturok.ru
Координатная плоскость (Г. Г. Гаицгори). Видеоурок. Алгебра 7 Класс
У чисел есть основные функции:
1. Задают порядок (например, нумерация вагонов: -й вагон, -й вагон, -й вагон).
2. Задают количество (например, «в поезде вагонов» или «мы купили яблок»).
3. Задают имя (например, номер автомобиля или телефона).
Но чаще всего числа выполняют несколько функций одновременно. Так, места в кинотеатре нумеруются и числа являются именами для каждого места (Рис. 1).
Рис. 1. Нумерация мест в кинотеатре
Но вместе с тем использование чисел упрощает поиск места благодаря тому, что числа задают порядок и количество: если вы возле -го кресла в ряду, то знаете, что через кресел будет -е (Рис. 2).
Рис. 2. Числа задают порядок и упрощают поиск места в кинотеатре
Представьте, насколько сложнее было бы искать место, если бы кресла в кинотеатре были обозначены картинками или даже подписаны пофамильно.
Обратите внимание, что для нумерации кресел в зале используют именно числа. Так определить место будет удобнее. Представьте, что в кинотеатре все места будут просто пронумерованы от до – поиск своего места всё равно будет затруднительным.
Итак, у каждого кресла есть имя (адрес), состоящий из двух чисел: номер ряда и номер кресла в ряду. Точки на глобусе тоже задаются двумя числами – долготой и широтой. Это адрес географической точки, ее географические координаты (Рис. 3).
Рис. 3. Географические координаты точки
Таким образом, адрес или координаты точки – это числовое или буквенное обозначение того места, где находится объект.
Математиками была разработана удобная модель, которая, в частности, позволяет описать любой зрительный зал (точнее, расположение мест в этом зале). Такая модель получила название координатная плоскость.
Вы уже знакомы с тем, как это делают на прямой. Для вычисления расстояний на прямой и задания порядка на ней вводят ось координат (Рис. 4).
- Выбирают – начало координат.
- Выбирают направление.
- Выбирают единичный отрезок.
Рис. 4. Координатная ось
Тогда каждой точке можно присвоить свою координату (расстояние от нее до нуля с соответствующим знаком) (Рис. 5).
Рис. 5. Определение координат точек на оси
И точно так же по любой координате можно восстановить точку (Рис. 6-7).
Рис. 6. Построение точки
Рис. 7. Построение точки
Т.е. на прямой нам достаточно одного числа, чтобы определять положение точки. На плоскости одного числа уже не хватает. Почему?
Пусть нам известно, что мы отъехали от города на км. В таком случае мы не можем точно определить свое положение, но мы знаем, что находимся на окружности с центром в городе и радиусом км (Рис. 8).

Рис. 8. Положение машины, отъехавшей от города на км
Чтобы задать положение машины точно, нужно еще задать направление, в котором мы ехали (Рис. 9).
То есть нужно второе число.
Рис. 9. Задание направления движения автомобиля
Присвоить каждой точке на плоскости имя из двух чисел можно разными способами. Остановимся подробно на уже известном нам способе – прямоугольной системе координат.
Она состоит из двух взаимно перпендикулярных осей (отсюда название – прямоугольная): икс и игрек (

Рис. 10. Прямоугольная система координат
Указав по каждой из осей координату, мы можем однозначно восстановить точку на плоскости (как ряд и место в кинотеатре).
Такую систему координат называют декартовой, в честь учёного Рене Декарта, который ее придумал (Рис. 11).
Рис. 11. Рене Декарт
Другие системы координат
Чтобы присвоить точке числовой адрес (ее координаты), используются и другие системы координат.
Есть несколько причин для использования различных систем координат, а именно:
1. Размерность.
На этом уроке мы рассматриваем прямоугольную систему координат на плоскости (Рис. 1).
Рис. 1. Прямоугольная система координат
Точка на плоскости однозначно задаётся двумя числами. В таком случае говорят, что размерность плоскости равна . А вот у прямой – другая размерность, равная .
Точка на прямой может менять свое положение только в одном направлении (двигаться вперед-назад, вверх-вниз). В качестве примера можно привести движение автомобиля по ровной дороге или движение лифта (Рис. 2).
Рис. 2. Пример изменения положения точки в одном направлении
Для указания местоположения точки нужна только одна координата. Эта координата будет обозначать то расстояние, которое проехал автомобиль (Рис. 3), или этаж, на котором находится лифт (Рис. 4).
Рис. 3. Координата обозначает расстояние, которое проехал автомобиль
Рис. 4. Координата обозначает этаж, на котором находится лифт
В математике такая система координат называется числовой или координатной осью.
Размерность пространства может быть и больше, например, (пространство, в котором мы живем, имеет три измерения). Для указания места положения точки в этом случае нужны координаты. Например, если в высотном здании на каждом этаже находится кинотеатр, то для указания места в билете должны быть указаны три координаты – этаж, ряд, номер кресла. Такая система координат строится точно так же, как на плоскости, только добавляется третья ось (ось аппликат) (Рис. 5).
Рис. 5. Построение прямоугольной системы координат в пространстве
2. Цель использования.
В нашем примере мы устанавливали положение автомобиля с помощью расстояния до города и направления движения. На самом деле мы использовали полярную систему координат. В полярной системе координат есть точка отсчета – начало координат и направление отсчета (Рис. 6).
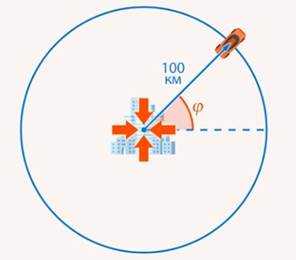
Рис. 6. Полярная система координат
Для того чтобы задать точку, мы указываем расстояние до начала координат и угол отклонения от направления отсчета.
Если на плоскости задать одновременно и полярную, и декартову системы координат, то можно выразить декартовы координаты и через полярные и и наоборот (Рис. 7).
Рис. 7. На плоскости заданы и полярная, и декартова системы координат
Т.е. все системы координат на плоскости эквивалентны, мы можем от одной перейти к другой.
Итак, прямоугольная система координат широко используется в математике, но не является единственной.
Координатные оси разбивают плоскость на четыре части – координатные четверти. Порядковые номера четвертей принято считать против часовой стрелки (Рис. 12).
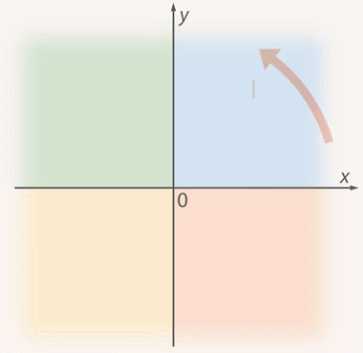
Рис. 12. Нумерация координатных четвертей
1. Если точка имеет положительную координату и положительную координату , то она лежит в I четверти. 2. Если точка имеет отрицательную координату и положительную координату , то она лежит во II четверти. 3. Если точка имеет отрицательную координату
interneturok.ru
| 1. |
Координаты точек
Сложность: лёгкое |
2 |
| 2. |
Определение положения точки в плоскости
Сложность: лёгкое |
1 |
| 3. |
Определение координат точки
Сложность: лёгкое |
2 |
| 4. |
Точки на прямой в координатной плоскости
Сложность: лёгкое |
1 |
| 5. |
Симметрия отрезков в координатной плоскости
Сложность: среднее |
2 |
| 6. |
Вершины четырёхугольника
Сложность: среднее |
4 |
| 7. |
Выбор уравнения прямой
Сложность: среднее |
2 |
| 8. |
Координаты вершин квадрата
Сложность: сложное |
8 |
| 9. |
Нахождение вершин квадрата, используя симметрию
Сложность: сложное |
6 |
| 10. |
Координаты середины отрезка
Сложность: сложное |
4 |
www.yaklass.ru
7 класс. Алгебра. Линейная функция. — Координатная плоскость.
Комментарии преподавателя
Этот урок посвящён изучению координатной плоскости. Мы рассмотрим, для чего используются координатные оси и координатные плоскости, разберём основные сведения. Также на уроке мы узнаем способ получения координатной плоскости из обычной. А также решим задачи, в которых научимся строить точки по заданным координатам, определять координатные углы и находить уравнения прямых по координатам лежащих на данной прямой точек.
Введение.
Координатная ось и координатная плоскость нужны для того, чтобы связать местность, точку пространства с числом или упорядоченной парой чисел. Такая связь используется давно. Например, на дороге ставят указатель расстояния до какого-либо объекта, месторасположение которого характеризуется одним числом. Математики разработали модель, удобную для описания любой прямолинейной дороги – это координатная ось. Чтобы из любой прямой получить координатную ось, необходимо отметить на прямой начало отсчёта, масштаб и направление отсчёта (на прямой отмечаем точку 0 и точку 1 (см. Рис. 1)). Этим мы добились взаимооднозначного соответствия между точками и числами (например, числу 3 сопоставляется единственная точкаA на координатной прямой, точке B сопоставляется единственное число -2 – координата этой точки).
Рис. 1. Координатная ось
Математиками также была разработана модель, которая, в частности, позволяет описать любой зрительный зал (расположение мест в зале), так как известно, что в билете указывается номер ряда и номер места, то есть пара чисел, в которой номера упорядочены. Такая модель получила название координатная плоскость. На данном уроке, тема которого: «Координатная плоскость. Терминология», мы рассмотрим координатную плоскость с прямоугольной системой координат.
Координатная плоскость
Чтобы из обычной плоскости получить координатную с прямоугольной системой координат, необходимо провести две координатные оси, пересекающиеся в точках начала отсчёта. Горизонтальная ось называется ось абсцисс (направление отсчёта – слева направо), вертикальная – ось ординат (направление отсчёта – снизу вверх) (см. Рис. 2).
Любой точке M координатной плоскости сопоставляются два числа (две координаты): . Для получения этих координат необходимо через точку M провести две прямые, параллельные координатным осям. Одна прямая пересечёт ось абсцисс (ось X) в точке с координатами , вторая прямая пересечёт ось ординат (ось Y) в точке с координатами (см. Рис. 2).
Четыре прямых угла, образованных координатными осями, называются координатными углами.
Рис. 2. Координатная плоскость
Построение точек по заданным координатам.
Построить точки по заданным координатам , .
Решение
Для построения точки M необходимо отложить единицу на оси X и провести перпендикулярную прямую; на оси Y откладываем число 3 и проводим перпендикулярную оси Y
www.kursoteka.ru
Открытый урок по алгебре «Координатная плоскость». 7-й класс
Разделы: Математика
Цель урока: Обобщение понятий, связанных с координатной плоскостью и координатами точек на плоскости; закрепление алгоритмов нахождения координат точки на плоскости и отыскания точки по ее координатам.
Оборудование: приложение 1, приложение 2.
Ход урока
I. Организационный момент. Сообщение темы и целей урока.
Здравствуйте, ребята! Сегодня у нас на уроке присутствуют гости. Поздоровайтесь с ними. Садитесь. Тема нашего урока «Координатная плоскость» (слайд 1). Сегодня на уроке мы:
- Обобщим понятия, связанные с координатной плоскостью и координатами точки на плоскости.
- Закрепим алгоритмы отыскания точки по ее координатам и нахождения координат точки на координатной плоскости (слайд 2).
II. Актуализация опорных знаний.
А начнем мы с повторения. Смотрите на экран и отвечайте на вопросы: (слайд 3)
- Что образуют построенные таким образом координатные прямые?
- Что называется координатной плоскостью? (слайд 4)
- Как называется координата а?
- Как называется координата б?
- Как называются прямые углы, образованные осями координат?
- Сколько таких координатных углов? Их нумеруют так, как показано на рисунке.
- Какой знак имеют координаты точки, принадлежащей I координатному углу? II ? III ? IV?
Давайте повторим алгоритм отыскания координат точки заданной в прямоугольной системе координат. В этом нам поможет компьютер. Внимание на экран. Сформулируйте этот алгоритм (см. слайды 5-7).
Давайте вспомним особенности некоторых точек. Внимание на экран.
- Что особенного в расположении точек А и В?
- Назовите координаты точки А и координаты точки В.
- Что особенного в координатах точек, лежащих на оси абсцисс?
- Что особенного в координатах точек, лежащих на оси ординат?
- Как расположены точки Д и С? Назовите их координаты. Что в них особенного?
- Как расположены точки С и Е? Назовите их координаты. Что в них особенного?
Повторим алгоритм построения точки М (а, в) в прямоугольной системе координат (слайд 8). Смотрите на экран (слайд 9). Сформулируйте алгоритм построения тоски М (а, в) в прямоугольной системе координат.
Молодцы! Вы хорошо работали. Мы повторили все понятия, связанные с координатной плоскостью.
III. Практическая работа на компьютере с элементами творчества (построение рисунка на ПК по заданным координатам точек).
А теперь вы должны свои умения и знания проявить при выполнении практического задания с элементами творчества.
Представьте, что вы художники. Вам предстоит нарисовать на компьютере рисунок по точкам с заданными координатами.
В вашем расположении будет 10 минут.
Кто справится с заданием раньше, получит дополнительное задание.
Около каждого ПК лежит лист с координатами, по которым вы будете рисовать рисунок (см. приложение 1).
Заняли свои места за ПК и приступили к «творчеству».
IV. Проверка и подведение итогов.
А теперь давайте посмотрим какой рисунок должен был получиться и что вы «натворили» (см. слайд 10).
Воспитательное слово учителя: При выполнении этого задания вы увидели как важно быть внимательным, аккуратным в работе и хорошо знать алгоритм построения точки по заданным координатам. Чтобы не получился глаз на хвосте, а лапы на голове.
Займите свои места за партами.
V. Контроль знаний, умений и навыков.
1. Инструктаж по работе с тестовым заданием (слайд 11).
Ребята, мы приступаем к заключительной части урока. Я предлагаю вам тестовое задание по двум вариантам, которые вы выполните на оценку. В вашем расположении будет 10 минут. Посмотрите на экран. В тесте три группы заданий, каждое из которых будет оценено отдельно, а потом будет выведен средний балл. Прочитайте самостоятельно, что надо сделать в каждой группе заданий. У каждого на парте лежит текст теста. Вы работаете на этом листе (см. приложение 1).
Запишите фамилию и имя.
2. Работа с тестовым заданием.
3. Взаимопроверка тестового задания (слайды 12-15).
Обменяйтесь тестами с соседом по парте. Приступаем к взаимопроверке. Внимание на экран. Вы видите верные ответы первой группы заданий и критерии оценок к нему. Проверяем и выставляем оценку под этой группой заданий.
Аналогично проверяем вторую и третью группу заданий и выставляем оценку.
4. Выставление оценки.
Найдите среднее арифметическое трех оценок. Если вы получили дробное число, то округлите до целого числа. Это и есть средний балл, который вы получили за тестовое задание.
Обменяйтесь вариантами и посмотрите, какие ошибки вы допустили. Сдайте тесты.
VI. Итог урока.
- Вспомните название темы урока?
- Какая цель стояла перед вами на уроке?
- Чему новому вы научились на уроке?
- Какие ранее полученные знания вы использовали на уроке?
- В какой новой ситуации вы применили свои знания на этом уроке?
- Выскажите свое отношение к уроку.
VII. Домашнее задание.
На отдельном листе построить рисунок в координатной плоскости и записать координаты точек, по которым этот рисунок можно построить. Из лучших рисунков будет оформлена выставка.
20.04.2010
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Конспект урока алгебры в 7 классе по теме «Координатная плоскость»
Предмет: алгебра
Класс: 7
Учебник: Колягин Ю.М.
Тема урока: Координатная плоскость
Цели урока:
-организовать деятельность учащихся по закреплению понятия координатной плоскости, координаты точек, построения точки по координатам и нахождения координат точки;
— развивать внимание и память учащихся.
ХОД УРОКА
1. Организационный момент.
«Учится можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом» А. Франс
2. Сообщение темы урока.
Из центра квадрата ходом шахматного коня отгадайте тему урока.
К
А
О
Е
О
О
П
С
Т
Р
Н
О
Т
Л
М
Я
К
Т
Д
Н
С
И
А
А
Ь
21
12
7
2
19
6
17
20
13
8
11
22
1
18
3
16
5
24
9
14
13
10
15
4
25
3. Историческая справка. (Слайд № 2) Более чем за 100 лет до нашей эры греческий ученый Гиппарх предложил провести на карте Земли параллели и меридианы. В ХIV веке французский ученый Оресле по аналогии с географическими координатами создал координатную плоскость. Он поместил на плоскость прямоугольную сетку и назвал широтой и долготой то, что сейчас мы называем абсциссой и ординатой. Термины абсцисса и ордината были введены в употребление Лейбницем в XVII веке. Однако основная роль в создании метода координат принадлежит французскому ученому Рене Декарту (1596-1650). Введенные на плоскости координаты х , у называют декартовыми.
4. Изучение нового материала.
Учитель: С именем какого выдающегося математикасвязано понятие прямоугольной системы координат?
Ученик:…….
Учитель: В какой области математики Рене Декарт использовал прямоугольную систему координат?
Ученик:…(анал. геом)
Учитель: Вспомните, что представляет собой прямоугольная система координат? Сформулируйте определение.Начертите в тетради прямоугольную систему координат
Ученик:…..
Учитель: Что мы называем координатой точки?
Ученик:……..
Учитель: Постройте произвольную точку М и назовите ее координаты. Представьте что вы ученые-математики, как бы вы назвали углы, образованные осями координат? Эти углы называют квадрантами или координатными углами. Их нумеруют против часовой стрелки. Назовите номер координатного угла, в котором вы поставили точку. Предположим, что точка лежит на оси абсцисс(ординат) чему равна ее ордината(абсцисса)?
Ученик:
Межпредметная связь
В географии положение точек на земной поверхности тоже определяют двумя числами географическими координатами: широтой и долготой.
Определить название города по широте и долготе, если его координаты — 39º в.д. и 47 º с.ш. (Ростов на Дону)
5. Первичное повторение материала
1. Игра «Охотники» на заранее начерченной координатной плоскости учитель прикрепляет фигурки животных, учащиеся «стреляют» (определяют координаты точки). Игру можно организовать в соревновательной форме.
2. Постройте рисунок по координатам
Ёжик
(2;-1), (3,5;0,5), (4;-1), (5;0), (4;2), (2;1), (2;3), (4;5), (4;6), (2;5), (1;7), (1;8), (0;7), (0;9), (-1;7), (-2;8),(-2;7), (-3;7), (-2;6), (-4;6), (-3;5), (-4;5), (-3;4), (-5;4), (-4;3), (-5;3), (-4;2), (-6;2), (-5;1), (-6;1), (-5;0),(-6;0), (-5;-1), (-6;-2), (-4;-2), (-5;-3), (-3;-4), (-4;-5), (-2;-5), (-1;-6), (3;-6), (3;-5), (1;-5), (1;-4), (2;-3), (2;-1)
Что изображено на рисунке? В Ростовской области ушастый еж занесен в Красную книгу.
Сообщение учащегося(Ушастый ёж — вид семейства ежовых отряда насекомоядных. Длина тела 12—27 см, хвоста до 2 см. Отличается от обыкновенного ежа большим размером ушной раковины: длина его ушей до 5 см. Ареал вида: степи, полупустыни ипустыни Северной Африки, Юго-восточной Европы, Центральной Азии. Активен в сумерки и ночью. В первой половине XX века довольно часто встречался, нередко вместе с белогрудым ежом, в окрестностях Ростова-на-Дону. В начале 2000-х годов отмечен в Орловском, Ремонтненском,Пролетарском районах области, где до 1960—1970-х годов был единственным видом ежей, однако широкое обводнение степей и их распашка привели к проникновению сюда и увеличению численности белогрудого ежа и падению популяции ушастого ежа.)
6.Самостоятельная работа
Самостоятельно с последующей проверкой по вариантам под копирку на листочках постройте на координатной плоскости точки по указанным координатам, соедините их последовательно. Один экземпляр сдается учителю, по второму проверяем и выставляем себе оценки.
Постройте фигуру по точкам
Вариант 1
Вариант 2
A (6; 6)
B (3; 7)
C ( 0; 8)
D (-3; 5)
E (-6; 3)
F (-8; 5)
G (-5; 7)
D (-3, 5)
K (-15;-7)
L (-10;-5)
M ( -6;-5)
N ( -3;-6)
O ( -1;-10)
P ( 5;- 10)
R ( 6; -6)
N (-3; -6)
Проверка: Что напоминают эти фигуры?
7. Рефлексия.
Ребята по кругу высказываются одним предложением, выбирая начало фразы из рефлексивного экрана на доске:
сегодня я узнал…
было интересно…
было трудно…
я выполнял задания…
я понял, что…
теперь я могу…
я почувствовал, что…
я приобрел…
я научился…
у меня получилось …
я смог…
я попробую…
меня удивило…
урок дал мне для жизни…
мне захотелось…
8. Итог урока.
Итак, ответим на следующие вопросы:
Как называют пару чисел, определяющих положение точки на плоскости?
Как отметить на координатной плоскости точку по заданным ее координатам?
Выставление оценок учащимся за работу на уроке.
Домой: А теперь домашнее задание, оно сегодня не обычное. У меня на столе лежат конверты с творческими заданиями, уходя, вы можете взять любой конверт, а можете и не брать, но если возьмете, то точно не пожалеете (в конвертах задание: по соответствующим координатам изобразить рисунок животного).
infourok.ru
Координатная плоскость — Математика — 7 класс
Просмотр содержимого документа
«Координатная плоскость»
Урок 76. Координатная плоскость.
Цели урока: развивать умение работать с координатной прямой и с координатной плоскостью.
1. Актуализация знаний.
Провести фронтальный опрос:
Как называется ось ?
Назовите ординату точки .
В какой четверти находится точка ?
На какой координатной оси находится точка ?
Какую координату показывает число 3 для точки ?
Предложите значение переменной a такое, чтобы точка располагалась в третьей координатной плоскости.
Назовите знаки для второй координатной четверти.
2. Решение задач.
1) Работа у доски (2): № 788(а, г), 789, 794, 796.
2) Устно ответить на вопросы заданий: № 767(б, в), 768(б, в), 779.
3. Самостоятельная работа.
Вариант I.
1. Заполнить таблицу:
Геометрическая модель | Аналитическая модель | Обозначение промежутка | Название промежутка |
|
|
| |
|
|
| |
|
|
| Интервал от 2 до 9 |
|
|
|
2. Постройте прямые AB, CD, MN, для которых , , , , , . Найдите координаты точек пересечения данных прямых.
3. Постройте прямую, удовлетворяющую уравнению .
Вариант II.
1. Заполнить таблицу:
Геометрическая модель | Аналитическая модель | Обозначение промежутка | Название промежутка |
|
|
| |
|
|
| |
|
|
| Луч от – 4 до |
|
|
|
2. Постройте прямые AB, CD, MN, для которых , , , , , . Найдите координаты точек пересечения данных прямых.
3. Постройте прямую, удовлетворяющую уравнению .
Домашнее задание: выполнить задания № 786(а), 792(а, в), 795.
multiurok.ru
