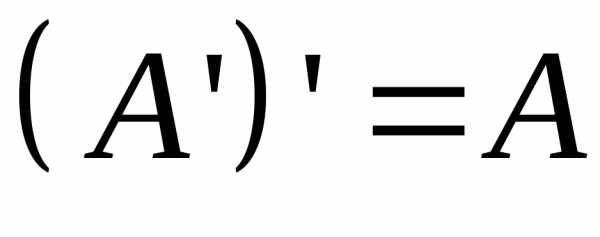Линейная алгебра Матрицы и определители.
Большинство математических моделей в экономике описываются с помощью матриц и матричного исчисления.
Матрица — это прямоугольная таблица, содержащая числа, функции, уравнения или другие математические объекты, расположенные в строках и столбцах.
Объекты, составляющие матрицу, называют ее элементами. Матрицы обозначают заглавными латинскими буквами
а их элементы – строчными.
Символ 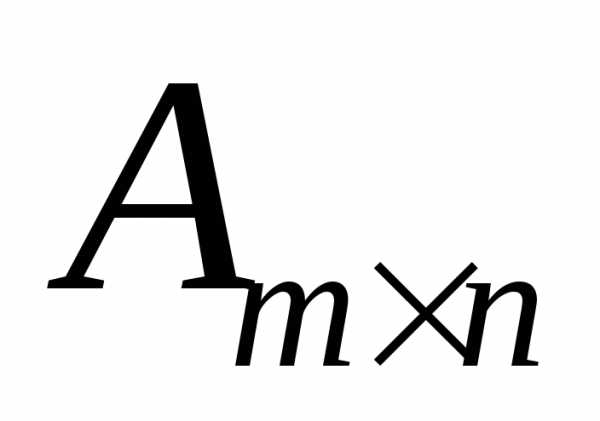 означает, что матрица
означает, что матрица имеет
имеет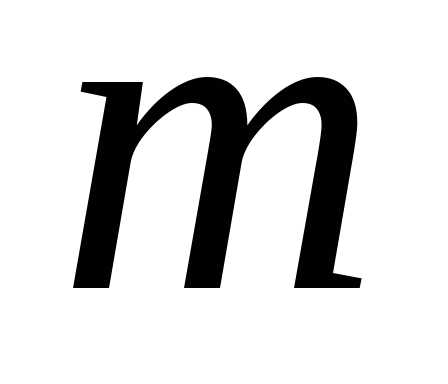 строк и
строк и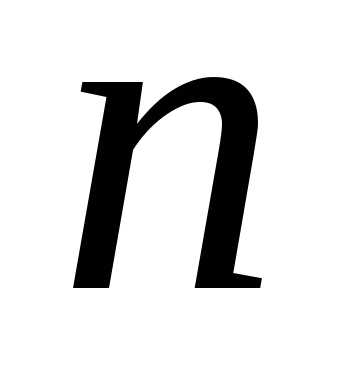 столбцов,
столбцов,
 –й
строки и
–й
строки и –го
столбца.
–го
столбца..
Говорят,
что матрица А равна матрице В: А=В, если они
имеют одинаковую структуру (то есть
одинаковое число строк и столбцов) и их
соответсвующие элементы тождественно
равны  ,
для всех.
,
для всех.
Частные виды матриц
На практике довольно часто встречаются матрицы специального вида. Некоторые методы предполагают также преобразования матриц от одного вида к другому. Наиболее часто встречающиеся виды матриц приведены ниже.
| квадратная матрица, число строк n равно числу столбцов n |
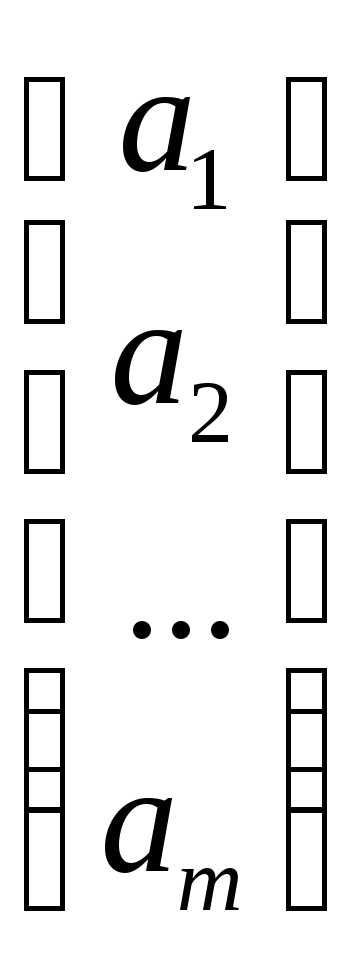
| матрица-столбец |
матрица-строка | |
| нижняя треугольная матрица |
| верхняя треугольная матрица |
| нулевая матрица |
| диагональная матрица |
Е = | единичная матрица Е (квадратная) |
| унитарная матрица |
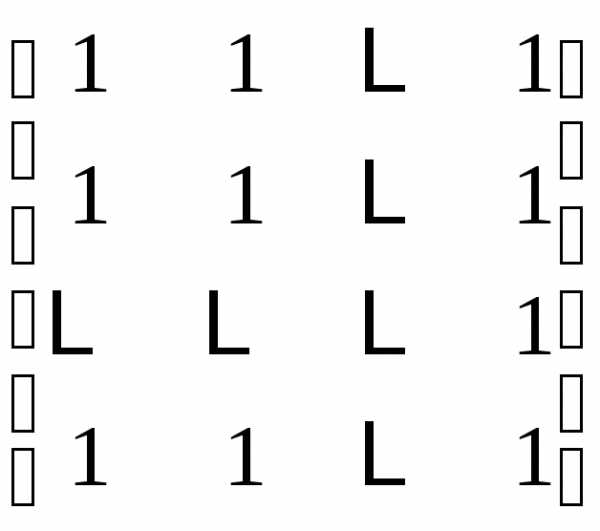
| ступенчатая матрица |
( ) | Пустая матрица |
Элементы матрицы, с равными номерами строк и столбцов, то есть aii образуют главную диагональ матрицы.
Операции над матрицами.
При умножении матрицы А на скаляр (число), необходимо умножить на это число все элементы матрицы . Общий множитель всех элементов можно вынести за знак матрицы.
Сложение матрицы и числа,
Сложение матриц
Вычитание матриц
Умножение двух матриц возможно только тогда, когда число строк первой равно числу строк второй. Произведением , где каждый элемент матрицыС —
 есть сумма произведений всех элементов
есть сумма произведений всех элементов –й
строки
–й
строки на соответсвующие элементы
на соответсвующие элементы –го
столбца
–го
столбца .
.
.
Свойства операций над матрицами
Специфические свойства оперций
Если
произведение матриц 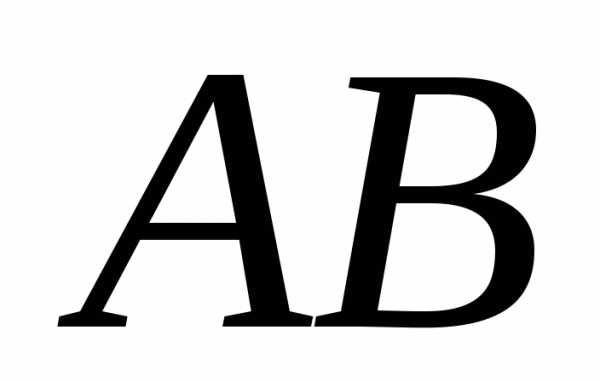 – существует, то произведение
– существует, то произведение может и не существовать. Вообще говоря,.
То есть умножение матриц не коммутативно.
Если же,
то
может и не существовать. Вообще говоря,.
То есть умножение матриц не коммутативно.
Если же,
то и
и называют коммутативными. Например,
диагональные матрицы одного порядка
коммутативны.
называют коммутативными. Например,
диагональные матрицы одного порядка
коммутативны.
Если 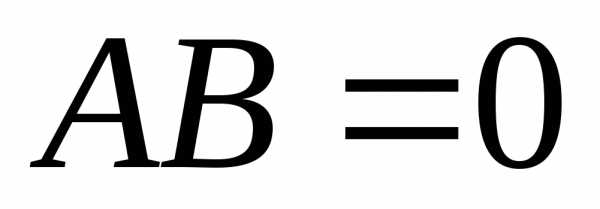 ,
то необязательно
,
то необязательно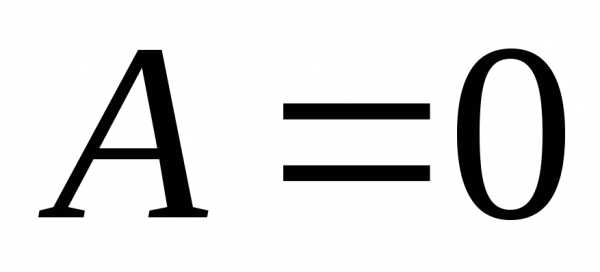
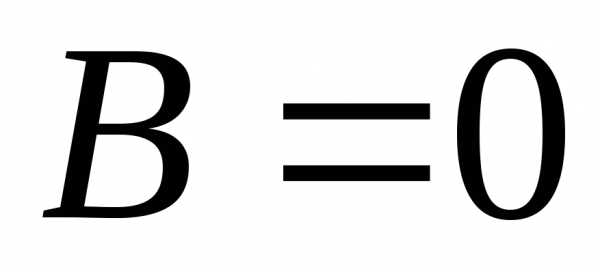 .
Т.е., произведение ненулевых матриц
может дать нулевую матрицу. Например
.
Т.е., произведение ненулевых матриц
может дать нулевую матрицу. Например Операция
возведения в степень определена только для квадратных матриц.
Если 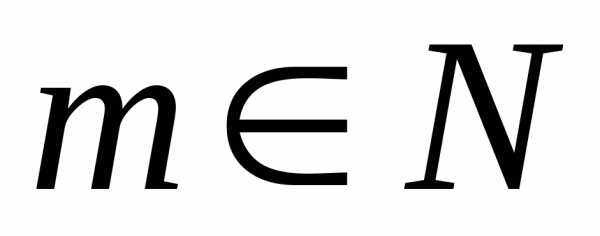 ,
то
,
то
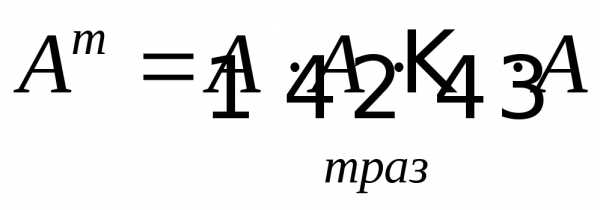 .
.
По
определению полагают
,
и нетрудно показать, что,.
Отметим,
что из 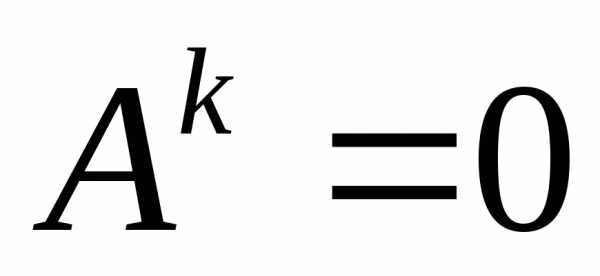 не следует, что
не следует, что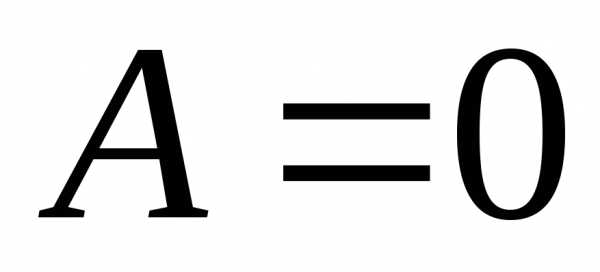 .
.
Поэлементное
возведение в степень А.m = 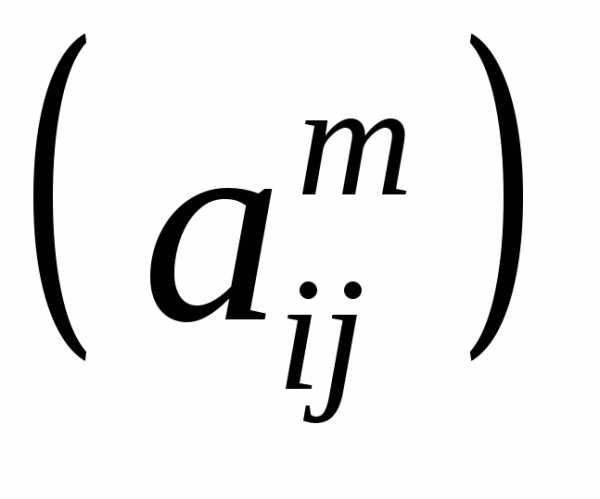 .
.
Операция транспонирования матрицы заключается в замене строк матрицы ее столбцами:
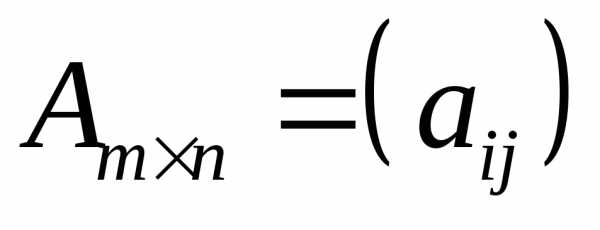
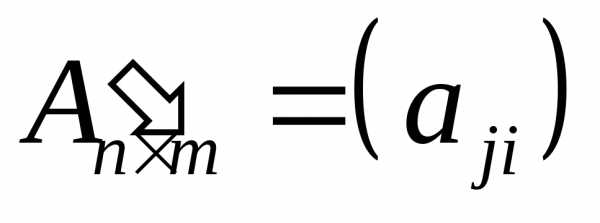
Например
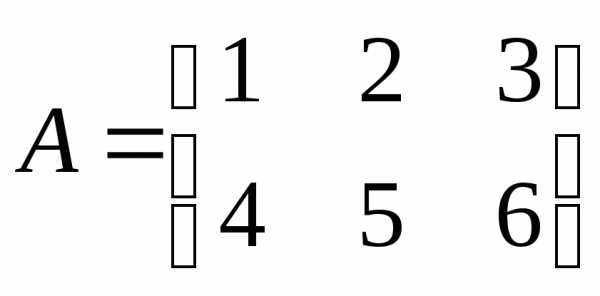 ,
, 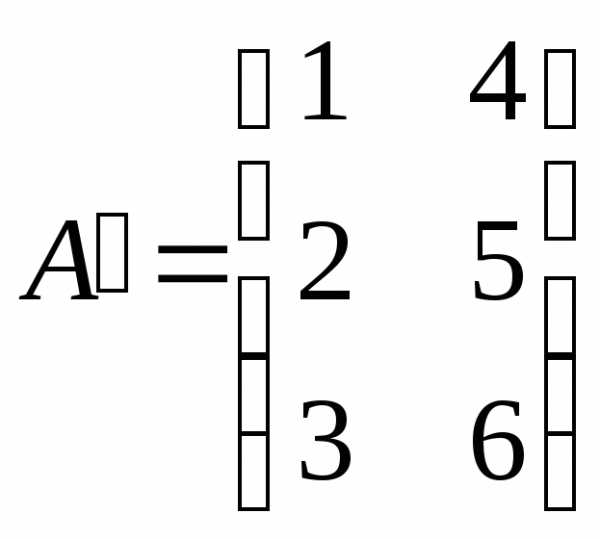 .
.
Свойства транспонирования:
Определители и их свойства.
Для квадратных матриц часто используется понятие определителя – числа, которое вычисляется по элементам матрицы с использованием строго определенных правил. Это число является важной характеристикой матрицы и обозначается символами
.
Определителем
матрицы
является ее элемент .
.
.
Определитель матрицы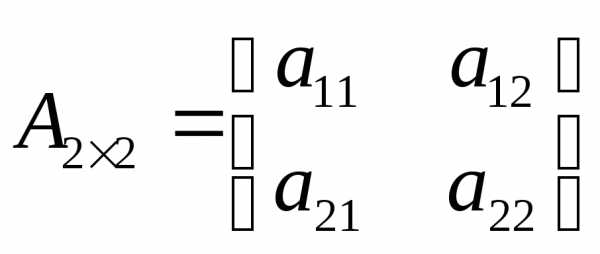 вычисляется
по правилу:
вычисляется
по правилу:,
т.е., из произведения элементов главной диагонали вычитается произведение элементов дополнительной диагонали.
Для
вычисления определителей более высокого
порядка (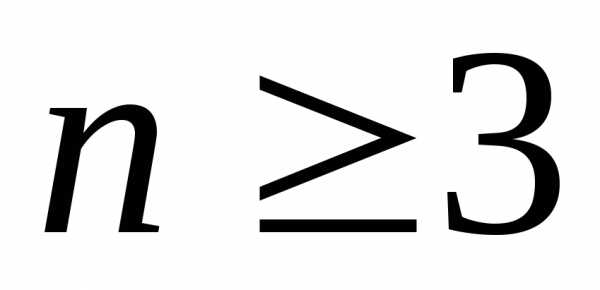 )
необходимо ввести понятия минора и
алгебраического дополнения элемента.
)
необходимо ввести понятия минора и
алгебраического дополнения элемента.
Минором 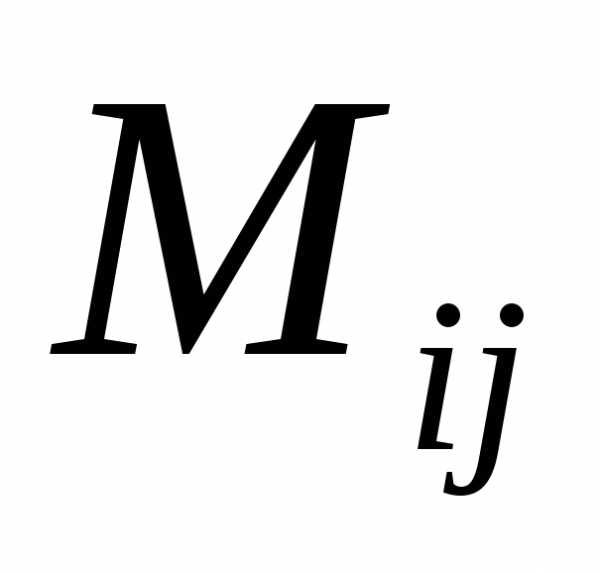 элемента
элемента  называют определитель, который получают
из матрицы
называют определитель, который получают
из матрицы ,
вычеркивая-ю
строку и
,
вычеркивая-ю
строку и -й
столбец.
-й
столбец.
Рассмотрим
матрицу  размером
размером :
:
тогда, например,
Алгебраическим
дополнением  элемента
элемента называют его минор, умноженный на
называют его минор, умноженный на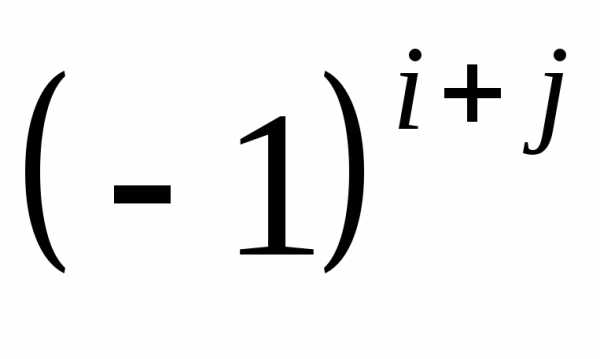 .
.
,
.
Теорема Лапласа: Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.
Например,
разлагая 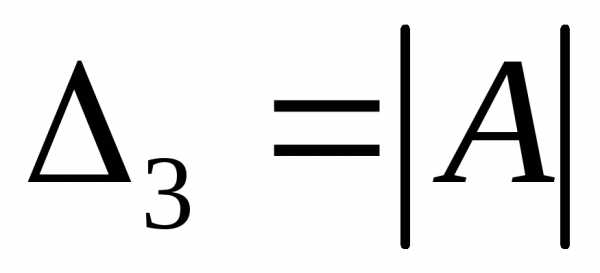 по элементам первой строки, получим:
по элементам первой строки, получим:
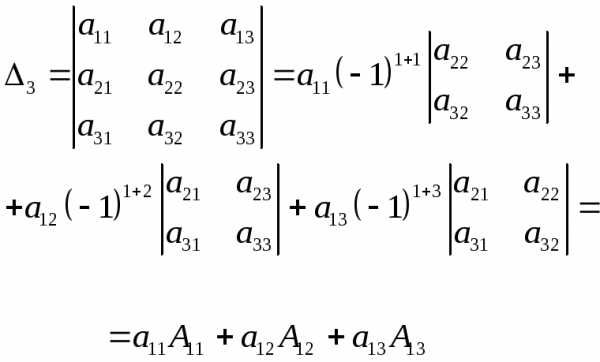
Последняя теорема дает универсальный способ вычисления определителей любого порядка, начиная со второго. В качестве строки (столбца) всегда выбирают тот, в котором имеется наибольшее число нулей. Например, требуется вычислить определитель четвертого порядка
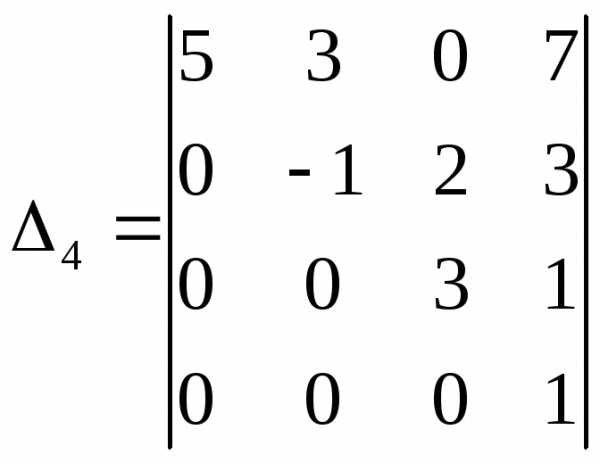
В данном случае можно разложить определитель по первому столбцу:
,
или последней строке:
.
Этот пример показывает также, что определитель верхней треугольной матрицы равен произведению ее диагональных элементов. Нетрудно доказать, что этот вывод справедлив для любых треугольных и диагональных матриц.
Теорема
Лапласа дает возможность свести
вычисление определителя 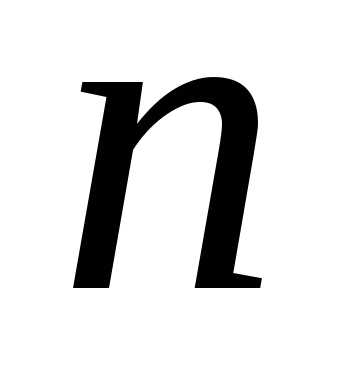 -го
порядка к вычислению
-го
порядка к вычислению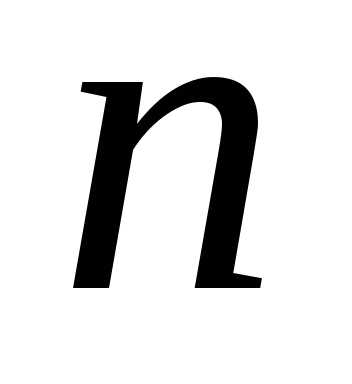 определителей
определителей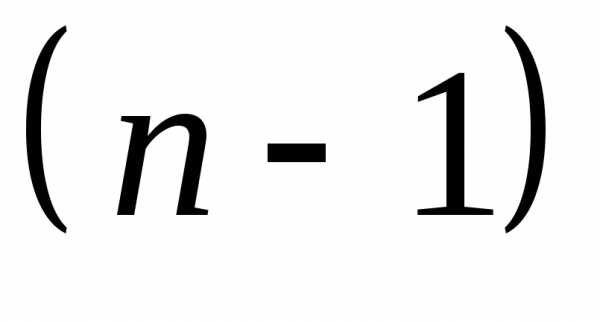 -го
порядка и, в конечном итоге, к вычислению
определителей второго порядка.
-го
порядка и, в конечном итоге, к вычислению
определителей второго порядка.
studfiles.net
Определители и их свойства
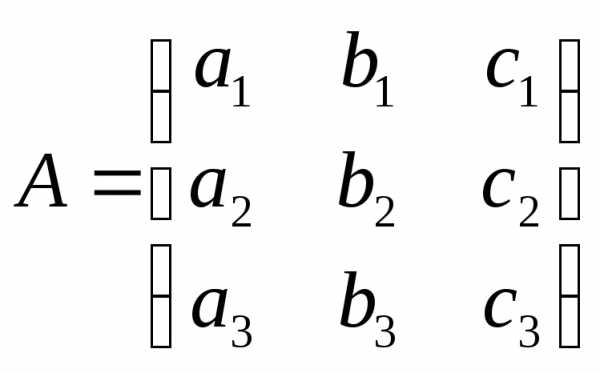
Определение. Определителем (или детерминантом) третьего порядка, соответствующим матрице А, называют число, обозначаемое символом
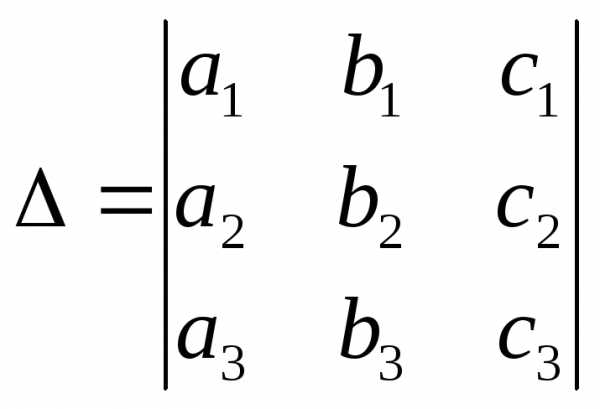
и определяемое равенством
Числа
называются
элементами определителя. Диагональ,
образованная элементами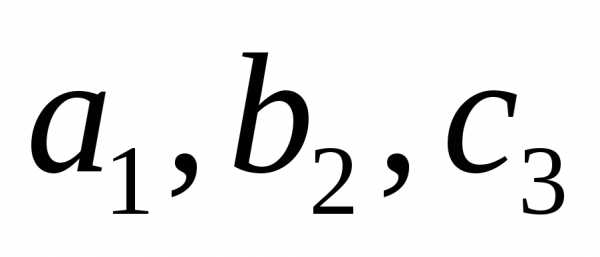 называется
главной , а диагональ, образованная
элементами
называется
главной , а диагональ, образованная
элементами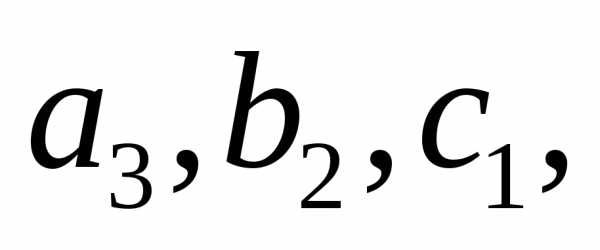 -побочной.
-побочной.
Чтобы запомнить, какие произведения в правой части равенства (*) берутся со знаком +, а какие со знаком — , полезно пользоваться правилом треугольников.
Пример.
Замечание
Определителем
2-го порядка 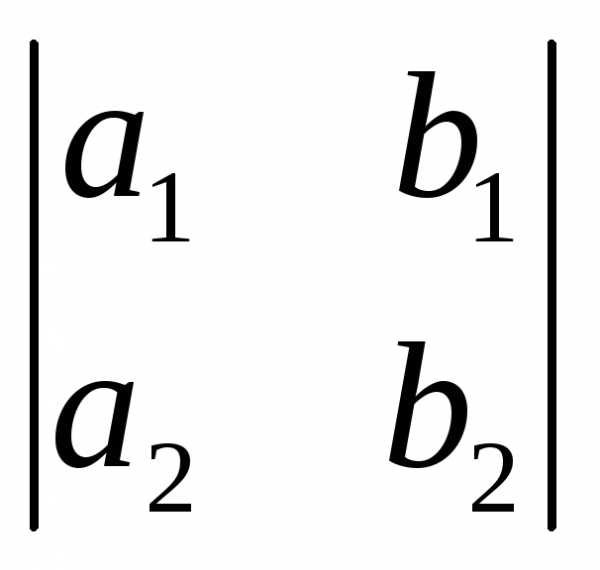 ,
соответствующим матрице
,
соответствующим матрице ,
называется число, равное.
,
называется число, равное.
Определение. Минором 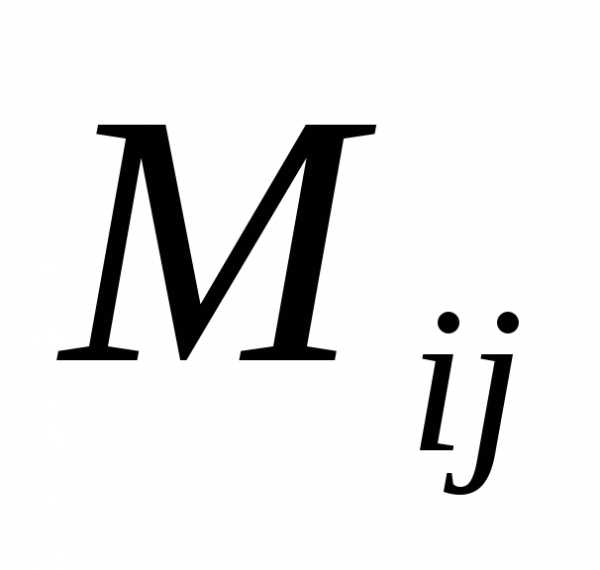 элемента
элемента определителя называется определитель,
полученный из данного, вычеркиваниемi-й
строки и j-го
столбца, на пересечении которых расположен
этот элемент.
определителя называется определитель,
полученный из данного, вычеркиваниемi-й
строки и j-го
столбца, на пересечении которых расположен
этот элемент.
Алгебраическим
дополнением  элемента
элемента называется
минор этого элемента
называется
минор этого элемента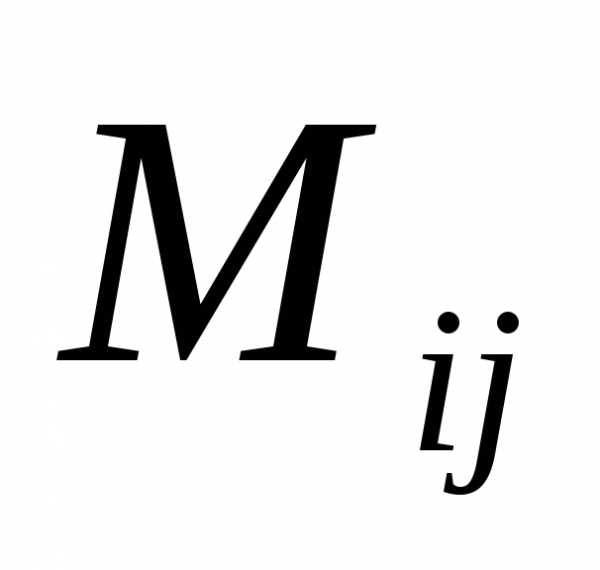 ,
умноженный на
,
умноженный на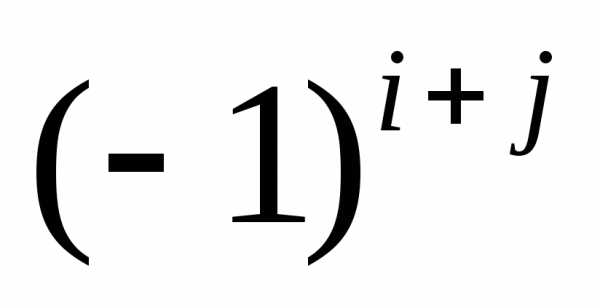 , т.е.
, т.е.
.
Свойства определителей рассмотрим на примере определителей третьего порядка.
1. Величина определителя не изменится, если строки и столбцы определителя поменять местами.
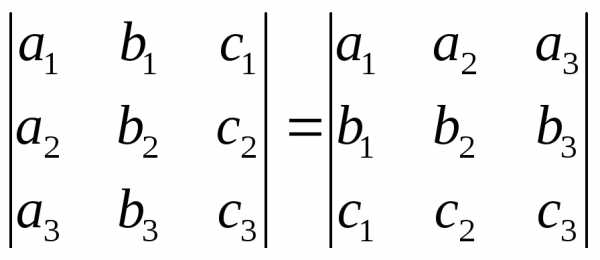
2. При перестановке двух рядом стоящих строк (или столбцов) определителя знак определителя меняется на противоположенный, т.е.
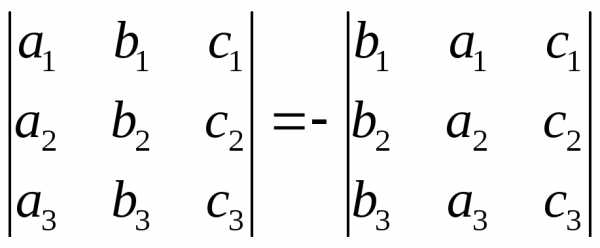
3. Если определитель имеет два одинаковых столбца или две одинаковых строки, то он равен нулю.
4. Общий множитель всех элементов некоторого столбца (или строки) выносится за знак определителя
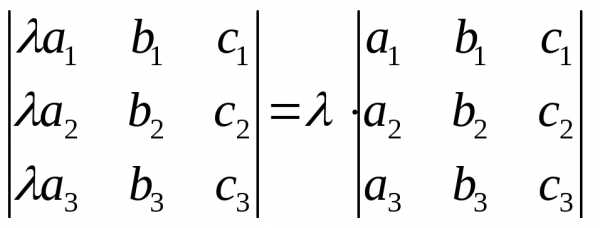
5. Если все элементы столбца (строки) равны нулю, то определитель равен нулю.
6. Если элементы двух столбцов (строк) определителя пропорциональны, то определитель равен нулю.
7. Если каждый элемент некоторого столбца (строки) есть сумма двух слагаемых, то определитель равен сумме двух определителей: в одном на месте суммы стоит первое слагаемое, в другом –второе.
8. Если к элементам некоторого столбца (строки) определителя прибавить соответствующие элементы другого столбца (строки), умноженные на одно и то же число, то определитель при этом не изменится.
9. Определитель равен сумме произведений элементов какого-нибудь столбца (строки) на их алгебраические дополнения.
Представление определителя в соответствии со свойством 9 называется разложением определителя по элементам некоторого столбца (строки).
10. Сумма произведений элементов какого-нибудь столбца (строки) на алгебраическое дополнение соответствующих элементов другого столбца (строки) равна нулю.
Пример.
Вычислить определитель, разлагая его по элементам первой строки.
1.2. Векторная алгебра
Прямоугольная система координат в пространстве определяется заданием единицы измерения длины и трёх пересекающихся в одной точке взаимно перпендикулярных осей: Ox,Oy, и Oz.
Точка 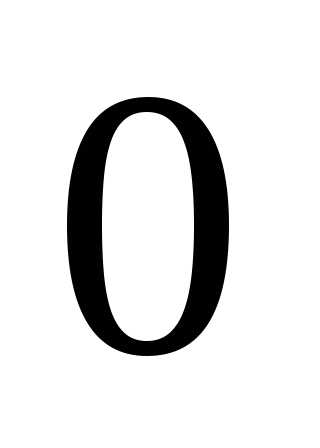 — начало координат,Ox—
ось абсцисс, Oy-ось
ординат,
— начало координат,Ox—
ось абсцисс, Oy-ось
ординат,
Oz – ось аппликат.
Пусть М— произвольная точка пространства (рис. 1.1). Проведем через точку М три плоскости, перпендикулярные координатным осям Ox, Oy, и Oz. Точка пересечения построенных плоскостей обозначается через соответственно.
Прямоугольными координатами точки М называются числа
При
этом называют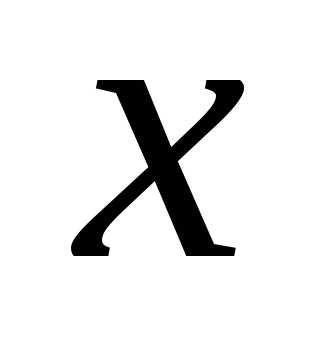 —
абсциссой,
—
абсциссой, – ординатой,
– ординатой, –
аппликатой точки М.
–
аппликатой точки М.
При заданной системе координат каждой точкеМ соответствует единственная упорядоченная тройка чисел (x, y, z) – её прямоугольные координаты и, наоборот, каждой упорядоченной тройке чисел (x, y, z) соответствует, и при том одна, точка М в пространстве.
Плоскости Oxy,Oxz,Oyz называются координатными плоскостями.
studfiles.net
Линейная алгебра Матрицы и определители.
Большинство математических моделей в экономике описываются с помощью матриц и матричного исчисления.
Матрица — это прямоугольная таблица, содержащая числа, функции, уравнения или другие математические объекты, расположенные в строках и столбцах.
Объекты, составляющие матрицу, называют ее элементами. Матрицы обозначают заглавными латинскими буквами
а их элементы – строчными.
Символ 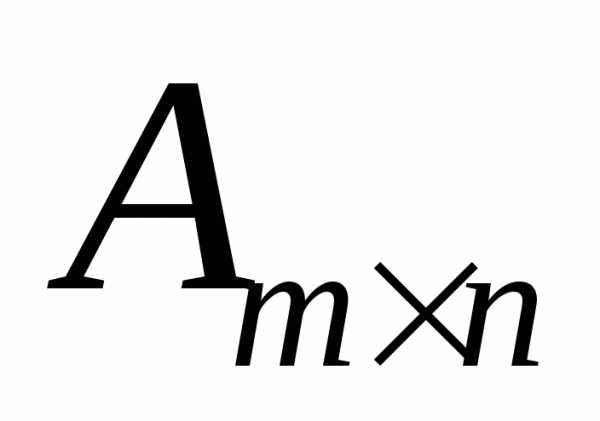 означает, что матрица
означает, что матрица имеет
имеет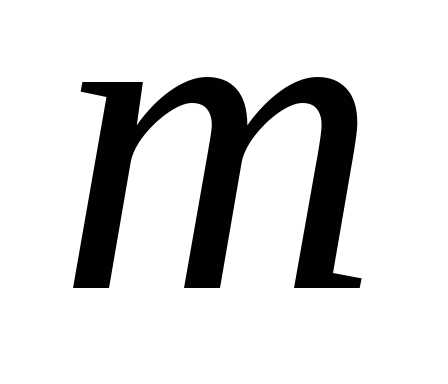 строк и
строк и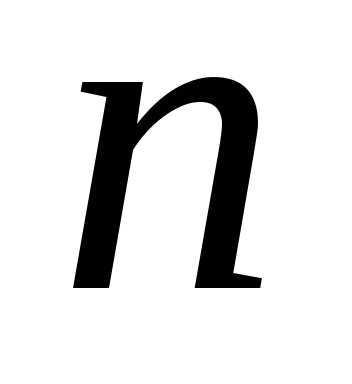 столбцов,
столбцов, элемент, находящийся на пересечении
элемент, находящийся на пересечении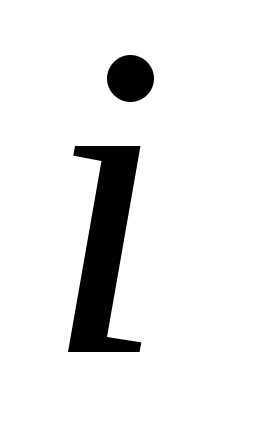 –й
строки и
–й
строки и –го
столбца.
–го
столбца.
.
Говорят,
что матрица А равна матрице В: А=В, если они
имеют одинаковую структуру (то есть
одинаковое число строк и столбцов) и их
соответсвующие элементы тождественно
равны 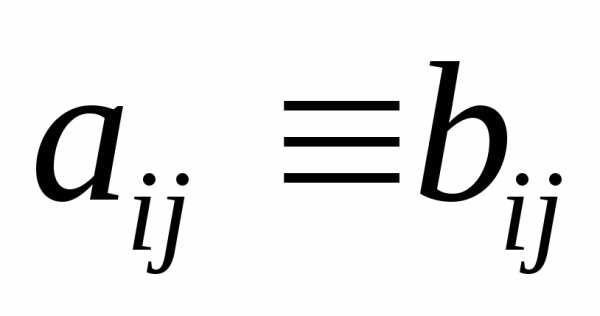 ,
для всех.
,
для всех.
Частные виды матриц
На практике довольно часто встречаются матрицы специального вида. Некоторые методы предполагают также преобразования матриц от одного вида к другому. Наиболее часто встречающиеся виды матриц приведены ниже.
| квадратная матрица, число строк n равно числу столбцов n |
| матрица-столбец |
матрица-строка | |
| нижняя треугольная матрица |
| верхняя треугольная матрица |
| нулевая матрица |
| диагональная матрица |
Е = | единичная матрица Е (квадратная) |
| унитарная матрица |
| ступенчатая матрица |
( ) | Пустая матрица |
Элементы матрицы, с равными номерами строк и столбцов, то есть aii образуют главную диагональ матрицы.
Операции над матрицами.
При умножении матрицы А на скаляр (число), необходимо умножить на это число все элементы матрицы . Общий множитель всех элементов можно вынести за знак матрицы.
Сложение матрицы и числа,
Сложение матриц
Вычитание матриц
Умножение двух матриц возможно только тогда, когда число строк первой равно числу строк второй. Произведением , где каждый элемент матрицыС —
 есть сумма произведений всех элементов
есть сумма произведений всех элементов –й
строки
–й
строки на соответсвующие элементы
на соответсвующие элементы –го
столбца
–го
столбца .
.
.
Свойства операций над матрицами
Специфические свойства оперций
Если
произведение матриц 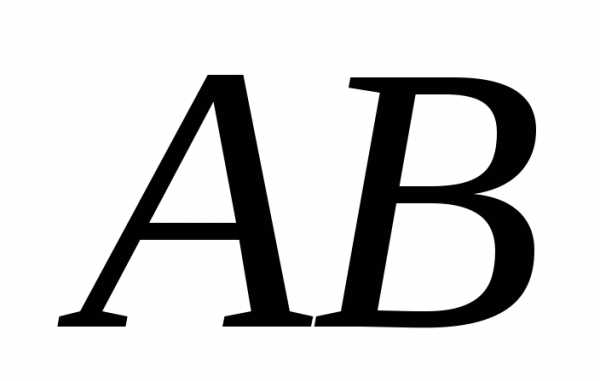 – существует, то произведение
– существует, то произведение может и не существовать. Вообще говоря,.
То есть умножение матриц не коммутативно.
Если же,
то
может и не существовать. Вообще говоря,.
То есть умножение матриц не коммутативно.
Если же,
то и
и называют коммутативными. Например,
диагональные матрицы одного порядка
коммутативны.
называют коммутативными. Например,
диагональные матрицы одного порядка
коммутативны.
Если 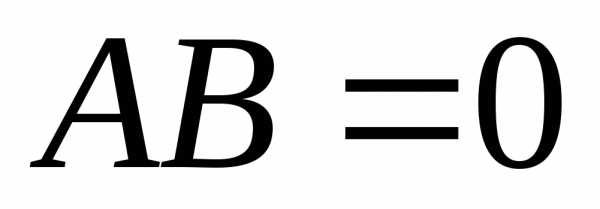 ,
то необязательно
,
то необязательно или
или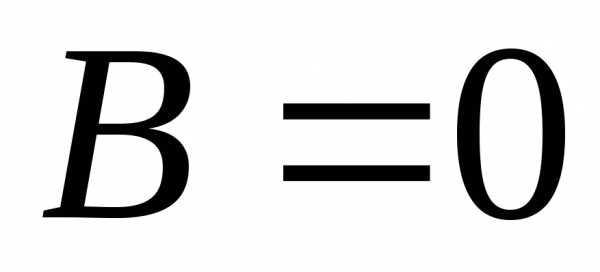 .
Т.е., произведение ненулевых матриц
может дать нулевую матрицу. Например
.
Т.е., произведение ненулевых матриц
может дать нулевую матрицу. Например
Операция
возведения в степень определена только для квадратных матриц.
Если 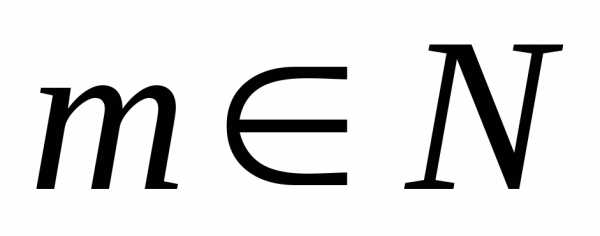 ,
то
,
то
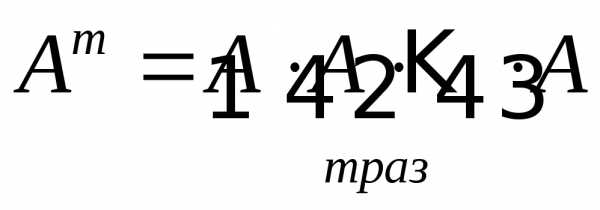 .
.
По
определению полагают
,
и нетрудно показать, что,.
Отметим,
что из 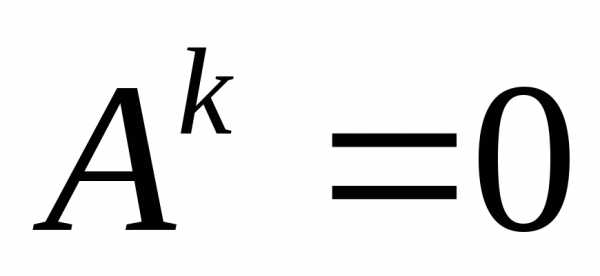 не следует, что
не следует, что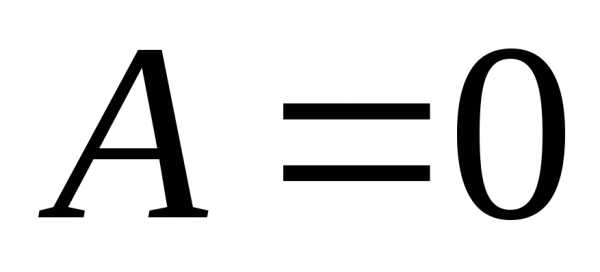 .
.
Поэлементное
возведение в степень А.m = 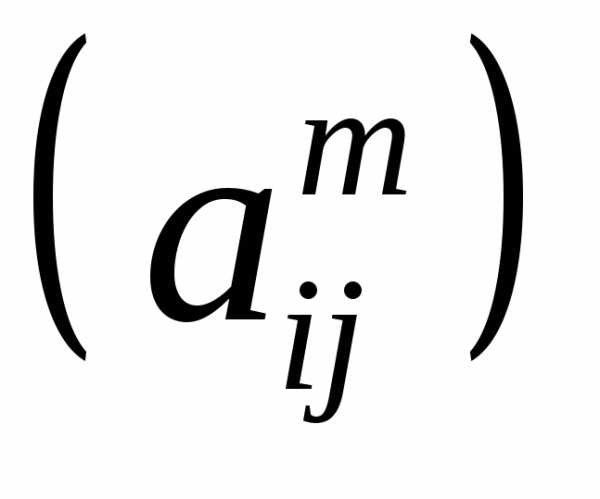 .
.
Операция транспонирования матрицы заключается в замене строк матрицы ее столбцами:
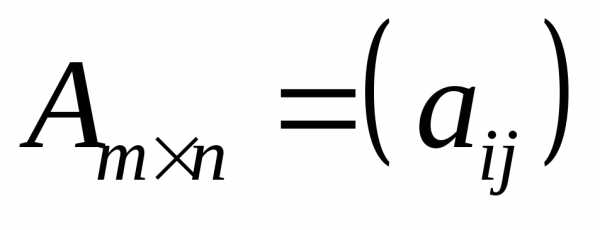 ,
, 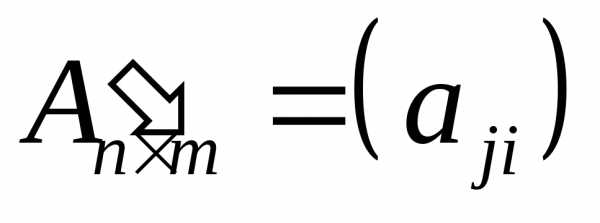
Например
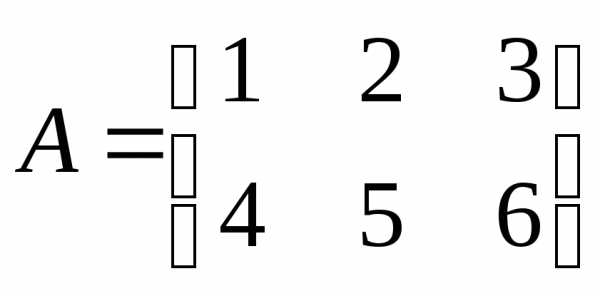 ,
, 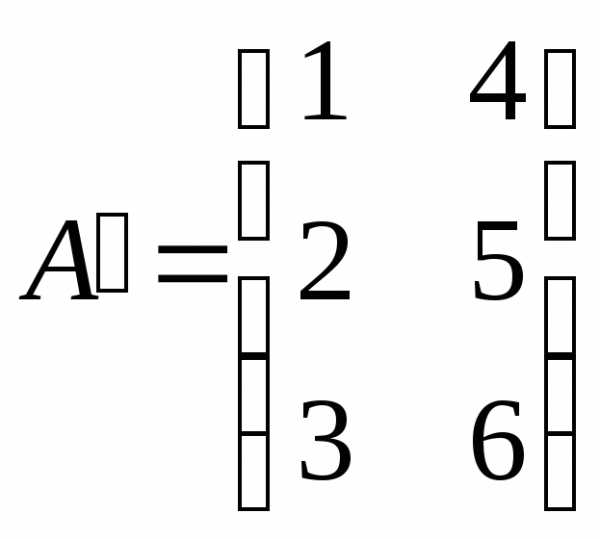 .
.
Свойства транспонирования:
Определители и их свойства.
Для квадратных матриц часто используется понятие определителя – числа, которое вычисляется по элементам матрицы с использованием строго определенных правил. Это число является важной характеристикой матрицы и обозначается символами
.
Определителем
матрицы
является ее элемент .
.
.
Определитель
матрицы 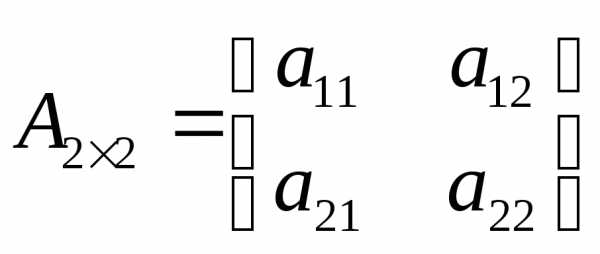 вычисляется
по правилу:
вычисляется
по правилу:
,
т.е., из произведения элементов главной диагонали вычитается произведение элементов дополнительной диагонали.
Для
вычисления определителей более высокого
порядка (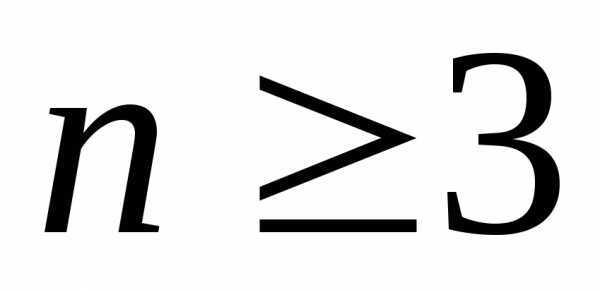 )
необходимо ввести понятия минора и
алгебраического дополнения элемента.
)
необходимо ввести понятия минора и
алгебраического дополнения элемента.
Минором 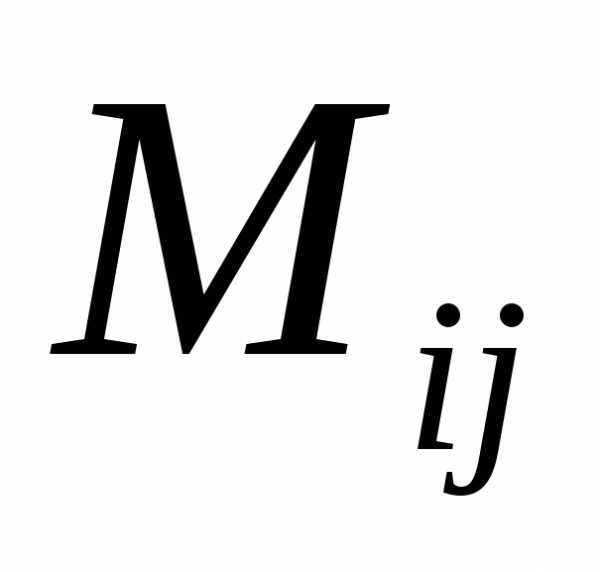 элемента
элемента  называют определитель, который получают
из матрицы
называют определитель, который получают
из матрицы ,
вычеркивая
,
вычеркивая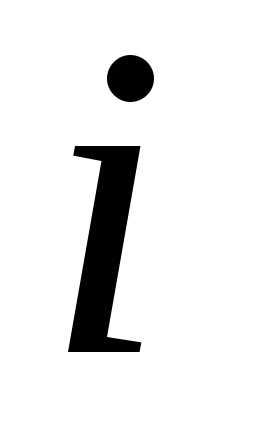 -ю
строку и
-ю
строку и -й
столбец.
-й
столбец.
Рассмотрим
матрицу  размером
размером :
:
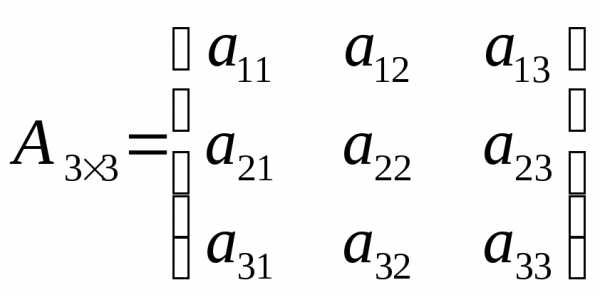 ,
,
тогда, например,
Алгебраическим
дополнением  элемента
элемента называют его минор, умноженный на
называют его минор, умноженный на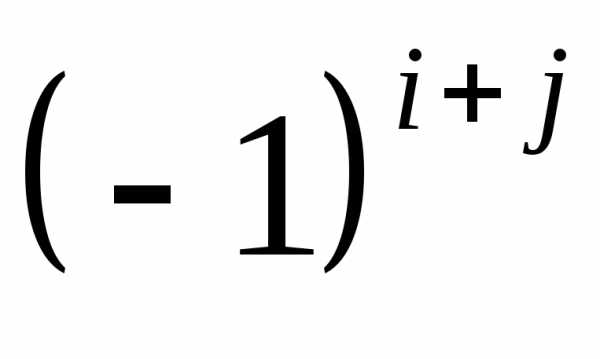 .
.
,
.
Теорема Лапласа: Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.
Например,
разлагая 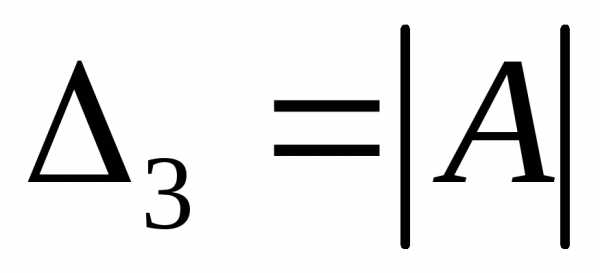 по элементам первой строки, получим:
по элементам первой строки, получим:
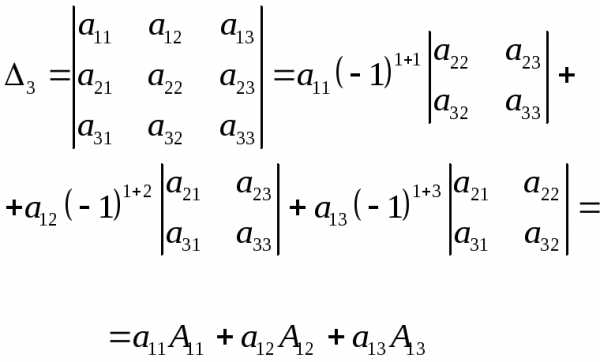
Последняя теорема дает универсальный способ вычисления определителей любого порядка, начиная со второго. В качестве строки (столбца) всегда выбирают тот, в котором имеется наибольшее число нулей. Например, требуется вычислить определитель четвертого порядка

В данном случае можно разложить определитель по первому столбцу:
,
или последней строке:
.
Этот пример показывает также, что определитель верхней треугольной матрицы равен произведению ее диагональных элементов. Нетрудно доказать, что этот вывод справедлив для любых треугольных и диагональных матриц.
Теорема
Лапласа дает возможность свести
вычисление определителя  -го
порядка к вычислению
-го
порядка к вычислению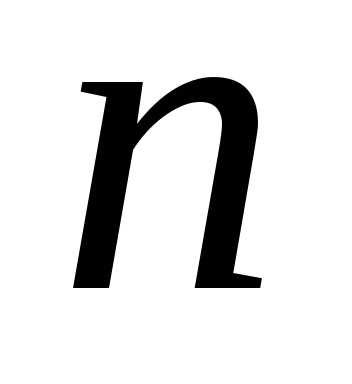 определителей
определителей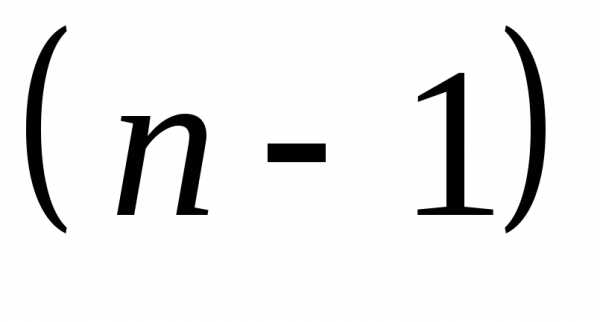 -го
порядка и, в конечном итоге, к вычислению
определителей второго порядка.
-го
порядка и, в конечном итоге, к вычислению
определителей второго порядка.
studfiles.net
Линейная алгебра. Основные определения.
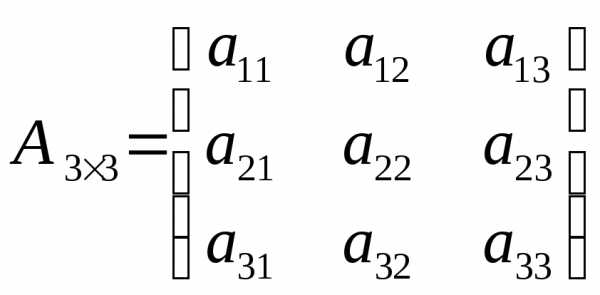
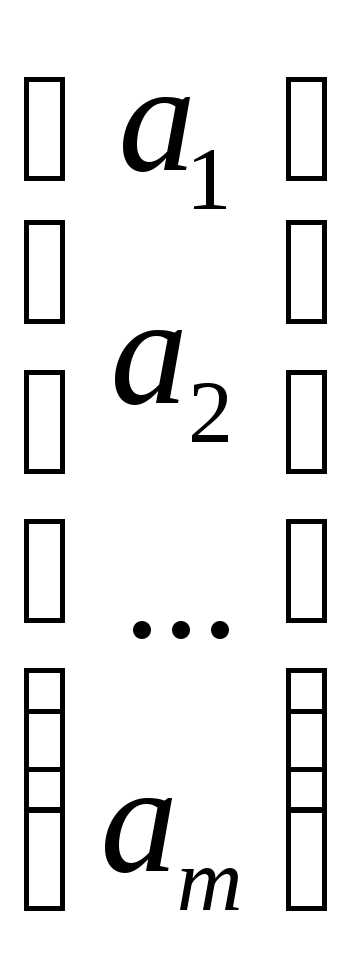
Определение. Матрицей размера mn, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i- номер строки, а j- номер столбца.
А
= 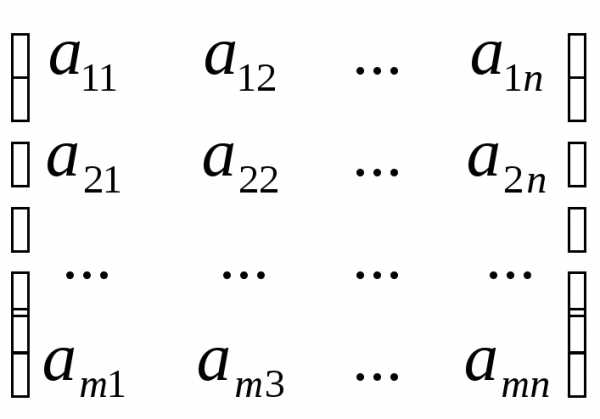
Основные действия над матрицами.
Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.
Определение. Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.
Определение. Матрица вида:
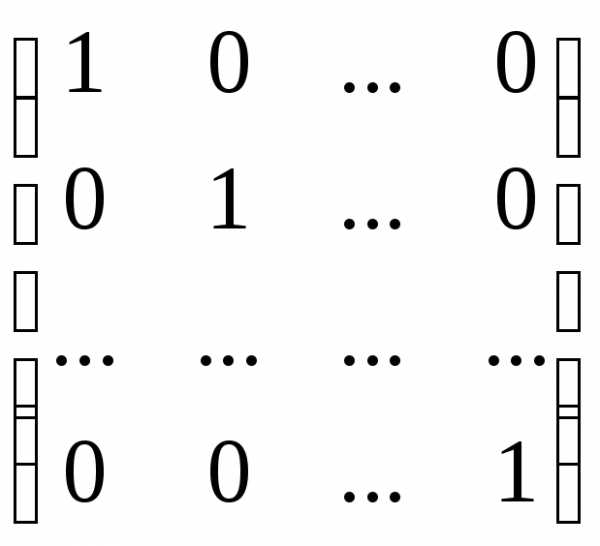 = E,
= E,
называется единичной матрицей.
Определение. Если amn = anm , то матрица называется симметрической.
Пример. 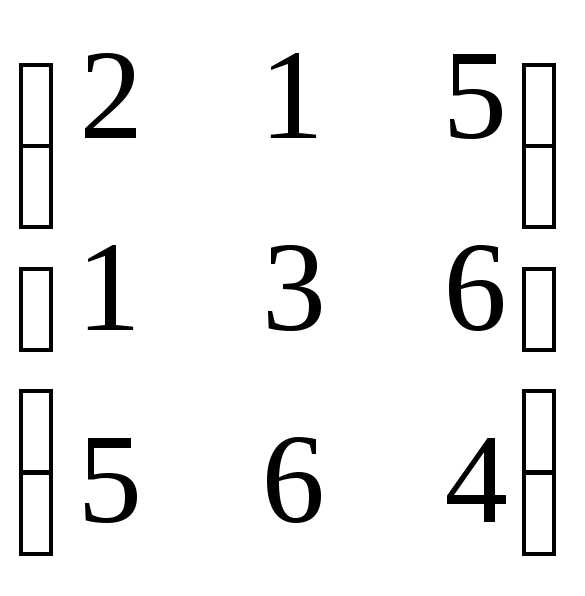 -симметрическая
матрица
-симметрическая
матрица
Определение. Квадратная
матрица вида  называетсядиагональной матрицей.
называетсядиагональной матрицей.
Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:
Определение.Суммой (разностью)матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.
cij=aijbij
С = А + В = В + А.
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.

(А+В) =А В
А() = А А
Пример. Даны матрицы А = 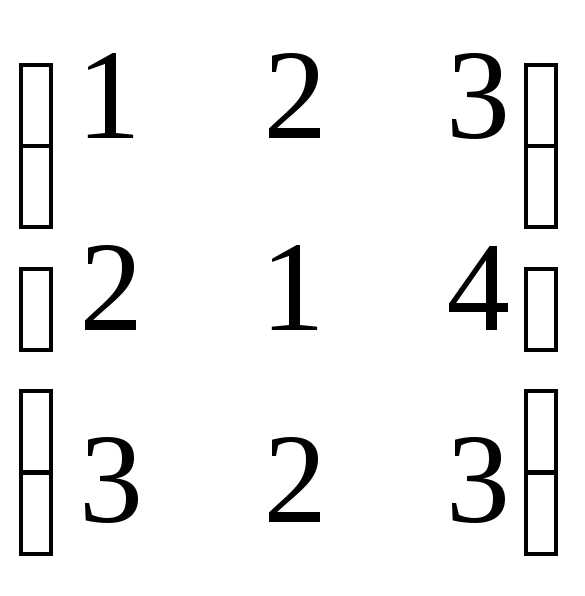 ;
B
=
;
B
= 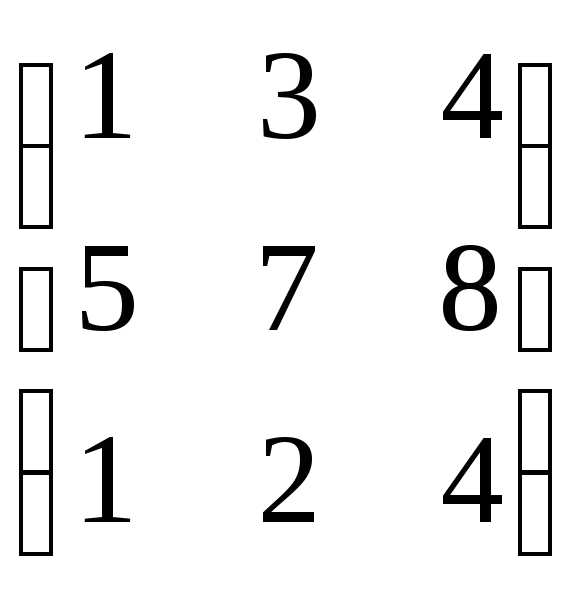 ,
найти 2А + В.
,
найти 2А + В.
2А
=  ,
2А + В =
,
2А + В = 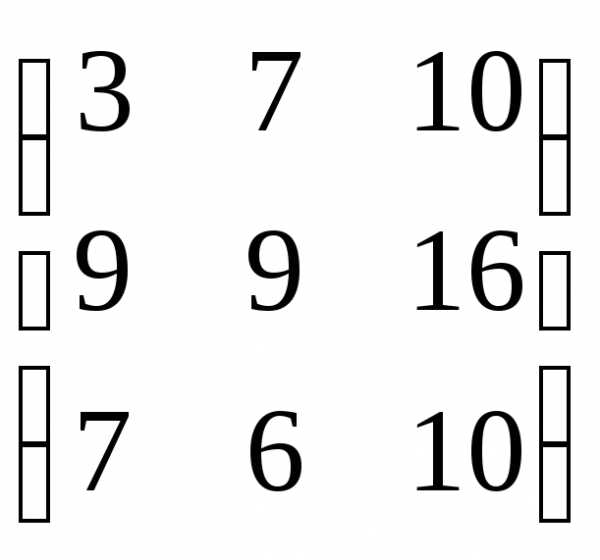 .
.
Операция умножения матриц.
Определение: Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:
AB = C;
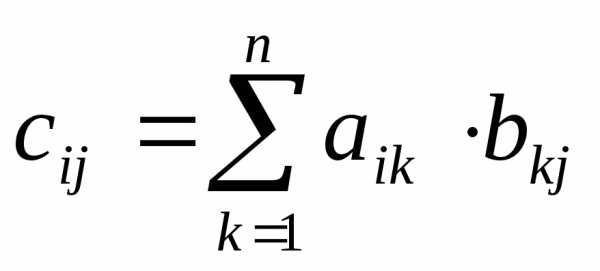 .
.
Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.
Свойства операции умножения матриц.
1)Умножение матриц не коммутативно, т.е. АВ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.
Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера.
Перестановочными могут быть только квадратные матрицы одного и того же порядка.
АЕ = ЕА = А
Очевидно, что для любых матриц выполняются следующее свойство:
AO = O; OA = O,
где О – нулевая матрица.
2) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:
(АВ)С=А(ВС).
3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно:
А(В + С) = АВ + АС
(А + В)С = АС + ВС.
4) Если произведение АВ определено, то для любого числа верно соотношение:
(AB) = (A)B = A(B).
5) Если определено произведение АВ , то определено произведение ВТАТ и выполняется равенство:
(АВ)Т = ВТАТ, где
индексом Т обозначается транспонированная матрица.
6) Заметим также, что для любых квадратных матриц det (AB) = detAdetB.
Понятие det (определитель, детерминант) будет рассмотрено ниже.
Определение. Матрицу В называют транспонированной матрицей А, а переход от А к В транспонированием, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В.
А
=  ;
В = АТ=
;
В = АТ=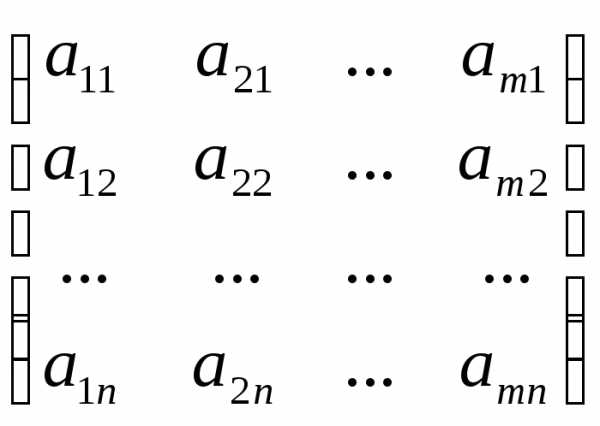 ;
;
другими словами, bji = aij.
В качестве следствия из предыдущего свойства (5) можно записать, что:
(ABC)T = CTBTAT,
при условии, что определено произведение матриц АВС.
Пример. Даны матрицы А = 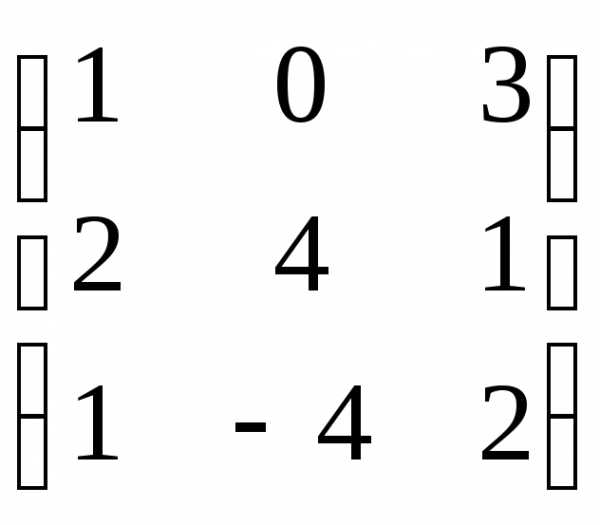 ,
В =
,
В = 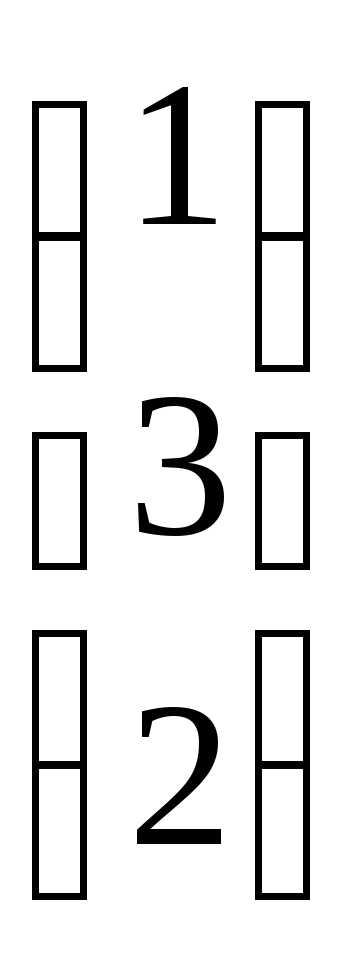 ,
С =
,
С = 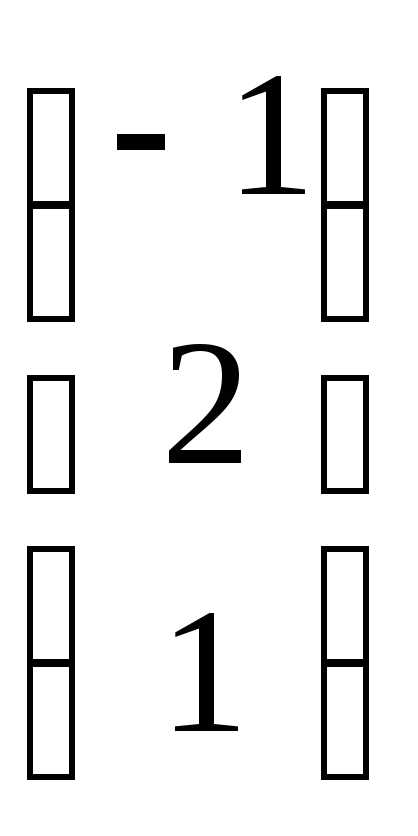 и число
= 2. Найти АТВ+С.
и число
= 2. Найти АТВ+С.
AT = 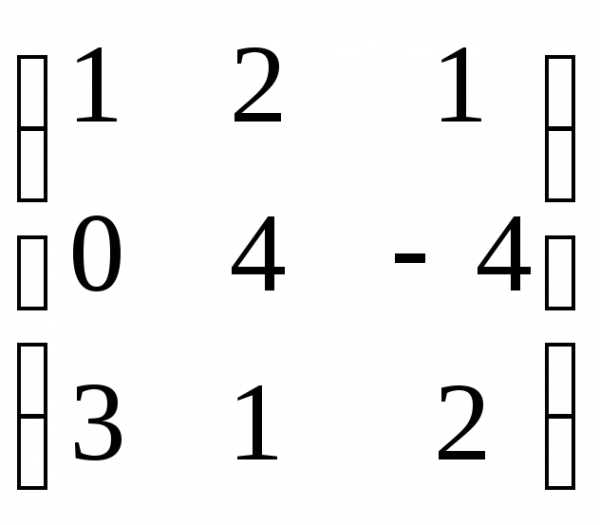 ;
ATB
=
;
ATB
= 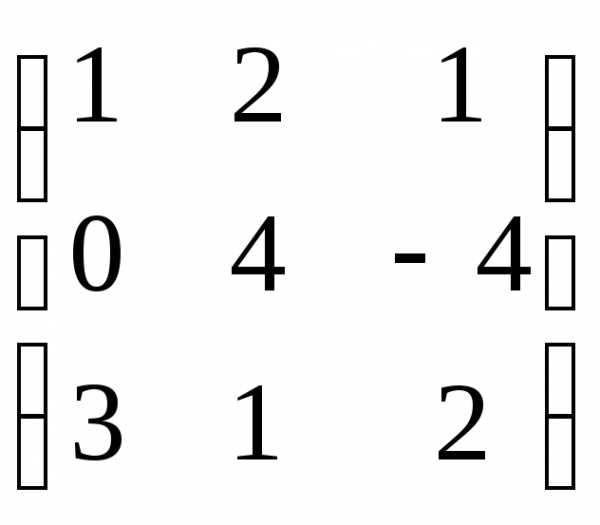
 =
= 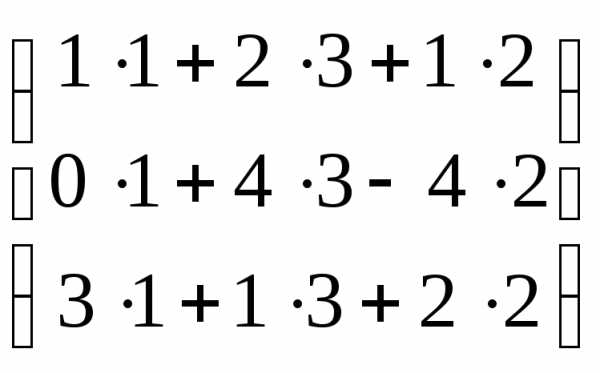 =
= 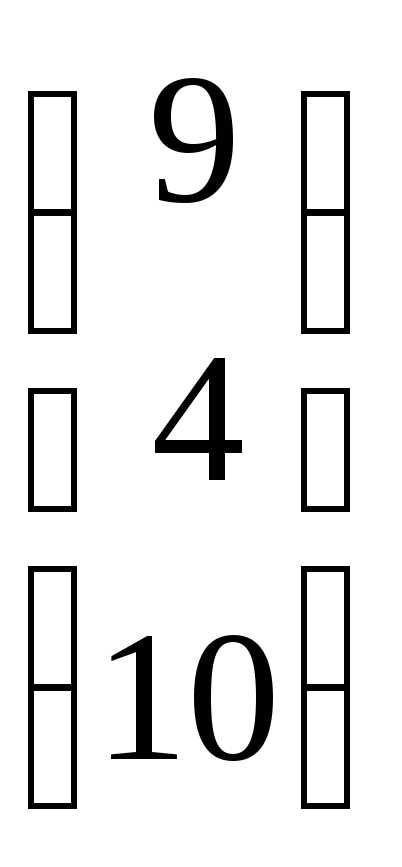 ;
;
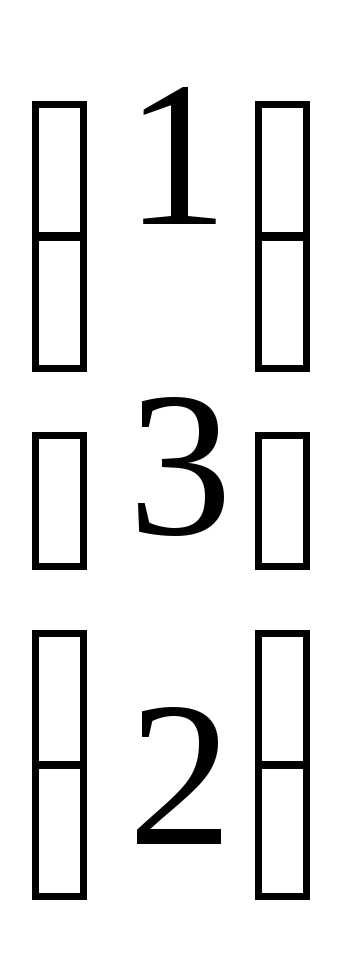
C
= 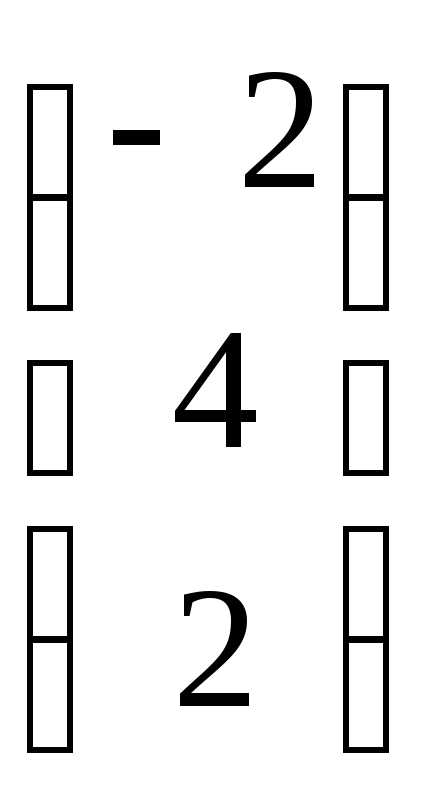 ;
АТВ+С
=
;
АТВ+С
= 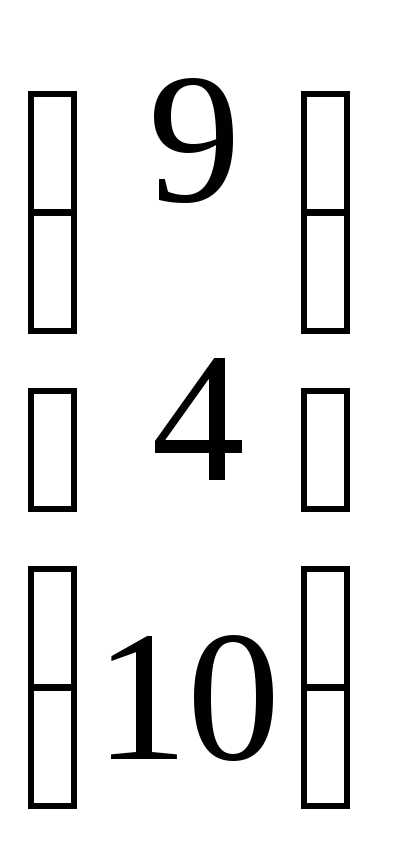 +
+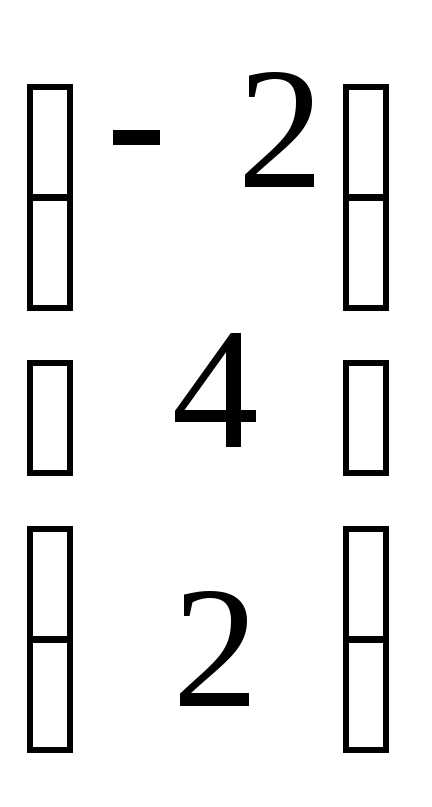 =
=  .
.
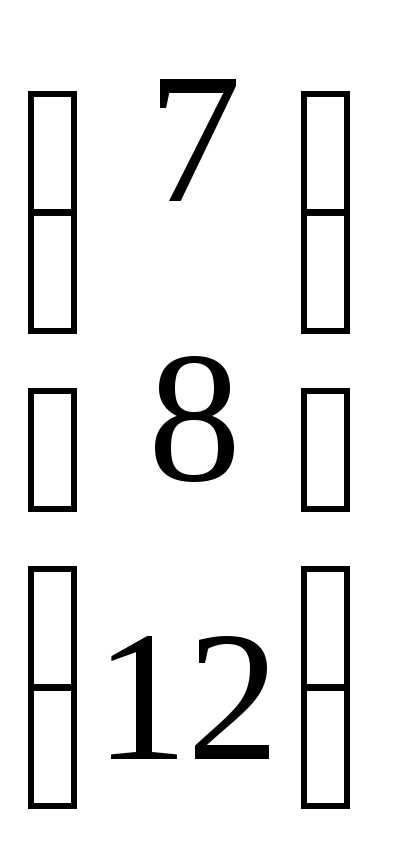
Пример. Найти произведение матриц А = 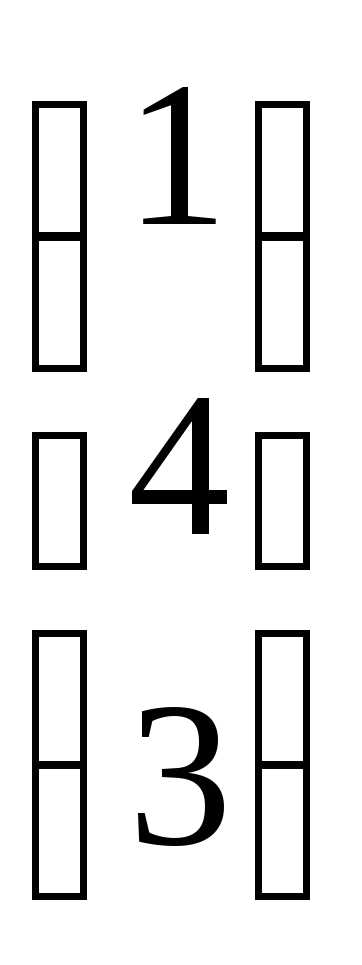 и В =
и В =  .
.
АВ
= 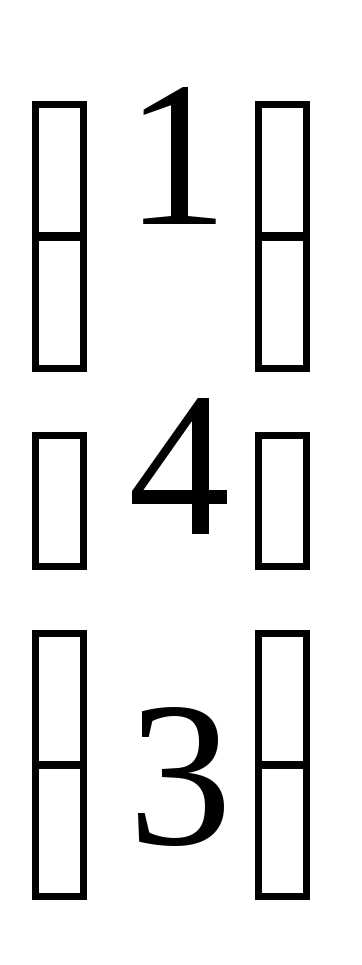
 =
= 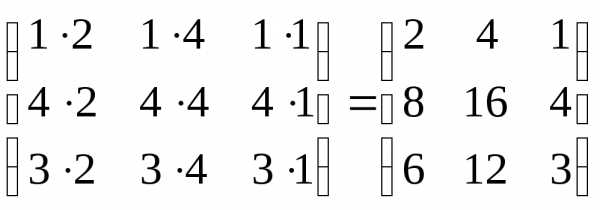 .
.
ВА
= 
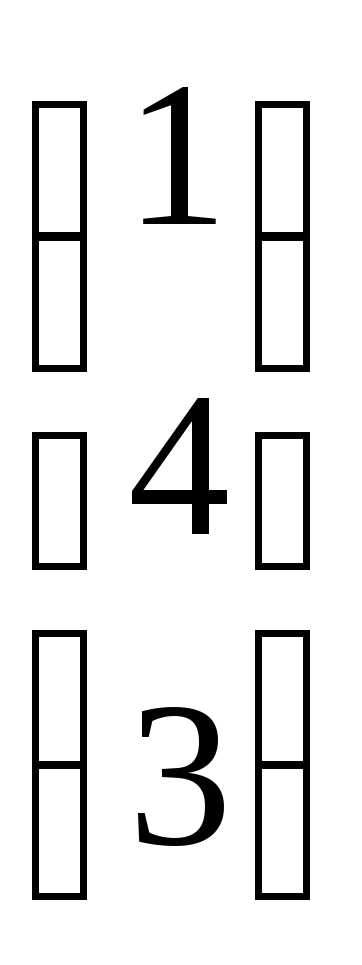 = 21
+ 44
+ 13
= 2 + 16 + 3 = 21.
= 21
+ 44
+ 13
= 2 + 16 + 3 = 21.
Пример. Найти произведение матриц А= ,
В =
,
В = 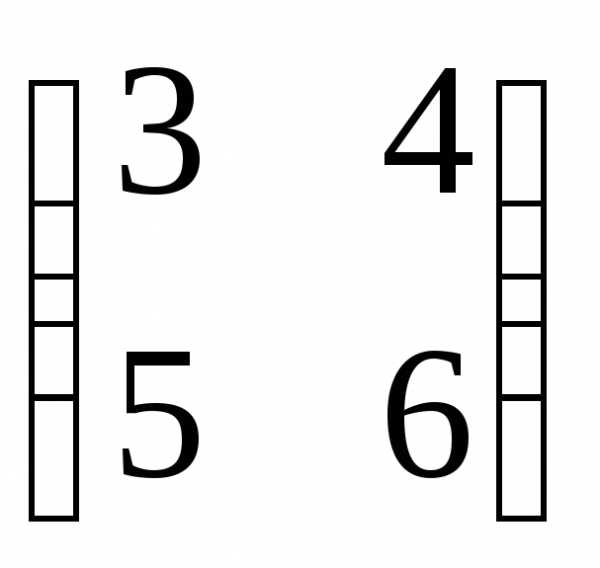
АВ
= 
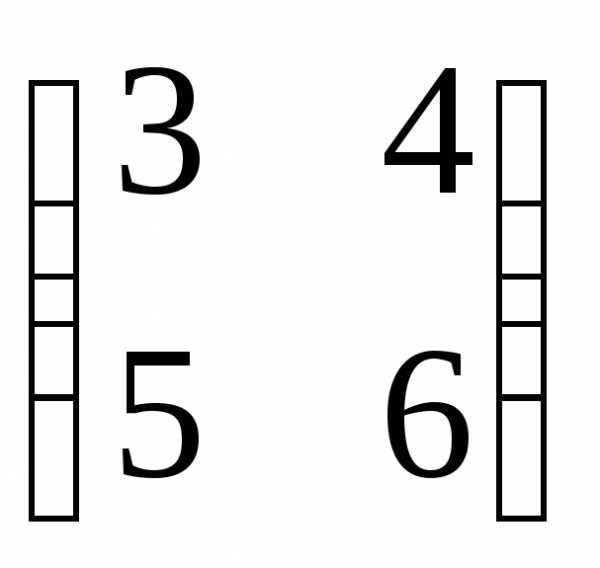 =
=
=
= 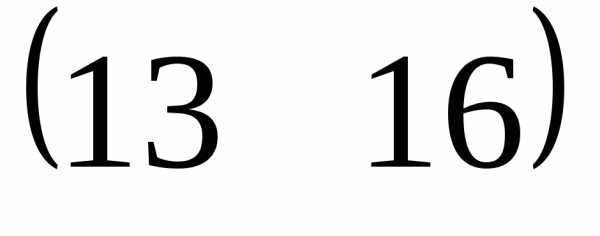 .
.
studfiles.net
Линейная алгебра Основные определения
Определение. Матрицей размера mn, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i- номер строки, а j- номер столбца.
А
= 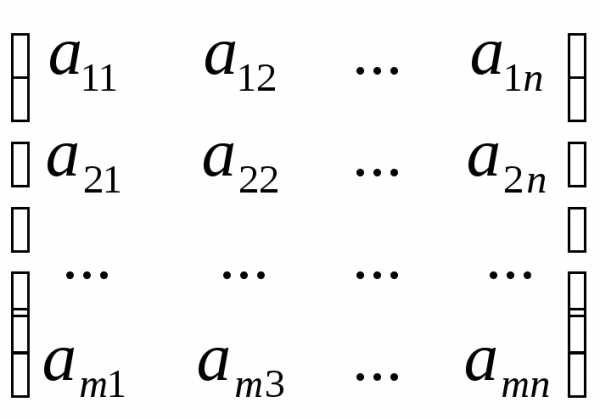
Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:
Определение. Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.
cij = aij bij
С = А + В = В + А.
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.

(А+В) =А В
А() = А А
Пример. Даны матрицы А = 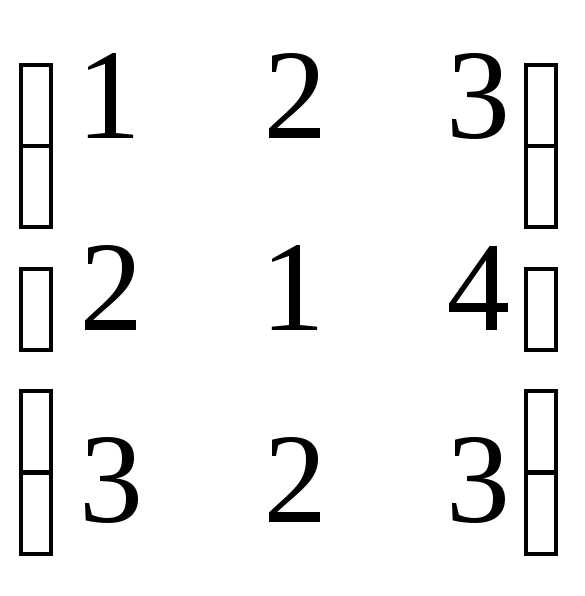 ;
B
=
;
B
= 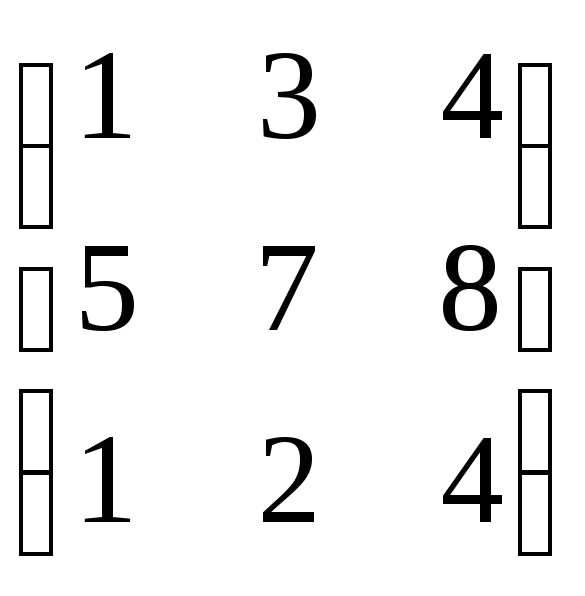 ,
найти 2А + В.
,
найти 2А + В.
2А
= 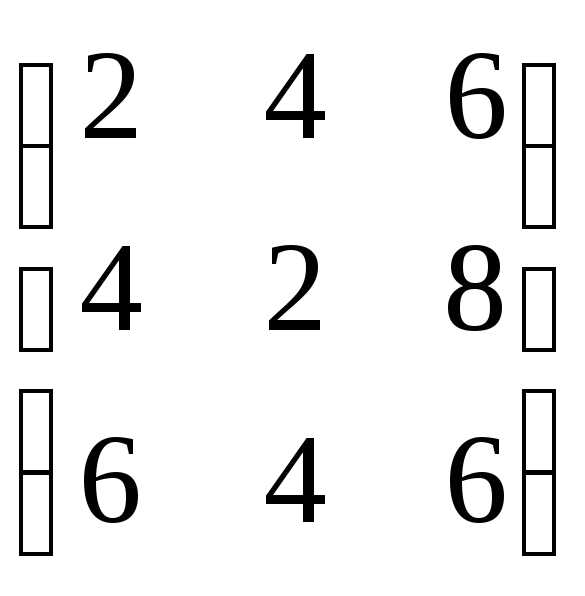 ,
2А + В =
,
2А + В =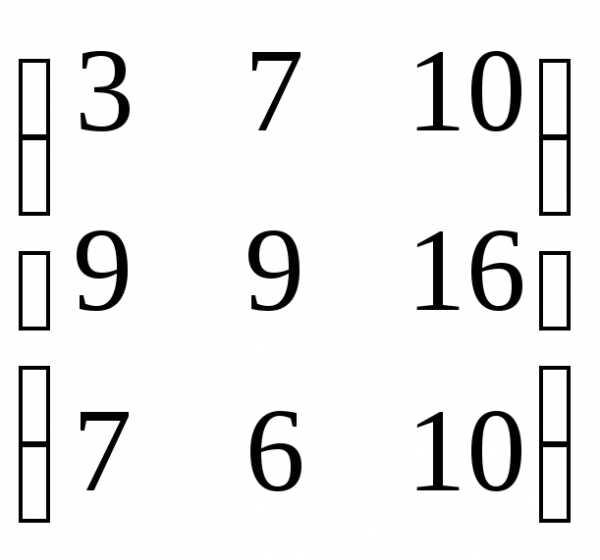 .
.
Операция умножения матриц
Определение: Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:
AB = C;
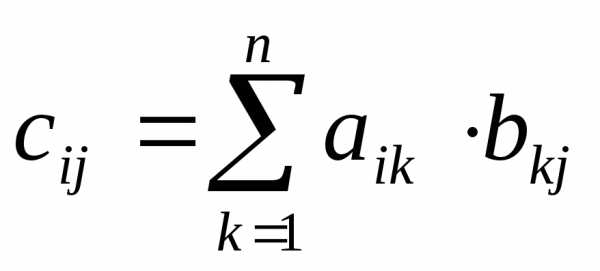 .
.
Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.
Свойства операции умножения матриц
1)Умножение матриц не коммутативно, т.е. АВ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.
Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера.
Перестановочными могут быть только квадратные матрицы одного и того же порядка.
АЕ = ЕА = А
Очевидно, что для любых матриц выполняются следующее свойство:
AO = O; OA = O,
где О – нулевая матрица.
2) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:
(АВ)С=А(ВС).
3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно:
А(В + С) = АВ + АС
(А + В)С = АС + ВС.
4) Если произведение АВ определено, то для любого числа верно соотношение:
(AB) = (A)B = A(B).
5) Если определено произведение АВ , то определено произведение ВТАТ и выполняется равенство:
(АВ)Т = ВТАТ, где
индексом Т обозначается транспонированная матрица.
6) Заметим также, что для любых квадратных матриц det (AB) = detAdetB.
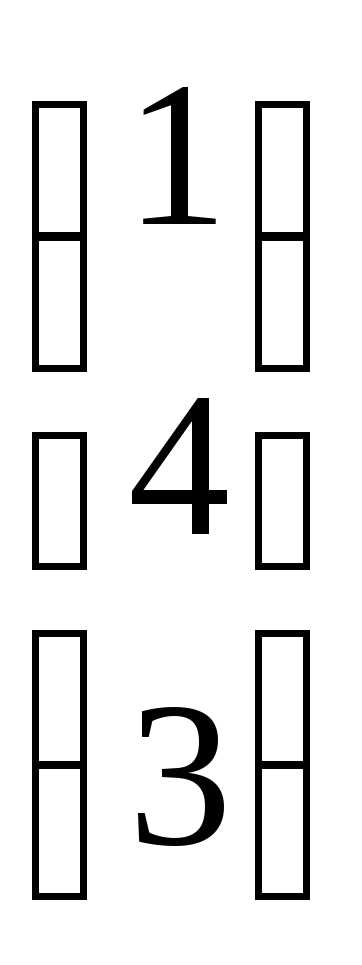
Пример. Найти произведение матриц А = 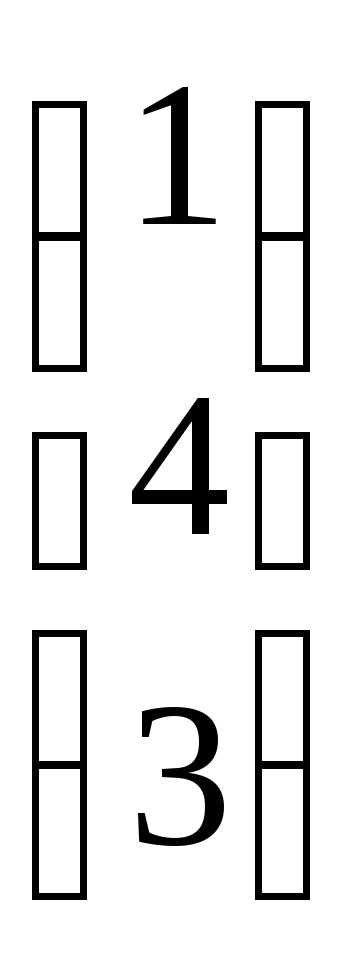 и В =
и В = .
.
АВ
= 
 =
=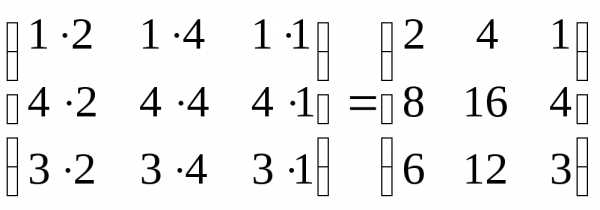 .
.
ВА
= 
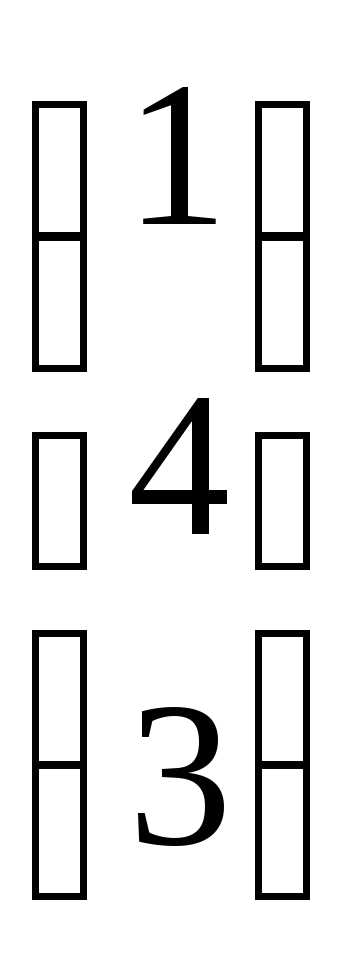 = 21
+ 44
+ 13
= 2 + 16 + 3 = 21.
= 21
+ 44
+ 13
= 2 + 16 + 3 = 21.
Пример. Найти произведение матриц А= ,
В =
,
В =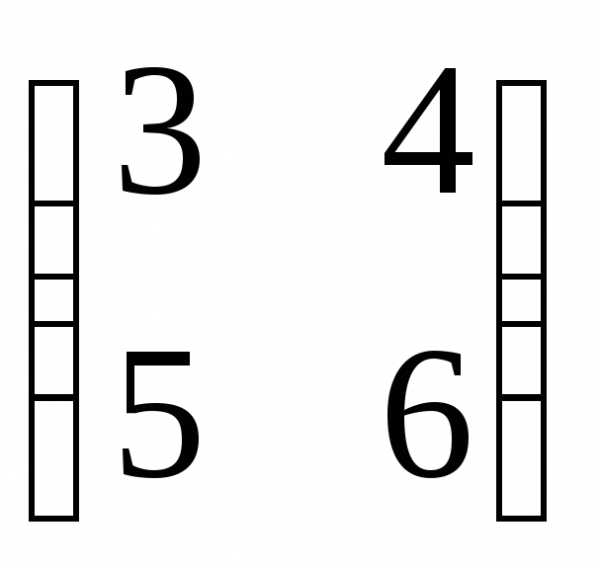
АВ
= 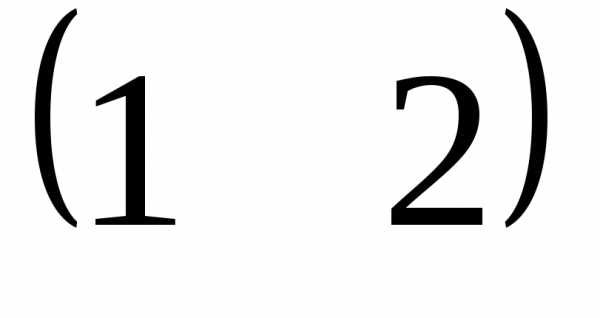
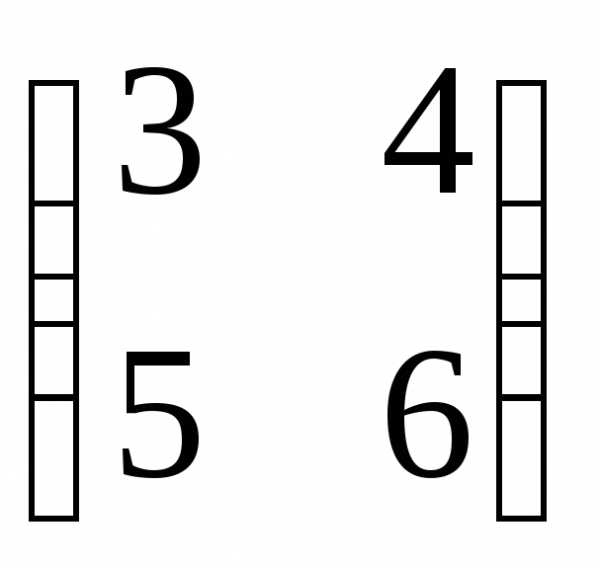 ==
==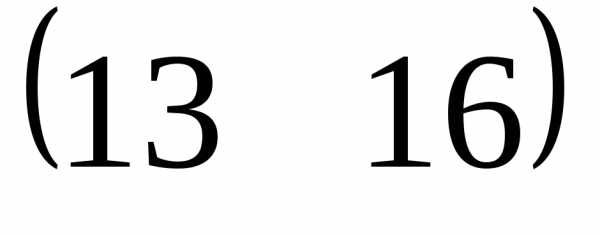 .
.
Определители (детерминанты)
Определение. Определителем квадратной
матрицы А= называется число, которое может быть
вычислено по элементам матрицы по
формуле:
называется число, которое может быть
вычислено по элементам матрицы по
формуле:
det
A
= 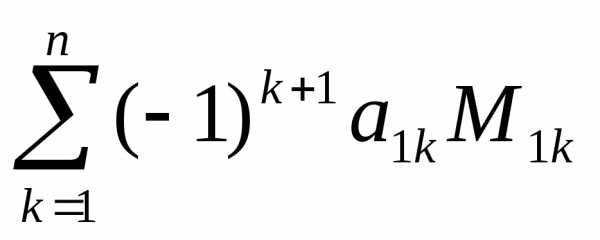 ,
где
,
где
М1к – детерминант матрицы, полученной из исходной вычеркиванием первой строки и k – го столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.
Предыдущая формула позволяет вычислить определитель матрицы по первой строке, также справедлива формула вычисления определителя по первому столбцу:
det
A
= 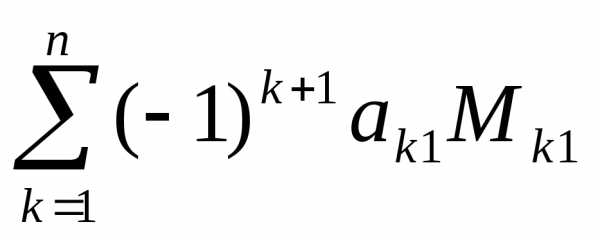
Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула:
detA
= 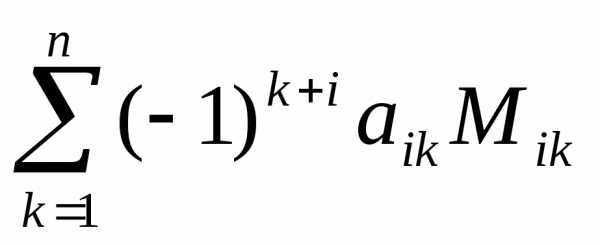 ,
i
= 1,2,…,n.
,
i
= 1,2,…,n.
Очевидно, что различные матрицы могут иметь одинаковые определители.
Определитель единичной матрицы равен 1.
Для указанной матрицы А число М1к называется дополнительным минором элемента матрицы a1k. Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.
Определение. Дополнительный минор произвольного элемента квадратной матрицы aij равен определителю матрицы, полученной из исходной вычеркиванием i-ой строки и j-го столбца.
Пример. Вычислить определитель матрицы А = 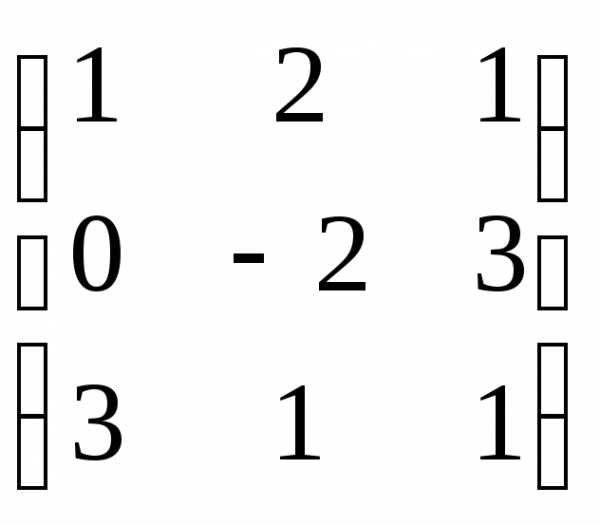
= -5 + 18 + 6 = 19.
Пример:.
Даны матрицы А = 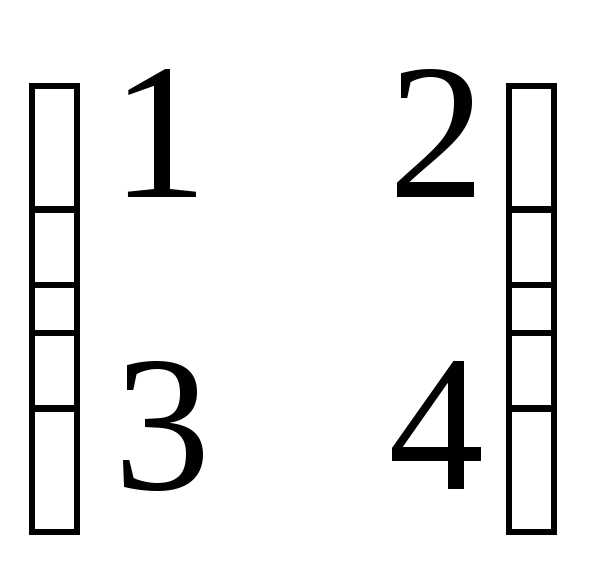 ,
В =
,
В = .
Найти
det (AB).
.
Найти
det (AB).
1-й способ: det A = 4 – 6 = -2; det B = 15 – 2 = 13;
det (AB) = det A det B = -26.
2- й способ: AB = ,
det (AB) = 718 — 819 = 126 – 152 = -26.
Миноры
Определение. Если в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется минором матрицы А. Если выделено s строк и столбцов, то полученный минор называется минором порядка s.
Заметим, что вышесказанное применимо не только к квадратным матрицам, но и к прямоугольным.
Если вычеркнуть из исходной квадратной матрицы А выделенные строки и столбцы, то определитель полученной матрицы будет являться дополнительным минором.
studfiles.net
Определители и их применение в алгебре и геометрии
Медико-биологический лицей г. Саратова.
Предмет: математика.
ОПРЕДЕЛИТЕЛИ И ИХ ПРИМЕНЕНИЕ В АЛГЕБРЕ И ГЕОМЕТРИИ.
Выполнили: Дёмин Дмитрий,
Грачёв Денис ученики 11 «б» класса МБЛ.
Руководитель: Винник Нина Дмитриевна
Учитель математики.
Саратов 2007 г.
Содержание
1. Определения.
2. Пример вычисления определителя второго порядка в общем виде.
3. Свойства определителя.
4. Доказательства свойств определителя.
5. Пример применения правила Крамера для решения систем из n уравнений с n неизвестными.
1. Определения.
2. Свойства векторного произведения.
3. Доказательства свойств векторного произведение.
4. Смешанное произведение.
5. Векторное произведение векторов заданных проекциями.
6. Примеры решение задач (с использованием определителей).
Введение
В алгебре существует широкий класс задач, решение которых является громоздким и трудным методами элементарной математики. Например, решение системы n линейных уравнений, с n неизвестными методом Жордана – Гаусса требует длительных вычислений и, как правило, часто ведёт к ошибке.
Теория определителей позволяет решать и исследовать системы с малыми затратами используя правило Крамера, рассматриваемое в этой работе.
(данную часть работы приготовил ученик 11 «б» класса Медико-биологического лицея Дёмин Дмитрий).
При вычислении площадей, объёмов в пространстве часто удобно пользоваться векторным и смешанным произведениями векторов, вычисляя определитель координат векторов, что представлено в работе.
(данную часть работы приготовил ученик 11 «б» класса Грачёв Денис).
Глава 1. Определители
1. Определения
Опр. Матрица – прямоугольная таблица, составленная из элементов произвольной природы. Элементы матрицы располагаются в строки и столбцы (иногда их называют колонками). Строки и столбцы часто называют собирательным термином «ряды матрицы». Элементы матрицы часто обозначают двойными индексами – aij ; первый индекс i означает номер строки матрицы, в которой стоит элемент aij , а второй индекс j означает номер столбца матрицы, в котором стоит aij . Матрицы символически обозначают заключёнными в круглые или квадратные скобки, или двойные вертикальные черточки. (Кратко: (aij ) или IIaij II).
Каждой квадратной матрице, элементами которой являются числа, ставится в соответствие число, называемое определителем матрицы .
Опр. Определитель (детерминант) n-го порядка – алгебраическая сумма n! слагаемых членов из элементов квадратной матрицы (таблицы), которое вычисляется по следующему закону: каждое слагаемое есть произведение n элементов взятых по одному и только по одному из каждой строки и из каждого столбца матрицы. Каждый член определителя берётся со знаком (-1)t , где t – число инверсий во вторых индексах члена, когда первые индексы члена расположены в натуральном порядке.
2. Пример вычисления определителя второго порядка в общем виде
Пусть матрица A=
, тогда ее определитель будет содержать 2!=2 слагаемых:a11 a22 и + a21 a12 , так как в перестановке
нет инверсий, следовательно, (-1)0 = -1, а в перестановке есть одна инверсия и (-1)1 = -1.Значит,
= a11 a22 – a21 a12Минором или алгебраическим дополнением элемента aij квадратной матрицы или ее определителя, называется определитель порядка n-1, который получается из исходного вычеркиванием i – той строки и j – того столбца.
3. Свойства определителя
Определитель обладает рядом свойств:
1) Определитель не изменяется при транспортировании матриц (строк и столбцов).
2) Если один из столбцов (строк) состоит из нулей, то определитель равен нулю.
3) Если один из определителей получен из другого определителя перестановкой двух столбцов (строк), то определители отличаются друг от друга знаком.
4) Если все элементы какого-либо i-го столбца (строки) определителя являются суммами двух слагаемых, то такой определитель равен сумме двух определителей в первом из которых в качестве i-го столбца (строки) взяты первые слагаемые, а во втором – вторые слагаемые; при этом элементы всех остальных строк (столбцов) у каждого из трёх определителей одинаковы.
5) Определитель, содержащий два пропорциональных, в частности два равных, столбца (строки), равен нулю.
6) Определитель не меняется, если к какому-нибудь столбцу (строке) прибавить линейную комбинацию других столбцов (строк).
7) Если все элементы какого-нибудь столбца (строки) определителя умножить на некоторое число k, то есть весь определитель умножается на k, то общий множитель любой строки или любого столбца можно выносить за знак определителя.
4. Доказательства свойств определителя
Свойство №1: Определитель не изменяется при транспортировании матриц (строк и столбцов).
Доказательство:
Опр. Матрицы Aji называется транспонированной матрицей Aij
= det A = det AT
det A = det AT
Выберем любое слагаемое из суммы определителя.
a1i a2j … ank
ai1 aj2 … akn сумме det AT
Следовательно определители равны.
Свойство №2: Если один из столбцов (строк) состоит из нулей, то определитель равен нулю.
Доказательство:
Пусть дана матрица, один столбец которой равен 0.
=detA подсчитаем определитель данной матрицы.Подсчитаем определитель данной матрицы, используя правило равнобедренных треугольников, основания которых параллельны главной и побочной диагоналям.
=0*а22 *а33 +а12 *а23 *0+а32 *а13 *0 = 0 =-(а13 *а22 *0+а12 *а33 *0+а23 *а32 *0)=0Свойство доказано.
Свойство №3: Если один из определителей получен из другого определителя перестановкой двух столбцов (строк), то определители отличаются друг от друга знаком.
Доказательство: Возьмём матрицу определитель которой равен detA и переставим в ней 2 столбца. Получим:
, после перестановки получим: .Посчитаем определители обеих матриц. Получим:
det A=(-1)0 *((a11 *a22 *a33 +a12 *a23 *a31 +a21 *a32 *a13 )-(a13 *a22 *a31 +a21 *a12 *a33 +a32 *a23 *a11 ))
det B=(-1)2 *((a31 *a22 *a13 +a21 *a12 *a33 +a32 *a23 *a11 )-(a33 *a22 *a11 +a12 *a23 *a31 +a21 *a32 *a13 ))
(a11 *a22 *a33 +a12 *a23 *a31 +a21 *a32 *a13 )-(a13 *a22 *a31 +a21 *a12 *a33 +a32 *a23 *a11 ) +(a31 *a22 *a13 +a21 *a12 *a33 +a32 *a23 *a11 )-(a33 *a22 *a11 +a12 *a23 *a31 +a21 *a32 *a13 )=0
mirznanii.com
Примеры решений Элементы линейной алгебры и аналитической геометрии
Линейная алгебра Определители
Составитель: Смирном А. Н.
Издание первое, 2014.
Оглавление
Линейная алгебра
1. Определители 2
2. Матрицы 4
3. Решение систем линейных уравнений 8
4. Ранг матрицы. Разрешимость систем 12
5. Линейное пространство 17
6. Векторная алгебра 28
Аналитическая геометрия
7. Плоскость в пространстве 39
8. Прямая в пространстве 43
9. Прямая на плоскости 48
10. Кривые второго порядка 53
11. Полярная система координат 58
Линейная алгебра
Определители
1.1. Вычислить определитель второго порядка
Ответ: 5
1.2. Вычислить определитель третьего порядка
Способ 1. Метод треугольника
Ответ: 184
Способ 2. Метод раскрытия по строке (или столбцу). Раскроем по второй строке.
Ответ: 184
1.3. Вычислить определитель четвертого порядка, преобразовав его так, чтобы три элемента некоторого ряда равнялись нулю, и разложить полученный определитель по элементам этого ряда.
И спользуя
свойства определителей, его нужно
преобразовать так, чтоб в каком, либо
столбце или строке стало три элемента
нуля.
спользуя
свойства определителей, его нужно
преобразовать так, чтоб в каком, либо
столбце или строке стало три элемента
нуля.
В данном задании проще всего к такому виду привести вторую строку, т.к. в ней уже содержится один ноль, а остальные числа не большие и удобны для преобразования.
Т еперь
во второй строке появилось два нуля.
Далее, ко второму столбцу прибавим
четвёртый, умноженный на два.
еперь
во второй строке появилось два нуля.
Далее, ко второму столбцу прибавим
четвёртый, умноженный на два.
К первому столбцу прибавим четвёртый, т.е. почленно прибавим элементы четвёртого столбца к элементам первого.
Теперь во второй
строке появилось три нуля. То, ч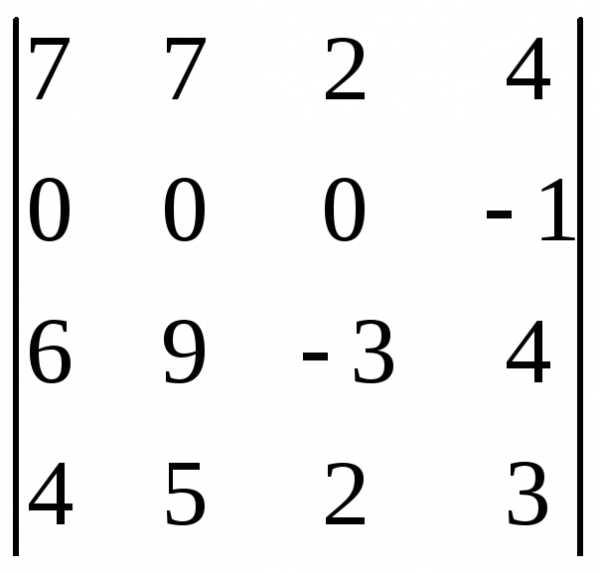 то
и требовалось сделать. Далее раскроем
данный определитель по второй строке.
то
и требовалось сделать. Далее раскроем
данный определитель по второй строке.
Получилось, что в первых трёх определителях множители равны нулю, значит дальше их можно и не раскрывать, т.к. они всё равно обернутся в ноль. Раскроем только определитель в четвёртом слагаемом и найдём его значение.
Ответ: -51
1.4. Решить неравенство (или уравнение) с определителями
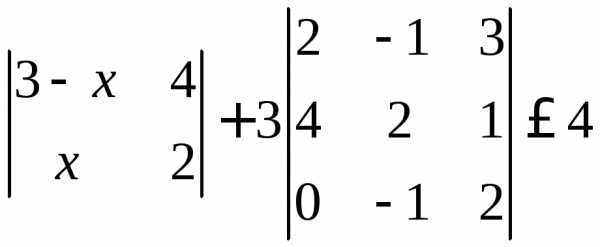
Для его решения необходимо раскрыть определители и решить обычное неравенство (или уравнение).
Упрощаем
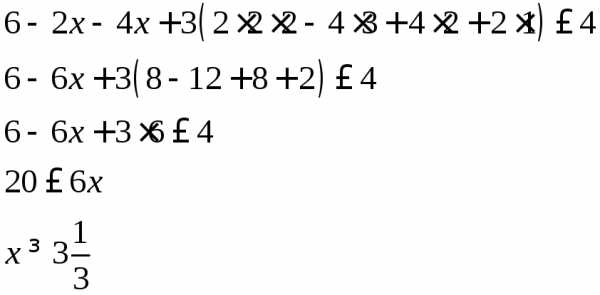

Ответ: 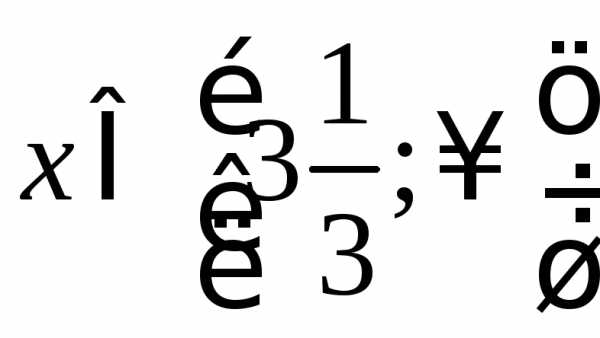
Матрицы
2.1. Операции над матрицами.
Дано матрицы
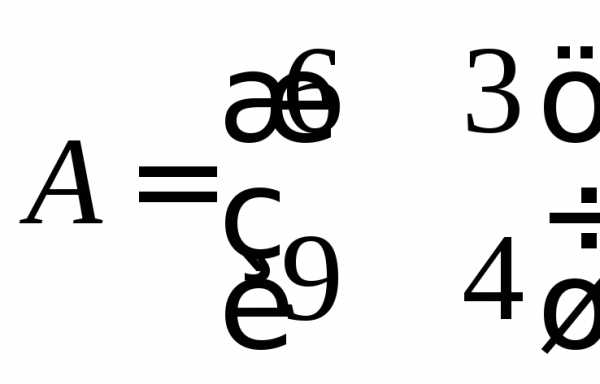 ,
, 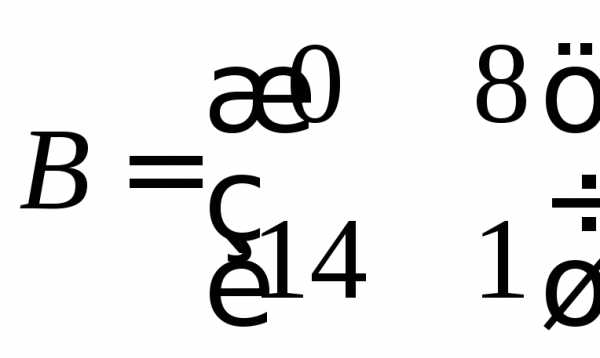 ,
,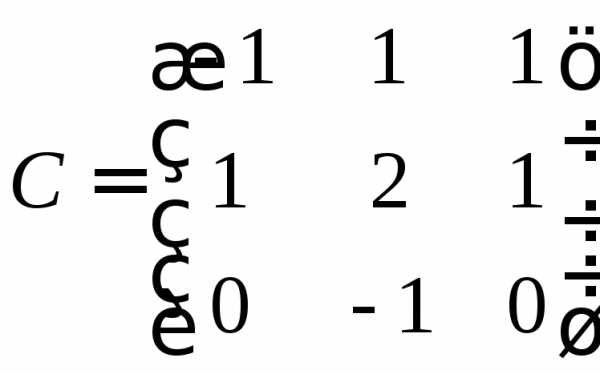 ,
,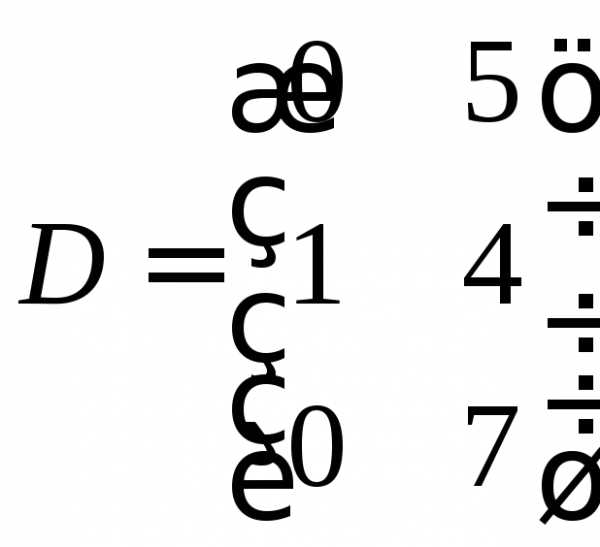
Выполнить операции
a)
б)
в)
г)
д)
е)
ж)
Примечание: , перестановка не тождественна.
з)
2.2. Найти обратные матрицы
а) Обратная матрица
второго порядка 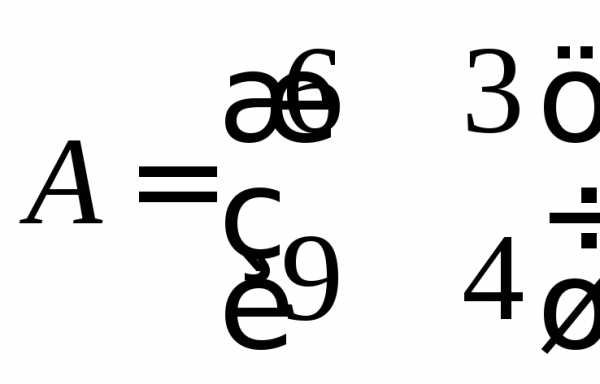
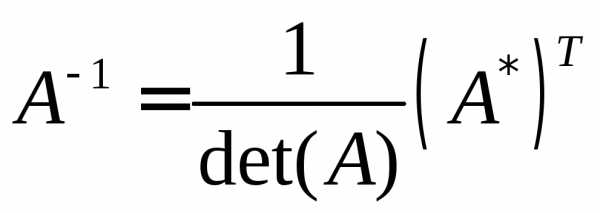 ,
, 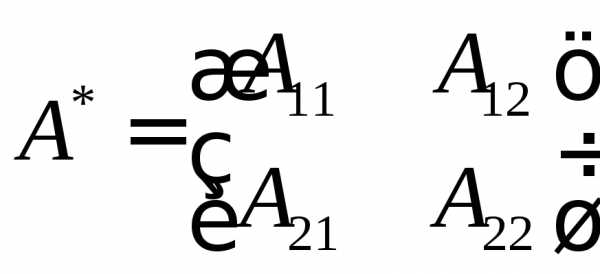
Союзная матрица
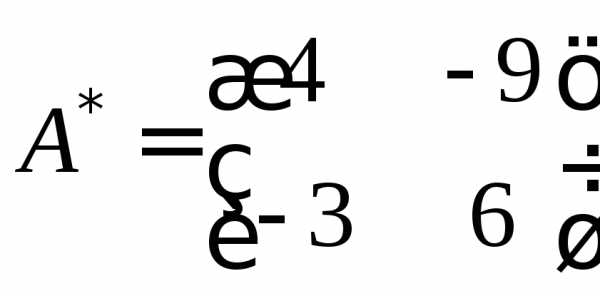
Находим ответ
Ответ: 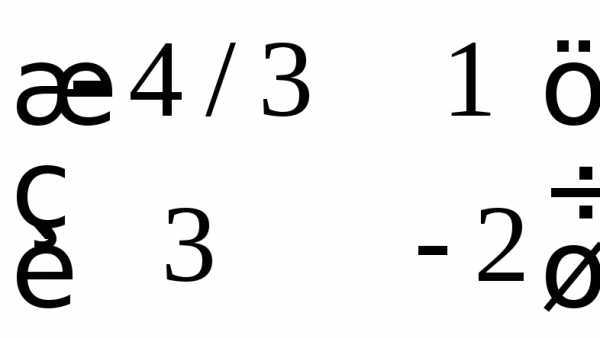
б) Обратная матрица
третьего порядка 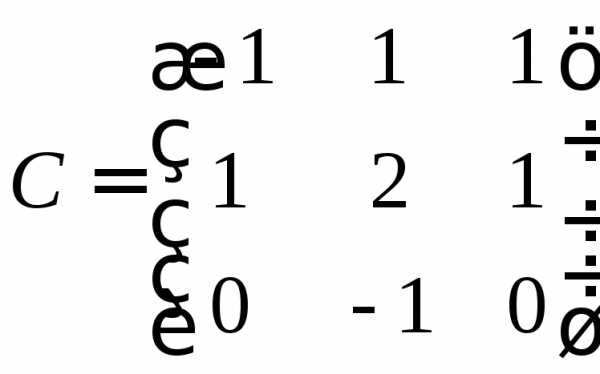 .
.
Способ 1. Метод миноров.
Этот метод заключается в составлении союзной матрицы и в дальнейшем делении её на определитель матрицы.
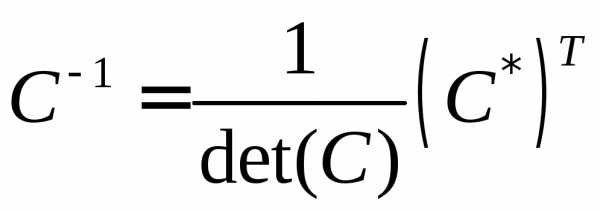 ,
, 
В матрице C в нижнем ряду два нулевых элемента, так что будет проще раскрыть определитель по этой строке.
Союзная матрица
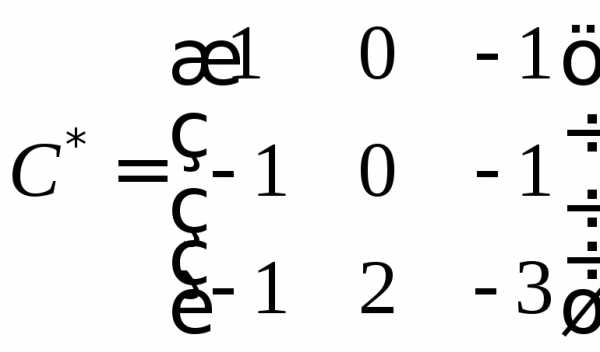
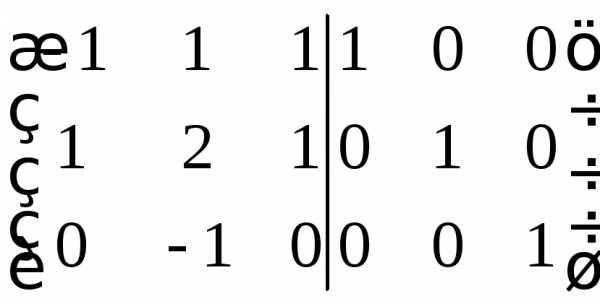
Способ 2. Метод Гаусса.
Расширим исходную матрицу единичной матрицей и методом Гаусса преобразуем исходную матрицу в единичную. Расширение матрицы и будет обратной матрицей.
Дальнейшая последовательность действий приводится без объяснений
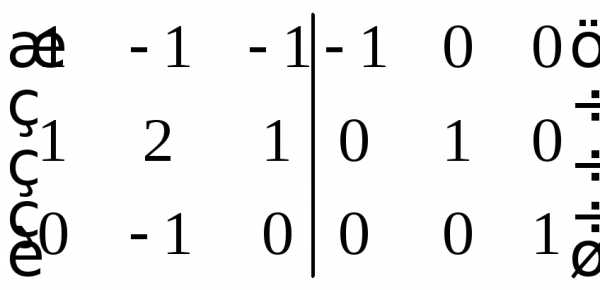


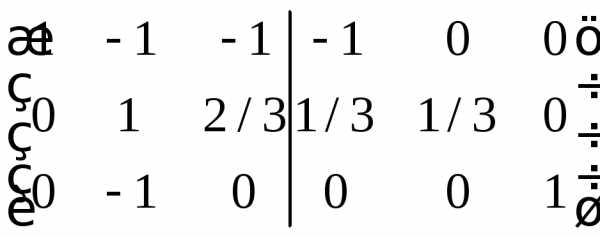


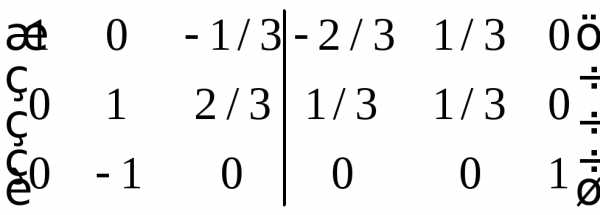

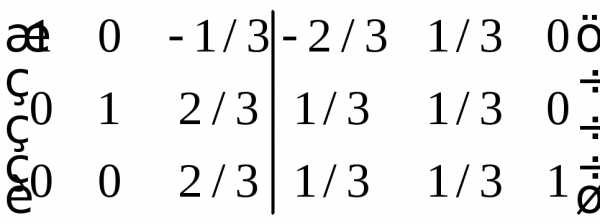

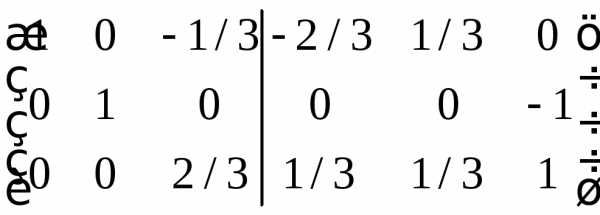

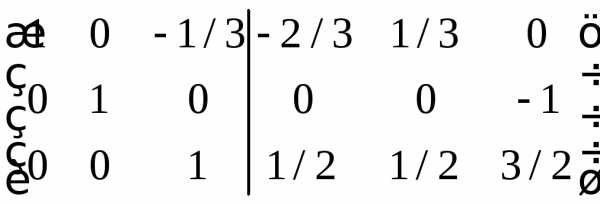

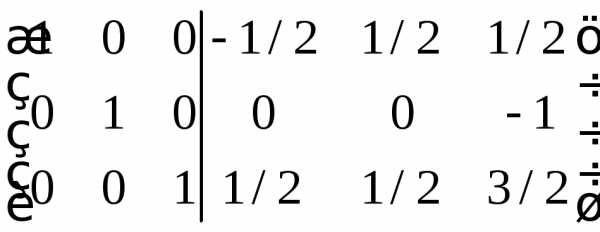
Ответ совпал с предыдущим методом.
Ответ: 
studfiles.net



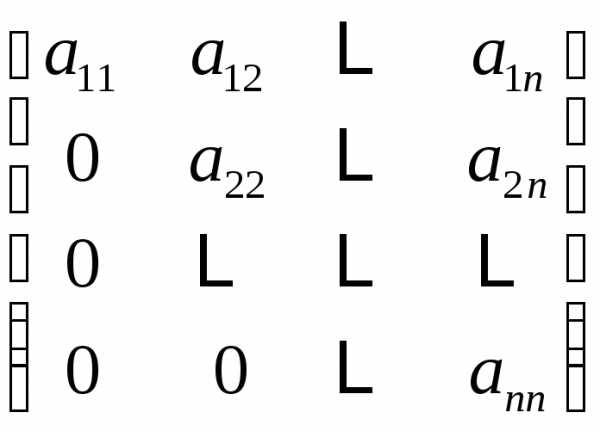
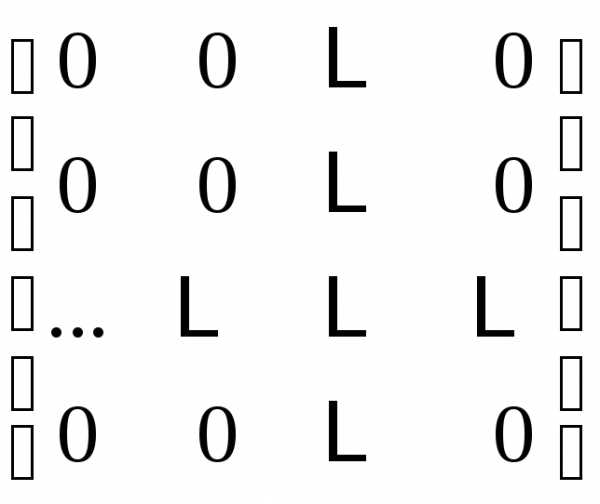
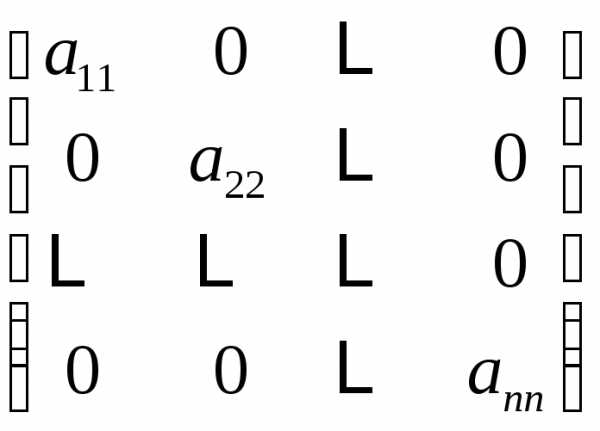
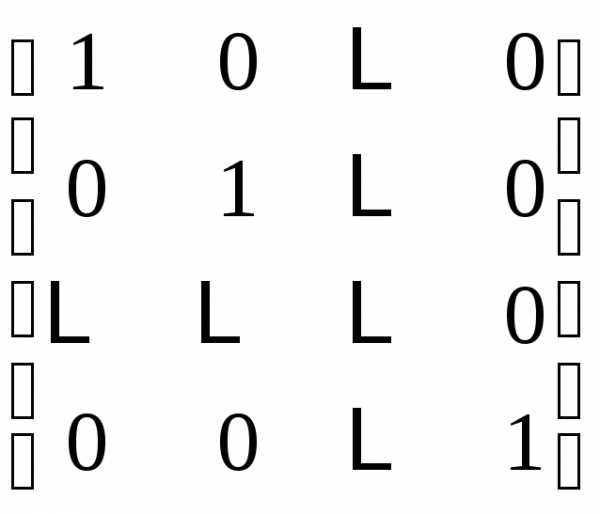

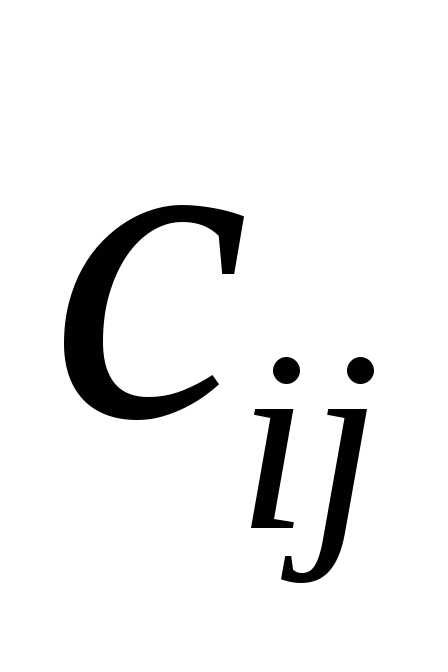 есть сумма произведений всех элементов
есть сумма произведений всех элементов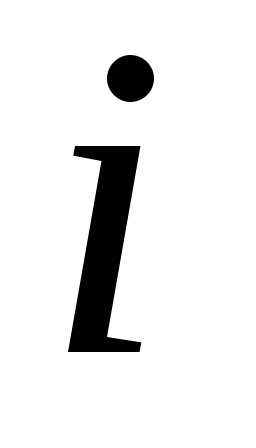 –й
строки
–й
строки на соответсвующие элементы
на соответсвующие элементы –го
столбца
–го
столбца .
.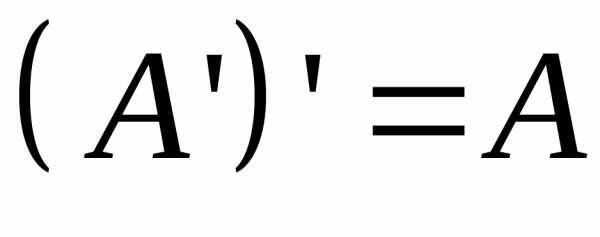
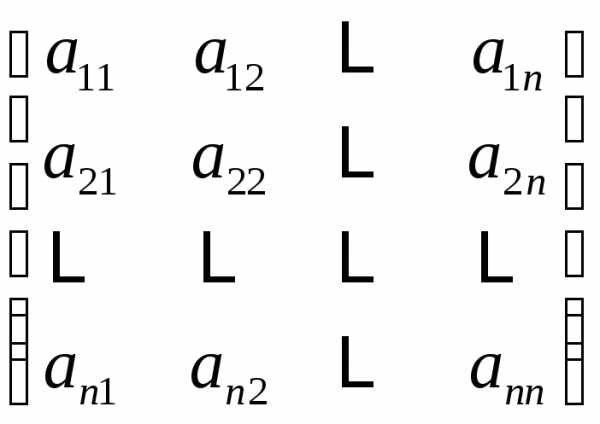

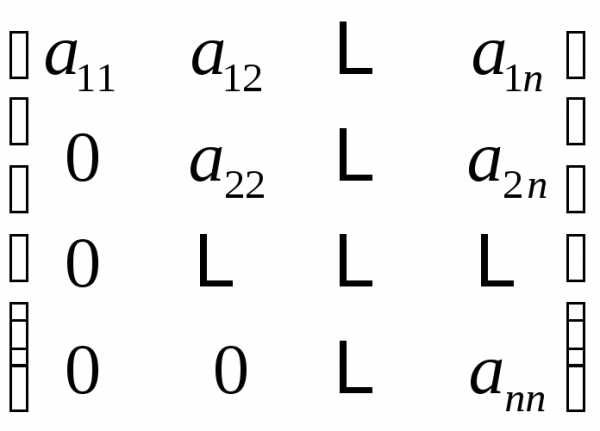
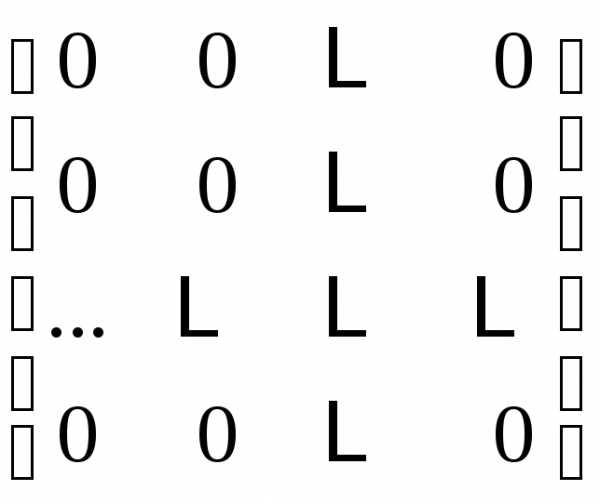
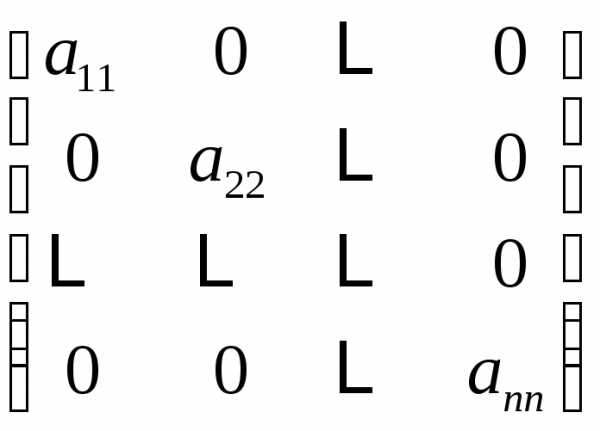
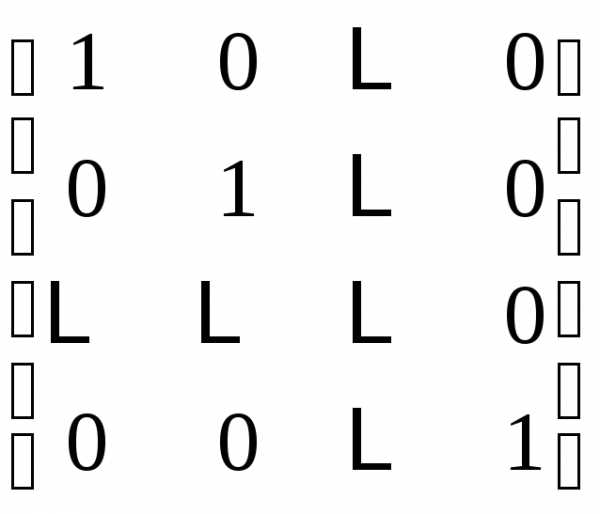

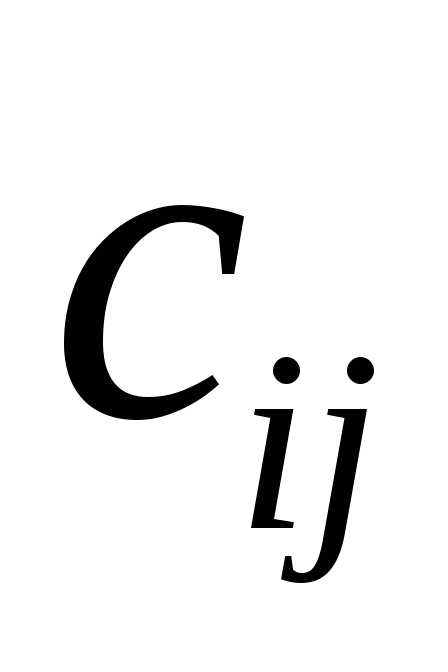 есть сумма произведений всех элементов
есть сумма произведений всех элементов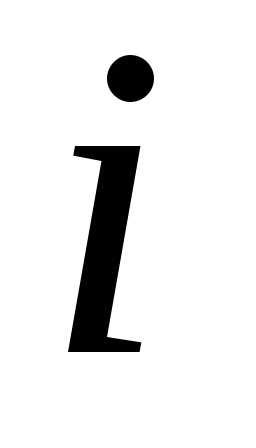 –й
строки
–й
строки на соответсвующие элементы
на соответсвующие элементы –го
столбца
–го
столбца .
.