Действия с числовыми и алгебраическими выражениями (Г.Г. Гаицгори)
На этом уроке мы вспомним, что такое алгебраическое выражение, как найти его значение при заданных значениях переменных. Выясним, какие значения переменных могут быть недопустимыми для данного выражения. А также научимся выполнять различные действия с числовыми и алгебраическими выражениями.
Определение: алгебраическое выражение – это любая составленная со смыслом запись, которая может содержать только числа, буквы, знаки действия и скобки. Например, .
Можно вычислить значение алгебраического выражения при заданных значениях переменных, для этого достаточно подставить значение в выражение и выполнить вычисления. Например, при значение выражения : .
Задача . Найдите значение выражения при .
Решение. Подставим значение в выражение и выполним вычисления:
Ответ: .
В задаче получилось деление на . Можно попробовать поделить на , например, на калькуляторе. Убедитесь сами, что калькулятор не смог найти значение этого выражения. Не получится и у нас. Деление на не имеет смысла, не определено.
Почему деление на ноль не определено?
был введен как часть большого механизма под названием целые числа для обозначения отсутствия чего-то. облегчает счет и запись чисел, но нулевого количества нет, на него не укажешь пальцем, поэтому сказать, сколько содержится в другом числе нельзя.
Разделить на означает сказать, сколько раз в ничего нет. Ответить на вопрос, сколько в гараже квадратных метров можно, но ответить, сколько в нем пустоты, – нет.
Если бы был придуман какой-то смысл для выражения , то это противоречило бы некоторым известным свойствам и определениям, например свойствам умножения, поэтому деление на не определяют.
Можно все же попробовать разделить на . Деление – это действие, обратное умножению, т.е., если .
Но при умножении на всегда получается , т.е. такого просто не существует.
Рассмотрим случай деления на , чтобы не возникало ощущения, что он – особый и отличается от деления на .
Равенство будет справедливым для любого , потому что Но результат деления должен быть конкретным числом. Снова получаем противоречие.
Поэтому деление на в математике не определено.
Подставить в алгебраическое выражение можно любое число, но не всегда получится посчитать его значение.
Определение: такие значения переменной, при которых выражение не определено (нельзя вычислить его значение), называют недопустимыми значениями.
На данный момент мы знакомы только с одним таким случаем. Например, если в выражении есть дробь или деление , то мы не будем подставлять в выражение такие значения переменной, при которых знаменатель обращается в : .
Есть и другие случаи появления недопустимых значений переменных, но о них мы узнаем позже, по мере изучения различных функций.
Рассмотрим примеры на определение недопустимых значений переменных в выражениях.
Пример . Определить недопустимые значения переменной в выражении .
Решение. Выражение представляет собой дробь, поэтому её знаменатель не может обращаться в : .
Таким образом, недопустимым значением переменной является , т.е. выражение определено для любых .
Ответ: .
Пример . Определить недопустимые значения переменной в выражении .
Решение. Выражение представляет собой дробь, поэтому её знаменатель не может обращаться в : .
Таким образом, недопустимым значением переменной является , т.е. выражение определено для любых .
Ответ: .
Где еще можно встретить деление на ноль?
Докажем, что . Введем переменные , пусть .
Запишем:
Получим равенство:
Перегруппируем слагаемые и получим:
Вынесем общий множитель за скобки в каждой из частей равенства:
Разделим обе части равенства на и получим:
Получили, что . В чём подвох? Дело в том, что в наше «доказательство» вкралась ошибка: было выполнено деление на при делении обеих частей равенства на выражение (по предположению эти числа равны: ).
Это пример математического софизма – утверждения с доказательством, в котором кроются ошибки. Софизмы бывают не только математическими,
interneturok.ru
Контрольная работа по алгебре на тему «Многочлены. Разбиение на множители и упрощение выражений» (7 класс)
Вариант 1
№ 1 Упростите выражение: а) б)
в) г)
№ 2 Раскрыть скобки: а) ; б) ;
в) ; г) .
№ 3 Разложить на множители: а) 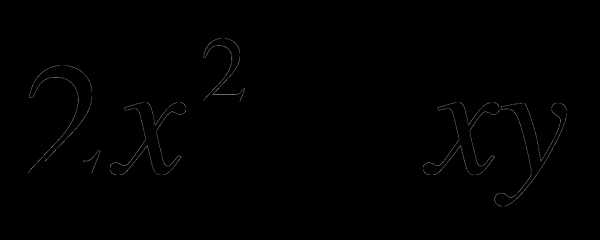 б)
б)
в) г)
№ 4 Разложить на множители: а) ; б) ;
в) .
№ 5 Доказать тождество: .
№ 6 Упростить выражение и найти его значение при 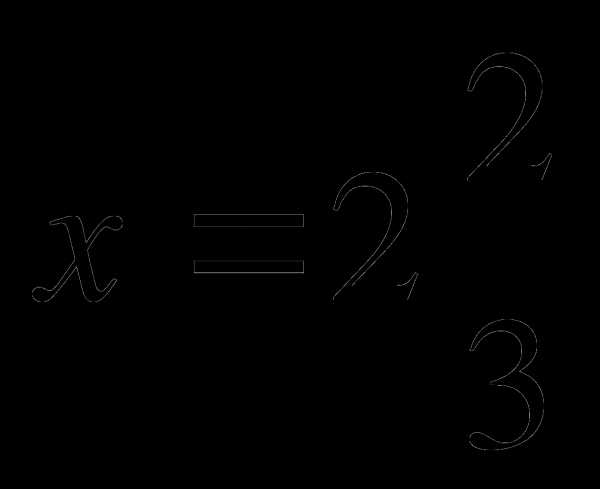 ,
, 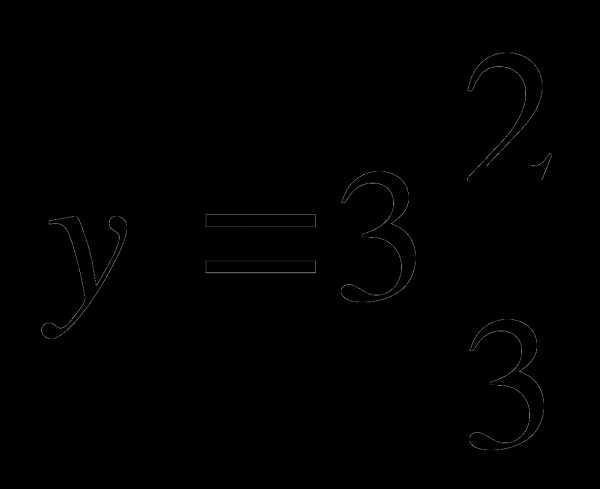 .
.
________________________________________________________________________
Вариант 2
№ 1 Упростите выражение: а) б)
в) г)
№ 2 Раскрыть скобки: а) ; б) ;
в) ; г) .
№ 3 Разложить на множители:
а) б)в) г)
№ 4 Разложить на множители: а) ; б) ;
в) .
№ 5 Доказать тождество: .
№ 6 Упростить выражение и найти его значение при  ,
,  .
.
________________________________________________________________________
Вариант 3
№ 1 Упростите выражение: а) б)
в) г)
№ 2 Раскрыть скобки: а) ; б) ;
в) ; г) .
№ 3 Разложить на множители: а) б)
в) г)
№ 4 Разложить на множители: а) ; б) ;
№ 5 Доказать тождество: .
№ 6 Упростить выражение и найти его значение при 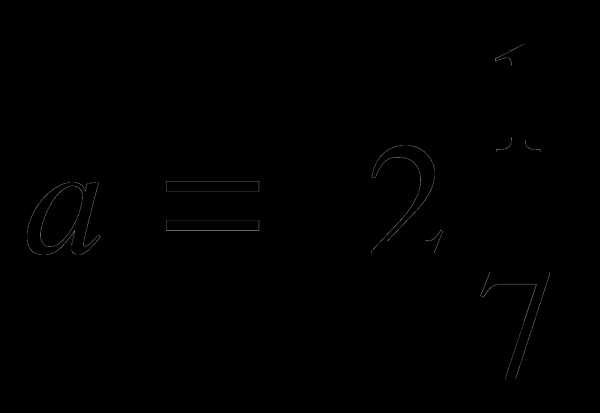 ,
, 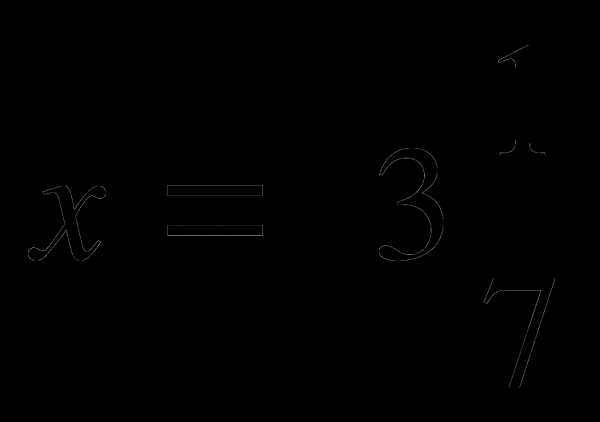 .
.
________________________________________________________________________
Вариант 4
№ 1 Упростите выражение: а) б)
в) г)
№ 2 Раскрыть скобки: а) ; б) ;
в) ; г) .
№ 3 Разложить на множители: а) 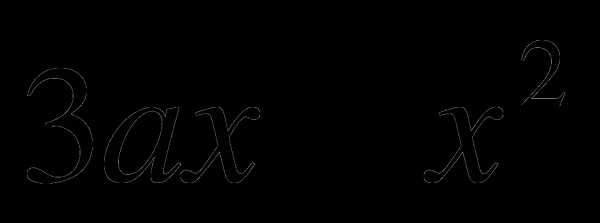 б)
б)
в) г)
№ 4 Разложить на множители: а) ; б) ;
в) .
№ 5 Доказать тождество: .
№ 6 Упростить выражение и найти его значение при ,
,  .
.________________________________________________________________________
infourok.ru
Числовые и алгебраические выражения — урок. Алгебра, 7 класс.
Числовым выражением называют всякую запись из чисел, знаков арифметических действий и скобок, составленную со смыслом.
Например:3+5⋅7−4 — числовое выражение;
3+:−5 — не числовое выражение, а бессмысленный набор символов.
Очень часто вместо конкретных чисел употребляются буквы, тогда получается алгебраическое выражение.
Алгебраическим выражением называется запись из букв, знаков арифметических действий, чисел и скобок, составленная со смыслом.
Например:a2−3b — алгебраическое выражение.
Поскольку буквам, входящим в состав алгебраического выражения, можно придавать различные числовые значения (т. е. можно менять значения букв), эти буквы называют переменными.
Алгебраические выражения могут быть очень громоздкими, и алгебра учит их упрощать, используя правила, законы, свойства, формулы.
При упрощении вычислений часто используются законы сложения и умножения.
Законы сложения
1) От перемены мест слагаемых сумма не изменяется, т. е.
a+b=b+a — переместительный закон сложения.
2) Чтобы к сумме двух слагаемых прибавить третье слагаемое, можно к первому слагаемому прибавить сумму второго и третьего слагаемых, т. е.
a+b+c=a+b+c — сочетательный закон сложения.
Законы умножения1) От перемены мест множителей произведение не меняется, т. е.
a⋅b=b⋅a — переместительный закон умножения.
2) Произведение не зависит от группировки его сомножителей, т. е.
a⋅b⋅c=a⋅b⋅c — сочетательный закон умножения.
3) Произведение суммы нескольких чисел на какое-нибудь число равно сумме произведений каждого слагаемого на это число, т. е.
a+b⋅c=ac+bc — распределительный закон умножения относительно сложения.
В результате упрощений числового выражения получается число, которое называют значением числового выражения.
Выполнив указанные действия в первом примере, получим
3+5⋅7−4=18.
Число \(18\) в ответе есть значение данного числового выражения.
О значении алгебраического выражения можно говорить только при конкретных значениях входящих в него букв.
Например, алгебраическое выражение a2−3b при \(a=-16\) и \(b=-14\) имеет значение \(298\), т. к.
a2−3b=−162−3⋅−14=256+42=298,
а вот алгебраическое выражение a2−3a+2 при \(a=-4\) имеет значение \(-6,5\),
т. к. −42−3−4+2=16−3−2=13−2=−6,5.
И это же алгебраическое выражение a2−3a+2 при \(a=-2\) не имеет смысла, т. к. a+2=−2+2=0, т. е. будет деление на ноль.
Обрати внимание!
А на ноль делить нельзя!
Вывод:если при конкретных значениях букв алгебраическое выражение имеет числовое значение, то указанные значения переменных называют допустимыми;
если же при конкретных значениях букв алгебраическое выражение не имеет смысла, то указанные значения переменных называют недопустимыми.
Так, в примере a2−3a+2 значение \(a=-4\) — допустимое, азначение \(a=-2\) — недопустимое, т. к. при нём будет деление на ноль, а делить на ноль нельзя!
www.yaklass.ru
Числовые и алгебраические выражения (В.А. Тарасов). Видеоурок. Алгебра 7 Класс
Числовые выражения – это те выражения, которые составлены из чисел и знаков арифметических операций – сложения, вычитания, умножения, деления.
Пример 1
.
Это числовое выражение, которое необходимо упрощать.
Рассмотрим ещё несколько примеров числовых выражений.
Пример 2
,
,
.
При замене некоторых чисел буквами образуется
Правило: от перемены мест слагаемых сумма не меняется – справедливо для чисел 4 и 5, для чисел 6 и 1. Если обобщить этот закон для всех чисел, то его можно записать в алгебраическом виде: обозначим первое слагаемое — , второе – . В результате получаем:
.
Значит данное правило применимо для алгебраических выражений.
Получаем, что для алгебраических выражений числовые выражения являются частным случаем. Поэтому действия с числовыми выражениями применимы и к алгебраическим выражениям. Рассмотрим несколько примеров на числовые выражения.
Пример 3
interneturok.ru
