Замечательные пределы. Эквивалентные бесконечно малые функции
При решении практических задач используются замечательные пределы [1, с. 123, 124]:
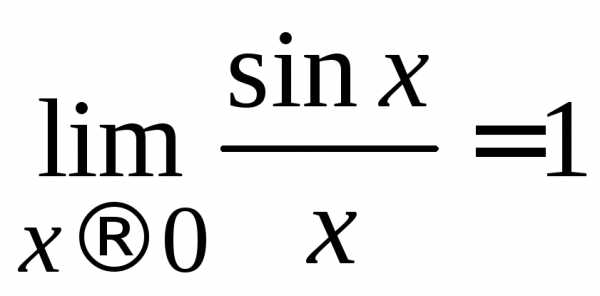 – первый замечательный предел;
(2.8)
– первый замечательный предел;
(2.8)
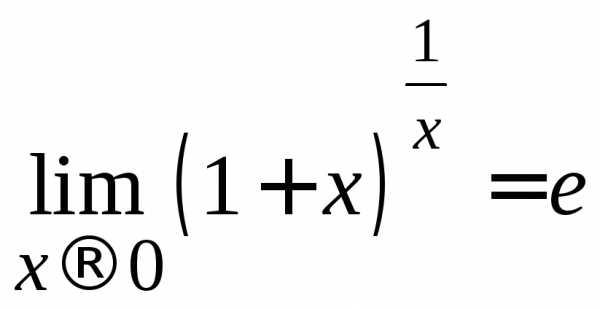 – второй замечательный предел.
(2.9)
– второй замечательный предел.
(2.9)
Замечательные пределы позволяют установить ряд полезных предельных соотношений:
1) 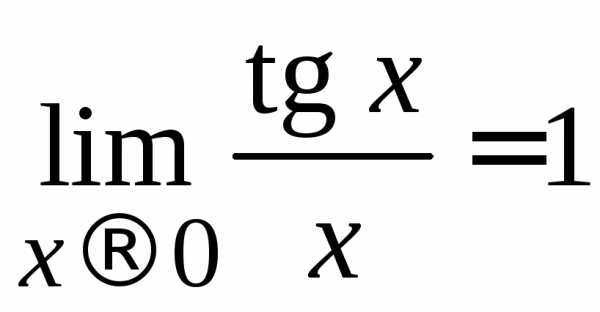 ;
2)
;
2)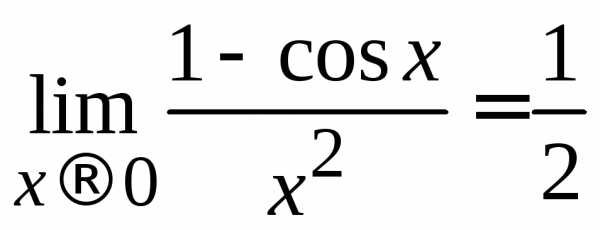 ;
3)
;
3)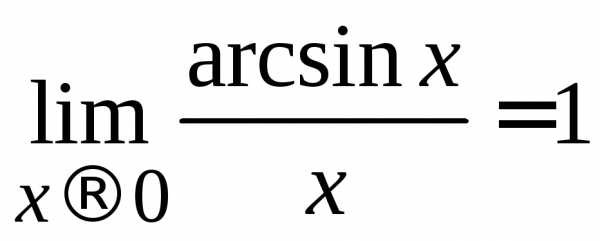 ;
;
4) 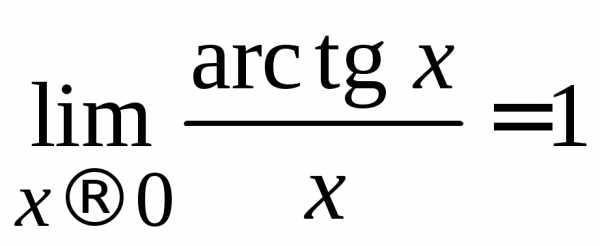
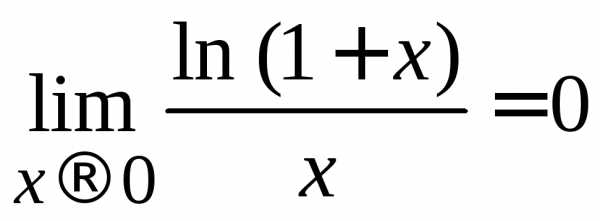 ;
6)
;
6)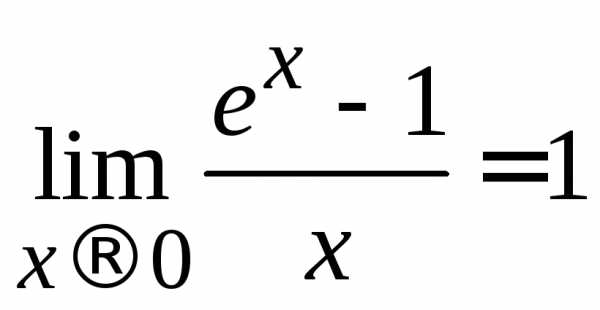 ;
;7) 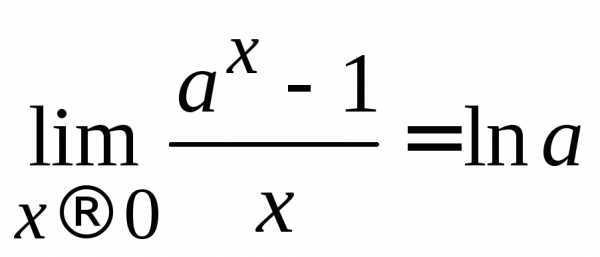 ;
8).
;
8).
Пример 2.16. Вычислить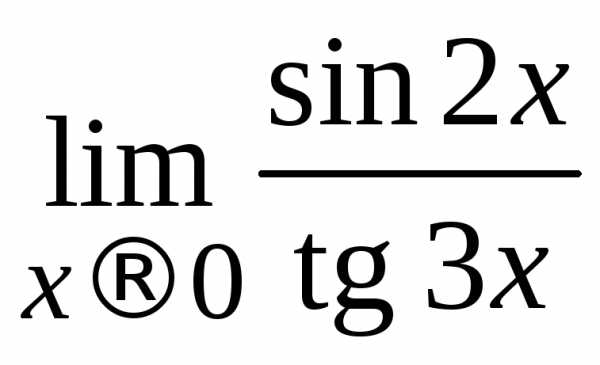 .
.
Решение.Сначала найдем предел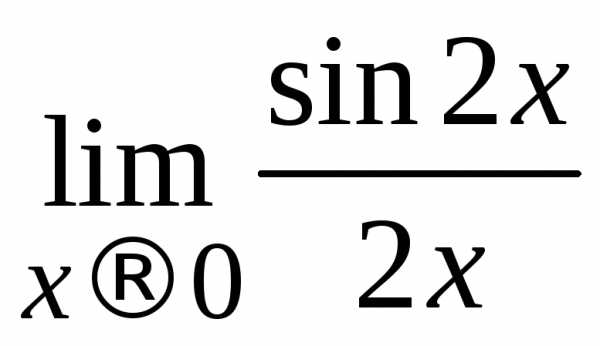 .
Для решения предложенной задачи сделаем
замену
.
Для решения предложенной задачи сделаем
замену .
Новая переменная
.
Новая переменная ,
когда
,
когда .
Тогда в силу первого замечательного
предела имеем:
.
Тогда в силу первого замечательного
предела имеем:
.
Рассуждая аналогичным образом, и
учитывая, что 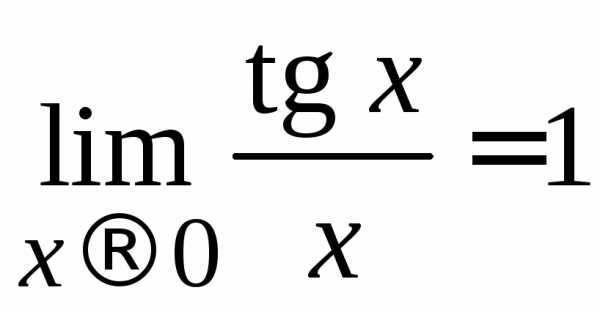
.
В числителе исходной дроби выделим
выражение 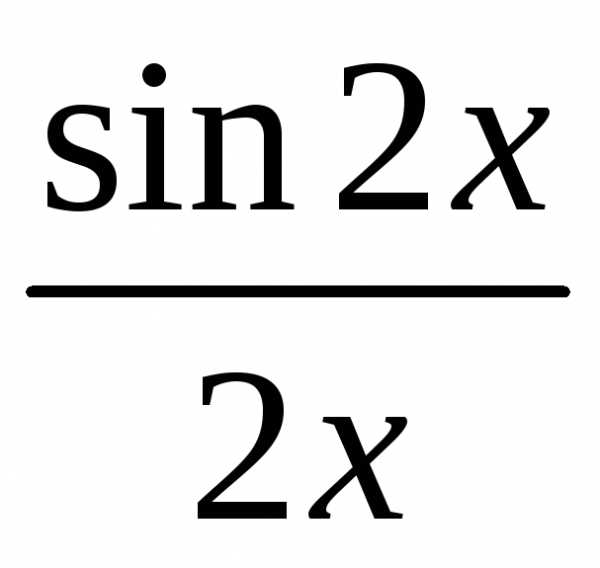 ,
а в знаменателе выражение
,
а в знаменателе выражение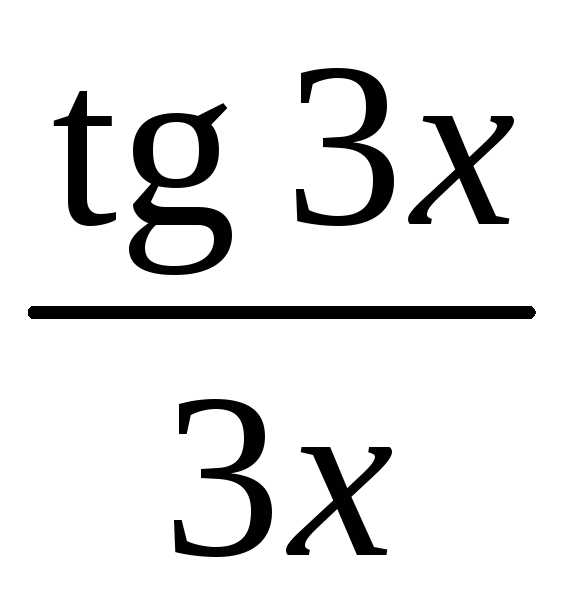 и применим формулы (2.3), (2.4). Тогда
и применим формулы (2.3), (2.4). Тогда
 .
.
Пусть 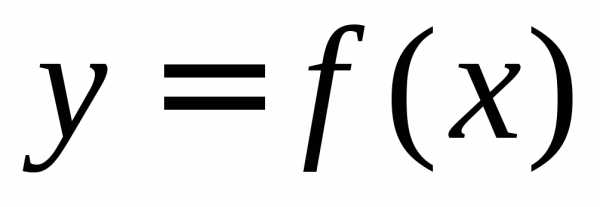 и
и есть бесконечно малые функции при,
т. е.
есть бесконечно малые функции при,
т. е.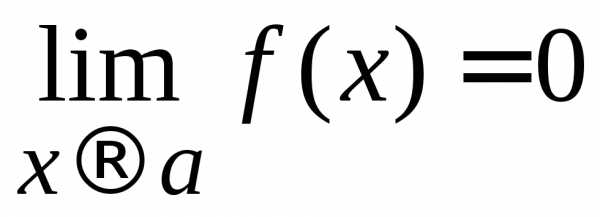 и
и .
Функции
.
Функции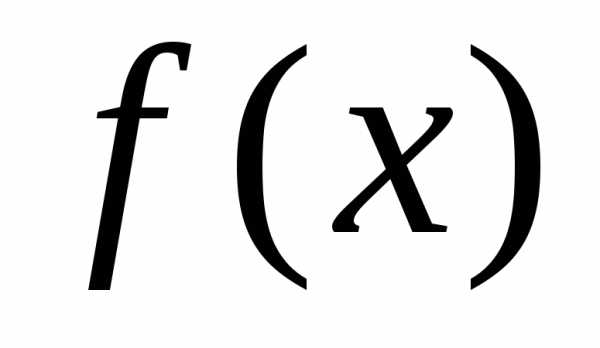 и
и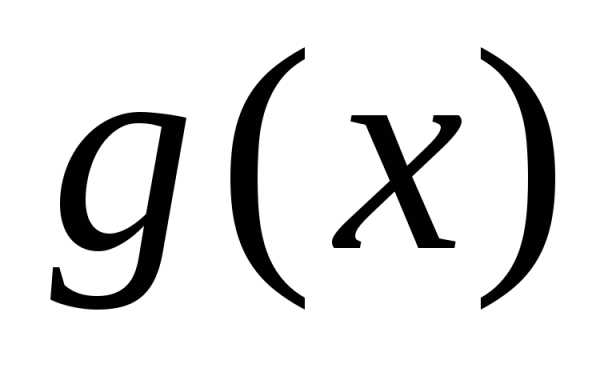
 .
Обозначается это так:.
.
Обозначается это так:.
Используя формулу (2.8) и предельные
соотношения 1 – 8, составим таблицу
важнейших эквивалентных бесконечно
малых функций при  .
.
З амечание. В качестве аргумента бесконечно
малых функций в таблице эквивалентностей
может выступать не только
амечание. В качестве аргумента бесконечно
малых функций в таблице эквивалентностей
может выступать не только ,
но и любая величинапри.
,
но и любая величинапри.
Поясним сказанное на примерах.
Пример 2.17. Найти бесконечно малые, эквивалентные функциям:
1) 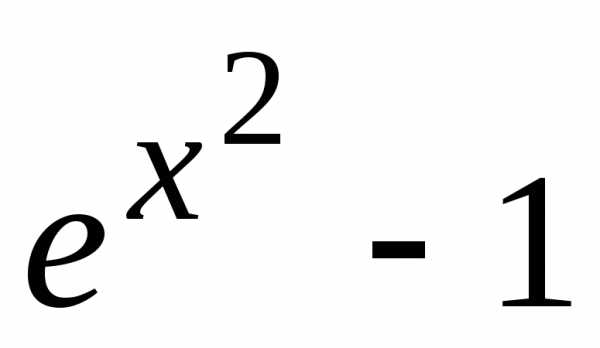
 ;
2)
;
2) при;
3)
при;
3)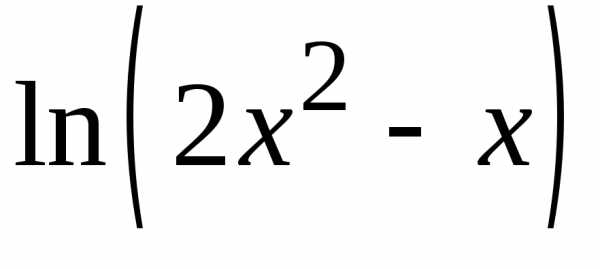 при
при .
.Решение:
1. Выражение
при 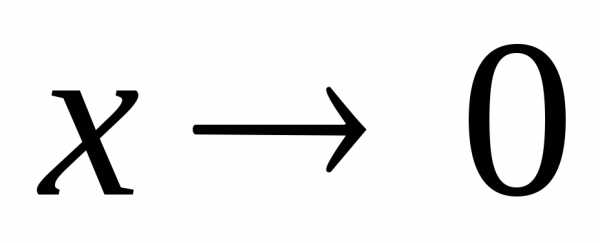 .Поэтому в роли бесконечно малого
аргумента показательной функции из
таблицы эквивалентностей выступает
величина
.Поэтому в роли бесконечно малого
аргумента показательной функции из
таблицы эквивалентностей выступает
величина .
Следовательно,
.
Следовательно,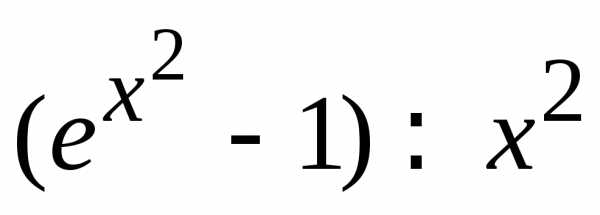 при
при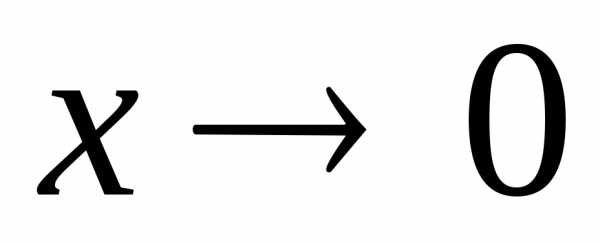 .
.
2. Рассматриваемая функция действительно
является бесконечно малой:
.
Выражение
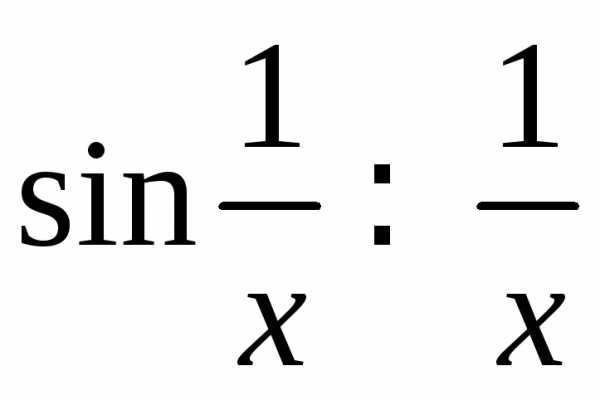 при.
при. 3. Проверкой убеждаемся, что
.
В аргументе логарифма выделим единицу:.
Выражениепри .
Тогда по таблице эквивалентностей
имеем:при
.
Тогда по таблице эквивалентностей
имеем:при .
.
Пример 2.18. Вычислить .
.
Решение. Подстановкой убеждаемся,
что имеет место неопределенность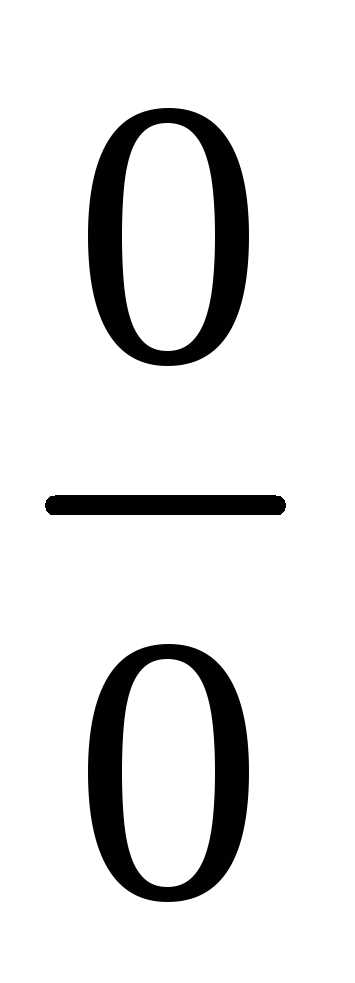 ,
для раскрытия которой применим следующее
утверждение.
,
для раскрытия которой применим следующее
утверждение.
Теорема 2.1.Предел отношения двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой.
И
числитель, и знаменатель дроби –
бесконечно малые. В примере 2.17 определена
бесконечно малая, эквивалентная
числителю:
при .
Рассуждая аналогичным образом, получаем:при
.
Рассуждая аналогичным образом, получаем:при .
После замены числителя и знаменателя
найденными эквивалентными бесконечно
малыми, придем к пределу отношения двух
многочленов:
.
После замены числителя и знаменателя
найденными эквивалентными бесконечно
малыми, придем к пределу отношения двух
многочленов:
 .
.
Замечание. Предел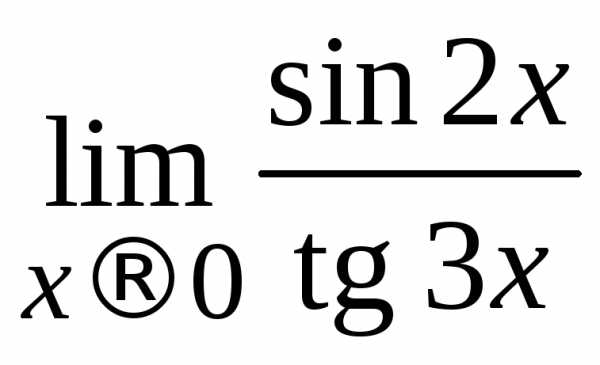 (пример 2.16) можно вычислить значительно
быстрее, если заменить числитель и
знаменатель эквивалентными им бесконечно
малыми. Так как,
апри
(пример 2.16) можно вычислить значительно
быстрее, если заменить числитель и
знаменатель эквивалентными им бесконечно
малыми. Так как,
апри ,
то.
,
то.
Согласно теореме 2.1, замена по таблице эквивалентностей разрешена в частном и произведении бесконечно малых функций, а вот в сумме или разности бесконечно малых функций она не законна. Однако некоторые пределы, содержащие сумму или разность бесконечно малых, можно вычислить, если перед тем, как осуществлять замену эквивалентными, воспользоваться теоремой о пределе суммы.
Пример 2.19. Вычислить .
.
Решение. Преобразуем выражение,
стоящее под знаком предела, следующим
образом:.
По таблице эквивалентностей: и
и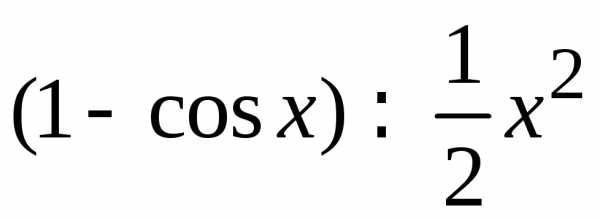 при
при .
Тогда, применив теорему о пределе суммы
и заменив бесконечно малые эквивалентными
уже в отношениях, получим:
.
Тогда, применив теорему о пределе суммы
и заменив бесконечно малые эквивалентными
уже в отношениях, получим:
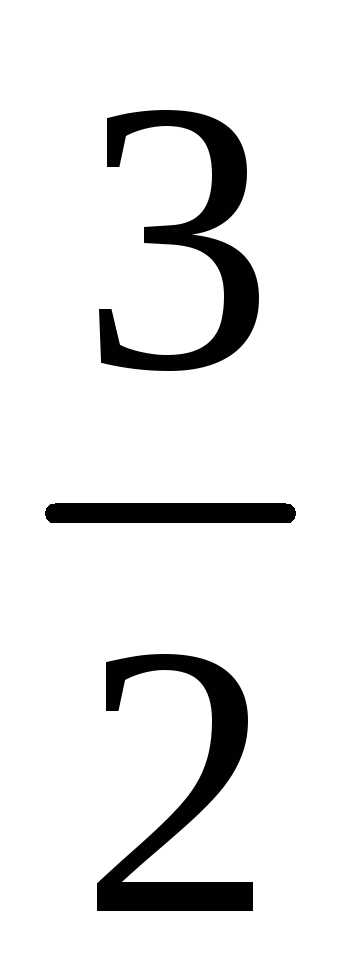 .
.
Но даже предварительное применение теоремы о пределе суммы или разности не гарантирует уничтожения неопределенности. Например,
.
studfiles.net
6. Сравнение бесконечно малых. Эквивалентные бесконечно малые.
1)
Пусть и—
бесконечно малые при.
1.
Если,
то говорят, чтоявляетсябесконечно
малой высшего порядка по
сравнению с .
В этом случае пишут.
2.
Если,
где—число,
отличное от нуля, то говорят,
чтои—бесконечно
малые одного и того же порядка.
В часности, если ,
то бесконечно малыеиназываются
эквивалентными. Запись~означает,
чтои—эквивалентные
бесконечно малые.
Если,
то это означает, что.
Таким образом,является
бесконечно малой высшего порядка по
сравнению с,
т. е.3.
Еслии—бесконечно
малые одного и того же порядка, причем,
то говорят, что бесконечно малаяимеет
порядокпо
сравнению с.
Отметим
некоторые свойства бесконечно малых
величин:
1
2) Б.м. функциииназываютсяэквивалентнымиилиравносильными б.м. одного порядка при, если
Обозначают:при.
Очень удобно пользоваться заменой эквивалентных бесконечно малых при нахождении пределов. Замена производится на основе таблицы.
Таблица эквивалентных бесконечно малых.
Пусть — бесконечно малая при .
7. Теорема о предельном переходе под знаком неравенства. Теорема о сжатой
переменной (формулировка).
1) ТЕОРЕМА: (о предельном переходе в неравенстве.).
Пусть при всех n выполняется неравенство ,и переменныеи имеют пределы:
;
Тогда:, т. е..
Теорема означает, что в неравенстве можно переходить к пределам, сохраняя знак неравенства.
Доказательство:
Предположим, что
Выделим вокруг точек истоль малыеE – окрестности, чтобы они не пересекались.
По определению предела, начиная с некоторого номера n, переменные ипопадут в своиE – окрестности предельных точек.
Замечание:
Если при всех n выполняется (строго), то гарантировать строгого неравенства в пределе нельзя (в общем случае), гарантируется лишь нестрогое неравенство.
2) ТЕОРЕМА: (о сжатой переменной).
Пусть, начиная с некоторого , выполняются неравенства, причем крайние переменные имеют одинаковый конечный предел, тогда переменнаятакже имеет предел, причем тот же самый.
8. Теорема о сохранении знака функции. Теорема о связи функции, имеющей
конечный предел, с бесконечно малой.
1) Теорема. (Теорема о сохранении знака непрерывной функции). Если ,, то.
Доказательство. Достаточно доказать, что если , то и. Действительно, взявполучаем по определению непрерывности окрестность.
2) Теорема Для того, чтобы функция имела предел в точкеaравный А, необходимо и достаточно, чтобы имело место представление :, где- бесконечно малая функция в точкеa .
ДОК. (1) Если , то функцияб.м.ф. Действительно,
(2) .
studfiles.net
6. Сравнение бесконечно малых. Эквивалентные бесконечно малые.
1) Пусть и— бесконечно малые при. 1. Если, то говорят, чтоявляетсябесконечно малой высшего порядка по сравнению с . В этом случае пишут. 2. Если, где—число, отличное от нуля, то говорят, чтои—бесконечно малые одного и того же порядка. В часности, если , то бесконечно малыеиназываются эквивалентными. Запись~означает, чтои—эквивалентные бесконечно малые. Если, то это означает, что. Таким образом,является бесконечно малой высшего порядка по сравнению с, т. е.3. Еслии—бесконечно малые одного и того же порядка, причем, то говорят, что бесконечно малаяимеет порядокпо сравнению с. Отметим некоторые свойства бесконечно малых величин: 1o. Произведение двух бесконечно малых есть бесконечно малая высшего порядка по сравнению с сомножителями, т. е. если , тои. 2o. Бесконечно малые иэквивалентны тогда и только тогда, когда их разностьявляется бесконечно малой высшего порядка по сравнению си, т. е. если ,. 3o. Если отношение двух бесконечно малых имеет предел, то этот предел не изменится при замене каждой из бесконечно малых эквивалентной ей бесконечно малой, т.е. если ,~,~, то.
2) Б.м. функциииназываютсяэквивалентнымиилиравносильными б.м. одного порядка при, если
Обозначают:при.
Очень удобно пользоваться заменой эквивалентных бесконечно малых при нахождении пределов. Замена производится на основе таблицы.
Таблица эквивалентных бесконечно малых.
Пусть — бесконечно малая при .
7. Теорема о предельном переходе под знаком неравенства. Теорема о сжатой
переменной (формулировка).
1) ТЕОРЕМА: (о предельном переходе в неравенстве.).
Пусть при всех n выполняется неравенство ,и переменныеи имеют пределы:
;
Тогда:, т. е..
Теорема означает, что в неравенстве можно переходить к пределам, сохраняя знак неравенства.
Доказательство:
Предположим, что
Выделим вокруг точек истоль малыеE – окрестности, чтобы они не пересекались.
По определению предела, начиная с некоторого номера n, переменные ипопадут в своиE – окрестности предельных точек.
Это означает, что, начиная с некоторого номера n, что противоречит условию. Противоречие доказывает теорему, ч. т. д.
Замечание:
Если при всех n выполняется (строго), то гарантировать строгого неравенства в пределе нельзя (в общем случае), гарантируется лишь нестрогое неравенство.
2) ТЕОРЕМА: (о сжатой переменной).
Пусть, начиная с некоторого , выполняются неравенства, причем крайние переменные имеют одинаковый конечный предел, тогда переменнаятакже имеет предел, причем тот же самый.
8. Теорема о сохранении знака функции. Теорема о связи функции, имеющей
конечный предел, с бесконечно малой.
1) Теорема. (Теорема о сохранении знака непрерывной функции). Если ,, то.
Доказательство. Достаточно доказать, что если , то и. Действительно, взявполучаем по определению непрерывности окрестность.
2) Теорема Для того, чтобы функция имела предел в точкеaравный А, необходимо и достаточно, чтобы имело место представление :, где- бесконечно малая функция в точкеa .
ДОК. (1) Если , то функцияб.м.ф. Действительно,
(2) .
studfiles.net
Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых функций. Эквивалентные функции и их применение к вычислению пределов.
361. Бесконечно малые и бесконечно большие функции.
Определение и основные свойства.Функция называется бесконечно малой при , если .
Функция называется бесконечно большой при , если .
Например, функция есть бесконечно большая функция при .
Утверждение 1.Для того, чтобы функция при была бесконечно малой функцией, необходимо и достаточно, чтобы функция была бесконечно большой функцией при .
Для бесконечно малой функции выполняются те же свойства, что и для бесконечно малых последовательностей.
Связь между функцией, ее пределом и бесконечно малой функцией.
Теорема 1. Для того, чтобы функция имела предел в точке , равный b, необходимо и достаточно, чтобы функция была бесконечно малой функцией при .
362. Сравнение бесконечно малых функций.
Как известно, сумма, разность и произведение двух бесконечно малых функций есть функция бесконечно малая (см. § 6). Отношение же двух бесконечно малых функций может быть конечным числом или вообще не имеет предела.
Пусть и – бесконечно малые функции при , т.е. и . Тогда:
1. Если , то и называются бесконечно малыми одного порядка.
2. Если , то называется бесконечно малой более высокого порядка, чем .
3. Если , то называется бесконечно малой более низкого порядка, чем .
4. Если не существует, то и называются несравнимыми бесконечно малыми функциями.
363. Эквивалентные функции и их применение к вычислению пределов.
Если , то и называются эквивалентными бесконечно малыми функциями (при ) и обозначаются: при .
Например, при , т. к. .
Для эквивалентных бесконечно малых функций справедливы следующие утверждения:
1. Предел отношения двух бесконечно малых функций не изменится, если каждую (или одну из них) заменить эквивалентной ей бесконечно малой функцией.
2. Разность двух эквивалентных бесконечно малых функций есть бесконечно малая функция более высокого порядка, чем каждая из них.
3. Сумма конечного числа бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.
Докажем последнее утверждение для двух функций.
Пусть при , причем –
бесконечно малая функция более высокого порядка, чем ,
т.е. . Тогда
.
Следовательно, при . □
Слагаемое, эквивалентное сумме бесконечно малых функций, называется главной частью этой суммы.
Применение эквивалентных бесконечно малых функций к вычислению пределов.Для раскрытия неопределенностей вида часто бывает полезным применять замену бесконечно малой функции на эквивалентную ей.
Приведем важнейшие эквивалентности, которые используются при вычислении пределов:
1. при ;
2.
3.
4.
5.
6.
7.
8.
9.
10. в частности .
Непрерывность функции в точке и на отрезке. Свойства функций, непрерывных в точке.
371. Непрерывность функции в точке и на отрезке.
cyberpedia.su
Эквивалентные бесконечно малые функции и их
применение для вычисления пределов
Определение.
Бесконечно малые функции называются эквивалентными бесконечно малыми при , если
Пишут так: при .
Теорема.
Пусть в окрестности точки , за исключением, быть может, ее самой, задана функция и бесконечно малые функции . Тогда
Это равенство понимается в смысле: если существует предел его правой части, то существует равный ему предел левой части (и обратно). Отсюда же следует, что если один из пределов не существует, то не существует и другой.
Доказательство.
Пусть тогда
Аналогично доказывается обратное утверждение.
Пары эквивалентных бесконечно малых, которые используют при вычислении пределов:

9) при
Монотонные функции. Теорема о существовании
И непрерывности обратной функции
Определение.
Функция называется неубывающей (невозрастающей) на отрезке , если для любых
выполняется неравенство .
Неубывающие и невозрастающие функции называются монотонными.
Если неравенства строгие, то функция называется возрастающей (убывающей) на отрезке. Возрастающие и убывающие функции называются строго монотонными.
Теорема.
Рассмотрим непрерывную строго возрастающую функцию на отрезке , причем Тогда существует обратная к f функция , однозначная, строго возрастающая и непрерывная на .
Доказательство существования.
Поскольку каждому значению соответствует только одно значение , то любому значению y из можно поставить в соответствие именно то значение x, для которого обозначим это соответствие так: . Тем самым определена обратная функция.
Доказательство возрастания.
Из условия возрастания следует: если Верно и обратное утверждение: если
Но и получаем: если т.е. обратная функция – возрастающая.
Доказательство непрерывности обратной функции.
Докажем непрерывность обратной функции в произвольной точке . Обозначим и выберем произвольное , такое, что . Пусть
Выберем Тогда, очевидно,
а . (*)
Пусть теперь , т.е. .
С учетом (*) можно записать, что .
В силу возрастания функции следует, что
Но , поэтому или А это и означает, что функция непрерывна в точке
Разрывы первого и второго рода
Определение.
Пусть функция определена на интервале (a, b), кроме, быть может, точки . Точка с называется точкой разрыва функции , если функция f не определена при , или если она определена в этой точке, но не является в ней непрерывной.
Рассмотрим график . Кружок в точке А означает, что эта точка входит в область значений , т.е. . Стрелка в точке В означает, что точка В в область значений функции не входит. Поскольку , функция имеет разрыв в точке с.
Другие возможные случаи разрывов.
Если функция f имеет конечные пределы и , но , то функция имеет в точке разрыв I рода.
Если , то в точке устранимая особенность.
Если доопределить так, что , то получим непрерывную функцию.
Пример разрывной функции (функция Кронекера):
Точка является точкой разрыва I рода.
Если у функции не существует ни левого, ни правого предела, либо одного из них, либо эти пределы бесконечны в точке С, то функция имеет разрыв II рода.
Пример 1.
;
–точка разрыва II рода.
Пример 2.
Ее график имеет вид:
 |
Эта функция не имеет в точке ни левого, ни правого предела. – точка разрыва II рода.
Пример 3.
Точки , – точки разрыва II рода. В них не определена, а пределы слева и справа бесконечны.
Функции, непрерывные на отрезке
Определение.
Функция называется непрерывной на отрезке , если она непрерывна во всех точках интервала , непрерывна справа в точке a, слева в точке b.
Теорема 1.
Если функция непрерывна на отрезке , то она ограничена на нем, т.е. существует число , такое, что для всех .
Теорема 2 (теорема Вейерштрасса).
Если функция непрерывна на отрезке , то она достигает минимума и максимума на , т.е. существуют точки , такие, что для всех .
Теорема 3.
Если функция непрерывна на и числа не равны нулю и имеют противоположные знаки, то на интервале имеется по крайней мере одна точка c, такая, что .
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
infopedia.su
