1.2 Бинарные отношения
1.2.1 Декартово произведение множеств. Соответствие множеств
Декартовым
произведением  двух множеств X и Y называется множество всех упорядоченных пар ( x,y ) таких, что
двух множеств X и Y называется множество всех упорядоченных пар ( x,y ) таких, что 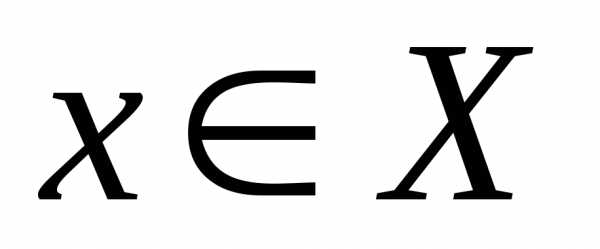 ,
а
,
а 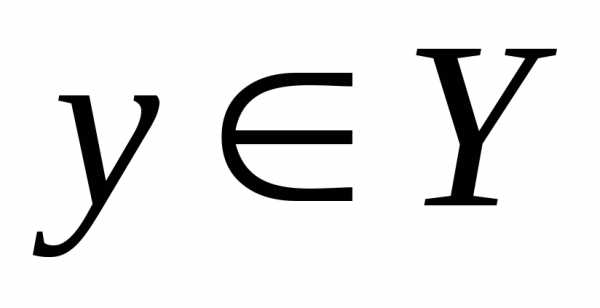 .
.
Пример 1. Пусть .
Тогда , .
Очевидно, что , т.е. операция декартова произведения множеств не является коммутативной.
Декартовым
произведением множеств называется
множество
всех упорядоченных наборовтаких, чтоЕсли,
то декартово произведение обозначают
Будем говорить, что задано соответствие q между множествами X и Y, если задана упорядоченная тройка , где.Множество X называется областью отправления, а Y – областью прибытия соответствия q (обозначают ). Каждый элементy в паре называется образом элементаx (x – прообразом элемента y) при данном соответствии q.
Соответствие
называетсяотображением множества X во множество Y,
если каждый элемент  имеет образ,
т.е..
имеет образ,
т.е..
Отображение
называетсяфункциональным,
если каждый элемент  имеетединственный образ
:.
Множество образов при данном отображенииобозначается:.
имеетединственный образ
:.
Множество образов при данном отображенииобозначается:.
Если множество 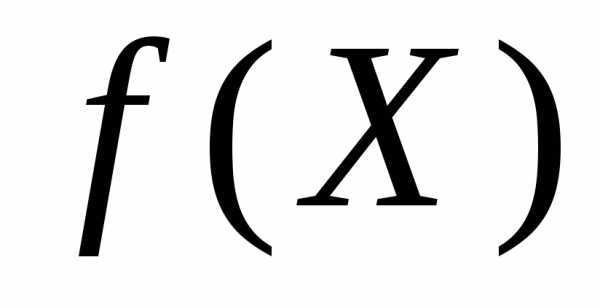
Соответствие
называетсявзаимно
однозначным (биекцией),
если а) является отображением; б)
функционально; в) отображает X «на» множество Y;
г) из условия
следует 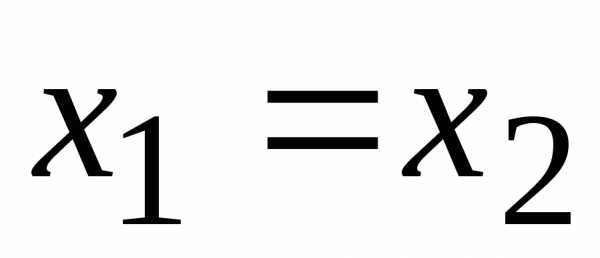 .
.
Другими словами,
является биекцией, если каждый элемент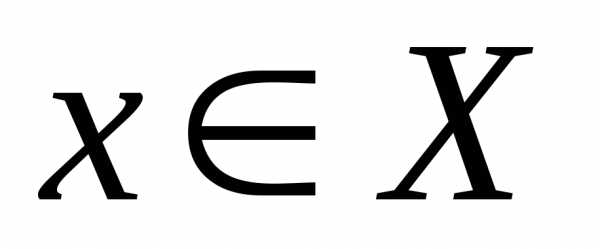 имеет единственный образ,
а каждый элемент
имеет единственный образ,
а каждый элемент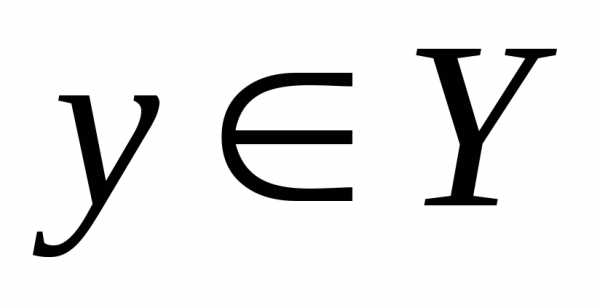 имеет единственный прообразпри данном отображении:
имеет единственный прообразпри данном отображении:
(1.2)
1.2.2 Определение бинарного отношения
Определение. Говорят, что на множестве X задано бинарное отношение R
 (т.е.
).
(т.е.
).Пример 2. Пусть Зададим наХ следующие отношения:
–отношение равенства;
–отношение предшествования;
делится
на  –
отношение делимости.
–
отношение делимости.
Все эти отношения заданы с помощью характеристического свойства. Ниже перечислены элементы этих отношений:
Тот факт, что пара (x, y) принадлежит данному отношению R, будем записывать: или xRy. Например, для отношения Q запись 4Q2 означает, что 4 делится на 2 нацело, т.е.
Областью
определения 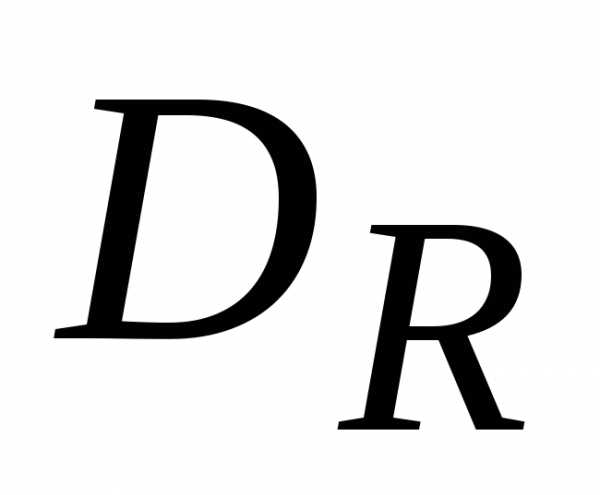 бинарного
отношения R называется множество Областью
значений
бинарного
отношения R называется множество Областью
значений  называется
множество
называется
множество
Так, для отношения Р из примера 2 областью определения является множество , а областью значений –.
1.2.3 Способы задания бинарного отношения
Бинарное отношение можно задать, указав характеристическое свойство или перечислив все его элементы. Более наглядными способы задания бинарного отношения являются график отношения, схема отношения, граф отношения, матрица отношения.
График отношения изображается в декартовой системе координат; на горизонтальной оси отмечается область определения, на вертикальной – множество значений отношения; элементу отношения (х,у) соответствует точка плоскости с этими координатами. На рис. 1.7,а) приведен график отношения Q примера 2.
Схема отношения изображается с помощью двух вертикальных прямых, левая из которых соответствует области определения отношения, а правая – множеству значений отношения. Если элемент (
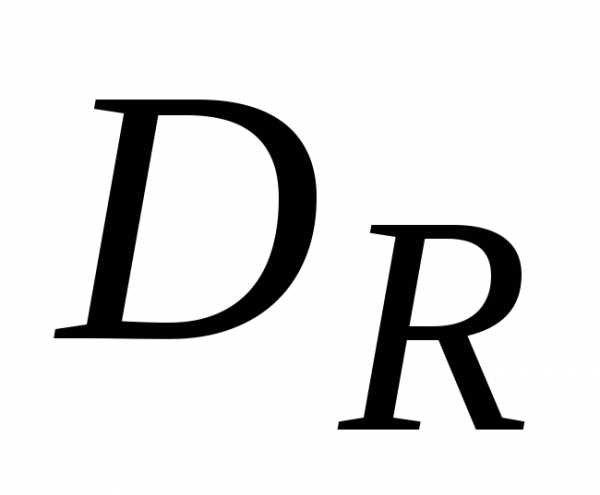 и
и  соединяются
отрезком прямой. На рис. 1.7,б) приведена
схема отношения Q из примера 2.
соединяются
отрезком прямой. На рис. 1.7,б) приведена
схема отношения Q из примера 2.Граф отношения строится следующим образом. На плоскости в произвольном порядке изображаются точки – элементы множестваХ. Пара точек х и у соединяется дугой (линией со стрелкой) тогда и только тогда, когда пара ( х,у ) принадлежит отношению R. На рис. 1.8,а) приведен граф отношения Q примера 2.
Пусть
. Матрица отношения имеет n строк и n столбцов, а ее элемент 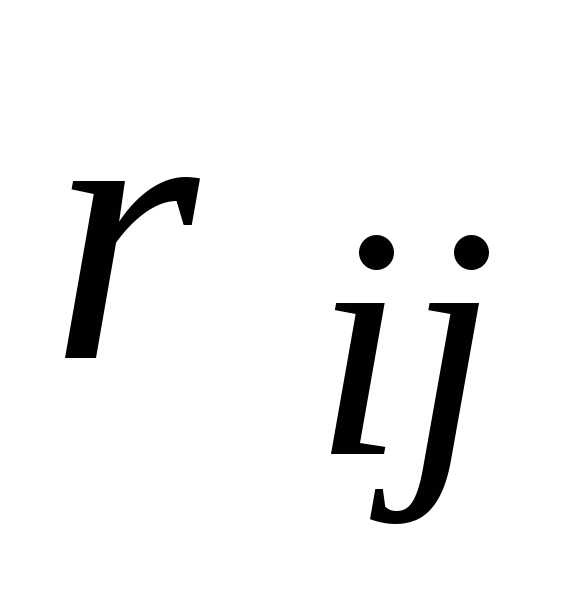 определяется
по правилу:
определяется
по правилу:
На рис.1.8,б) приведена матрица отношения Q примера 2.
studfiles.net
Бинарное отношение — Википедия. Что такое Бинарное отношение
Бина́рное (двухместное) отноше́ние — отношение между двумя множествами A{\displaystyle A} и B{\displaystyle B}, то есть всякое подмножество декартова произведения этих множеств: R⊆A×B{\displaystyle R\subseteq A\times B}[1]. Бинарное отношение на множестве A{\displaystyle A} — любое подмножество R⊆A2=A×A{\displaystyle R\subseteq A^{2}=A\times A}, такие бинарные отношения наиболее часто используются в математике, в частности, таковы равенство, неравенство, эквивалентность, отношение порядка.
Связанные определения
- Множество всех первых компонент пар из R⊆A×B{\displaystyle R\subseteq A\times B} называется областью определения отношения R{\displaystyle R} и обозначается как DomR{\displaystyle \mathrm {Dom} \,R}.
- DomR={x∣∃y((x,y)∈R)}.{\displaystyle \mathrm {Dom} \,R=\{x\mid \exists y((x,\;y)\in R)\}.}
- Множество всех вторых компонент пар из R{\displaystyle R} называется областью значения отношения R{\displaystyle R} и обозначается как ImR{\displaystyle \mathrm {Im} \,R}.
- ImR={y∣∃x((x,y)∈R)}.{\displaystyle \mathrm {Im} \,R=\{y\mid \exists x((x,\;y)\in R)\}.}
Свойства отношений
Бинарное отношение R{\displaystyle R} на некотором множестве M{\displaystyle M} может обладать различными свойствами, например:
- рефлексивность: ∀x∈M(xRx){\displaystyle \forall x\in M(xRx)},
- антирефлексивность (иррефлексивность): ∀x∈M¬(xRx){\displaystyle \forall x\in M\neg (xRx)},
- корефлексивность: ∀x,y∈M(xRy⇒x=y){\displaystyle \forall x,y\in M(xRy\Rightarrow x=y)},
- симметричность: ∀x,y∈M(xRy⇒yRx){\displaystyle \forall x,\;y\in M(xRy\Rightarrow yRx)},
- антисимметричность: ∀x,y∈M(xRy∧yRx⇒x=y){\displaystyle \forall x,\;y\in M(xRy\wedge yRx\Rightarrow x=y)},
- асимметричность: ∀x,y∈M(xRy⇒¬(yRx)){\displaystyle \forall x,\;y\in M(xRy\Rightarrow \neg (yRx))},
- транзитивность: ∀x,y,z∈M(xRy∧yRz⇒xRz){\displaystyle \forall x,\;y,\;z\in M(xRy\wedge yRz\Rightarrow xRz)},
- евклидовость: ∀x,y,z∈M(xRy∧xRz⇒yRz){\displaystyle \forall x,y,z\in M(xRy\wedge xRz\Rightarrow yRz)},
- полнота (или связность[2]): ∀x,y∈M(xRy∨yRx){\displaystyle \forall x,y\in M(xRy\lor yRx)},
- связность (или слабая связность[2]): ∀x,y∈M(x≠y⇒xRy∨yRx){\displaystyle \forall x,y\in M(x\neq y\Rightarrow xRy\lor yRx)},
- коннексность (англ. connex): ∀x,y∈M(xRy∨yRx∨x=y){\displaystyle \forall x,y\in M(xRy\lor yRx\lor x=y)},
- трихотомия: ∀x,y∈M{\displaystyle \forall x,y\in M} верно ровно одно из трех утверждений: xRy{\displaystyle xRy}, yRx{\displaystyle yRx} или x=y{\displaystyle x=y}.
Виды отношений
Виды бинарных отношений
- Обратное отношение[уточнить] (отношение, обратное к R{\displaystyle R}) — это двухместное отношение, состоящее из пар элементов (y,x){\displaystyle (y,x)}, полученных перестановкой пар элементов (x,y){\displaystyle (x,y)} данного отношения R{\displaystyle R}. Обозначается: R−1{\displaystyle R^{-1}}. Для данного отношения и обратного ему верно равенство: (R−1)−1=R{\displaystyle (R^{-1})^{-1}=R}.
- Взаимо-обратные отношения (взаимообратные отношения) — отношения, являющиеся обратными друг по отношению к другу. Область значений одного из них служит областью определения другого, а область определения первого — областью значений другого.
- Рефлексивное отношение — двухместное отношение R{\displaystyle R}, определённое на некотором множестве и отличающееся тем, что для любого x{\displaystyle x} этого множества элемент x{\displaystyle x} находится в отношении R{\displaystyle R} к самому себе, то есть для любого элемента x{\displaystyle x} этого множества имеет место xRx{\displaystyle xRx}. Примеры рефлексивных отношений: равенство, одновременность, сходство.
- Антирефлексивное отношение (иррефлексивное отношение; так же, как антисимметричность не совпадает с несимметричностью, иррефлексивность не совпадает с нерефлексивностью) — бинарное отношение R{\displaystyle R}, определённое на некотором множестве и отличающееся тем, что для любого элемента x{\displaystyle x} этого множества неверно, что оно находится в отношении R{\displaystyle R} к самому себе (неверно, что xRx{\displaystyle xRx}).
- Транзитивное отношение — двухместное отношение R{\displaystyle R}, определённое на некотором множестве и отличающееся тем, что для любых x,y,z{\displaystyle x,y,z} из xRy{\displaystyle xRy} и yRz{\displaystyle yRz} следует xRz{\displaystyle xRz} (xRy∧yRz→xRz{\displaystyle xRy\wedge yRz\to xRz}). Примеры транзитивных отношений: «больше», «меньше», «равно», «подобно», «выше», «севернее».
- Нетранзитивное отношение[уточнить] — двухместное отношение R{\displaystyle R}, определённое на некотором множестве и отличающееся тем, что для любых x,y,z{\displaystyle x,y,z} этого множества из xRy{\displaystyle xRy} и yRz{\displaystyle yRz} не следует xRz{\displaystyle xRz} (¬(xRy∧yRz→xRz){\displaystyle \neg (xRy\wedge yRz\to xRz)}). Пример нетранзитивного отношения: «x отец y»
- Симметричное отношение — бинарное отношение R{\displaystyle R}, определённое на некотором множестве и отличающееся тем, что для любых элементов x{\displaystyle x} и y{\displaystyle y} этого множества из того, что x{\displaystyle x} находится к y{\displaystyle y} в отношении R{\displaystyle R}, следует, что и y{\displaystyle y} находится в том же отношении к x{\displaystyle x} — xRy→yRx{\displaystyle xRy\to yRx}. Примером симметричных отношений могут быть равенство, отношение эквивалентности, подобие, одновременность.
- Антисимметричное отношение — бинарное отношение R{\displaystyle R}, определённое на некотором множестве и отличающееся тем, что для любых x{\displaystyle x} и y{\displaystyle y} из xRy{\displaystyle xRy} и yRx{\displaystyle yRx} следует x=y{\displaystyle x=y} (то есть R{\displaystyle R} и R−1{\displaystyle R^{-1}} выполняются одновременно лишь для равных между собой членов).
- Асимметричное отношение — бинарное отношение R{\displaystyle R}, определённое на некотором множестве и отличающееся тем, что для любых x{\displaystyle x} и y{\displaystyle y} из xRy{\displaystyle xRy} следует ¬yRx{\displaystyle \neg yRx}. Пример: отношения «больше» (>) и «меньше» (<).
- Отношение эквивалентности — бинарное отношение R{\displaystyle R} между объектами x{\displaystyle x} и y{\displaystyle y}, являющееся одновременно рефлексивным, симметричным и транзитивным. Примеры: равенство, равномощность двух множеств, подобие, одновременность.
- Отношение порядка — отношение, обладающие только некоторыми из трёх свойств отношения эквивалентности: отношение рефлексивное и транзитивное, но несимметричное (например, «не больше») образует нестрогий порядок, а отношение транзитивное, но нерефлексивное и несимметричное (например, «меньше») — строгий порядок.
- Функция одного переменного — бинарное отношение R{\displaystyle R}, определённое на некотором множестве, отличающееся тем, что каждому значению x{\displaystyle x} отношения xRy{\displaystyle xRy} соответствует лишь единственное значение y{\displaystyle y}. Свойство функциональности отношения R{\displaystyle R} записывается в виде аксиомы: (xRy∧xRz)→(y≡z){\displaystyle (xRy\wedge xRz)\to (y\equiv z)}.
- Биекция (взаимно-однозначное отношение) — бинарное отношение R{\displaystyle R}, определённое на некотором множестве, отличающееся тем, что в нём каждому значению x{\displaystyle x} соответствует единственное значение y{\displaystyle y}, и каждому значению y{\displaystyle y} соответствует единственное значение x{\displaystyle x}.
- Связанное отношение — бинарное отношение R{\displaystyle R}, определённое на некотором множестве, отличающееся тем, что для любых двух различных элементов x{\displaystyle x} и y{\displaystyle y} из этого множества, одно из них находится в отношении R{\displaystyle R} к другому (то есть выполнено одно из двух соотношений: xRy{\displaystyle xRy} или yRx{\displaystyle yRx}). Пример: отношение «меньше» (<).
Операции над отношениями
Так как отношения, заданные на фиксированной паре множеств A{\displaystyle A} и B{\displaystyle B} суть подмножества множества A×B{\displaystyle A\times B}, то совокупность всех этих отношений образует булеву алгебру относительно операций объединения, пересечения и дополнения отношений. В частности, для произвольных a∈A{\displaystyle a\in A}, b∈B{\displaystyle b\in B}:
- a(R∪S)b⇔aRb∨aSb{\displaystyle a\,(R\cup S)\,b\Leftrightarrow a\,R\,b\vee a\,S\,b},
- a(R∩S)b⇔aRb∧aSb{\displaystyle a\,(R\cap S)\,b\Leftrightarrow a\,R\,b\wedge a\,S\,b},
- aR¯b⇔¬aRb{\displaystyle a\,{\overline {R}}\,b\Leftrightarrow \neg a\,R\,b}.
Часто вместо объединения, пересечения и дополнения отношений говорят об их дизъюнкции, конъюнкции и отрицании.
Например, (=)∪(<)=(⩽){\displaystyle ({=})\cup ({<})=({\leqslant })}, (=)∩(<)=∅{\displaystyle ({=})\cap ({<})=\varnothing }, то есть объединение отношения строгого порядка с отношением равенства совпадает с отношением нестрогого порядка, а их пересечение пусто.
Кроме перечисленных важное значение имеют ещё операции обращения и умножения отношений, определяемые следующим образом. Если R⊆A×B{\displaystyle R\subseteq A\times B}, то обратным отношением называется отношение R−1{\displaystyle R^{-1}}, определённое на паре B{\displaystyle B}, A{\displaystyle A} и состоящее из тех пар (b,a){\displaystyle (b,a)}, для которых aRb{\displaystyle a\,R\,b}. Например, (<)−1=(⩾){\displaystyle ({<})^{-1}=(\geqslant )}.
Пусть R⊆A×B{\displaystyle R\subseteq A\times B}, S⊆B×C{\displaystyle S\subseteq B\times C}. Композицией (или произведением) отношений R{\displaystyle R} и S{\displaystyle S} называется отношение R∘S⊆A×C{\displaystyle R\circ S\subseteq A\times C} такое, что:
- a(R∘S)c⇔∃b∈B:a(R)b∧b(S)c{\displaystyle a\,(R\circ S)\,c\Leftrightarrow \exists b\in B:\,a\,(R)\,b\wedge b\,(S)\,c}.
Например, для отношения строгого порядка на множестве натуральных числе его умножение на себя определено следующим образом: a(<)(<)b⇔a+1<b{\displaystyle a({<})({<})b\Leftrightarrow a+1<b}.
Бинарные отношения R{\displaystyle R} и S{\displaystyle S} называются перестановочными, если RS=SR{\displaystyle RS=SR}. Для любого бинарного отношения R{\displaystyle R}, определённого на A{\displaystyle A}, имеет место RIdA=IdAR{\displaystyle R{\mathsf {Id}}_{A}={\mathsf {Id}}_{A}R}, где символом IdA{\displaystyle {\mathsf {Id}}_{A}} обозначено равенство, определённое на A{\displaystyle A}. Однако равенство RR−1=Id{\displaystyle RR^{-1}={\mathsf {Id}}} не всегда справедливо.
Имеют место следующие тождества:
Аналоги последних двух тождеств для пересечения отношений не имеют места.
Примечания
- ↑ Кострикин А. И. Введение в алгебру. Основы алгебры.. — М.: Физматлит, 1994. — С. 47-48. — 320 с. — ISBN 5-02-014644-7.
- ↑ 1 2 Дубов Ю. А., Травкин СИ., Якимец В. Н. Многокритериальные модели формирования и выбора вариантов систем. — М.: Наука, 1986. (с. 48)
Литература
- Алескеров Ф.Т., Хабина Э.Л., Шварц Д.А. Бинарные отношения, графы и коллективные решения. — М.: Учебники Высшей школы экономики, 2006. — 300 с.
- Учебник: Математика без формул (Ю.В. Пухначев, Ю.П. Попов, 1995)
Ссылки
wiki.sc
БИНАРНОЕ ОТНОШЕНИЕ — это… Что такое БИНАРНОЕ ОТНОШЕНИЕ?
- БИНАРНОЕ ОТНОШЕНИЕ
двуместный предикат на заданном множестве. Под Б. о. иногда понимают подмножество множества упорядоченных пар (а, 6) элементов заданного множества А. Б. о.- частный случай отношения. Пусть . Если , то говорят, что элемент «находится в бинарном отношении R к элементу b. Вместо пишут также .
Пустое подмножество в и само множество наз., соответственно, нуль-отношением и универсальным отношением в множестве А. Диагональ множества , т. е. множество есть отношение равенст-в а, или единичное бинарное отношение в А.
Пусть — Б. о. в множестве А. Наряду с теоретико-множественными операциями объединения пересечения и дополнения для Б. о. рассматривают также операцию обращения:
и операцию умножения:
Б. о. наз. обратным для R. Умножение Б. о. ассоциативно, но, вообще говоря, не коммутативно.
Б. о. R в A называется: а) рефлексивным, если ; б) транзитивным, если ; в) симметричным, если ; г) антисимметричным, если . Если Б. о. R обладает нек-рым из свойств а), б), в), г), то обратное отношение обладает этим же свойством. Б. р. наз. функциональным, если
Наиболее важными типами Б. о. являются эквивалентности, порядки (линейные и частичные) и функциональные отношения. д. м. Смирнов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
- БИНАРНО ЛИЕВА АЛГЕБРА
- БИНОМ
Смотреть что такое «БИНАРНОЕ ОТНОШЕНИЕ» в других словарях:
Бинарное отношение — [binary relation]. Иначе: двуместное или двойственное. «Бинарным отношением на множестве X» называется подмножество упорядоченных пар элементов из X. Примерами Б.о. являются равенство (=), неравенства (< или >), отношение включения A Ì B.… … Экономико-математический словарь
бинарное отношение — Иначе: двуместное или двойственное. «Бинарным отношением на множестве X» называется подмножество упорядоченных пар элементов из X. Примерами Б.о. являются равенство (=), неравенства (), отношение включения A ? B. В широком смысле слова… … Справочник технического переводчика
Бинарное отношение — У этого термина существуют и другие значения, см. Отношение. В математике бинарным отношением называется подмножество декартова произведения двух множеств. В частности, бинарным отношением на множестве называется… … Википедия
ОТНОШЕНИЕ — в логике то, что в отличие от свойства характеризует не отдельный предмет, а пару, тройку и т.д. предметов. Традиционная логика не рассматривала О.; в современной логике О. пропозициональная функция от двух или большего числа переменных. Бинарным … Философская энциклопедия
отношение — ОТНОШЕНИЕ множество упорядоченных п ок индивидов (где п > 1), т.е. двоек, троек и т.д. Число п называется «местностью», или «арностью», О. и, соответственно, говорят о n местном (п арном) О. Так, например, двуместное О. называют… … Энциклопедия эпистемологии и философии науки
Отношение предпочтения — в теории потребления это формальное описание способности потребителя сравнивать (упорядочивать по желательности) разные наборы товаров (потребительские наборы). Чтобы описать отношение предпочтения, не обязательно измерять желательность… … Википедия
Отношение (математика) — У этого термина существуют и другие значения, см. Отношение. Отношение математическая структура, которая формально определяет свойства различных объектов и их взаимосвязи. Отношения обычно классифицируются по количеству связываемых объектов … Википедия
Отношение (логика) — У этого термина существуют и другие значения, см. Отношение. Отношение в логике первого порядка двух и более аргументный предикат (многоместный предикат), двух и более предикатное свойство. Знак отношения: R.[уточнить] В терминах отношений… … Википедия
Отношение эквивалентности — У этого термина существуют и другие значения, см. Эквивалентность. Отношение эквивалентности ( ) на множестве это бинарное отношение, для которого выполнены следующие условия: Рефлексивность: для любого в , Симметричность: если … Википедия
Отношение порядка — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей. Бинарное отношение на мно … Википедия
dic.academic.ru
Бинарное отношение — это… Что такое Бинарное отношение?
- Бинарное отношение
Бинарное отношение [binary relation]. Иначе: двуместное или двойственное. «Бинарным отношением на множестве X» называется подмножество упорядоченных пар элементов из X. Примерами Б.о. являются равенство (=), неравенства (< или >), отношение включения A Ì B. В широком смысле слова понятие функции, ставящей в соответствие каждому числу x (аргументу) определенное значение функции f(x), также является Б.о.
Б.о. могут отображаться матрицами и графами. Например, отношение равенства можно описать единичной матрицей. Изучаются кроме Б.о. также тернарные (тройственные) и n-арные отношения.
Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело. Л. И. Лопатников. 2003.
- Бинарная переменная
- Бинарный опцион
Смотреть что такое «Бинарное отношение» в других словарях:
бинарное отношение — Иначе: двуместное или двойственное. «Бинарным отношением на множестве X» называется подмножество упорядоченных пар элементов из X. Примерами Б.о. являются равенство (=), неравенства (), отношение включения A ? B. В широком смысле слова… … Справочник технического переводчика
БИНАРНОЕ ОТНОШЕНИЕ — двуместный предикат на заданном множестве. Под Б. о. иногда понимают подмножество множества упорядоченных пар (а, 6) элементов заданного множества А. Б. о. частный случай отношения. Пусть . Если , то говорят, что элемент находится в бинарном… … Математическая энциклопедия
Бинарное отношение — У этого термина существуют и другие значения, см. Отношение. В математике бинарным отношением называется подмножество декартова произведения двух множеств. В частности, бинарным отношением на множестве называется… … Википедия
ОТНОШЕНИЕ — в логике то, что в отличие от свойства характеризует не отдельный предмет, а пару, тройку и т.д. предметов. Традиционная логика не рассматривала О.; в современной логике О. пропозициональная функция от двух или большего числа переменных. Бинарным … Философская энциклопедия
отношение — ОТНОШЕНИЕ множество упорядоченных п ок индивидов (где п > 1), т.е. двоек, троек и т.д. Число п называется «местностью», или «арностью», О. и, соответственно, говорят о n местном (п арном) О. Так, например, двуместное О. называют… … Энциклопедия эпистемологии и философии науки
Отношение предпочтения — в теории потребления это формальное описание способности потребителя сравнивать (упорядочивать по желательности) разные наборы товаров (потребительские наборы). Чтобы описать отношение предпочтения, не обязательно измерять желательность… … Википедия
Отношение (математика) — У этого термина существуют и другие значения, см. Отношение. Отношение математическая структура, которая формально определяет свойства различных объектов и их взаимосвязи. Отношения обычно классифицируются по количеству связываемых объектов … Википедия
Отношение (логика) — У этого термина существуют и другие значения, см. Отношение. Отношение в логике первого порядка двух и более аргументный предикат (многоместный предикат), двух и более предикатное свойство. Знак отношения: R.[уточнить] В терминах отношений… … Википедия
Отношение эквивалентности — У этого термина существуют и другие значения, см. Эквивалентность. Отношение эквивалентности ( ) на множестве это бинарное отношение, для которого выполнены следующие условия: Рефлексивность: для любого в , Симметричность: если … Википедия
Отношение порядка — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей. Бинарное отношение на мно … Википедия
economic_mathematics.academic.ru
Бинарные отношения. Примеры бинарных отношений
Бинарные отношения.
Пусть A и B – произвольные множества. Возьмем по одному элементу из каждого множества, a из A, b из B и запишем их так: <a, b> (сначала элемент первого множества, затем элемент второго множества – т.е. нам важен порядок, в котором берутся элементы). Такой объект будем называть
Декартовым произведением произвольных множеств A и B (обозначается: AB) называется множество, состоящее из всех возможных упорядоченных пар, первый элемент которых принадлежит A, а второй принадлежит B. По определению: AB = {<a, b> | aA и bB}. Очевидно, что если A≠B, то AB ≠ BA. Декартово произведение множества A само на себя n раз называется декартовой степенью A (обозначается: An).
Пример 5. Пусть A = {x, y} и B = {1, 2, 3}.
AB = {<x, 1>, <x, 2>, <x, 3>, <y, 1>, <y, 2>, <y, 3>}.
BA = {<1, x>, <2, x>, <3, x>, <1, y>, <2, y>, <3, y>}.
AA = A2 = {<x, x>, <x, y>, <y, x>, <y, y>}.
BB = B2 = {<1, 1>, <1, 2>, <1, 3>, <2, 1>, <2, 2>, <2, 3>, <3, 1>, <3, 2>, <3, 3>}.
Бинарным отношением на множестве M называется множество некоторых упорядоченных пар элементов множества M. Если r – бинарное отношение и пара <x, y> принадлежит этому отношению, то пишут: <x, y> r или x r y. Очевидно, r Í M2.
Пример 6. Множество {<1, 2>, <2, 2>, <3, 4>, <5, 2>, <2, 4>} является бинарным отношением на множестве {1, 2, 3, 4, 5}.
Пример 7. Отношение ³ на множестве целых чисел является бинарным отношением. Это бесконечное множество упорядоченных пар вида <x, y>, где x ³ y, x и y – целые числа. Этому отношению принадлежат, например, пары <5, 3>, <2, 2>, <324, -23> и не принадлежат пары <5, 7>, <-3, 2>.
Пример 8. Отношение равенства на множестве A является бинарным отношением: IA = {<x, x> | x Î A}. IA называется диагональю множества A.
Поскольку бинарные отношения являются множествами, то к ним применимы операции объединения, пересечения, дополнения и разности.
Областью определения бинарного отношения r называется множество D(r) = { x | существует такое y, что xry }. Областью значений бинарного отношения r называется множество R(r) = { y | существует такое x, что xry }.
Отношением, обратным к бинарному отношению r Í M2, называется бинарное отношение r-1 = {<y, x> | <x, y> Î r}. Очевидно, что D(r‑1) = R(r), R(r‑1) = D(r), r‑1 Í M2.
Композицией бинарных отношений r1 и r2, заданных на множестве M, называется бинарное отношение r2 o r1 = { <x, z> | существует y такое, что <x, y> Î r1 и <y, z> Í r2 }. Очевидно, что r2 o r1 Í M2.
Пример 9. Пусть бинарное отношение r задано на множестве M = {a, b, c, d}, r = {<a, b>, <a, c>, <c, c>, <c, d>}. Тогда D(r) = {a, c}, R(r) = {b, c, d}, r‑1 = {<b, a>, <c, a>, <c, c>, <d, c>}, r o r = {<a, c>, <a, d>, <c, c>, <c, d>}, r‑1 o r = {<a, a>, <a, c>, <c, a>, <c, c>}, r o r‑1 = {<b, b>, <b, c>, <c, b>, <c, c>, <c, d>, <d, c>, <d, d>}.
Пусть r – бинарное отношение на множестве M. Отношение r называется рефлексивным, если x r x для любого x Î M. Отношение r называется симметричным, если вместе с каждой парой <x, y> оно содержит и пару <y, x>. Отношение r называется транзитивным, если из того, что x r y и y r z следует, что x r z. Отношение r называется антисимметричным, если оно не содержит одновременно пары <x, y> и <y, x> различных элементов x ¹ y множества M.
Укажем критерии выполнения этих свойств.
Бинарное отношение r на множестве M рефлексивно тогда и только тогда, когда IM Í r.
Бинарное отношение r симметрично тогда и только тогда, когда r = r‑1.
Бинарное отношение r на множестве M антисимметрично тогда и только тогда, когда r Ç r‑1 = IM.
Бинарное отношение r транзитивно тогда и только тогда, когда r o r Í r.
Пример 10. Отношение из примера 6 является антисимметричным, но не является симметричным, рефлексивным и транзитивным. Отношение из примера 7 является рефлексивным, антисимметричным и транзитивным, но не является симметричным. Отношение IA обладает всеми четырьмя рассматриваемыми свойствами. Отношения r‑1 o r и r o r‑1 являются симметричными, транзитивными, но не являются антисимметричными и рефлексивными.
Отношением эквивалентности на множестве M называется транзитивное, симметричное и рефлексивное на М бинарное отношение.
Отношением частичного порядка на множестве М называется транзитивное, антисимметричное и рефлексивное на М бинарное отношение r.
Пример 11. Отношение из примера 7 является отношением частичного порядка. Отношение IA является отношением эквивалентности и частичного порядка. Отношение параллельности на множестве прямых является отношением эквивалентности.
vunivere.ru
Что такое бинарное отношение? — КиберПедия
Что такое бинарное отношение?
Пусть A , B – непустые множества, A xB– их декартово произведение. Любое
подмножество alphа включается в Ax B называется бинарным отношением на множествах A , B.
Какое бинарное отношение называется однородным?
Пусть A , B – непустые множества, A xB– их декартово произведение. Любое
подмножество alphа включается в Ax B называется бинарным отношением на множествах A , B.
Если A =B , то бинарное отношение называется однородным.
Какое бинарное отношение называется рефлексивным?
Рефлексивность. Отношение alphа включается в Ax A называется рефлексивным, если
(a ,a )принадлежит alphа,для любого a принадлежащего A
Какое бинарное отношение называется симметричным?
Симметричность. Отношение alphа включается в Ax A называется симметричным, если
(a ,b ) принадлежат alphа тогда и только тогда,когда (b,a) принадлежит alphа
Какое бинарное отношение называется транзитивным?
Транзитивность. Отношение alphа включается в Ax A называется транзитивным, если
(a ,b )принадлежит alphа , (b,c ) принадлежит alphа следовательно (a ,c ) принадлежит alphа
Какое бинарное отношение называется антисимметричным?
Отношение alphа включается в Ax A называется антисимметричным,если
(a ,b )принадлежит alphа , (b,a)принадлежит alphа,следовательно a=b
Какое бинарное отношение называется отношением эквивалентности?
Если бинарное отношение является одновременно рефлексивным, симметричным
и транзитивным, то оно называется отношением эквивалентности. Отношение экви-
валентности на множестве A задаёт разбиение A на непересекающиеся классы экви-
валентных элементов: A =A1∪А2∪……∪Aк, A∩ A=∅ при i ≠j . Внутри каждого
класса Ai все элементы попарно эквивалентны, а элементы из разных классов не экви-
валентны.
Какое бинарное отношение называется отношением частичного порядка?
Однородное бинарное отношение alphа включается в Ax A называется отношением частичного порядка на множестве A (или просто частичным порядком на A ), если оно рефлексивно, транзитивно и антисимметрично
Какое бинарное отношение называется отношением линейного порядка?
Если, для любых a ,b принадлежащих A (a ,b )принадлежит alphа или (b,a)принадлежит alphа , то alphа называется полным порядком. Множество, на котором определено отношение полного порядка называется вполне упорядоченным. Примером может служить множество действительных чисел R : отношение >= («больше») является полным порядком на R .
Какое бинарное отношение на множествах А, В называется отображением А в В
Важным классом бинарных отношений (не обязательно однородных) являются
отображения. Бинарное отношение f включенное в Ax B называется отображением множества A во множество B , если:
1) для любого a принадлежащего A существует b принадлежащее B : (a,b)
принадлежит f
2) (a ,b)принадлежит f , (a ,b1)принадлежит f следовательно b1= b2 .
Для отображений вместо (a,b )принадлежащее f обычно пишут f( a)= b . Среди отображений выделяют инъективные, сюръективные, биективные
11.Какие способы задания однородного бинарного отношения вы знаете?
а).Перечисление всех его элементов: Пусть А={a,b,c}.Однородное отношение a={(a,a),(b,b),(c,c)} можно назвать отношение совпадения.Действительно,(x,y)принадлежат а тогда и только тогда,когда элементы x,y совпадают.
б)Предикатный: Пусть beta={(x,y)принадлежат RxR|x<=y}.Однородное бинарное отношение beta называется отношением ”меньше или равно”.Вместо записи (5,6)принадлежит betaобычно употребляется другая запись 5<=6.
//Думаю матрицу и графики можно не расписывать//
в).Матричный
г).Графический
Что такое ориентированный граф?
Графом называется совокупность,состоящая из произвольного множества точек и множества линий соединяющих некоторые из этих точек.Точки называются вершинами графа,линии называются ребрами.Могут встречаться ребра с концами в одной и той же вершине-они называются петлями.Если на каждом ребре указана ориентация,то такие ребра называются дугами,а граф-ориентированным графом(орграфом).
Что такое неориентированный граф?
см. опред выше)
Что такое отношение достижимости?
Это отношение эквивалентности на множестве вершин неориентированного графа.
Что такое отношение взаимной достижимости?
Вершины x и y называются взаимно достижимыми,если существует путь из x в y, а также путь из y в x.
Что такое бинарное отношение?
Пусть A , B – непустые множества, A xB– их декартово произведение. Любое
подмножество alphа включается в Ax B называется бинарным отношением на множествах A , B.
cyberpedia.su
бинарное отношение — это… Что такое бинарное отношение?
- бинарное отношение
binary relation
Англо-русский словарь технических терминов. 2005.
- бинарное кодирование
- бинарное соединение
Смотреть что такое «бинарное отношение» в других словарях:
Бинарное отношение — [binary relation]. Иначе: двуместное или двойственное. «Бинарным отношением на множестве X» называется подмножество упорядоченных пар элементов из X. Примерами Б.о. являются равенство (=), неравенства (< или >), отношение включения A Ì B.… … Экономико-математический словарь
бинарное отношение — Иначе: двуместное или двойственное. «Бинарным отношением на множестве X» называется подмножество упорядоченных пар элементов из X. Примерами Б.о. являются равенство (=), неравенства (), отношение включения A ? B. В широком смысле слова… … Справочник технического переводчика
БИНАРНОЕ ОТНОШЕНИЕ — двуместный предикат на заданном множестве. Под Б. о. иногда понимают подмножество множества упорядоченных пар (а, 6) элементов заданного множества А. Б. о. частный случай отношения. Пусть . Если , то говорят, что элемент находится в бинарном… … Математическая энциклопедия
Бинарное отношение — У этого термина существуют и другие значения, см. Отношение. В математике бинарным отношением называется подмножество декартова произведения двух множеств. В частности, бинарным отношением на множестве называется… … Википедия
ОТНОШЕНИЕ — в логике то, что в отличие от свойства характеризует не отдельный предмет, а пару, тройку и т.д. предметов. Традиционная логика не рассматривала О.; в современной логике О. пропозициональная функция от двух или большего числа переменных. Бинарным … Философская энциклопедия
отношение — ОТНОШЕНИЕ множество упорядоченных п ок индивидов (где п > 1), т.е. двоек, троек и т.д. Число п называется «местностью», или «арностью», О. и, соответственно, говорят о n местном (п арном) О. Так, например, двуместное О. называют… … Энциклопедия эпистемологии и философии науки
Отношение предпочтения — в теории потребления это формальное описание способности потребителя сравнивать (упорядочивать по желательности) разные наборы товаров (потребительские наборы). Чтобы описать отношение предпочтения, не обязательно измерять желательность… … Википедия
Отношение (математика) — У этого термина существуют и другие значения, см. Отношение. Отношение математическая структура, которая формально определяет свойства различных объектов и их взаимосвязи. Отношения обычно классифицируются по количеству связываемых объектов … Википедия
Отношение (логика) — У этого термина существуют и другие значения, см. Отношение. Отношение в логике первого порядка двух и более аргументный предикат (многоместный предикат), двух и более предикатное свойство. Знак отношения: R.[уточнить] В терминах отношений… … Википедия
Отношение эквивалентности — У этого термина существуют и другие значения, см. Эквивалентность. Отношение эквивалентности ( ) на множестве это бинарное отношение, для которого выполнены следующие условия: Рефлексивность: для любого в , Симметричность: если … Википедия
Отношение порядка — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей. Бинарное отношение на мно … Википедия
dic.academic.ru
