Целые и рациональные числа
Вы уже знаете, что числа, которые мы используем в счёте, называют натуральными. Кстати, натуральные числа – это один из первых математических объектов, который стал изучать человек, так как повседневная жизнь требовала использования натуральных чисел на практике, и в частности, в счёте.
Поэтому и изучение математики в школе мы начинали именно со знакомства с натуральными числами.
Итак, давайте перечислим натуральные числа: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 и так далее. Все натуральные числа образуют множество натуральных чисел, которое обозначают заглавной латинской буквой .
С понятием натуральных чисел мы с вами разобрались, а теперь давайте перейдём к действиям с ними. И ответим на вопрос: какие числа получают при сложении и умножении натуральных чисел?
Конечно же, вам не составит труда ответить на этот вопрос. И вы сразу скажете, что при сложении натуральных чисел всегда получают натуральные числа.
И при умножении натуральных чисел тоже всегда получают натуральные числа.
Тогда возникает новый вопрос: а какие числа мы получим при вычитании и делении натуральных чисел?
Так вот, при нахождении разности и частного натуральных чисел не всегда получаются натуральные числа.
В связи с этим математикам пришлось расширять знания, связанные с числами.
Если мы добавим к натуральным числам нуль и отрицательные числа (то есть числа, которые противоположны натуральным), то множество натуральных чисел расширится до множества целых чисел.
Множество целых чисел принято обозначать заглавной латинской буквой . Оно состоит из следующих элементов: .
Мы с вами разобрались с понятием целых чисел, а теперь давайте перейдём к действиям с ними. Понятно, что при сложении, вычитании и умножении целых чисел всегда получают целые числа.
Чего нельзя сказать о делении целых чисел. При нахождении частного двух целых чисел в результате не всегда получают целые числа.
(
Следовательно, понятия, связанные с числами, пришлось расширять дальше. Так, множество целых чисел расширили, введя множество рациональных чисел.
Итак, числа вида , где m – целое число, n – натуральное число, составляют множество рациональных чисел. Это множество принято обозначать заглавной латинской буквой . Кстати, любое целое число можно представить в виде рационального, например, число m можно представить в виде .
Множество рациональных чисел позволило находить частное любых двух целых чисел при условии, что делитель не равен нулю.
Кроме того, при выполнении всех четырёх арифметических действий (кроме деления на нуль) над рациональными числами всегда получают рациональные числа.
Рациональное число можно представить в виде дроби , где m – целое число, k – натуральное число. Если рациональное число можно представить в виде дроби , где m – целое число, k – натуральное число, то его можно записать в виде конечной десятичной дроби.
Заметим, что одно и то же рациональное число можно представить различными дробями, которые получаются из несократимой дроби умножением её числителя и знаменателя на одно и то же целое число, отличное от нуля.
Существуют и рациональные числа, которые нельзя записать в виде конечной десятичной дроби.
Если, например, мы попытаемся записать число в виде десятичной дроби, используя алгоритм деления уголком, то получим бесконечную десятичную дробь ….
Напомним, что такую бесконечную десятичную дробь называют периодической, а повторяющуюся цифру 3 – её периодом. Нашу периодическую дробь … коротко записывают так: . А читают нашу периодическую дробь так: «нуль целых и три в периоде».
Тогда можем сделать такой вывод: любая периодическая дробь – это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или группа цифр – период дроби.
Например, десятичная дробь …. Она равна . Это периодическая дробь с периодом 23. Читают эту дробь так: «пятнадцать целых семнадцать сотых и двадцать три в периоде».
Заметим, что каждое целое число или конечную десятичную дробь можно считать и бесконечной десятичной периодической дробью с периодом, равным нулю.
Вообще, любую конечную десятичную дробь можно записать в виде бесконечной дроби двумя способами: с периодом 0 и с периодом 9.
Давайте договоримся в дальнейшем не использовать бесконечные десятичные дроби с периодом 9. Вместо таких дробей будем записывать конечные десятичные дроби или бесконечные десятичные дроби с периодом 0.
Таким образом, можем сделать следующий вывод: каждое рациональное число можно представить в виде бесконечной периодической десятичной дроби. Справедливо и обратное утверждение: каждая бесконечная периодическая десятичная дробь является рациональным числом, так как может быть представлена в виде дроби , где m – целое число, n – натуральное число.
Вообще, при делении целого числа m на натуральное число n на некотором шаге остаток может стать равным нулю, тогда в результате деления получается целое число или конечная десятичная дробь. Либо же при делении целого числа m на натуральное число n на некотором шаге остатки начинают повторяться, так как каждый из остатков меньше n, тогда в результате деления получается бесконечная десятичная периодическая дробь.
А теперь давайте приступим к практической части нашего урока.
Итак, задание первое. Запишите в виде бесконечной десятичной дроби: а) ; б) .
Решение.
Задание второе. Запишите в виде обыкновенной дроби: а) ; б) .
Решение.
И последнее задание. Покажите, что … .
Решение.
videouroki.net
рациональные числа — ПриМат
Натуральные, целые и рациональные числа
В процессе счёта возникли натуральные числа.
.
Сложение и умножение натуральных чисел снова даёт натуральное число. Операция «вычитание» во множестве натуральных чисел приводит к целым числам.
.
Операция «деление» во множестве целых чисел приводит к рациональным числам.
.
Например:
Во множестве рациональных чисел выполняются все 4 арифметических действия. В данном множестве можно решать уравнения 1-ой степени , однако, простейшее уравнение , не всегда разрешимо в , в частности, уравнение не имеет решений в .
Необходимость иррациональных чисел
Докажем, что уравнение не имеет решений в .
Теорема
Не существует рационального числа, квадрат которого равен 2.
Предположим противное. Предположим, что существует такое рациональное число, квадрат которого равен 2. Числа и — числитель и знаменатель данного рационального числа; и — взаимно простые (числа, наибольший общий делитель которых равен 1).
— чётное число, тогда — чётное.
Отсюда:
— чётное — чётное.
Получили противоречие того утверждения, что и — взаимно простые.
Таким образом, проблема решения уже таких уравнений приводит к необходимости расширения множества рациональных чисел путём добавления к ним иррациональных чисел.
Бесконечные дроби: периодические десятичные дроби
Зная рациональное число, его можно представить либо в виде конечной десятичной дроби, либо в виде бесконечной периодической десятичной дроби.
— конечная десятичная дробь;
.
— бесконечная периодическая десятичная дробь.
.
Используем формулу суммы бесконечно убывающей геометрической прогрессии: , где — первый член геометрической прогрессии, — знаменатель прогрессии.
Получим:
.
Договоримся, конечную десятичную дробь будем отождествлять с бесконечной десятичной дробью с в периоде.
.
Между множеством множеством всех рациональных чисел и множеством всех периодических бесконечных десятичных дробей установлена связь, если отождествлять бесконечную периодическую дробь с с бесконечной периодической периодической дробью с .
Тест «Существование иррациональных чисел».
Лимит времени: 0
Информация
Тестовые задания по вышеизложенной теме.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 5
Ваше время:
Время вышло
| Средний результат |
|
| Ваш результат |
|
- С ответом
- С отметкой о просмотре
Источники:
- З. М. Лысенко. Лекции по математическому анализу.
- В. И. Коляда, А.А.Кореновский «Курс лекций по мат.анализу, часть 1» (Одесса, «Астропринт», 2009г.), стр.1.
- В. И. Ильин, Э.Г.Позняк «Основы мат.анализа, часть 1, выпуск 2» (Издание четвёртое, переработанное и дополненное, 1982г.) стр.40. (скачать учебник можно здесь).
Подробнее про «существование иррациональных чисел» на:
Wikipedia
Викизнание
Поделиться ссылкой:
ib.mazurok.com
Рациональные числа: определения, примеры
Данная статья посвящена изучению темы «Рациональные числа». Ниже приведены определения рациональных чисел, даны примеры, рассказано о том, как определить, является ли число рациональным, или нет.
Yandex.RTB R-A-339285-1Рациональные числа. Определения
Прежде чем дать дефиницию рациональных чисел вспомним, какие еще есть множества чисел, и как они связаны между собой.
Натуральные числа, в совокупности с противоположными им и числом ноль образуют множество целых чисел. В свою очередь, совокупность целых дробных чисел образует множество рациональных чисел.
Определение 1. Рациональные числаРациональные числа — числа, которые можно представить в виде положительной обыкновенной дроби ab, отрицательной обыкновенной дроби -ab или числа ноль.
Таким образом, можно оставить ряд свойств рациональных чисел:
- Любое натуральное число является рациональным числом. Очевидно, каждое натуральное число n можно представить в виде дроби 1n.
- Любое целое число, включая число 0, является рациональным числом. Действительно, любое целое положительное и целое отрицательное число легко представляется в виде соответственно положительной или отрицательной обыкновенной дроби. Например, 15=151, -352=-3521.
- Любая положительная или отрицательная обыкновенная дробь ab является рациональным числом. Это следует напрямую из данного выше определения.
- Любое смешанное число является рациональным. Действительно, ведь смешанное число можно представить в виде обыкновенной неправильной дроби.
- Любую конечную или периодическую десятичную дробь можно представить в виде обыкновенной дроби. Поэтому, каждая периодическая или конечная десятичная дробь является рациональным числом.
- Бесконечные и непериодическое десятичные дроби не являются рациональными числами. Их невозможно представить в форме обыкновенных дробей.
Приведем примеры рациональных чисел. Числа 5, 105, 358, 1100055 являются натуральными, положительными и целыми. Сдедовательно, это рациональные числа. Числа -2, -358, -936 представляют собой целые отрицательные числа, и они также рациональны в соответствии с определением. Обыкновенные дроби 35, 87, -358 также являются примерами рациональных чисел.
Приведенное выше определение рациональных чисел можно сформулировать более кратко. Еще раз ответим на вопрос, что такое рациональное число.
Определение 2. Рациональные числаРациональные числа — это такие числа, которые можно представить в виде дроби ±zn, где z — целое число, n — натуральное число.
Можно показать, что да
zaochnik.com
Целые и рациональные числа
Целые и рациональные числа.
Тип занятия:
Урок овладения новым материалом.
Вид занятия:
Аудиторное теоретическое занятие
Цели занятия:
Образовательные:
— рассмотреть множество натуральных чисел;
— рассмотреть множество целых чисел;
— рассмотреть множество рациональных чисел;
— ввести понятие конечной и бесконечной десятичной дроби;
— дать определение бесконечной периодической десятичной дроби.
— сформировать умение переводить обыкновенную дробь в десятичную;
— сформировать умение переводить бесконечную периодическую дробь в обыкновенную;
— сформировать желание самостоятельно изучать материал;
Воспитательные:
— воспитывать положительное отношение к приобретению новых знаний;
— воспитывать ответственность за свои действия и поступки;
— вызвать заинтересованность новым для студентов подходом изучения математики.
Развивающие:
— формировать навыки познавательного мышления;
— формировать умения и навыки учебного труда.
Методы обучения:
Лекция объяснительно — иллюстрированная
Планируемый результат:
знаеть:
Определение бесконечной периодической десятичной дроби. Знает множество натуральных чисел. Знает множество целых чисел. Знает множество рациональных чисел. Умеет представлять обыкновенную дробь в виде десятичной. Умеет представлять бесконечную периодическую дробь в виде обыкновенной дроби.
Структура занятия:
1. Устная работа
2. Объяснение темы «Целые и рациональные числа»
Множество натуральных чисел
Множество целых чисел
Множество рациональных чисел
Конечные десятичные дроби
Бесконечные десятичные дроби
Бесконечная периодическая десятичная дробь
3. Решение ключевых задач.
Представить обыкновенную дробь в виде десятичной.
Представить бесконечную периодическую дробь в виде обыкновенной дроби.
4. Решение упражнений (нечетные пункты) на закрепление темы (№1,2,4,5)
5. Самостоятельная работа. 6. Домашнее задание
1
Устная работа:
Вычислите:
Вычислите:
Вычислите:
Вычислите:
2
Объяснение
новой темы:
Множество натуральных чисел:
Числа, которые мы используем при счете предметов, называются натуральными. При сложении и умножении натуральных чисел всегда получаются натуральные числа. Однако разность и частное натуральных чисел не всегда являются натуральными числами.
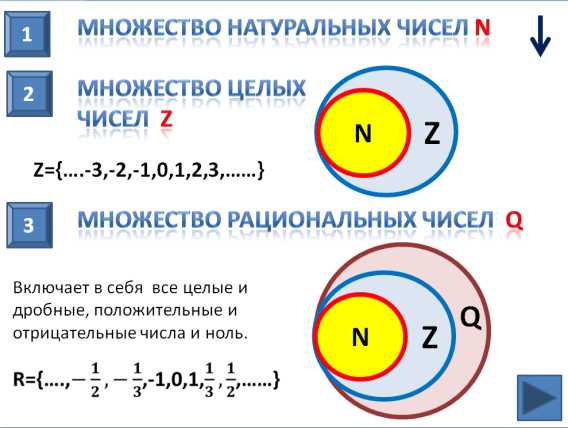
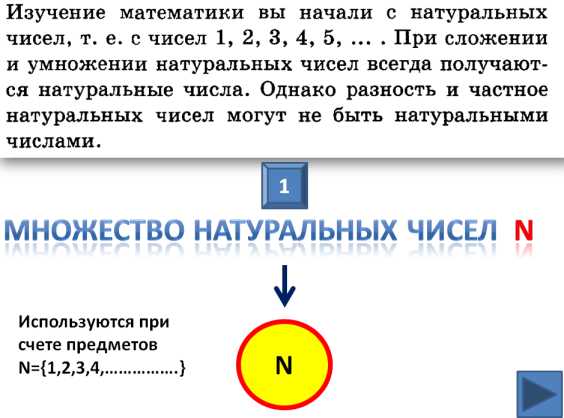

Множество целых чисел
Дополним множество натуральных чисел, нулем и отрицательными числами(т.е. числами противоположными натуральным). Мы получим множество целых чисел. Надо заметить, что при сложении, вычитании, умножении целых чисел, всегда образуются целые числа. Однако частное двух целых чисел, не обязятельно будет целым числом.

Множество рациональных чисел
Введение рациональных чисел, то есть чисел вида , где – целое число, – натуральное число, дает возможность находить частное двух рациональных чисел при условии, что делитель не равен нулю.
Каждое целое число также является рациональным, так как его можно представить в виде
При выполнении четырех арифметических действий (кроме деления на нуль) над рациональными числами всегда получаются рациональные числа.

Конечные десятичные дроби
Если рациональное число можно представить в виде дроби – целое число, – натуральное число, то его можно записать в виде конечной десятичной дроби.
Например, можно записать
Например,
Бесконечные десятичные дроби
Существуют рациональные числа, которые нельзя записать в виде конечной десятичной дроби, например
Если, например, попытаться записать число в виде десятичной дроби, разделив числитель на знаменатель, то получится бесконечная десятичная дробь
Бесконечную деятичную дробь называют периодической, а повторяющуюся цифру 3 — ее периодом.
Коротко записывают так: (ноль целых три десятых в периоде)
Бесконечная периодическая десятичная дробь.
Определение
Периодическая дробь – это бесконечная десятичная дробь, у которой начиная с некоторого десятичного знака повторяется одна и та же цифра или несколько цифр – период дроби.

3
Решение ключевых задач.
Задача 1. Записать число в виде бесконечной десятичной дроби.
Решение:
Задача 2. Представить бесконечную периодическую десятичную дробь в виде обыкновенной.
Решение:
1.Пусть Так как в записи этого числа до периода содержится только один десятичный знак, то, умножая на 10, получаем
(1)
2)Период этой дроби состоит из двух цифр. Поэтому, умножая обе части последнего равенства на находим
(2)
3)Вычитая из равенства (2) равенство (1), получаем
4
Решение тренировочных упражнений из учебника «Алгебра и начала анализа 10-11» на закрепление темы:
№1. Записать в виде десятичной дроби:
Решение:
№2. Выполнить действия и записать результат в виде десятичной дроби:
№4.Вычислить:
2) 3) 4) 5)
2) 3) 4)
№5.Вычислить:
5
Самостоятельная работа
1 вариант
2 вариант
Закончите предложения таким образом, чтобы высказывание стало истинным
Натуральное число делится на 3 если, …….сумма цифр этого числа делится на 3
Натуральное число делится на 4 если, ……. две его последние цифры нули или число, кратное 4.
Натуральное число делится на 5 если, …….если число оканчивается на цифру ноль или цифру 5
Натуральное число делится на 9 если, ……. сумма цифр этого числа делится на 9
Каждое натуральное число можно записать в виде бесконечной периодической дроби с периодом….. ноль
Каждое целое число можно записать в виде бесконечной периодической дроби с периодом….. ноль
Представьте бесконечную периодическую десятичную дробь в виде десятичной
Решение:
Так как в записи нашего числа до периода содержится только один десятичный знак, то, умножая на 10, получаем
Период нашей дроби состоит из одной цифры. Поэтому, умножая обе части последнего равенства на находим
….
Вычитая из равенства (2) равенство (1), получаем
Решение:
Так как в записи нашего числа до периода содержится только один десятичный знак, то, умножая на 10, получаем
Период нашей дроби состоит из одной цифры. Поэтому, умножая обе части последнего равенства на находим
Вычитая из равенства (2) равенство (1), получаем
Решение:
Так как в записи нашего числа до периода содержится только один десятичный знак, то, умножая на 10, получаем
Период нашей дроби состоит из двух цифр. Поэтому, умножая обе части последнего равенства на находим
….
Вычитая из равенства (2) равенство (1), получаем
Решение:
Так как в записи нашего числа до периода содержится только один десятичный знак, то, умножая на 10, получаем
Период нашей дроби состоит из двух цифр. Поэтому, умножая обе части последнего равенства на находим
….
Вычитая из равенства (2) равенство (1), получаем
Итак, , значит
6
Домашнее задание: Решение №1, №2, №4, №5 – четные пункты.
Литература
Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева и др. Алгебра и начала математического анализа 10-11 классы. — Москва: Просвещение, 2011г.
М.И. Шабунин, М.В. Ткачева и Н.Е. Федорова, Р.Г. Газарян. Алгебра и начала математического анализа. Дидактические материалы 10 класс. – Москва: Просвещение, 2011г
infourok.ru
Рациональные числа
Определение рациональных чисел
Определение 1
К рациональным числам относятся числа, которые можно представить как положительную или отрицательную обыкновенную дробь или число нуль.
К рациональным числам относятся:
- Натуральные числа, которые можно представить как обыкновенную дробь. Например, $7=\frac{7}{1}$.
- Целые числа, включая число нуль, которые можно представить как положительную или отрицательную обыкновенную дробь, или как нуль. Например, $19=\frac{19}{1}$, $-23=-\frac{23}{1}$.
- Обыкновенные дроби (положительные или отрицательные).
- Смешанные числа, которые можно представить как неправильную обыкновенную дробь. Например, $3 \frac{11}{13}=\frac{33}{13}$ и $-2 \frac{4}{5}=-\frac{14}{5}$.
- Конечная десятичная дробь и бесконечная периодическая дробь, которую можно представить как обыкновенную дробь. Например, $-7,73=-\frac{773}{100}$, $7,(3)=-7 \frac{1}{3}=-\frac{22}{3}$.
Замечание 1
Заметим, что бесконечная непериодическая десятичная дробь не относится к рациональным числам, т.к. ее нельзя представить как обыкновенную дробь.
Пример 1
Натуральные числа $7, 670, 21 \ 456$ являются рациональными.
Целые числа $76, –76, 0, –555 \ 666$ – рациональные.
Обыкновенные дроби $\frac{7}{11}$, $\frac{555}{4}$, $-\frac{7}{11}$, $-\frac{100}{234}$ – рациональные числа.
Таким образом, рациональные числа делятся на положительные и отрицательные. Число нуль является рациональным, но не относится ни к положительным, ни к отрицательным рациональным числам.
Сформулируем более краткое определение рациональных чисел.
Определение 2
Рациональными называются числа, которые могут быть записаны в виде дроби $\frac{m}{n}$ с целым числом в числителе и натуральным числом в знаменателе.
Определение 3
Рациональными называют числа, которые могут быть представлены в виде конечной или бесконечной периодической десятичной дроби.
Можно сделать следующие выводы:
- положительные и отрицательные целые и дробные числа относятся к множеству рациональных чисел;
- рациональные числа могут быть представлены в виде дроби, у которой целый числитель и натуральный знаменатель и которая является рациональным числом;
- рациональные числа могут быть представлены в виде любой периодической десятичной дроби, которая является рациональным числом.
Как определить, является ли число рациональным
- Число задано в виде числового выражения, которое состоит только из рациональных чисел и знаков арифметических операций. В таком случае значением выражения будет рациональное число.
- Квадратный корень из натурального числа – рациональное число только в том случае, когда под корнем стоит число, которое является полным квадратом некоторого натурального числа. Например, $\sqrt{9}$ и $\sqrt{121}$ – рациональные числа, так как $9=3^2$ и $121=11^2$.
- Корень $n$-ой степени из целого числа – рациональное число только в том случае, когда число под знаком корня является $n$-ой степенью какого-либо целого числа. Например, $\sqrt[3]{8}$ – рациональное число, т.к. $8=2^3$.
На числовой оси рациональные числа располагаются повсюду плотно: между каждыми двумя рациональными числами, которые не равны друг другу, можно расположить хотя бы одно рациональное число (следовательно, и бесконечное множество рациональных чисел). В то же время, множество рациональных чисел характеризуется счетной мощностью (т. е. все элементы множества можно пронумеровать). Древние греки доказали, что существуют числа, которые невозможно записать как дробь. Они показали, что не существует такое рациональное число, квадрат которого равен $2$. Тогда рациональных чисел оказалось недостаточно для выражения всех величин, что и привело в дальнейшем к появлению вещественных чисел. Множество рациональных чисел, в отличие от вещественных чисел, является нульмерным.
spravochnick.ru
