что такое сумма?что такое разность?что такое произведение?что такое частное?
сумма это плюс, разность — минус, произведение — умножение, частное — деление
это ответы в: сложении, вычитании, умножении, делении. Хоть бы класс писали, а то можно по этим четырём знакам и реферат накромсать на 10 страниц
Сумма (математика) — результат сложения. Разность — результат вычитания Произведение — результат умножения Частное — результат деления
touch.otvet.mail.ru
Деление / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Деление
В этом разделе познакомимся с делением и узнаем, что деление – это математическая операция, обратная умножению.
Умножение – это последовательное сложение чисел, а деление – это последовательное вычитание чисел.
В математике существует знак для умножения — это точка ( • ) посередине строки между числами, которые нужно перемножить, а для деления существует особый знак — это две точки (
Как ёжикам поделить между собой яблоки поровну?
Нужно воспользоваться действием деления и узнать, сколько раз по 3 содержится в 6.
1) 6 : 3 = 2 (яб.) — мы узнали, сколько яблок получит каждый ёжик.
2) 6 : 2 = 3 (ёж.) — мы узнали, сколько ёжиков получат по 2 яблока.
3) 2 • 3 = 6 (яб.) — мы узнали, сколько яблок нужно, чтобы у каждого из трёх ёжиков было по 2 яблока.
Любой пример на умножение можно представить двумя примерами на деление.
Например, для выражения 6 • 4 = 24 есть два обратных выражения:
24 : 4 = 6 — нужно из 24 вычесть число 4 ровно 6 раз.
24 : 6 = 4 — нужно из 24 вычесть число 6 ровно 4 раз.
Числа при делении
При делении, как и при другом математическом действии, каждое число имеет свое название.
Число, которое делят, называется делимое.
Число, на которое делят, называется делитель.
Результат деления называется частное.
Чтение числовых выражений
24 : 6 = 4
Этот пример можно прочитать по-разному.
- 24 разделить на 6 равняется 4.
- 24 уменьшить в 6 раз – получится 4.
- Делимое – 24, делитель – 6, частное – 4.
- Частное от деления числа 24 на 6 равно 4.
Деление на 1
4 : 1 = 4
23 : 1 = 23

Деление на 0
Деление числа само на себя

Связь деления и умножения

Чётные и нечётные числа
Числа, которые делятся на 2 без остатка, называются чётными, а числа, которые не делятся на 2 без остатка, называются нечётными.
Чётные: 6, 22 44, 60, 74, 82, 96
Нечётные: 7, 13, 21, 37, 45, 97
В несколько раз меньше
Для примера решим задачу:
В магазине было 8 котят, а лисичек в 4 раза меньше. Сколько было лисичек?
составим схему:
Значит, чтобы узнать, сколько было лисичек, нужно 8 : 4 = 2 (л.)
Вывод: Если в задаче есть слова «в … раз меньше», то задача решается делением.
Во сколько раз больше? Во сколько раз меньше?
Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?
Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?
8 : 2 = 4 (раза)
Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Табличное деление
Внетабличное деление
Деление с остатком
Деление суммы на число
Деление на однозначное число
Деление чисел, оканчивающихся нулями
Деление на двузначное и трёхзначное число
Правило встречается в следующих упражнениях:
2 класс
Страница 56. Вариант 1. № 3, Моро, Волкова, Проверочные работы
Страница 58. Вариант 1. № 1, Моро, Волкова, Проверочные работы
Страница 59. Вариант 2. № 1, Моро, Волкова, Проверочные работы
Страница 67. Вариант 2. Тест 2, Моро, Волкова, Проверочные работы
Страница 59, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 64, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 72, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 73, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 75, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 92, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
3 класс
Страница 79, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 26, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 29, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 53, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 34. Вариант 1. № 3, Моро, Волкова, Проверочные работы
Страница 43. Вариант 2. Тест 1, Моро, Волкова, Проверочные работы
Страница 14, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 25, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 47, Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 53, Моро, Волкова, Рабочая тетрадь, 2 часть
5 класс
Упражнение 36, Мерзляк, Полонский, Якир, Учебник
Упражнение 1, Мерзляк, Полонский, Якир, Учебник
© 2019 — budu5.com, Буду отличником!
budu5.com
Что такое разность и частное
Определим, что такое разность и что такое частное
Разность и частное относятся к математическим понятиям. Так же, есть такие понятия, как сумма и произведение. Все эти понятия взаимосвязаны с математическими терминами:
- Сложение;
- Вычитание;
- Умножение;
- Деление.
Определим понятие разности
Разность – это результат действия вычитания. Разность состоит уменьшаемого, вычитаемого и разности.
Рассмотрим на примере: 9 – 3 = 6, где 9 – уменьшаемое, 3 – вычитаемое, 6 – разность. Для того, чтобы сделать проверку разности, нужно найти сумму вычитаемого и разности.
Рассмотрим примеры разностей:
- 5 – 3 = 2;
- 15 – 8 = 7;
- 36 – 12 = 24;
- 45 – 12 = 33;
- 65 – 25 = 40.
Определим понятие частного
Частное – это результат действия деления. Частное состоит из делимого, делителя и частного.
Рассмотрим на примере: 15/5 = 3, где 15 – делимое, 5 – делитель, 3 – частное. Для того, чтобы сделать проверку, нужно найти произведение делителя и частного.
Рассмотрим примеры частных:
- 8/2 = 4;
- 75/15 = 5;
- 100/5 = 20;
- 50/25 = 2;
- 3/6 = 0.5.
Свойства суммы, разности, произведения и частного:
- Сумма двух положительных чисел равна положительному числу. Например, 5 + 3 = 8;
- Произведение двух положительных чисел дает положительное число. Например, 6 * 8 = 48;
- Частное двух положительных чисел будет положительным числом. Например, 72/8 = 9;
- Сумма двух отрицательных чисел равна отрицательному числу. Например, — 6 – 5 = — 11;
- Произведение двух отрицательных чисел равна положительному числу. Например, — 9 * (- 3) = 27;
- Частное двух отрицательных чисел равна положительному числу. Например, — 36/(- 2) = 18;
- Произведение двух отрицательных чисел равна отрицательному числу. Например, — 8 * 5 = — 40;
- Частное двух отрицательных чисел равна отрицательному числу. Например, — 81/9 = — 9.
vashurok.ru
Что такое частное чисел? Ответ на webmath.ru
Задание. Найти частное чисел:
1) ; 2)
Решение. Для нахождения частного в первом примере выполним деление в столбик. Для этого запишем делимое и делитель следующим образом
Берем первую цифру слева, она не делится на 12, значит, берем две цифры: 56 и делим их на 12 с остатком. Возьмем по . Записываем 48 под 56 и находим остаток: . Восьмерку записываем под чертой и сносим к ней следующее число из делимого, получим 84. Делим 84 на 12, получаем 7. остаток от деления 0 и цифр в делимом больше нет. Деление окончено.
Таким образом,
Для нахождения частного во втором примере, сведем деление десятичных дробей к делению десятичной дроби на целое число. Для этого будем передвигать запятую вправо у делимого и делителя до тех пор, пока делимое не станет целым числом. Далее запишем полученные числа в столбик, как и в первом примере:
Берем в делимом первые две цифры слева и делим их на делимое с остатком. Получаем , можно взять по 2. Двойку записываем в частное. И так как целая часть делимого закончилась, ставим в частном запятую. Умножаем , записываем 42 под 56 и вычитаем: . Остаток 14 списываем к нему следующую незадействованную цифру делимого 7. Полученное число 147 делим на 12, получаем 7. Записываем семерку в частное, и, так как на этом делимое закончилось, а остаток после последнего деления 0, деление окончено.
Таким образом
Ответ.
Десятичные дроби Деления чисел столбиком онлайн
www.webmath.ru
разность это деление или минус?
это минус (а-б) это разность
— разность : частное
РАЗНОСТЬ ЭТО —
разность это минус
———————————————————————————————————————————————————————————
touch.otvet.mail.ru
Свойства деления. Деление произведения, суммы и разности на число
Деление произведения на число
Произведение можно разделить на число двумя способами:
1)Чтобы разделить произведение на какое-нибудь число, можно сначала вычислить значение произведения (выполнить умножение) и полученный результат разделить.
Например, чтобы найти значение выражения:
(12 · 5) : 3
можно сначала умножить 12 на 5:
12 · 5 = 60
и полученное произведение разделить на 3:
60 : 3 = 20, значит (12 · 5) : 3 = 60 : 3 = 20
Если один из сомножителей делится на число, на которое надо разделить произведение, то можно воспользоваться вторым способом нахождения частного от деления произведения на число.
2)Чтобы разделить произведение на какое-нибудь число, можно разделить на это число один любой сомножитель, оставив другие без изменений.
Например, чтобы найти значение выражения:
(8 · 20) : 4
можно сначала разделить любой из сомножителей (8 или 20) на 4:
8 : 4 = 2
и полученное частное умножить на другой сомножитель:
2 · 20 = 40, значит (8 · 20) : 4 = (8 : 4) · 20 = 2 · 20 = 40
данное выражение можно решить ещё так:
(8 · 20) : 4 = 8 · (20 : 4) = 8 · 5 = 40
Деление числа на произведение
Число можно разделить на произведение двумя способами:
1) Чтобы разделить какое-нибудь число на произведение, можно сначала вычислить значение произведения (выполнить умножение), а затем разделить число на полученный результат.
Например, чтобы найти значение выражения:
60 : (3 · 2)
можно сначала умножить 3 на 2:
3 · 2 = 6
и разделить 60 на полученный результат:
60 : 6 = 10, значит 60 : (3 · 2) = 60 : 6 = 10
Если число, которое нужно разделить на произведение, делится на каждый сомножитель, из которого состоит данное произведение, то можно воспользоваться вторым способом нахождения частного от деления числа на произведение.
2) Чтобы разделить какое-нибудь число на произведение, можно разделить это число на первый сомножитель, полученное частное разделить на второй сомножитель, это частное на третий и т. д.
Например, чтобы найти значение выражения:
120 : (5 · 3)
можно сначала разделить 120 на 5:
120 : 5 = 24
а теперь, полученное частное 24 разделить на 3
24 : 3 = 8, значит 120 : (5 · 3) = (120 : 5) : 3 = 24 : 3 = 8
Так как от перестановки множителей произведение не изменится, то множители можно поменять местами:
120 : (3 · 5)
и разделить 120 сначало на 3, а затем полученный результат разделить на 5:
120 : (3 · 5) = (120 : 3) : 5 = 40 : 5 = 8
получается, что не важно на какой множитель сначала делить число, результат будет одинаковым:
120 : (5 · 3) = (120 : 5) : 3 = 24 : 3 = 8
тоже самое, что и
120 : (5 · 3) = (120 : 3) : 5 = 40 : 5 = 8
Из данного примера можно сделать вывод, что значение частного не изменится от порядка выполнения действий.
Деление суммы на число
Сумму можно разделить на число двумя способами:
1) Чтобы разделить сумму на какое-нибудь число, можно сначала вычислить значение суммы (выполнить сложение) и полученный результат разделить.
Например, чтобы найти значение выражения:
(15 + 12) : 3
можно сначала сложить числа 15 и 12:
15 + 12 = 27
и полученную сумму разделить на 3:
27 : 3 = 9, значит (15 + 12) : 3 = 27 : 3 = 9
Если все слагаемые в записи суммы делятся на число, на которое надо разделить сумму, то можно воспользоваться вторым способом нахождения частного от деления суммы на число.
2) Чтобы разделить сумму на какое-нибудь число, можно разделить на это число каждое слагаемое отдельно и полученные частные сложить.
Например, чтобы найти значение выражения:
(42 + 28 + 70) : 7
можно каждое слагаемое разделить на число 7:
42 : 7 = 6, 28 : 7 = 4 и 70 : 7 = 10
и полученные частные (6, 4 и 10) сложить:
6 + 4 + 10 = 20, значит
(42 + 28 + 70) : 7 = 42 : 7 + 28 : 7 + 70 : 7 = 6 + 4 + 10 = 20
Деление разности на число
Разность можно разделить на число двумя способами:
1) Чтобы разделить разность на какое-нибудь число, можно сначала вычислить значение разности (выполнить вычитание) и полученный результат разделить.
Например, чтобы найти значение выражения:
(24 — 8) : 2
можно сначала вычесть из 24 число 8:
24 — 8 = 16
и полученную разность разделить на 2:
16 : 2 = 8, значит (24 — 8) : 2 = 16 : 2 = 8
Если и уменьшаемое и вычитаемое в записи разности делятся на число, на которое надо разделить разность, то можно воспользоваться вторым способом нахождения частного от деления разности на число.
2) Чтобы разделить разность на какое-нибудь число, можно разделить на это число отдельно уменьшаемое и вычитаемое, а потом из первого частного вычесть второе.
Например, чтобы найти значение выражения:
(42 — 28) : 7
можно отдельно уменьшаемое и вычитаемое разделить на число 7:
42 : 7 = 6, 28 : 7 = 4
и найти разность полученных частных:
6 — 4 = 2, значит (42 — 28) : 7 = 42 : 7 — 28 : 7 = 6 — 4 = 2
Общие формулы свойств деления
Все свойства деления можно представить в виде формул:
| Распределительные свойства | |
|---|---|
| (a + b) : c = a : c + b : c | |
| (a — b) : c = a : c — b : c | |
| (a · b) : c = (a : c) · b = (b : c) · a | |
| a : (b · c) = (a : b) : c = (a : c) : b | |
| Действия с единицей и нулём | |
| a : 1 = a | |
| a : a = 1 | |
| 0 : a = 0 (a ≠ 0) | |
| На нуль делить нельзя | |
naobumium.info
Вычитание и деление
___________________________________________________________________
Определение 6. Вычитанием натуральных чисел а и b называется операция «–» , удовлетворяющая условию: а – b = с, тогда и только тогда, когда b + с = а.
или
Вычитанием натуральных чисел а и b называется операция по нахождению разности (а – b).
______________________________________________________________________________________________
___________________________________________________________________
Определение 7. Разностью натуральных чисел а и b называется число с (если оно существует), такое, что b + с = а.
______________________________________________________________________________________________
Символическая запись: а – b ( с) а = с + b.
Число а называется уменьшаемым, число b – вычитаемым, число (а – b) – разностью.
Например:
Разностью чисел 7 и 3 будет число 4, т.к. 3 + 4 = 7. (7 – 3 = 4, т.к. 3 + 4 = 7).
Разность чисел 5 и 9 не существует, т.к. не существует натурального числа с, такого, что 9 + с = 5.
((5
– 9) –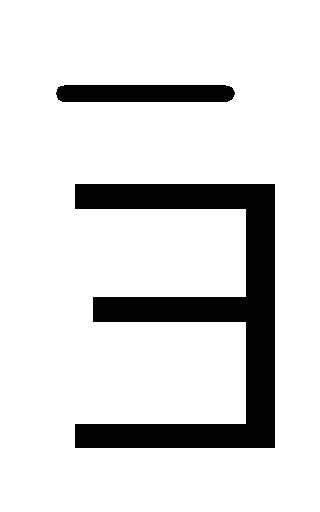 ,т.к. (
,т.к. (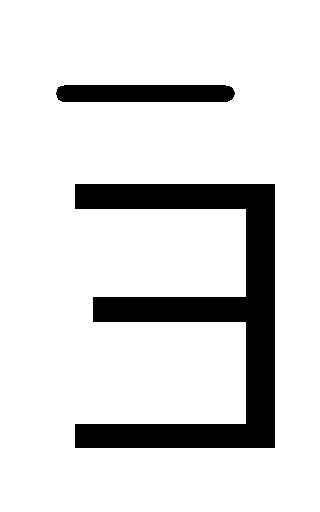 с)( 9 + с = 5).
с)( 9 + с = 5).
Теорема 5. Разность натуральных чисел (а – b) существует тогда и только тогда, когда b < а.
Теорема 6. Если разность натуральных чисел а и b существует, то она единственна.
Пользуясь определением разности, можно доказать истинность следующих утверждений: (а + b) – а = b; (а + b) – b = а.
Исходя из определения разности натуральных чисел, и условия существования, можно объяснить известные правила вычитания.
Правило вычитания числа из суммы
s – c, где s = a + b > c
(a + b)– c = (a + b) – c = (a –c)+b, если a > c
a + (b – c) , если b > c
Число из суммы можно вычесть одним из трех способов:
• найти сумму (а + b) и из нее вычесть число с.
Например (11 + 8) — 13 = 19 -13 = 6;
• вычесть число из первого слагаемого и к полученному результату прибавить второе слагаемое.
Например (13 + 8) — 9 = (13 -9) + 8 = 4 + 8 = 12;
• вычесть число из второго слагаемого, и полученный результат прибавить к первому слагаемому.
Например (5 + 13) – 6 = 5 + (13 -6) = 5 + 7 = 12.
Правило вычитания суммы из числа
a – s , s = b + c,
a – (b + c)= (a – b) – c, если а > b + с
(a – c) – b
Сумму из числа можно вычесть одним из трех способов:
• найти сумму (b + с), и полученный результат вычесть из числа a;
Например: 19 – (2 + 7) =19 – 9 = 10;
• из числа а вычесть первое слагаемое b, и из полученного результата (а – b) вычесть второе слагаемое с;
Например: 17 – (7 + 5) = (17 – 7) – 5 = 10 – 5 = 5;
• из числа а вычесть второе слагаемое и из полученного результата вычесть первое слагаемое;
Например: 13 – (5 + 3) = (13 – 3) – 5 = 10 – 5 = 5.
Правило вычитания суммы из суммы
S1 – S2, если S1=a + b, S2 = с + d и S1 S2
(а + b)-(с + d) = (а – с) + (b – d), если а > с, b > d;
(а — d) + (b – с), если а > d, b > с.
 (7+
8) – (4+ 9) = 15 – 13 = 2;
(7+
8) – (4+ 9) = 15 – 13 = 2;
Например, (7 + 4) – (5 + 3) = (7 – 5) + (4 – 3) = 2 + 1 = 3;
(6 + 8) – (7 + 4) = (6 – 4) + (8 – 7) = 2 + 1 = 3.
______________________________________________________________________
Определение 8. Делением натуральных чисел а и b называется операция «:», удовлетворяющая условию: а: b = с тогда и только тогда, когда b с = а, или
Делением натуральных чисел а и b называется операция по нахождению частного а : b.
___________________________________________________________________________________________________
______________________________________________________________________
Определение 9. Частным натуральных чисел а и b называется число с, такое, что b с = а.
___________________________________________________________________________________________________
Символическая
запись: а
: b = с  (с)b с = а.
(с)b с = а.
Число а называется делимым, число b — делителем, число (а :b) – частным и число с – тоже частным.
Например:
Частным чисел 42 и 7 будет число 6, т.к. 7 6 = 42, (42 : 7 = 6, т.к. 7 6 = 42).
Частное чисел 15 и 7 не существует, т.к. не существует такого натурального числа с, что 7 с = 15, (15 : 7 –
 ;т.к. (
;т.к. ( с N с = 15).
с N с = 15).
Теорема 7. Для того чтобы существовало частное двух натуральных чисел а и b, необходимо, чтобы b < а.
Теорема 8. Если частное натуральных чисел а и b существует, то оно единственно.
Из определения частного следует истинность утверждения (а : b) b = а.
(Частное умножим на делитель – получим делимое).
Исходя из определения частного и условия его существования можно обосновать известные правила деления суммы, разности, произведения на число.
studfiles.net

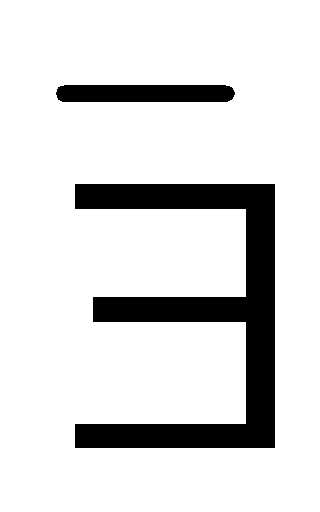 ;т.к. (
;т.к. (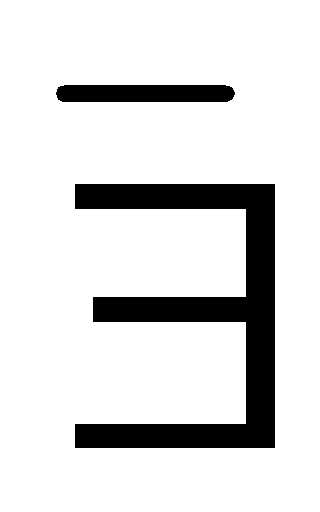 с N с = 15).
с N с = 15).