Высшая математика. Теория рядов
Разделы: Математика
ВВЕДЕНИЕ
Методическое пособие предназначено для преподавателей математики в техникумах, а также для студентов второго курса, всех специальностей.
В данной работе излагаются основные понятия теории рядов. Теоретический материал соответствует требованиям Государственного образовательного стандарта среднего профессионального образования (Министерство образования Российской Федерации. М., 2002г.).
Изложение теоретического материала по всей теме сопровождается рассмотрением большого количества примеров и задач, ведется на доступном, по-возможности строгом языке. В конце пособия приведены примеры и задания, которые студенты могут выполнять в режиме самоконтроля.
Пособие предназначено для студентов заочной и дневной форм обучения.
ОСНОВНЫЕ ПОНЯТИЯ
Решение задачи, представленной в математических терминах, например, в виде комбинации различных функций, их производных и интегралов, нужно уметь “довести до числа”, которое чаще всего и служит окончательным ответом. Для этого в различных разделах математики выработаны различные методы.
Раздел математики, позволяющий решить любую корректно поставленную задачу с достаточной для практического использования точностью, называется теорией рядов.
Даже если некоторые тонкие понятия математического анализа появились вне связи с теорией рядов, они немедленно применялись к рядам, которые служили как бы инструментом для испытания значимости этих понятий. Такое положение сохраняется и сейчас.
Выражение вида
,
где ;;;…;;… — члены ряда; — n-ый или общий член ряда, называется бесконечным рядом (рядом).
Если члены ряда :
- числа, то ряд называется числовым;
- числа одного знака, то ряд называется знакопостоянным;
- числа разных знаков, то ряд называется знакопеременным;
- положительные числа, то ряд называется знакоположительным;
- числа, знаки которых строго чередуются, то ряд называется знакочередующимся;
- функции, то ряд называется функциональным;
- степени, то ряд называется степенным;
- тригонометрические функции, то ряд называется тригонометрическим.
1.1. Основные понятия числового ряда.
Числовым рядом называется сумма вида
, (1.1)
где ,,,…,,…, называемые членами ряда, образуют бесконечную последовательность; членназывается общим членом ряда.
Суммы
…………..
,
составленные из первых членов ряда (1.1), называются частичными суммами этого ряда.
Каждому ряду можно сопоставить последовательность частичных сумм .
Если при бесконечном возрастании номера n частичная сумма ряда стремится к пределу, то ряд называется сходящимся, а число - суммой сходящегося ряда, т.е.
и .
Эта запись равносильна записи
.
Если частичная сумма ряда (1.1) при неограниченном возрастании n не имеет конечного предела (стремится к или ), то такой ряд называется расходящимся.
Если ряд сходящийся, то значение при достаточно большом n является приближенным выражением суммы ряда S.
Разность называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т.е., и наоборот, если остаток стремится к нулю, то ряд сходится.
1.2. Примеры числовых рядов.
Пример 1. Ряд вида
(1.2)
называется геометрическим .
Геометрический ряд образован из членов геометрической прогрессии.
Известно, что сумма её первых n членов . Очевидно: это n-ая частичная сумма ряда (1.2).
Возможны случаи:
:
.
Ряд (1.2) принимает вид:
,
, ряд расходится;
Ряд (1.2) принимает вид:
,
не имеет предела, ряд расходится.
,
— конечное число, ряд сходится.
,
— ряд расходится.
Итак, данный ряд сходится при и расходится при .
Пример 2. Ряд вида
(1.3)
называется гармоническим.
Запишем частичную сумму этого ряда:
.
Сумма больше суммы, представленной следующим образом:
или .
Если , то , или .
Следовательно, если , то , т.е. гармонический ряд расходится.
Пример 3. Ряд вида
(1.4)
называется обобщенным гармоническим.
Если , то данный ряд обращается в гармонический ряд, который является расходящимся.
Если , то члены данного ряда больше соответствующих членов гармонического ряда и, значит, он расходится. При имеем геометрический ряд, в котором ; он является сходящимся.
Итак, обобщенный гармонический ряд сходится при и расходится при .
1.3. Необходимый и достаточные признаки сходимости.
Необходимый признак сходимости ряда.
Ряд может сходиться только при условии, что его общий член при неограниченном увеличении номера стремится к нулю: .
Если , то ряд расходится – это достаточный признак расходимости ряда.
Достаточные признаки сходимости ряда с положительными членами.
Признак сравнения рядов с положительными членами.
Исследуемый ряд сходится, если его члены не превосходят соответствующих членов другого, заведомо сходящегося ряда; исследуемый ряд расходится, если его члены превосходят соответствующие члены другого, заведомо расходящегося ряда.
Признак Даламбера.
Если для ряда с положительными членами
выполняется условие , то ряд сходится при и расходится при .
Признак Даламбера не дает ответа, если . В этом случае для исследования ряда применяются другие приемы.
Упражнения.
Записать ряд по его заданному общему члену:
;
;
.
Решение.
Полагая ,,,…, имеем бесконечную последовательность чисел:
,,. Сложив его члены, получим ряд
.
Поступая так же, получим ряд
.
Придаваязначения 1,2,3,… и учитывая, что,,,…, получим ряд
.
Найти n-ый член ряда по его данным первым членам:
;
.
Решение.
Знаменатели членов ряда, начиная с первого, являются четными числами; следовательно, n-ый член ряда имеет вид .
Числители членов ряда образуют натуральный ряд чисел, а соответствующие им знаменатели – натуральный ряд чисел, а соответствующие им знаменатели – натуральный ряд чисел, начиная с 3. Знаки чередуются по закону или по закону . Значит, n-й член ряда имеет вид . или .
Исследовать сходимость ряда, применяя необходимый признак сходимости и признак сравнения:
;
;
.
Решение.
Находим .
Необходимый признак сходимости ряда выполняется, но для решения вопроса о сходимости нужно применить один из достаточных признаков сходимости. Сравним данный ряд с геометрическим рядом
который сходится, так как.
Сравнивая члены данного ряда, начиная со второго, с соответствующими членами геометрического ряда, получим неравенства
т.е. члены данного ряда, начиная со второго, соответственно меньше членов геометрического ряда, откуда следует, что данный ряд сходится.
Имеем
.
Здесь выполняется достаточный признак расходимости ряда; следовательно, ряд расходится.
Находим .
Необходимый признак сходимости ряда выполняется. Сравним данный ряд с обобщенным гармоническим рядом
,
который сходится, поскольку, следовательно, сходится и данный ряд.
Исследовать сходимость ряда, используя признак Даламбера:
;
.
Решение.
Подставив в общий член ряда вместо n число n+1, получим . Найдем предел отношения -го члена к n-му члену при :
.
Следовательно, данный ряд сходится.
Имеем
Значит, данный ряд расходится.
, т.е. ряд расходится.
II. Знакопеременный ряд
2.1 Понятие знакопеременного ряда.
Числовой ряд
называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.
Числовой ряд называется знакочередующимся, если любые два стоящие рядом члена имеют противоположные знаки.
,
где для всех (т.е. ряд, положительные и отрицательные члены которого следуют друг за другом поочередно). Например,
;
;
.
Для знакочередующихся рядов имеет место достаточный признак сходимости (установленный в 1714г. Лейбницем в письме к И.Бернулли).
2.2 Признак Лейбница. Абсолютная и условная сходимость ряда.
Теорема (Признак Лейбница).
Знакочередующийся ряд сходится, если:
Последовательность абсолютных величин членов ряда монотонно убывает, т.е. ;
Общий член ряда стремится к нулю:.
При этом сумма S ряда удовлетворяет неравенствам
.
Замечания.
Исследование знакочередующегося ряда вида
(с отрицательным первым членом) сводится путем умножения всех его членов на к исследованию ряда .
Ряды, для которых выполняются условия теоремы Лейбница, называются лейбницевскими (или рядами Лейбница).
Соотношение позволяет получить простую и удобную оценку ошибки, которую мы допускаем, заменяя сумму S данного ряда его частичной суммой .
Отброшенный ряд (остаток) представляет собой также знакочередующийся ряд , сумма которого по модулю меньше первого члена этого ряда, т.е.. Поэтому ошибка меньше модуля первого из отброшенных членов.
Пример. Вычислить приблизительно сумму ряда .
Решение: данный ряд Лейбницевского типа. Он сходится. Можно записать:
.
Взяв пять членов, т.е. заменивна
, сделаем ошибку, меньшую,
чем. Итак,.
Для знакопеременных рядов имеет место следующий общий достаточный признак сходимости.
Теорема. Пусть дан знакопеременный ряд
.
Если сходится ряд
,
составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд.
Признак сходимости Лейбница для знакочередующихся рядов служит достаточным признаком сходимости знакочередующихся рядов.
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов, т.е. всякий абсолютно сходящийся ряд является сходящимся.
Если знакопеременный ряд сходится, а составленный из абсолютных величин его членов ряд расходится, то данный ряд называется условно (неабсолютно) сходящимся.
2.3. Упражнения.
Исследовать на сходимость (абсолютную или условную) знакочередующийся ряд:
;
Решение.
Члены данного ряда по абсолютной величине монотонно убывают:
и
Следовательно, согласно признаку Лейбница, ряд сходится. Выясним, сходится ли этот ряд абсолютно или условно.
Ряд , составленный из абсолютных величин данного ряда, является гармоническим рядом, который, расходится. Поэтому данный ряд сходится условно.
Решение.
Члены данного ряда по абсолютной величине монотонно убывают:
, но
.
Ряд расходится, так как признак Лейбница не выполняется.
;
Решение.
Используя признак Лейбница, получим
;,
т.е. ряд сходится.
Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:
.
Это геометрический ряд вида, где, который сходится. Поэтому данный ряд сходится абсолютно.
;
Решение.
Используя признак Лейбница, имеем
;
, т.е. ряд сходится.
Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:
, или
.
Это обобщенный гармонический ряд, который расходится, так как. Следовательно, данный ряд сходится условно.
III. Функциональный ряд
3.1. Понятие функционального ряда.
Ряд, членами которого являются функции от , называется функциональным:
.
Придавая определенное значение , получим числовой ряд
,
который может быть как сходящимся, так и расходящимся.
Если полученный числовой ряд сходится, то точка называется точкой сходимости функционального ряда; если же ряд расходится – точкой расходимости функционального ряда.
Совокупность числовых значений аргумента , при которых функциональный ряд сходится, называется его областью сходимости.
В области сходимости функционального ряда его сумма является некоторой функцией от :.
Определяется она в области сходимости равенством
, где
— частичная сумма ряда.
Пример. Найти область сходимости ряда .
Решение. Данный ряд является рядом геометрической прогрессии со знаменателем . Следовательно, этот ряд сходится при , т.е. при всех ; сумма ряда равна ;
, при .
3.2. Степенные ряды.
Степенным рядом называется ряд вида
,
где числа называются коэффициентами ряда, а член — общим членом ряда.
Областью сходимости степенного ряда называется множество всех значений , при которых данный ряд сходится.
Число называется радиусом сходимости степенного ряда, если при ряд сходится и притом абсолютно, а при ряд расходится.
Радиус сходимости найдем, используя признак Даламбера:
(не зависит от),
urok.1sept.ru
Формулы и уравнения рядов
Примеры решения рядов здесь.
Числовые ряды
Факториал и двойные факториалы:
— формула Стирлинга.
Геометрическая прогрессия:
|q|<1.
Основные определения и теоремы о рядах:
{un} — заданная бесконечная числовая последовательность,
— числовой ряд,
un — члены ряда,
– частичные суммы ряда.
Сумма ряда:
сходится, S — сумма ряда.
или ряд сходится и суммы нет.
Отбрасывание конечного числа членов ряда не влияет на его сходимость (но влияет на сумму).
Свойства сходящихся рядов:
- Теоремы сравнения рядов с положительными членами:
- ≤
Если сходится, то сходится;
если расходится, то расходится. - vn ≠ 0, 0 < k < ∞.
Либо и , и сходятся,
либо и , и расходятся.
≥ 0, ≥ 0.
- Достаточные признаки сходимости числовых рядов с положительными членами (un > 0)
- Признак Даламбера
Если существует , то : сходится, если l < 1; расходится, если l > 1; признак не дает ответа, если l = 0. - Признак Коши
Если существует , то : сходится, если l < 1; расходится, если l > 1; признак не дает ответа, если l = 0. - Интегральный признак сходимости
1) un > 0; 2) un ≥ un+1; 3) f(x) — непрерывная невозрастающая функция, f(n) = un.
Либо и , и сходятся,
либо и , и расходятся.
- Примеры числовых рядов
- : сходится, если a > 1; расходится, если a ≤ 1.
- : сходится, если a < 1; расходится, если a ≥ 1.
- : сходится.
- : сходятся, |q| < 1; расходятся, |q| ≥ 1.
- : сходится;
- : сходится, если a > 1; расходится, если a ≤ 1.
- : сходится условно.
- : сходится абсолютно.
- : сходится абсолютно.
Функциональные ряды
Функциональный ряд – сумма вида
При из функционального ряда получается числовой ряд
Если для числовой ряд сходится, то точка называется точкой сходимости функционального ряда. Если в каждой точке числовые ряды сходятся, то функциональный ряд называется сходящимся в области . Совокупность всех точек сходимости образует область сходимости функционального ряда.
– частичные суммы ряда. Функциональный ряд сходится к функции f(x), если
Равномерная сходимость
Функциональный ряд, сходящийся для всех из области сходимости, называется равномерно сходящимся в этой области, если ∀ε > 0 существует не зависящий от x номер N(ε), такой, что при n > N(ε) выполняется неравенство Rn(x) < ε для всех x из области сходимости, где — остаток ряда.
Геометрический смысл равномерной сходимости: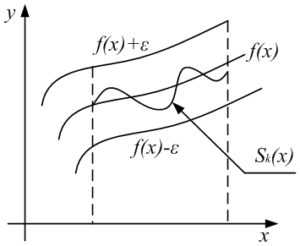
если окружить график функции y = f(x) «ε-полоской», определяемой соотношением f(x)−ε > y > f(x)+ε, то графики всех частичных сумм Sk(x), начиная с достаточно большого k, ∀x ∈ [a, b] целиком лежат в этой «ε-полоске», окружающей график предельной функции y = f(x).
— называется мажорируемым в области , если существует такой сходящийся числовой ряд un > 0, что для ∀x ∈ D fn(x) ≤ un, n = 1, 2, …. Ряд называется мажорантой ряда
Признак Вейерштрасса (признак равномерной сходимости функционального ряда): функциональный ряд сходится равномерно в области сходимости, если он является мажорируемым в этой области.
Степенные ряды:
— степенной ряд по степеням
При – степенной ряд по степеням x.
Область сходимости степенного ряда:
Радиус сходимости, интервал сходимости R, x ∈ (-R, R):
или
При |x| < R ряд сходится, при |x| > R – расходится;
в точках x = ±R – дополнительное исследование.
На интервале сходимости ряд сходится абсолютно;
на любом отрезке из интервала сходимости он сходится равномерно.
- Свойства степенных рядов
- Степенной ряд сходится равномерно на [−R′, R′]
∀R′ < R, его можно почленно дифференцировать и интегрировать в интервале сходимости. - Ряды, полученные почленным дифференцированием и интегрированием, имеют тот же интервал сходимости.
- Разложение элементарных функций в степенные ряды
- , x ∈ (−∞; ∞).
- ,
x ∈ (−∞; ∞). - , x ∈ (−∞; ∞).
- , x ∈ (−∞; ∞).
- , x ∈ (−∞; ∞).
, x ∈ (−1; 1].
, x ∈ [−1; 1).- ,
x ∈ (−1; 1). - , x ∈ [−1; 1].
- , x ∈ [−1; 1].
- , x ∈ (−1; 1).
- , x ∈ (−1; 1).
- , x ∈ (−1; 1).
- , x ∈ (−1; 1).
- , x ∈ (−1; 1].
Тригонометрические ряды
- Ряд Фурье для периодической функции с периодом 2π
- Ряд Фурье функции f(x):
- Коэффициенты Фурье:
Ряд Фурье для функции с произвольным периодом Т=2l, f(x+2l) = f(x):
где
- Разложение в ряд Фурье непериодических функций, заданных на отрезке x ∈ [0; l] или на отрезке x ∈ [-l; l]
- f1(x)=f(-x), x ∈ [-l; 0] (четное продолжение)
где x ∈ [0; l] n = 0, 1, 2,… - f1(x) = —f(−x), x ∈ [-l; 0]
(нечетное продолжение)
где x ∈ [0; l] n = 1, 2,… - На всю действительную ось ϕ(x) продолжается периодически с периодом 2l, ϕ(x) = ϕ(x + 2l). Функция ϕ(x) разлагается в ряд Фурье, причем в точках x = ±l выполняется условие: где то есть,
– левый предел f(x) в точке x = l,
– правый предел f(x) в точке x = l.
Произвольная функция f(x) задана на отрезке [0; l]; на отрезок [-l; 0] она может быть продолжена произвольным образом:
– некоторая кусочно-монотонная функция.
Наиболее часто встречающиеся продолжения:
matematika.electrichelp.ru
Как найти сумму ряда 🚩 найти сумму ряда 🚩 Математика
Автор КакПросто!
Из курса высшей математики известно определение – числовым рядом называется сумма видаu1 + u2 + u3 + … + un + … = ∑un, n – натуральные числагде u1, u2, …, un, … — члены некоторой бесконечной последовательности, при этом un – называется общим членом ряда, который задаётся некоторой формулой определяющей всю последовательность.Чтобы посчитать сумму ряда, необходимо ввести понятие частичной суммы.

Статьи по теме:
Инструкция
Рассмотрим сумму первых n членов заданного ряда и обозначим SnSn = u1 + u2 + u3 + … + un = ?un, n – натуральные числа.
Сумма Sn называется частичной суммой ряда.
Перебирая n начиная с 1 до бесконечности, получим последовательность вида
S1, S2, …, Sn, …
которая называется последовательностью частичных сумм. Таким образом, сумму ряда можно определить следующим способом.
Заданный ряд будет называться сходящимся, если последовательность его частичных сумм Sn сходится, т.е. имеет конечный предел S
lim Sn = S,
тогда число S будем суммой заданного ряда
?un = S, n – натуральные числа.
Если же последовательность частичных сумм Sn не имеет предела или имеет бесконечный придел, то заданный ряд называется расходящимся и соответственно не имеет суммы.
Числовым рядом называют сумму членов бесконечной последовательности. Частичными суммами ряда называют сумму первых n членов ряда. Ряд будет являться сходящимся, если сходится последовательность его частичных сумм.
Вам понадобится
- Умение вычислять пределы последовательностей.
Инструкция
Определите формулу общего члена ряда. Пусть дан ряд x1+x2+…+xn+…, его общий член имеет вид xn. Воспользуйтесь признаком Коши определения сходимости ряда. Посчитайте предел lim((xn)^(1/n)) при n стремящимся к ∞. Пусть он существует и равен L, тогда если L1, то ряд расходится, а если L=1, то необходимо дополнительно исследовать ряд на сходимость. Рассмотрите примеры. Пусть дан ряд 1/2+1/4+1/8+…, общий член ряда представляется в виде 1/(2^n). Найдите предел lim((1/(2^n)^(1/n)) при n стремящимся к ∞. Этот предел равен 1/2формулы (2×n/(n+1))^n. Посчитайте предел lim(((2×n/(n+1))^n)^(1/n))=lim(2×n/(n+1)) при n стремящимся к ∞. Предел равен 2>1, то есть данный ряд расходится. Определите сходимость ряда по признаку Даламбера. Для этого посчитайте предел lim((xn+1)/xn) при n стремящимся к ∞. Если этот предел существует и равен M1, то ряд расходится. Если M=1, то ряд может быть сходящимся и расходящимся.Изучите несколько примеров. Пусть дан ряд Σ(2^n/n!). Посчитайте предел lim((2^(n+1)/(n+1)!)×(n!/2^n))=lim(2/(n+1)) при n стремящимся к ∞. Он равен 0<1 и данный ряд является сходящимся. Пусть теперь дан ряд Σn!×(6/n)^n. Вычислите предел lim((n+1)!×6^(n+1)×n^n)/((n+1)^(n+1)×n!×6^n)=lim (6/(1+1/n)^n)=6/e>1 и значит данный ряд расходится.
Воспользуйтесь признаком Лейбница для знакочередующегося ряда при условии, что xn>x(n+1). Посчитайте предел lim(xn) при n стремящимся к ∞. Если этот предел равен 0, то ряд сходится, его сумма положительна и не превосходит первого члена ряда. Например, пусть дан ряд 1−1/2+1/3−1/4+…. Заметьте, что 1>1/2>1/3>…>1/n>…. Общий член ряда будет 1/n. Посчитайте предел lim(1/n) при n стремящимся к ∞. Он равен 0 и, следовательно, ряд сходится.
Обратите внимание
Знак ^ обозначает возведение в степень.
Из названия числового ряда очевидно, что это последовательность чисел. Применяется этот термин в математическом, а также комплексном анализе как система приближений к числам. Понятие числового ряда неразрывно связано с понятием предела, а основной характеристикой является сходимость.

Инструкция
Пусть есть числовая последовательность вида a_1, a_2, a_3, …, a_n и некоторая последовательность s_1, s_2, …, s_k, где n и k стремятся к ∞, а элементы последовательности s_j представляют собой суммы некоторых членов последовательности a_i. Тогда последовательность a является числовым рядом, а s — последовательностью его частичных сумм:s_j = Σa_i, где 1 ≤ i ≤ j. Задачи на решение числовых рядов сводятся к определению его сходимости. Говорят, что ряд сходится, если сходится последовательность его частичных сумм и абсолютно сходится, если последовательность модулей его частичных сумм сходится. И наоборот, если расходится последовательность частичных сумм ряда, то он расходится.
Чтобы доказать сходимость последовательности частичных сумм, необходимо перейти к понятию ее предела, который называют суммой ряда:
S = lim_n→∞ Σ_(i=1)^n a_i.
Пример1.
Определите сходимость ряда 1/3 + 2/5 + 3/7 + … + n/(2*n+1) + ….
Решение.
Примените необходимый признак сходимости – стремится ли общий член к нулю:
lim a_i = lim n/(2*n+1) = ½.
Итак, a_i ≠ 0, следовательно, ряд расходится.
Пример2.
Определите сходимость ряда 1 + ½ + 1/3 + … + 1/n + ….
Решение.
Стремится ли общий член к нулю:
lim 1/n = 0. Да, стремится, выполнен необходимый признак сходимости, однако этого недостаточно. Теперь с помощью предела последовательности сумм попробуем доказать, что ряд расходится:
s_n = Σ_(k=1)^n 1/k = 1 + ½ + 1/3 + … + 1/n. Последовательность сумм, хоть и очень медленно, но очевидно стремится к ∞, следовательно, ряд расходится.
Признак сходимости Даламбера.
Пусть существует конечный предел отношения последующего и предыдущего членов ряда lim (a_(n+1)/a_n) = D. Тогда:
D 1 – ряд расходится;
D = 1 – решение неопределенно, нужно воспользоваться дополнительным признаком.
Радикальный признак сходимости Коши.
Пусть существует конечный предел вида lim √(n&a_n) = D. Тогда:
D 1 – ряд расходится;
D = 1 – нет однозначного ответа.
Эти два признака можно использовать в совокупности, однако признак Коши более сильный. Существует также интегральный признак Коши, согласно которому для определения сходимости ряда необходимо найти соответствующий определенный интеграл. Если он сходится, то сходится и ряд, и наоборот.
Видео по теме
www.kakprosto.ru
Числовые ряды
ВЫСШАЯ МАТЕМАТИКА
Числовые ряды
Содержание
Лекция. Числовые ряды
1. Определение числового ряда. Сходимость
2. Основные свойства числовых рядов
3. Ряды с положительными членами. Признаки сходимости
4. Знакочередующиеся ряды. Признак сходимости Лейбница
5. Знакопеременные ряды
Вопросы для самопроверки
Литература
Лекция. ЧИСЛОВЫЕ РЯДЫ
1. Определение числового ряда. Сходимость.
2. Основные свойства числовых рядов.
3. Ряды с положительными членами. Признаки сходимости.
4. Знакочередующиеся ряды. Признак сходимости Лейбница.
5. Знакопеременные ряды.
1. Определение числового ряда. Сходимость
В математических приложениях, а также при решении некоторых задач в экономике, статистике и других областях рассматриваются суммы с бесконечным числом слагаемых. Здесь мы дадим определение того, что понимается под такими суммами.
Пусть задана бесконечная числовая последовательность
, , …, , …Определение 1.1 . Числовым рядом или просто рядом называется выражение (сумма) вида
. (1.1)Числа
называются членами ряда , – общим или n – м членом ряда.Чтобы задать ряд (1.1) достаточно задать функцию натурального аргумента
вычисления -го члена ряда по его номеруПример 1.1 . Пусть
. Ряд (1.2)называется гармоническим рядом .
Пример 1.2 . Пусть
, Ряд (1.3)называется обобщенным гармоническим рядом . В частном случае при
получается гармонический ряд.Пример 1.3 . Пусть
=. Ряд (1.4)называется рядом геометрической прогрессии .
Из членов ряда (1.1) образуем числовую последовательность частичных сумм где
– сумма первых членов ряда, которая называется n —й частичной суммой , т. е. , , ,…………………………….
, (1.5)…………………………….
Числовая последовательность
при неограниченном возрастании номера может:1) иметь конечный предел;
2) не иметь конечного предела (предел не существует или равен бесконечности).
Определение 1.2 . Ряд (1.1) называется сходящимся, если последовательность его частичных сумм (1.5) имеет конечный предел, т. е.
В этом случае число
называется суммой ряда (1.1) и пишется .Определение 1.3. Ряд (1.1) называется расходящимся, если последовательность его частичных сумм не имеет конечного предела .
Расходящемуся ряду не приписывают никакой суммы.
Таким образом, задача нахождения суммы сходящегося ряда (1.1) равносильна вычислению предела последовательности его частичных сумм.
Рассмотрим несколько примеров.
Пример 1.4. Доказать, что ряд
сходится, и найти его сумму.
Найдем n — ю частичную сумму данного ряда
.Общий член
ряда представим в виде .Тогда
Отсюда имеем:
. Следовательно, данный ряд сходится и его сумма равна 1:Пример 1.5 . Исследовать на сходимость ряд
(1.6)Для этого ряда
. Следовательно, данный ряд расходится.Замечание. При
ряд (1.6) представляет собой сумму бесконечного числа нулей и является, очевидно, сходящимся.Пример 1.6. Исследовать на сходимость ряд
(1.7)Для этого ряда
В этом случае предел последовательности частичных сумм
не существует, и ряд расходится.Пример 1.7. Исследовать на сходимость ряд геометрической прогрессии (1.4):
Нетрудно показать, что n -я частичная сумма ряда геометрической прогрессии при
задается формулой .Рассмотрим случаи:
1)
Тогда и .Следовательно, ряд сходится и его сумма равна
2)
.Тогда
и .Следовательно, ряд расходится.
3)
или Тогда исходный ряд имеет вид (1.6) или (1.7) соответственно, которые расходятся. Окончательно имеем (1.8)Пример 1.8. Найти сумму ряда
Очевидно, что данный ряд является рядом геометрической прогрессии. В наше
mirznanii.com
Числовые ряды.
Пусть дана числовая последовательность .
Выражение вида называется числовым рядом или просто рядом.
При
этом числа называются членами ряда, а член 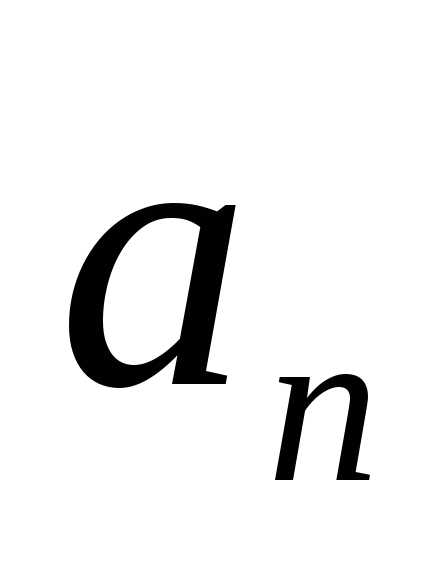 с произвольным номером —общим
членом ряда.
с произвольным номером —общим
членом ряда.
Суммы конечного числа членов ряда:
называются частичными суммами ряда. Так как число членов ряда бесконечно, то частичные суммы ряда образуют бесконечную последовательность частичных сумм .
Если все члены ряда положительны, то ряд называется знакоположительным.
Ряд
называется сходящимся,
если предел 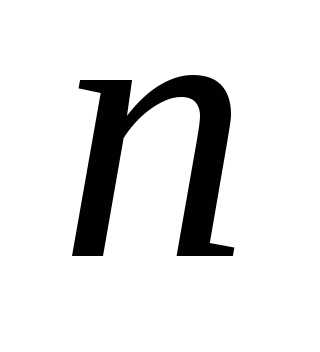 -частичной суммы существует и конечен,
т.е.
-частичной суммы существует и конечен,
т.е.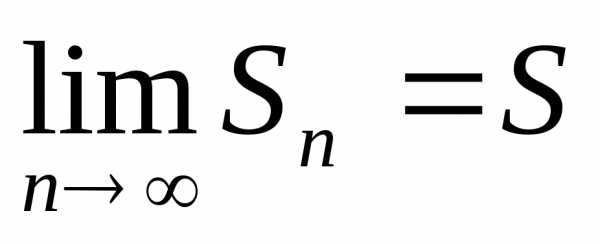 ,
в противном случае говорят, что рядрасходится. При этом
,
в противном случае говорят, что рядрасходится. При этом  называется суммой ряда.
называется суммой ряда.
Ряд: ,
где  — знаменатель геометрической прогрессии,
называется рядом геометрической прогрессии.
— знаменатель геометрической прогрессии,
называется рядом геометрической прогрессии.
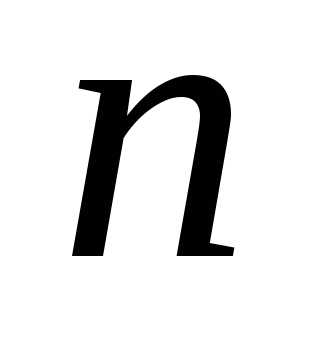 -частичная
сумма ряда геометрической прогрессии
равна:
-частичная
сумма ряда геометрической прогрессии
равна:
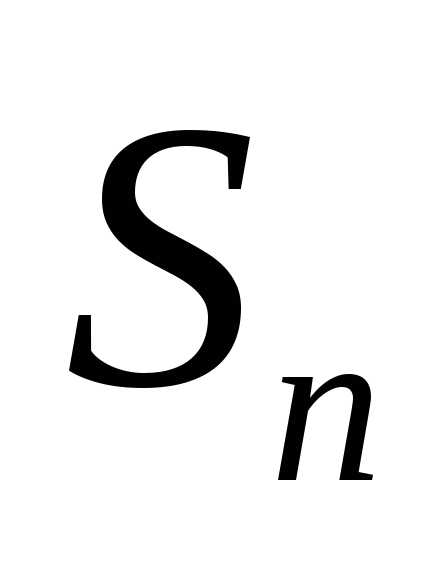 =.
=.
Ряд
геометрической прогрессии является
сходящимся
при 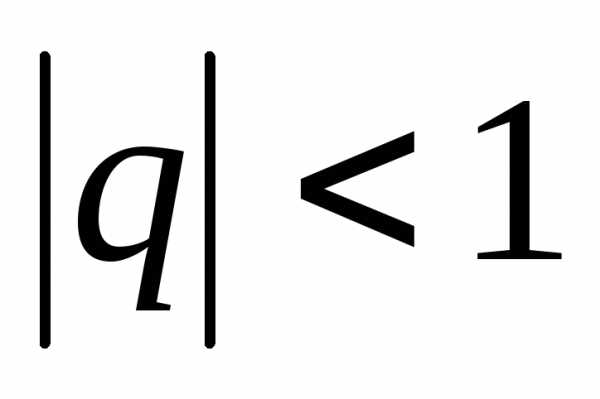 (его сумма
(его сумма 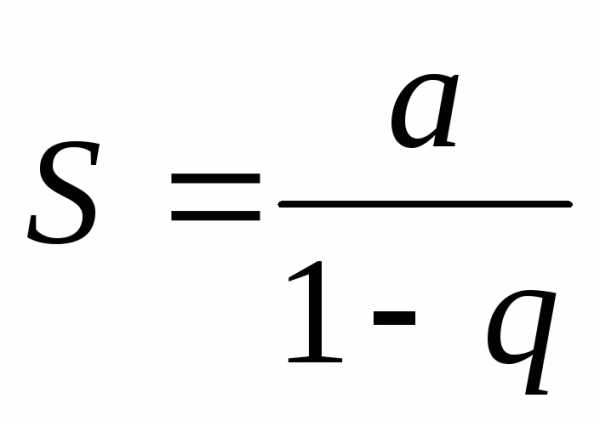 )и расходящимся
при
)и расходящимся
при 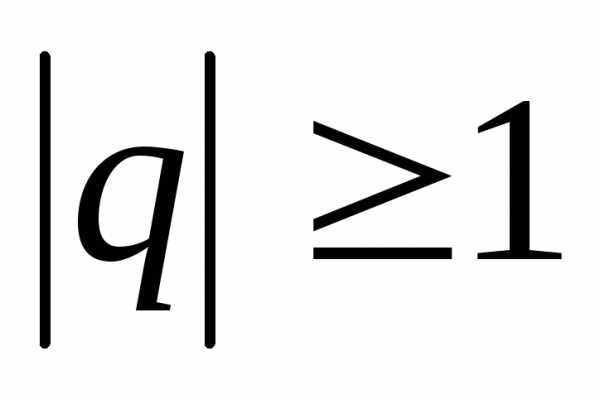 .
.
Свойства сходящихся рядов:
Если сходится ряд:
то сходится и ряд
и обратно, если сходится второй ряд, то сходится и первый.
Другими словами, на сходимость ряда не влияет отбрасывание любого конечного числа его первых членов.
Если ряд
 сходится и
его сумма равна
сходится и
его сумма равна  ,
то и ряд
,
то и ряд  ,где с — некоторое число, также сходится, и
его
сумма
равна
,где с — некоторое число, также сходится, и
его
сумма
равна  .
.
Если ряды
 и
и  сходятся и их
суммы
соответственно равны
сходятся и их
суммы
соответственно равны  и
и ,
то и ряд
,
то и ряд  cходится
и его сумма равна
cходится
и его сумма равна  .
.
Таким образом, установлено, что сходящиеся ряды можно умножать на число, почленно складывать и вычитать так же, как и конечные суммы.
Необходимое и достаточные условия сходимости ряда.
При рассмотрении рядов возникают две задачи: 1) исследовать ряд на сходимость и 2) зная, что ряд сходится, найти его сумму. Будем решать в основном первую задачу, имеющую теоретический характер. Приведем необходимое условие сходимости рядов.
Если
ряд 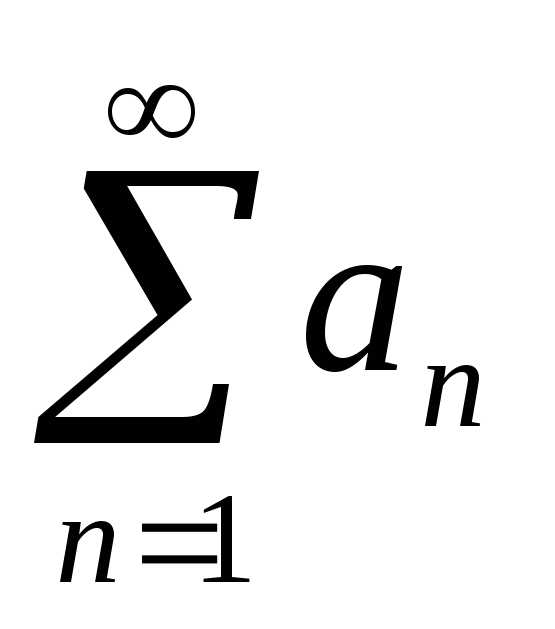 сходится,
то его общий член стремится к нулю, т.е.
сходится,
то его общий член стремится к нулю, т.е. 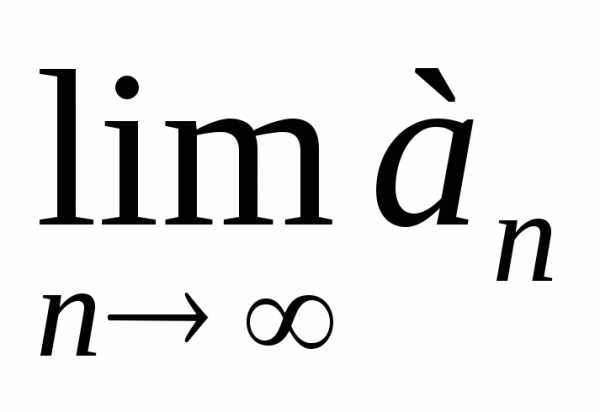 =0.
=0.
Числовой ряд:
называется гармоническим рядом.
Только
невыполнение необходимого условия
сходимости позволяет делать определённый
вывод, а его выполненине, как в данном
случае 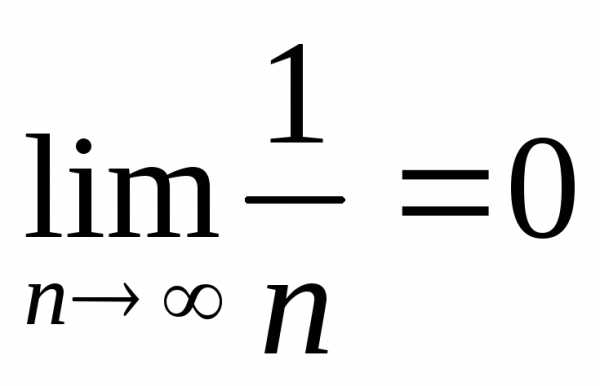 ,
не позволяет судить о сходимости.
,
не позволяет судить о сходимости.
Лекция 42
Признаки сходимости рядов
Перейдем теперь к рассмотрению некоторых достаточных условий сходимости рядов с неотрицательными членами.
Для
того чтобы, ряд 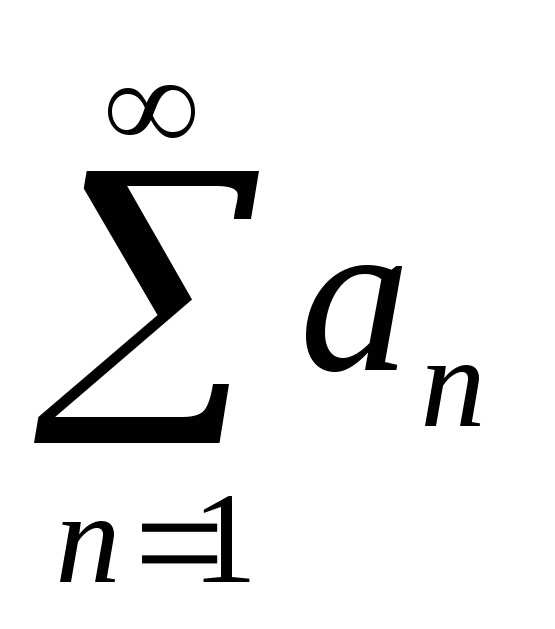 снеотрицательными
членами сходился, необходимо и достаточно,
чтобы последовательность частичных
сумм этого ряда была ограничена.
снеотрицательными
членами сходился, необходимо и достаточно,
чтобы последовательность частичных
сумм этого ряда была ограничена.
Это значит, что последовательность его частичных сумм имеет предел. Всякая сходящаяся последовательность является ограниченной.
Установим ряд признаков, позволяющих сделать вывод о сходимости (расходимости) рассматриваемого ряда.
Признак сравнения.
Пусть
даны два ряда с неотрицательными членами 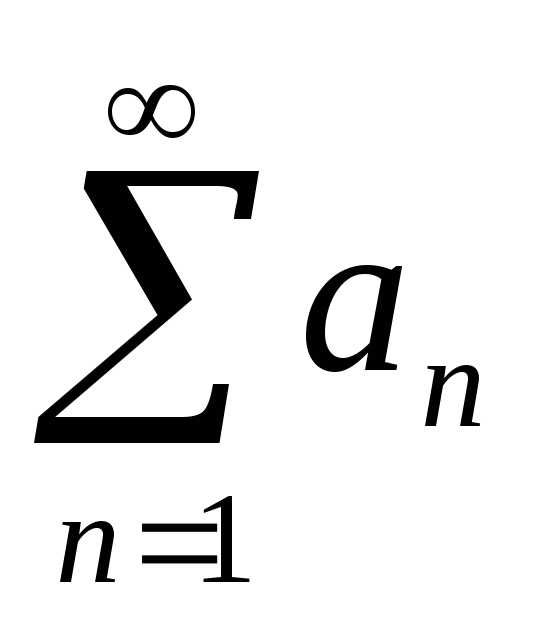 и
и 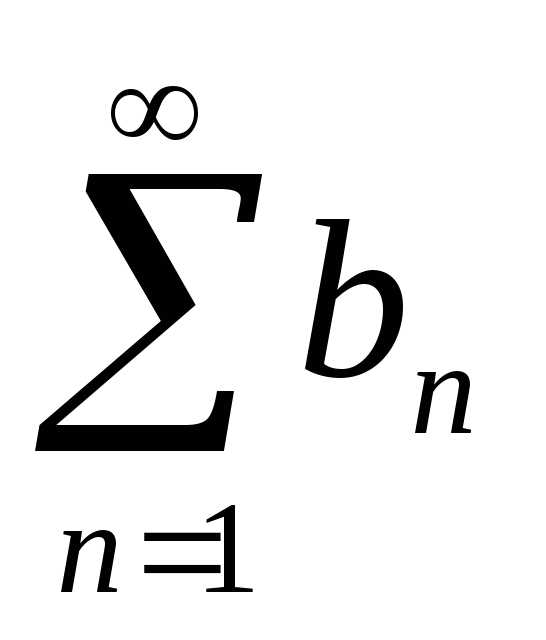 и для всех n
выполняется неравенство
и для всех n
выполняется неравенство 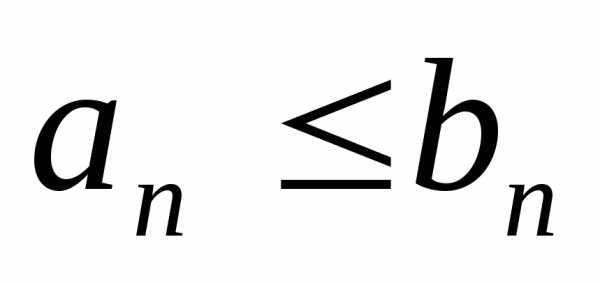 . Тогда:
из сходимости ряда
. Тогда:
из сходимости ряда 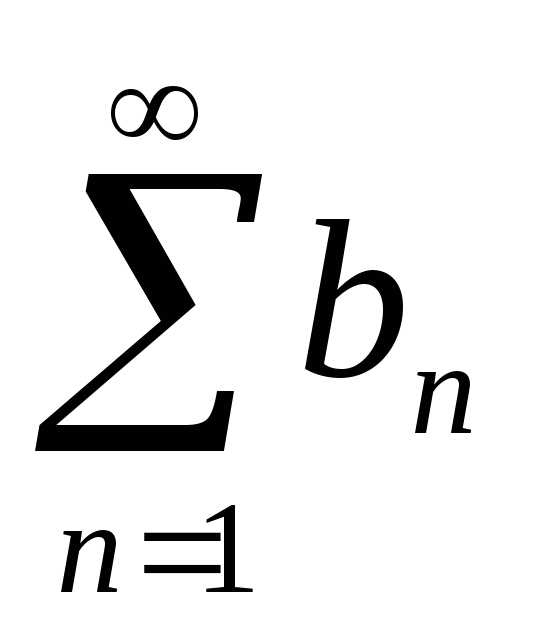 следует
сходимость ряда
следует
сходимость ряда 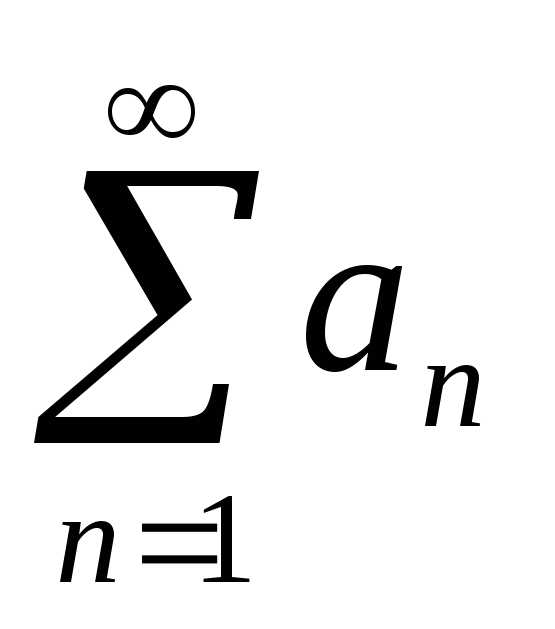 ,
а из
расходимости ряда
,
а из
расходимости ряда 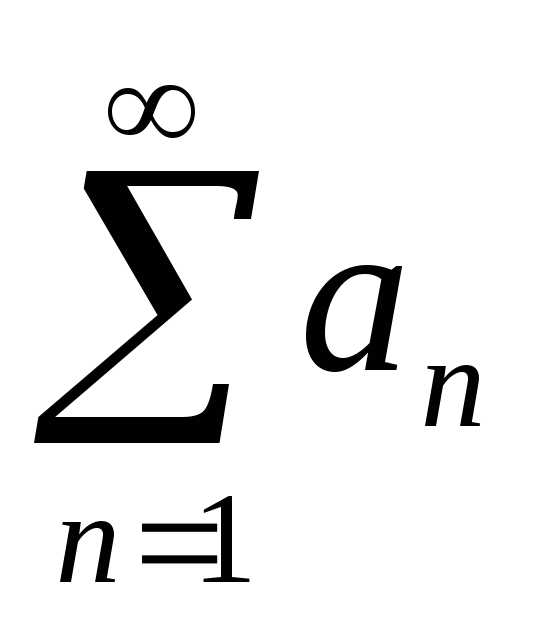 следует
расходимость ряда
следует
расходимость ряда 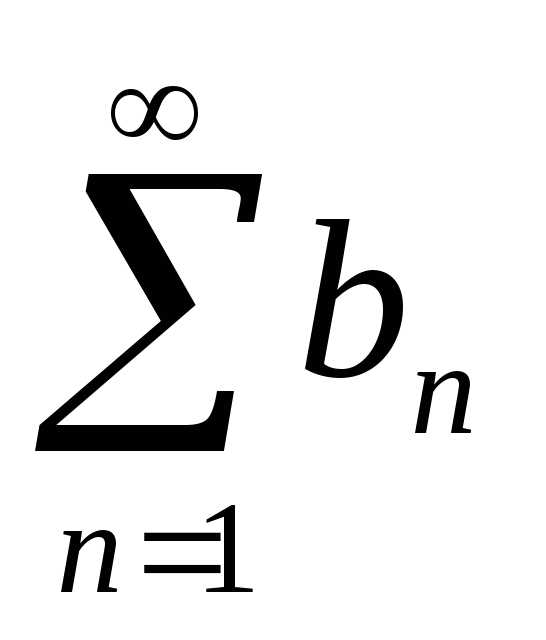 .
.
Признак Даламбера (Даламбер Жан Лерон (1717-1783)-французский математик, механик и философ-просветитель).
Пусть
дан ряд 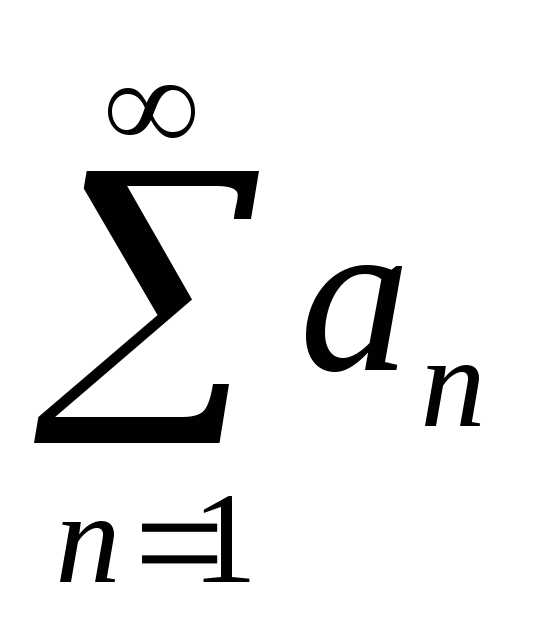 с
положительными членами
и существует предел
с
положительными членами
и существует предел 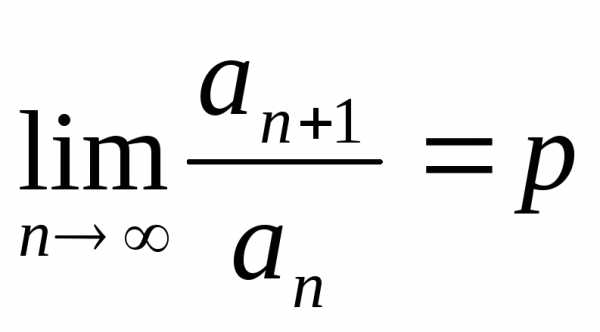 .Тогда: а) при
.Тогда: а) при 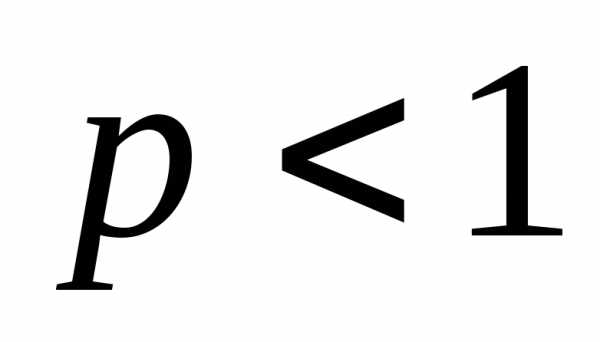 ряд
сходится; б) при
ряд
сходится; б) при 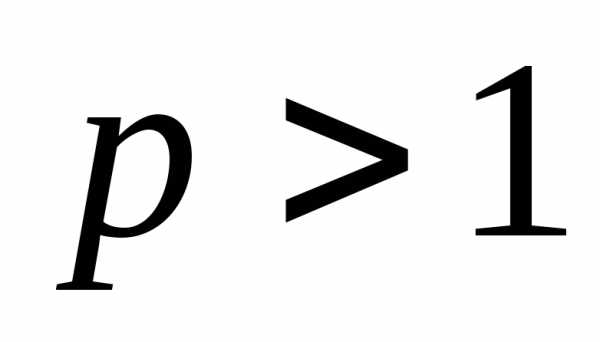 ряд расходится.
ряд расходится.
Интегральный признак.
Пусть
дан ряд ,члены
которого являются значениями некоторой
функции 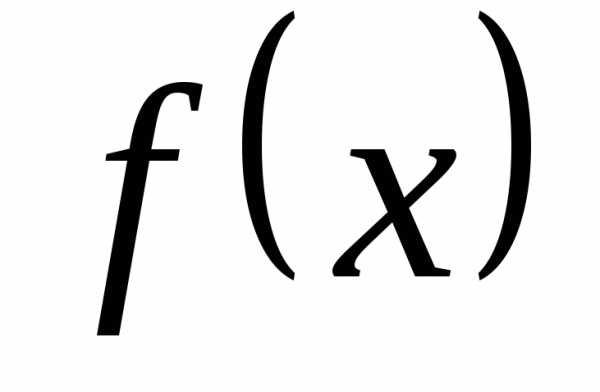 , положительной,
непрерывной и убывающей на полуинтервале
, положительной,
непрерывной и убывающей на полуинтервале 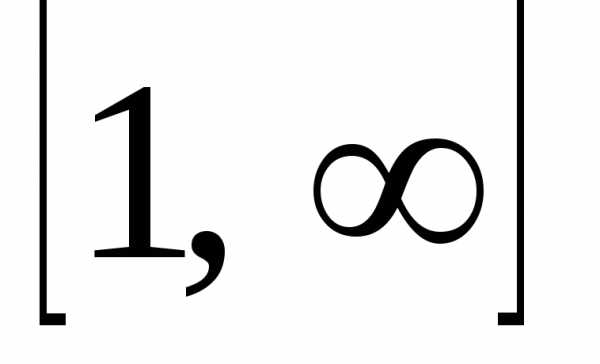 .
.
Тогда,
если 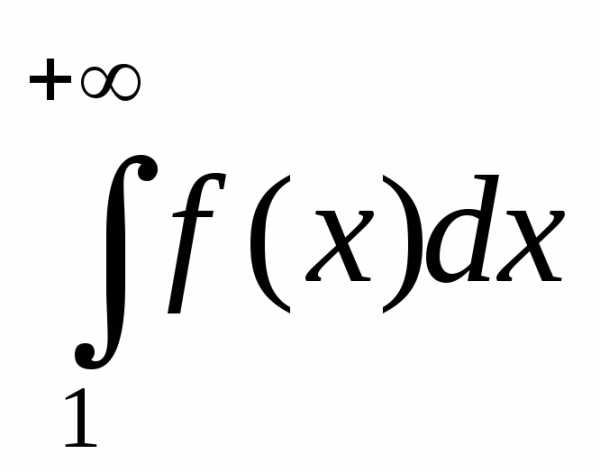 сходится, то сходится и ряд
сходится, то сходится и ряд 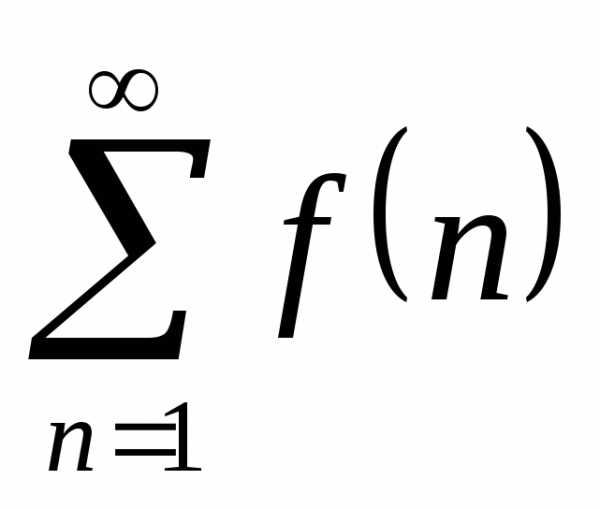 ;
;
если же 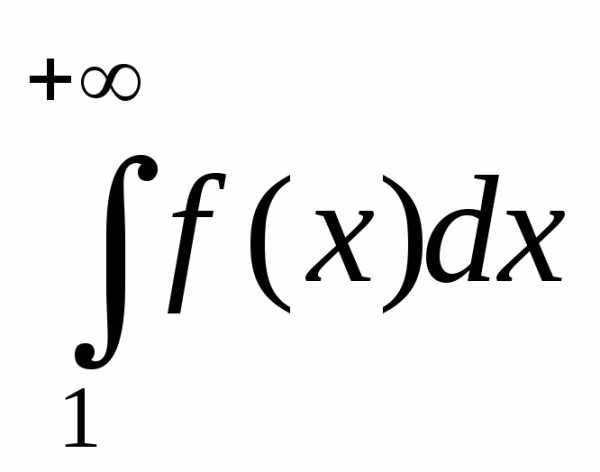 расходится, то ряд
расходится, то ряд 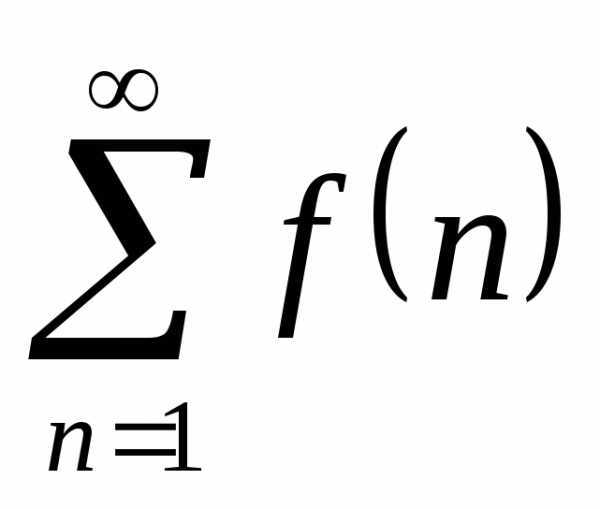 также расходится.
также расходится.
Гармонический ряд:
расходится, так как .
До сих пор мы рассматривали ряды с неотрицательными членами. Ряды с неположительными членами отличаются от соответствующих рядов с неотрицательными членами только множителем (-1), поэтому вопрос об их сходимости решается аналогично.
Перейдем теперь к рассмотрению знакочередующихся рядов, члены которых имеют чередующиеся знаки. Для удобства будем считать, что первый член такого ряда положителен. Тогда знакочередующийся ряд можно записать в виде:
,
где 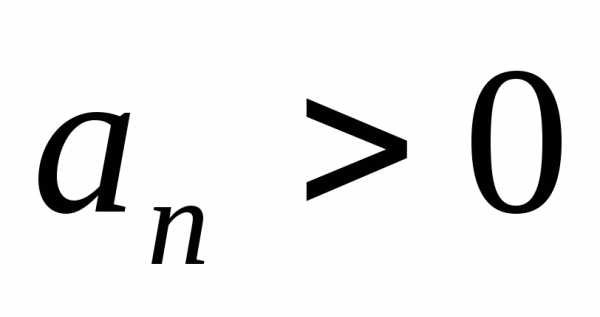 .
.
Для знакочередующихся рядов имеет место следующий очень простой достаточный признак сходимости.
ПризнакЛейбница.
Если
абсолютные величины членов знакочередующегося
ряда монотонно
убывают: и общий член ряда стремится к нулю 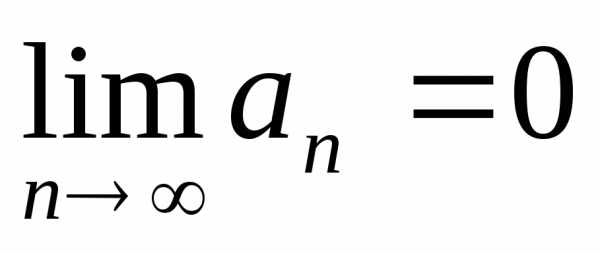 ,
то ряд сходится.
,
то ряд сходится.
Рассмотрим теперь ряды с членами произвольных знаков. Такие ряды называются знакопеременными рядами.
Возьмем какой-нибудь знакопеременный ряд
,
где числа могут быть как положительными, так и отрицательными, причем расположение положительных и отрицательных членов в ряде произвольно.
Абсолютная и условная сходимость рядов.
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд из модулей его слагаемых:
Знакопеременный ряд называется условно сходящимся, если он сходится, но ряд из модулей его слагаемых расходится.
studfiles.net
Числовые и функциональные ряды. Лекция 15. Числовые ряды.
1.Числовые ряды: основные понятия, необходимые условия сходимости ряда. Остаток ряда.
2.Ряды с положительными членами и признаки их сходимости: признаки сравнения, Даламбера, Коши.
3. Знакочередующиеся ряды, признак Лейбница.
1. Определение числового ряда. Сходимость
В математических приложениях, а также при решении некоторых задач в экономике, статистике и других областях рассматриваются суммы с бесконечным числом слагаемых. Здесь мы дадим определение того, что понимается под такими суммами.
Пусть задана бесконечная числовая последовательность
, , …,, …
Определение 1.1. Числовым рядом или просто рядом называется выражение (сумма) вида
. (1.1)
Числа называютсячленами ряда, –общим или n–м членом ряда.
Чтобы задать ряд (1.1) достаточно задать функцию натурального аргумента вычисления-го члена ряда по его номеру
Пример 1.1. Пусть . Ряд
(1.2)
называется гармоническим рядом.
Пример 1.2. Пусть ,Ряд
(1.3)
называется обобщенным гармоническим рядом. В частном случае при получается гармонический ряд.
Пример 1.3. Пусть =. Ряд
(1.4)
называется рядом геометрической прогрессии.
Из членов ряда (1.1) образуем числовую последовательность частичных сумм где – суммапервых членов ряда, которая называетсяn—й частичной суммой, т. е.
,
,
,
…………………………….
, (1.5)
…………………………….
Числовая последовательность при неограниченном возрастании номераможет:
1) иметь конечный предел;
2) не иметь конечного предела (предел не существует или равен бесконечности).
Определение 1.2. Ряд (1.1) называется сходящимся, если последовательность его частичных сумм (1.5) имеет конечный предел, т. е.
В этом случае число называетсясуммой ряда (1.1) и пишется
.
Определение 1.3. Ряд (1.1) называется расходящимся, если последовательность его частичных сумм не имеет конечного предела.
Расходящемуся ряду не приписывают никакой суммы.
Таким образом, задача нахождения суммы сходящегося ряда (1.1) равносильна вычислению предела последовательности его частичных сумм.
Рассмотрим несколько примеров.
Пример 1.4. Доказать, что ряд
сходится, и найти его сумму.
Найдем n-ю частичную сумму данного ряда .
Общий член ряда представим в виде.
Отсюда имеем: . Следовательно, данный ряд сходится и его сумма равна 1:
Пример 1.5. Исследовать на сходимость ряд
(1.6)
Для этого ряда
. Следовательно, данный ряд расходится.
Замечание. При ряд (1.6) представляет собой сумму бесконечного числа нулей и является, очевидно, сходящимся.
2. Основные свойства числовых рядов
Свойства суммы конечного числа слагаемых отличаются от свойств ряда, т. е. суммы бесконечного числа слагаемых. Так, в случае конечного числа слагаемых их можно группировать в каком угодно порядке, от этого сумма не изменится. Существуют сходящиеся ряды (условно сходящиеся, которые будут рассмотрены в разделе 5), для которых, как показал Риман*, меняя надлежащим образом порядок следования их членов, можно сделать сумму ряда равной какому угодно числу, и даже расходящийся ряд.
Пример 2.1. Рассмотрим расходящийся ряд вида (1.7)
Сгруппировав его члены попарно, получим сходящийся числовой ряд с суммой, равной нулю:
С другой стороны, сгруппировав его члены попарно, начиная со второго члена, получим также сходящийся ряд, но уже с суммой, равной единице:
Сходящиеся ряды обладают некоторыми свойствами, которые позволяют действовать с ними, как с конечными суммами. Так их можно умножать на числа, почленно складывать и вычитать. У них можно объединять в группы любые рядом стоящие слагаемые.
Теорема 2.1. (Необходимый признак сходимости ряда).
Если ряд (1.1) сходится, то его общий член стремится к нулю при неограниченном возрастании n, т. е.
(2.1)
Доказательство теоремы следует из того, что , и если
S – сумма ряда (1.1), то
Условие (2.1) является необходимым, но недостаточным условием для сходимости ряда. Т. е., если общий член ряда стремится к нулю при , то это не значит, что ряд сходится. Например, для гармонического ряда (1.2)однако, как будет показано ниже, он расходится.
Следствие (Достаточный признак расходимости ряда).
Если общий член ряда не стремится к нулю при, то этот ряд расходится.
Пример 2.2. Исследовать на сходимость ряд
.
Для этого ряда
Следовательно, данный ряд расходится.
Рассмотренные выше расходящиеся ряды (1.6), (1.7) также являются таковыми в силу того, что для них не выполняется необходимый признак сходимости.Для ряда (1.6) пределдля ряда (1.7) пределне существует.
Свойство 2.1. Сходимость или расходимость ряда не изменится, если произвольным образом удалить из него, добавить к нему, переставить в нем конечное число членов (при этом для сходящегося ряда его сумма может измениться).
Доказательство свойства следует из того, что ряд (1.1) и любой его остаток сходятся или расходятся одновременно.
Свойство 2.2. Сходящийся ряд можно умножать на число, т. е., если ряд (1.1) сходится, имеет сумму S и c – некоторое число, тогда
Доказательство следует из того, что для конечных сумм справедливы равенства
Свойство 2.3. Сходящиеся ряды можно почленно складывать и вычитать, т. е. если ряды ,
сходятся,
то и ряд
сходится и его сумма равна т. е.
.
Доказательство следует из свойств предела конечных сумм, т. е.
studfiles.net
Числовые ряды
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.
Написать пять первых членов ряда,
 -ый
член которого имеет вид:
-ый
член которого имеет вид: .
.
РЕШЕНИЕ:
Первые пять членов ряда имеют порядковые номера, соответственно, . Подставляя эти значения в формулу общего члена, получим:
Написать
 -ый
член ряда.
-ый
член ряда.
РЕШЕНИЕ:
Так
как все члены ряда с четными номерами
отрицательны, а с нечетными – положительны,
то в записи общего члена будет 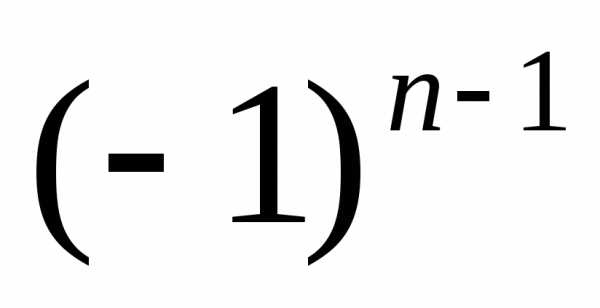 .
.
Величина
под квадратным корнем в числителе
отличается от порядкового номера на 1:
при  имеем
имеем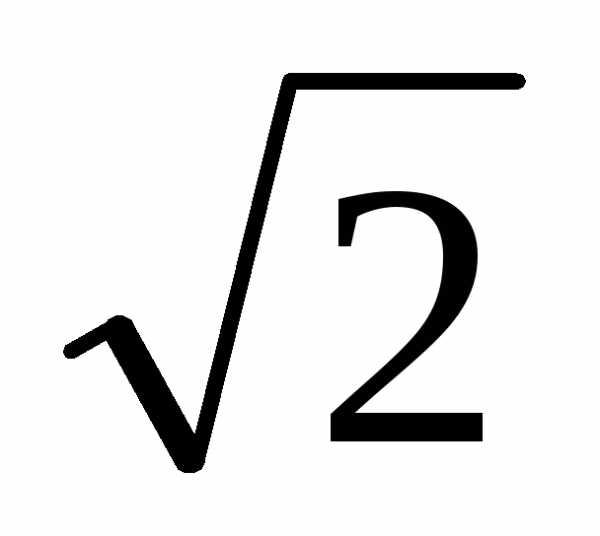 ,
при
,
при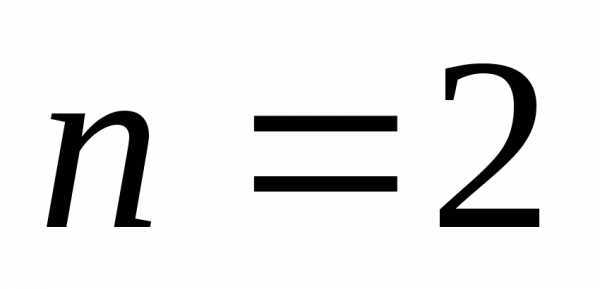 имеем
имеем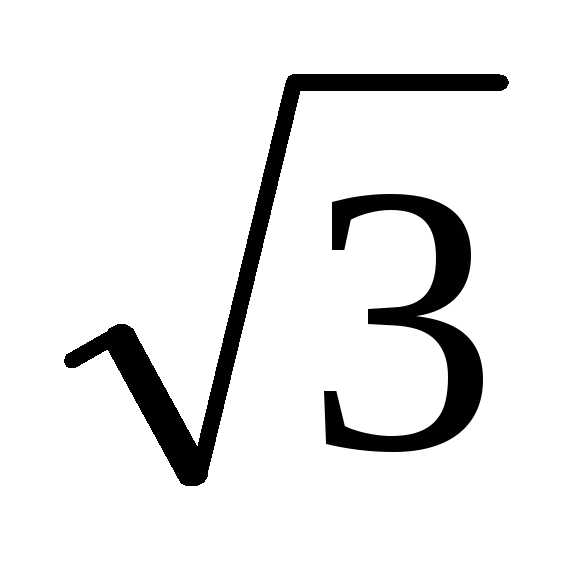 ,
при
,
при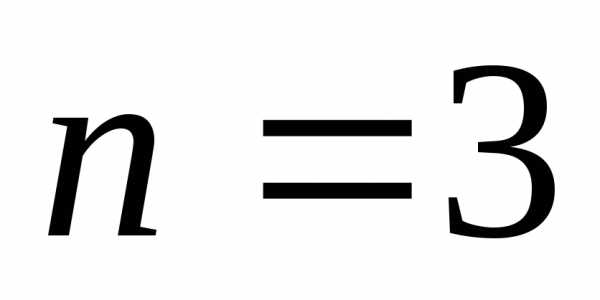 имеем
имеем .
Следовательно, в общем случае, при
.
Следовательно, в общем случае, при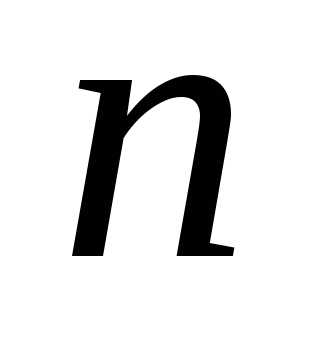 имеем
имеем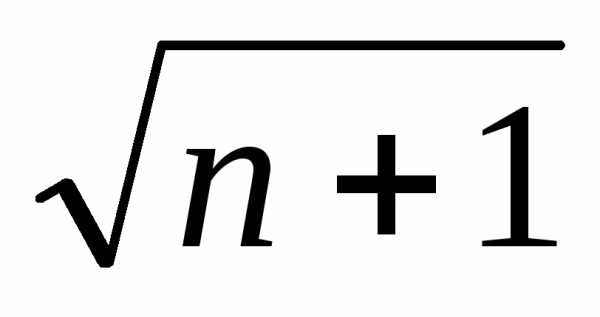 .
.
В знаменателе, очевидно, будет стоять факториал некоторой величины. Напомним, что
.
Тогда
при 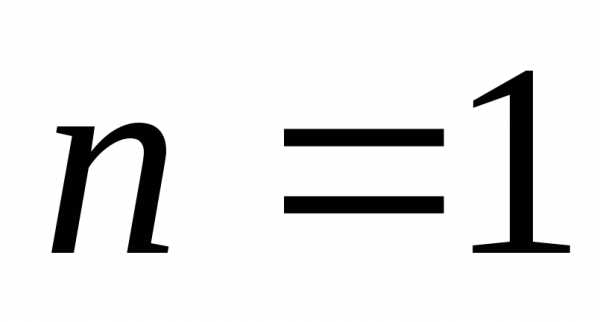 имеем в знаменателе
имеем в знаменателе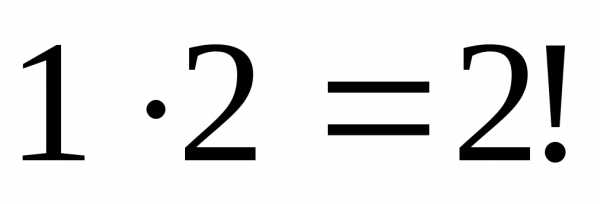 ,
при
,
при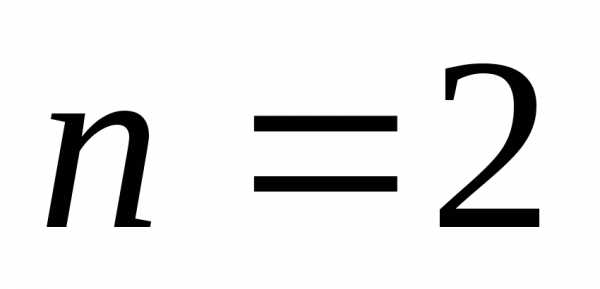 имеем,
при
имеем,
при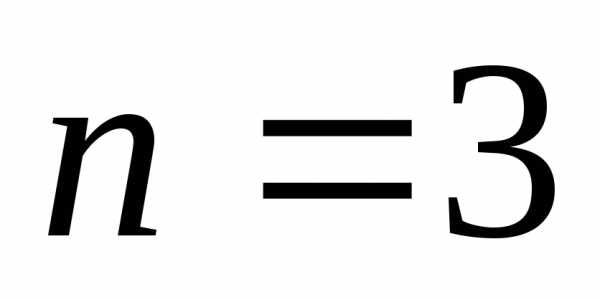 имеем.
Тогда, в общем случае, при
имеем.
Тогда, в общем случае, при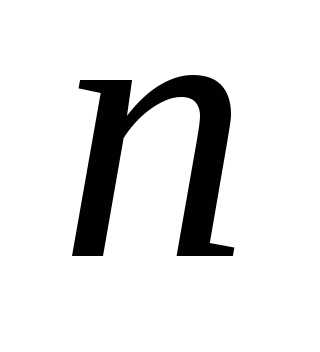 имеем
имеем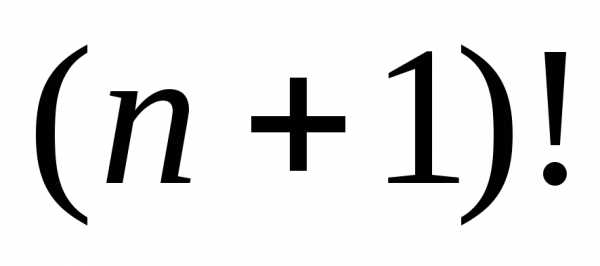 .
.
Получаем общий член ряда в виде:
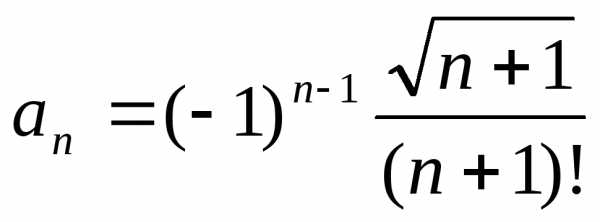 .
.
Используя необходимый признак сравнения, исследовать сходимость ряда
 .
.
РЕШЕНИЕ:
Согласно необходимому признаку сходимости ряда, если числовой ряд сходится, то предел его общего члена при будет равен нулю:
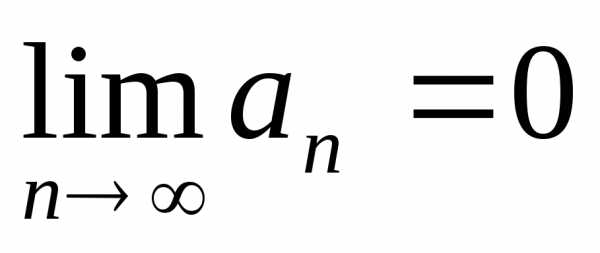 .
.
В нашем примере общий член ряда
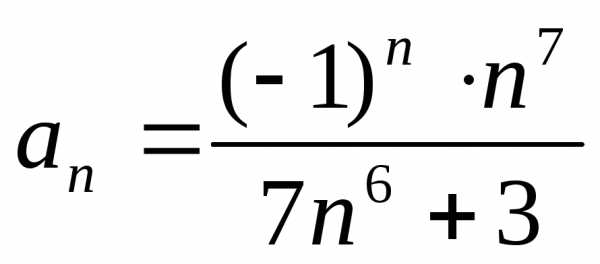 .
.
Найдем предел общего члена:
.
Необходимое условие сходимости ряда не выполняется, следовательно, данный ряд расходится.
Отметим, что, так как данный признак является необходимым, но не достаточным, то из равенства предела общего члена нулю, еще не следует сходимость данного ряда. В этом случае нужно применить дополнительные методы исследования сходимости рядов.
Используя признак сравнения, исследовать сходимость ряда:
РЕШЕНИЕ:
Согласно
признаку сравнения рядов, если для двух
рядов с неотрицательными членами  и
и для всехn выполняется
неравенство
для всехn выполняется
неравенство 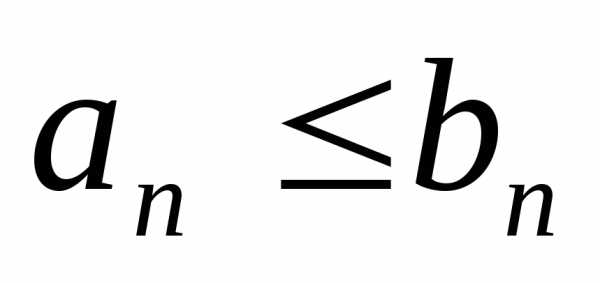 ,
то из сходимости второго ряда следует
сходимость первого, а из расходимости
первого ряда, следует расходимость
второго.
,
то из сходимости второго ряда следует
сходимость первого, а из расходимости
первого ряда, следует расходимость
второго.
Для того, чтобы воспользоваться признаком сравнения, нужно выбрать для сравнения один из эталонный рядов:
1. 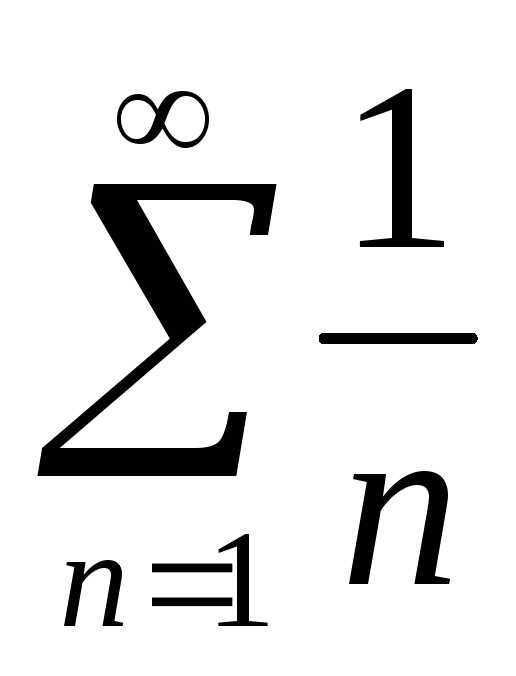 — гармонический ряд. Этот ряд расходится.
— гармонический ряд. Этот ряд расходится.
2. 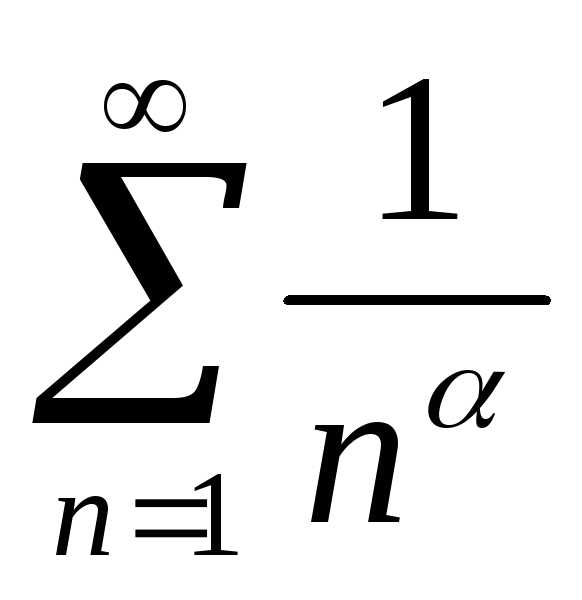 — обобщенный гармонический ряд. Сходится
при
— обобщенный гармонический ряд. Сходится
при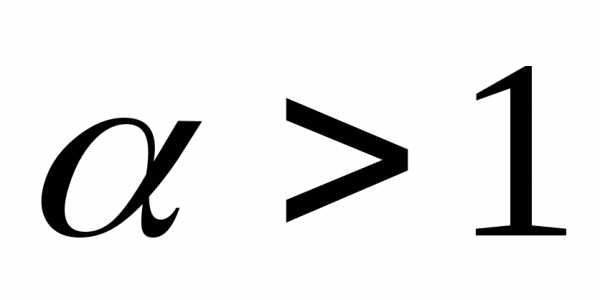 ,
расходится при
,
расходится при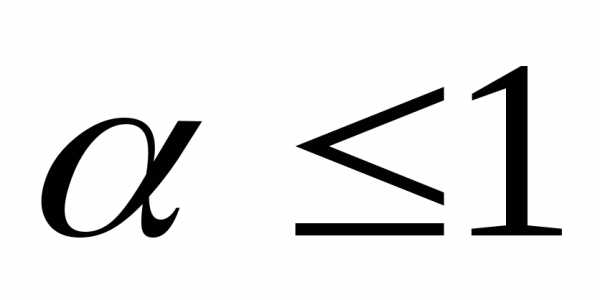 .
.
3. 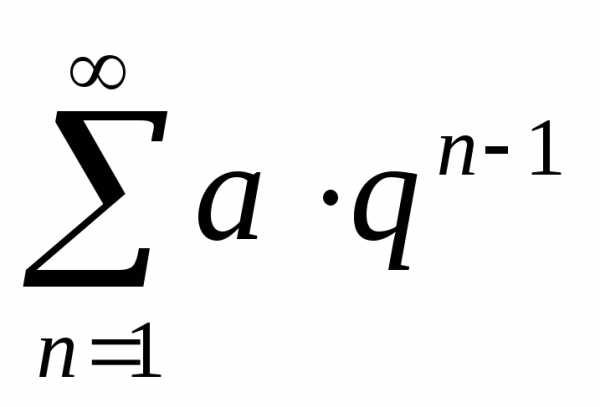 — геометрический ряд. Сходится при
— геометрический ряд. Сходится при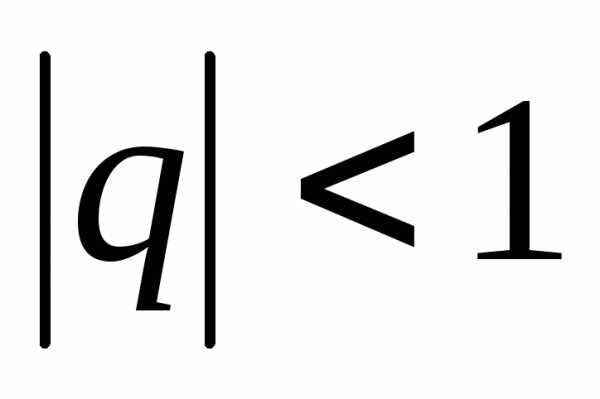 ,
расходится при
,
расходится при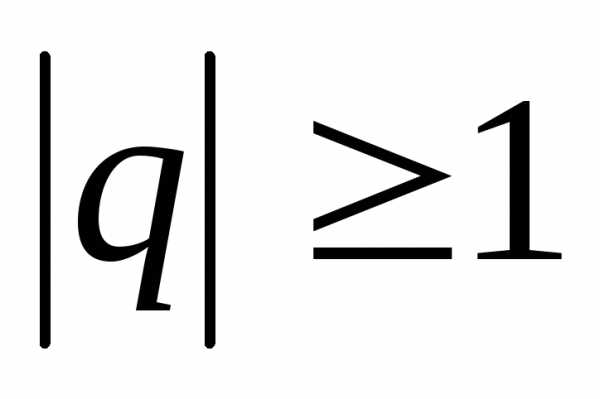 .
.
В нашем случае для сравнения выберем геометрический ряд
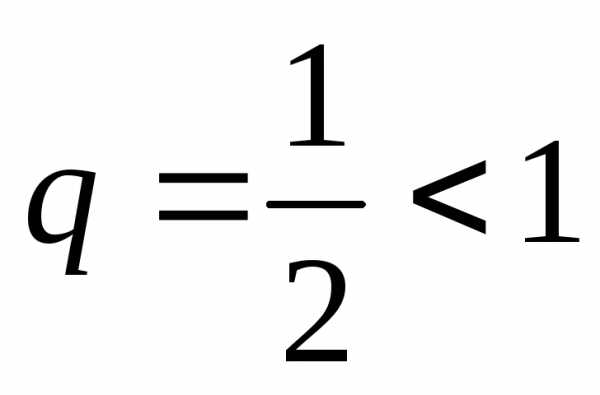 ,
следовательно, эталонный ряд будет
сходящимся.
,
следовательно, эталонный ряд будет
сходящимся.
Каждый
член исходного ряда 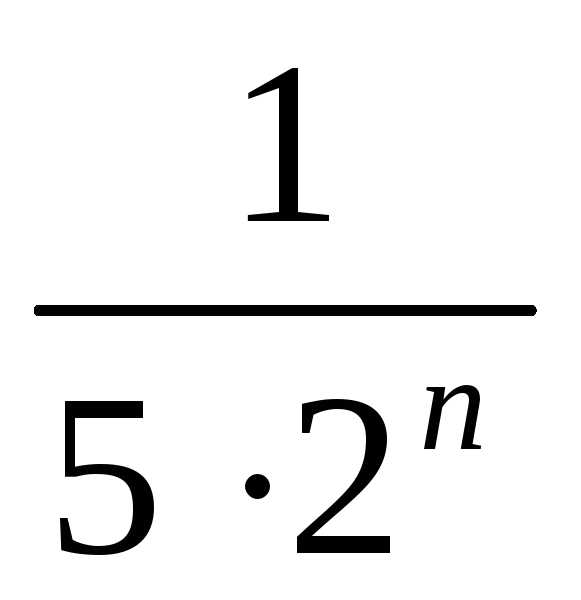 будет меньше соответствующего члена
эталонного ряда
будет меньше соответствующего члена
эталонного ряда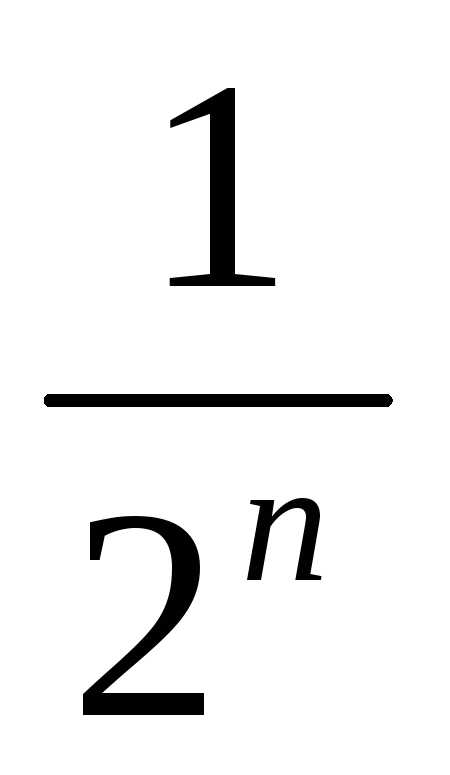 ,
т.е.
,
т.е.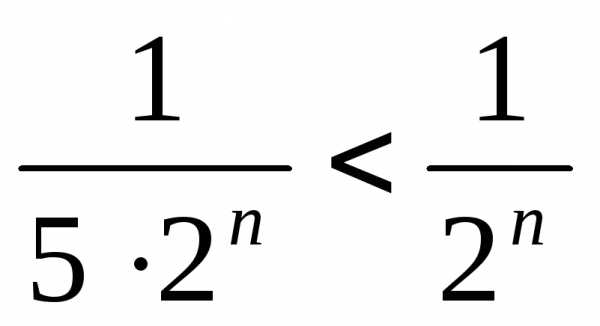 .
.
Поэтому исходный ряд тоже будет сходиться.
Используя признак сравнения, исследовать сходимость ряда:
 .
.
РЕШЕНИЕ:
В
качестве эталонного ряда выберем для
сравнения гармонический ряд 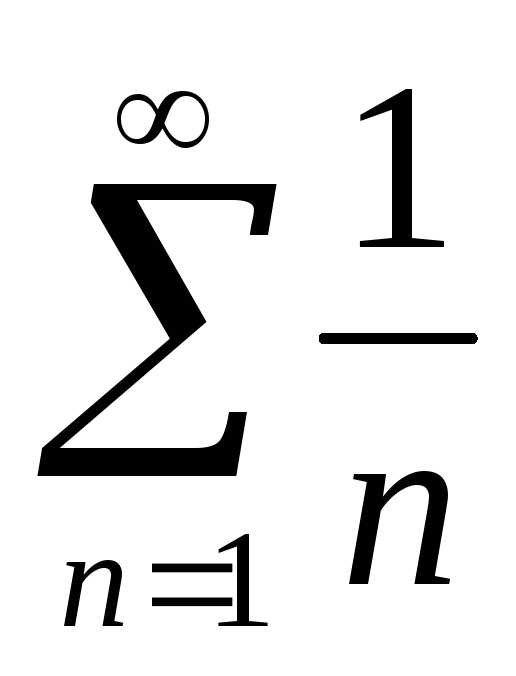 .
.
Так
как, начиная со второго члена ( ),
каждый член исходного ряда будет больше
соответствующих членов расходящегося
эталонного ряда
),
каждый член исходного ряда будет больше
соответствующих членов расходящегося
эталонного ряда
 ,
,
то исходный ряд тоже будет расходиться.
Используя признак Даламбера, исследовать на сходимость ряд
 .
.
РЕШЕНИЕ:
Согласно
признаку Даламбера, если предел отношения  -го
члена ряда к
-го
члена ряда к -му
-му
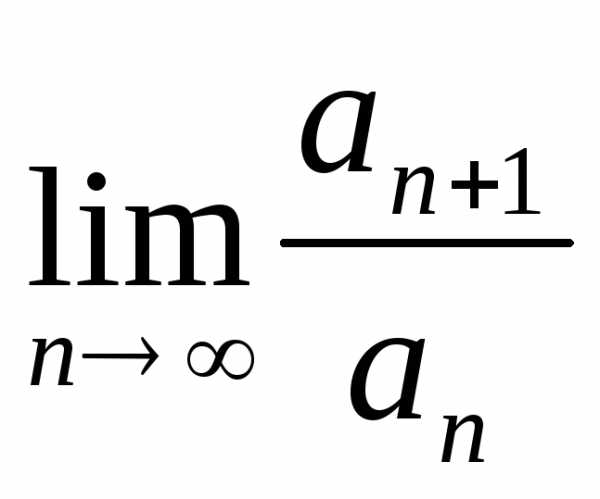
будет меньше единицы, то ряд сходится, если же этот предел больше единицы, то ряд расходится. Если такой предел окажется равным единице, то о сходимости данного ряда судить на основании этого признака нельзя.
В нашем примере:
Составляем предел:
Следовательно, по признаку Даламбера, ряд будет сходиться.
Используя признак Лейбница, исследовать на сходимость знакочередующийся ряд
РЕШЕНИЕ:
По признаку Лейбница, знакочередующийся ряд будет сходиться, если выполняются два условия:
Члены ряда убывают по абсолютной величине:
Предел общего члена при равен нулю:
 .
.
Проверим заданный ряд на выполнение этих условий.
1.
— каждый последующий член ряда меньше предыдущего, поэтому первое условие признака Лейбница выполняется.
2.
(При нахождении этого предела мы свели предел числителя и знаменателя ко второму замечательному пределу и учли, что
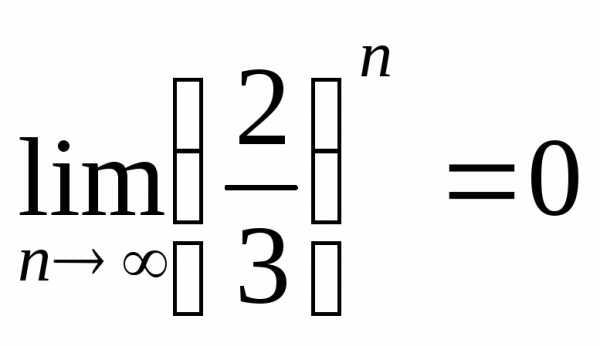
Следовательно, и второе условие признака Лейбница выполняется, поэтому данный ряд будет сходиться.
Исследовать на абсолютную и условную сходимость знакопеременный ряд
РЕШЕНИЕ:
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из модулей членов данного ряда.
Исследуем заданный ряд на абсолютную сходимость. Для этого составим ряд из модулей членов исходного ряда:
Для исследования сходимости применим признак Даламбера:
Тогда
Следовательно, данный ряд сходится абсолютно.
9. Исследовать на абсолютную и условную сходимость знакопеременный ряд
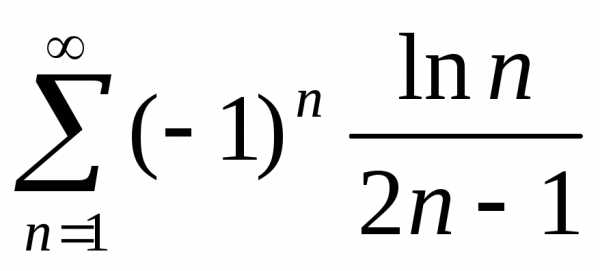
РЕШЕНИЕ:
Сначала исследуем данный ряд на абсолютную сходимость. Составляем ряд из модулей членов данного ряда:
Для
исследования сходимости полученного
ряда, применим признак сравнения. В
качестве эталонного ряда для сравнения
используем гармонический ряд: 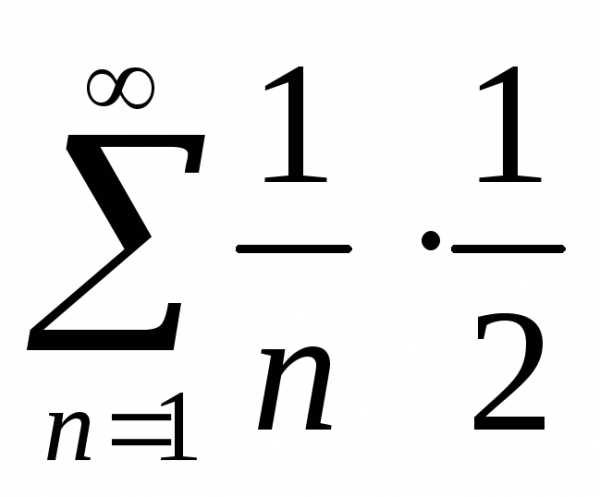 :
:
.
Так как члены нашего ряда больше соответствующих членов расходящегося гармонического ряда, то наш ряд не будет иметь абсолютной сходимости.
Исследуем ряд на условную сходимость. Так как ряд знакочередующийся, то применим признак Лейбница:
1.
— каждый последующий член ряда меньше предыдущего, поэтому первое условие признака Лейбница выполняется.
2.
Второе условие признака Лейбница также выполняется: предел общего члена ряда равен нулю. (Отметим, что предел находили, используя правило Лопиталя).
Следовательно, ряд будет условно сходящимся.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
Написать пять первых членов ряда,
 -ый
член которого имеет вид:
-ый
член которого имеет вид:
а)  б)
б)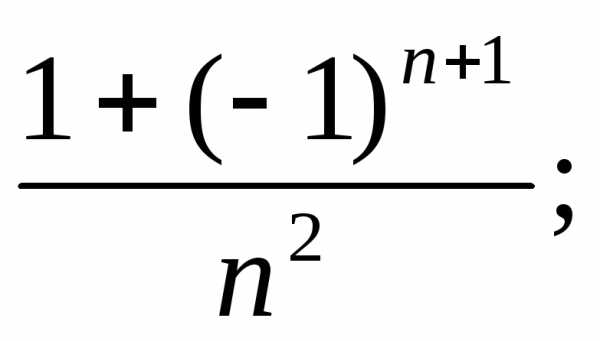 в)
в)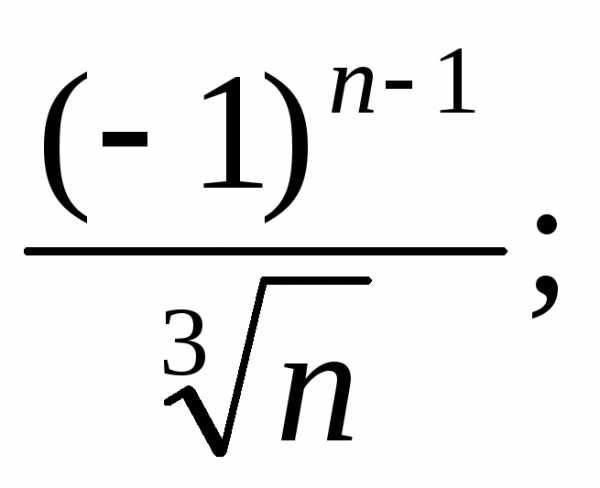 г)
г)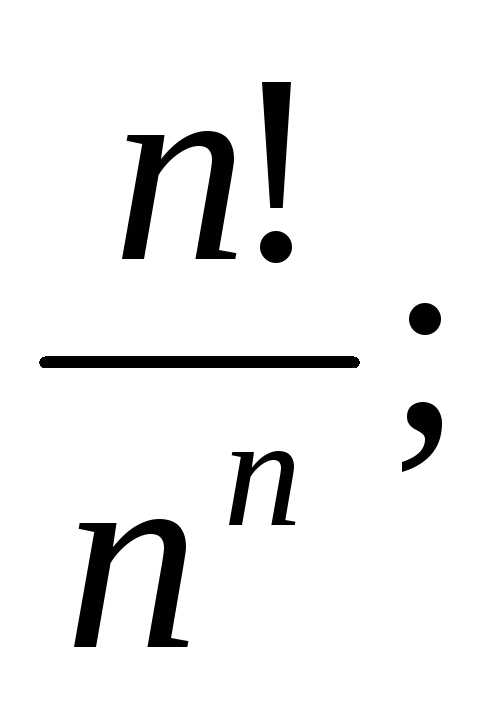 д)
д)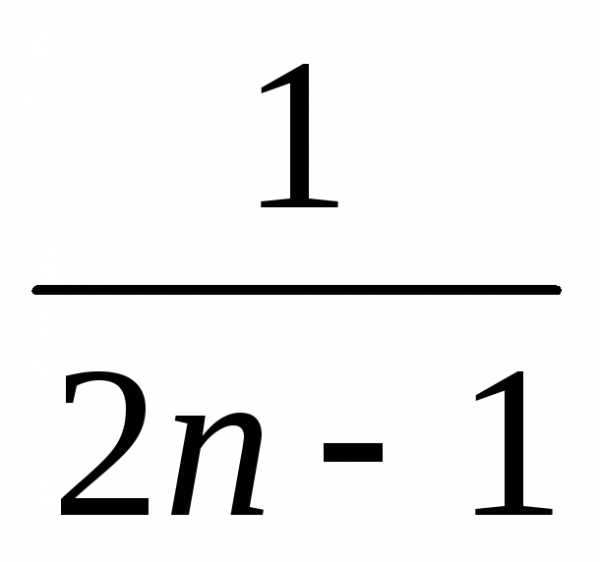 ;
е)
;
е)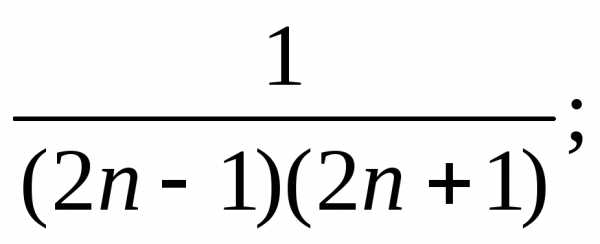
Написать
 -ый
член ряда:
-ый
член ряда:
а)
б)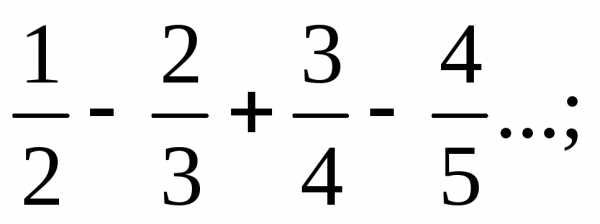 в)г)
в)г)
д)
е)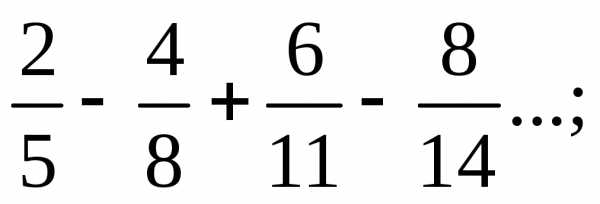 ж)
ж)
Используя необходимый признак сравнения, исследовать сходимость ряда:
а) 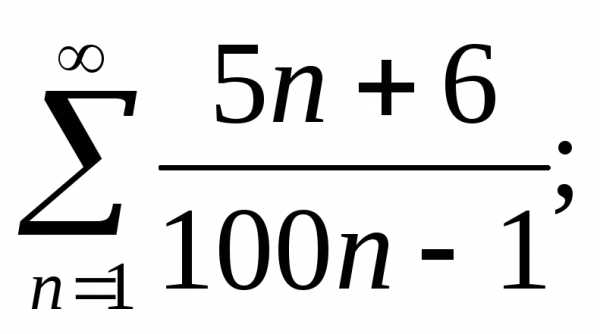 б)
б)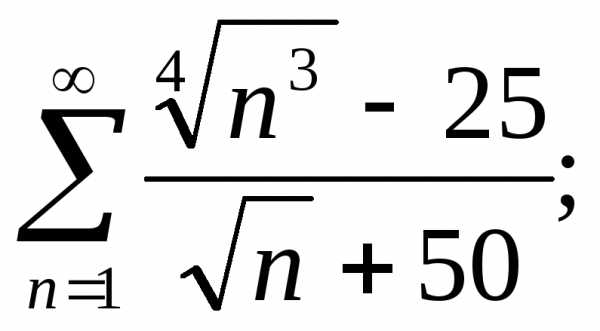 в)
в)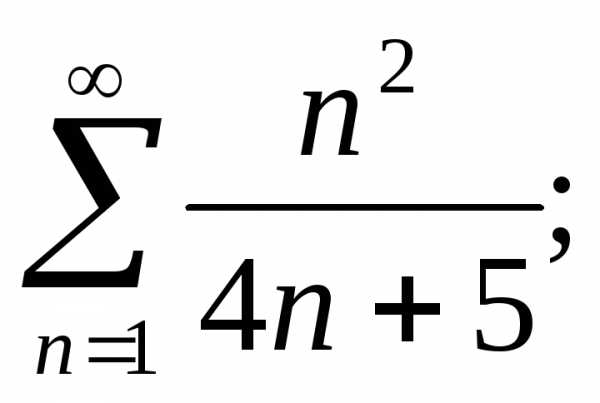 г)
г)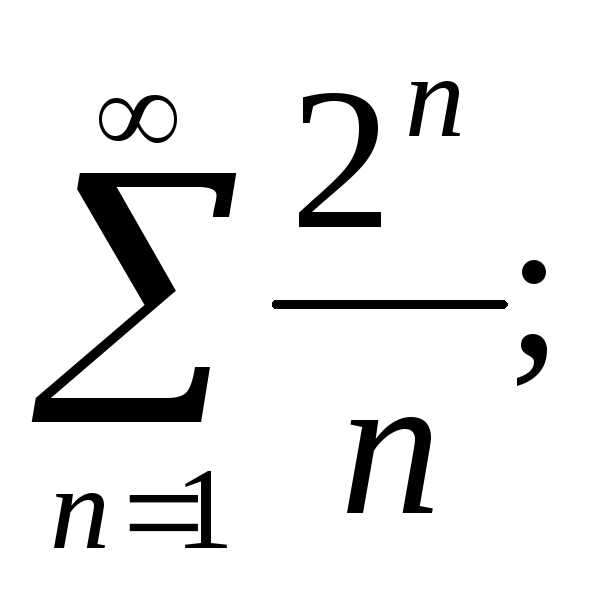 д)
д)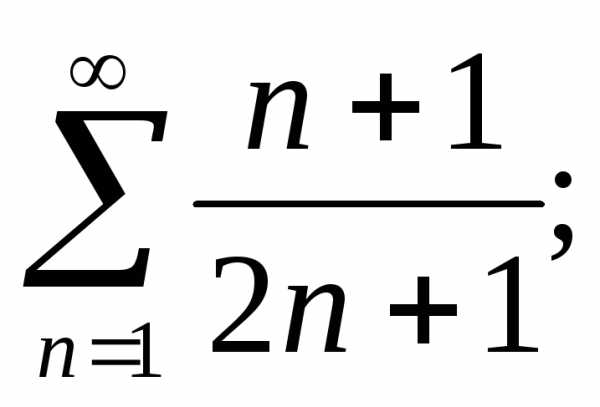
Используя признак сравнения, исследовать сходимость ряда:
а)б)
в)г)д)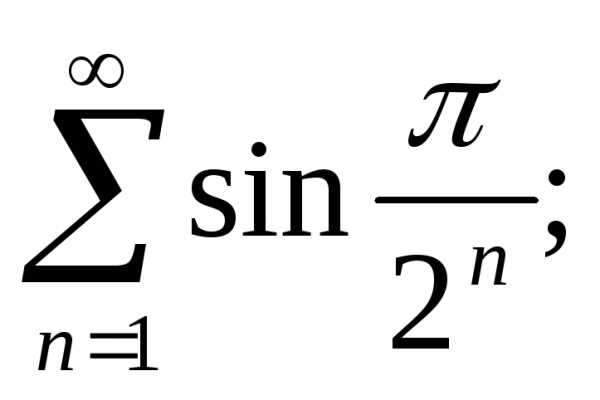 е)
е)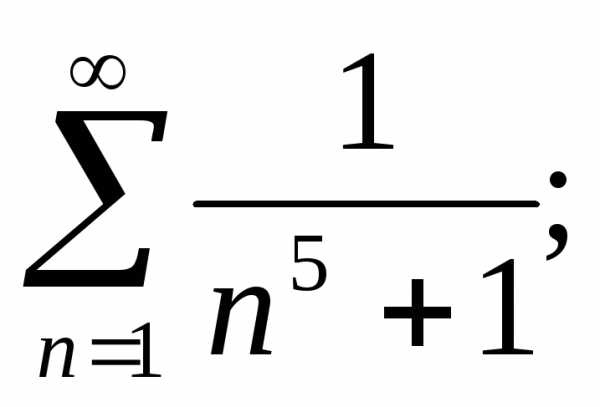
ж) 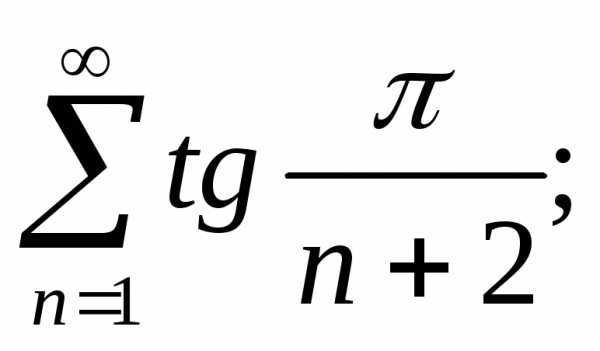 з)
з)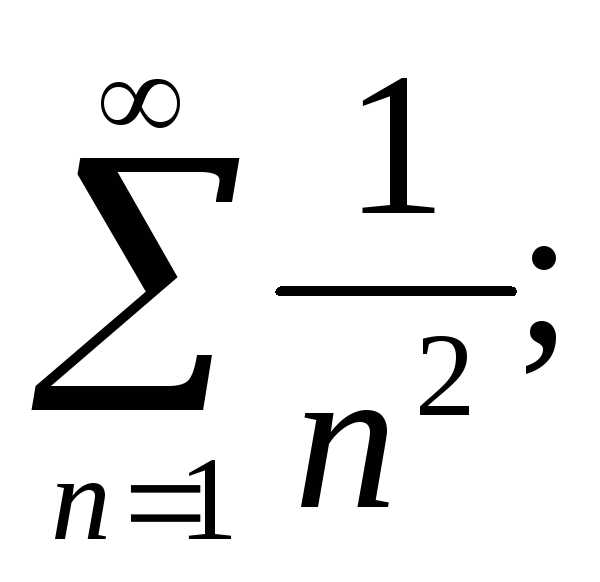
8.5. Используя признак Даламбера, исследовать на сходимость ряд:
а)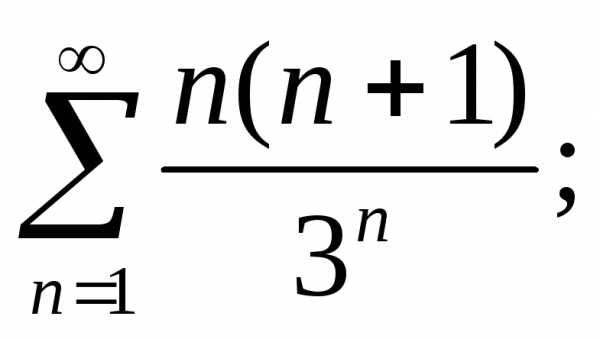 б)
б)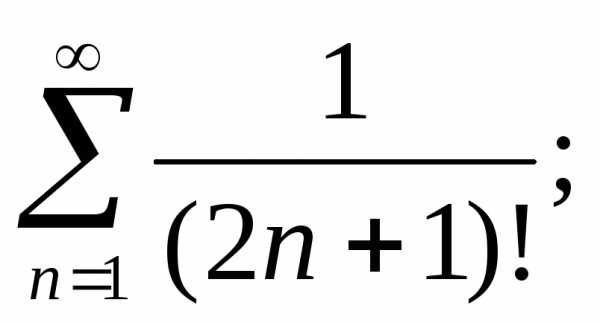 г)
г)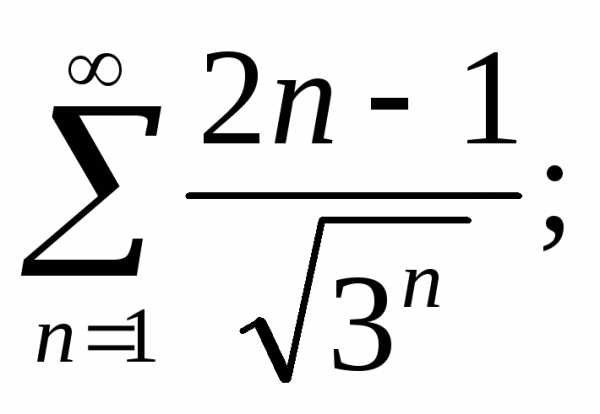 д)
д)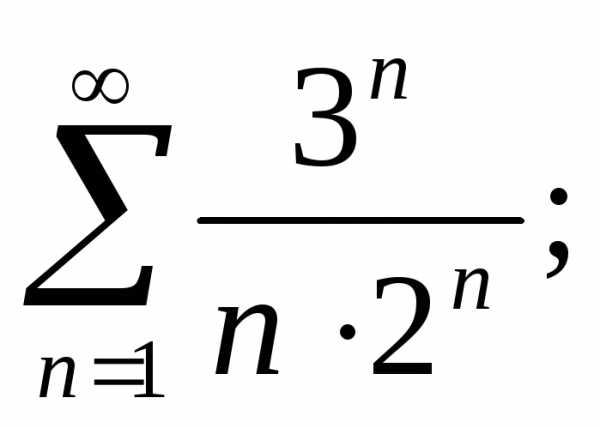 е)
е)
ж)з)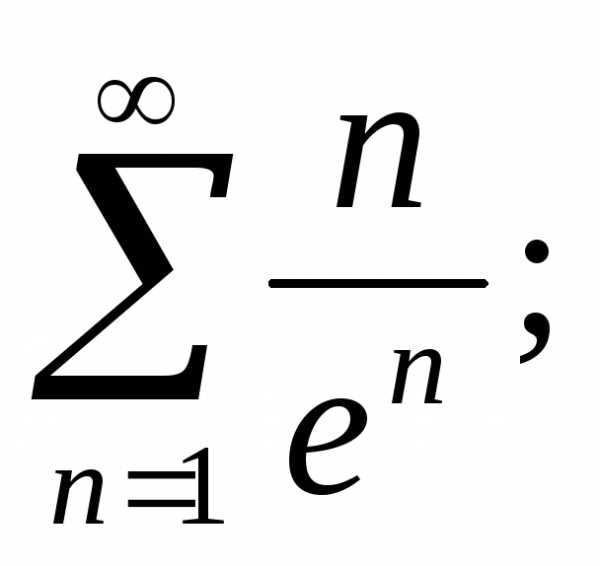 и)
и)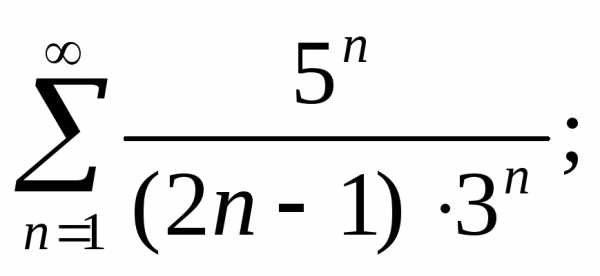 к)
к)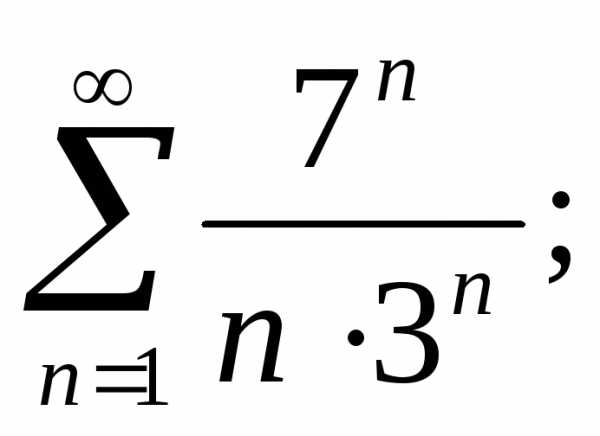
8.6. Используя признак Лейбница, исследовать на сходимость знакочередующийся ряд:
а)б)
в)г)
д)
Исследовать на абсолютную и условную сходимость знакопеременный ряд:
а) б)
в)г)д)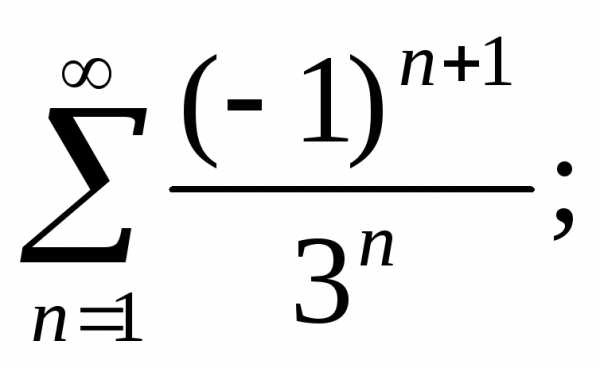
е)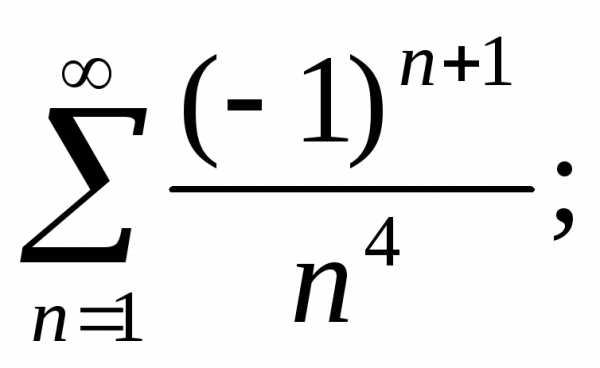 ж)
ж)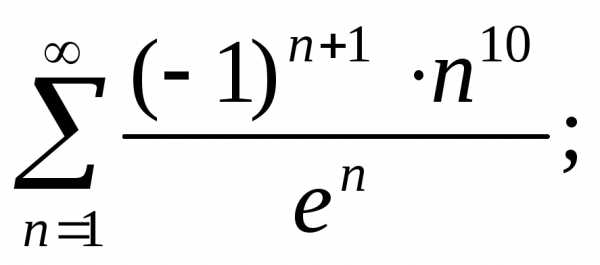 з)
з)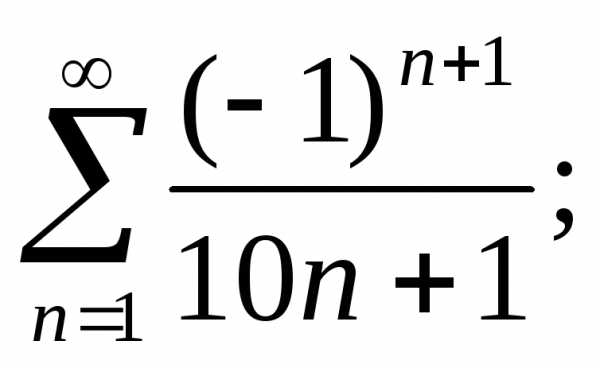
studfiles.net

 сходится и
его сумма равна
сходится и
его сумма равна  ,
то и ряд
,
то и ряд 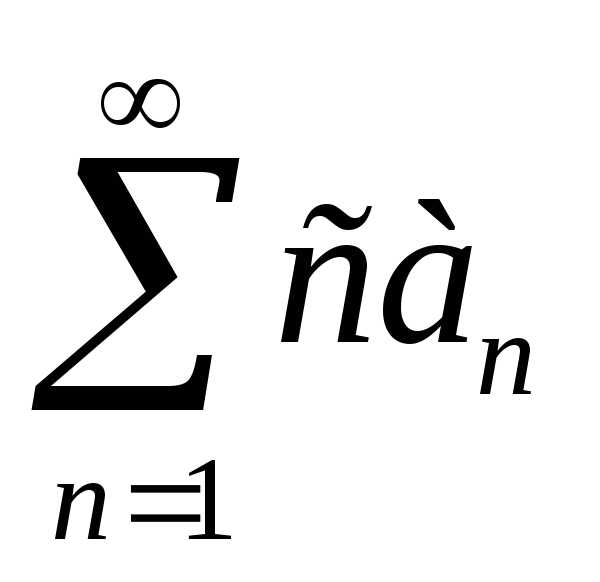 ,где с — некоторое число, также сходится, и
его
сумма
равна
,где с — некоторое число, также сходится, и
его
сумма
равна  .
.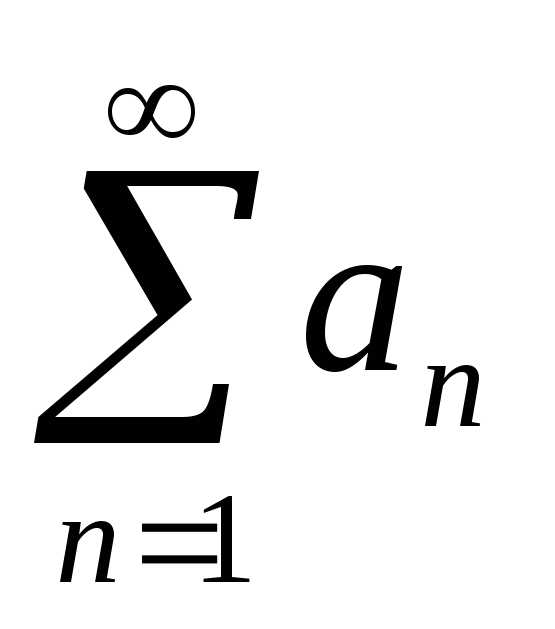 и
и 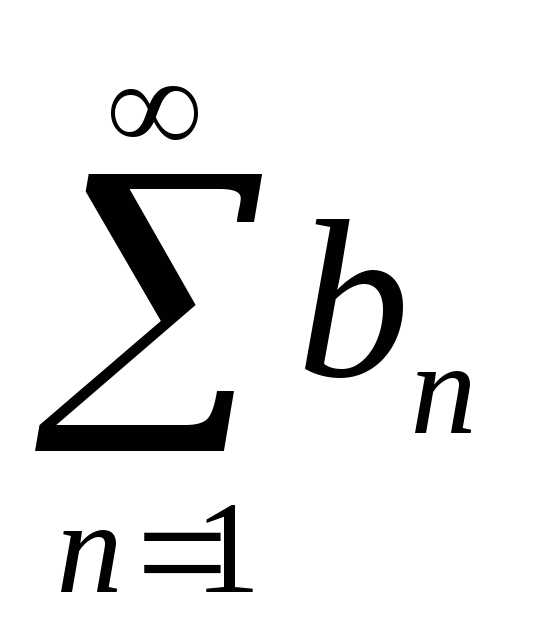 сходятся и их
суммы
соответственно равны
сходятся и их
суммы
соответственно равны  и
и ,
то и ряд
,
то и ряд 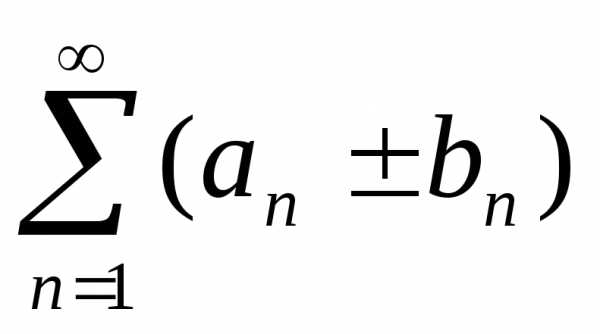 cходится
и его сумма равна
cходится
и его сумма равна 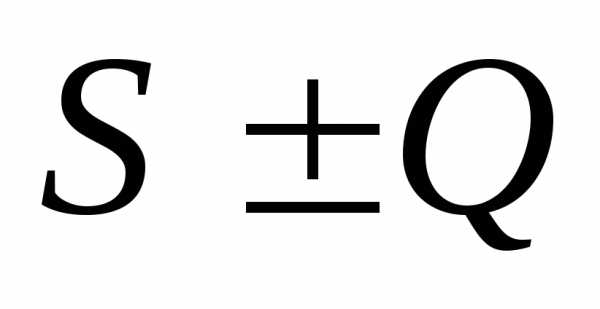 .
. -ый
член которого имеет вид:
-ый
член которого имеет вид: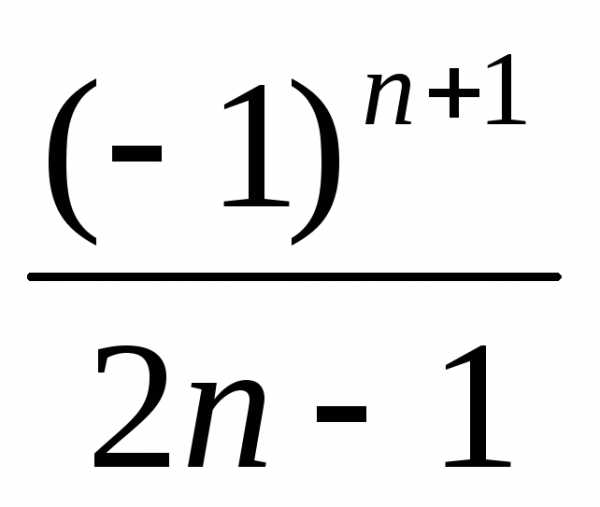 .
. -ый
член ряда.
-ый
член ряда.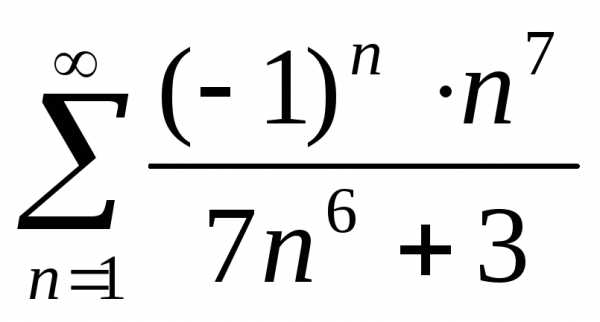 .
.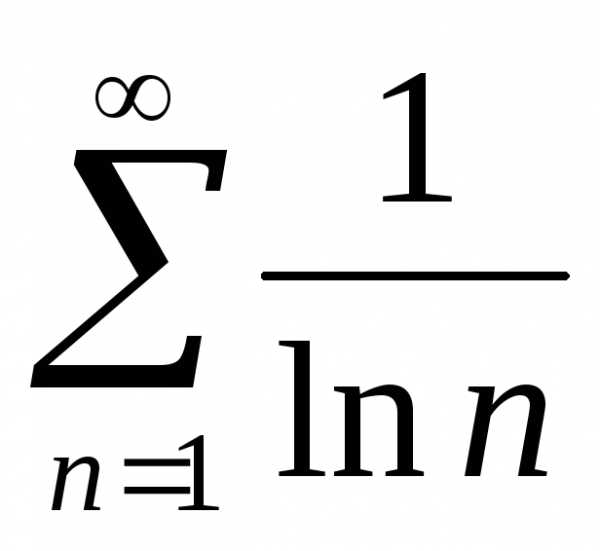 .
.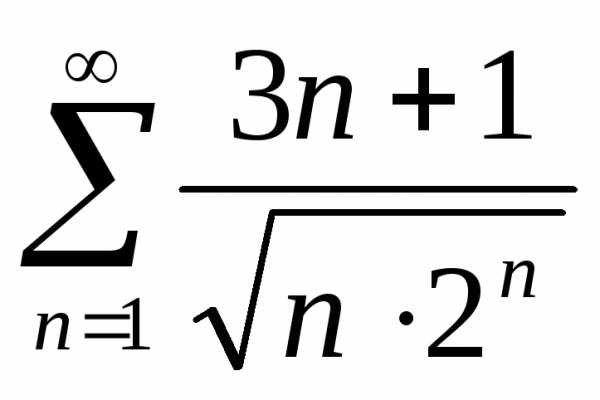 .
.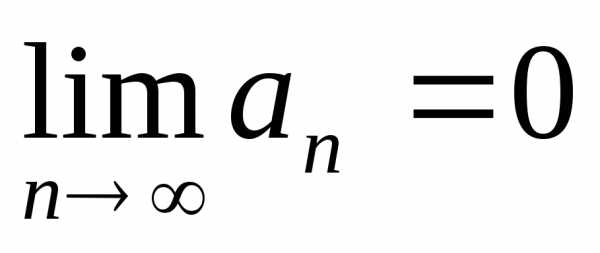 .
. -ый
член которого имеет вид:
-ый
член которого имеет вид: -ый
член ряда:
-ый
член ряда: