Что такое формулы и как их понимать? – boeffblog.ru

Изначально, формулы были придуманы математиками для того, чтобы описать простые физические явления. Например формула скорости: скорость = путь/время. Эта формула говорит о том, что если двигаться с одинаковой скоростью, то за определенное время мы пройдем определенное расстояние. То есть она показывает связь между двумя изменяющимися величинами: путь и время. Если же одно и то же расстояние два человека пройдут с разной скоростью, то они потратят на это разное время, и первым финиширует тот, кто шел с большей скоростью.
Таким образом, формулы нужны для более короткой записи (математическими символами или буквами) взаимосвязей между некоторыми величинами (смотрите пример в статье).
Решение заданий с формулами обычно подразумевает нахождение какой-либо величины, зная остальные величины входящие в формулу.
Например:
Закон Ома выражается формулой: U = I•R, где U – напряжение в Вольтах, I – сила тока в Амперах, R – сопротивление в Омах. Зная, что сила тока равна 2 А, а сопротивление равно 10 Ом, найдите напряжение.
Все, что требуется в данном задании – подставить вместо букв их значения и посчитать. U = 2 • 10 = 20 В.
Встречаются задания и посложнее. Например:
Площадь четырехугольника находится по формуле: S = 1/2 d1d2 Sinα. Где d1 и d2 – диагонали четырехугольника, α – угол между ними. Вычислите Sinα. S = 21, d1 = 7, d2 = 15.
Для начала нужно выразить величину, которую нужно найти (то есть, чтобы эту величину и остальные величины разделял знак равно). Для этого нужно избавиться от лишних величин, стоящих возле Sinα.
Разделим обе части на 1/2 d 1d2. В результате получим: = Sinα.
Теперь осталось подставить числа и посчитать: Sinα = = 0,4.
Из закона всемирного тяготения F = G выразите массу m и найдите её величину (в килограммах), если F = 13,4 Н, r = 5 м, M = 5·109 кг и гравитационная постоянная G = 6,7 ·10-11.
Первым действием разделим обе части на G, чтобы масса была отделена от других величин знаком равно.
Получим:
F : G = m
F : = m
F • = m
= m
Теперь подставляем численные значения и находим наконец-то массу:
= m
m = 1000.
Таким образом происходит решение задач на расчет по формулам.
boeffblog.ru
Ответы@Mail.Ru: Как научиться понимать математику?
Считать научись!!!
В математике и понимать нечего. Это как бы аксиоматическая наука. Соображать надо, когда решаешь примеры и задачи. Но тут есть только один способ: для того, чтобы научиться решать задачи, надо решать задачи. У меня в школе был уникальный учитель математики. Он задавал примеры так: от номера такого-то …и до конца параграфа, кого на сколько хватит. А понимать надо естественные науки: физику, химию, биологию.
Я думаю, чтобы понимать математику нужно знать ее историю. Ведь каждый термин, каждое понятие не явились с потолка, они не выдуманы, а появились как ответ на поставленный жизнью (или каким-либо человеком) вопрос. Каждое математическое понятие прежде чем оформилось прошло длинный исторический путь. Я думаю, что просмотрев этот путь, ученик проникнется уважением к этому понятию (читай к мыслителям) , и знания его будут увереннее. А вообще, чтобы что-либо понимать, надо ЗАГОРЕТЬСЯ. И здесь многое зависит от учителя, и от окружения. Еще в математике надо уметь отделять второстепенное, научиться мыслить рассчетными схемами (к гению это конечно не относится) . Сам я дилетант.
Математика гавно!!!
математика самый легкий предмет я его тяну спокойно даже без обьяснений учителей даже контрохи на 5 пишу без подготовки
математика гавно считать надо
как понять физику и математику?
Надо полюбить математике. А потом если ты в школе делать все домашние задания. Если не понимаешь тему подойти в преподавателю и попроси, чтобы тебе объяснили.
touch.otvet.mail.ruКак запоминать формулы по математике
Голова идёт кругом от множества математических формул, которые необходимо знать. Зубрёжка и шпаргалки — удел слабых. А вот тем, кто хочет стать в математике сильнее, мы подскажем несколько советов, как запоминать формулы по математике так, чтобы они не выветрились из головы до контрольной, экзамена или ЦТ.
Понимай формулу
В школе учат читать формулы, потому что так ты запоминаешь их суть, а не просто сочетание символов. Возьмём простой пример:
Если ты будешь заучивать только последовательность переменных, рискуешь «потерять» всю формулу, когда забудешь символ или знак.
Задействуй все виды памяти
Читай формулы вслух, прописывай на листке по нескольку раз, пока не запомнишь. Задействуй все виды памяти, делая упор на ведущую. Визуальная и двигательная память вместе дают больший эффект. Конечно, потенциал для запоминания у каждого разный. Есть специальные методики, которые помогают тренировать память.
Обязательно делай формулы наглядными: обводи формулу в рамку, пиши её другим цветом. Так будет легче найти в конспекте и запомнить. А лучше выписывай формулы в отдельный блокнот, структурируя их по темам. Помечай, в какого рода задачах та или иная формула пригодится, в чём её особенность. Заведи привычку пополнять список формул. Подобный «дневник наблюдений за формулами» поможет освежить в памяти важную информацию перед контрольной, экзаменом или ЦТ по математике.
Многие школьники ещё вот что делают: когда раздают проштампованные черновики, ты берёшь и сразу же записываешь на них важные формулы, которые тебе тяжело даются. За полчаса до ЦТ ты эти формулы зрительно запомнил, а потом быстренько написал. Это экономит время. Особенно такой лайфхак хорош в тригонометрии. Чем больше знаешь формул, тем лучше.
Дмитрий Судник, преподаватель математики в образовательном центре Адукар
 Заучивание формул похоже на заучивание стихов: вызубрив только слова, прочесть стих выразительно не получится. А вот когда прочувствуешь содержание, научишься правильно расставлять паузы, произведение зазвучит и отложится в памяти надолго
Заучивание формул похоже на заучивание стихов: вызубрив только слова, прочесть стих выразительно не получится. А вот когда прочувствуешь содержание, научишься правильно расставлять паузы, произведение зазвучит и отложится в памяти надолгоПроверяй себя
Нужно постоянно возвращаться к выученному материалу, чтобы не забыть его. Попробуй метод «Две карточки», он подойдёт для запоминания формул приведения, сокращённого умножения, тригонометрических формул. Возьми две стопки карточек разного цвета, на одной напиши левую часть формулы, а на другой — правую. Раздели таким образом все формулы, что тебе нужно запомнить, затем перемешай обе стопки. Тяни по порядку карточку с левой частью формулы и подбирай её продолжение среди «правых» и наоборот.
Карточки хороши и в геометрии
Чтобы запомнить формулы по геометрии, заведи себе карточки по темам («Формулы площади», «Фомулы для треугольника», «Фомулы для квадрата» и т. д.) и записывай в них информацию следующим образом.
Можно фиксировать формулы в отдельном блокноте и всегда был под рукой — как тебе удобноБудь на позитиве
Если ты учишь что-либо из-под палки, мозг сам желает избавиться от груза знаний. Воспринимай заучивание формул как хорошее упражнение для тренировки памяти. Да и настроение поднимается, когда вспоминаешь нужную формулу для решения. И конечно же, решай как можно больше тестов и задач для подготовки к контрольной, экзамену или ЦТ!
ЦТ по математике — это типовые задачи: чем больше тестов решаешь, тем выше шанс встретить что-то похожее на ЦТ. Невозможно подготовиться к ЦТ по одной задаче. Но когда ты прорешал 100 задач, то 101 задача не вызовет затруднений.
Дмитрий Судник, преподаватель математики в образовательном центре Адукар
***
Если материал был для тебя полезен, не забудь поставить «мне нравится» в наших соцсетях ВКонтакте, Instagram, Facebook, ASKfm и поделись постом с друзьями. А мы сделаем ещё больше материалов, которые пригодятся тебе для учёбы.
Перепечатка материалов с сайта adukar.by возможна только с письменного разрешения редакции. [email protected]
adukar.by
Zero To Hero
У меня непростые отношения с матанализом: с одной стороны он демонстрирует всю красоту и мощь математики, а с другой — агонию математического образования.
Математический анализ связывает различные темы в элегантной, но довольно сложной для ума манере. Ближайшая аналогия, которая приходит мне на ум, — Дарвиновская теория эволюции: стоит ее понять, и весь мир видится с позиции выживания. Вы понимаете, почему лекарства привели к резистентным микробам (выживает наиболее приспособленный). Вы понимаете, почему сахар и жир сладкие на вкус (вкус стимулирует потребление высококалорийных продуктов в условиях дефицита резервов организма). И все эти моменты складываются в единую, логическую картину.
Матанализ таким же образом проливает свет на всю систему математики. Не кажется ли вам, что все эти формулы как-то связаны?
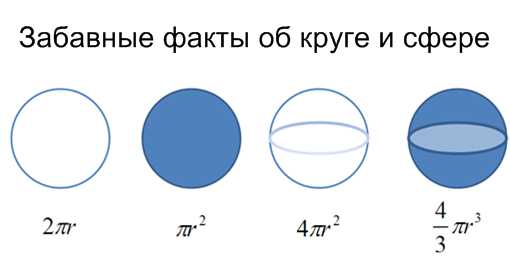
Так и есть. Но большинство из нас изучают эти формулы независимо друг от друга. Математический анализ позволяет начать с «длина окружности = 2 * π * r» и вывести остальные формулы для вычисления площади круга, сферы и даже объема шара — древним грекам очень бы пригодился подобный подход.
К сожалению, матанализ олицетворяет собой все трудности в изучении математики. Большинство уроков объясняются на натянутых, неправдоподобных примерах, заумных доказательствах и банальном заучивании, которое напрочь убивает интуицию.
Так действительно не должно происходить.
Математика, искусство и идеи
Кое-что я понял еще со школы: математика — не самая сложная часть математики; самое тяжелое — мотивация к ее освоению. Особенно, умение не терять энтузиазм, несмотря на:
- Преподавателей, больше сконцентрированных на штамповке публикаций и своей карьере, чем на преподавании
- Небеспочвенные опасения, что математика — это сложно, скучно, непопулярно или «не ваш предмет»
- Учебники и учебные планы, больше нацеленные на получение прибыли и хорошую статистику по тестированиям знаний, чем на пояснение сущности предмета.
‘Плач математика’ [pdf] — отличное эссе на эту тему, которое вызвало бурный резонанс среди многих прочитавших его:
«…если бы мне пришлось создавать механизм с единственной целью разрушить природное любопытство ребенка и его любовь к моделированию, вряд ли бы у меня получилось лучше, чем это уже реализовано — у меня бы просто не хватило фантазии, чтобы тягаться с такими бесчувственными, унылыми идеями, которые воплощены в современных методах изучения математики».
Представьте изучение изобразительного искусства так: Детки, никакого рисования в детском садике. Вместо этого, давайте-ка изучим химию лакокрасочных изделий, физику света и анатомию глаза. После 12 лет изучения этих аспектов, если дети (точнее уже подростки) всё еще не возненавидят искусство, они смогут начать рисовать самостоятельно. В конечном итоге, они теперь владеют полноценным фундаментом для того, чтобы начать уважать искусство. Верно?
Также и с поэзией. Представьте изучение этой цитаты (формулы):
«Но главное: будь верен сам себе; Тогда, как вслед за днем бывает ночь, Ты не изменишь и другим.» —Вильям Шекспир, Гамлет
Это элегантный способ сказать «будь собой» (и если это означает непочтительно писать о математике, пусть будет так). Но если бы мы рассматривали поэзию на уроке математики, вместо поиска смысла мы бы занялись подсчётом количества слогов, анализировали пятистопный ямб, разметкой существительных, глаголов и прилагательных.
Математика и поэзия — это как разные способы пояснить, охарактеризовать одно и то же. Формулы — это средства к достижению цели, способ выражения математической истины.
Мы забыли, что математика оперирует идеями, это не машинальное маниппулирование формулами, которые выражают эти идеи.
Ну это всё понятно, так в чем же твоя великая мысль?
Вот, что я не буду делать: я не буду пересказывать уже написанные учебники. Если вам нужны ответы здесь и сейчас, есть масса вебсайтов, видеоуроков и 20-минуток в помощь.
Вместо этого давайте освоим основные положения матанализа. Уравнений недостаточно — я хочу моментов озарения, чтобы вы действительно видели их смысл и понимали язык математики.
Формальный математический язык — это просто способ коммуникации. Графики, информативные анимированные модели и разговор простым языком могут дать больше знаний, чем целая страница заумных доказательств.
Но матанализ — это сложно!
Я думаю, что любой человек сможет понять основные положения матанализа. Нам не обязательно быть поэтами, чтобы наслаждаться произведениями Шекспира.
Вам будет гораздо проще, если вы знаете алгебру и интересуетесь математикой. Не так давно, чтение и письмо были работой специально обученных писцов. А сегодня это может сделать любой 10-летний ребенок. Почему?
Потому что мы этого ожидаем. Ожидания играют огромную роль в развитии возможностей. Так что ожидайте, что матанализ — это просто еще один предмет. Некоторые люди доходят до мельчайших подробностей (писатели/математики). Но остальные из нас могут просто восторгаться происходящим и попытаться его понять. Я бы хотел, чтобы каждый освоил основные понятия матанализа и сказал «Вот это да!».
Так о чем же матанализ?
Некоторые определяют матанализ как «область математики, которая изучает пределы, дифференцирование, интегрирование функций с одной или более переменных». Это определение верно, но оно совсем не полезно для новичков.
Вот мой ход: Матанализ делает с алгеброй то, что алгебра сделала с арифметикой.
- Арифметика — это манипуляция числами (сложение, умножение и т.д.).
- Алгебра находит связи между числами: a2 + b2 = c2 — очень известная связь, описывающая соотношение сторон в прямоугольном треугольнике. Алгебра находит целые наборы чисел — если вы знаете a и b, вы можете вычислить и c.
- Матанализ находит связи между уравнениями: вы можете видеть, как одно уравнение (длина окружности = 2 * π * r) связано с другим (площадь круга = π * r2).
Используя матанализ, мы можем спросить самые разные вопросы:
- Как уравнение растет и сокращается? Наращивается со временем?
- Когда оно достигнет самой высокой/низкой точки?
- Как мы используем переменные, которые постоянно меняются? (Тепло, движение, популяции, …).
- И многое, многое другое!
Алгебра и матанализ решают задачи вместе: матанализ находит новые уравнения, а алгебра их решает. Как эволюция, матанализ расширяет ваше понимание того, как работает матушка-природа.
Пример, пожалуйста
Представим, что мы знаем уравнение длины окружности (2 * π * r), и нам нужно найти площадь. С чего начнем?
Представьте, что заполненный диск круга — это как набор матрешек.
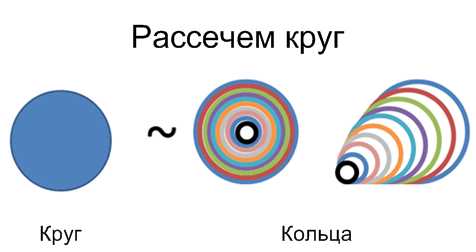
Тут есть два способа нарисовать этот диск:
- Нарисовать окружность и закрасить ее
- Нарисовать набор колец толстым маркером
Количество «пространства» (площадь) должно быть одинаковым в обоих случаях, верно? И сколько пространства занимает кольцо?
Самое большое кольцо имеет радиус «r», и длина окружности кольца вычисляется как 2 * π * r. По мере того, как кольца уменьшаются, окружность также становится меньше, но всё равно сохраняется соотношение 2 * π * текущий радиус. Последнее кольцо больше похоже на булавочную головку, и длину окружности уже не вычислишь.
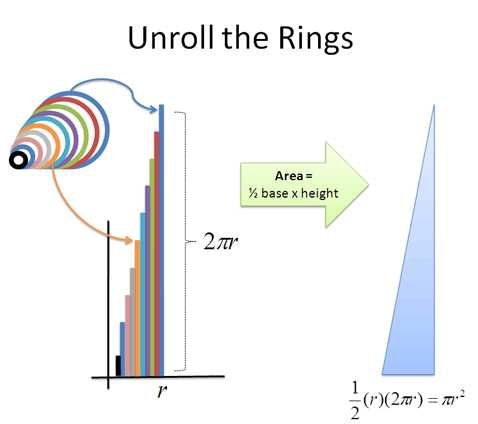
А теперь начинается самое интересное. Давайте раскрутим эти кольца и выровняем их. Что произойдет?
- У нас получится набор линий, который составит зубчатый треугольник. Но если взять более тонкие кольца, то треугольник становится уже менее зубчатым (об этом мы еще поговорим в других статьях).
- С одной стороны будет самое маленькое кольцо (0), а с другой — самое большое (2* π * r)
- Кольца имеют радиусы от 0 до «r». Для каждого возможного радиуса из этого диапазона (от 0 до r), мы просто помещаем раскрученное кольцо на свое место.
- Общая площадь «кольцевого треугольника» = 1/2 основания * высоту = 1/2 * r *(2 * π * r) = π * r2, а это и есть формула поиска площади круга!
Ух ты! Общая площадь колец = площадь треугольника = площадь круга!
(Изображение из Википедии)
Это был простой пример, но вы уловили основную идею? Мы взяли диск, разделили его, и сложили части вместе немного другим путем. Матанализ показал, что диск и кольцо тесно связаны друг с другом: диск — это действительно набор колец. Это очень популярная тема в матанализе: Большие предметы состоят из более мелких предметов. И иногда именно с этими мелкими предметами работается проще и понятнее.
Немного о примерах
Множество примеров в матанализе основано на физике. Это, конечно, замечательно, но бывает сложно их воспринимать: честно, далеко не всегда удается держать в голове разные физические формулы вроде формулы скорости объекта.
Я предпочитаю начать с простых визуальных примеров, потому что именно так и работает наш мозг. Кольцо/круг, которое мы исследовали — вы бы могли смоделировать то же самое из нескольких отрезков трубок разного диаметра: разделить их, выровнять и уложить в грубый треугольник, чтобы убедиться, что математика действительно работает. С простой физической формулой такое вряд ли удастся провернуть.
Немного о математической строгости (для фанатиков этой науки)
Я чувствую, как математики-педанты жгут свои клавиатуры. Поэтому я вставлю всего несколько слов о «строгости». Знаете ли вы, что мы не учим матанализ способами, которыми его открыл Ньютон или Лейбниц? Они использовали интуитивные идеи «флюксии» и «бесконечно малых величин», которые были заменены пределами, потому что «Конечно, это работает на практике. Но работает ли это в теории?».
Мы создали сложные механические модели, чтобы «точно» доказать матанализ, но мы утратили интуитивное восприятие предмета в процессе таких доказательств.
Мы смотрим на сладость сахара с точки зрения химии мозга, вместо того, чтобы пояснять это языком науки «В сахаре много энергии. Ешьте его».
Я не хочу (и не могу) преподавать матанализ студентам или обучать ученых. Но будет ли плохо, если каждый сможет понимать матанализ на том «неточном» уровне, на котором его понимал Ньютон? Чтобы это также изменило мир для вас, как когда-то изменило для него?
Преждевременная концентрация на точности рассредоточивает учеников и делает математику сложной для изучения. Вот хороший пример: число е технически определено пределом, но открыто оно было именно с помощью интуитивной догадки о росте. Натуральный логарифм может выглядеть как интеграл, или время, которому нужно расти. Какие объяснения лучше помогут новичкам?
Давайте немного порисуем от руки, а в химию погрузимся уже по ходу дела. Приятных вычислений.
(P.S: Один любезный читатель создал анимированное слайд-шоу powerpoint, которое помогает презентовать эту идею более наглядно (лучше посмотреть ее в PowerPoint, там будут видны анимации). Спасибо!)
Перевод статьи «A Gentle Introduction To Learning Calculus»
zero2hero.org
Как научиться понимать математику? | Учебный блог
Алгебра, геометрия, высшая математика… Некоторых эти слова заставляют нервно грызть ногти и хвататься за голову. Да, математика действительно требует серьезного подхода и старания, но и не только способность.
Проблема в том, что для многих математика ассоциируется с такими терминами как «дипломная», «курсовая», «контрольная», «семестровая» и другие виды отчетных работ. К счастью, сегодня это совсем не проблема, так как существуют такие сайты, как 5orka.ru, которые помогают справиться с выполнением таких работ. Важно полюбить математику.
Именно постоянная работа и интересные упражнения превратят математику в сплошное удовольствие с интересными задачами и примерами. И не обязательно без понимания сути заучивать формулы и зазубривать теоремы из аксиом, они сами «отложатся» в вашей голове с помощью специальных упражнений на основе математической логики.
Почему не все понимают математику?
Для школьников и студентов с гуманитарным направлением изучения математики может превратиться в сплошной кошмар. Это возникает ввиду отсутствия понимания всей сущности математических законов. Что же тогда делать? Как постичь все тайны математического мира когда все желания изучать эту науку отпали?
Первые шаги для понимания математики
Чтобы научиться понимать математику, нужно начать изучать эту науку заново. Да, нужно изучить все формулы и начальные законы снова, с пониманием и умением объяснить собственными словами. Таким образом, вы будете иметь хорошее математическое основание, которое поможет при дальнейшем изучении и углублении в мир математики. Обязательно спрашивайте у преподавателей или учителей, что вам не ясно, ведь промедление с непонятным материалом как снежный шарик катится по снегу, набирая все больше снега на себя, может привести к плохим последствиям.
Учимся понимать способы решения математических задач
Не менее важным в овладении математики есть и способы решения математических задач. Они бывают разными: от противного, от противоположного, с помощью индукции… Но вы не сможете ими пользоваться, если не поймете сути метода. Именно поэтому вам необходимо сначала ознакомиться с основными методами, понять их, освоить и научиться использовать. Для этого нужно просматривать уже готовые задачи, представленные в учебниках, и логично в них разобраться.
Чтобы научиться понимать математику, старайтесь находить решение задачи собственным путем, а не по шаблону. Ведь каждая задача требует своего подхода и решения. Даже Евклид, основатель геометрии, говорил, что математика не имеет царских путей. Это означает, что для того, чтобы решать задачи и постичь мир математики, нужно иметь только ум, и ни чего более. А решать задачи можно и с помощью начальных формул и логических рассуждений.
Например, не обязательно подносить к квадрату двузначное число с 5 на конце, нужно только воспользоваться специально выведенной формуле. Например число 65. Сначала добавляем первую цифру с единицей, а затем ту первую цифру умножаем на полученное число: 6 * (6 + 1) = 42. Итак, мы получили 42, к которому нужно подставить 25 и вуаля — 4225, а это 65 в квадрате!
Конечно, именно изучение математики требует не только ваших усилий, но и консультации специалистов. В таком случае, вы можете воспользоваться помощью репетитора или онлайн-помощи, предоставляемой талантливыми математиками через программы-мессенджеры.
Поэтому, все в ваших руках! Не забывайте об этом и идите к своей цели!
xn--80ablbaanka7beun6ae4de9e.xn--p1ai
Отношения между объектами…………………………………… | — 16 — | |
Прямые второго порядка…………………………………………….. | — 17 — | |
Окружность…………………………………………………………………… |
| — 17 — |
Эллипс……………………………………………………………………………… |
| — 17 — |
Гипербола……………………………………………………………………….. |
| — 17 — |
Парабола………………………………………………………………………… |
| — 18 — |
Системы координат…………………………………………………….. |
| — 18 — |
Приложения……………………………………………………………………. |
| — 18 — |
Аналитическая геометрия (R3)……………………………………….. | — 19 — | |
Плоскость………………………………………………………………………. |
| — 19 — |
Прямая……………………………………………………………………………. |
| — 19 — |
Расстояния…………………………………………………………………….. |
| — 19 — |
Вектор…………………………………………………………………………….. |
| — 20 — |
Отношения между объектами…………………………………… | — 20 — | |
Приложения……………………………………………………………………. |
| — 21 — |
Матрицы……………………………………………………………………………… |
| — 22 — |
Операции над матрицами…………………………………………… | — 22 — | |
Свойства определителей…………………………………………….. | — 22 — | |
Операции над определителями…………………………………… | — 23 — | |
Обратная матрица………………………………………………………. |
| — 23 — |
Производные функций………………………………………………………… |
| — 24 — |
Определение производной…………………………………………….. | — 24 — | |
Таблица производных……………………………………………………. |
| — 24 — |
Правила дифференцирования……………………………………… | — 25 — | |
Логарифмическая производная…………………………………… | — 25 — | |
Параметрические функции…………………………………………. | — 26 — | |
Приложения……………………………………………………………………. |
| — 26 — |
Пределы………………………………………………………………………………… |
| — 27 — |
Свойства пределов………………………………………………………… |
| — 27 — |
Замечательные (классические) пределы …………………… | — 27 — | |
Эквивалентность бесконечно-малых………………………… | — 28 — | |
Сравнение бесконечно-малых………………………………………. | — 28 — | |
Способы раскрытия неопределенностей………………….. | — 28 — | |
Исследование графика функции……………………………………….. | — 29 — | |
Дифференциальное исчисление…………………………………………. | — 30 — | |
Основные понятия………………………………………………………… |
| — 30 — |
Интегралы…………………………………………………………………………… |
| — 31 — |
Таблица интегралов…………………………………………………….. |
| — 31 — |
Основные правила…………………………………………………………. |
| — 32 — |
Подстановки Эйлера…………………………………………………….. |
| — 33 — |
Универсальная тригонометрическая подстановка.. | — 34 — | |
Метод неопределённых коэффициентов…………………… | — 34 — | |
Андрей Ивашов | — 58 — |
|
studfiles.net
Как понять математику?
Вопрос, как понять математику, чаще возникает у людей с гуманитарным складом ума. Проблема состоит в том, что математику необходимо именно понять, уловить суть, а заучивание формул и теорем, без первой составляющей становится бесполезным делом. При систематических занятиях даже люди, которым математика дается с трудом, могут научиться логически думать, сопоставлять и просчитывать на несколько шагов вперед, что просто необходимо при решении математических задач.
Если ребенок не понимает математику, помогите ему разбираться в сути явлений, где и откуда что-то берется, как это взаимосвязано, как получить то, чего не достает.
Вот инструкция для всех тех, кто ищет ответ на вопрос — не понимаю математику, что делать?
- Начните изучать материал с самого начала, так как в точных науках невозможно понять что-либо без знания предыдущего материала. С самого первого урока разберитесь в формулировках теорем и правил так, чтобы для вас эти строчки не были пустым звуком. Читая правило, пишите на бумаге из чего оно состоит, для чего необходимо. Так, возможно чертите схемки или пишите тезисы до тех пор, пока точно не будете уверенны в том, что вам все понятно. Не стесняйтесь переспрашивать учителя, если что-либо не уловили или не ясно. Потеряв нить рассуждения, придется начинать все заново.
- Если внимательно прочитать несколько тем из алгебры или геометрии, можно заметить, что постоянно применяется несколько методов доказательств – метод от противного или метод индукции. Запомните их раз и навсегда. Не допускайте пробелов в знаниях, так как недопонимание одной темы закрывает вам дверь в понимание следующей. Часто математику не понимают из-за слабых начальных знаний.
- Основоположник геометрии Евклид говорил, что в математике нет царских путей. Универсальных легких способов для понимания математических законов нет. Вашим спасением будет регулярные занятия, нахождение решений по готовым формулам, развитее логики, редкое использ
elhow.ru
