Действия над десятичными дробями, формулы и примеры решений
Задание. Найти сумму дробей и
Решение. Распишем решение пошагово. Итак, нам надо найти сумму
Действия будем производить в столбик, то есть запишем сумму следующим образом (помним, что для десятичных дробей при выполнении сложения/вычитания десятичные запятые дробей должны находиться на одной вертикальной линии):
Вначале к первой дроби справа дописываем нуль, чтобы уравнять количество десятичных знаков:
Складываем по одной цифре (знаку, разряду) справа налево. Результат сложения записываем под соответствующими слагаемыми под чертой. На первом этапе складываем 0 и 4: :
Теперь складываем 5 и 7: , в результате получилось число большее 10, а поэтому под чертой записываем только последнюю цифру полученного числа, то есть 2, а над соседним левым разрядом — 4 — ставим оставшиеся цифры, то есть 1. (Обычно при решении говорят так: «два пишем, один в уме»):
Единица над 4 означает, что после того как будет выполнено сложение следующего разряда: , к полученной сумме надо будет прибавить 1, которую мы «держим в уме».
Итак, складываем далее, к 4 прибавляем 2: и прибавляем «красную» единицу: . То есть под чертой под десятыми пишем 7:
Под десятичными запятыми слагаемых, ставим запятую суммы:
И продолжаем сложение далее по выше описанному алгоритму: :
И, снеся 3 (под ней во втором слагаемом нет соответствующей цифры), окончательно будем иметь:
Таким образом,
Ответ.
www.webmath.ru
Конспект по математике «Десятичная дробь»
Ключевые слова конспекта: десятичная дробь, сравнение дробей, арифметические действия с дробями, нахождение части от целого и целого по его части, представление десятичной дроби в виде обыкновенной и обыкновенной в виде десятичной.
Дробные числа, знаменатель которых равен 10, 100, 1000 и т. д., можно записать не только в виде обыкновенных, но и в виде десятичных дробей.
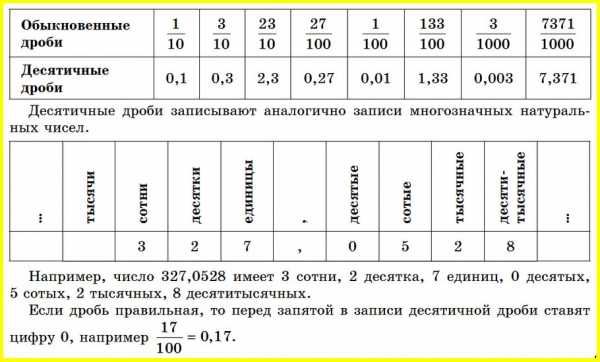
Сравнение десятичных дробей
- Из двух десятичных дробей больше та, у которой целая часть больше: 7,99 > 6,399.
- Если целые части дробей равны, то больше та дробь, у которой десятых больше. Если и десятые равны, то больше та дробь, у которой больше сотых, и т. д.: 85,7 > 85,679; 35,87 > 35,8695; 5,09 < 5,1.
Арифметические действия с десятичными дробями
Сложение и вычитание десятичных дробей
Чтобы сложить (вычесть) десятичные дроби, нужно:
- уравнять в этих дробях количество знаков после запятой;
- записать их друг под другом так, чтобы запятая была записана под запятой;
- поставить в ответе запятую под запятой в данных дробях.
Умножение десятичных дробей
При умножении десятичных дробей сначала нужно выполнить умножение, не обращая внимания на запятую, а затем в произведении отделить запятой справа столько знаков, сколько их имеется после запятой в обоих множителях вместе.
Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001, нужно перенести запятую влево на сколько цифр, сколько нулей стоит перед единицей в множителе.
Деление десятичных дробей
Чтобы разделить десятичную дробь на натуральное число, нужно:
- разделить дробь на это число, не обращая внимания на запятую;
- поставить в частном запятую после того, как закончено деление целой части;
- если целая часть меньше делителя, то частное начинается с нуля целых.
Чтобы разделить десятичную дробь на 10, 100, 1000, …, нужно перенести влево запятую в этой дроби на сколько цифр, сколько нулей стоит после единицы в делителе.

Чтобы разделить число на десятичную дробь, нужно:
- в делимом и делителе перенести запятую вправо на сколько цифр, сколько их после запятой в делителе;
- выполнить деление на натуральное число.
Чтобы разделить десятичную дробь на 0,1; 0,01; 0,001, нужно перенести в ней запятую вправо на столько цифр, сколько нулей стоит в делителе перед единицей (т. е. умножить дробь на 10, 100, 1000, …).
Представление десятичной дроби в виде обыкновенной
и обыкновенной в виде десятичной
Чтобы обратить десятичную дробь в обыкновенную, достаточно в числителе дроби записать число, стоящее после запятой, а в знаменателе — единицу с нулями, причем нулей должно быть столько, сколько цифр справа от запятой. Если можно, дробь сократить.
Чтобы обратить обыкновенную дробь в десятичную, следует разделить числитель на знаменатель по правилу деления десятичной дроби на целое число.
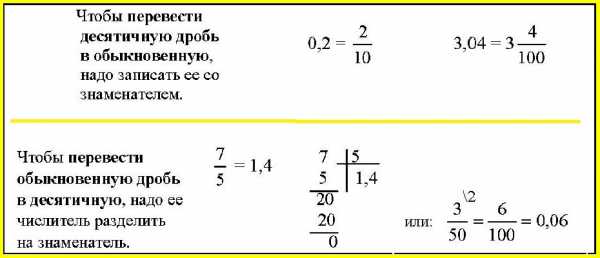
Не каждую обыкновенную дробь можно перевести в десятичную. Если знаменатель обыкновенной дроби не содержит простых множителей, кроме 2 и 5, то эту обыкновенную дробь можно перевести в десятичную.
Учитывая это правило, можно переводить обыкновенную дробь в десятичную не с помощью деления, а приведением ее к знаменателю 10, 100, 1000 путем умножения числителя и знаменателя этой дроби на недостающие множители.
Это конспект по теме «Десятичная дробь». Выберите дальнейшие действия:
Десятичная дробь
5 (100%) 3 vote[s]uchitel.pro
определения, запись, примеры, действия с десятичными дробями, бесконечные периодические десятичные дроби
Данный материал мы посвятим такой важной теме, как десятичные дроби. Сначала определимся с основными определениями, приведем примеры и остановимся на правилах десятичной записи, а также на том, что из себя представляют разряды десятичных дробей. Далее выделим основные виды: конечные и бесконечные, периодические и непериодические дроби. В финальной части мы покажем, как точки, соответствующие дробным числам, расположены на оси координат.
Yandex.RTB R-A-339285-1Что такое десятичная запись дробных чисел
Так называемая десятичная запись дробных чисел может быть использована как для натуральных, так и для дробных чисел. Она выглядит как набор из двух и более цифр, между которыми есть запятая.
Десятичная запятая нужна для того, чтобы отделять целую часть от дробной. Как правило, последняя цифра десятичной дроби не бывает нулем, за исключением случаев, когда десятичная запятая стоит сразу после первого же нуля.
Какие можно привести примеры дробных чисел в десятичной записи? Это может быть 34,21, 0,35035044, 0,0001, 11 231 552,9 и др.
В некоторых учебниках можно встретить использование точки вместо запятой (5.67, 6789.1011 и др.) Это вариант считается равнозначным, но он более характерен для англоязычных источников.
Определение десятичных дробей
Основываясь на указанном выше понятии десятичной записи, мы можем сформулировать следующее определение десятичных дробей:
Определение 1Десятичные дроби представляют собой дробные числа в десятичной записи.
Для чего нам нужна запись дробей в такой форме? Она дает нам некоторые преимущества перед обыкновенными, например, более компактную запись, особенно в тех случаях, когда в знаменателе стоят 1000, 100, 10 и др. или смешанное число. Например, вместо 610 мы можем указать 0,6, вместо 2510000 – 0, 0023, вместо 5123100 – 512,03.
О том, как правильно представить в десятичном виде обыкновенные дроби с десятками, сотнями, тысячами в знаменателе, будет рассказано в рамках отдельного материала.
Как правильно читать десятичные дроби
Существуют некоторые правила чтения записей десятичных дробей. Так, те десятичные дроби, которым соответствуют их правильные обыкновенные эквиваленты, читаются почти так же, но с добавлением слов «ноль десятых» в начале. Так, запись 0,14, которой соответствует 14100, читается как «ноль целых четыр
zaochnik.com
Вариант 1 | |
1 | 15,3 * 5,4 — 4,2* (5,12 – 4,912) + 16,0036 |
2 | 9,84 — 16,32 * ( 8 – 7,45) + 2,186 |
3 | (2,12 + 1,07) * (2,12 – 1,07) |
4 | 86,4 * (17,01 : 4,2) : 6,4 |
5 | 42,26 – 34,68 : (33,32 : 9,8) |
6 | 40 – ( 7,12 + 11,043 : 2,7) |
7 | 12,6 : (2,04 + 4,26) – 0,564 |
8 | 7,371 : (5 – 3,18) + 2,05 *(17,82 – 7) |
9 | (5,2 : 26 + 26 : 5,2) *6,1 + 5,25 : 5 |
10 | 27,5967 : (8 – 1,186) + 3,02 |
11 | (20 – 13,7 ) * 7,4 + 18 : 0,6 |
12 | ( 4,694 — 3,998) : 4,35 + ( 4,5 * 5,4 – 0,06) |
13 | (4,6 * 3,5 + 15,32) : 31,42 + ( 7,26 – 5,78) : 0,148 |
14 | (101,96 – 6,8 * 7,2) : 4,24 – 3,4 * ( 10 – 6,35) |
15 | 7,72 * 2,25 – 4,06 : ( 0,824 + 1,176) – 12,423 |
16 | 51,328 : 6, 4 + 3,2 * (10 – 4,7) * 2,05 |
17 | (42,12 * 0,12 + 112,016* 0,1) : 1,6 – 9,424 |
18 | ( (4,2 *0,81 – 6,8*0,05) : 0,5) ) : 200 |
19 | 2,6* (4,4312 + 15,5688) – 6,66 : (8,2 – 6,72) |
20 | ( 0,624 : 4,16 + 6,867 : 2,18) *2,08 – 4,664 |
21 | 4260 + 42,6 : (62,06 + 37,94) – 42,6 : (52,44 — 52,43) |
22 | 5 : 0,25 + 0,6 *(9,275 – 4,275) : 0,1 |
23 | 3,1 : 100 + ( 6 – 0,3 : 100) *10 |
24 | 0,415 +(2,85 : 0,6*3,2 – 2,72 : 8) + 5,134 : 0,17 |
25 | 0,1: 0,002 – 0,5*( 7,91 : 0,565 – 11,1 :1,48) |
26 | 0,2 : 0,004 + (7,91 : 0,565 – 44,4 : 5,92) *0,5 |
27 | 4,735 : 0,5 + 14,95 : 1,3 + 2,121 : 0,7 |
28 | ( 0,1955 + 0,187) : 0,085 |
29 | (86,9 + 667,6) : (37,1 + 13,2) |
30 | (0,008 + 0,992) * (5 *0,6 – 1,4) |
Вариант 2 | |
1 | (130,2 – 30,8) : 2,8 — 21,84 |
2 | 3,712 : ( 7 – 3,8) + 1,3* (2,74 + 0,66) |
3 | ( 3,4 : 1,7 + 0,57 : 1,9)* 4,9 + 0,0825 : 2,75 |
4 | 10,79 : 8,3*0,7 — 0,46 * 3,15 : 6,9 |
5 | ( 21,2544 : 0,9 + 1,02 * 3,2 ) : 5,6 |
6 | 4,36 : ( 3,15 + 2,3) + ( 0,792 – 0,78) * 350 |
7 | ( 3,91 : 2,3 * 5,4 – 4,03 ) * 2,4 |
8 | 6,93 : ( 0,028 + 0,36 * 4,2 ) — 3,5 |
9 | 42,165 – 22,165 : ( 0,61 + 3,42) |
10 | ( (4 : 0,128 + 14628,25) : 1,011* 0,00008 + 6,84) : 12,5 |
11 | 687,8 + ( 88,0802 – 85,3712) : 0,045 |
12 | (3,1 * 5,3 – 14,39) : 1,7 + 0,8 |
13 | ( 3,8 * 1,75 : 0,95 – 1,02) : 2,3 + 0,4 |
14 | ( ( 23,79 : 7,8 – 6,8 : 17) * 3,04 – 2,04 ) * 0,85 |
15 | 0,15 : 0,01 + ( 6 + 9,728 : 3,2) * 2,5 – 1,4 |
16 | 1,44 : 3,6 + 0,8 + 3,6 : 1,44* ( 0,1 — 0,02) |
17 | 3,45 * ( 11,2 + 75,6) – 0,93 * 1,26 |
18 | 4,25 : 0,25 – 0,06 * 82 + 0,4 |
19 | ( 0,237 + 45,6) * 12,01 — 11,1* ( 237,1 – 229,9) |
20 | 5,8 – 0,27 * 3,6 + 5,172 |
21 | 12 – 5,3 : ( 19,6 : 0,35 — 0,06 * 50) |
22 | ( 0,6 + 0,25 – 0,125) * 3,2 + 4,5 : 100 |
23 | ( 15,5 : 0,25 – 0,08 * 200) : 2,3 – 1,3 |
24 | ( 87,05 * 2,7 – 55,68 :32) * 0,8 : 0,02 |
25 | 522,348 : 87 + 2,7 * ( 0,84 – 0,128 : 0,16) |
26 | 6400 * 0,0145 – ( 1272,6 : 0,42 – 3000) |
27 | ( 0,7 : 1,4 – 0,02) : 0,012 + 1,6 * (0,548 – 0,023) |
28 | ( 1,184 : 3,2 + 0,832 : 0,4) : 0,5 + 1,5 |
29 | 4,96 ; 10 + 35,8 : 100 — 0,0042 |
30 | ( 0,04 + 3,59) * ( 7,35 + 2,65 ) : 300 |
Вариант 3 | |
1 | 2,5 + 0,56* 28 + 0,125*15 – 0,12*7 |
2 | 12,8 : 4 + 76,8 : 12 – 42,6 : 6 – 2,4 |
3 | 4,01 + 43,6 : 10 – 73,2 : 30 + 15,4 : 100 |
4 | 176,4 : 100 – 0,041*40 + 13,5 :50 +0,3 |
5 | (16,4 + 13,2)*3 – ( 10,6 + 4,8) *2 – 23,2 |
6 | (40,65 — 32,6) : 5 + ( 4,72 _ 2,24)*3 |
7 | 4,735 : 0,5 + 14,95 : 1,3 + 2,121 : 0,7 – 21,6 |
8 | 0,01105 + 0,05 — 0,3417 : 34 -_ 0,875 : 125 |
9 | (5,72 – 3,21 )*5 + ( 86,9 + 667,6) : (37,1 + 13,2) |
10 | ( 0,1955 + 0,187) : 0,085 – (4,72 – 4,72 )*0,157 |
11 | 4,9 – (0,008 + 0,992) * (5 *0,6 – 1,4) |
12 | (50000 – 1397,3) : (20,4 + 33,603) – 856 |
13 | 3,7 *0,18 + 35,9 *0,26 – 0,109 *91 |
14 | 34,98 : 6,6 + 5,141 : 0,53 – 0,8379 : 0,057 |
15 | 0,131 *470 + 26,97 : 2,9 — 50,4 *1,4 |
16 | 0,439 *97 – 182,75 : 4,3 + 31,9 *0,43 |
17 | (20,4 – 18,23)* 4,3 + (0,40713 + 0,44176) : 0,67 |
18 | (0,357 + 7,043)*0,85 + (52 – 1,928) : 5,69 |
19 | (1,5 — 0,4732)* 35 – (0,6092 + 0,0718) : 0,75 |
20 | (139,4 + 16,6)* 0,039 — ( 20 – 17,54) : 2,5 |
21 | 4,1819 + 0,73 *( 5,375 + 2,595) |
22 | 5,0143 – 65,9*( 0,0612 + 0,0058) |
23 | (0,83 *3,7 + 9,741 :51 – 0,012) : 0,325 |
24 | (67,21 : 0,143 – 0,546*850 + 2,1) : 1,25 |
25 | ( 79* 0,63 – 9,558 : 5,4 – 26,94) : 0,324 |
26 | (11,328 : 16 + 7,752 : 7,6) : 0,16 |
27 | 13,7 – (0,53 *6,7 + 1,77*3,1 + 0,004) : 0,66 |
28 | 5,3 : (2,87* 0,53 – 0,043 *7,7 – 0,19) |
29 | (3,06 – 2,97) * (5,6*0,93 – 0,84*6,2) |
30 | (5,4*0,77 – 0,008) : (2,747 : 0,67+ 0,05) |
Вариант 4 | |
1 | 589,72 :16 – 18,305 :7 + 5,67 : 4 |
2 | (86,9 + 667,6 ) : (37,1 +13,2) |
3 | ( 0,93 + 0,07 ) : (0,93 – 0,805) |
4 | 1,35 : 2,7 + 6,02 – 5,9 + 0,4 : 2,5 *(4,2 – 1,075) |
5 | ( (14,068 + 15,78) : (1,875 + 0,175)) : (0,325+ 0,195) |
6 | (0,578 + 0,172)* ( 0,823 + 0,117) – 1,711 : (4,418 + 1,382) |
7 | (39,3 + 116,7) *0,39 – (19,01 -16,56) : 2,5 |
8 | (2,747 : 0,67 + 0,05) : (0,54* 7,7 – 0,008) |
9 | 5,76*4,76 : 6,12 + 81,9 : 58,5*2,05 |
10 | 25,6 : (38,07 + 1,93) + 0,037 *10 |
11 | (3,7011: 0,73 – 9,27: 4,5 – 1,41) :1,6 |
12 | 40,86 : 4,5 – 0,6039 : 5,49 + 0.338: 0,13 |
13 | (85,9 +667,1) : ((37 +13,2) + (11,44 – 6,42)*10 |
14 | 1,224 : (7 – 2,92) + 1,06*(13,5 – 3) |
15 | (7,5* 48 – 8,2* 9,5 + 141,4) : (254,1 :4,2) |
16 | 0,63*69 – 10,048 : 6,4 – 19,44 : 32,4 *0,8 |
17 | (3,8 : 19 + 1,9 : 3,8) *5,2 + 7,28 : 7 |
18 | (4,9 + 1,06 – 0,98) : ( 0,83*0,6) : 2,4 |
19 | (28,7 *0,15) : (0,25 *0,21) + 22,5 :1,25 |
20 | 0,1 : 0,002 + (7,91 : 0,565 — 11,1 : 1,48) |
21 | (0,2028 :0,24 – 0,32 *1,5) *(4,05 – 13,1625 : 4,05) |
22 | (97,44 : 0,48 + 128,64 : 3,2) *0,25 – 17,89 |
23 | 5,4 + ( (4,7 – 2,85)*1,8 + 0,0156 : 0,13) |
24 | (1,2 *0,15 + 12 :100 – 1,4 : 10) : 0,1 |
25 | 0,545 : 0,5 +2,75 *0,4 – 0,45 *3,8 |
26 | 0,6 * (7,24 : 0,8 – 0,968 : 0,16) + 2,25 *0,04 |
27 | (6,4 *0,025 + 7,07 : 3,5 – 3,68 : 4) : 0,9 |
28 | 2,5 *( 3 : 6 – 0,2 : 5 + 1,2 *0,15) |
29 | ( 5,508 : 0,27 – 10,2 *1,3) : 0,7 + 1,3 : 0,1 |
30 | 1,5 + 0,5*( 4,214 : 0,14 – 5,436 : 1,8) * 0,1 |
kopilkaurokov.ru
Действия с десятичными дробями — Десятичные дроби — Математика — Алгебра
Действия с десятичными дробями
Сложение и вычитание
Для сложения (вычитания) десятичных дробей необходимо:1) уравнять в дробях количество знаков после запятой;
2) записать дроби друг под другом так, чтобы ком была записана под запятой;
3) выполнить сложение (вычитание), не обращая внимания на запятую;
4) в ответе поставить ком под запятыми данных чисел.
Примеры
1)
2)
Для сложения и вычитания десятичных дробей имеют место те же свойства действий, что и для действий с натуральными числами.
Примеры
1) ;
2)
Умножения и деления
Для умножения двух десятичных дробей необходимо:1) выполнить умножение этих чисел как натуральных, несмотря на запятые;
2) в произведении отделить справа запятой столько десятичных знаков, сколько их имеют множители оба вместе.
Если в произведении меньше цифр, чем надо отделить запятой, то впереди пишут нужное количество нулей.
Примеры
Чтобы разделить число на десятичную дробь, нужно в деленному и делителе перенести запятую вправо на столько десятичных знаков, сколько их в делителе, а затем выполнить деление на натуральное число: .
Деление на натуральное число
Деление десятичной дроби на натуральное число выполняется как деление натуральных чисел, но после окончания деления целой части числа надо в доле поставить запятую. Например:Для умножения и деления десятичных дробей имеют место те же свойства, что и для действий с натуральными числами.
Отдельные случаи умножения и деления десятичных дробей
Чтобы умножить десятичную дробь на 10, 100, 1000 и так далее, надо перенести кому дроби справа на одну, две, три и так далее цифры.Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т.д., надо перенести запятую дроби влево на одну, две, три и так далее цифры.
Примеры
;
;
;
.
;
Чтобы разделить десятичную дробь на 10, 100, 1000 и так далее, надо перенести в ней запятую вправо на одну, две, три и так далее цифры.
Примеры
; ;
; ;
; .
Следовательно, если число умножить на 0,1; 0,01; 0,001 и так далее, то оно уменьшится в 10, 100, 1000 и так далее раз, а если поделить на 0,1; 0,01; 0,001 и так далее, то оно увеличится в 10, 100, 1000 и так далее раз.
na-uroke.in.ua
Этапы урока | Деятельность учителя | Деятельность ученика | Примечание | ||
1. Самоопределение к учебной деятельности.
| Приветствие, мобилизация внимания детей. | Включаются в деловой ритм урока. Девиз урока: | Слайд 2 | ||
2. Актуализация знаний | Задание 1. Организует устную работу по теоретическому материалу. Задаёт вопросы. Вопросы для первой команды. Вопросы для второй команды. Вопросы для третьей команды. | Команды отвечают на теоретические вопросы. За каждый правильный ответ команда получает один балл.
|
Слайд 3
Слайд 4 | ||
3. Постановка учебной проблемы | Задание 2. Учитель организует устный счет. Ответ: 0,06; 0,16; 0,2; 0,54; 1,02; 1,2; 1,3; 2,1; 3,1. Здесь заканчивается 5 слайд. | Команды считают устно. Первой отвечает та команда, которая первой поднимет сигнальную карточку. Если ответ неверный, то отвечает другая команда. |
Слайд 5.
Слайд 6. | ||
| 4. Поиск решения
| Задание 3. Игра «Найди ошибки». | Отвечает команда, которая первой найдет пример, в котором ошибка и скажет ответ. Правильный ответы: | Слайд 7 Щелкая на неправильные ответы, будут появляться – правильные. | ||
Задание 4. Выполните задание и найдите правильный ответ. б) (41 – 38,7) ∙ 8,8 + 4 : 0,8 | Команды выполняют тестовые задания. Та команда, которая первой поднимет сигнальную карточку, отвечает. Если ответ неверный, право отвечать переходит к другой команде. Каждый правильный ответ – один балл. Работа с сигнальными карточками. | Слайд 8 | |||
2. Решите уравнение. б) 4,42 – 14х = 3.3 | Слайд 9 | ||||
3. Найдите среднее арифметическое чисел: 23,86; 22,7 и 36,6. 4. Пешеход шел 2 ч со скоростью 2,5 км/ч и 3 ч со скоростью 3,2 км/ч. Найдите среднюю скорость пешехода. Здесь заканчивается 10 слайд. |
| Слайд 10 | |||
5. Физминутка | Учитель читает стихотворение | Учащиеся выполняют движения. |
| ||
| 6. Включение в систему знаний
| Задание 5. Игра «Кто быстрее». | Каждая команда выполняет задание. Та команда, которая первой выполнит задание, выбирает своего представителя, и он записывает решение на доске. Правильное выполнение задания – один балл. | Слайд 11. По щелчку будет показано правильное решение примеров и уравнений. | ||
| 2. Решите уравнение. а) 11 + 2,3у + 1,3у = 38 б) (4,5 – х) ∙ 5,8 = 8,7 Здесь заканчивается 11 слайд. | Решение. б) 4,5 – х = 8,7: 5,8 | ||||
Задание 6. | Каждая команда получает задачу, обсуждает решение и выбирает участника, который будет объяснять решение задачи и записывать его на доске. Если ошибки при решении задач исправляют другие команды, то они получают дополнительные баллы. За правильное решение задачи – один балл. | Слайд 12. По щелчку мышкой появляется решение задачи. | |||
Задача для первой команды. Здесь заканчивается 12 слайд. | Решение первой задачи. 2,3 – 0,8 = 1,5 (дм) – ширина. 2) 1,5 ∙ 1,2 = 1,8 (дм) – высота. 3) 2,3 ∙ 1,5 ∙ 1,8 = 6,21 (дм³) – объём. 6,21 ≈ 6,2 Ответ: 6,21 дм³ | ||||
Задача для второй команды. Здесь заканчивается 13 слайд. | Решение второй задачи. 8,3 ∙ 9 = 74,7 (т) – на 9 автомобилях. 2) 7,2 ∙ 6 = 43,2 (т) – на 6 автомобилях. 3) 74,7 + 43,2 = 117,9 (т) – всего. 4) 9 + 6 = 15 (авт.) – всего. 5) 117,9 : 15 = 7,86 (т) – средняя грузоподъёмность одного автомобиля. Ответ: 7,86 тонн. | Слайд 13 По щелчку мышкой появляется решение задачи. | |||
Задача для третьей команды. | Решение третьей задачи. | Слайд 14 | |||
7. Информация о домашнем задании | Записывает на доске д/з | Записывают домашнее задание в дневник. |
| ||
8. Рефлексия и итог урока | 1. Предлагает продолжить предложение
| 1. Продолжают предложение учителя.
2. Учащиеся поднимают карточку с ответом на вопрос, тем самым оценивают, как они усвоили эту тему. | Слайд 15
Карточки для рефлексии
|
xn--i1abbnckbmcl9fb.xn--p1ai
Десятичные дроби и действия с ними. Деление и умножение десятичных дробей :: SYL.ru
Десятичная дробь используется, когда нужно выполнять действия с нецелыми числами. Это может показаться нерациональным. Но такой вид чисел существенно облегчает математические операции, которые с ними необходимо выполнять. Это понимание приходит со временем, когда их запись становится привычной, а прочтение не вызывает трудностей, и освоены правила десятичных дробей. Тем более что все действия повторяют уже известные, которые усвоены с натуральными числами. Только нужно запомнить некоторые особенности.
Определение десятичной дроби
Десятичная дробь — это особое представление нецелого числа со знаменателем, который делится на 10, а ответ получается в виде единицы и, возможно, нулей. Другими словами, если в знаменателе 10, 100, 1000 и так далее, то удобнее переписать число с использованием запятой. Тогда до нее будет расположена целая часть, а потом — дробная. Причем запись второй половины числа будет зависеть от знаменателя. Количество цифр, которые находятся в дробной части, должно быть равно разряду знаменателя.
Проиллюстрировать вышесказанное можно этими числами:
9/10=0,9; 178/10000=0,0178; 3,05; 56 003,7006.

Причины, по которым понадобилось применение десятичных дробей

Математикам потребовались десятичные дроби по нескольким основаниям:
Упрощение записи. Такая дробь расположена вдоль одной линии без черточки между знаменателем и числителем, при этом наглядность не страдает.
Простота в сравнении. Достаточно просто соотнести цифры, находящиеся в одинаковых позициях, в то время как с обыкновенными дробями пришлось бы приводить их к общему знаменателю.
Упрощение вычислений.
Калькуляторы не рассчитаны на введение обыкновенных дробей, они для всех операций используют десятичную запись чисел.

Как правильно прочитать такие числа?
Ответ прост: так же, как обыкновенное смешанное число со знаменателем, кратным 10. Исключение составляют только дроби без целого значения, тогда при чтении нужно произносить «ноль целых».
Например, 45/1000 нужно произнести как сорок пять тысячных, в то же время 0,045 будет звучать как ноль целых сорок пять тысячных.
Смешанное число с целой частью равной 7 и дробью 17/100, что запишется как 7,17, в обоих случаях будет прочитано как семь целых семнадцать сотых.
Роль разрядов в записи дробей
Верно отметить разряд — это то, что требует математика. Десятичные дроби и их значение могут существенно измениться, если записать цифру не в том месте. Впрочем, это было справедливо и раньше.
Для прочтения разрядов целой части десятичной дроби нужно просто воспользоваться правилами, известными для натуральных чисел. А в правой части они зеркально отражаются и по-другому читаются. Если в целой части звучало «десятки», то после запятой это будут уже «десятые».
Наглядно это можно увидеть в этой таблице.
| класс | тысячи | единицы | , | дробная часть | |||||||
| разряд | сот. | дес. | ед. | сот. | дес. | ед. | десятая | сотая | тысячная | десятитысячная | |
Как правильно записать смешанное число десятичной дробью?
Если в знаменателе стоит число, равное 10 или 100, и прочие, то вопрос о том, как дробь перевести в десятичную, несложен. Для этого достаточно по-другому переписать все ее составные части. В этом помогут такие пункты:
немного в стороне написать числитель дроби, в этот момент десятичная запятая располагается справа, после последней цифры;
переместить запятую влево, здесь самое главное — правильно сосчитать цифры — передвинуть ее нужно на столько позиций, сколько нолей в знаменателе;
если их не хватает, то на пустых позициях должны оказаться нули;
нули, которые были в конце числителя, теперь не нужны, и их можно зачеркнуть;
перед запятой приписать целую часть, если ее не было, то здесь тоже окажется нуль.
Внимание. Нельзя зачеркивать нули, которые оказались окружены другими цифрами.
О том, как быть в ситуации, когда в знаменателе число не только из единицы и нулей, как дробь переводить в десятичную, можно прочитать чуть ниже. Это важная информация, с которой обязательно стоит ознакомиться.
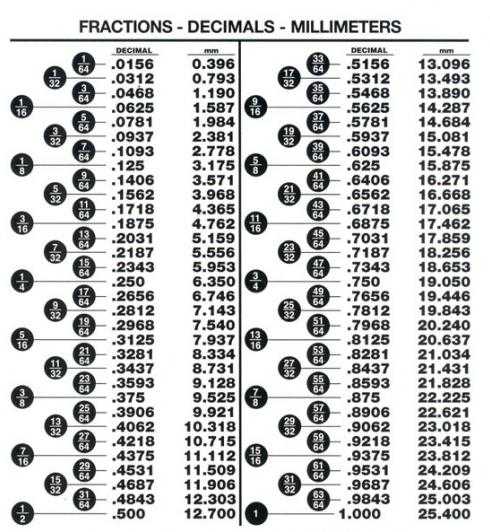
Как дробь перевести в десятичную, если знаменатель — произвольное число?
Здесь возможны два варианта:
Когда знаменатель можно представить в виде числа, которое равно десяти в любой степени.
Если такую операцию проделать нельзя.
Как это проверить? Нужно разложить знаменатель на множители. Если в произведении присутствуют только 2 и 5, то все хорошо, и дробь легко преобразуется в конечную десятичную. В противном случае, если появляются 3, 7 и другие простые числа, то результат будет бесконечным. Такую десятичную дробь для удобства использования в математических операциях принято округлять. Об этом будет речь немного ниже.
Изучает, как получаются такие десятичные дроби, 5 класс. Примеры здесь будут очень кстати.
Пусть в знаменателях находятся числа: 40, 24 и 75. Разложение на простые множители для них будет такое:
- 40=2·2·2·5;
- 24=2·2·2·3;
- 75=5·5·3.
В этих примерах только первая дробь может быть представлена в виде конечной.
Алгоритм перевода обыкновенной дроби в конечную десятичную
Проверить разложение знаменателя на простые множители и убедиться в том, что оно будет состоять из 2 и 5.
Добавить к этим числам столько 2 и 5, чтобы их стало равное количество. Они дадут значение дополнительного множителя.
Произвести умножение знаменателя и числителя на это число. В результате получится обыкновенная дробь, под чертой у которой стоит 10 в некоторой степени.
Дальше действовать так, как было описано в пункте, расположенном немного выше.

Если в задаче эти действия выполняются со смешанным числом, то его сначала нужно представить в виде неправильной дроби. А уже потом действовать по описанному сценарию.
Представление обыкновенной дроби в виде округленной десятичной
Этот способ того, как дробь переводить в десятичную, кому-то покажется даже проще. Потому что в нем нет большого количества действий. Нужно только разделить значение числителя на знаменатель.
К любому числу с десятичной частью справа от запятой можно приписать бесконечное количество нулей. Этим свойством и нужно воспользоваться.
Сначала записать целую часть и поставить после нее запятую. Если дробь правильная, то написать ноль.
Потом полагается выполнить деление числителя на знаменатель. Так, чтобы количество цифр у них было одинаковым. То есть приписать справа у числителя нужное количество нолей.
Выполнять деление в столбик до тех пор, пока не будет набрано нужное количество цифр. Например, если округлить нужно будет до сотых, то в ответе их должно быть 3. В общем, цифр должно быть на одну больше, чем нужно получить в итоге.
Записать промежуточный ответ после запятой и округлить по правилам. Если последняя цифра — от 0 до 4, то ее нужно просто отбросить. А когда она равна 5-9, то стоящую перед ней нужно увеличить на единицу, отбросив последнюю.
Возврат от десятичной дроби к обыкновенной
В математике встречаются задачи, когда десятичные дроби удобнее представить в виде обыкновенных, в которых есть числитель со знаменателем. Можно вздохнуть с облегчением: эта операция возможна всегда.
Для этой процедуры нужно сделать следующее:
записать целую часть, если она равна нулю, то ничего писать не надо;
провести дробную черту;
над ней записать цифры из правой части, если первыми идут нули, то их нужно зачеркнуть;
под чертой написать единицу с таким количеством нолей, сколько цифр стоит после запятой в первоначальной дроби.
Это все, что нужно сделать, чтобы перевести десятичную дробь в обыкновенную.
Что можно делать с десятичными дробями?
В математике это будут определенные действия с десятичными дробями, которые ранее выполнялись для других чисел.
Ими являются:
Первое действие, сравнение, похоже на то, как это делалось для натуральных чисел. Чтобы определить, какое больше, нужно сравнивать разряды целой части. Если они окажутся равными, то переходят к дробной и так же по разрядам сравнивают их. То число, где окажется большая цифра в старшем разряде, и будет ответом.
Сложение и вычитание десятичных дробей
Это, пожалуй, самые простые действия. Потому что выполняются по правилам для натуральных чисел.
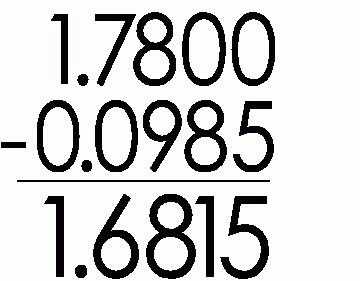
Так, чтобы выполнить сложение десятичных дробей, их нужно записать друг под другом, разместив запятые в столбик. При такой записи слева от запятых оказываются целые части, а справа — дробные. И теперь нужно сложить цифры поразрядно, как это делается с натуральными числами, снеся вниз запятую. Начинать сложение нужно с самого маленького разряда дробной части числа. Если в правой половине не хватает цифр, то дописывают нули.
При вычитании действуют так же. И здесь действует правило, которое описывает возможность занять единицу у старшего разряда. Если в уменьшаемой дроби после запятой меньше цифр, чем у вычитаемого, то в ней просто приписывают нули.
Немного сложнее обстоит дело с заданиями, где нужно выполнить умножение и деление десятичных дробей.
Как умножить десятичную дробь в разных примерах?
Правило, по которому производится умножение десятичных дробей на натуральное число, такое:
записать их в столбик, не обращая внимания на запятую;
перемножить, как если бы они были натуральными;
отделить запятой столько цифр, сколько их было в дробной части исходного числа.
Частным случаем является пример, в котором натуральное число равно 10 в любой степени. Тогда для получения ответа нужно просто передвинуть запятую вправо на столько позиций, сколько нулей в другом множителе. Иными словами, при умножении на 10 запятая сдвигается на одну цифру, на 100 — их будет уже две, и так далее. Если цифр в дробной части не хватает, то нужно записать на пустых позициях нули.
Правило, которым пользуются, когда в задании нужно произвести умножение десятичных дробей на другое такое же число:
записать их друг под другом, не обращая внимания на запятые;
умножить, как если бы они были натуральными;
отделить запятой столько цифр, сколько их было в дробных частях обеих исходных дробях вместе.
Частным случаем выделяются примеры, в которых один из множителей равен 0,1 или 0,01 и далее. В них нужно выполнить перемещение запятой влево на количество цифр в представленных множителях. То есть если умножается на 0,1, то запятая сдвигается на одну позицию.
Как разделить десятичную дробь в разных заданиях?
Деление десятичных дробей на натуральное число выполняется по такому правилу:
записать их для деления в столбик, как если бы они были натуральными;
делить по привычному правилу до тех пор, пока не закончится целая часть;
поставить в ответ запятую;
продолжить деление дробной составляющей до получения в остатке нуля;
если нужно, то можно приписать нужное количество нулей.
Если целая часть равна нулю, то и в ответе ее тоже не будет.
Отдельно стоит деление на числа, равные десятке, сотне и так далее. В таких задачах нужно передвинуть запятую влево на количество нулей в делителе. Бывает, что цифр в целой части не хватает, тогда вместо них используют нули. Можно заметить, что эта операция подобна умножению на 0,1 и подобным ей числам.
Чтобы выполнить деление десятичных дробей, нужно воспользоваться этим правилом:
превратить делитель в натуральное число, а для этого перенести в нем запятую вправо до конца;
выполнить перемещение запятой и в делимом на такое же число цифр;
действовать по предыдущему сценарию.
Выделяется деление на 0,1; 0,01 и прочие подобные числа. В таких примерах запятая сдвигается вправо на число цифр в дробной части. Если они закончились, то нужно приписать недостающее количество нулей. Стоит отметить, что это действие повторяет деление на 10 и подобные ему числа.

Заключение: все дело в практике
Ничто в учебе не дается легко и без усилий. Для надежного освоения нового материала требуются время и тренировка. Математика не исключение.
Чтобы тема про десятичные дроби не вызывала затруднений, нужно решать с ними примеров как можно больше. Ведь было время, когда и сложение натуральных чисел ставило в тупик. А теперь все нормально.
Поэтому, перефразируя известную фразу: решать, решать и еще раз решать. Тогда и задания с такими числами будут выполняться легко и непринужденно, как очередная головоломка.
Кстати, и головоломки поначалу решаются сложно, а потом нужно делать привычные движения. Так же и в математических примерах: пройдя по одному пути несколько раз, потом уже не будешь задумываться над тем, куда повернуть.
www.syl.ru
