Дифференциальные уравнения с разделяющимися переменными [wiki.eduVdom.com]
subjects:diffury:уравнения_с_разделяющимися_переменными
Уравнения вида $\varphi_1(x)\Psi_1(y)dx=\varphi_2(x)\Psi_2(y)dy$ , в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от X и только от Y называется уравнением с разделяющими переменными. Путём деления на произведение $\varphi_1(y)\varphi_2(x)$ оно приводится к уравнению с разделёнными переменными:
$$ \frac{\varphi_1(x)}{\varphi_2(x)}dx = \frac{\Psi_2(y)}{\Psi_1(y)}dy $$
Общий интеграл этого уравнения имеет вид:
$$ \int \frac{\varphi_1(x)}{\varphi_2(x)}dx = \int \frac{\Psi_2(y)}{\Psi_1(y)}dy = C $$
Примеры
Пример 1. Найти общее решение дифференциального уравнения: ${xy}’-y=1$
Решение дифференциального уравнения:
Пример 2. Найти частное решение уравнения $(1+e^{x})y{y}’=e^{x}$, удовлетворяющее начальному условию $y|_{x=0}=1$ (задача Коши)
Решение. Имеем $(1+e^{x})y\frac{dy}{dx}=e^{x}$
Разделяя переменные, получаем: $$ y\;dy = \frac{e^{x}}{1+e^{x}}dx $$
Интегрируя, найдём общий интеграл: $$ \int y\;dy = \int \frac{e^{x}}{1+e^{x}}dx \\ \frac{y^{2}}{2}=\ln{(1+e^{x})} +C \qquad (1) $$
(1) – общее решение дифференциального уравнения
Полагая X=0 и Y=1, будем иметь $\frac{1}{2}=\ln{2}+C$ , откуда $C=\frac{1}{2} -\ln{2}$
Подставляя в (1) найденное значение C, получаем частное (решение задачи Коши)
$$
y^{2} =
1 +\ln{\left ( \frac{1+e^{x}}{2} \right )^{2}}
\;;
\\
y=
\pm\sqrt{
1 +\ln{\left ( \frac{1+e^{x}}{2} \right )^{2}}
}
$$
Из начального $u=\frac{y}{x}$ условия следует, что $y>0 ( y|_{x=0}=1 >0)$ поэтому перед корнем берём знак плюс. Итак, искомое частное решение
$$
y=\sqrt{
1 +\ln{\left ( \frac{1+e^{x}}{2} \right )^{2}}
}
$$
Пример 3.
Решение дифференциального уравнения:
Пример 4. Найти общее решение дифференциального уравнения: $$ \frac{dy}{dx}=x^{3} $$
Решение дифференциального уравнения:
Пример 5. Найти общее решение дифференциального уравнения: $$ \frac{dy}{dx}=2\frac{y}{x} $$
Решение дифференциального уравнения:
Пример 6. Найти общее решение дифференциального уравнения: $$ \frac{dy}{dx}=-xy $$
Решение дифференциального уравнения:
Пример 7. $$ {y}’={\rm tg}\,x\cdot{\rm tg}\,y $$
Решение:
Пример 8.
Решение дифференциального уравнения:
subjects/diffury/уравнения_с_разделяющимися_переменными.txt · Последние изменения: 2014/12/15 20:25 — ¶
Дифференциальные уравнения с разделенными переменными
Многие студенты спрашивают «Как найти решение дифференциального уравнения?» Ответ возможно неординарен, но что Вы знаете о дифференциальных уравнениях (ДУ), их типах, какие распространенные схемы вычислений ДУ? С этого нужно начинать.
Сферы применения дифференциальных уравнений были в общем очерчены на предыдущем уроке. Здесь речь пойдет об одном из самых простых (в плане вычислений) типов ДУ первого порядка среди всех возможных уравнений что Вас ждут. Начнем с базовых понятий теории которые Вы должны знать и мы будем использовать в терминологии. Для одних это не нужно, потому что они ищут готовые ответы по дифференциальным уравнениям и думают, что таким образом решат все проблемы. Но это ошибка, потому что не знание элементарных понятий по теории ДУ сравнимо с тем, что Вы пытаетесь говорить, предварительно не изучив звуки и алфавит.
Дифференциальное уравнение первого порядка, которое можно записать формулой
N(х)dx+М(у)dy=0 (1)
называют уравнением с разделенными переменными.
Их не трудно обнаружить среди других уравнений, основной признак — множители при dx и dy являются функциями (константами), которые зависят только от х при множителе dx и у при dy.
Чтобы найти общее решение (общий интеграл) уравнения с разделенными переменными необходимо проинтегрировать уравнение (1)
Int(N(x), x) + Int(M(y),y) = С,
Для понимания дифференциальное уравнение (1) можно принимать, как условие равенства нулю полного дифференциала некоторой функции двух переменных U(x,y)
Отсюда следует что функция U(x,y)=С=const равна постоянной.
Дифференциальное уравнение вида
f1(x)*g1(y)dx+f2(x)*g2(y)dy=0 (2)
называют дифференциальным уравнением с разделяющимися переменными в симметричной форме.
В уравнении (2) коэффициенты при дифференциалах dx и dy является произведениями двух функций: одна зависит только от x, а вторая — от y. В области, где g1(y), f2(x) принимают отличные от нуля значения в уравнение с разделяющимися переменными (2) сводится к уравнению с разделенными переменными
Звучит как игра слов: разделенными, разделяющимися, однако между ними как видите есть маленькая разница, и теперь Вы ее знаете.
Рассмотрим типичные для практики задания на диф. уравнения первого порядка, которые в достаточно простой способ можно свести к уравнениям с разделенными переменными.
Пример 1 Решить дифференциальное уравнение
Решение:Имеем дифференциальное уравнение первого порядка, по теории его можно назвать уравнением с разделяющимися переменными или уравнением в дифференциалах. Для его упрощения сгруппируем слагаемые, содержащие dx, dy по разные стороны знака равенства
Далее выделим общие множители для каждой суммы и перепишем уравнение в дифференциалах в форме
После этого все, что содержит y переносим к dy, то же самое проделываем с множителями которые содержат переменную x.
В результате придем к дифференциальному уравнению с разделенными переменными
Теперь посмотрите почему данное уравнение называется уравнением с разделенными переменными? — Возле dx имеем функцию зависимую только от «икс», у dy — только от y.
Проинтегрируем дифференциальное уравнение
Выносим множители, чтобы при переменной в знаменателе стояли единицы. Также, чтобы в числителе получить дифференциалы знаменателя умножаем обе части на 2
Это позволяет упростить вычисления интеграла ДУ (после интегрирования получить логарифмы)
Константу рекомендуем внести в логарифм, для этого записывайте всегда ее в виде C1=ln(C)
Чтобы раскрыть логарифмическое уравнение экспонируем (находим экспоненту) правую и левую сторону зависимости
(3)
Также выделяем значение функции
Конечная запись имеет двойной корень и является общим решением уравнения с разделяющимися переменными. Это не совсем хороший тон подавать ответ, лучше решение оставить в виде формулы (3), только тройку перенести в правую сторону.
Пример 2 Найти общий интеграл дифференциального уравнения
Решение:Имеем уравнение в дифференциалах первого порядка. Разделим в уравнении переменные, содержащиеся при dx, dy и перенесем их по разные стороны знака равенства
С первых скобок выносим общий для двух слагаемых множитель y за скобки
Далее разделим множители так, чтобы при dy получить функцию только от y, а при dx — функцию аргумента x. В результате получим дифференциальное уравнение с разделенными переменными
После интегрирования
получим корневую зависимость для y и арктангенс в результате вычисления интеграла по аргументу (правая сторона).
Общий интеграл можем оставить в такой форме или перенести артангенс в левую часть зависимости.
Так же можем записать решение дифференциального уравнения в виде зависимости y(x) (явном виде). Для этого возведем обе части к квадрату
и перенеся сталую в правую сторону, вычислим корень квадратный
Это и есть искомое решение дифференциального уравнения.
Пример 3 Решить дифференциальное уравнение
Решение:Данное ДУ первого порядка необходимо свести под правило решения уравнений с разделенными переменными. Для этого второе слагаемое, что со знаком минус, переносим в правую сторону от знака равенства
и разделяем переменные
Проинтегрируем левую и правую сторону зависимости
В результате придем к логарифмическому уравнению вида
И снова обращаем Ваше внимание на то что в таком виде как правило не записывают.
Целесообразно, для компактности конечного решения, постоянную вносить под логарифм, то есть в форме
Взяв экспоненту от правой и левой части формулы придем к конечному виду решения дифференциального уравнения
Как Вы могли убедиться примеры достаточно просты, методика вычислений ДУ з разделенными переменными легкая для изучения.
Пример 4 Решить дифференциальное уравнениеРешение: Одно из слагаемых (не содержит производной) переносим за знак равенства
и записываем уравнение в дифференциалах..
Следующим шагом сводим зависимость к дифференциальному уравнению с разделенными переменными.
Для заданного уравнения всего лишь перекрестным делением записываем корни в знаменатели
В таком виде можем интегрировать уравнения
Левая сторона содержит функцию которая при иртегрировании даст корневую зависимость, для правой стороны по формулам получим арксинус.
Выполняем манипуляции с корнем, чтобы получить зависимость вида y=y(x)
Решение дифференциального уравнения будет иметь вид
На этом вводный урок закончен и основные выводы Вы должны сделать самостоятельно.
Для закрепления темы рекомендуем самостоятельно решить несколько из следующих примеров.
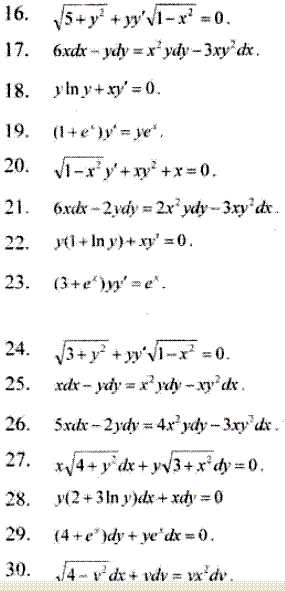Хотите верьте, а хотите — нет, но это самый простой тип дифференциальных уравнений, с которым Вам придетсяиметь дело на контрольной, экзаменах, практических занятиях, модулях. Это можно сказать важнейшая часть, поскольку сложные дифференциальные уравнения придется упрощать и сводить к уравнениям с разделенными переменными.
Схему вычислений должны заучить и знать на зубок — это один из основных методов решения сложных примеров на диф. уравнения.
yukhym.com
Дифференциальные уравнения с разделяющимися переменными
Дифференциальное уравнение с разделенными переменными записывается в виде: (1).В этом уравнении одно слагаемое зависит только от x, а другое – от y. Проинтегрировав почленно это уравнение, получаем: – его общий интеграл.
Пример: найти общий интеграл уравнения: .
Решение: данное уравнение
– дифференциальное уравнение с
разделенными переменными. Поэтому
или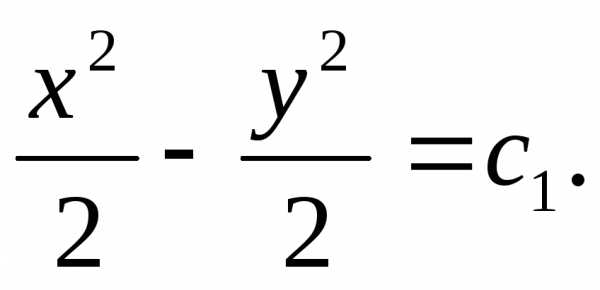
Обозначим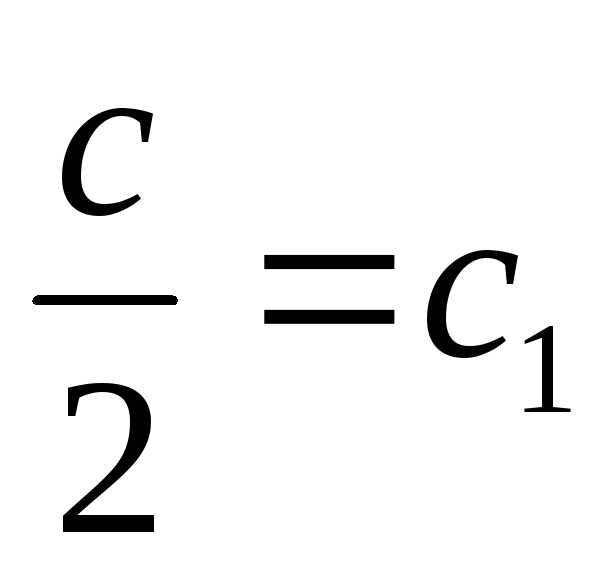
Уравнение с разделяющимися переменными имеет вид (2).Уравнение (2) легко сводиться к уравнению (1) путем почленного деления его на . Получаем:– общий интеграл.
Пример: Решить уравнение .
Решение: преобразуем левую
часть уравнения:
.
Делим обе части уравнения на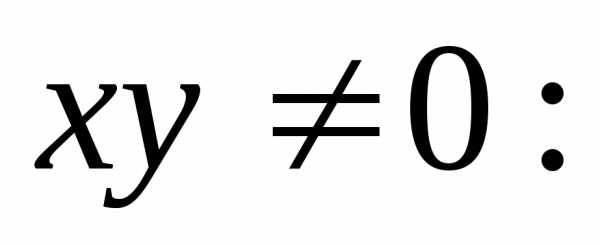
Решением является выражение:т.е.
Однородные дифференциальные уравнения. Уравнения Бернулли. Линейные дифференциальные уравнения первого порядка.
Уравнение вида
называетсяоднородным,
если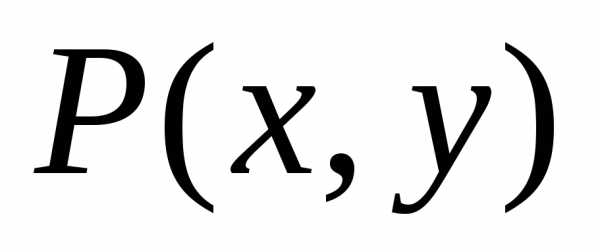 
и
–
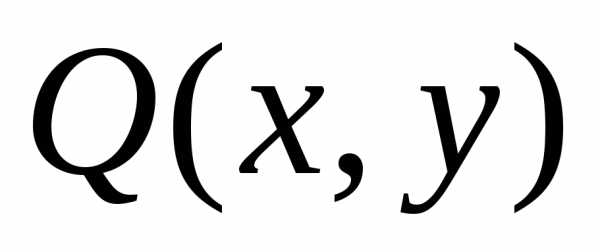однородные функции одного порядка
(измерения). Функция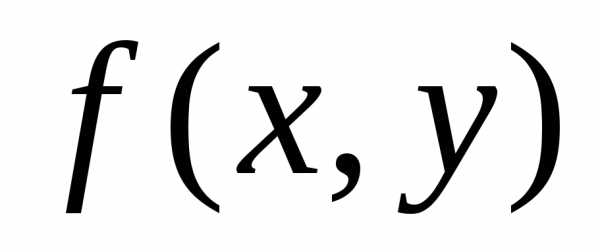
вся функция умножиться на
,
т.е.=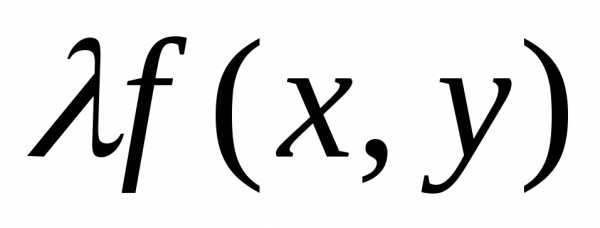
.
Однородное уравнение может быть приведено
к виду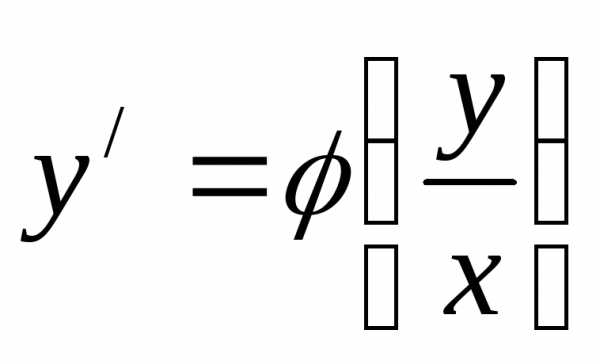
.
С помощью подстановки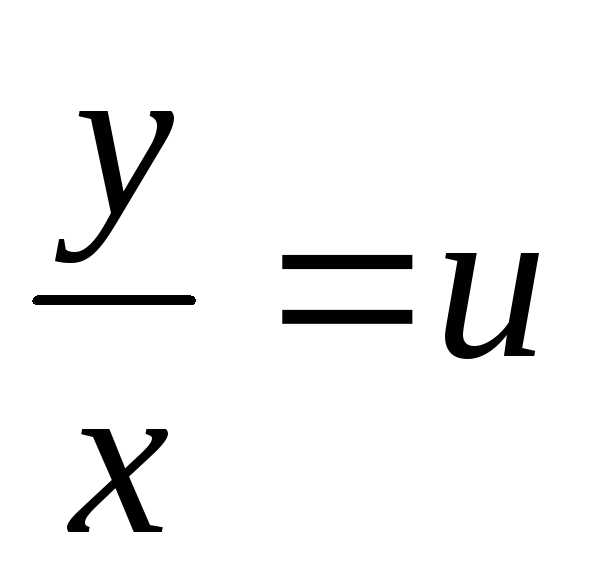
(
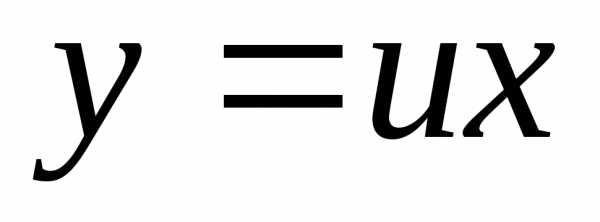
.Дифференциальное уравнение первого порядка называется линейным, если его можно записать в виде.
Метод Бернулли
Решение уравнения ищется в виде произведения двух других функций, т.е. с помощью подстановки().
Пример: проинтегрировать уравнение .
Полагаем
.
Тогда
,
т.е.
.
Сначала решаем уравнение=0: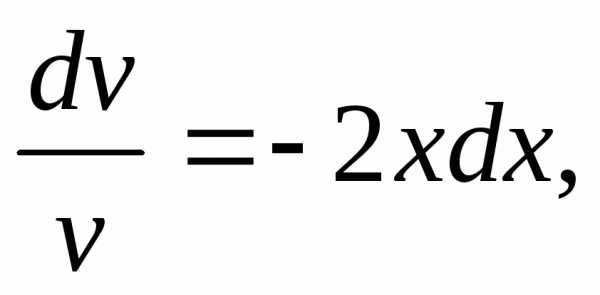
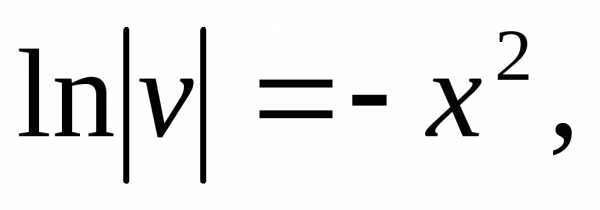
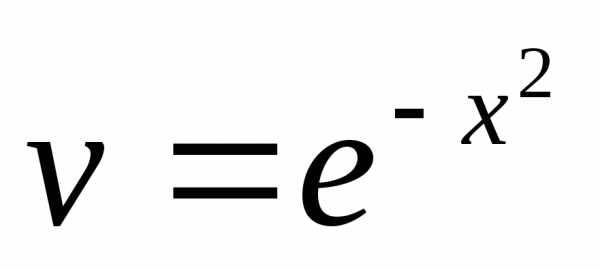
Теперь решаем уравнение
т.е.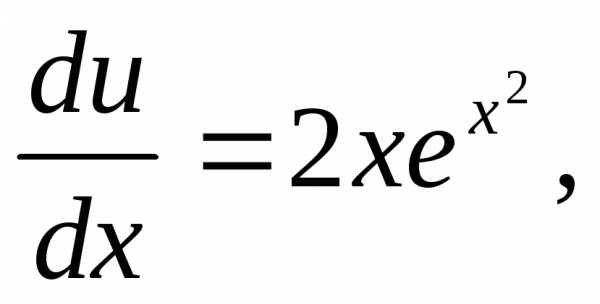
.
Итак, общее решение данного уравнения
естьт.е.
Уравнение Я. Бернулли
Уравнение вида , гденазываетсяуравнением Бернулли.Данное уравнение решается с помощью метода Бернулли.
Однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Однородным линейным дифференциальным
уравнением второго порядка называется
уравнение вида
(1), где
и
постоянны.
Частные решения уравнения (1) будем
искать в виде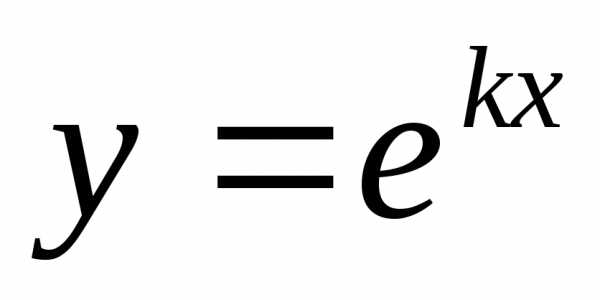
в
уравнение (1), получимт.е.или(2)(
).Уравнение 2 называется характеристическим уравнением дифференциального уравнения.
При решении характеристического уравнения (2) возможны три случая.
Случай 1.Корни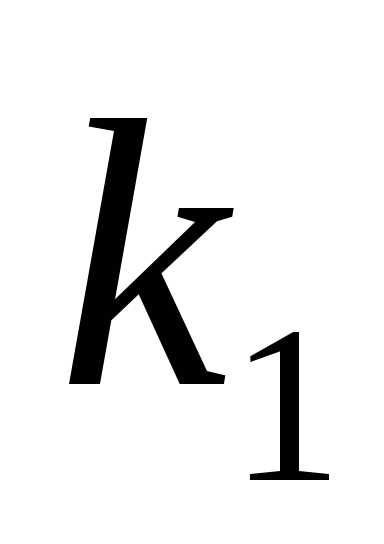
и
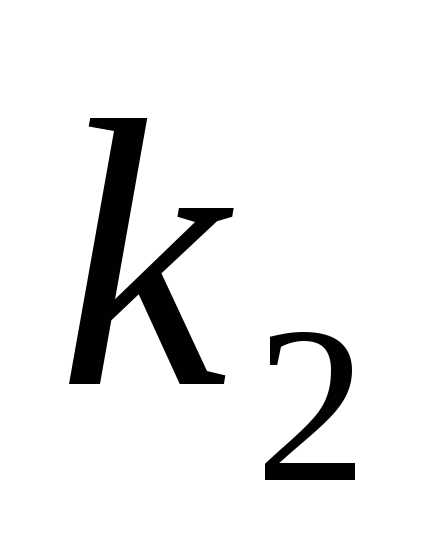уравнения (2) действительные и различные: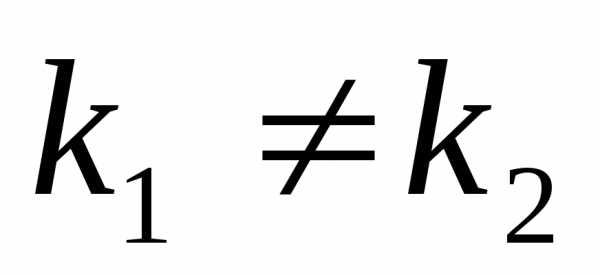
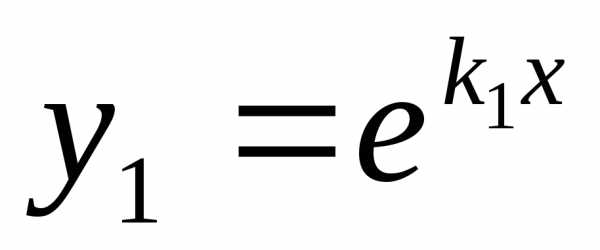и
.
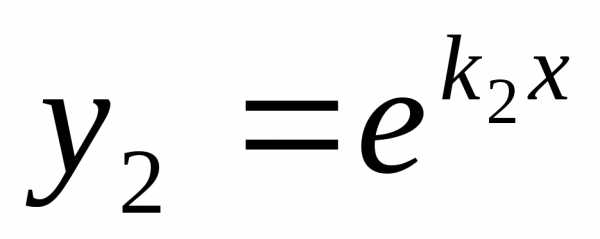Следовательно, общее решение уравнения
(1) имеет вид.
Случай 2.Корни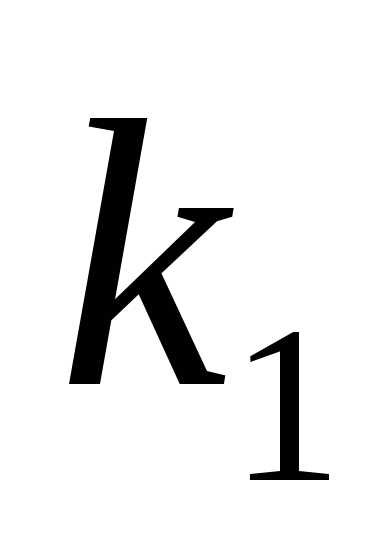
и
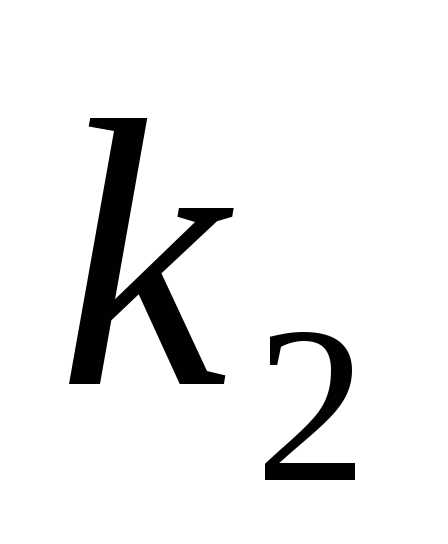уравнения (2) действительные и равные:
.
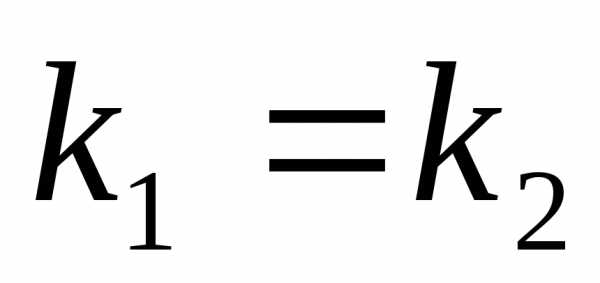В этом случае частными решениями
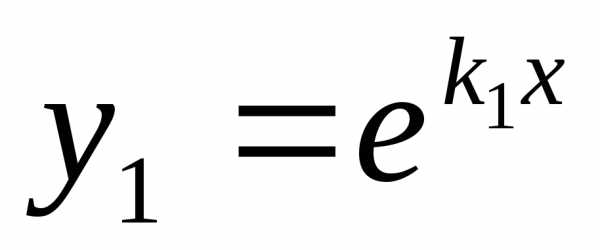уравнения (1) являются функции
и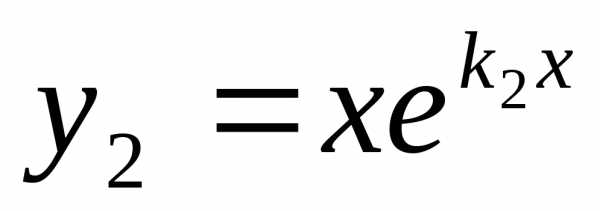
Случай 3.Корни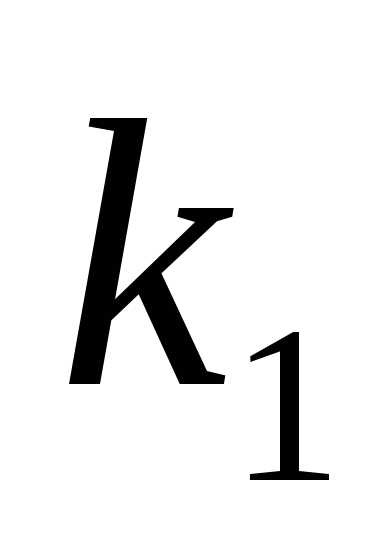
и
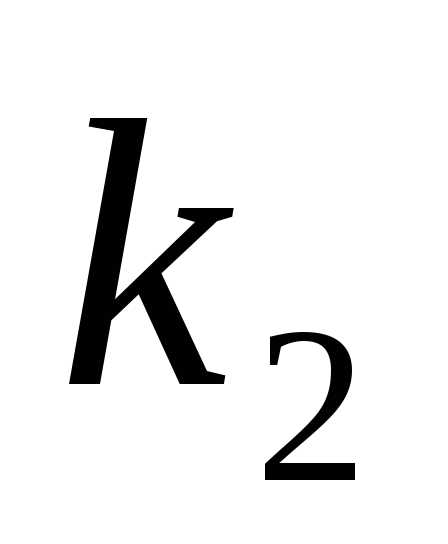уравнения (2) комплексные:,.
В этом случае частными решениями
уравнения (1) являются функциии.
Следовательно, общее решение уравнения
(1) имеет вид
Пример. Решить уравнение .
Решение: составим характеристическое уравнение:. Тогда. Общее решение данного уравнения.
Экстремум функции нескольких переменных. Условный экстремум.
Экстремум функции нескольких переменных
Определение. Точка М (хо,уо) называется точкой максимума (минимума)
На рис. 1 точка А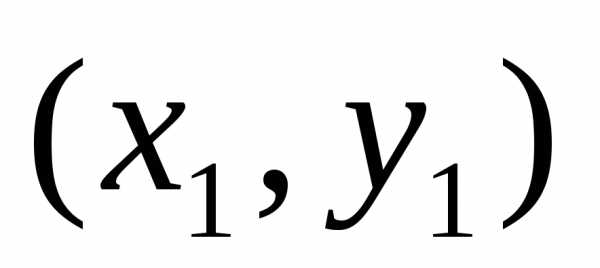
—
есть точка минимума, а точка В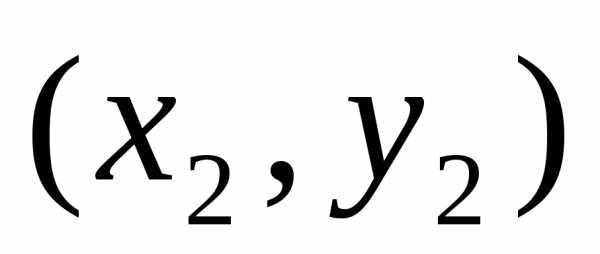
—точка максимума.
Необходимое условие экстремума — многомерный аналог теоремы Ферма.
Теорема. Пусть
точка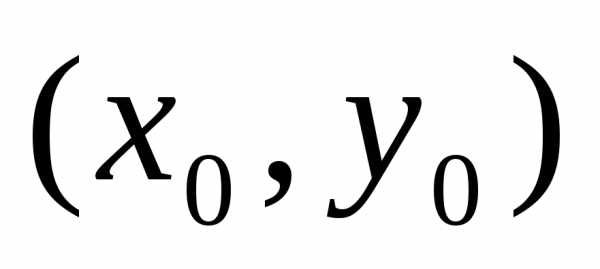
–
есть точка экстремума дифференцируемой
функцииz=f(x,
у). Тогда частные производные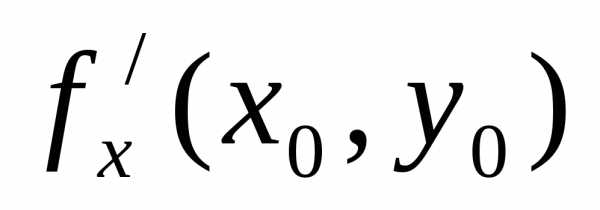
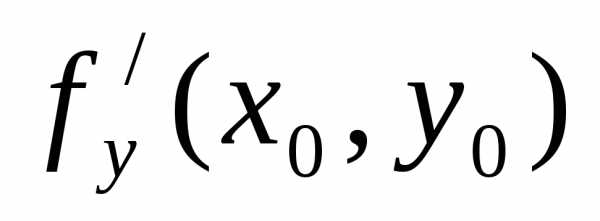в
этой точке равны нулю.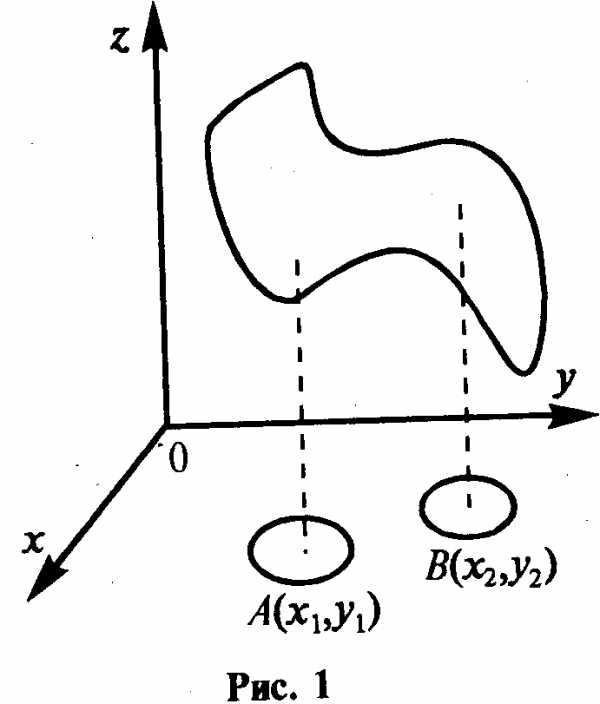
Точки, в которых выполнены необходимые условия экстремума функции z=f(x, у), т.е. частные производные z‘x и z‘y равны нулю, называются критическими или стационарными.
Равенство частных производных нулю выражает лишь необходимое, но недостаточное условие экстремума функции нескольких переменных.
На рис. изображена так называемая седловая точка М (хо,уо).
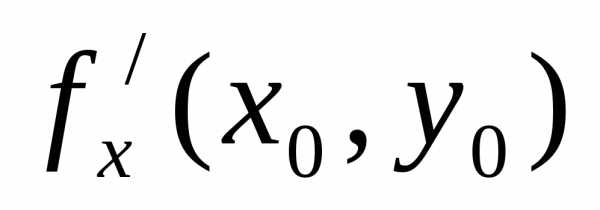и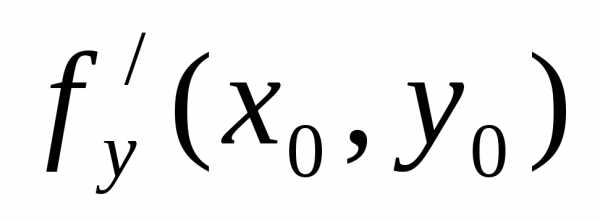
равны
нулю, но, очевидно, никакого экстремума
в точке М(хо,уо)
нет.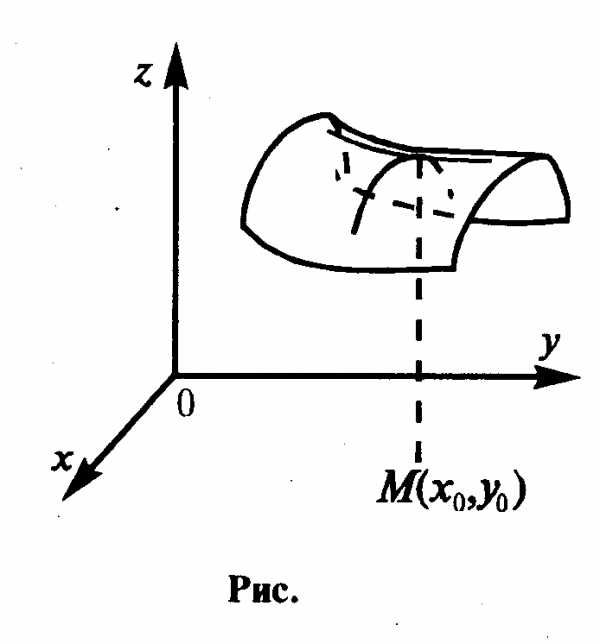
Такие седловые точки являются двумерными аналогами точек перегиба функций одной переменной. Задача заключается в том, чтобы отделить их от точек экстремума. Иными словами, требуется знать достаточное условие экстремума.
Теорема (достаточное
условие экстремума функции двух
переменных). Пусть
функция z=f(x,
у): а) определена
в некоторой окрестности критической
точки (хо,уо),
в которой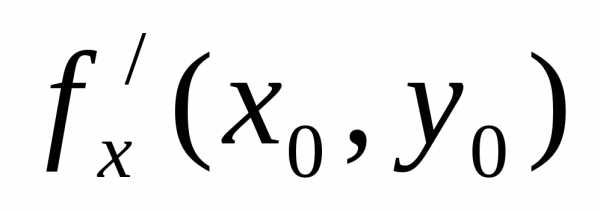
=0
и
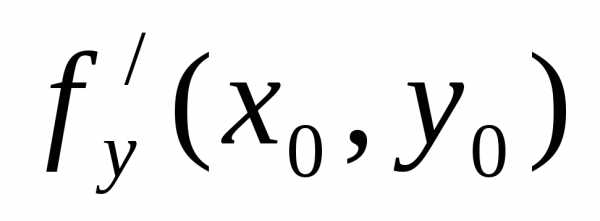=0;
б) имеет в этой точке непрерывные частные производные второго порядка;;Тогда, если ∆=АС— В2 >0, то в точке (хо,уо) функция z=f(x, у) имеет экстремум, причем если А<0 — максимум, если А>0 — минимум. В случае ∆=АС— В2<0, функция z=f(x, у) экстремума не имеет. Если ∆=АС— В2=0, то вопрос о наличии экстремума остается открытым.
Исследование функции двух переменных на экстремум рекомендуется проводить по следующей схеме:
Найти частные производные функции z‘x и z‘y.
Решить систему уравнений z‘x =0, z‘y =0 и найти критические точки функции.
Найти частные производные второго порядка, вычислить их значения в каждой критической точке и с помощью достаточного условия сделать вывод о наличии экстремумов.
Найти экстремумы (экстремальные значения) функции.
Пример. Найти экстремумы функции
Решение. 1. Находим частные производные
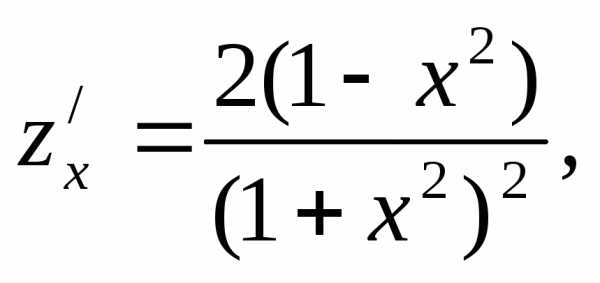
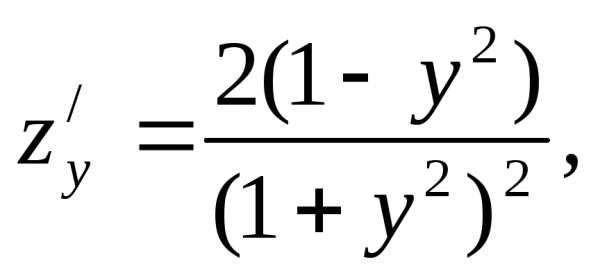
2. Критические точки функции находим из системы уравнений:
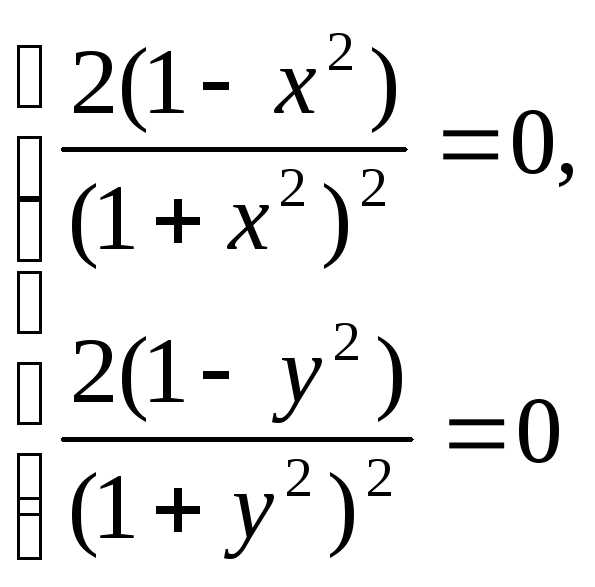
имеющей четыре решения (1; 1), (1; —1), (—1; 1) и (—1; -1).
3. Находим частные производные второго порядка:
;;,
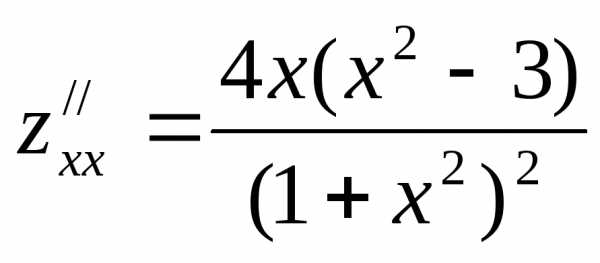вычисляем их значения в каждой критической
точке и проверяем в ней выполнение
достаточного условия экстремума.
Например, в точке (1; 1) A=z«(1; 1)= -1; В=0; С= -1. Так как ∆= АС— В2 = (-1)2-0=1 >0 и А=-1<0, то точка (1; 1) есть точка максимума.
Аналогично устанавливаем, что (-1; -1) — точка минимума, а в точках (1; —1) и (—1; 1), в которых ∆=АС— В2 <0, — экстремума нет. Эти точки являются седловыми.
4. Находим экстремумы функции zmax = z(l; 1) = 2, zmin = z(-l; -1) = -2,
Условный экстремум. Метод множителей Лагранжа.
Рассмотрим задачу, специфическую для функций нескольких переменных, когда ее экстремум ищется не на всей области определения, а на множестве, удовлетворяющем некоторому условию.
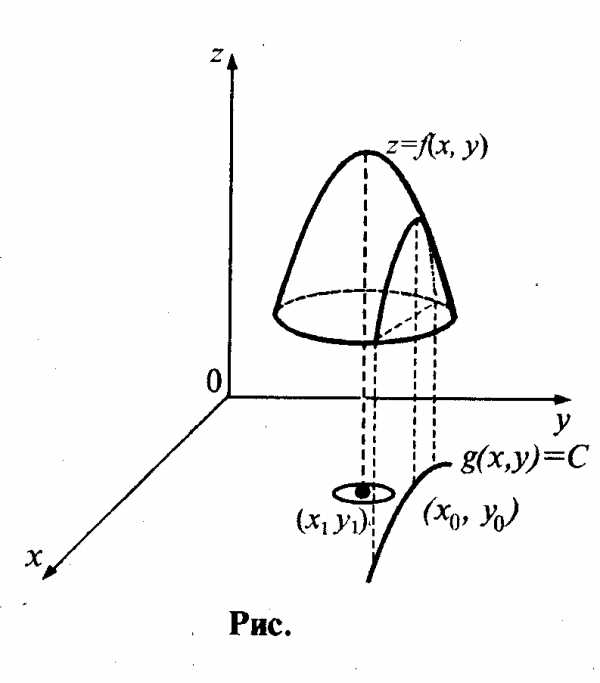
Пусть рассматривается функция z = f(x,y), аргументы х и у которой удовлетворяют условию g (х,у) = С, называемому уравнением связи.
Определение. Точка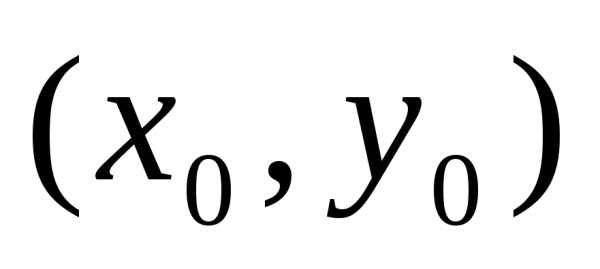
называется точкойусловного
максимума (минимума), если
существует такая окрестность этой
точки, что для всех точек (х,у) из этой
окрестности удовлетворяющих условию
g
(x,y)
= С, выполняется неравенство
().
На рис. изображена точка
условного максимума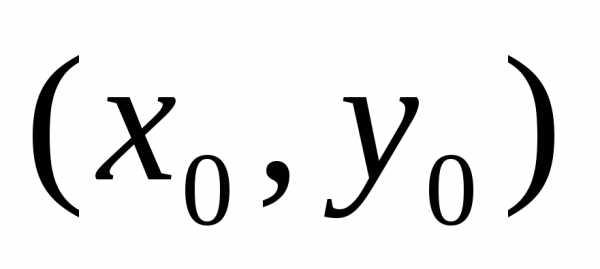
.Очевидно, что она не
является точкой безусловного экстремума
функции z
= f(x,y)
(на рис. это точка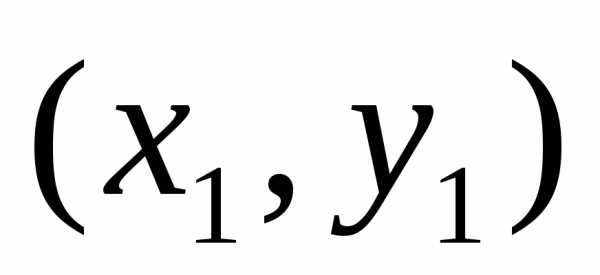
).
Наиболее простым способом
нахождения условного экстремума
функции двух переменных является
сведение задачи к отысканию экстремума
функции одной переменной. Допустим
уравнение связи g
(x,y)
= С
удалось разрешить
относительно одной из переменных,
например, выразить у
через х: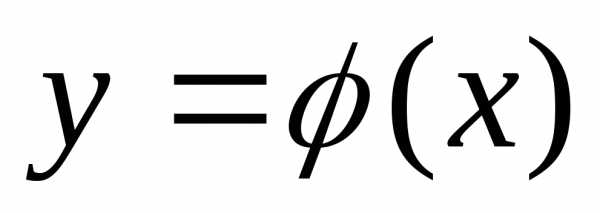
.Подставив полученное
выражение в функцию двух переменных,
получим z
= f(x,y)
=,
т.е. функцию одной
переменной. Ее экстремум и будет условным
экстремумом функции z
= f(x,y).
Пример. Найти точки максимума и минимума функции z = х2 + y2 при условии 3х +2у = 11.
Решение. Выразим из уравнения
3х +2у = 11
переменную y
через переменную x
и подставим полученное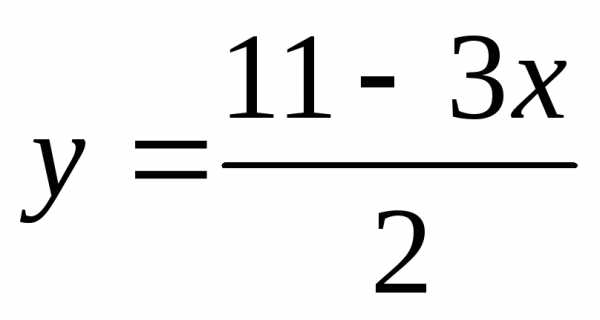
в функциюz.
Получим z=x2+2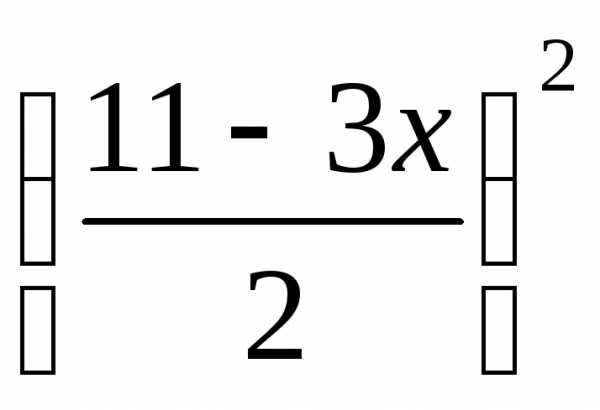
илиz
=
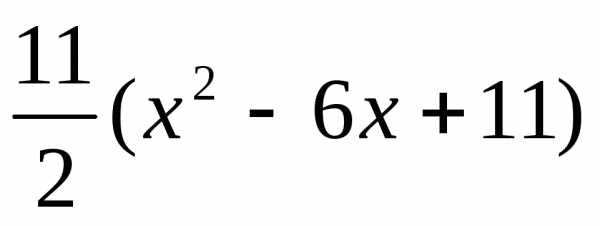.Эта функция имеет
единственный минимум при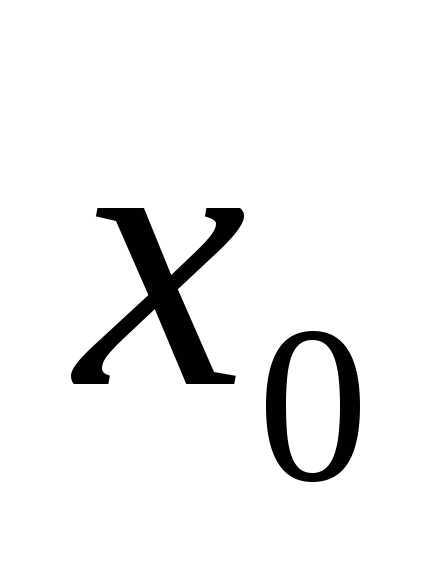
=
3. Соответствующее
значение функции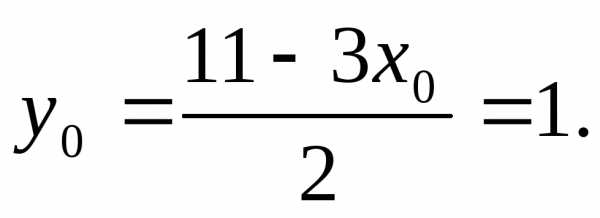
Таким образом, (3; 1) — точка условного
экстремума (минимума).
В рассмотренном примере уравнение связи g(x, у) = С оказалось линейным, поэтому его легко удалось разрешить относительно одной из переменных. Однако в более сложных случаях сделать это не удается.
Для отыскания условного экстремума в общем случае используется метод множителей Лагранжа.
Рассмотрим функцию трех переменных
Эта функция называется
функцией Лагранжа, а
—
множителем Лагранжа. Верна
следующая теорема.
Теорема. Если
точка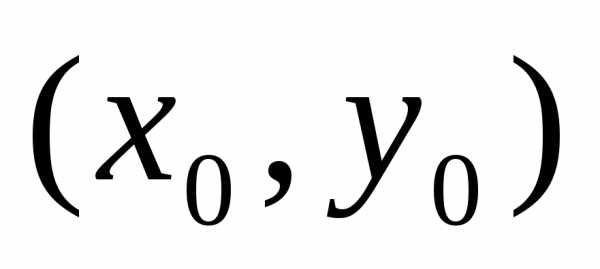
является
точкой условного экстремума функцииz
= f(x,y)
при условии g
(x,y)
= С, то существует значение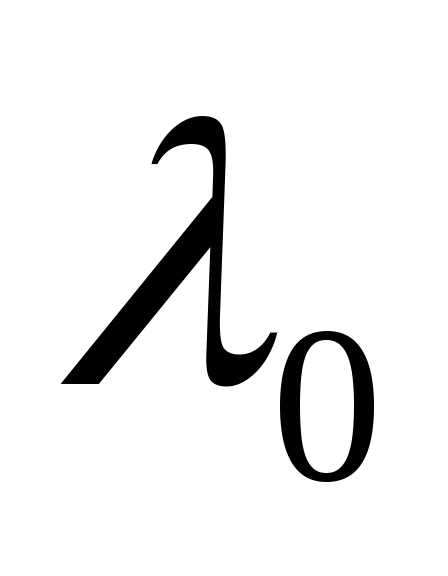
такое,
что точкаявляется
точкой экстремума функцииL{x,y,
).
Таким образом, для нахождения условного экстремума функции z = f(х,у) при условии g(x,y) = С требуется найти решение системы
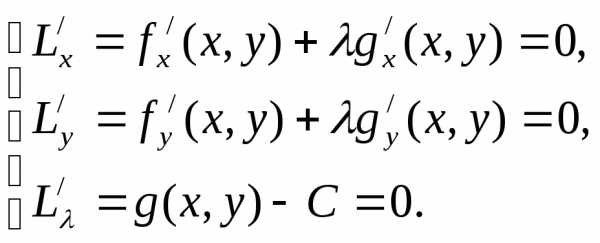
На рис. показан геометрический смысл условий Лагранжа. Линия g (х,у) = С пунктирная, линия уровня g(x,y) = Q функции z = f(x,y) сплошные.
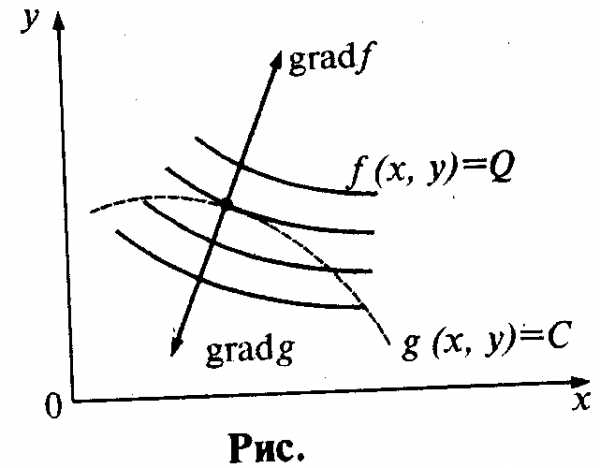
Из рис. следует, что в точке условного экстремума линия уровня функции z = f(x,y) касается линии g(x,y) = С.
Пример. Найти точки максимума и минимума функции z = х2 + y2 при условии 3х +2у = 11, используя метод множителей Лагранжа.
Решение. Составляем функцию Лагранжа L = х2 + 2у2 +
Приравнивая к нулю ее частные производные, получим систему уравнений
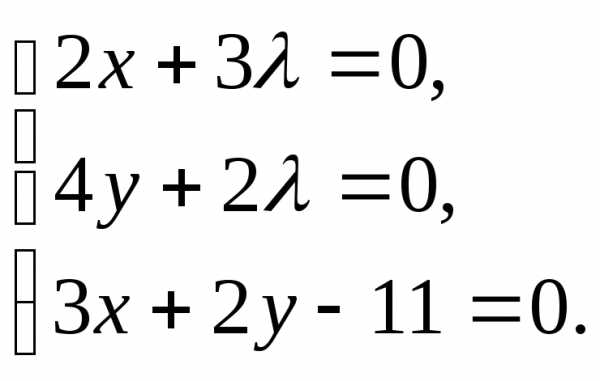
Ее единственное решение
(х=3, у=1,
=—2).
Таким образом, точкой
условного экстремума может быть только
точка (3;1). Нетрудно убедиться в том,
что в этой точке функция z=f(x,y)
имеет условный минимум.
studfiles.net