Как рассчитать теорию вероятности в лотерее 🚩 вероятность выпадения шаров одинакового цвета 🚩 Хобби и развлечения 🚩 Другое
В мире постоянно проводится множество лотерей с самыми различными правилами, условиями победы, призами, однако существуют общие принципы расчета вероятности выигрыша, которые можно адаптировать под условия той или иной конкретной лотереи. Но для начала желательно определиться с терминологией.
Итак, вероятность – это вычисленная оценка возможности того, что произойдет определенное событие, которая чаще всего выражается в форме отношения числа желаемых событий к общему числу исходов. Например, вероятность выпадения «орла» при подбрасывании монетки – один к двум.
Исходя из этого, очевидно, что вероятность выигрыша – это соотношение количества выигрышных комбинаций к числу всех возможных. Однако нельзя забывать, что критерии и определения понятия «выигрыш» тоже могут быть разными. К примеру, в большинстве лотерей используется такое определение как «класс выигрыша». Требования к выигрышу третьего класса ниже, чем к выигрышу первого, поэтому вероятность выигрыша первого класса самая низкая. Как правило, таким выигрышем является джек-пот.
Еще один значимый момент в расчетах заключается в том, что вероятность двух связанных событий вычисляется путем перемножения вероятностей каждого из них. Проще говоря, если вы подбросите монетку два раза, то вероятность выпадения «орла» каждый раз будет равна один к двум, но шанс, что «орел» выпадет оба раза, составит лишь один к четырем. В случае с тремя подбрасываниями шанс вообще упадет до одного к восьми.
Таким образом, для расчета шанса выигрыша джек-пота в абстрактной лотерее, где нужно верно угадать несколько выпавших значений из определенного числа шаров (например, 6 из 36), нужно рассчитать вероятность выпадения каждого из шести шаров и перемножить их между собой. Учтите, что с уменьшением числа шаров, оставшихся в барабане, вероятность выпадения нужного шара меняется. Если для первого шара вероятность того, что выпадет нужный, равна 6 к 36, то есть, 1 к 6, то для второго шанс составит 5 к 35 и так далее. В данном примере вероятность того, что билет окажется выигрышным составит 6x5x4x3x2x1 к 36x35x34x33x32x31, то есть 720 к 1402410240, что будет равно 1 к 1947792.
Несмотря на такие пугающие числа, люди регулярно выигрывают в лотереи по всему миру. Не забывайте, что даже если вы не возьмете главный приз, существуют еще выигрыши второго и третьего классов, вероятность получить которые намного выше. Кроме того, очевидно, что наилучшей стратегией является покупка нескольких билетов одного тиража, так как каждый дополнительный билет кратно увеличивает ваши шансы. Например, если купить не один билет, а два, то и вероятность победы будет в два раза больше: два из 1,95 миллиона, то есть примерно 1 к 950 тысячам.
Популярная лотерея «Мегалот» предполагает, что играющий должен выбрать и зачеркнуть 6 цифр из 36. Если игрок угадает несколько цифр, ему выплачивается выигрыш в зависимости от количества угаданных чисел. Угадать все числа чрезвычайно сложно, но систематически определять 3-5 выигрышных цифр вполне реально.

Инструкция
Настройтесь на серьезную и систематическую работу. Определите в семейном бюджете сумму, которую вы без ущерба для себя и близких можете ежемесячно тратить на приобретение билетов лотереи. Даже если возможности регулярно покупать билет нет, отсматривать все телевизионные розыгрыши и вести по ним свою статистику вы обязаны.
Отсматривая телепередачи с розыгрышами «Мегалота», собирайте статистические данные по каждому из чисел, участвующих в лотерее. Учитывайте, насколько часто каждое число выпадает и когда оно выпадало в последний раз. Чем большую статистику вы соберете, тем точнее будут сведения.
Выбирая цифры в лотерейном билете, которые намереваетесь зачеркнуть, делайте это на основании полученных вами статистических данных. Старайтесь выбрать числа, наиболее часто выпадающие и, желательно, не выпадавшие достаточно давно. Не доверяйте статистическим данным, полученным из интернета и даже от знакомых. В первом случае вы будете выбирать те цифры, которые выгодны автору, возможно, связанному с организаторами лотереи. Во втором можете быстро потерять веру в истинность данных и прекратить игру. Если у вас сильно развита интуиция, прислушивайтесь к своему внутреннему голосу при выборе чисел. Если интуиция слаба, ведение статистических данных и вычислений поможет вам ее развить.Чтобы улучшить методы анализа собранных вами сведений статистики, начните изучать математические теории вероятности, теории комбинаторики, теории игр и т.п. Базовую информацию об этих теориях можно узнать на сайте http://topfortuna.com/.
Если нет желания вести самостоятельную статистику, выберите те числа, которые, по вашему мнению, являются для вас счастливыми. Например, цифры из даты вашего рождения, номера дома и квартиры и т.п. В зависимости от выбранной стратегии меняйте их каждый раз или оставляйте неизменными.
Видео по теме
www.kakprosto.ru
Кубики и Вероятности
В настольных и кабинетных играх для генерации случайных чисел зачастую используются игральные кубики. Однако часто для разработки сбалансированной игры требуется получить более сложные распределения случайных величин, чем линейное, задаваемое одной игральной костью. Более того, порой требуется задать распределение в определенных числовых рамках и точно знать, какова вероятность выпадения того или иного значения.
Чтобы упростить себе разработку и балансировку игр в вышеописанных ситуациях, я в свое время создал для себя небольшую шпаргалку. Думаю, что такая подсказка может пригодиться как начинающим разработчикам, так и активным игрокам. Поэтому в данной статье я поделюсь своими расчетами, а так же методом, при помощи которого можно высчитывать вероятности для любых комбинаций игральных костей.
Общая вводная
Для начала я бы хотел немного раскрыть терминологию, которая будет использована в дальнейшем.
Исторически сложилось, что бросок игральной кости обозначается как XdY, где X — количество бросков, а Y — число граней или иное маркирование типа кости. Например 1d6 означает 1 бросок 6-гранного кубика. Буква d означает dice (мн. ч. от die — игральная кость, кубик (англ.)). Закоренелые игроки так и называют игровые кости — дайсы. Впрочем, иногда встречается и русский вариант записи — 1к6. Лично я предпочитаю использовать слово дайс, поскольку «кубик» у меня строго ассоциируется с 6-гранником 🙂
Соответственно, сам дайс в такой системе обозначается как dY. Так что если вам вдруг встретится запись вида d6, знайте, что это просто 6-гранный кубик. А запись 2d10 означает «результат двух бросков 10-гранного дайса».

Джентльменский набор дайсов
В качестве d2 может использоваться обыкновенная монета. Наиболее часто встречаются следующие форматы дайсов: d4, d6, d8, d10, d12, d20. Реже можно встретить d30. Особые ухищрения позволяют моделировать d100 с помощью двух d10, однако наибольшее распространение получил, конечно же, d6.
В некоторых старых компьютерных играх можно встретить такие интересные обозначения как 1d3 или 3d17. Естественно, представить себе 17-гранный кубик немного проблематично, так что, по сути дела, это — своеобразный переходный артефакт, когда компьютер уже позволял задавать случайное распределение в любом диапазоне, но игроки по старой привычке ориентировались по дайсовой схеме. В современных компьютерных играх обычно указан разброс случайных значений в формате X-Y. Например 15-85, что означает случайное значение от 15 до 85.
Впрочем, нас сейчас интересуют дайсы, так что вернемся к ним. Дайсовая форма записи имеет небольшое преимущество над записью формы X-Y. Хоть по-сути 2d6 означает случайную величину от 2 до 12, но в случае записи 2-12 нам неведом график распределения между этими значениями. Т.е. мы не знаем, одинакова ли вероятность выпадения, например 7 и 10. 2d6, в свою очередь, подразумевает не только границу значений 2-12, но и определенный порядок распределения случайных величин, о чем и пойдет речь далее.
Осталось добавить, что для смещения диапазона значений используются так называемые модификаторы броска. Фактически, это просто число, которое прибавляется или вычитается из результата броска. Записывается это в форме XdY+Z, где Z — и есть модификатор. Например, 1d6+3 означает 1 бросок 6-гранного кубика, к результату которого прибавляется 3.
С обозначениями разобрались, можно двигаться дальше.
1d6
В качестве подопытного возьмем знаменитый d6. При необходимости расчеты для любых других вариантов (включая экзотические d17) делаются без особых затруднений по аналогии. Главное — понять принцип.
Сначала проанализируем плотность вероятностей для броска 1d6.
Плотность вероятностей в нашем случае — это шанс выпадения тех или иных значений на кубике.
Очевидно что вероятность кубика упасть на ту или иную грань, в случае когда у нас идеально сбалансированный и не крапленый кубик, обратно-пропорциональна количеству его граней. Для d6 она, соответственно, составляет 1/6 или 16,67%. Т.е. любое из 6 значений выпадает с равной вероятностью в 16,67%.

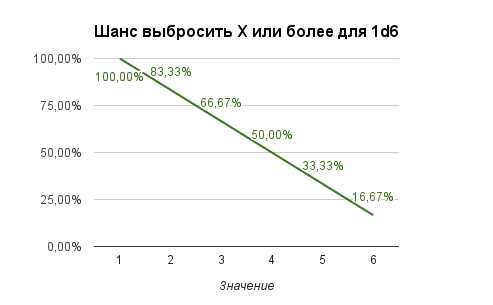
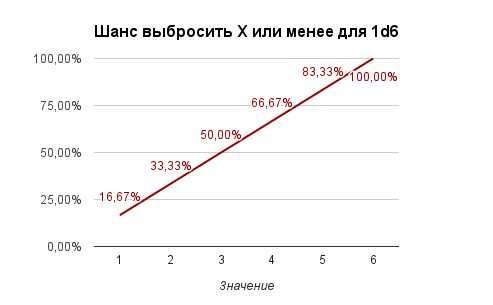
Порою весьма полезно бывает знать какова вероятность выбросить значение равное или превышающее какое-то число. Кстати, такое значение принято записывать как X+. Например, 4+ означает «4 и более». Впрочем, к обозначению 18+ уже многие привыкли, так что освоиться с такой записью не составляет никакого труда 🙂
Посчитать такую вероятность довольно просто. Достаточно просуммировать вероятности всех удовлетворяющих нас результатов. Например в случае 5+ для 1d6 нас интересует сумма шансов выбросить 5 и 6. А это 1/6+1/6=1/3 или 16,67%+16,67% = 33,33% (Все процентные значения указаны с округлением. На самом деле 16,67% это 16,666666…..6%. Поэтому не удивляйтесь тому, что иногда 7+7=13 🙂 ).
Таким образом получаем следующие графики:
Если свести все полученные данные в таблицу, то получим:
| Значение | Вероятность | Значение | Вероятность | Значение | Вероятность |
|---|---|---|---|---|---|
| 1 | 16,67% | 1+ | 100,00% | 1 | 16,67% |
| 2 | 16,67% | 2+ | 83,33% | 2- | 33,33% |
| 3 | 16,67% | 3+ | 66,67% | 3- | 50,00% |
| 4 | 16,67% | 4+ | 50,00% | 4- | 66,67% |
| 5 | 16,67% | 5+ | 33,33% | 5- | 83,33% |
| 6 | 16,67% | 6 | 16,67% | 6- | 100,00% |
Ничего необычного. Для любого единичного броска кубика с любым количеством граней мы будем получать равномерное линейное распределение. Но что будет, если мы будем рассматривать результат нескольких бросков?
2d6
Проанализируем плотность вероятностей для 2d6. Для этого нам потребуется составить матрицу, столбцы которой будут результатами первого броска, а строки — второго.
Теперь нам нужно высчитать вероятности всех возможных исходов при двух бросках и записать их в ячейки матрицы. Если вероятность выбросить на d6 1 равна 1/6, то вероятность получить 1 и во втором броске равна 1/6 от 1/6, то есть 1/36 или 2,78%.
Таким образом в каждой ячейке такой матрицы получаем значение 2,78%
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% |
| 2 | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% |
| 3 | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% |
| 4 | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% |
| 5 | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% |
| 6 | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% |
Однако если мы заполним ту же самую матрицу значениями, которые получаются в сумме двух бросков, то получим:
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Из таблицы видно, что к значению 2 от броска 2d6 ведет только 1 исход, когда оба броска показали 1. В то время как получить 4 можно одним из трех исходов: 3 и 1, 2 и 2, 1 и 3. Выходит, что вероятность получить 4 при броске 2d6 равна сумме вероятностей 3 исходов, вероятность каждого из которых равна 2,78%. Получаем 2,78%+2,78%+2,78%=8,33% (помним про округление процентов).
Если составить таблицу вероятности для всех значений, получим:
| Значение | Вероятность |
|---|---|
| 2 | 2,78% |
| 3 | 5,56% |
| 4 | 8,33% |
| 5 | 11,11% |
| 6 | 13,89% |
| 7 | 16,67% |
| 8 | 13,89% |
| 9 | 11,11% |
| 10 | 8,33% |
| 11 | 5,56% |
| 12 | 2,78% |
В графическом представлении это выглядит так:
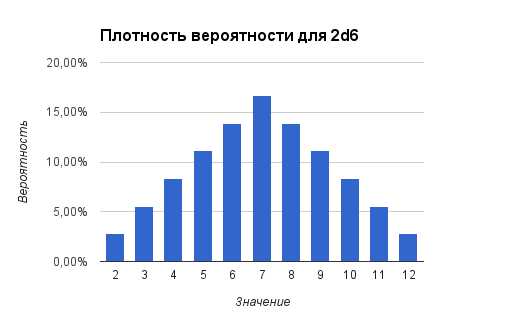
Заметим, что при учете двух бросков мы получаем распределение Гаусса (оно же нормальное распределение). Вероятность получить в результате двух бросков срединное значение (в нашем случае это 7) значительно выше, чем вероятность получить крайние значения (2 или 12). Соответственно гораздо чаще результаты бросков для 2d6 будут находится среди значений 5-9 и редко показывать 2-4 или 10-12. В некоторых случаях от случайной величины требуется именно такое поведение.
Кривые вероятности выбросить значение X+ или X- так же будут иметь нелинейный вид:
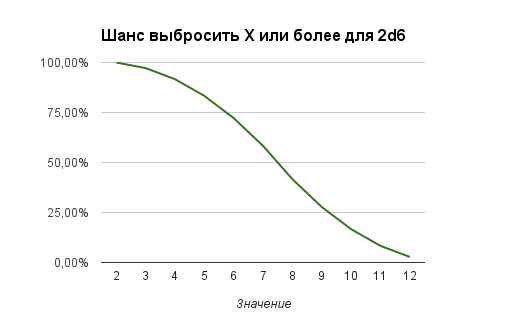

Если представить полученные данные в табличной форме, то:
| Значение | Вероятность | Значение | Вероятность | Значение | Вероятность |
|---|---|---|---|---|---|
| 2 | 2,78% | 2+ | 100,00% | 2 | 2,78% |
| 3 | 5,56% | 3+ | 97,22% | 3- | 8,33% |
| 4 | 8,33% | 4+ | 91,67% | 4- | 16,67% |
| 5 | 11,11% | 5+ | 83,33% | 5- | 27,78% |
| 6 | 13,89% | 6+ | 72,22% | 6- | 41,67% |
| 7 | 16,67% | 7+ | 58,33% | 7- | 58,33% |
| 8 | 13,89% | 8+ | 41,67% | 8- | 72,22% |
| 9 | 11,11% | 9+ | 27,78% | 9- | 83,33% |
| 10 | 8,33% | 10+ | 16,67% | 10- | 91,67% |
| 11 | 5,56% | 11+ | 8,33% | 11- | 97,22% |
| 2,78% | 12 | 2,78% | 12- | 100,00% |
Получается, что если мы хотим получить генератор случайных чисел, который выдает распределение близкое к тому, что встречается «в природе», то использование пары кубиков или учет двух бросков дает нам эту возможность.
Ровно как и запись 2d6 имеет преимущество над 2-12 как раз в том, что указывает не только на диапазон, но и на плотность вероятностей.
Если же нам требуется получить нормальное распределение в промежутке от 0 до 10, то с помощью дайсов это можно организовать как бросок 2d6 из результата которого будем вычитать 2. Вспоминая описанные ранее обозначения, это 2d6-2.
Если такая перемена в графике произошла когда мы добавили второй бросок, то что произойдет, если ввести третий?
3d6
Для анализа плотности вероятностей для 3d6 можно, конечно составить 3-х мерную матрицу и посчитать все точь-в-точь как для 2d6. Но поскольку вероятности для 2d6 нам уже известны, то мы можем значительно упростить себе задачу:
| 2d6 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| 2 | 2,78% | ||||||
| 3 | 5,56% | ||||||
| 4 | 8,33% | ||||||
| 5 | 11,11% | ||||||
| 6 | 13,89% | ||||||
| 7 | 16,67% | ||||||
| 8 | 13,89% | ||||||
| 9 | 11,11% | ||||||
| 10 | 8,33% | ||||||
| 11 | 5,56% | ||||||
| 12 | 2,78% |
Помножив вероятности результатов для 2d6 на 16,67% получим вероятности исходов для 3-х бросков:
| 2d6 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| 2 | 2,78% | 0,46% | 0,46% | 0,46% | 0,46% | 0,46% | 0,46% |
| 3 | 5,56% | 0,93% | 0,93% | 0,93% | 0,93% | 0,93% | 0,93% |
| 4 | 8,33% | 1,39% | 1,39% | 1,39% | 1,39% | 1,39% | 1,39% |
| 5 | 11,11% | 1,85% | 1,85% | 1,85% | 1,85% | 1,85% | 1,85% |
| 6 | 13,89% | 2,31% | 2,31% | 2,31% | 2,31% | 2,31% | 2,31% |
| 7 | 16,67% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% |
| 8 | 13,89% | 2,31% | 2,31% | 2,31% | 2,31% | 2,31% | 2,31% |
| 9 | 11,11% | 1,85% | 1,85% | 1,85% | 1,85% | 1,85% | 1,85% |
| 10 | 8,33% | 1,39% | 1,39% | 1,39% | 1,39% | 1,39% | 1,39% |
| 11 | 5,56% | 0,93% | 0,93% | 0,93% | 0,93% | 0,93% | 0,93% |
| 12 | 2,78% | 0,46% | 0,46% | 0,46% | 0,46% | 0,46% | 0,46% |
Ну а просуммировав исходы с одинаковым результатом, получим плотности вероятностей:
| Значение | Вероятность |
|---|---|
| 3 | 0,46% |
| 4 | 1,39% |
| 5 | 2,78% |
| 6 | 4,63% |
| 7 | 6,94% |
| 8 | 9,72% |
| 9 | 11,57% |
| 10 | 12,50% |
| 11 | 12,50% |
| 12 | 11,57% |
| 13 | 9,72% |
| 14 | 6,94% |
| 15 | 4,63% |
| 16 | 2,78% |
| 17 | 1,39% |
| 18 | 0,46% |
Графически это выглядит так:
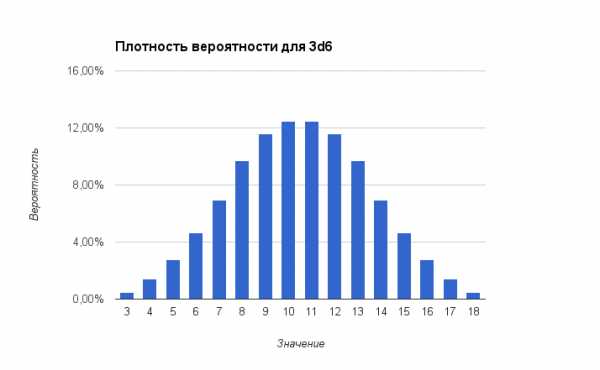
Графики вероятностей для X+ и X- тоже имеют более выраженные очертания нормального распределения:
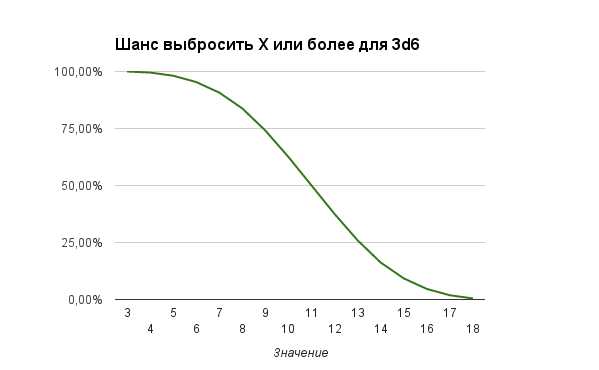

Итоговая таблица для 3d6 будет выглядеть так:
| Значение | Вероятность | Значение | Вероятность | Значение | Вероятность |
|---|---|---|---|---|---|
| 3 | 0,46% | 3+ | 100,00% | 3 | 0,46% |
| 4 | 1,39% | 4+ | 99,54% | 4- | 1,85% |
| 5 | 2,78% | 5+ | 98,15% | 5- | 4,63% |
| 6 | 4,63% | 6+ | 95,37% | 6- | 9,26% |
| 7 | 6,94% | 7+ | 90,74% | 7- | 16,20% |
| 8 | 9,72% | 8+ | 83,80% | 8- | 25,93% |
| 9 | 11,57% | 9+ | 74,07% | 9- | 37,50% |
| 10 | 12,50% | 10+ | 62,50% | 10- | 50,00% |
| 11 | 12,50% | 11+ | 50,00% | 11- | 62,50% |
| 12 | 11,57% | 12 | 37,50% | 12- | 74,07% |
| 13 | 9,72% | 13+ | 25,93% | 13- | 83,80% |
| 14 | 6,94% | 14+ | 16,20% | 14- | 90,74% |
| 15 | 4,63% | 15+ | 9,26% | 15- | 95,37% |
| 16 | 2,78% | 16+ | 4,63% | 16- | 98,15% |
| 17 | 1,39% | 17+ | 1,85% | 17- | 99,54% |
| 18 | 0,46% | 18 | 0,46% | 18- | 100,00% |
Из полученных результатов видно, что с увеличением количества бросков до 3 «колокол Гаусса» не только сохраняется, но и становиться более выраженным. Забегая вперед скажу что и для всех последующих повышений количества бросков (4d6, 5d6, 6d6 …) эта тенденция сохраняется.
Вместо итогов
Полученные таблицы можно использовать для балансировки вероятностных значений в разрабатываемых играх. Ровно как можно с помощью данных расчетов более точно оценивать свои шансы на исход броска во время игры.
Продемонстрированный метод применим для получения таблиц к любому количеству бросков любых дайсов.
Кстати, с помощью разнообразных дайсов можно задавать довольно большой диапазон случайных значений. Например 2d6+1d4 даст нормальное распределение в диапазоне 3-16. А с помощью двух d10 можно задать линейное распределение 0-99, для этого один кубик должен отвечать за десятки, другой — за единицы. Такую комбинацию двух d10 называют «процентником».
Надеюсь, эти таблицы будут Вам полезны.
Юрий Исаев
2015.07.27
ulf.tordenson.ru
Ответы@Mail.Ru: вероятность выпадения в костях
Вероятность выпадения любой комбинации =1=6/6*6/6*6/6, или 100% :))) 1/192 =1/6*1/6*1/6 — вероятность выпадения комбинации из трех ЗАДАННЫХ чисел. (1-2-3 захотел и выпало) Вероятность выпадения трех любых одинаковых чисел: 1/32= 6/6*1/6*1/6 Вероятность выпадения комбинации из двух любых одинаковых чисел: 1/6=6/6*1/6*6/6 Вероятность того что все числа будут разные 120/196= 0,6123 =6/6*5/6*4/6
Что значит ЛЮБОЙ? Ты не поверишь, но разных комбинаций разная и вероятность выпадения. Например, вероятность выпадения трех шестерок равна 1/216. А вероятность выпадения комбинации 1-2-3 равна 1/36. А вероятность выпадения комбинации 5-5-3 равна 1/72. Не все так просто в этом мире, детка.. . Этот мир устроен очень сложно, а многие просят объяснить его устройство на пальцах, не понимая даже, что сделать этого нельзя в принципе. Что для того, чтобы понять устройство данного мира нужно долго и упорно учиться, изучать дифференциальное и интегральное исчисления, теорию вероятностей, математическую статистику, квантовую механику, молекулярную биологию.. . А «вынь да положь» — не получается, хоть тресни. А поскольку учиться трудно и лень, да еще для этого и мозги нужны, то подавляющее большинство вместо учения начинает просто верить в бога.. . Ведь так проще! Не надо ничего изучать — бог придумал, и слава богу.. . Дебилизм процветает…
Задача решается просто: если для одной кости вероятность: 1/6, значит для двух = 1/6 * 1/6 = 1/32, для трёх = 1/6 * 1/6 * 1/6 = 1/192.
touch.otvet.mail.ru
Вероятность выпадения комбинаций флеша, пары и дро в покере
Многие люди, знающие о покере лишь понаслышке, считают, что победить в покере может любой и для этого нужно лишь немного удачи. Действительно, покер интересен тем, что невозможно заранее предугадать, кто выиграет. Ярким примером стала победа Ки Нгуена в финальном событии серии WSOP в 2016-ом году.
Удача в покере играет довольно существенную роль, но не решающую. Ведь, ежегодно количество игроков в покере увеличивается, и крупнейшие мировые турниры постоянно пополняются новыми участниками, но в призах всегда крутятся одни и те же люди. Пусть и не выигрывают регулярно, но стабильно заходят в финальные розыгрыши и получают хорошее денежное вознаграждение. И дело отнюдь не в том, что они более везучие, чем другие.
Все дело в том, что они имеют хорошие математические способности, трезво оценивают ситуацию и могут достаточно точно подсчитать вероятности в покере. И благодаря своим навыкам они имеют хорошие шансы дойти достаточно далеко в турнире, где уже в равной борьбе могут уступить не менее умелым игрокам, но с лучшими картами.
Никто не знает, какая карта появится на борде следующей, но проанализировав вероятность выпадения комбинации в покере, участник может оценить свои шансы на то, чтобы выиграть в конкретной раздаче. Сегодня для того чтобы стать хорошим игроком, не нужно быть гением математики и в уме проводить сложные математические операции. Все давно просчитано и сведено в конкретные таблицы. Хорошая память очень нужна покеристу, а тренировать ее можно начать с запоминания, какова вероятность выпадения дров в покере или непосредственно сильной комбинации.
Если же игрок принимает участие в онлайн покерном турнире, то подсчет вероятности собрать комбинацию в покере становится еще легче. Давно разработаны и существуют программы, помогающие в мгновение рассчитать шансы на успех в игре, и на то, чтобы появилась необходимая карта. Они демонстрируют реальную картину, но даже если шансы 80% на 20% — это не значит, что именно эти 80 процентов окажутся решающими. В этом вся прелесть покера. Даже при наличии всех передовых разработок невозможно дать 100-процентную гарантию успеха.
Вероятность собрать пару
Самой распространенной покерной комбинацией является пара. Она достаточно сильная в покерной иерархии и к тому же ее не так трудно собрать, как флеш или стрит. Многие рассчитывают вероятности покерных комбинаций еще с префлопа и появления карманных карт. Особенно везучим игрокам может сразу же выпасть карманная пара.
Вероятность пары в покере на стадии карманных карт достаточно низкая. Общее число карманных пар 13, а шансы на такой локальный успех не дотягивают и до 6%. Подсчет проводится путем простых математических операций.
Мы знаем, что всего есть 13 пар, при этом карт в покерной колоде – 52. Делим количество пар на общее число карт и умножаем на 12 и 51. Двенадцать означает количество оставшихся пар в колоде или на руках у других участников, а пятьдесят один – количество всех карт без одной, которая уже сдана игроку. Недолгие математические подсчеты демонстрируют, что вероятность пары в покере на префлопе не больше, чем в одной раздаче из семнадцати.
Конечно же, в идеале было бы неплохо получить пару тузов на префлопе. Но шансы на это ничтожно малы – меньше 0,5%. Вероятность пары в покере на флопе или ревере увеличивается в разы. На флопе в 32% случаев можно собрать пару, а сразу две пары, одна из которых является карманной – 16%. На ривере шансы еще выше. Пара собирается в 46% раздач, а две пары, если одна из них карманная, — в 40%.
Вероятность флеша
Флеш стоит в иерархии покерных комбинации выше, чем пара. Собрать ее на порядок сложнее, но если удается, то шансы на успех стают очень высокие. Для того чтобы собрать флеш у игрока должна быть комбинация из 5 карт одной масти. Номинал карт значения не имеет, но если сразу нескольким игрокам удалось собрать флеш, то победителем становится тот, у кого старшая карта.
Вероятность флеша в покере очень небольшая. Важную роль играют карманные карты. Они естественно должны быть одной масти. Если у участника пара, то вариант с флешем нужно сразу же отбросить. Шансы на флеш уже на флопе меньше одного процента. А вот если разобраться в том, какова вероятность дров в покере для флеша, то она будет чуть более 10%.
Если покерист надеется на флеш на ривере, то нужно понимать, что в лучшем случае шансы на успех не более 7% и это при условии, что у него две карманные карты одной масти. Если же карманные карты разной масти, то шансы на флеш не больше 2%.
Шансы на стрит
Стрит также в 95% случаев может гарантировать покеристу успех в раздаче. Эта комбинация состоит также из пяти карт, но в четкой последовательности, цепь которой не должна прерываться. Туз в этой руке может быть самой старшей картой или же самой младшей.
Стрит можно исключить уже на флопе, если в своих картах есть пара или случайные карты разной или одной масти. Случайные карты подразумевают, что разрыв в номинале карт будет превышать 3 карты, и его не получится восполнить с помощью трех общих карт.
Шансы на то, чтобы собрать стрит будут зависеть от разрыва в номиналах коннекторов. Если разрывы от трех до 1 значений, то вероятности покерной комбинации составляют от 0,64% до 1%. Если же карманные карты последовательны, то стрит-дро на флопе можно будет собрать с вероятностью почти в 10%.
На ривере самые большие шансы на стрит у участника с двумя последовательными по номиналу картами. Они составляют 10%. Как видим, вероятности в покере собрать стрит, даже при условии самых оптимальных раскладов, очень низкие и не дают возможности надеяться на успех чаще, чем в одном из 10 случаев.
Итоги
Математические шансы игрока на то, чтобы собрать комбинацию в покере увеличиваются по мере снижению по иерархии комбинаций. Также многое будет зависеть от того, какие карманные карты получил игрок, и в какой вид покера играют за столом. К примеру, вероятность выпадения комбинаций в пятикарточном покере будет рассчитываться отдельно на каждом этапе игры по мере того, какие карты будут появляться на борде. Мы же советуем не пытаться постоянно собирать Роял-Флеш или Каре, ведь, в долгосрочной перспективе это принесет лишь убыток. Вероятности таких комбинаций в покере очень низкие.
irakeback.net
Игральная кость сделана так, что вероятность выпадения определенного числа пропорциональна числу очков. Какова вероятность выпадения трех очков, если известно, что выпало нечетное число очков.
1 2 3 4 5 6
P x 2x 3x 4x 5x 6x
P(1)+P(2)+P(3)+P(4)+P(5)+P(6)=1
x+2x+3x+4x+5x+6x=1
21x=1
X=1/21
x 3x 5x
P(1)+P(3)+P(5)=1/21+3/21+5/21 = 9/21=3/7 –вероятность выпадения нечетного числа очков.
3x/9x=1/3
P=m/n=3x/9x=1/3
21. Брошены 2 игральные кости. Какова вероятность того, что абсолютная величина разности выпавших очков равна 3?
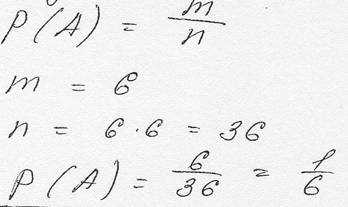
Студент в поисках книги посещает 3 библиотеки. Вероятность того, что они есть в библиотеке равны 0,4; 0,5; 0,1; а того, что они выданы или нет – равновероятные события. Какова вероятность того, что нужна книга найдена.
Решение:A-книга есть в библиотеке, B – книга не выдана.
P(B) = P(B—) = ½
P(A1) = 0,4 P(A2) = 0,5 P(A3) = 0,1
Определим вероятность того, что нужная книга найдена:
P = P(A1)* P(B) + P(A2)*P(B) + P(A3)*P(B) = P(B)(P(A1) + P(A2) + P(A3) = 1/2 * (0,4 + 0,5 +0,1) = 1/2 * 1 = ½
Ответ: 1/2
23. Найти вероятности того, что дни рождения 12 человек прийдутся на разные месяцы года.
Решение: P(A)= m/n
m = P12 = 12!
n = —A12= 1212
P = 12! / 1212 = 11! / 1211 = (11*10*9*8*7*6*5*4*3*2*1) / (12*12*12*12*127) = (11*5*7*5*1) / 127 = 7*8*25 / 127 = 1925 / 127
Ответ: 1925/127
24. В урне имеется 10 белых, 5 черных и 15 красных шаров. Извлекается последовательно 2 шара. Рассматриваются 2 события А — хотя бы один шар из двух вынутых красный, В — хотя бы один вынутый шар белый. Найти вероятность события С = А + В.
25.Наудачу набранный номер состоит из 5 цифр. Определить вероятность того, что все цифры в нем различны.

26.В магазин трикотажных изделий поступили носки, 60% которых получено от одной фабрики, 25% — другой и 15% — третьей. Найти вероятность того, что купленные покупателем носки изготовлены на второй или третьей фабрике.
Решение.A1-от 1 фабрики, P(A1) = 0,6;
А2 –от 2 фабрики; P(A2) = 0,25
A3 – от 3 фабрики; P(A3) = 0,15
P(A2+A3) = 0,25 + 0,15 = 0,4
Ответ: 0,4
Пассажир за получением билета может обратиться в одну из касс. Вероятность обращения в 1ую кассу составляет 0,4; во 2ую 0,35; и 3ью 0,25. Вероятность того, что к моменту прихода пассажира имеющиеся в кассе билеты будут проданы, равна для 1ой кассы 0,3; для 2ой 0,4, для 3ей 0,6. Найти вероятность того, что пассажир купит билет.
P(A) –вероятность не купить билет.
P(A) =0,4*0,3 + 0,35*0,4 + 0,25*0,6 =
0,12 + 0,14 + 0,15 = 0,41
P(A1) – вероятность купить билет = 1-P(A) = 1 – 0,41 = 0,59.
Ответ: P(A1) = 0,59.
28. Бросаются 4 игральные кости. Найти вероятность того, что: а) хотя бы на одной появится 2 очка, б) на них выпадет по одинаковому числу очков.
Решение: 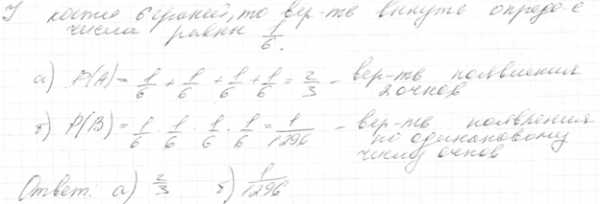
29. Из 9 жетонов, занумерованных разными однозначными цифрами, выбирается 3. Найти вероятность того, что последовательная запись их номеров покажет возрастание значений цифр.
Решение:

30. Вероятность выигрыша по лотерейному билету равна 0,1. Какова вероятность того, что выиграет хотя бы один билет из трех купленных?
31. Из полной колоды карт(52 листа) вынимают сразу 4 карты. Найти вероятность того, что все эти карты будут разным мастей.
Решение:Вероятность вытащить конкретную масть равна C113
C113 = 13(количество возможных способов).
Возможность вытащить карты из 52 = C452 = 52! / 4!* 48! = 48!*49*50*51* 52 / 2*3*4*48! = 270725
P(A) = C113 * C113 * C113 * C113 / C452 = 28561 /270725 = 0,1054982
Ответ: P(A) = 0,1054982.
32. Имеется 3 урны. В первой из них 5 белых и 6 черных шаров, во второй 4 белых и 3 черных шара, в третьей 5 белых и 3 черных шара. Некто наугад выбирает одну из урн и вынимает из нее шар. Этот шар оказался белым. Найти вероятность того, что этот шар вынут из второй урны.
Решение:

cyberpedia.su
вероятность шанса 0.01% а какова вероятность за 10000 попыток?
Как я понимаю, вероятность выпадения числа равна 0,01%. Надо найти вероятность выпадения этого числа один раз в десяти тысячах попыток. Используй локальную теорему Лапласа. Хотя вероятность так и останется 0,01%
100 раз, т. к. вероятность будет оставаться такой же 0,01% независимо от предыдущего броска. На десять тысяч попыток может выпасть 100 раз. Для 30000 вероятность останется такой 0,01%, т. е. может выпасть 300 раз
Знаю, что ответ слишком поздний, но не мог удержаться ответить: тут надо решать не от вероятности выпадения, а от вероятности НЕвыпадения, т. е. надо посчитать вероятность того, что за 10000 раз число не выпадет ни разу: 0,99^10000 = 2,24877*10^-44, а значит вероятность того, что число выпадет хотя бы раз = 1 — 2,24877e-44 = очень близко к 100%. А если надо посчитать вероятность, что выпадет всего лишь 1 раз, то расчет такой: 0,01*(0,99^9999)=2,27*10^-46
touch.otvet.mail.ru
МЕНДОС Д. 
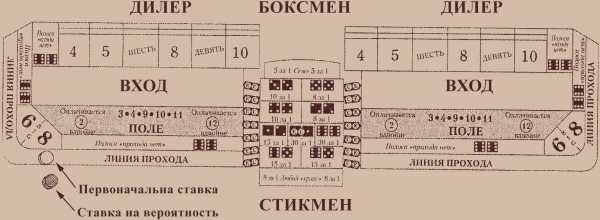
СОДЕРЖАНИЕ ДАННОЙ СТАТЬИ Определение истинной вероятности выпадения числа Истинная вероятность — это число способов выпадения семерки в сопоставлении с числом способов выпадения любых других чисел на данный момент. Используя эти цифры, вы получаете следующие истинные вероятности выпадения вашего числа до выпадения семи: пяти или девяти равняются три к одному. Верные шансы для шести или восьми равняются шесть к пяти.
Рисунок 4-2. Истинная вероятность выпадения различных чисел с двумя костями Ставки на вероятность не отмечены на разметке крэпса, вероятно, потому, что казино не имеет преимуществ над игроком при этих ставках и, следовательно, у него нет причины поощрять их. Для того, чтобы испытать вероятность на ставке линии прохода, просто увеличьте вплоть до удвоения сумму вашей ставки линии прохода, поместив ее прямо рядом с вашей ставкой линии прохода. Если шутер выбросит «очко» ранее семи, вы получите равные деньги за вашу ставку линии прохода и деньги в истинном соотношении выплат за вашу ставку на вероятность. Рисунок 4-3 показывает, как разместить ставку на вероятность на разметке стола крэпса. Например, если «очко» равнялось пяти и ваша ставка линии прохода составляет 5$ с 10$ на вероятность, вы выиграли бы 5$ по ставке линии прохода и 15$ по ставке на вероятность, когда шутер выбросил пять до семи. Истинная вероятность выпадения пяти перед семью составляет три к двум. Итак, для того, чтобы вычислить то, что вам должны заплатить, умножьте вашу 10$ ставку в полтора раза или на 1,5. Это 15$. Видите, как важно знать, какова истинная вероятность для каждого очка. Таким образом вы будете знать, правильно ли вам платят. Верьте или нет, но дилеры делают ошибки. Для того, чтобы поставить на вероятность на ставке входа, вы должны подождать, пока дилер подвинет ставку входа к номеру, затем сказать дилеру, что вы хотите ставить на вероятность на вашу ставку входа, и положить сумму, которую вы предназначили «на вероятность», на участок входа. Убедитесь, что дилер кладет ваши «вероятностные» на правильную ставку входа. Когда имеется несколько игроков, может возникнуть путаница, так что следите, куда идет ваша ставка входа.
Рисунок 4-3. Размещение фишек при ставке на вероятность Вероятностные ставки на лавки «входа нет» входа или «прохода нет» Эти ставки противоположны предыдущим. Когда вы делаете ставку «прохода нет» или «входа нет», вы хотите, чтобы семь выпало перед очком. Ставки простив вероятности приносят вам оплату по истинным соотношениям, только вы должны сделать ставку на большую сумму денег, чем вы выиграете, потому что шансы в вашу пользу, что семь выпадает перед очком. Например, если очко равняется четырем и вы имеете ставку 10$ «прохода нет» с 20$ вероятностей ставки, и шутер выбрасывает семь перед четырьмя, вы выиграете 10$ на «прохода нет» и 10$ на вероятностную ставку. Истинная вероятность того, что семь выпадает перед четырьмя, составляет один к семи. Вероятность выпадения 7 вдвое выше, чем 4. Поэтому вам оплатят один к двум вашу ставку «против вероятности», или половину вашей вероятностной ставки, когда семь выпадает перед четырьмя. Для того, чтобы соблюсти честность в отношении всех игроков, казино позволяет игрокам, ставящим на «прохода нет», класть сумму, которую они бы выиграли, если бы выиграли по ставке линии прохода с полными шансами. Игроки, ставящие на «прохода нет» и «входа нет», могут четырехкратно увеличить свою вероятностную ставку «прохода нет» или «входа нет», когда очко равняется четырем или десяти. Когда очко равняется пяти, шести, восьми или девяти, вам разрешается троекратно увеличить свою вероятностную ставку «прохода нет» или «входа нет». Для того, чтобы поставить «против вероятности» на «прохода нет», поместите сумму, которую вы хотите вложить в вероятность, рядом с вашей ставкой «прохода нет». Для того, чтобы поставить «против вероятности» на ставку «входа нет» входа, поместите сумму, которую вы хотите вложить в вероятность на участок входа, и скажите дилеру, что вам хотелось бы положить энную сумму на вашу ставку «входа нет». Номерные ставки Номерные ставки чрезвычайно похожи на ставки входа, за исключением того, что вам не надо помещать ставку сначала в полосы «входа нет» или «прохода нет» (как со ставками на вероятность). Если вы хотите сделать номерную ставку на четыре, например, скажите дилеру, что вам хотелось бы поставить энную сумму на четыре. Для того, чтобы ваша номерная ставка на четыре выиграла, вам нужно, чтобы шутер выбросил четыре перед семью. Единственные числа, на которые вы можете ставить, — это вероятные числа очков: 4, 5, 6, 8, 9 или 10. Номерные ставки на 4,5,9 или 10 должны делаться с шагом в 5$. Номерные ставки на шесть или восемь должны быть сделаны с шагом в 6$. Причиной этого является то, что соотношение семь к шести затрудняет оплату 5$ ставок на эти числа. Номерные ставки оплачиваются следующим образом: — номерные ставки на четыре или десять оплачиваются девять к пяти: на каждую 5$ ставку вы выиграете 9$; — номерные ставки на пять или девять оплачиваются семь к пяти: на каждую 5$ ставку вы выиграете 7$; — шесть или восемь номерные ставки дают оплату семь к шести: на каждую 6$ ставку вы выиграете 7$. Ваши номерные ставки остаются на числе после того, как это число выпало и дилер отсчитал перед вами ваш выигрыш. Если вы не хотите, чтобы ваша номерная ставка оставалась на этом номере, вы должны сказать дилеру, чтобы он снял вашу номерную ставку и возвратил вам фишки. Помните, чтобы номерная ставка выиграла, выбранное вами число должно выпасть перед семью. Если выпало семь, то ваша номерная ставка проиграна. Номерные ставки дают казино большее преимущество, чем ставки прохода или ставки входа. Преимущество казино на номерных четырех или десяти равняется 6,67 процента. Преимущество казино на номерных пяти или девяти равняется 4 процентам. Преимущество казино на номерных шести или восьми равняется 1,52 процента. Причина этих различий заключается в вероятности выпадения каждого из этих номеров, как показано на рисунке 4-2. ⇦ Ctrl предыдущая страница / страница 10 из 49 / следующая страница Ctrl ⇨мобильная версия страницы Смотрите также на этом сайте: ГАДАНИЯ, СОННИКИ, ЗАГОВОРЫ, НУМЕРОЛОГИЯ, ХИРОМАНТИЯ, ВУДУ, МАЯТНИК, ДЕНЕЖНАЯ МАГИЯ ВЯЗАНИЕ НА СПИЦАХ, КРЮЧКОМ, ТУНИССКОЕ ВЯЗАНИЕ, МОДЕЛИ ВЯЗАНОЙ ОДЕЖДЫ; ШИТЬЕ; МАШИННОЕ ВЯЗАНИЕ РАЗНООБРАЗНЫЕ КУЛИНАРНЫЕ РЕЦЕПТЫ; ГОРШОЧКИ, МИКРОВОЛНОВКА; КОНСЕРВИРОВАНИЕ СПРАВОЧНИКИ ПО ФИЗИКЕ, МАТЕМАТИКЕ, АНГЛИЙСКОМУ ЯЗЫКУ; ПОХУДЕНИЕ, АКУПУНКТУРА; НЕИСПРАВНОСТИ АВТОМОБИЛЯ МНОЖЕСТВО ИСТОРИЧЕСКИХ ФАКТОВ О СОБЫТИЯХ, ОРУЖИИ И ОБМУНДИРОВАНИИ ВТОРОЙ МИРОВОЙ ВОЙНЫ; АРМЕЙСКИЕ БОТИНКИ ВСЕХ ВРЕМЕН ПОПУЛЯРНЫЕ ПЕСЕННИКИ 1963-1987 гг.; ТОСТЫ, РОЗЫГРЫШИ, КОНКУРСЫ Пользуйтесь поиском вверху страницы! Все, что будет найдено со значком Ł — относится к данному сайту |  |
cartalana.org