Сколько в кубе доски 25х100х6000? -Полезные советы
Что такое куб доски?
По стандартам для измерения пиломатериалов принята такая мера как куб. Чаще всего есть необходимость рассчитать количество досок в одном кубе стройматериала определенного вида.
Существует несколько способов для расчётов:
- Воспользоваться готовыми таблицами (если доска идет стандартной ширины и длины)
- Воспользоваться калькулятором для расчета
- Рассчитать по формуле — способ подходит для любого вида пиломатериалов с любыми размерами, в том числе нестандартными
Расчет количества досок в кубометре по формуле
Для расчета нам необходимо знать следующие параметры доски:
- Толщина
- Длина
- Ширина
Все измерения проводятся в метрах.
Формула для расчета количества досок в кубометре:
Количество досок в кубометре = 1/(Длина доски Х Ширина Доски Х Толщина)
Измерения округляем до целого числа в большую сторону.
Для примера возьмем доску длиной 6000мм (переводим в метры – 6м), ширина 100 мм (или 0,1метра), толщина 25 мм (0,025м):
Количество досок = 1/ (6х0,1х0,025) = 66,7
Результат: в кубе доски 25х100х6000 находится 67 штук.
Калькулятор для расчета обычно работает по тому же принципу, что и формула, в него необходимо внести эти же данные.
Готовые справочки по расчету количества доски в кубометрах
В готовых справочниках предоставляется информация для стандартных размеров доски:
— толщина от 20 до 50мм
— длина – от 1 до 6 метров
— ширина – от 10 до 25 см
В справочниках есть информация для различных видов пиломатериалов – от обрезной доски до бруса.
При таких запросах как: Сколько 40 доски в кубе? Нужно понимать, что количество зависит не только от толщины («сороковка» или 40мм толщины), но и от длины и ширины доски.
Сколько доски в кубе – самые часто используемые размеры
Доска 50х150х600 (или шестиметровая доска 50х150) — 23 доски.
Доска 150х40х6000 сколько штук в кубе – 28 досок.
Доска обрезная 25х150х6000 сколько досок в кубе – 45 штук.
Сколько в кубе доски 25х100х6000 – 67 досок.
Как рассчитать количество досок необходимое для покрытия определенной площади?
Этот параметр рассчитывается умножением длины и ширины доски. Все данные указываются в метрах.
Если для примера берем доску: 25х100х6000 – для расчета покрытия показатель толщины доски нам не важен: 0,1м х 6 = 0,6 кв. м – покрывает одна доска. Как ранее мы сосчитали, что в кубе 67 досок, то получается из куба доски мы покроем:
67*0,6= 40,2 квадратных метра будет покрыто 1 кубометром доски.
Стоит учесть, что площадь покрытия считается исходя из поверхности доски без монтажных пазов, если они есть, например на евровагонке.
Остались вопросы?
Подобрать материал необходимого качества и проконсультировать по размерам, монтажу и обработке могут наши консультанты.
Наши контакты
Заказать звонок или позвоните по номеру +7(951)061-80-42, +7(843)216-49-36 или отправляйте ваш запрос на почту
Обращайтесь!
Возможно Вам будет интересно!
Баня из бруса Все полезные советы Сколько весит куб сосны? Покупайте доску у нас:
mathschallenge.
 net
netЕсть ли формула для сложения последовательности кубов?
При рассмотрении первых пяти сумм делается замечательное открытие:
1 3 = 1
1 3 +2 3 =9
1 3 +2 3 +3 3 =36
1 3 +2 3 +3 3 +4 3 =100
1 3 +2 3 +3 3 +4 3 +5 3 =225
Кажется, что сумма всегда квадратная, но еще более примечательно то, что сумма первых n кубов, 1 3 +2 3 +…+
Например, 1 3 +2 3 +…+10 3 =(10×11/2) 2 =55 2 = 3025.
Используется аналогичный метод докажите эту формулу суммы квадратов, мы докажем этот результат дедуктивно; есть надежда, что это даст некоторое представление о том, как дальше можно найти ряд сил.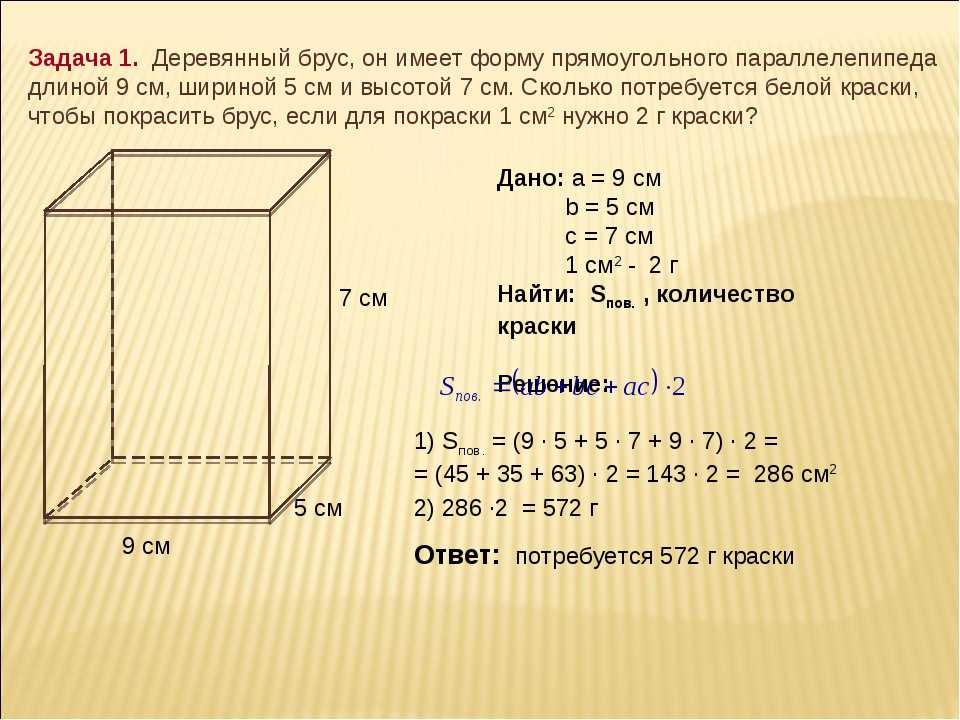
Доказательство
| р 4 –( р –1) 4 | = | n 4 –( n –1) 4 + ( n –1) 4 –( n –2) 4 + … + 3 4 –2 4 + 2 4 –1 4 + 1 4 9007 0 9 –0 9 4 | |||
| = | нет 4 |
, но R 4 — ( R –1) 4 = R 4 — ( R 4 –4 R 3 9008 +6 r 3 9008 +6 –4 R 3 9008 +6 –4 R 3 9008 +6 –4 R 3 9008 +6 –4 R 3 0044 2 –4 r +1) = 4 r 3 –6 r 2 +4 r –1.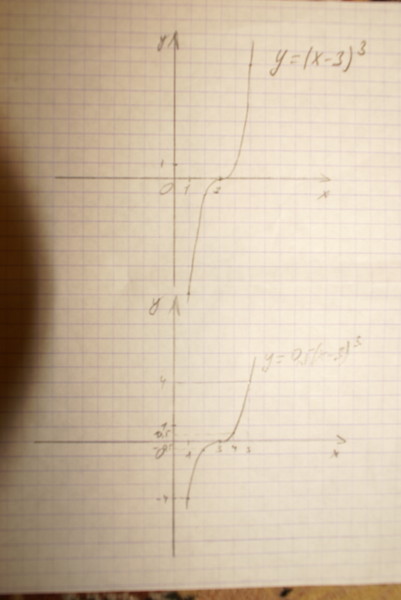
| ∴ ∑ 4 r 3 –6 r 2 +4 r –1 | = | 4∑ r 3 – 6∑ r 2 + 4∑ r – ∑1 |
| = | 4∑ р 3 – 6 n ( n +1)(2 n +1)/6 + 4 n ( n +1)/2 – n | |
| = | 4∑ r 3 – n ( n +1)(2 n +1) + 2 n ( n 904 – 4 904 9044 +4) | |
| = | п 4 . |
| ∴ 4∑ р 3 | = | n 4 + n ( n +1)(2 n +1) – 2 n ( n +1) + 3 |
| = | n ( n 3 + ( n +1)(2 n +1) – 2( n +1) + 1 | |
| = | n ( n 3 + 2 n 2 +3 n +1 – 2 n –2 + 1) | |
| = | n ( n 3 +2 n 2 + n ) | |
| = | n 2 ( n 2 +2 n +1) | |
| = | n 2 ( n +1) 2 | |
| ∴ ∑ р 3 | = | n 2 ( n +1) 2 /4 |
| = | ( н ( н +1)/2) 2 |
Другими словами, сумма первых n кубов — это квадрат суммы первых n натуральных чисел.
Факторизинг — выпуск выпускных экзаменов по математике по математике
Факторизинг — раскрывающиеся скобки
В этом разделе показано, как проводить факторизацию, а также приведены примеры, примеры вопросов и видеоролики.
Скобки должны быть раскрыты следующим образом:
Для выражения формы a(b + c) расширенная версия будет ab + ac, т. е. умножьте член вне скобок на все, что внутри скобок (например, 2 x ( x + 3) = 2x² + 6x [помните, что x × x равно x²]).
Для выражения формы (a + b)(c + d) расширенная версия будет ac + ad + bc + bd, другими словами, все, что в первой скобке, должно быть умножено на все, что во второй.
Пример
Расширение (2x + 3)(x — 1):
(2x + 3)(x — 1)
= 2x² — 2x + 3x — 3
= 2x² + x — 3
Разложение на множители — это действие, обратное раскрытию скобок, то есть, например, 2x² + x — 3 в форме (2x + 3)(x — 1). Это важный способ решения квадратных уравнений.
Это важный способ решения квадратных уравнений.
Первым шагом факторизации выражения является «удаление» любых общих факторов, которые имеют термины. Итак, если бы вас попросили разложить на множители x² + x, поскольку x входит в оба термина, вы бы написали x(x + 1) .
Факторизация квадратичных уравнений
В этом видео показано, как решить квадратное уравнение с помощью факторизации.
Не существует простого метода разложения квадратного выражения на множители, но после небольшой практики он станет проще. Однако один систематический метод заключается в следующем:
Пример
Факторизация 12y² — 20y + 3
= 12y² — 18y — 2y + 3 [здесь 20y разбито на два числа, кратное 36. 36 выбрано потому, что это произведение 12 и 3 , два других числа].
36 выбрано потому, что это произведение 12 и 3 , два других числа].
Первые два члена, 12y² и -18y, оба делятся на 6y, так что «вычтите» этот множитель 6y.
6y(2y — 3) — 2y + 3 [мы можем это сделать, потому что 6y(2y — 3) равно 12y² — 18y]
Теперь приведем два последних выражения к выражению в скобках:
Ответ: (2y — 3)(6y — 1)
Пример
Факторизация x² + 2x — 8
Нам нужно разделить 2x на два числа, которые умножаются на -8. Это должно быть 4 и -2.
x² + 4x — 2x — 8
x(x + 4) — 2x — 8
x(x + 4)- 2(x + 4)
(x + 4)(x — 2)
Однажды вы выяснить, что происходит, этот метод упрощает разложение любого выражения на множители. Стоит изучить эти примеры дальше, если вы не понимаете, что происходит. К сожалению, единственным другим методом факторизации является метод проб и ошибок.
Разность двух квадратов
Если вас попросят разложить на множители выражение, представляющее собой одно квадратное число минус другое, вы можете разложить его на множители немедленно.
