Как решать уравнения с факториалами онлайн
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Факториалом n! называется произведение n последовательных натуральных чисел, начиная с единицы:
\[n! = 1\cdot2\cdot3(n-1) \cdot n\]
Факториал нуля равен единице:
\[0! = 1\]
Так же используются факториалы по четным и нечетным числам. Обозначаются они следующим образом:
\[ (2n)!! = 2\cdot4\cdot6\ldots(2n — 2)( 2n) \] (1)
\[ (2n + 1)!!\] — факториал по всем нечетным числам до \[(2n +1) \]
Факториал — частое явление в комбинаторике, поэтому знание их способов решения очень важно.

Так же читайте нашу статью «Решить уравнение с дробями онлайн решателем»
Допустим, дано уравнение с факториалом следующего вида:
\[\frac{8!-6!}{55}\]
Для решения данного дробного уравнения с факториалом необходимо вынести за пределы скобок 6!:
\[\frac{8!-6!}{55} = \frac{6!(7\cdot8-1)}{55} = \frac{6!(56-1)}{55} = \frac{6!\cdot55}{55} = 6! = 1\cdot2\cdot3\cdot4\cdot5\cdot6 = 720\]
Ответ: \[720\]
Решим дробное уравнение с двойным факториалом следующего вида:
\[\frac{7!-7!!}{47}\]
Из вышеописанного равенства (1) следует:
\[7! = 6!! \cdot7!! \]
Соответственно получим:
\[\frac{7!-7!!}{47} = \frac{6!!\cdot7!!-7!!)}{47} = \frac{7!!(6!!-1)}{47} = \frac{7!!(2\cdot4\cdot6-1)}{47} = \frac{7!!(48-1)}{47} = \frac{7!!(48-1)}{47} = \frac{7!!47}{47} = 7!! = 1\cdot3\cdot5\cdot7 = 105\]
Ответ: \[105.\]
Как видите, уравнения с факториалами довольно легко решаются с помощью несложных преобразований и арифметических операций, главное знать алгоритм их решения и формулы преобразования.
Где можно решить уравнение с факториалом онлайн?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
www.pocketteacher.ru
Fast Factorial Functions
- Установите .
- Создать
- F = вход? Если да, то является N.
- Если нет, то установите , а затем снова начните с # 2.
Вы можете оптимизировать, используя предыдущий результат для вычисления нового ( ).
Это так же быстро, как движение в противоположном направлении, если не быстрее, учитывая, что разделение обычно занимает больше времени, чем умножение. Данный факториал гарантировано, что все целые числа, меньшие, чем качестве факторов в дополнение к А, так что вы потратили бы столько времени на факторинг, как вы просто вычисляли бы факториал.
Ну, если вы знаете, что M действительно является факториалом какого-то целого, то вы можете использовать
Вы можете решить эту проблему (или, действительно, решить ) и найти ближайшее целое число. Он все еще нелинейный, но вы можете легко получить приближенное решение путем итерации (на самом деле, я ожидаю, что коэффициент достаточен).
Вот код clojure:
Пусть n = 120, div = 2. 120/2 = 60, 60/3 = 20, 20/4 = 5, 5/5 = 1, возврат 5
Пусть n = 12, div = 2. 12/2 = 6, 6/3 = 2, 2/4 = .5, return ‘nil’
Если вы не знаете , является ли число или нет, достойным тестом является проверка, если он делится на все мелкие простые числа, пока приближение Стерлинга этого числа больше, чем В качестве альтернативы, если у вас есть таблица факториалов, но она не подходит достаточно высоко, вы можете выбрать самый большой фактор в своей таблице и убедиться, что делится на это.
В C из моего приложения Advanced Trigonometry Calculator v1.6.8
Что вы думаете об этом? Правильно работает для целых чисел факториалов.
Большинство чисел не находятся в диапазоне выходов факториальной функции. Если это то, что вы хотите проверить, легко получить приближение, используя формулу Стирлинга или количество цифр целевого номера, как упомянуто другими, а затем выполнить бинарный поиск, чтобы определить факториалы выше и ниже заданного числа.
Более интересным является построение обратной функции Гамма, которая расширяет факториальную функцию до положительных действительных чисел (и к наиболее сложным числам тоже). Оказывается, что построение обратного является трудной задачей. Тем не менее, он был определен явно для большинства положительных реальных чисел в 2012 году в следующем документе: http://www.ams.org/journals/proc/2012-140-04/S0002-9939-2011-11023-2/S0002- 9939-2011-11023-2.pdf . Явная формула приведена в следствии 6 в конце статьи.
Обратите внимание, что он включает интеграл в бесконечной области, но при тщательном анализе я считаю, что разумная реализация может быть построена. То, что лучше, чем простая схема последовательных приближений на практике, я не знаю.
п!
Как решать уравнения с факториалами
очень легко оценить. Поэтому продолжайте делиться на 2,3,5,7 … и проверьте экспоненты, сколько раз вы могли бы разделить.
Теперь вопрос в том, что у вас есть n! что представляет собой показатель простого p в нем?
Во-первых, n! может иметь только простые числа вплоть до n, включая n, если он является простым.
Вы добавляете один за каждый раз простой p, или любая его сила находится в пределах n. Сколько раз вы увидите p. Ну, это должен быть самый большой k, для которого
имея в виду
то же самое от премьер-министра
Алгоритм следует.
Предположим, что у нас есть 10888869450418352160768000000
Мы можем разделить
2, 23 раза
3, 13 раз
5, 6
7, 3
11, 2
13, 2
17, 1
23, 1
не делится на 29
Это означает, что это число от 23 до 29. (Обычно диапазон намного больше, но этот пример по-прежнему полезен).
Теперь мы можем использовать бинарный поиск между 23 и 29, чтобы получить набор, который можно разделить на 2, 23 раза. Обратите внимание, что может быть только два таких числа. Мы пробуем 26 и легко обнаруживаем, что это
Если это не так, мы продолжим сегмент 23-26 или 26-29 в зависимости от результата.
Таким образом, это либо 26, либо 27. Мы делаем то же самое для 3 и остальных, пока не получим совпадение ни с одним из двух возможных чисел. Числа будут иметь разный результат для хотя бы одного из заданных простых чисел.
Поэтому, если вышеперечисленное является факториалом, это факторный показатель 27. Проверка того же, что и выше для 5,7,11,13,17,19 и 23, показывает, что все в порядке и что это действительно 27.
steptosleep.ru
Как упростить факториальные выражения — макеты 2019
Наборы элементов имеют специальные операции, используемые для их объединения или их изменения. Другая операция, которая используется с наборами (но не только для наборов), — это factorial, , обозначаемая восклицательным знаком.
Вы используете факториальную операцию в формулах, используемых для подсчета количества элементов в объединении, пересечении или дополнении множеств. Факториалы появляются в формулах, которые вы используете для подсчета элементов в наборах, которые действительно велики.
Факториальная операция, n ! , определяется как n ! = n ( n — 1) ( n — 2) ( n — 3) · · · 4 · 3 · 2 · 1. Другими словами, вы умножаете число n , на которое воздействует каждое положительное целое число меньше n . Некоторые значения n ! являются: 1! = 1, 2! = 2, 3! = 6, 4! = 24, 5! = 120, 6! = 720 и т. Д. Вы видите, что они становятся довольно крупными довольно быстро.
Еще одно факторное значение, которое вам нужно, — 0! = 1. Вы можете подумать, что это опечатка. Неа. По определению факториал 0 равен 1. Это одна из тех причудливых вещей, которые заявляют математики и заставляют всех использовать, чтобы ответы на проблемы выходили правильно. Люди хотели, чтобы формулы для подсчета были согласованными для всех используемых чисел.
Упрощение факториалов не сложно, но это не так просто, как вы думаете на первый взгляд. Чтобы упростить
вы не можете просто уменьшить 6 и 3. Вы должны посмотреть на все факторы, связанные с каждой факториальной операцией. Запишите факториалы, и вы получите
Теперь уменьшите аналогичные факторы и упростите:
Пример вопроса
Упростите факториальное выражение:
816. Сначала выпишите разложения факториалов. Но ждать! (Обратите внимание, что, несмотря на восклицательный знак, факториал не работает над словом wait. ) Вместо того, чтобы записывать все факторы из 18! , просто напишите 18! как 18 · 17 · 16 · 15! , Вы решили остановиться с 15 из-за 15! в знаменателе.
15! условия будут отменены, поэтому не стоит записывать все эти идентичные термины как в числителе, так и в знаменателе:
Теперь разделите любые другие общие факторы и упростите:
Вопросы практики
Упростите выражение: > Упростите выражение:
Упростите выражение:
Упростите выражение:
Ниже приведены ответы на вопросы практики:
Ответ 1, 680.
Разверните числитель и оставьте знаменатель как 4! , Затем уменьшите и упростите:
Ответ 2, 652.
Разверните числитель и оставьте знаменатель равным 50!, Затем уменьшите и упростите:
Ответ будет 10.
Развернуть числитель и первый множитель знаменателя. Уменьшите общие факторы и упростите:
Ответ будет равен 15, 504.
Разверните числитель и первый множитель знаменателя. Уменьшите общие факторы и упростите:
ru.no-dummy.com
Перестановки и факториалы. Способы вычисления факториала. Рекурсия
Разделы: Математика, Информатика
Вид урока: Бинарный (математика – информатика)
Место проведения: компьютерный класс .
Тема:
Алгебра: Перестановки и факториалы.
Оборудование: компьютерная сеть из 14 компьютеров, мультимедийный проектор, экран, маркерная доска.
Цели и задачи урока:
- Повторить понятие перестановки и правила вычисления числа перестановок.
- Повторить понятие факториала и рассмотреть рекурсивный способ его вычисления в среде программирования Турбо Паскаль.
- Сравнить итерационный и рекурсивный способы вычисления факториала.
- Рассмотреть типичные задачи и отработать способы их решения.
- Отработать применение подпрограммы при программировании решения комбинаторной задачи.
- Закрепить изученный материал, используя ИКТ.
Ход урока
I. Понятие факториала и перестановки.
Рассмотрим задачу, которая хорошо известна Вам как гуманитарному классу, хотя возможно Вы и не догадывались, что перед Вами именно задача (иллюстрируем презентацией).
“Проказница Мартышка, Осел,
Козел,
Да косолапый Мишка
Затеяли сыграть Квартет.
Вот пуще прежнего пошли у них разборы
И споры,
Кому и как сидеть.
А вы, друзья, как ни садитесь,
Всё в музыканты не годитесь».
И.А. Крылов”.
Итак, данной группе пришлось решать не такой уж простой вопрос: “Как расположить 4 объекта по 4 местам?”. Баснописец Крылов предложил только 2 способа рассадки участников квартета. А сколько их было на самом деле?
У нас 4 объекта:
1) Проказница мартышка;
2) Осёл;
3) Козёл;
4) Косолапый мишка.
И мест тоже 4: первое, второе, третье, четвертое.
Записываем решение на слайде.
Допустим, мартышка, как дама, выбирает место первой. Сколько у неё возможностей? Ведь она может занять любое из 4 мест, следовательно – 4.
Мишка по старшинству будет выбирать вторым, но уже только из 3 мест, так как одно занято, следовательно, у него 3 возможности.
Допустим, следующим будет козел, как имеющий неоспоримое преимущество в виде рогов. У него всего 2 возможности выбора, так как незанятых мест всего 2.
И последнему, ослу, остается только занять единственное свободное место, то есть его выбор – 1.
Напоминаю правило умножения для конечного числа испытаний: “Число всех возможных исходов независимого проведения n испытаний равно произведению количества исходов этих испытаний”.
Значит, число возможных вариантов рассадки членов квартета составит:
4•3•2•1=24.
И если бы баснописец Крылов описал все возможные способы, то мы получили бы не басню, а поэму. А как называется полученное нами произведение идущих подряд n натуральных чисел? Факториалом!
Определение.
Произведение идущих подряд n натуральных чисел обозначают n! и называют “эн факториал”.
n!=1•2•3• … • (n – 1)• n.
Фактически мы с Вами решали задачу о количестве перестановок некоторого n – элементного множества (в нашем случае 4-х элементного множества).
Теорема.
Число всех перестановок n – элементного множества равно n!.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| n! | 1 | 2 | 6 | 24 | 120 | 720 | 5040 | 40320 |
II. Рассмотрим ещё несколько задач. (Тексты перед Вами)
№1. У мамы и папы – один сын. К ним в гости пришла другая семья – мама, папа и дочь. За круглым обеденным столом есть 6 мест. Сколькими способами можно рассадить людей за столом, если:
а) место хозяина в доме неприкосновенно;
б) первыми садятся дети, и они садятся рядом;
в) первыми садятся дети, но не рядом друг с другом;
г) жены садятся рядом со своими мужьями?
Ответы:
№1 а) 120; б) 288; в) 432; г) 72.
Обратите внимание, какие числовые выражения, значения которых надо найти, получены в ответах. Что же может помочь нам в этом?
Используется презентация “Алгоритм вычисления факториала”
III. Самостоятельная работа.
Учащиеся работают на компьютерах, выполняя задания и заполняя индивидуальные бланки самостоятельной работы:
Самостоятельная работа
Домашнее задание.№5. В зоопарке 5 львов надо распределить по одному по пяти клеткам, четырех тигров – по четырем другим клеткам и трех слонов – по трем вольерам.
а) Найдите число всех возможных распределений
львов, тигров и слонов в зоопарке.
б) То же, но если есть четыре льва и львица и
одного льва (известно какого именно) вместе с
львицей надо посадить в одну клетку.
в) То же, что и в пункте а), но если у львов есть две
семейные пары.
г) то же, что и в пункте а), но если между клетками
для тигров и клетками для львов нет разницы.
Ответ: а) 5!•4!•3!=17280; б) 17280; в)( 5•4•3)•4!•3!=8640; г) 2177280.
IV. Подводим итоги урока.
1. Чему равно количество перестановок в
множестве из n элементов?
2. Сколько алгоритмов вычисления факториала нами
изучено?
Какие это алгоритмы? В чём различия между ними?
Презентация
24.01.2011
xn--i1abbnckbmcl9fb.xn--p1ai
Тема «деление дробей факториал » основные цели
Тип урока: ОНЗ
Тема: «Деление дробей. Факториал.»
Основные цели:
1) вывести алгоритм n! факториала и сформировать способность к его выполнению;
2) повторить и закрепить определение, взаимосвязь между умножением и делением, тренировать способность к сокращению дробей.
Оборудование, демонстрационный материал
Сложение и вычитание дробей
Суммой (разностью) дробей является дробь
Привести дроби к НОЗ
Общий знаменатель записать в знаменатель суммы (разности)
Сложить (вычесть) числители и записать ответ
в числитель суммы (разности)
Если возможно, сократить полученную дробь
и выделить и нее целую часть
задания для актуализации знаний:
Алгоритм умножения дробей
1) Произведение дробей записать в виде дроби, в числители, которой записано произведение числителей, в знаменателе произведение знаменателей.
2) Если возможно сократить, получившуюся дробь.
3) Найти произведение чисел, стоящих в числителе и чисел, стоящих в знаменателе.
4. Если получилась неправильная дробь, выделить целую часть.
Алгоритм деления дробей
1. Деление заменить умножением.
2. Делитель заменить числом, обратным.
3. Выполнить умножение по известному алгоритму.
Оборудование, демонстрационный материал
№ 1
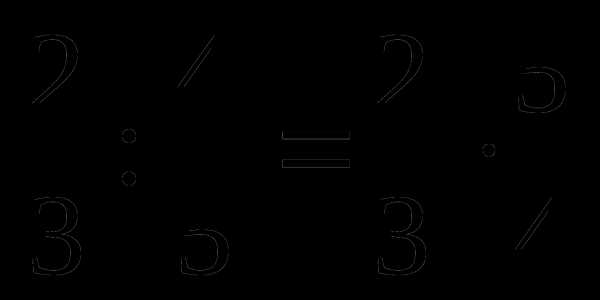 ;
;  ;
;  ;
; 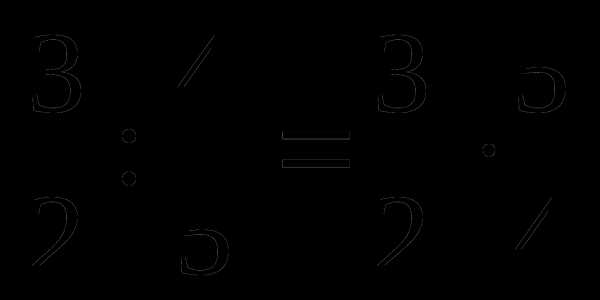
№ 2.
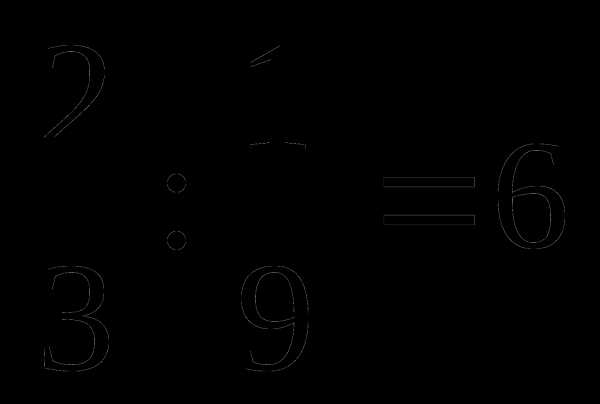 ;
; 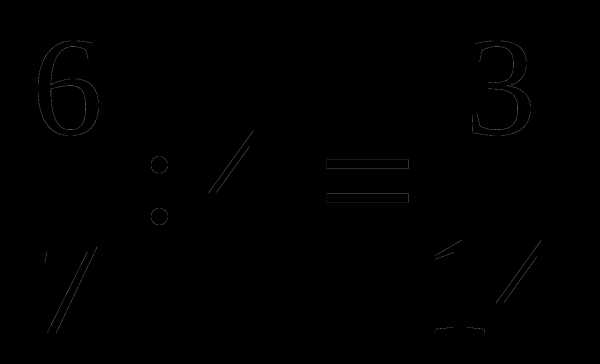 ;
;  ;
; 
№3
Алгоритм Факториала Факториалом числа n называется произведение всех натуральных чисел от 1 до n: n! = 1· 2 · 3 · 4 · …· n (n! читается: «эн факториал» ) |
Ход урока
1. Самоопределение к учебной деятельности
Цель этапа:
1) включить учащихся в учебную деятельность;
2) определить содержательные рамки урока: продолжаем работать над действиями с обыкновенными дробями.
Организация учебного процесса на этапе 1:
– Какие действия с обыкновенными дробями мы научились выполнять? (Сравнивать, складывать, вычитать, умножать обыкновенные дроби и смешанные числа.)
– Вспомните, по какому плану мы изучали тему сложение и вычитание дробей. (Алгоритм сложения дробей.)
– Молодцы! Для успешной работы выполним следующие задания.
2. Актуализация знаний и фиксация затруднения в деятельности
Цель этапа:
1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: сложение и вычитание, умножение и деление дробей, сравнение дробей;
2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;
3) зафиксировать все повторяемые понятия и алгоритмы в виде схем и символов: в виде свойств и определения;
4) зафиксировать индивидуальное затруднение в деятельности, демонстрирующее на личностно значимом уровне недостаточность имеющихся знаний: найти частное дробей.
Организация учебного процесса на этапе 2:
Вспомните, по какому плану мы изучали тему умножение, деление дробей.
(1. Сформулируйте определение взаимно обратных чисел. (Числа взаимно обратные, если их произведение равно 1).
2.Сформулируйте взаимно обратных действия. (Сложение и вычитание, умножение и деление.)
Организация учебного процесса на этапе 3:
1). Слайд 2 ( Показ презентации Факториал)
— Быль: «Однажды на экзамене…»
Преподаватель: Прочитайте выражение:
Студент: Единица, деленная на два-а-а!..
Плюс единица, деленная на три-и-и!..
Плюс единица, деленная на четы-ы-ыре!…
Преподаватель: Простите, постойте…
Почему вы кричите?
Студент: Нотам же написаны восклицательные знаки?!..
– Как бы вы назвали такие числа? (Варианты детей.)
— Что студенту необходимо знать?
— В чем возникло затруднение?
— Какую цель мы поставим перед собой? (Найти способ решения)
— А, зачем нам нужен, этот способ?
Организация учебного процесса на этапе 4:
— Сформулируйте тему урока (Показать Алгоритм факториала)
-Запишите тему в тетрадь.
слайд 3 ( Показ презентации Факториал)
– В математике их называют Факториалы
Сформулируйте определение n!
(n! называется произведение всех натуральных чисел. )
– Какую цель мы поставим перед собой? (Найти способ решения примеров с факториалами, не используя определение делимости.)
слайд 4 ( Показ презентации).
– А зачем нам нужен, будет этот способ? (Чтобы научится быстро выполнять решения с дроби.)
– Сформулируйте тему урока. (Факториал.)
– Запишите тему в тетрадь.
Индивидуальное задание.
Вычисли : 2!, 3!, 4!, 5!, 6! Слайд 5 ( Показ презентации).
— Какое задание вы должны были сделать?
-Вы знаете алгоритм факториала?
-Почему данное задание вызвало у вас затруднение? (нехватка времени)
-Чтобы быстро и правильно выполнить задание, что необходимо знать?
(алгоритм факториала)
-Какая цель урока? (Построить алгоритм и научится быстро выполнять задание)
Какой следующий шаг вы должны сделать?(Найти закономерность и ей воспользоваться)
С проверкой Презентация
3) Выявление причины затруднения и постановка цели деятельности
Цель этапа:
1) организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности: возможность найти по определению умножения и делимости результат первого примера
2) согласовать цель и тему урока: вывести правило сравнения факториала, научиться делить дроби, тема урока: «деление дробей, факториал».
Сравни: а) и ( > ) ;
б) 1/59! < 1/49! ; d) 1/n! > 1/(n+3)!
С теми учащими, которые допустили ошибки организовать диалог по локализации затруднения.
– Какой следующий шаг вы должны сделать после проверки работы и фиксации результатов? (Надо найти место ошибки и понять её причину.)
– Что нужно сделать для этого? (Постараться подробно расписать задание, если это не сделано при выполнении работы.)
– Каков может быть результат такой работы? (Можем получить правильный ответ или опять получить не правильный ответ.)
– Если ответ не совпал с образцом, что необходимо сделать? (Определить, какие правила необходимо использовать при выполнении задания и повторить эти правила.)
–Какую цель вы ставите для себя на этом уроке? (Определить причину ошибки и исправить её.)
3. Самостоятельная работа с самопроверкой по эталону.
Цель этапа: проверить своё умение применять алгоритм сложения и вычитания в типовых условиях на основе сопоставления своего решения с эталоном для самопроверки.
слайд 6 ( Показ презентации) ½! > 1/3!
1) ¼! > 1/9!; 2) 1/59! > 1/49!; 3) 1/n! > 1/(n+3)!
4. Построение проекта выхода из затруднения
Цель этапа:
1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;
2) зафиксировать новый способ действия в знаковой, вербальной форме и с помощью эталона.
Алгоритм факториала
Факториал заменить умножением чисел.
Выполнить умножение (вычитание) по известному алгоритму.
№ 400 слайд 7 ( Показ презентации)
Приведите к несократимому виду дроби: ;
1) ;
2) ;
3) 5!/3! *4! = 5/3! = 5/6; 4) 8!/4!*4! = 5*6*7*8/4! = 5*2*7 = 70;
5) 12!/5!*7!= 8*7*11=56*11=616
5. Первичное закрепление во внешней речи
Цель этапа: зафиксировать изученное учебное содержание во внешней речи.
6. Самостоятельная работа с самопроверкой по эталону.
Цель этапа: проверить своё умение применять алгоритм сложения и вычитания в типовых условиях на основе сопоставления своего решения с эталоном для самопроверки.
Организация учебного процесса на этапе 5:
№400 слайд 7 ( Показ презентации)
Найти значение разности
№ 400 (6)
2) 1/3! – ¼! = (4-1)/4! = ¾! = 1/8;
4) 1/5! – 1/6! = (6-1)/6! = 1/6*24= 1/144
7. Включение в систему знаний и повторение
Цель этапа: 1) тренировать навыки использования нового содержания совместно с ранее изученным: нахождение разности дробей;
2) повторить учебное содержание, которое потребуется на следующих уроках: сокращение дробей.
Организация учебного процесса на этапе 6:
№ 400 (5) 1) ½!=60/5! и 1/5!; 2) 1/3! = 4/4! и ¼!;
3) 1/7! и 1/5! = 42/7!; 4) 1/99! = 100/100! и 1/100!;
(4 учащихся) у доски с проговариванием правила или алгоритма деления дробей.
После проверки по эталону анализируются и исправляются ошибки.
8. Рефлексия деятельности на уроке
1) зафиксировать новое содержание, изученное на уроке: алгоритм факториала;
2) оценить собственную деятельность на уроке;
3) поблагодарить одноклассников, которые помогли получить результат урока;
4) зафиксировать неразрешённые затруднения как направления будущей учебной деятельности;
5) обсудить и записать домашнее задание.
Организация учебного процесса на этапе 8:
– Что нового мы узнали на уроке сегодня? (понятие о факториале)
– С каким правилом тесно связано правило факториал? (С правилом деления и умножения дробей.)
– Проанализируйте свою деятельность на уроке и дайте своей работе оценку.
Домашнее задание
№400 (6) ( Показ презентации)
½! + 1/3! + ¼! +1/5! = (60+20+5+1)/5! = 43/60;
1/n! -1/(n+1)! = n/(n+1)!
Самоанализ урока
Предмет – математика 5 Б класс
Учитель – Мирошина Галина Леонидовна.
Тема урока «Факториал»
Тип урока – изучение нового материала.
Цели урока 1) вывести алгоритм n! факториала и сформировать способность к его выполнению; 2) повторить и закрепить определение, взаимосвязь между умножением и делением, тренировать способность к сокращению дробей.
Структура урока –
Самоопределение к учебной деятельности
Актуализация знаний и фиксация затруднения в деятельности Цель этапа:
1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: сложение и вычитание, умножение и деление дробей, сравнение дробей;
2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;
3) зафиксировать все повторяемые понятия и алгоритмы в виде схем и символов: в виде свойств и определения;
Выявление причины затруднения и постановка цели деятельности
Построение проекта выхода из затруднения
Первичное закрепление во внешней речи
Включение в систему знаний и повторение
Рефлексия деятельности на уроке
Приемы и организационные формы, помогающие достичь поставленной цели – закрепление знаний пройденного материала, дидактическое и техническое оснащение урока, при изучении нового материала создание проблемной ситуации, организация самостоятельных работ с проверкой у доски.
textarchive.ru
