Площадь параллелограмма | Треугольники
Площадь параллелограмма можно найти по стороне и проведённой к этой стороне высоте, по двум сторонам и углу, по диагоналям и углу между ними.
I. Площадь параллелограмма по стороне и высоте
Площадь параллелограмма равна произведению стороны параллелограмма на высоту, проведённую к этой стороне.
Формула для нахождения площади параллелограмма через сторону и высоту:
Например,площадь параллелограмма ABCD через высоту можно найти по одной из формул:
или
II. Площадь параллелограмма по сторонам и углу
Площадь параллелограмма равна произведению его сторон на синус угла между ними.
Формула для нахождения площади параллелограмма через стороны и угол:
Например, площадь параллелограмма ABCD
По свойствам параллелограмма, противоположные углы параллелограмма равны:
Сумма углов параллелограмма, прилежащих к одной стороне, равна 180º, то есть,
А так как синус тупого угла равен синусу смежного ему угла, то
Таким образом, площадь параллелограмма можно найти как произведение его двух любых не смежных сторон на синус любого угла.
III. Площадь параллелограмма по диагоналям
Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.
Формула площади параллелограмма через диагонали:
Например, площадь параллелограмма ABCD
А так как
то в качестве угла между диагоналями можно брать любой угол — как острый, так и тупой (прямой — в ромбе и квадрате).
www.treugolniki.ru
Формула нахождения площади параллелограмма онлайн
Параллелограмм — это четырехугольник с попарно параллельными и равными противоположными сторонами. В параллелограмме равны между собой и противоположные углы. Диагонали параллелограмма в точке пересечения друг с другом делятся пополам. Прямоугольник, квадрат, ромб являются тоже параллелограммами. Площадь параллелограмма определяется несколькими способами через высоту, стороны, диагонали и углы.
1-й способ, классический. Определяем S параллелограмма, зная его сторону и высоту, путем умножения стороны на высоту, которая проведена к этой стороне, по формуле:
где a, b — стороны параллелограмма;
h × a — высота на сторону a;
h × b — высота на сторону b.
Расчет площади параллелограмма через сторону и высоту
2-й способ. S параллелограмма рассчитывается через стороны и углы, как произведение двух сторон на синус угла между ними, по формуле:
где S — площадь параллелограмма;
a, b — его стороны;
Расчет площади параллелограмма через стороны и углы
3-й способ. S параллелограмма, в котором даны диагонали и угол между ними, рассчитывается как полупроизведение диагоналей на синус угла между ними по формуле:
где D — величина большей диагонали;
d — величина меньшей диагонали;
α,β — углы между диагоналями.
Расчет площади параллелограмма через диагонали и угол между ними
infofaq.ru
11. Формулы площади параллелограмма
1. Формула площади параллелограмма через стороны и углы
a, b — стороны параллелограмма
α, β — углы параллелограмма
Формула площади через стороны и углы параллелограмма, (S):
2. Формула площади параллелограмма через сторону и высоту
a, b — стороны параллелограмма
Hb — высота на сторону b
Ha — высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):
3. Формула площади параллелограмма через диагонали и угол между ними
D — большая диагональ
d — меньшая диагональ
α, β — углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):
Площадь параллелограмма | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Первый способ вычисления площади параллелограмма связан с одной из самых простых фигур – прямоугольником. Доказательство: если провести в параллелограмме высоту h, то мы разделим его на две фигуры – треугольник и трапецию.
Совершив несложное перемещение треугольника по другую сторону трапеции, мы получим прямоугольник, равный по площади нашему параллелограмму. И поскольку площадь прямоугольника находится умножением его сторон, то в данном случае мы поступим аналогично, только вместо длины прямоугольника в формуле будет сторона параллелограмма, а вместо ширины – его высота.
Второй способ использует для нахождения площади параллелограмма его стороны и синус острого угла между ними. Это логически вытекает из первого способа, в случае если высота неизвестна. Доказательство: высота в параллелограмме всегда образует прямоугольный треугольник с одной из сторон, в котором действуют тригонометрические отношения.
Синус угла, по определению, это отношение противолежащего катета к гипотенузе – то есть высоты к стороне для параллелограмма: , следовательно . Подставляем в формулу из первого способа:
Третий способ основан на диагоналях параллелограмма и углу между ними. Доказательство: Диагонали делят параллелограмм на 4 треугольника, соответственно площадь параллелограмма будет состоять из площадей этих треугольников: .
Используем следующую формулу для нахождения площади треугольника , а учитывая, что , то во всех площадях треугольников будет фигурировать один и тот же sin γ, потому что между диагоналями все углы дополнительные друг другу до 180°, то есть или γ, или 180°-γ.
Тогда получаем:
.
Выносим за скобки: Методом группировки собираем скобку в множители (помним, что AO и OA это одно и то же): И здесь уже из чертежа видно,что AO+OC вместе составляют диагональ AC,
и BO+OD=BD. Таким образом, получаем формулу:
или в общем виде, для любого параллелограмма , где d
geleot.ru
Площадь параллелограмма, треугольника и трапеции — урок. Геометрия, 8 класс.
Площадь параллелограмма
Необходимо определить, что такое высота параллелограмма.
Это перпендикуляр, проведённый из любой точки стороны параллелограмма к прямой, содержащей противоположную параллельную сторону. Обычно высоту проводят из вершины параллелограмма. Так как параллелограмм имеет две пары параллельных сторон, то он имеет высоты двух различных длин.
Высота \(BE\), проведённая между длинными сторонами, короче высоты \(BF\), проведённой между короткими сторонами.
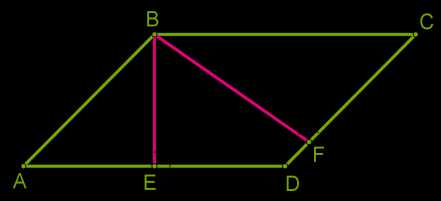
Так как стороны ромба одинаковы, то высоты ромба также одинаковы: \(BE = BF\).
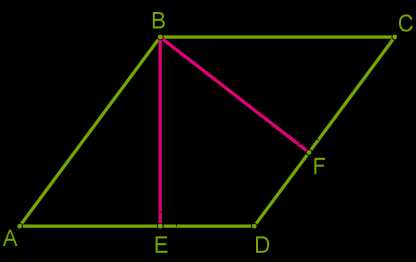
Площадь произвольного параллелограмма
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена высота.
Проведём высоты из двух вершин \(B\) и \(C\) к стороне \(AD\) .
Прямоугольные треугольники \(ABE\) и \(DCF\) равны (равные гипотенузы как противоположные стороны параллелограмма и равные катеты как расстояние между параллельными прямыми).
Параллелограмм \(ABCD\) и прямоугольник \(EBCF\) — равновеликие, так как состоят из равных фигур:
SABCD=SABE+SEBCD;SEBCF=SEBCD+SDCF.
Значит, площадь параллелограмма определяется так же, как площадь прямоугольника:
SEBCF=BE⋅BC;SABCD=BE⋅BC=BE⋅AD.
Если обозначить сторону через \(a\), высоту — через \(h\), то:
Sп−гр=a⋅h.
Для определения площади параллелограмма можно использовать короткую сторону и высоту, проведённую к короткой стороне.
Площадь ромба
Диагонали ромба в точке пересечения делятся пополам, они перпендикулярны и делят ромб на четыре равных прямоугольных треугольника.
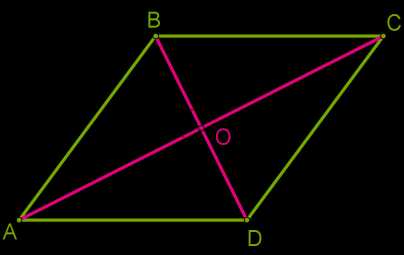
SABCD=4⋅SABO=4⋅BO⋅AO2=2⋅BO⋅AO.
Формула определения площади ромба:
Sромба=d1⋅d22.
Эта формула справедлива для определения площади любого четырёхугольника, если его диагонали перпендикулярны.
Так как диагонали квадрата равны, то для определения площади квадрата в формуле достаточно длины одной диагонали:
Sквадрата=d22.
Площадь произвольного треугольника
Так как диагональ параллелограмма делит его на два равных треугольника, то площадь треугольника равна половине площади параллелограмма.
Sтреуг=aha2, где \(h\) — высота (на рисунке — \(BE\)), проведённая к стороне \(a\) (на рисунке — \(AD\)).
Для определения площади треугольника можно использовать любую сторону и высоту, проведённую к этой стороне.
Удобно иногда использовать формулу Герона, если известны длины всех трёх сторон треугольника.
SΔ=pp−ap−bp−c;p=a+b+c2
— формула Герона, где \(a\), \(b\) и \(c\) — стороны треугольника, \(p\) — полупериметр треугольника.
Площадь прямоугольного треугольника
Так как катеты прямоугольного треугольника взаимно перпендикулярны, то один катет может быть высотой, а другой катет — стороной, к которой проведена высота. Получаем формулу:
S=a⋅b2, где \(a\) и \(b\) — катеты.
Для прямоугольного треугольника также можно применять формулы площади произвольного треугольника.
Пример:
1. вычислим площадь треугольника со сторонами \(17\) см, \(39\) см, \(44\) см.
Решение:
p=17+39+442=50;SΔ=50⋅50−17⋅50−39⋅50−44=50⋅33⋅11⋅6==25⋅2⋅3⋅11⋅11⋅2⋅3=5⋅2⋅3⋅11=330см2.
Чтобы легче было вычислить корень, необходимо не перемножать все числа, а раскладывать их на множители: a⋅a=a.
Формулу Герона можно использовать для вычисления высоты треугольника.Пример:
2. вычислим меньшую высоту треугольника, стороны которого равны \(15\) см, \(13\) см, \(4\) см.
Решение:
используем две формулы вычисления площади: SΔ=aha2 и SΔ=pp−ap−bp−c.
Меньшая высота в треугольнике — та, которая проведена к большей стороне, поэтому \(a =\) \(15\) см.
SΔ=pp−ap−bp−c=16⋅1⋅3⋅12=24см2.
Составляем уравнение:
15⋅h3=24⋅215⋅h=48;h=4815=3,2(см).
Иногда формула Герона используется для вычисления площади параллелограмма, если даны стороны параллелограмма и его диагональ.
Пример:
3. дан параллелограмм со сторонами \(17\) см и \(39\) см, длина диагонали равна \(44\) см. Вычислим площадь параллелограмма.
Решение:
диагональ делит параллелограмм на два равных треугольника. Используем результат, полученный в первом примере:
Sпараллелограмма=2⋅SΔ=2⋅330=660(см2).
Площадь трапеции
Трапеция имеет одну пару параллельных сторон, следовательно, имеет одну высоту — перпендикуляр, проведённый между параллельными сторонами.
Чаще всего высоту трапеции проводят из вершин или через точку пересечения диагоналей.
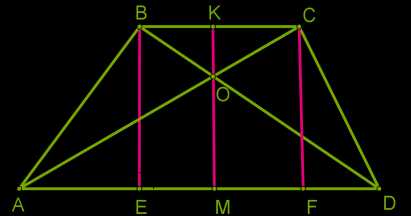
Площадь трапеции определим как сумму площадей треугольников, на которые трапецию делит диагональ.
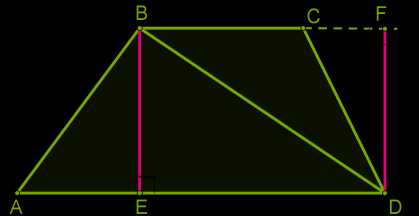
SABCD=SABD+SDBC;SABCD=AD⋅BE2+BC⋅DF2=AD⋅BE2+BC⋅BE2==AD+BC⋅BE2.
Если обозначить параллельные стороны (основания) трапеции через \(a\) и \(b\), высоту через \(h\), то:
Sтрап=a+b2⋅h.
Обрати внимание!
Важные следствия:
1. если высоты треугольников равны, то их площади относятся как длины оснований.
2. Если основания треугольников равны, то их площади относятся как длины высот.
3. Если высоты треугольников равны и их основания равны, то они равновелики, например, медиана делит треугольник на две равновеликие части.
www.yaklass.ru
Площадь параллелограмма
Площадь параллелограмма равна произведению его основания (a) на высоту (h)
Что такое параллелограмм? Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
1. Площадь параллелограмма вычисляется по формуле:
\[ \LARGE S = a \cdot h_{a}\]
где:a – сторона параллелограмма,ha – высота, проведенная к этой стороне.
2. Если известны длины двух смежных сторон параллелограмма и угол между ними, то площадь параллелограмма вычисляется по формуле:
\[ \LARGE S = a \cdot b \cdot sin(\alpha) \]
3. Если заданы диагонали параллелограмма и известен угол между ними, то площадь параллелограмма вычисляется по формуле:
\[ \LARGE S = \frac{1}{2} \cdot d_{1} \cdot d_{2} \cdot sin(\alpha) \]
Свойства параллелограмма
В параллелограмме противоположные стороны равны: \( AB = CD \), \( BC = AD \)
В параллелограмме противоположные углы равны: \( \angle A = \angle C \), \( \angle B = \angle D \)
Диагонали параллелограмма в точке пересечения делятся пополам \( AO = OC \), \( BO = OD \)
Диагональ параллелограмма делит его на два равных треугольника.
Сумма углов параллелограмма, прилежащих к одной стороне равна 180 o:
\( \angle A + \angle B = 180^{o} \), \( \angle B + \angle C = 180^{o}\)
\( \angle C + \angle D = 180^{o} \), \( \angle D + \angle A = 180^{o}\)
Диагонали и стороны параллелограмма связаны следующим соотношением:
\( d_{1}^{2} + d_{2}^2 = 2a^{2} + 2b^{2} \)
В параллелограмме угол между высотами равен его острому углу: \( \angle K B H =\angle A \).
Биссектрисы углов, прилежащих к одной стороне параллелограмма, взаимно перпендикулярны.
Биссектрисы двух противоположных углов параллелограмма параллельны.
Признаки параллелограмма
Четырехугольник будет параллелограммом, если:
\( AB = CD \) и \( AB || CD \)
\( AB = CD \) и \( BC = AD \)
\( AO = OC \) и \( BO = OD \)
\( \angle A = \angle C \) и \( \angle B = \angle D \)
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
Поделитесь с другими:
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
calcsbox.com
Вычисление площади параллелограмма
В геометрии параллелограммом называется геометрическая фигура, представляющая собой четырехугольник, имеющий стороны, расположенные попарно параллельно. Квадрат, прямоугольник и ромб являются частными случаями параллелограмма. Тому, как найти площадь параллелограмма, учат в средней школе, причем эту величину можно определить тремя различными способами в зависимости от того, какие именно параметры фигуры известны.
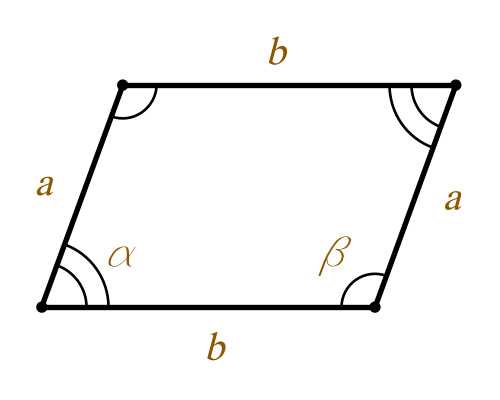
Нахождение площади параллелограмма
S = ab × sinα = ab × sinβ
a, b – стороны параллелограмма
α, β – углы параллелограмма
S – площадь параллелограмма
В повседневной жизни с параллелограммами мы сталкиваемся достаточно часто, а что касается определения площади фигуры, то этой работой нередко занимаются инженеры-конструкторы, разрабатывающие всевозможные машины и механизмы, а также архитекторы и даже строители. К примеру, в некоторых домах, построенных по индивидуальным проектам, можно увидеть окна, имеющие форму параллелограмма. Выглядят они достаточно оригинально, а их разработка и изготовление стоит несколько дороже, чем обычных. Архитекторы, создающие такие конструкции, производят расчет площади параллелограмма для того, чтобы эти окна пропускали в помещение достаточное количество света.
Зачастую параллелограммы можно увидеть, что называется, под ногами. Речь идет о тротуарной плитке, которая сейчас широко используется вместо асфальтового покрытия и имеет соответствующую форму. Для того чтобы точно узнать количество единиц этого материала, необходимого, для покрытия заранее определенной поверхности, нужно узнать площадь параллелограмма формула которой, как известно, достаточно проста и незатейлива.
В технике существует такое понятие, как « параллелограмм Уатта », который представляет собой относительно несложный механизм, с помощью которого происходит преобразование возвратно-поступательного движения во вращательное движение. Эти конструкции достаточно широко применяются в паровых машинах, а также подвесках легковых автомобилей.
В процессе ремонта транспорта и для поднятия различных тяжелых предметов часто используются такие агрегаты, как домкраты. Некоторые из них, в качестве рабочих частей, оснащаются штангами, соединенными между собой в форме параллелограмма и образующими подвижные шарниры. За счет этого они могут легко изменять свою высоту, что и обеспечивает, в итоге, поднятие и опускание тяжестей. Поэтому же принципу устроены и широко распространенные складские подъемные платформы, при помощи которых в логистических комплексах производится перемещение грузов на верхние полки стеллажей.
Форму параллелограмма имеют и такие устройства, как токосъемники, которыми оснащаются железнодорожные локомотивы, работающие на электрической тяге, а также почти все типы современных городских трамваев. Эти устройства также представляют собой подвижные шарниры, способные изменять свою высоту благодаря тем свойствам, которыми обладают параллелограммы.
Ячейки практически всех раздвижных решеток, которые часто устанавливаются на окнах первых этажей зданий, также имеют форму параллелограммов. Соединения элементов, из которых состоят эти конструкции, являются подвижными шарнирами. Наконец, подвижные штанги настольных ламп, которые можно увидеть в любом офисе, представляют собой параллелограммы.
simple-math.ru
