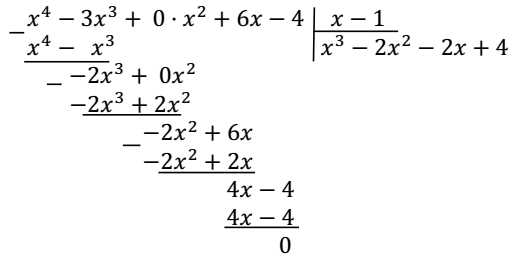Деление полиномов – Деление полиномов

Деление полиномов

Введение

Общий вид одночлена

f(x)=axⁿ, где:

—a — коэффициент, который может принадлежать любому из множеств N, Z, Q, R, C

—x — переменная

—n показатель степени, который принадлежит множеству N

Два одночлена подобны, если они имеют одну и ту же переменную и одинаковый показатель степени.

Примеры: 3x² и -5x²; ½x⁴ и 2√3x⁴

Сумма одночленов, не подобных друг другу, называется многочленом (или полиномом). В этом случае одночлены являются слагаемыми полинома. Полином, содержащий два слагаемых, называется биномом (или двучленом).
Пример: p(x)=3x²-5; h(x)=5x-1
Полином, содержащий три слагаемых, называется трехчленом.

Общий вид многочлена с одной переменной
p(x)=a_nxⁿ+a_n-1x^n-1+…+a₁x¹

+a₀
где:

• a_n,a_n-1,a_n-2,…,a₁,a₀ — коэффициенты полинома. Они могут быть натуральными, целыми, рациональными, действительными или комплексными числами.
• a_n — коэффициент при слагаемом с наибольшим показателем степени (ведущий коэффициент)
• a₀ — коэффициент при слагаемом с наименьшим показателем степени (свободный член, или константа)
• n — степень полинома

Пример 1
p(x)=5x³-2x²+7x-1

• полином третьей степени с коэффициентами 5, -2, 7 и -1
• 5 — ведущий коэффициент
• -1 — свободный член
• x — переменная

Пример 2
h(x)=-2√3x⁴+½x-4

• полином четвертой степени с коэффициентами -2√3,½ и -4
• -2√3 — ведущий коэффициент
• -4
  — свободный член
• x — переменная

Деление полиномов

p(x) и q(x) — два полинома:
p(x)=a_nxⁿ+a_n-1x^n-1+…+a₁x¹ +a₀
q(x)=a_px^p+a_p-1x^p-1+…+a₁x¹ +a₀

Чтобы найти частное и остаток от деления p(x) на q(x), нужно использовать следующий алгоритм:

1. Степень p(x) должна быть больше либо равной степени q(x).
2. Мы должны записать оба полинома в порядке понижения степени. Если в p(x) нет члена с какой-либо степенью, его надо дописать с коэффициентом 0.
3. Ведущий член p(x) делится на ведущий член q(x), и результат записывается под разделительной линией (в знаменателе).
4. Умножаем полученный результат на все члены q(x) и записываем результат с противоположными знаками под членами p(x) с соответствующими степенями.
5. Складываем почленно слагаемые с одинаковыми степенями.
6. К результату приписываем оставшиеся члены p(x).
7. Делим ведущий член полученного полинома на первый член полинома q(x) и повторяем шаги 3-6.
8. Эта процедура повторяется до тех пор, пока вновь полученный полином не будет иметь меньшую степень, чем q(x). Этот полином будет являться остатком от деления.
9. Полином, записанный под разделительной линией, является результатом деления (частным).

Пример 1
Шаг 1 и 2) $p(x)=x^5-3x^4+2x^3+7x^2-3x+5 \\ q(x)=x^2-x+1$

3)    x⁵-3x⁴+2x³+7x²-3x+5

4)    x⁵-3x⁴+2x³+7x²-3x+5

      -x⁵+x⁴-x³

5)    x⁵-3x⁴+2x³+7x²-3x+5

      -x⁵+x⁴-x³

       /  -2x⁴-x³

6)    x⁵-3x⁴+2x³+7x²-3x+5

      -x⁵+x⁴-x³

       /  -2x⁴-x³+7x²-3x+5

7)    x⁵-3x⁴+2x³+7x²-3x+5

      -x

www.math10.com

Деление многочленов «столбиком» («уголком»).

Начнём с некоторых определений. Многочленом n-й степени (или n-го порядка) будем именовать выражение вида $P_n(x)=\sum\limits_{i=0}^{n}a_{i}x^{n-i}=a_{0}x^{n}+a_{1}x^{n-1}+a_{2}x^{n-2}+\ldots+a_{n-1}x+a_n$. Например, выражение $4x^{14}+87x^2+4x-11$ есть многочлен, степень которого равна $14$. Его можно обозначить так: $P_{14}(x)=4x^{14}+87x^2+4x-11$.

Коэффициент $a_0$ называют старшим коэффициентом многочлена $P_n(x)$. Например, для многочлена $4x^{14}+87x^2+4x-11$ старший коэффициент равен $4$ (число перед $x^{14}$). Число $a_n$ называют свободным членом многочлена $P_n(x)$. Например, для $4x^{14}+87x^2+4x-11$ свободный член равен $(-11)$. Теперь обратимся к теореме, на которой, собственно говоря, и будет основано изложение материала на данной странице.

Для любых двух многочленов $P_n(x)$ и $G_m(x)$ можно найти такие многочлены $Q_p(x)$ и $R_k(x)$, что будет выполнено равенство

\begin{equation} P_n(x)=G_m(x)\cdot Q_p(x)+R_k(x) \end{equation}

причём $k < m$.

Словосочетание «разделить многочлен $P_n(x)$ на многочлен $G_m(x)$» означает «представить многочлен $P_n(x)$ в форме (1)». Будем называть многочлен $P_n(x)$ – делимым, многочлен $G_m(x)$ – делителем, многочлен $Q_p(x)$ – частным от деления $P_n(x)$ на $G_m(x)$, а многочлен $R_k(x)$ – остачей от деления $P_n(x)$ на $G_m(x)$. Например, для многочленов $P_6(x)=12x^6+3x^5+16x^4+6x^3+8x^2+2x+1$ и $G_4(x)=3x^4+4x^2+2$ можно получить такое равенство:

$$ 12x^6+3x^5+16x^4+6x^3+8x^2+2x+1=(3x^4+4x^2+2)(4x^2+x)+2x^3+1 $$

Здесь многочлен $P_6(x)$ является делимым, многочлен $G_4(x)$ – делителем, многочлен $Q_2(x)=4x^2+x$ – частным от деления $P_6(x)$ на $G_4(x)$, а многочлен $R_3(x)=2x^3+1$ – остатком от деления $P_6(x)$ на $G_4(x)$. Замечу, что степень остатка (т.е. 3) меньше степени делителя, (т.е. 4), посему условие равенства (1) соблюдено.

Если $R_k(x)\equiv 0$, то говорят, что многочлен $P_n(x)$ делится на многочлен $G_m(x)$ без остатка. Например, многочлен $21x^6+6x^5+105x^2+30x$ делится на многочлен $3x^4+15$ без остатка, так как выполнено равенство:

$$ 21x^6+6x^5+105x^2+30x=(3x^4+15)\cdot(7x^2+2x) $$

Здесь многочлен $P_6(x)=21x^6+6x^5+105x^2+30x$ является делимым; многочлен $G_4(x)=3x^4+15$ – делителем; а многочлен $Q_2(x)=7x^2+2x$ – частным от деления $P_6(x)$ на $G_4(x)$. Остаток равен нулю.

Чтобы разделить многочлен на многочлен часто применяют деление «столбиком» или, как его ещё называют, «уголком». Реализацию этого метода разберём на примерах.

Перед тем, как перейти к примерам, я введу ещё один термин. Он не является общепринятым, и использовать его мы будем исключительно для удобства изложения материала. До конца этой страницы будем называть старшим элементом многочлена $P_n(x)$ выражение $a_{0}x^{n}$. Например, для многочлена $4x^{14}+87x^2+4x-11$ старшим элементом будет $4x^{14}$.

Пример №1

Разделить $10x^5+3x^4-12x^3+25x^2-2x+5$ на $5x^2-x+2$, используя деление «столбиком».

Решение

Итак, мы имеем два многочлена, $P_5(x)=10x^5+3x^4-12x^3+25x^2-2x+5$ и $G_2(x)=5x^2-x+2$. Степень первого равна $5$, а степень второго равна $2$. Многочлен $P_5(x)$ – делимое, а многочлен $G_2(x)$ – делитель. Наша задача состоит в нахождении частного и остатка. Поставленную задачу будем решать пошагово. Будем использовать ту же запись, что и для деления чисел:

Первый шаг

Разделим старший элемент многочлена $P_5(x)$ (т.е. $10x^5$) на старший элемент многочлена $Q_2(x)$ (т.е. $5x^2$):

$$ \frac{10x^5}{5x^2}=2x^{5-2}=2x^3. $$

Полученное выражение $2x^3$ – это первый элемент частного:

Умножим многочлен $5x^2-x+2$ на $2x^3$, получив при этом:

$$ 2x^3\cdot (5x^2-x+2)=10x^5-2x^4+4x^3 $$

Запишем полученный результат:

Теперь вычтем из многочлена $10x^5+3x^4-12x^3+25x^2-2x+5$ многочлен $10x^5-2x^4+4x^3$:

$$ 10x^5+3x^4-12x^3+25x^2-2x+5-(10x^5-2x^4+4x^3)=5x^4-16x^3+25x^2-2x+5 $$

Этот многочлен допишем уже под чертой:

На этом первый шаг заканчивается. Тот результат, что мы получили, можно записать в развёрнутой форме:

$$ 10x^5+3x^4-12x^3+25x^2-2x+5=(5x^2-x+2)\cdot 2x^3+5x^4-16x^3+25x^2-2x+5 $$

Так как степень многочлена $5x^4-16x^3+25x^2-2x+5$ (т.е. 4) больше степени многочлена $5x^2-x+2$ (т.е. 2), то процесс деления надобно продолжить. Перейдём ко второму шагу.

Второй шаг

Теперь уже будем работать с многочленами $5x^4-16x^3+25x^2-2x+5$ и $5x^2-x+2$. Точно так же, как и на первом шаге, разделим старший элемент первого многочлена (т.е. $5x^4$) на старший элемент второго многочлена (т.е. $5x^2$):

$$ \frac{5x^4}{5x^2}=x^{4-2}=x^2. $$

Полученное выражение $x^2$ – это второй элемент частного. Прибавим к частному $x^2$

Умножим многочлен $5x^2-x+2$ на $x^2$, получив при этом:

$$ x^2\cdot (5x^2-x+2)=5x^4-x^3+2x^2 $$

Запишем полученный результат:

Теперь вычтем из многочлена $5x^4-16x^3+25x^2-2x+5$ многочлен $5x^4-x^3+2x^2$:

$$ 5x^4-16x^3+25x^2-2x+5-(5x^4-x^3+2x^2)=-15x^3+23x^2-2x+5 $$

Этот многочлен допишем уже под чертой:

На этом второй шаг заканчивается. Полученный результат можно записать в развёрнутой форме:

$$ 10x^5+3x^4-12x^3+25x^2-2x+5=(5x^2-x+2)\cdot (2x^3+x^2)-15x^3+23x^2-2x+5 $$

Так как степень многочлена $-15x^3+23x^2-2x+5$ (т.е. 3) больше степени многочлена $5x^2-x+2$ (т.е. 2), то продолжаем процесс деления. Перейдём к третьему шагу.

Третий шаг

Теперь уже будем работать с многочленами $-15x^3+23x^2-2x+5$ и $5x^2-x+2$. Точно так же, как и на предыдущих шагах, разделим старший элемент первого многочлена (т.е. $-15x^3$) на старший элемент второго многочлена (т.е. $5x^2$):

$$ \frac{-15x^3}{5x^2}=-3x^{2-1}=-3x^1=-3x. $$

Полученное выражение $(-3x)$ – это третий элемент частного. Допишем к частному $-3x$

Умножим многочлен $5x^2-x+2$ на $(-3x)$, получив при этом:

$$ -3x\cdot (5x^2-x+2)=-15x^3+3x^2-6x $$

Запишем полученный результат:

Теперь вычтем из многочлена $-15x^3+23x^2-2x+5$ многочлен $-15x^3+3x^2-6x$:

$$ -15x^3+23x^2-2x+5-(-15x^3+3x^2-6x)=20x^2+4x+5 $$

Этот многочлен допишем уже под чертой:

На этом третий шаг заканчивается. Полученный результат можно записать в развёрнутой форме:

$$ 10x^5+3x^4-12x^3+25x^2-2x+5=(5x^2-x+2)\cdot (2x^3+x^2-3x)+20x^2+4x+5 $$

Так как степень многочлена $20x^2+4x+5$ (т.е. 2) равна степени многочлена $5x^2-x+2$ (т.е. 2), то продолжаем процесс деления. Перейдём к четвёртому шагу.

Четвёртый шаг

Теперь уже будем работать с многочленами $20x^2+4x+5$ и $5x^2-x+2$. Точно так же, как и на предыдущих шагах, разделим старший элемент первого многочлена (т.е. $20x^2$) на старший элемент второго многочлена (т.е. $5x^2$):

$$ \frac{20x^2}{5x^2}=4x^{2-2}=4x^0=4. $$

Полученное число $4$ – это четвёртый элемент частного. Допишем к частному $4$

Умножим многочлен $5x^2-x+2$ на $4$, получив при этом:

$$ 4\cdot (5x^2-x+2)=20x^2-4x+8 $$

Запишем полученный результат:

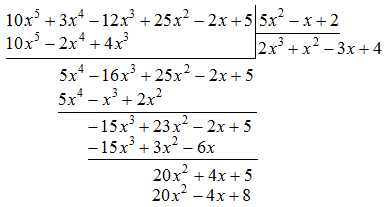
Теперь вычтем из многочлена $20x^2+4x+5$ многочлен $20x^2-4x+8$:

$$ 20x^2+4x+5-(20x^2-4x+8)=8x-3 $$

Этот многочлен допишем уже под чертой:

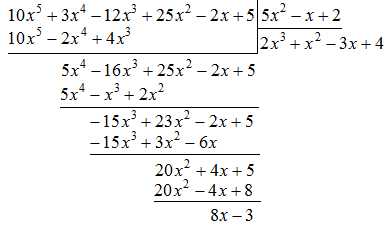
На этом четвёртый шаг заканчивается. Полученный результат можно записать в развёрнутой форме:

$$ 10x^5+3x^4-12x^3+25x^2-2x+5=(5x^2-x+2)\cdot (2x^3+x^2-3x+4)+8x-3 $$

Так как степень многочлена $8x-3$ (т.е. 1) меньше степени многочлена $5x^2-x+2$ (т.е. 2), то процесс деления завершён. Частным от деления многочлена $P_6(x)$ на многочлен $G_2(x)$ есть многочлен $Q_3(x)=2x^3+x^2-3x+4$. Остаток от деления $P_6(x)$ на $G_2(x)$ – это многочлен $R_1(x)=8x-3$. По сути, мы представили исходный многочлен $P_6(x)$ в форме (1):

$$ P_6(x)=G_2(x)\cdot Q_3(x)+R_1(x) $$

Ответ: частное от деления – многочлен $2x^3+x^2-3x+4$, остаток – многочлен $8x-3$.

Пример №2

Разделить $4x^3+2x-11$ на $x+5$, используя деление «столбиком».

Решение

Здесь можно использовать схему Горнера (и это было бы несколько менее громоздко). Однако для сугубо демонстрационных целей используем деление «столбиком». Подробные пояснения есть в примере №1, посему здесь укажем только ход решения.

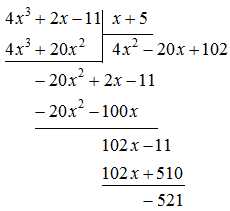
Результат можно записать в такой форме:

$$ 4x^3+2x-11=(x+5)\cdot(4x^2-20x+102)-521 $$

Следовательно, частным от деления $4x^3+2x-11$ на $x+5$ является многочлен $4x^2-20x+102$, а остаток есть число $(-521)$ (по сути, это многочлен нулевого порядка).

Ответ: частное – многочлен $4x^2-20x+102$, остаток – число $-521$.

Пример №3

Разделить $7x^3+9x^2-5x+9$ на $5x^7+10x^6-17x^2+14x-7$.

Решение

Степень делителя (т.е. многочлена $5x^7+10x^6-17x^2+14x-7$) равна $7$. Степень делимого (многочлена $7x^3+9x^2-5x+9$) равна 3. В этом ситуации, когда степень делителя больше степени делимого ($7 > 3$) разложение вида (1) возможно лишь в такой форме:

$$ 7x^3+9x^2-5x+9=0\cdot(5x^7+10x^6-17x^2+14x-7)+7x^3+9x^2-5x+9 $$

Ответ: частное есть 0, остаток – многочлен $7x^3+9x^2-5x+9$.

math1.ru

Деление многочленов «уголком»

Сегодня учимся делить многочлены “уголком”, так, как это делают с обычными числами. Рассмотрим несколько примеров подробно. Например, разделим многочлен на двучлен  (Здесь деление можно произвести без остатка. Этот вопрос – можно или нельзя поделить данный многочлен на предлагаемый двучлен обсуждается в статье “Схема Горнера”). Итак, за работу!

Выписываем наш многочлен и рядом, “на полочке” – двучлен, на который будем делить – все как с числами:

 

Теперь сравниваем старшую степень многочлена и старшую степень делителя, и определяем, во сколько раз первая больше второй (по сути, делим на ):

Результат деления записываем под полочку – это первый “кусочек” ответа:

Теперь нам предстоит умножить полученный одночлен  на двучлен , который стоит на полочке (на наш делитель). Умножаем почленно, сначала на первое слагаемое:

А теперь на второе:

Результаты умножения пишем, как показано, под соответствующие степени делимого многочлена – кубы под кубы, квадраты – под квадраты и т. п.  Теперь производим вычитание:

И сносим вниз следующий одночлен ():

Переходим на новый уровень и продолжаем в том же духе. Опять сравниваем старшие степени и результат деления на  записываем под полочку, получилось (не забудем про минус!):

И опять умножаем полученный одночлен () на оба слагаемых делителя. Сначала на первое слагаемое:

Теперь на второе:

 

И снова вычитаем, и к полученному результату сносим вниз новый одночлен, который собираемся подвергнуть казни операции деления:

 

И вот мы опять на новом уровне! Но… здесь все надо начинать сызнова. Сравниваем старшие степени, делим старшую степень делимого на старшую степень делителя, результат пишем под полку:

 

Умножаем почленно, сначала  на , потом  на :

 

Вычитаем, сносим последнее слагаемое, сравниваем старшие степени, производим деление  на , результат (-15) – пишем под полку.

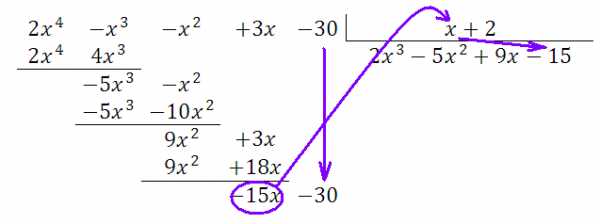
Ну, чем кончилось данное приключение, понятно:

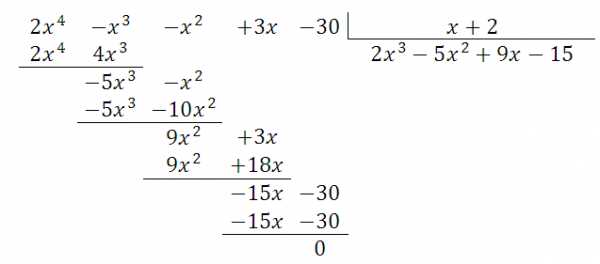
Деление закончилось без остатка – то есть исходный многочлен поделился на  нацело. Ответ: . Заметим, что исходный многочлен был четвертой степени, деление производили на двучлен первой степени – получили в ответе многочлен третьей степени.

Попробуем еще раз?

Разделим многочлен на .

Выполняем те же шаги: сравниваем старшие степени делимого и делителя. Производим деление:

Полученное частное записываем под полочку. Умножаем его почленно на слагаемые делителя: на , затем на  , и наконец на  :

 

Выполняем вычитание, “спускаем” вниз очередное слагаемое делимого. После этого все начинаем сначала: сравниваем старшие члены делимого и делителя…:

 

Дальше – можно уже без комментариев:

 

И наконец:

 

Ответ: . Заметим, что исходный многочлен был третьей степени, деление производили на квадратный трехчлен – получили в ответе двучлен первой степени. Вообще степень делимого многочлена понижается всегда на степень делителя.

Пример 3:

 

 

Во всех примерах получалось разделить многочлен на многочлен без остатка, однако так бывает не всегда. Вот, например, случай, когда остаток от деления ненулевой:

 

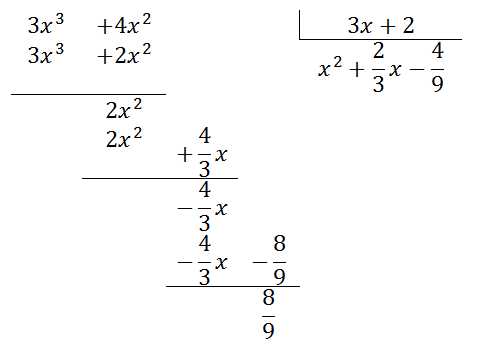
Деление необходимо продолжать, пока степень делимого не станет равной, а лучше – меньшей, чем у делителя.

Задача:

при делении многочлена на двучлен  образовался остаток 42. Найти результат деления.

Решение: рассмотрим случай, когда остается остаток от деления. Если  разделить на  и при этом остается остаток N, то это можно записать так: . Тогда V можно найти так: . Определим ту часть многочлена, которая полностью делится на  (без остатка):

 

Теперь произведем деление:

Ответ:  .

Еще задача:

при делении многочлена на двучлен  образовался остаток . Найти результат деления.

Решение:  V можно найти так: . Определим ту часть многочлена, которая полностью делится на  (без остатка):

 

Теперь можно делить:

 

Ответ:  .

Достоинства способа: делить можно что угодно на что угодно, лишь бы степень делимого не была меньше, чем степень делителя. Делить можно на двучлен, на трехчлен и т.д. Делить можно даже в том случае, если остается остаток.

easy-physic.ru

Деление многочлена на многочлен «уголком»

В этой статье рассмотрим один из способов разложения на множители многочленов высших степеней. С его помощью вы сможете решать уравнения и неравенства вида:

\(x^3+6x^2+11x+6=0\)
\(x^3-2x-4=0\)
\(x^3+2x^2-5x-6<0\)
\(x^4-3x^3+6x-4≥0\)

Пошаговый алгоритм разложения на множители с помощью деления «уголком»:

0) Запишите многочлен в стандартном виде, то есть так, чтоб степени одночленов стояли по убыванию.

Пример:
\(6x^2+6+x^3+11x\) записываем как \(x^3+6x^2+11x+6\)

1) Подбором найдите один из корней многочлена.

Для этого вместо \(x\) подставьте по очереди числа: \(±1,±2,±3,±4,±5\) и т.д. Число, которое сделает многочлен нулем и будет его корнем.

Пример:
\(x^3+6x^2+11x+6\)
Подставим \(1\). Имеем: \(1^3+6 \cdot 1^2+11\cdot 1+6=24\) — не равно нулю. Ищем дальше.
Подставим \(-1\). Получим: \((-1)^3+6\cdot (-1)^2+11\cdot (-1)+6=-1+6-11+6=0\) – значит \(-1\) корень нашего многочлена.

Матхак! Пробуйте сначала числа, на которые свободный член делиться нацело. В данном случае свободный член \(6\), поэтому в первую очередь нужно пробовать числа: \(±1,±2,±3\) и \(±6\).

2) Поделите исходный многочлен на \(x-x_0\), где \(x_0\) – найденный корень. Процесс деления многочлена на многочлен сильно похож на обычное деление в столбик — поэтому и называется деление «уголком».

       а) Запишите многочлены как числа при делении столбиком:

       б) Подберите такой одночлен, чтобы при умножении его на \(x\), получалось первое слагаемое исходного многочлена, то есть в нашем случае \(x^3\). Очевидно, что таким одночленом будет \(x^2\).

        в) Умножьте этот одночлен на делитель и запишите результат под исходным многочленом. Таким образом, мы умножаем \(x^2\) на \(x+1\) и получаем \(x^3+x^2\).

        г) Теперь точно так же, как в случае деления натуральных чисел, поставьте знак минус, проведите горизонтальную черту и сделайте вычитание.

        д) Повторите шаги б) – г) только уже с новым многочленом:
                — подберите такой одночлен, чтобы при умножении на \(x\) первое слагаемое было таким же, как в новом многочлене: в нашем примере этим одночленом будет \(5x\).
              — умножьте этот одночлен на делитель: умножив \(5x\) на \(x+1\) получим \(5x^2+5x\).
              — вычтите получившиеся многочлены:

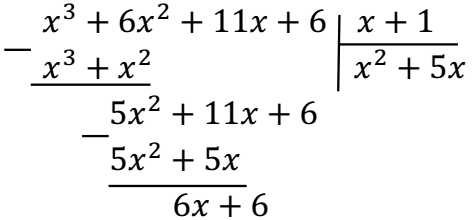
        е) И вновь повторяем шаги б) – г) до тех пор, пока после вычитания не останется ноль.

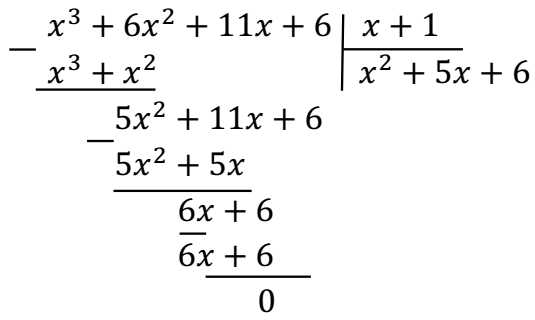
3) Запишите новый вид многочлена, представив его как произведение делителя и частного.
\(x^3+6x^2+11x+6=(x+1)(x^2+5x+6)\)

Матхак! Если есть сомнения в правильности разложения, можно проверить его раскрытием скобок – в результате должен получиться исходный многочлен.
Проверим наш случай: \((x+1)(x^2+5x+6)=x^3+5x^2+6x+x^2+5x+6=x^3+6x^2+11x+6\).
Получен исходный многочлен, значит, поделили правильно.

Матхак! Если в результате деления у вас в остатке получился не ноль, значит, скорее всего, в решении есть ошибка.

Давайте теперь решим пример с применением изученного материала.

Пример: Решите неравенство \(x^4-3x^3+6x-4≥0\).

Решение:

\(x^4-3x^3+6x-4≥0\)	Найдем один из корней многочлена слева. Проверим \(1\).
\(1: 1^4-3·1^3+6·1-4=0\)	Поделим многочлен \(x^4-3x^3+6x-4\) на \((x-1)\) уголком. Однако замечаем, что у нас нет слагаемого с квадратом. Чтоб нам было удобнее решать, запишем вместо него выражение \(0·x^2\) (ведь его значение равно нулю, а значит оно ничего не меняет в исходном многочлене).
	Запишем новый вид нашего неравенства.
\((x-1)(x^3-2x^2-2x+4)≥0\)	С первой скобкой все хорошо, а вот вторую надо бы разложить еще. Так как высшая степень в ней — куб, то мы можем попробовать разложить методом группировки, что проще чем деление в столбик. У первых двух слагаемых вынесем за скобку \(x^2\), а у третьего и четвертого – минус двойку.
\((x-1)(x^2 (x-2)-2(x-2))≥0\)	Теперь выносим общую скобку \((x-2)\) за скобку.
\((x-1)(x-2)(x^2-2)≥0\)	Но и это еще не все, потому что \(x^2-2\) можно разложить с помощью формулы сокращенного умножения «разность квадратов»: \(a^2-b^2=(a-b)(a+b)\).
\((x-1)(x-2)(x-\sqrt{2})(x+\sqrt{2})≥0\)	Вот сейчас все готово для применения метода интервалов.
	Запишем ответ.

Ответ: \((-∞;-\sqrt{2}]∪[1;\sqrt{2}]∪[2;∞)\).

Скачать статью

cos-cos.ru

Деление многочлена на многочлен | Математика

Пусть требуется

(2x³ – 7x² + x + 1) ÷ (2x – 1).

Здесь дано произведение (2x³ – 7x² + x + 1) и один множитель (2x – 1), – надо найти другой множитель. В данном примере сразу ясно (но вообще этого установить нельзя), что и другой, искомый, множитель, или частное, есть многочлен. Это ясно потому, что данное произведение имеет 4 члена, а данный множитель лишь 2. Однако, сказать заранее, сколько членов у искомого множителя – нельзя: может быть 2 члена, 3 члена и т. д. Вспоминая, что старший член произведения всегда получается от умножения старшего члена одного множителя на старший член другого (см. умножение многочлена на многочлен) и что членов, подобных этому, быть не может, мы уверены, что 2x³ (старший член данного произведения) получится от умножения 2x (старший член данного множителя) на неизвестный старший член искомого множителя. Чтобы найти последний, придется, следовательно, разделить 2x³ на 2x – получим x². Это и есть старший член частного.

Вспомним затем, что при умножении многочлена на многочлен приходится каждый член одного многочлена умножать на каждый член другого. Поэтому данное произведение (2x³ – 7x² + x + 1) представляет собою произведение делителя (2x – 1) на все члены частного. Но мы можем теперь найти произведение делителя на первый (старший) член частного, т. е. (2x – 1) ∙ x²; получим 2x³ – x². Зная произведение делителя на все члены частного (оно = 2x³ – 7x² + x + 1) и зная произведение делителя на 1-ый член частного (оно = 2x³ – x²), вычитанием мы можем найти произведение делителя на все остальные, кроме 1-го, члены частного. Получим

(2x³ – 7x² + x + 1) – (2x³ – x²) = 2x³ – 7x² + x + 1 – 2x³ + x² = –6x² + x + 1.

Старший член (–6x²) этого оставшегося произведения должен представлять собою произведение старшего члена делителя (2x) на старший член остального (кроме 1-го члена) частного. Отсюда найдем старший член остального частного. Надо –6x² ÷ 2x, получим –3x. Это и есть второй член искомого частного. Мы можем опять найти произведение делителя (2x – 1) на второй, только что найденный, член частного, т. е. на –3x.

Получим (2x – 1) ∙ (–3x) = –6x² + 3x. Из всего данного произведения мы уже вычли произведение делителя на 1-ый член частного и получили остаток –6x² + x + 1, представляющий собою произведение делителя на остальные, кроме 1-го, члены частного. Вычитая из него только что найденное произведение –6x² + 3x, получим остаток, представляющий собою произведение делителя на все остальные, кроме 1-го и 2-го, члены частного:

–6x² + x + 1 – (–6x² + 3x) = –6x² + x + 1 + 6x² – 3x = –2x + 1.

Разделив старший член этого оставшегося произведения (–2x) на старший член делителя (2x), получим старший член остального частного, или его третий член, (–2x) ÷ 2x = –1, – это и есть 3-й член частного.

Умножив на него делителя, получим

(2x – 1) ∙ (–1) = –2x + 1.

Вычтя это произведение делителя на 3-й член частного из всего оставшегося до сих пор произведения, т. е.

(–2x + 1) – (–2x + 1) = –2x + 1 + 2x – 1 = 0,

мы увидим, что в нашем примере произведение делится на остальные, кроме 1-го, 2-го и 3-го, члены частного = 0, откуда заключаем, что у частного больше членов нет, т. е.

(2x³ – 7x² + x + 1) ÷ (2x – 1) = x² – 3x – 1.

Из предыдущего мы видим: 1) удобно располагать члены делимого и делителя по нисходящим степеням, 2) необходимо установить какой-либо порядок для выполнения вычислений. Таким удобным порядком можно считать тот, который употребляется в арифметике при делении многозначных чисел. Следуя ему, все предыдущие вычисления расположим так (сбоку даны еще краткие пояснения):

Те вычитания, какие здесь нужны, выполняются переменою знаков у членов вычитаемого, причем эти переменные знаки пишутся сверху.

Так, написано

Это значит: вычитаемое было 2x³ – x², а после перемены знаков получили –2x³ + x².

Благодаря принятому расположению вычислений, благодаря тому, что члены делимого и делителя расположены по нисходящим степеням и благодаря тому, что степени буквы x в обоих многочленах идут, понижаясь всякий раз на 1, оказалось, что подобные члены приходятся написанными друг под другом (напр.: –7x² и +x²), почему легко выполнить их приведение. Можно подметить, что не все члены делимого нужны во всякий момент вычисления. Напр., член +1 не нужен в тот момент, где был найден 2-й член частного, и эту часть вычислений можно упростить.

Еще примеры:

1. (2a⁴ – 3ab³ – b⁴ – 3a²b²) ÷ (b² + a² + ab).

Расположим по нисходящим степеням буквы a и делимое и делитель:

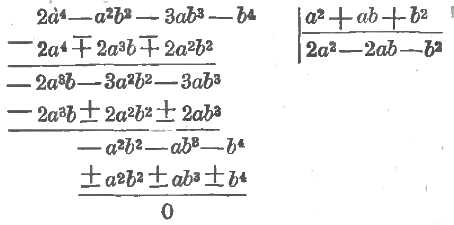
(Заметим, что здесь, благодаря отсутствию в делимом члена с a³, в первом вычитании оказалось, что подписаны друг под другом не подобные члены –a

2b² и –2a³b. Конечно, они не могут быть приведены в один член и написаны под чертою оба по старшинству).

В обоих примерах надо внимательнее относиться к подобным членам: 1) друг под другом часто оказываются написанными не подобные члены и 2) иногда (как, напр., в последнем примере, члены –4aⁿ и –aⁿ при первом вычитании) подобные члены выходят написанными не друг под другом.

Возможно выполнять деление многочленов в ином порядке, а именно: всякий раз разыскивать младший член или всего или остающегося частного. Удобно в этом случае располагать данные многочлены по восходящим степеням какой-либо буквы. Напр.:

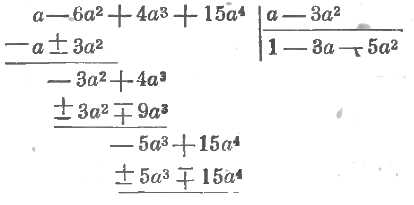
maths-public.ru

Деление многочленов уголком

1 октября 2013

Сегодня мы узнаем, как выполняется деление многочленов друг на друга, причем выполнять деление мы будем уголком по аналогии с обычными числами. Это очень полезный прием, который, к сожалению, не изучают в большинстве школ. Поэтому внимательно прослушайте данный видеоурок. Ничего сложного в таком делении нет.

Для начала давайте разделим друг на друга два числа:

\[595:17=35\]

Как можно это сделать? В первую очередь, мы отсекаем столько разрядов, чтобы полученное числовое значение было больше чем то, на которое мы делим. Если мы отсечем один разряд, то получим пять. Очевидно, семнадцать в пять не вмещается, поэтому этого недостаточно. Берем два разряда — у нас выйдет 59 — оно уже больше, чем семнадцать, поэтому мы можем выполнить операцию. Итак, сколько раз семнадцать помещается в 59? Давайте возьмем три. Перемножаем и записываем результат под 59. Итого у нас получилось 51. Вычитаем и у нас вышло «восемь». Теперь сносим следующий разряд — пять. Делим 85 на семнадцать. Берем пять. Перемножим семнадцать на пять и получаем 85. Вычитаем и у нас получается ноль.

Решаем реальные примеры

Задача № 1

Теперь выполним те же самые шаги, но не с числами, а с многочленами. Для примера возьмем такое:

\[\frac{{{x}^{2}}+8x+15}{x+5}=x+3\]

Обратите внимание, если при делении чисел друг на друга мы подразумевали, что делимое всегда больше делителя, то в случае деления полиномов уголком, необходимо, чтобы степень делимого была больше, чем делителя. В нашем случае все в порядке — мы работаем с конструкциями второй и первой степени.

Итак, первый шаг: сравниваем первые элементы. Вопрос: на что нужно домножить $x$, чтобы получилось ${{x}^{2}}$? Очевидно, что на еще один $x$. Умножаем $x+5$ на только что найденное число $x$. У нас есть ${{x}^{2}}+5$, которое вычитаем из делимого. Остается $3x$. Теперь сносим следующее слагаемое — пятнадцать. Снова посмотрим на первые элементы: $3x$ и $x$. На что следует домножить $x$, чтобы вышло$3x$? Очевидно, что на три. Домножаем почленно $x+5$ на три. Когда мы вычтем, то получим ноль.

Как видите, вся операция деления уголком свелась к сравнению старших коэффициентов при делимом и делителе. Это даже проще, чем когда вы делите числа. Тут не требуется выделять какое-то количество разрядов — мы просто на каждом шаге сравниваем старшие элементы. Вот и весь алгоритм.

Задача № 2

Давайте попробуем еще:

\[\frac{{{x}^{2}}+x-2}{x-1}=x+2\]

Первый шаг: посмотрим на старшие коэффициенты. На сколько нужно домножить $x$, чтобы записать${{x}^{2}}$? Домножаем почленно. Обратите внимание, при вычитании у нас получится именно $2x$, потому что

\[x-\left( -x \right)=x+x=2x\]

Сносим -2 и снова сравним первый полученный коэффициент со старшим элементом делителя. Итого у нас вышел «красивый» ответ.

Переходим ко второму примеру:

\[\frac{{{x}^{3}}+2{{x}^{2}}-9x-18}{x+3}={{x}^{2}}-x-6\]

В этот раз в качестве делимого выступает полином третьей степени. Сравним между собой первые элементы. Для того чтобы получилось ${{x}^{3}}$, необходимо $x$ домножить на ${{x}^{2}}$. После вычитания сносим $9x$. Домножаем делитель на $-x$ и вычитаем. В итоге наше выражение полностью разделилось. Записываем ответ.

Задача № 3

Переходим к последней задаче:

\[\frac{{{x}^{3}}+3{{x}^{2}}+50}{x+5}={{x}^{2}}-2x+10\]

Сравниваем ${{x}^{3}}$ и $x$. Очевидно, нужно домножить на ${{x}^{2}}$. В итоге мы видим, что мы получили очень «красивый» ответ. Записываем его.

Вот и весь алгоритм. Ключевых моментов здесь два:

1. Всегда сравнивайте первую степень делимого и делителя — повторяем это на каждом шаге;
2. Если в исходном выражении пропущены какие-либо степени, при делении уголком их обязательно следует добавить, но с нулевыми коэффициентами, иначе ответ будет неправильным.

Больше никаких премудростей и хитростей в таком делении нет.

Краткое содержание

Материал сегодняшнего урока нигде и никогда не встречается в «чистом» виде. Его редко изучают в школах. Однако умение делить многочлены друг на друга очень поможет вам при решении уравнений высших степеней, а также всевозможных задач «повышенной трудности». Без данного приема вам придется раскладывать многочлены на множители, подбирать коэффициенты — и результат при этом отнюдь не гарантирован. Однако многочлены можно делить и уголком — так же, как и обычные числа! К сожалению, данный прием не изучают в школах. Многие учителя считают, что деление многочленов уголком — это что-то безумно сложное, из области высшей математики. Спешу вас заверить: это не так. Более того, делить многочлены даже проще, чем обычные числа! Посмотрите урок — и убедитесь в этом сами.:) В общем, обязательно возьмите этот прием на вооружение. Умение делить многочлены друг на друга очень пригодится вам при решении уравнений высших степеней и в других нестандартных задачах.

Я надеюсь, этот ролик поможет тем, кто работает с полиномами, особенно высших степеней. Это относится и к старшеклассникам, и к студентам университетов. А у меня на этом все. До встречи!     

Смотрите также:

1. Теорема Безу: разложение на множители
2. Что такое схема Горнера
3. Тест к уроку «Площади многоугольников на координатной сетке» (легкий)
4. Задача 7 — геометрический смысл производной
5. Как решать задачи B15 без производных
6. Симметрия корней и оптимизация ответов в тригонометрии

www.berdov.com

Онлайн калькулятор: Синтетическое деление полиномов

Синтетическое деление это простой способ евклидова деления полиномов с небольшим количеством записей и вычислений. Калькулятор ниже выполняет деление полиномов этим методом. Описание метода можно найти сразу под калькулятором.

Введите коэффициенты многочлена, который надо разделить, через пробел.

Введите коэффициенты многочлена-делителя через пробел.

Точность вычисления

Знаков после запятой: 2

Схема синтетического деления

 

Сохранить share extension

Подготовка к синтетическому делению

Будем рассматривать подготовку к делению на примере: 3x⁴+5x³+2x+4 / x²+2x+1.

	Шаги подготовки
	1) Взять коэффициенты делителя с обратным знаком. 2) Записать коэффициенты делимого в верхней строке. Если коэффициента нет — записываем ноль. 3) Отбросим коэффициент делителя самой большой степени 4) Запишем коэффициенты делителя диагонально слева. Свободный член в самом верху

Синтетическое деление для монических делителеф

Изначально метод был разработан для делителей, являющихся моническими полиномами (коэффициент старшего члена = 1). Рассмотрим деление на примере: 3x⁴+5x³+2x+4 / x²+2x+1.

	Алгоритм деления для монического делителя
	1) Опустим старший коэффициент делимого в строку результата 2) Умножим диагональ с коэффициентами делителя на крайний левый коэффициент из строки результатов 3) Поместим результат умножения диагонально справа от последнего столбца с результатами 4) Выполним сложение значений в следующем столбце и результат занесем в строку результата 5) Будем повторять шаги 2-4 до тех пор пока будет куда заносить результат умножения. (Последний столбец — столбец со свободным членом делимого.) 6) Просуммируем значения всех оставшихся столбцов и впишем результат в строку результата 7) Отделим частное и остаток. Количество членов остатка будет равно количеству членов делителя за минусом одного.

Пример 1 (монический делитель)

Не монический делитель

Алгоритм работает так же и для обычных делителей ( не монических полиномов).
Рассмотрим на примере: 3x³+5x²+7x+2 / 3x²-x-2.

	Алгоритм для не монического делителя
	1) Опустим старший коэффициент делимого в строку остатка (предпоследняя строка). 2) Поделим последний коэффициент в строке остатка на старший коэффициент делителя, результат запишем в строку результата (последняя строка) 3) Умножим диагональ с коэффициентами делителя на крайний левый коэффициент из строки результатов 4) Поместим результат умножения диагонально справа от последнего столбца с результатами 5) Выполним сложение значений в следующем столбце и результат занесем в строку остатка 6) Повторим шаги 2-5 тех пор пока будет куда заносить результат умножения. (Последний столбец — столбец со свободным членом делимого.) 6) Просуммируем значения всех оставшихся столбцов и впишем результат в строку остатка 7) Отделим частное и остаток. Коэффициенты частного будут в последнем столбце. Коэффициенты остатка — в предпоследнем. Количество членов остатка будет равно количеству членов делителя за минусом одного.

Пример 2 (не монический делитель)

planetcalc.ru