Угол / Начальные геометрические сведения / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Начальные геометрические сведения
- Угол
Угол — геометрическая фигура
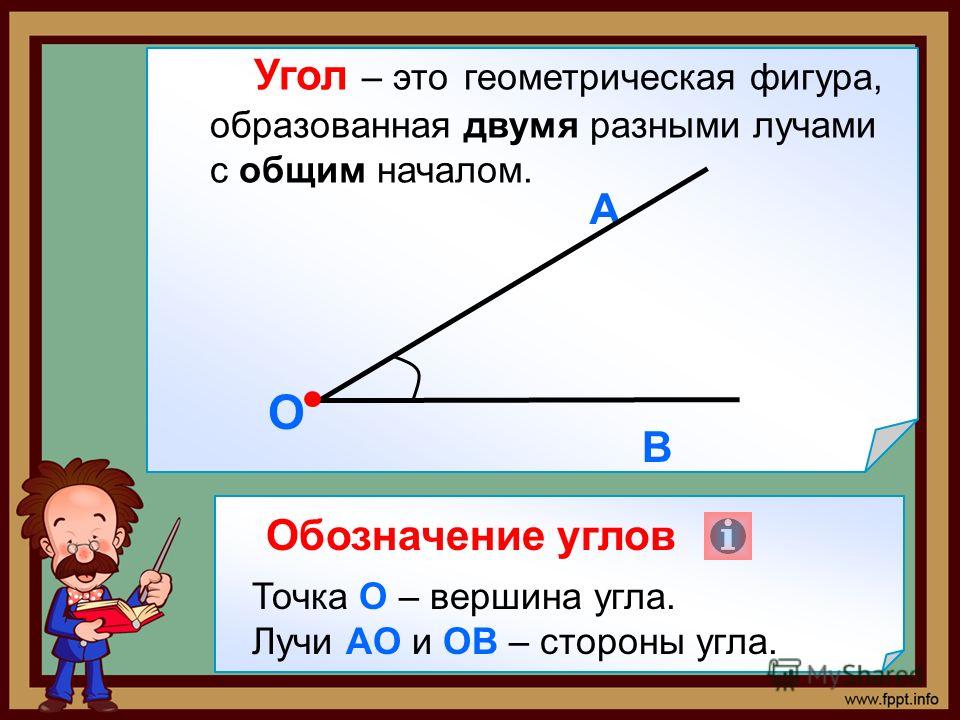
Мы знаем, что углом называется геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
Лучи — это стороны угла, а точка (их общее начало) — вершина угла
Изображать угол можно и так (не отмечаем точкой общее начало, считаем, что точка есть)
Обозначения угла
1)
На сторонах угла не отмечены точки (только обозначены большими латинскими буквами А и В)
Считается, что буква А обозначает любую точку на верхней стороне угла (по данному рисунку)
Точка В обозначает любую точку на нижней стороне угла (по данному рисунку)
Читаем: угол АОВ
Пишем: АОВ
2)
На сторонах угла отмечены и обозначены произвольные точки А и В
Читаем: угол АОВ
Пишем: АОВ
3)
Стороны угла (лучи) обозначены малыми латинскими буквами k и m
Читаем: угол km
Пишем: km
4)
Обозначена только вершина угла
Читаем: угол О
Пишем: О
Развернутый угол
Построим прямую АВ и отметим на этой прямой точку О
Лучи ОА и ОВ лежат на одной прямой (являются дополнительными)
Угол АОВ называется развернутым
Угол на плоскости
Изобразим часть плоскости
(так как плоскость бесконечна, мы не можем изобразить ее всю, только часть ее)
Построим на этой плоскости неразвернутый угол
Этот угол делит плоскость на две части (области) — внешнюю и внутреннюю
Замечание
Любой угол разделяет плоскость на две части. Названия этих частей ( внутренняя область и внешняя область) применяется для неразвернутого угла.
Названия этих частей ( внутренняя область и внешняя область) применяется для неразвернутого угла.
Если угол развёрнутый, то любую из двух частей, на которые он разделяет плоскость, можно считать внутренней областью угла.
Расположение точек относительно угла
По рисунку определим положение отмеченных точек A, B, C, D, K, M
Точки А и В лежат на сторонах угла
Точки D и C лежат вне угла (во внешней области угла)
Точки К и М, лежат внутри угла (во внутренней области угла)
При необходимости мы можем продолжить стороны угла, например, чтобы уточнить положение точки М
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Точки, прямые, отрезки
Луч
Равенство геометрических фигур
Сравнение отрезков
Сравнение углов
Длина отрезка
Единицы измерения длины, расстояний
Градусная мера угла
Измерение углов на местности
Смежные углы
Вертикальные углы
Перпендикулярные прямые
Построение прямых углов на местности
Начальные геометрические сведения
Правило встречается в следующих упражнениях:
7 класс
Задание 10, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 21, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 84, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 12, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 556, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 15, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 619, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 812, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 14, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1176, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Сравнение углов / Начальные геометрические сведения / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Начальные геометрические сведения
- Сравнение углов
Мы знаем, что геометрические фигуры можно сравнивать методом наложения, а угол — это геометрическая фигура, следовательно, сравнить углы мы можем, наложив один угол на другой.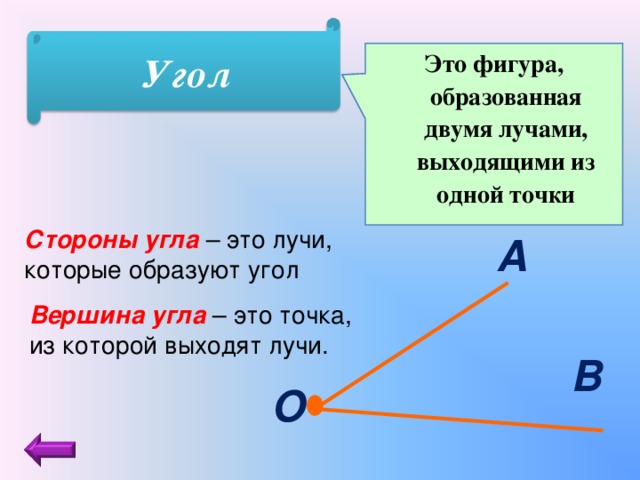
Рассмотрим два неразвёрнутых угла LOK и BAC
Совместим их вершины (точка O и точка A).
Затем повернём BAC так, чтобы сторона AC совпала со стороной OK, при этом стороны OL и AB должны быть по одну сторону от совпавших сторон.
Мы видим, что BAC составляет только часть LOK, следовательно, LOK > BAC.
Если LOB = BOK, то луч OB называется биссектрисой угла.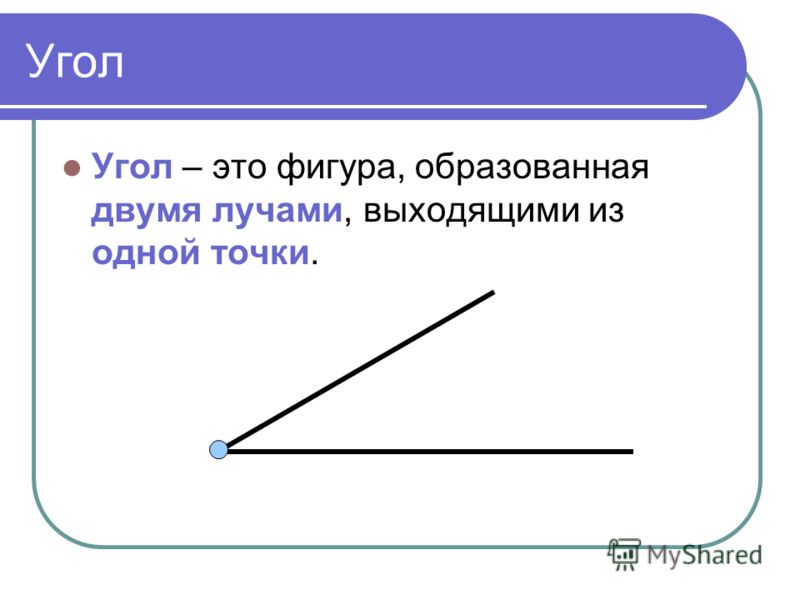
Теперь сравним LOK и TNS.
Совместим их вершины (точка O и точка N).
Затем повернём TNS так, чтобы сторона NS совпала со стороной
Мы видим, что стороны OL и NT также совпали, следовательно, LOK = TNS.
Неразвёрнутый угол всегда составляет часть развёрнутого угла, следовательно, развёрнутый угол больше любого неразвёрнутого угла.
Пример:
DXJ — развёрнутый угол, HXJ, RXJ, HXD, RXD, HXR — неразвёрнутые углы, и все они составляют лишь часть DXJ и все они меньше его.
Очевидно, что любые два развёрнутых угла равны друг другу.
- Угол, который составляет часть другого угла, считается меньшим.
- Если при наложении одного угла на другой, совпадают обе стороны данных углов, то они равны.
- Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.
- Развёрнутый угол больше любого неразвёрнутого угла.
- Любые два развёрнутых угла равны друг другу.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Точки, прямые, отрезки
Провешивание прямой на местности
Луч
Угол
Равенство геометрических фигур
Сравнение отрезков
Длина отрезка
Единицы измерения длины, расстояний
Градусная мера угла
Измерение углов на местности
Смежные углы
Вертикальные углы
Перпендикулярные прямые
Построение прямых углов на местности
Начальные геометрические сведения
Правило встречается в следующих упражнениях:
7 класс
Задание 21, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 132, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 175, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 212, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 425, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 426, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 428, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 433, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 862, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 885, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Angle — определение математического слова
Angle — определение математического слова — Math Open ReferenceОткрытый справочник по математике
Главная Контакт О Тематический указатель
Определение: Фигура, образованная двумя линиями или лучами, расходящимися из общей точки (вершины).
Попробуйте это Отрегулируйте угол ниже, перетащив оранжевую точку.
Атрибуты
| Вершина | Вершина является общей точкой, в которой соединяются две линии или лучи. Точка B на фигуре выше является вершиной угла ∠Азбука. |
| Ноги | Ножки (борта) угла – это две линии, из которых он состоит. На рисунке выше отрезки AB и BC являются катетами угла ∠ABC. |
| Интерьер | Внутренняя часть угла — это пространство в «челюстях» угла, простирающееся до бесконечности. Видеть Интерьер угла |
| Внешний вид | Все пространство в самолете, кроме салона. Видеть Интерьер угла |
Определение угла
Угол можно определить двумя способами.Вот так: ∠ABC
Символ угла, за которым следуют три точки, определяющие угол, при этом средняя буква является вершиной, а две другие — ребрами. Таким образом, на рисунке выше угол будет равен ∠ABC или ∠CBA.
Пока вершина является средней буквой, порядок не важен. Как стенография
мы можем использовать символ «угол». Например, «∠ABC» будет читаться как «угол ABC».
Таким образом, на рисунке выше угол будет равен ∠ABC или ∠CBA.
Пока вершина является средней буквой, порядок не важен. Как стенография
мы можем использовать символ «угол». Например, «∠ABC» будет читаться как «угол ABC».Или вот так: ∠B
Просто по вершине, если это не двусмысленно. Так что на рисунке выше угол также можно было бы назвать просто ‘∠Б’
Мера угла
Величина угла измеряется в градусах (см. Угловые меры). Когда мы говорим «угол ABC», мы имеем в виду фактический угол объекта. Если мы хотим говорить о величине или мере угла в градусах, мы должны сказать «мера угла ABC» — часто пишут m∠ABC.Типы уголков
Всего существует шесть типов углов, перечисленных ниже. Щелкните изображение, чтобы просмотреть полное описание этого типа и соответствующий интерактивный апплет.| Острый угол Менее 90° | Прямой угол Ровно 90° | Тупой угол Между 90° и 180° |
| Угол прямой Ровно 180° | Угол рефлекса Между 180° и 360° | Полный угол Точно 360° |
Тригонометрия
При использовании в тригонометрии
углы обладают некоторыми дополнительными свойствами:
Они могут иметь размер более 360°, могут быть положительными и отрицательными и расположены на координатной сетке с осями x и y.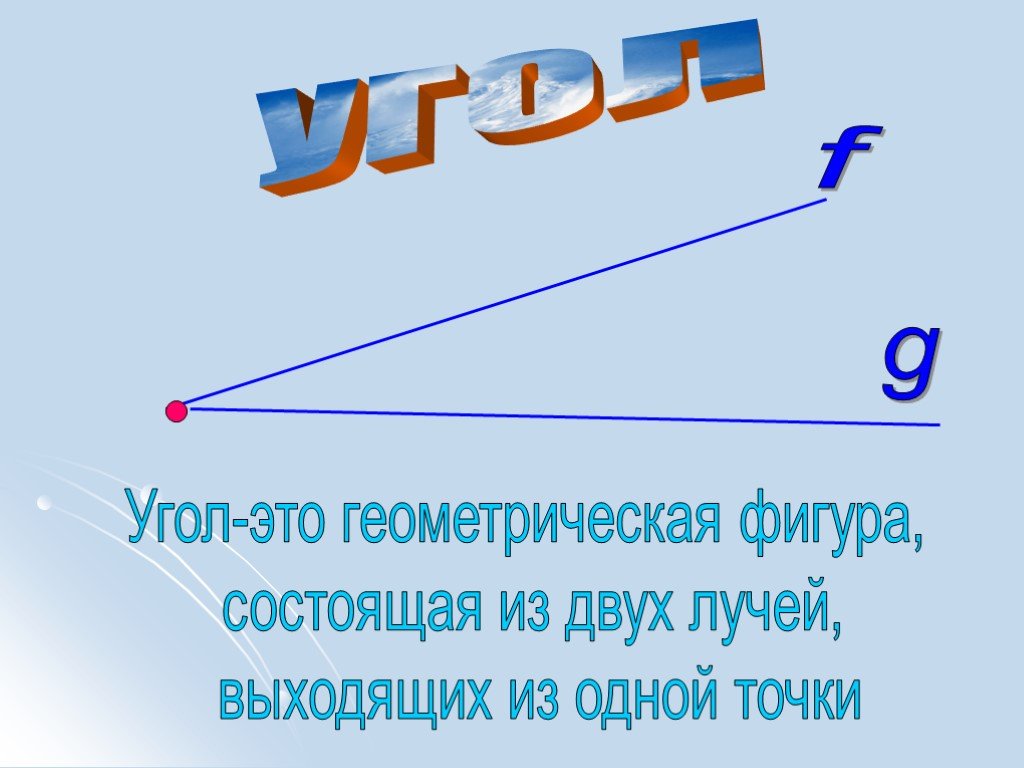 Обычно они измеряются в радианах, а не в
градусов.
Подробнее об этом см. в разделе Определение и свойства угла (тригонометрия).
Обычно они измеряются в радианах, а не в
градусов.
Подробнее об этом см. в разделе Определение и свойства угла (тригонометрия).
Угловая конструкция
В разделе «Конструкции» представлены анимированные демонстрации различных конструкции углов, используя только циркуль и линейку.- Копирование угла
- Построение угла 30°
- Построение угла 45°
- Построение угла 60°
- Построение угла 90° (перпендикулярного, прямого угла) при:
- конец отрезка
- точка на отрезке
- через точку не на отрезке
- середина отрезка
Другие ракурсы
Общий
- Определение угла
- градусов
- Радиан
- Биссектриса угла
- Угол наклона
- Внутренняя часть угла
- Угол в комплекте
Угловые типы
- Острый угол
- Прямой угол
- Тупые углы
- Прямой уголок
- Угол рефлекса
- Полный угол
Соотношение углов
- Вертикальные уголки
- Дополнительные уголки
- Дополнительные уголки
- Линейная пара
- Смежные углы
- Соответствующие углы
- Альтернативные внутренние углы
- Альтернативные внешние углы
- Внутренние углы поперечной
- Наружные углы поперечной
(C) 2011 Copyright Math Open Reference.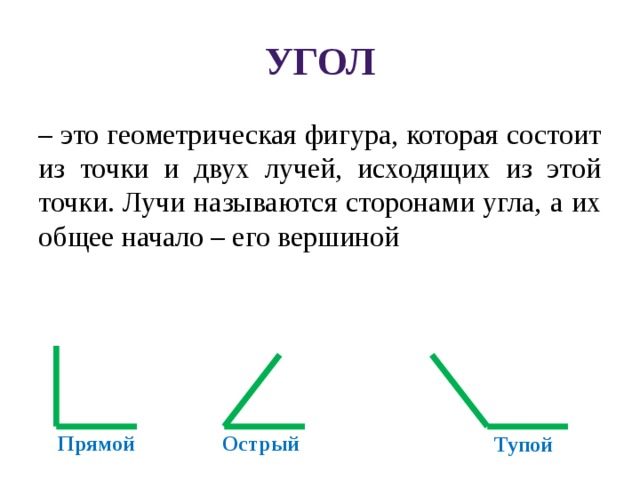
Все права защищены
Блог фактов об углах формы для детей от PlanBee
Делиться:25 февраля 2022 г. Кэтрин Линч
Если вы хотите узнать больше об углах формы, вы находитесь в правильном месте! Прочтите информацию ниже, загрузите бесплатное руководство по углам формы, бесплатный постер с математическими углами и прочтите наш блог о 2D-формах, чтобы получить дополнительную информацию о 2D-фигурах.
Словарь важных углов
Угол — это размер поворота между двумя сторонами в вершине. Углы измеряются в градусов с помощью транспортира.
Острый угол — это угол, который больше 90º, но меньше 180º.
Прямой угол равен 90º. Прямые углы образуются, когда пересекаются две прямые, перпендикулярные друг другу на 90 199 и 90 200. Например, у квадрата четыре прямых угла.
Тупой угол — это угол, который больше 90°, но меньше 180°.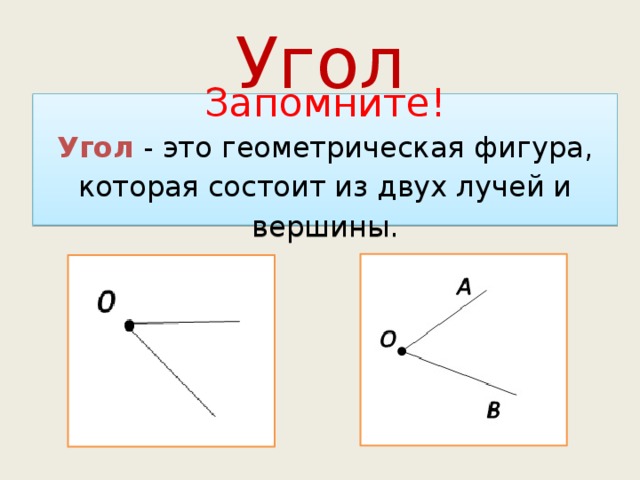
Прямой угол — это угол, равный 180º. Прямой угол – это точка на прямой.
Угол рефлекса — это угол, который больше 180º, но меньше 360º.
Полный угол — это угол, равный 360º. Это полный оборот вокруг точки.
Внутренние углы — это углы внутри линий фигуры.
Внешние углы — это углы вне линий формы.
Плакаты углов 2D формы
Уголы в полигонах
Углы внешних углов у Полигона Всегда равны 360º
. Внутренние углы треугольников Всегда равны 180º
Внутренние углы Кабирки АВАЛЬНЫЕ
Внутренние углы 9019 Образ.
Внутренние углы пятиугольника всегда равны 540º
Внутренние углы гексагона Hexagon Всегда равны 720º
Внутренние углы Гептагона Всегда равны 900º
Внутренние углы Octagon Всегда равны 1080 °
. polygons
Суммарный размер внутренних углов фигуры можно вычислить по формуле (n — 2) x 180 , где n равно количеству сторон.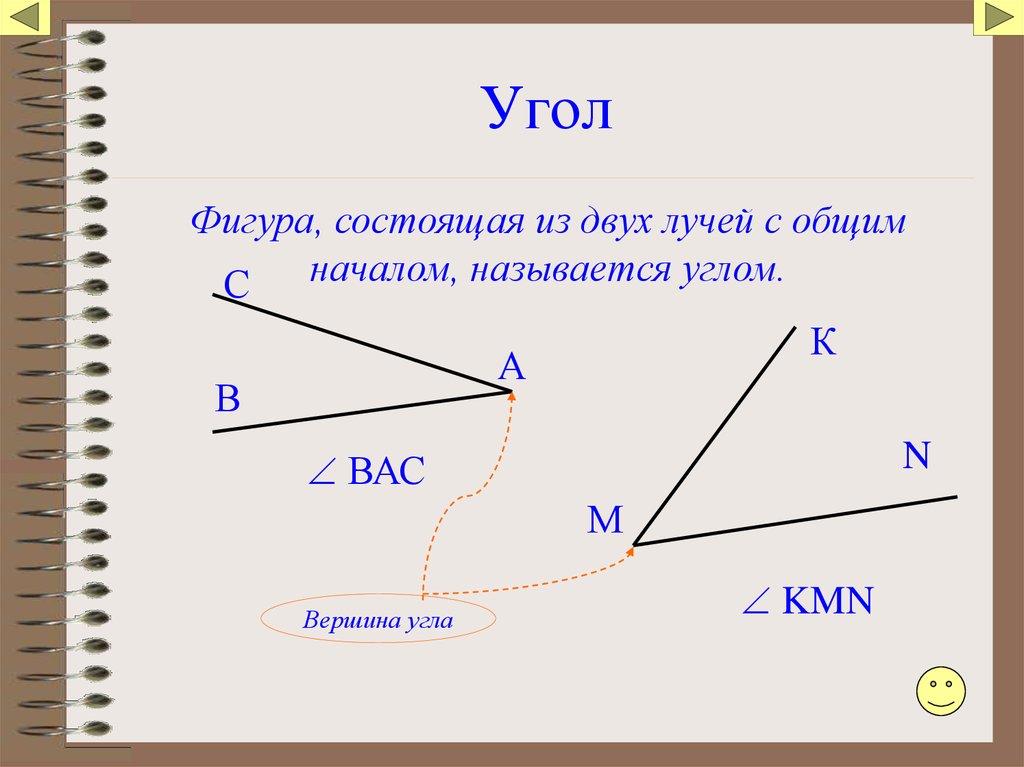
A Square имеет 4 стороны, SO N = 4
( N — 2) x 180
= (4 — 2) x 180
= 2 x 180
= 360 °
= 2 x 180= 360 °
= 2 x 180= 360 3
= 2 x 180
= 360 3
= 2 x 180
= 360 3
= 2 x 180
= 360 3
= 2 x 180
= 360 3
9A Hexagon имеет 6 сторон, SO N = 6
( N — 2) x 180
= (6 — 2) x 180
= 4 x 180
= 720 3
A
= 4 x 180= 720 3
A
9 = 4 x 180= 7203
A
= 4 x 180= 720 000
A
имеет 9 сторон, поэтому n = 9( n — 2) x 180
= (9 — 2) х 180
= 7 х 180
= 1260º
Когда углы преподаются в национальной учебной программе по математике?
Углы преподаются как часть геометрии в учебной программе по математике. Эти нити представляют собой геометрию — положение и направление и геометрию — свойства форм .
Эти нити представляют собой геометрию — положение и направление и геометрию — свойства форм .
Углы впервые изучаются во втором классе, когда дети:
- используют математический словарь для описания положения, направления и движения, в том числе движения по прямой линии и различают вращение как поворот и прямой угол как четверть, Половина и три четверти оборота (по часовой стрелке и против часовой стрелки).
В 3 классе детей учат:
- распознавать углы как свойство формы или описание поворота
- определять прямые углы, признавать, что два прямых угла составляют пол-оборота, три — три четверти оборота и четыре — полный оборот; определить, больше или меньше углы, чем прямой угол
- определяют горизонтальные и вертикальные линии и пары перпендикулярных и параллельных линий.
Все эти цели преподаются в нашей готовой к обучению схеме работы «Формы и углы».
В 4 классе дети учатся:
- определять острые и тупые углы, сравнивать и упорядочивать углы до двух прямых по величине
Эта цель описана в нашей загружаемой схеме работы Shape Angles.
В 5 классе дети учатся:
- знать, что углы измеряются в градусах: оценивать и сравнивать острые, тупые и рефлекторные углы
- начертите заданные углы и измерьте их в градусах (º)
- определить:
- углы в точке и один полный оборот (всего 360)º)
- углов в точке на прямой и поворот (всего 180º)
- другие кратные 90º
- использовать свойства прямоугольников для вывода связанных фактов и нахождения недостающих длин и углов
- различать правильные и неправильные многоугольники на основе рассуждений о равенстве сторон и углов.
В 6-м классе детей учат:
- рисовать двумерные фигуры, используя заданные размеры и углы
- распознавать, описывать и строить простые трехмерные фигуры, включая создание сетей
- сравнивать и классифицировать геометрические фигуры на основе их свойств и размеров и находить неизвестные углы в любых треугольниках, четырехугольниках и правильных многоугольниках
- изображать и называть части кругов, включая радиус, диаметр и длину окружности, и знать, что диаметр в два раза больше радиуса
- распознает углы, где они сходятся в одной точке, лежат на прямой или противоположны по вертикали, и находит отсутствующие углы.

Подано в: увлекательные факты, математика
Делиться: Предыдущая статья Что такое симметрия? Следующая статья 2-D формыПохожие сообщения
Ваш простой путеводитель по международному месяцу школьных библиотек
Международный месячник школьных библиотек — это возможность рассказать вашим ученикам все о школьной библиотеке. Этот удобный блок
Подробнее
Факты о Дивали для детей и учителей
Этот блог фактов Дивали полон интересной информации о Дивали, фестивале огней.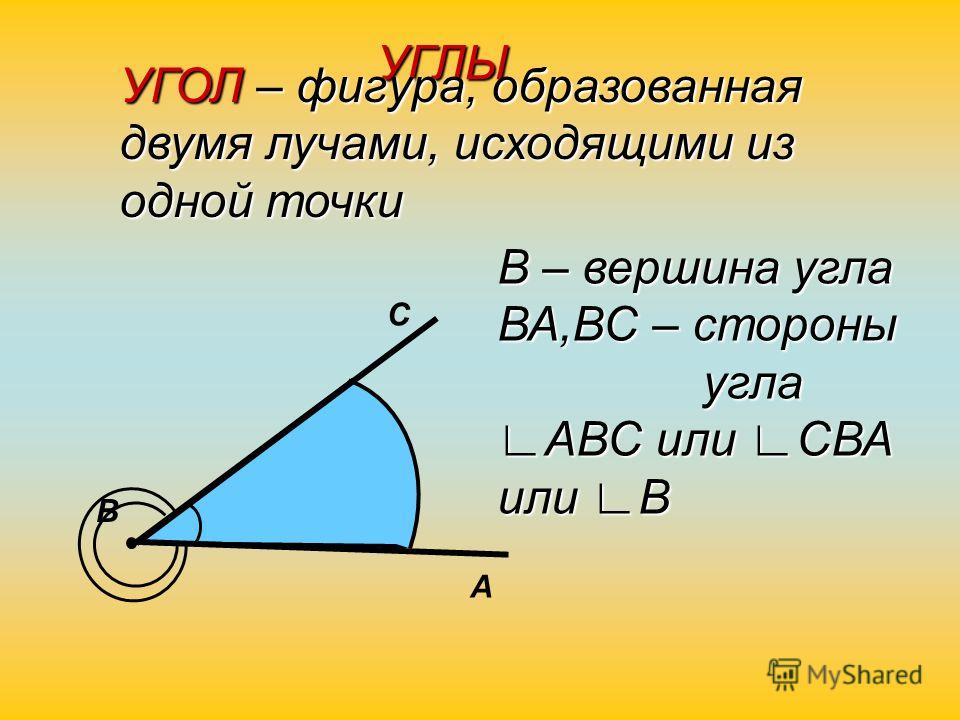

 Таким образом, на рисунке выше угол будет равен ∠ABC или ∠CBA.
Пока вершина является средней буквой, порядок не важен. Как стенография
мы можем использовать символ «угол». Например, «∠ABC» будет читаться как «угол ABC».
Таким образом, на рисунке выше угол будет равен ∠ABC или ∠CBA.
Пока вершина является средней буквой, порядок не важен. Как стенография
мы можем использовать символ «угол». Например, «∠ABC» будет читаться как «угол ABC».