Площадь круга
Площадь круга, формулы для вычисления площади при различных исходных данных и калькулятор для решения онлайн. Площадь круга — это численная характеристика, характеризующая размер плоскости, ограниченной линией окружности. Вычислить площадь круга можно с помощью числа Пи и радиуса окружности, или с помощью других известных исходных данных.
Наш калькулятор поможет вам бесплатно в режиме онлайн вычислить площадь круга или проверить уже выполненные вычисления.
1
Площадь круга через радиус
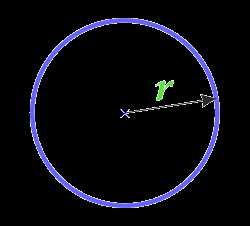
r — радиус
… подготовка …
2
Площадь круга через диаметр
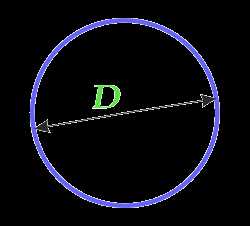
D — диаметр
… подготовка …
3
Площадь круга по длине окружности
— длина окружности
… подготовка …
4
Площадь круга через вписанный в круг квадрат
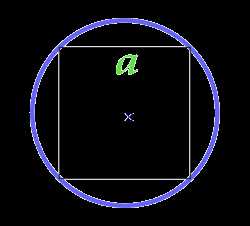
a — сторона
… подготовка …
5
Площадь круга вписанного в квадрат
A — сторона
… подготовка …
6
Площадь круга описанного около произвольного треугольника
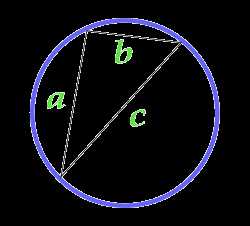
Данная формула применима только, если вокруг треугольника можно описать круг, то есть все три вершины треугольника должны лежать на линии окружности. Треугольник в данном случае может быть любым.
Для вычисления площади круга, предварительно рассчитаем полупериметр треугольника
a — сторона
b — сторона
c — сторона
… подготовка …
7
Площадь круга описанного около равностороннего треугольника
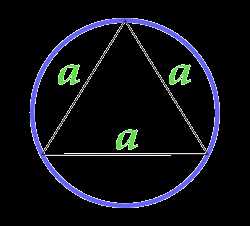
a — сторона
… подготовка …
8
Площадь круга описанного около равностороннего треугольника, вычисляемая по высоте треугольника
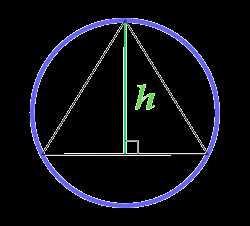
h — высота
… подготовка …
9
Площадь круга описанного около равнобедренного треугольника
a — сторона
b — основание
… подготовка …
10
Площадь круга описанного около прямоугольного треугольника
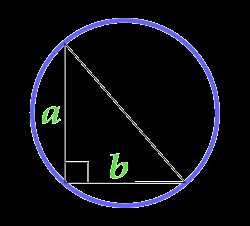
a — сторона
b — сторона
… подготовка …
11
Площадь круга вписанного в равнобедренный треугольник
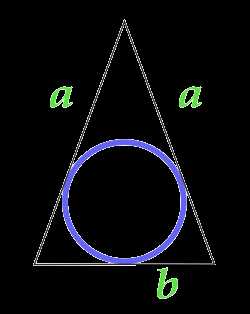
a — сторона
b — основание
… подготовка …
12
Площадь круга вписанного в равнобедренный треугольник, вычисляемая по боковым сторонам треугольника и углу между ними
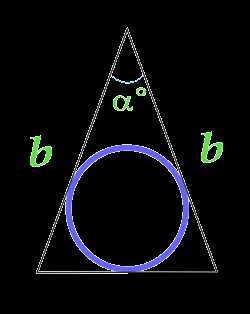
b — сторона
α — угол между сторонами
… подготовка …
13
Площадь круга вписанного в прямоугольный треугольник
a — сторона
b — сторона
c — сторона
… подготовка …
14
Площадь круга вписанного в прямоугольный треугольник, вычисляемая по стороне и углу
b — сторона
α — угол при основании
… подготовка …
15
Площадь круга вписанного в равносторонний треугольник
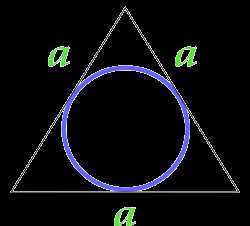
a — сторона
… подготовка …
16
Площадь круга вписанного в равнобедренную трапецию, вычисленная по основанию трапеции и углу при основании
b — сторона
α — угол при основании
… подготовка …
17
Площадь круга описанного около равнобедренной трапеции, рассчитанная по боковым сторонам трапеции, ее диагонали и основанию
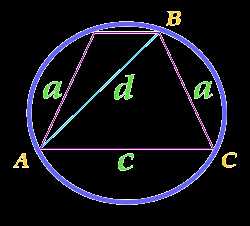
a — сторона
c — сторона
d — диагональ
… подготовка …
18
Площадь круга описанного около прямоугольника
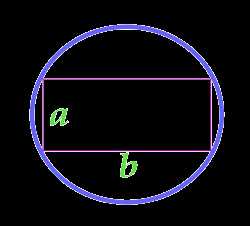
a — сторона
b — сторона
… подготовка …
19
Площадь круга описанного около правильного многоугольника
a — сторона
N — количество сторон многоугольника
… подготовка …
20
Площадь круга описанного около правильного шестиугольника
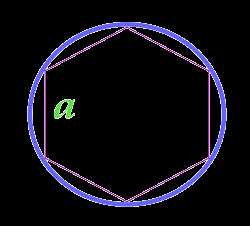
a — сторона
… подготовка …
Определения
Круг – это геометрическая плоская фигура, ограниченная линией состоящей из множества точек равноудаленных от одной точки – центра круга. Кривая замкнутая линия проведенная через равноудаленные точки, образует окружность.
Диаметр круга – это отрезок в виде прямой линии, проходящей через центр окружности и соединяющий две точки лежащие на окружности.
Радиус круга – это прямой отрезок соединяющий центр окружности с любой точкой лежащей на окружности.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см
doza.pro
Площадь круга | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Для того чтобы найти площадь круга, существует единственная формула, которую нужно запомнить – это произведение числа π на квадрат радиуса.
Доказательством этой формулы будет служить следующий расчет. На чертеже внутри и снаружи круга рисуем правильный многоугольник – многоугольник с равными сторонами.
Из центра круга проводим радиусы в указанные вершины многоугольников. Радиусы во вписанном многоугольнике делят его на определенное количество n одинаковых равнобедренных треугольников. Таким образом, площадь вписанного многоугольника – это n площадей треугольников Sв=nS∆. Тогда как площадь каждого треугольника, исходя из его свойств, равна . Так как конгруэнтные стороны a этого треугольника являются радиусами, то формула приобретает вид , а формула площади всего многоугольника – , считая сумму всех сторон nc, как периметр многоугольника P. Аналогично получаем площадь описанного многоугольника: . Если считать, что количество nc, как сторон многоугольника стремится к бесконечности, то его форма максимально приближается к кругу, и периметр становится близок по значению к длине окружности, а cosα стремится к 1. В этом случае обе формулы – и для вписанного, и для описанного многоугольника приобретают следующий вид:
Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр или длину окружности.
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два. Так как в первоначальной формуле S=πr2 радиус возводится во вторую степень, полученная половина диаметра также должна будет быть в квадрате, и это уже будет выглядеть как .
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель: . Подставляя это в основную формулу, не забываем возвести выражение во вторую степень, и получаем, что площадь круга через длину окружности равна .
geleot.ru
Как находить площадь круга
Большое количество точек расположенных на равном расстоянии от центра и находящиеся на одном расстоянии — образуют круг, плоскую фигуру. Радиус круга — это прямая которая соединяет середину круга с любой из точек находящейся в его окружности. При этом в одной окружности, какая бы точка не была, радиус будет одинаков. Диаметр круга — это отрезок исходящий от любой точки окружности, проходящий через середину круга и заканчивающийся в параллельной точке той же окружности.
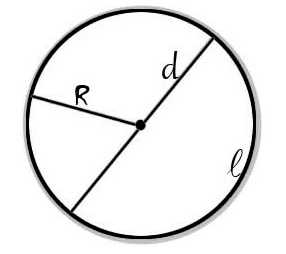
Как находить площадь круга? Площадь круга находится с помощью формулы в которой участвует число ?.
Интересный факт: Числом ? представляется отношение между длиной окружности и длиной диаметра этой же окружности. При этом имеет постоянную величину. А как нам известно ?= 3,1415926 и стало применяться с 1737 года.
Заметка: Ни как не можете определиться, какую машину выбрать? В автосалоне москва автомобили с пробегом (http://center-carauto.ru/), вы сможете в комфортных условиях подобрать наилучший вариант и при этом сэкономить. Согласитесь, заманчивое предложение!
Как рассчитать площадь круга? Как и говорилось выше благодаря формуле, в которой участвует число ? и радиус, записывается так:
S = ?R2
Разберем для наглядности
Найдем площадь круга с помощью его радиуса который равен 4 см.
Площадь круга равна
Решение
S= 3,14 * 42 = 3,14 * 16 = 50,24 кв/см
Так же площадь круга через диаметр находиться по формуле
S = (?/4)d2
Разберем для наглядности
Найдем площадь круга с помощью его диагонали. Возьмем радиус равный 4 см.
Решение
1) Вычислим диаметр, который больше радиуса в два раза.
d=2R
d = 2 * 4 =8
2) Подставляем значения в формулу
S =(3,14/4) * 82 = 0,785 * 64 = 50,24
Если сверить полученный ответ с предыдущим, то они равны.
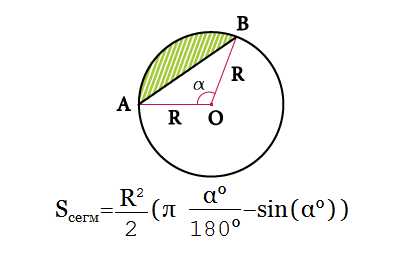
Когда мы ищем площадь сегмента круга или сектора, очень помогает знание основных формул. С их помощью них можно узнавать не известные значения.
Сегментом — называется ограниченная часть круга, которую ограничивают хорда и дуга данного круга.
Как нам уже известно расчет площади круга вычисляется с использованием числа ? умноженного на радиус в квадрате. Используя длину окружности, мы сможем найти радиус.
R = (l/2)?
Если подставить эту формулу в формулу расчета площади., у нас получится:
S = ? ((l/2)?)2 = l2/4?
Разберем для наглядности
Найти площадь круга с окружностью равной 8 см.
Решение
Используем формулу S= 82/4*3,14 = 64 / 12,56 = 5 см
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
Формулы площади окружности и примеры применения
Сделаем рисунок (рис. 1).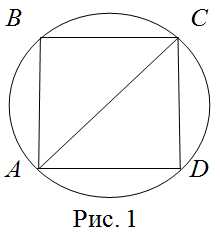
Диагональ вписанного квадрата является диаметром описанной вокруг него окружность. Найдем диагональ . Так как – квадрат, то треугольник прямоугольный. Запишем для него теорему Пифагора, выражая сторону :
Подставляя значения , получим
(см)
Далее для вычисления площади круга, ограниченного заданной окружностью, используем формулу: . Подставляя в неё , получим
(см)
ru.solverbook.com
Как найти площадь полукруга 🚩 Площадь полукруга формула 🚩 Математика
Автор КакПросто!
Необходимость найти площадь полукруга или сектора возникает регулярно при проектировании архитектурных сооружений. Это может понадобиться и при расчете ткани, например, на рыцарский или мушкетерский плащ. В геометрии встречаются самые разные задания на вычисление этого параметра. В условиях может быть предложено определить площадь полкруга, построенного на определенной стороне треугольника или параллелепипеда. В этих случаях необходимы дополнительные вычисления.
Вам понадобится
- — радиус полуокружности;
- — линейка;
- — циркуль;
- — лист бумаги;
- — карандаш;
- — формула площади круга.
Инструкция
Постройте окружность с заданным радиусом. Центр ее обозначьте как О. Чтобы получить полукруг, достаточно провести через эту точку отрезок до пересечения с окружностью. Этот отрезок является диаметром данной окружности и равен двум ее радиусам. Вспомните, что такое окружность и что такое круг. Окружность — это линия, все точки которой удалены от центра на одинаковое расстояние. Круг — часть плоскости, ограниченная этой линией. Вспомните формулу площади круга. Она равна квадрату радиуса, умноженному на постоянный коэффициент π, равный 3,14. То есть площадь круга выражается формулой S=πR2, где S – площадь, а R — радиус окружности. Вычислите площадь полукруга. Она равна половине площади круга, то есть S1= πR2/2. В случае, когда вам в условиях дана только длина окружности, найдите сначала радиус. Длина окружности вычисляется по формуле P=2πR. Соответственно, чтобы найти радиус, необходимо длину окружности разделить на удвоенный коэффициент. Получается формула R=P/2π.Полукруг можно представить и как сектор. Сектором называется часть круга, которая ограничена его двумя радиусами и дугой. Площадь сектора равна площади круга, умноженной на отношение центрального угла к полному углу окружности. То есть, в данном случае она выражается формулой S=π*R2*n°/360°. Угол сектора известен, он составляет 180°. Подставив его значение, вы снова получите ту же самую формулу — S1= πR2/2.
Обратите внимание
Встречаются задания, где угол дуги указан не в градусах, а в радианах. В этом случае необходимо воспользоваться формулой перевода Ar = Ad *π / 180°, где Ar — угол в радианах, а Ad — он же в градусах. Для вычисления площади полукруга это не особенно важно. Даже если вы представляете полукруг как сектор, в конечной формуле никаких градусов нет. Но это может оказаться нужным для вычисления площади сектора, имеющего другой центральный угол.В некоторых задачах требуется найти площадь круга или полукруга, построенного на определенной стороне правильного или неправильного многоугольника. Без дополнительных построений в этом случае не обойтись. Необходимо разделить заданную фигуру на другие, параметры которых вам заданы или вы легко можете их найти. После этого вычислите нужную сторону, которая чаще всего и представляет собой диаметр круга или полукруга.
Источники:
- формула как найти площадь
Эта линия совершенна — говорит нам рассудок, когда мы видим перед собою окружность. Действительно, благодаря ее свойству — все точки ее равноудалены от центра — она кажется такой соразмерной и изящной. Но эта соразмерность таит в себе «подводный камень» — как вычислить ее длину?
Инструкция
Как известно из школьных учебников, окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое ее радиусом. Измерение ее длины, по сравнению с измерением длины отрезка прямой или периметра геометрических фигур, является более сложной операций в связи с тем, что окружность не состоит, в силу определения, из набора отрезков прямой, а является кривой, каждая точка которой равно удалена от центра окружности.Для нахождения длины окружности необходимы две величины — радиус (отрезок прямой, соединяющий центр окружности и точку на окружности) и математическая константа ? (пи), понимаемая как длина окружности с диаметром, равным единице (диаметр — отрезок прямой, соединяющий две точки окружности (хорда) и проходящий через ее центр). Измерение радиуса, если он заранее неизвестен, можно произвести при помощи линейки: максимальное расстояние между двумя точками окружности является ее диаметром. Радиус, в свою очередь — это половина диаметра. Число ? — постоянное, примерно равное 3.1415926535.
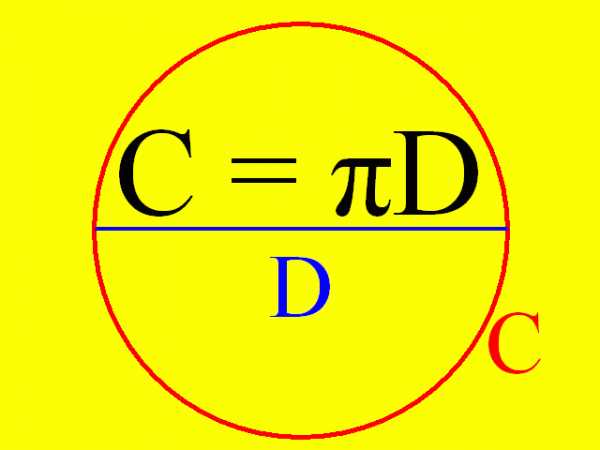
Зная радиус окружности и число ?, можно рассчитать длину окружности, равную произведению указанной константы и радиуса, умноженного на 2 (см. формулу на рис. 1, где C — длина окружности, R — радиус).
Видео по теме
Окружность — это плоская геометрическая фигура, которая представляет собой совокупность точек, которые удалены от центра окружности на равное расстояние, образуя при этом замкнутую фигуру. Посчитать радиус окружности достаточно легко, обладая лишь некоторыми данными.
Вам понадобится
- В зависимости от случая, необходимо знать диаметр окружности, длину окружности, значение числа π («пи»), которое является постоянным: π = 3.14
Инструкция
Пусть в данном случае дана окружность, у которой известна длина окружности (L).Тогда найти радиус окружности можно будет, воспользовавшись формулой:
R = L/2?.
Известно, что длина окружности L = 2?R = ?D, где D — диаметр окружности.
Тогда радиус окружности R можно найти следующим образом:
R = ?D/2? = D/2. Таким образом, можно сделать вывод, что длина радиуса равна половине длине диаметра окружности.
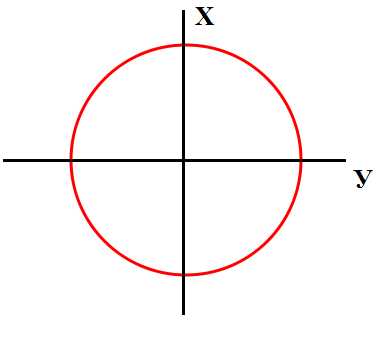
Если дана координатная плоскость, а центр окружности расположен в начале координат, радиус окружности можно посчитать, зная уравнение окружности:
R?=x?+y?
Обратите внимание
Диаметр окружности — это отрезок, проходящий через центр окружности и соединяющий 2 точки окружности между собой.
Окружностью называется место точек плоскостей, одинаково удаленных от единой заданной точки, которая является центром, на определенное расстояние, именуемое радиусом. Также существует такое понятие, как диаметр окружности. Для того чтобы его найти, воспользуйтесь инструкцией.
Вам понадобится
Инструкция
Увеличьте радиус в два раза D=2R. Диаметр – это хорда, проходящая через центр окружности, также диаметр имеет максимальную длину среди всех остальных возможных в окружности хорд. В таком случае можно сделать вывод, что он равен сумме двух радиусов одной и той же представленной окружности. Этот способ удачно применяется только в том случае, если в задаче есть данные по радиусу. В противном случае выберите что-то иное для решения поставленной задачи. Поделите длину окружности на число Пи. Обычно в математике это число используется как обозначение определенной иррациональной величины. Число Пи приравнивается к 3,14. Но это относительное значение, которое применяют для удобства при несложных вычислениях. В итоге получается такая, совсем несложная формула: D=L/π. При наличии данных в условии о длине окружности её можно применить и легко найти диаметр заданной фигуры. Также, слегка изменив данную формулу, вы можете найти радиус. Достаточно будет лишь увеличить число Пи в два раза и также поделить результат на длину окружности. Простая и достаточно универсальная формула радиуса будет иметь такой вид: D=L/2π. В этом случае опять же прослеживается пропорциональная связь между диаметром и радиусом. Главное, при их нахождении не перепутать, в каком из случаев нужно перемножать число Пи с двойкой, а в каком из них, например, не следует. Учтите тот, факт, что диаметр всегда относится к радиусу как 2 к 1. Соответственно здесь же могут частично применяться формулы для нахождения радиуса окружности. Например, зная площадь окружности, можно поделить её на число Пи, из результата извлечь корень, а далее полученное число увеличить в два раза. Действия в таком случае будут иметь вид, подобный этому: 2SQR(S/π). Такой вариант вычислений также удобен в том случае, если вам уже известна площадь.Видео по теме
Зная лишь длину диаметра окружности, можно вычислить не только площадь круга, но и площади некоторых других геометрических фигур. Это вытекает из того, что диаметры вписанных или описанных вокруг таких фигур окружностей совпадают с длинами их сторон либо диагоналей.
Инструкция
Если надо найти площадь круга (S) по известной длине его диаметра (D), умножайте число пи (π) на возведенную в квадрат длину диаметра, а результат делите на четыре: S=π ²*D²/4. Например, если диаметр круга равен двадцати сантиметрам, то его площадь можно вычислить так: 3,14² * 20² / 4 = 9,86 * 400 / 4 = 986 квадратных сантиметров. Если надо найти площадь квадрата (S) по диаметру описанной вокруг него окружности (D), возводите длину диаметра в квадрат, а результат разделите пополам: S=D²/2. Например, если диаметр описанной окружности равен двадцати сантиметрам, то площадь квадрата можно вычислить так: 20² / 2 = 400 / 2 = 200 квадратных сантиметров.Если площадь квадрата (S) нужно найти по диаметру вписанной в него окружности (D), достаточно возвести длину диаметра в квадрат: S=D². Например, если диаметр вписанной окружности равен двадцати сантиметрам, то площадь квадрата можно вычислить так: 20² = 400 квадратных сантиметров.
Если надо найти площадь прямоугольного треугольника (S) по известным диаметрам вписанной (d) и описанной (D) вокруг него окружностей, то возводите длину диаметра вписанной окружности в квадрат и делите на четыре, а к результату прибавляйте половину произведения длин диаметров вписанной и описанной окружностей: S=d²/4 + D*d/2. Например, если диаметр описанной окружности равен двадцати сантиметрам, а вписанной – десяти сантиметрам, то площадь треугольника можно вычислить так: 10² / 4 + 20*10/2 = 25 + 100 = 125 квадратных сантиметров.
Используйте встроенный в поисковую систему Google калькулятор для проведения необходимых расчетов. Например, чтобы рассчитать с помощью этого поисковика площадь прямоугольного треугольника по данным примера из четвертого шага, надо ввести такой поисковый запрос: «10^2 / 4 + 20*10/2», а затем нажать клавишу Enter.
Источники:
- как найти площадь окружности по диаметру
Круг – это несложная геометрическая фигура, не имеющая углов. Если измерить расстояние от центра круга до любой его крайней точки, оно всегда будет равно радиусу. В задачах, как правило, требуется вычислить диаметр или найти площадь круга. Эти показатели легко высчитать, если радиус круга известен.
Вам понадобится
- — калькулятор.
Инструкция
Для определения площади круга сначала его радиус возведите в квадрат, то есть во вторую степень. А затем результат умножьте на число π (пи). Если в задаче вместо радиуса дан диаметр фигуры, можете предварительно разделить его на 2. Теперь полученный при делении радиус фигуры используйте для удобства вычисления площади круга. Для нахождения значения квадрата радиуса круга воспользуйтесь калькулятором. Для начала введите величину радиуса круга, а затем найдите специальную кнопку с обозначением х2. Этот символ на кнопке показывает, что число будет возведено во вторую степень. Если у вас возникли сложности, умножьте радиус круга сам на себя. Чтобы найти площадь круга, можете использовать и диаметр. Радиус составляет ½ от диаметра, а значит его можно представить в виде дроби, где в числителе будет величина диаметра, а в знаменателе — 2. При вычислении квадрата такой дроби на калькуляторе возведите значение диаметра круга во вторую степень, а затем разделите полученное число на 4.Значение квадрата радиуса круга умножьте на коэффициент π (пи). Чтобы найти площадь круга, можете использовать более точное или округленное его значение. Для этого наберите соответствующее число (3,1415926535897932384626433832795 или 3,14). Часто есть возможность использовать специальную кнопку, обозначенную символом π (пи), предусмотренную на многих моделях калькуляторов.
Площадь круга измеряйте в квадратных величинах. Если радиус был дан в сантиметрах (см), то площадь будет выражаться в квадратных сантиметрах (см2). При вычислении радиуса из диаметра круга единица измерения не меняется. Например, если диаметр был дан в дюймах, то и радиус будет измеряться в дюймах, а искомая площадь будет получена в дюймах квадратных. В условии задачи не всегда сразу указан радиус. Иногда изначально дан диаметр круга. Если не заметить это и использовать диаметр для вычислений вместо радиуса, то неизбежны ошибки в вычислениях. Чтобы найти радиус, величину диаметра поделите на 2.
Полезный совет
Для расчета площади круга используйте число π (пи), приблизительно равное 3,1415926535897932384626433832795. Если большая точность не требуется, можете округлить этот коэффициент до 3,14.
Длиной окружности называют протяженность границы круга — простейшей плоской геометрической фигуры. По определению каждая точка этой границы находится на одинаковом расстоянии от центра, поэтому при заданной длине окружности эту границу можно найти только одним единственным способом. Из этого вытекает, что одной лишь длины окружности достаточно, чтобы определить площадь плоскости, заключенной внутри границ круга.
Инструкция
Исходите из формулы, которая определяет площадь круга (S) как половину от произведения длины окружности (L) на ее радиус (r): S=½*L*r. Известное всем со школы число Пи (π) определяет постоянное соотношение между периметром круга (длиной окружности) и ее диаметром (d) — хордой, проходящей через центр: L/d=π. Это соотношение позволяет выразить через длину окружности и неизвестный по условиям радиус: r=L/(2*π).Подставьте выражение радиуса через длину окружности в формулу нахождения площади круга через его радиус. В результате выяснится, что для вычисления площади круга длину окружности надо возвести в квадрат и разделить на учетверенное число Пи: S=L*(L/(2*π))/2=¼*L²/π.
Используйте встроенные в некоторые поисковые системы калькуляторы, чтобы найти конкретное значение площади по выведенной в предыдущем шаге формуле. Например, если известная длина окружности равна 50 см, то перейдите на сайт Google и введите в поле поискового запроса 50^2/(4*пи). Поисковик произведет указанные математические операции и покажет результат: 198,943679 см².Запустите программный калькулятор, встроенный в операционную систему вашего компьютера, если доступ к интернету отсутствует. Его использование требует немного больше операций для вычисления площади круга по длине окружности. Запустить это приложение можно через главное меню «Пуск» или воспользовавшись стандартным диалогом запуска программ. Этот диалог открывается одновременным нажатием клавиш win + r, а для вызова калькулятора надо набрать в нем команду calc и щелкнуть по кнопке OK.
Интерфейс калькулятора имитирует обычный гаджет, поэтому сложностей с вводом данных и вычислениями по формуле из второго шага быть не должно.
Источники:
- как найти длину границ
Круг – это плоская геометрическая фигура. Ее основными числовыми характеристиками являются площадь, диаметр (радиус) и периметр (длина ограничивающей его окружности). В зависимости от конкретной ситуации, под длиной круга может подразумеваться или длина окружности, или его диаметр.
Вам понадобится
- — калькулятор;
- — линейка;
- — циркуль;
- — веревка.
Инструкция
Если требуется определить длину круга, то в первую очередь уточните: что конкретно требуется рассчитать или измерить. Проблема в том, что строго говоря, такого понятия как «длина круга» в геометрии не существует. Однако, на практике, слово «круг» часто применяют вместо слова «окружность» — в этом случае определите длину ограничивающей круг окружности.С другой стороны, на практике часто используется такое понятие, как «габариты» предмета, или длина и ширина «описанного» прямоугольника. Так, например, современные автомобили имеют далеко не прямоугольную форму. Тем не менее, «длина автомобиля» — вполне привычное понятие. Таким образом, под длиной круга могут подразумеваться и его габаритные размеры – в этом случае измерьте или рассчитайте его диаметр.
Чтобы измерить длину окружности материального круга (колеса, бочки, торца бревна), возьмите кусок веревки и намотайте ее на этот круг в один оборот. Отметьте на веревке начало и конец измерений (можно завязать узелки). После чего, измерьте длину этого куска веревки линейкой или строительной рулеткой. Полученное число и будет длиной окружности (периметром круга).
Если имеется возможность прокатить круг, то прокатите его на расстояние полного оборота. Затем измерьте линейкой длину пройденного пути. Веревка в данном случае не понадобится, однако не забудьте отметить точки начала и конца движения. Расстояние между ними и будет длиной окружности.
Чтобы измерить длину окружности очень маленького круга (например, гвоздя), то для большей точности обмотайте его веревкой (ниткой) несколько раз или прокатите на несколько оборотов. После чего, разделите длину веревки или пройденного пути на количество оборотов.
Если измерить периметр круга (веревкой или качением) проблематично, то измерьте его диаметр. Здесь вам также пригодится веревка. Закрепите один конец веревки на границе круга и найдите на нем самую удаленную точку. Затем измерьте длину веревки и умножьте ее на число «пи» (3,14). Это и будет периметр (длина окружности) круга. Если же требуется определить «длину и ширину круга», то в качестве ответа предложите величину его диаметра.
Окружность является линией, а линия еще в «Началах» Евклида определялась как «длина без толщины». Поэтому определить, что такое площадь окружности, теоретически невозможно. Однако, на практике, понятие «толщина линии» встречается в любом графическом реакторе. А чтобы начертить эту самую окружность, потребуется определенное количество красителя, которое напрямую зависит от ее площади.
Вам понадобится
- — линейка;
- — циркуль;
- — калькулятор.
Инструкция
Если требуется определить площадь окружности, то обязательно уточните: что подразумевается под площадью окружности и кому это нужно. Узнайте также радиус окружности, а если под окружностью имеется ввиду кольцо, то определите его внутренний и внешний радиусы. Если определить площадь окружности требует учитель, то заявите ему, что окружность является линией, а понятие площади для линии не определено. При этом не используйте такие распространенные утверждения как «площадь (толщина) окружности равна нулю» или «площадь окружности бесконечно мала». Если площадь окружности требует определить не очень грамотный человек, то подразумевается, скорее всего, площадь ограниченного этой окружностью круга. В этом случае, воспользуйтесь формулой для нахождения площади круга:S = ?r?, где ? – число «пи» (примерное значение 3,14),r – радиус окружности (круга),S – площадь круга.Вполне реальная площадь имеется у нарисованных окружностей. Чтобы посчитать площадь начерченной окружности (например, чтобы оценить – сколько понадобится на ее распечатку порошка или краски), умножьте длину окружности на толщину линии:S = С * T = 2?r * Т,где:Т – толщина окружности,S – площадь окружности (линии).
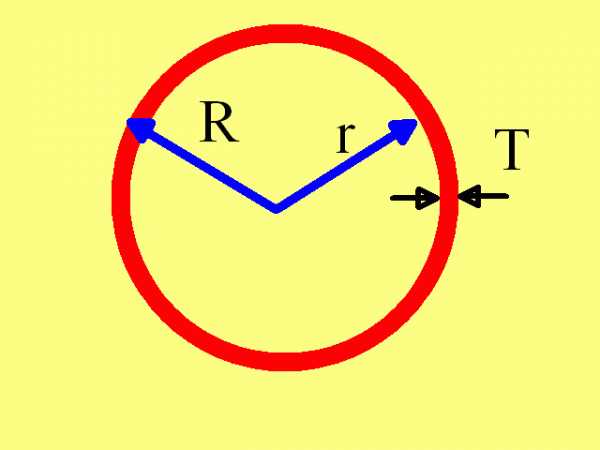
Если рассматривать окружность, имеющую толщину, как геометрическую фигуру, то правильнее было бы назвать такую окружность кольцом. Для определения площади кольца уточните его внутренний и внешний диаметр и воспользуйтесь следующей формулой:S = ?R? — ?r? = ?(R? — r?),где:r – внутренний радиус кольца,R –. внешний радиус кольца
Если заданы только радиус окружности и толщина линии, которой она проведена, то уточните: какой радиус – внешний или внутренний.Если задан внутренний радиус (r), то наружный радиус будет равен внутреннему плюс толщина окружности (R = r + T).Если задан наружный радиус (R), то внутренний радиус будет равен наружному минус толщина окружности (r = R — T).Если не указано, какой радиус подразумевается, то это, как правило, «средний радиус». В этом случае внутренний и внешний радиусы для подстановки в вышеприведенную формулу будут равняться: r = Rc – T/2 и R = Rc + T/2, где Rc – величина среднего радиуса.
Задачи на вычисление площади круга часто встречаются в школьном курсе геометрии. Чтобы найти площадь круга, необходимо знать длину диаметра или радиуса окружности, в которую он заключен.
Вам понадобится
- — длина диаметра окружности.
Инструкция
Окружность — фигура на плоскости, состоящая из множества точек, удалённых на одинаковое расстояние от другой точки, называемой центром. Круг — плоская геометрическая фигура, представляет собой множество точек, заключённых в окружность, которая является границей круга. Диаметр — это отрезок, соединяющий две точки на окружности и проходящий через её центр. Радиус — это отрезок, соединяющий точку на окружности и с её центром. π — число «пи», математическая константа, постоянная величина. Она показывает отношение длины окружности к длине её диаметра. Вычислить точное значение числа π невозможно. В геометрии пользуются приблизительным значением этого числа: π ≈ 3,14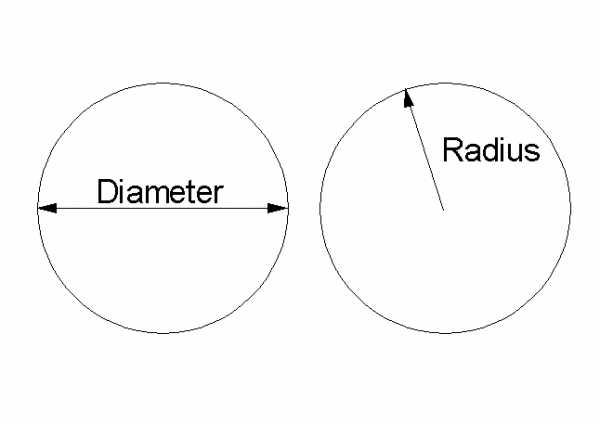
Площадь круга равна произведению квадрата радиуса на число и вычисляется по формуле: S=πR^2, где S — площадь круга, R — длина радиуса окружности.Из определения радиуса следует, что он равен половине диаметра. Следовательно, формула приобретает вид: S=π(D/2)^2, где D — длина диаметра окружности. Подставьте в формулу значение диаметра, вычислите площадь круга.
Площадь круга измеряется в единицах площади — мм2, см2, м2 и т.п. В каких единицах выражается полученная вами площадь круга, зависит от того, в каких единицах был дан диаметр окружности.
Если вам необходимо вычислить площадь кольца, воспользуйтесь формулой: S=π(R-r)^2, где R, r — радиусы внешней и внутренней окружностей кольца соответственно.
Полезный совет
Существует Международный день числа «пи», который отмечается 14 марта. Точное время наступления торжественной даты — 1 час 59 минут 26 секунд, согласно цифрам числа — 3,1415926…
www.kakprosto.ru
Как найти площадь круга по формулам через диаметр, радиус, длину окружности, расчет площади сектора круга
Как найти площадь круга?
Для того, чтобы рассчитать площадь круга, необходимо знать следующие данные:
- Длину диаметра – отрезка, проходящего через центр круга и соединяющего две противоположные точки окружности, либо радиуса – отрезка, одна из крайних точек которого находится в центре круга, а вторая – на дуге окружности. Таким образом, диаметр равен длине радиуса, умноженной на два.
- Значение числа π. Эта величина представляет собой константу – иррациональную дробь, не имеющую конца. При этом она не является периодической. Данное число выражает соотношение длины окружности к ее радиусу. Для вычисления площади круга в заданиях школьного курса используется значение π, приведенное с точностью до сотых – 3,14.
Формулы для нахождения площади круга, его сегмента или сектора
В зависимости от специфики условий геометрической задачи применяются две формулы нахождения площади круга:
- Если известен радиус r, то расчет производится следующим образом: S= π*r2
- Площадь круга через диаметр d вычисляется другим способом: S = π*d2/ 4
Чтобы определить, как найти площадь круга проще всего, нужно тщательно проанализировать условия задания.
Школьный курс геометрии также включает в себя задачи на расчет площади сегментов или секторов, для которых применяются специальные формулы:
- Сектор представляет собой часть круга, ограниченную окружностью и углом с вершиной, расположенной в центре. Площадь сектора рассчитывается по формуле: S = (π*r2/360)*А;
- r – радиус;
- А – величина угла в градусах.
- r – радиус;
- р – длина дуги.
- Сегмент – представляет собой часть, ограниченную сечением круга (хордой) и окружностью. Его площадь можно найти по формуле S=(π*r2/360)*А± S∆;
Также существует второй вариант S = 0,5*р*r;
- r – радиус;
- А – величина угла в градусах;
- S∆ – площадь треугольника, сторонами которого являются радиусы и хорда круга; при этом одна из его вершин располагается в центре круга, а две других – в точках соприкосновения дуги окружности с хордой. Важный момент – знак “минус” ставится в том случае, если значение А меньше 180 градусов, а знак “плюс” – если больше 180 градусов.
Чтобы упростить решение геометрической задачи, можно вычислить площадь круга он-лайн. Специальная программа быстро и безошибочно сделает расчет за пару секунд. Как рассчитать он-лайн площадь фигур? Для этого необходимо известные ввести исходные данные: радиус, диаметр, величину угла.
Структура раздела Справочные материалы:
beta-ege.ru
Ответы@Mail.Ru: как найти площадь окружности?
Круг — это часть плоскости, лежащая внутри окружности. Соответственно, площадь круга — это площадь ограниченная окружностью. Круг имеет замечательное свойство, это фигура с самым большим отношением площади к периметру. Иными словами, отношение площади круга к длине ограничивающей его окружности, самое большое. 1. Площадь круга S = пи * R2 Где S — площадь круга, R — радиус круга 2. Площадь круга вписанного в квадрат. S = пи * (a / 2)2 Где a/2 — радиус круга, a — длина стороны квадрата. 3. Площадь круга описанного около квадрата. S = пи * 0.5*a2 Где a — длина стороны квадрата. В этом случае радиус круга равен 0.5*a*√‾2, используя формулу 1, получаем формулу 3. 4. Площадь круга вписанного в треугольник. Используя формулу радиуса вписанной окружности R = (p-a)*tg(A/2) Где a, A — сторона и противолежащий угол соответственно, p — полупериметр. Можем записать формулу площади круга вписанного в треугольник: S = пи * ((p-a)*tg(A/2))² 5. Площадь круга описанного около треугольника. Используя формулу радиуса описанной окружности R = a/(2*sin(A)) Где a, A — сторона и противолежащий угол соответственно. Можем записать формулу площади круга описанного около треугольника: S = пи * (a/(2*sin(A)))² Выбирай формулу которая соответствует твоей задаче и вперёд. И вт ещё что правилино говорить площадь круга, а окружность это периметр. Удачи .Не болей.
S = число «пи» (оно равно 3,14) умножить на радиус круга в квадрате
S=пи умножить на радиус в квадрате
окружность — линия, у нее нет площади.
Круг — это часть плоскости, лежащая внутри окружности. Соответственно, площадь круга — это площадь ограниченная окружностью. Круг имеет замечательное свойство, это фигура с самым большим отношением площади к периметру. Иными словами, отношение площади круга к длине ограничивающей его окружности, самое большое. 1. Площадь круга S = пи * R2 Где S — площадь круга, R — радиус круга 2. Площадь круга вписанного в квадрат. S = пи * (a / 2)2 Где a/2 — радиус круга, a — длина стороны квадрата. 3. Площадь круга описанного около квадрата. S = пи * 0.5*a2 Где a — длина стороны квадрата. В этом случае радиус круга равен 0.5*a*√‾2, используя формулу 1, получаем формулу 3. 4. Площадь круга вписанного в треугольник. Используя формулу радиуса вписанной окружности R = (p-a)*tg(A/2) Где a, A — сторона и противолежащий угол соответственно, p — полупериметр. Можем записать формулу площади круга вписанного в треугольник: S = пи * ((p-a)*tg(A/2))² 5. Площадь круга описанного около треугольника. Используя формулу радиуса описанной окружности R = a/(2*sin(A)) Где a, A — сторона и противолежащий угол соответственно. Можем записать формулу площади круга описанного около треугольника: S = пи * (a/(2*sin(A)))² Выбирай формулу которая соответствует твоей задаче и вперёд. И вт ещё что правилино говорить площадь круга, а окружность это периметр. Удачи .Не болей.
touch.otvet.mail.ru