Дифференциал производная функции – Производная и дифференциал

34. Производная от функции. Дифференцируемость функции. Дифференциал.

Производной функции y=f(x) в точке х₀ называется предел отношения приращения функции к приращению аргумента, когда аргумент стремится к нулю.

Производная функции f(x) есть некоторая функция

f ’(x), произведенная из данной функции.

Функция y=f(x), имеющая производную в каждой точке интервала (a;b) называется дифференцируемой в этом интервале.

Операция нахождения производной называется дифференцированием.

Дифференциал функции y=f(x) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dy (или df(x) ).

Иначе. Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

35. Правила дифференцирования суммы, произведения, частного функции. Производные сложных функций.

Для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.

Производная обратной функции равна обратной величине производной данной функции.

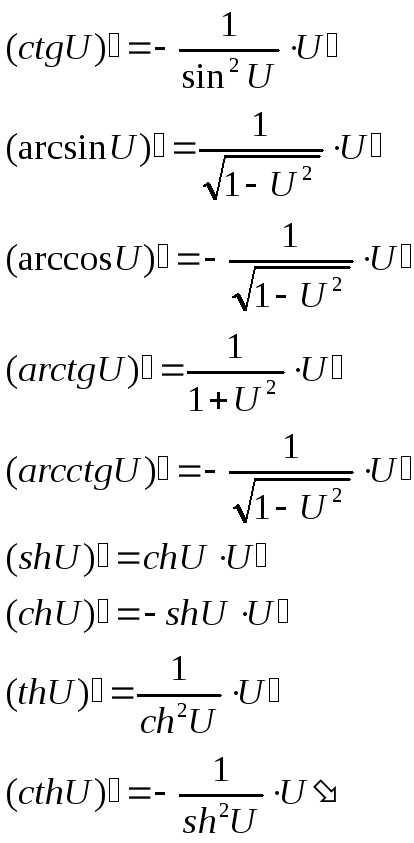
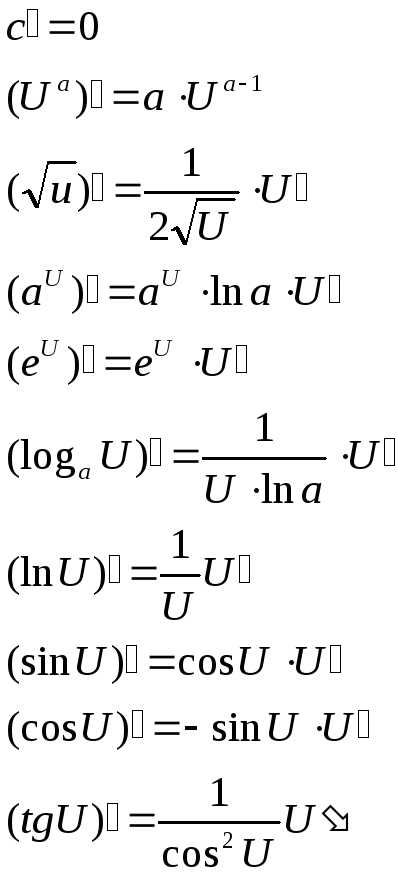
36. Логарифмическое дифференцирование.

Логарифмическое дифференцирование — в некоторых случаях целесообразнее функцию сначала прологарифмировать, а результат продифференцировать.

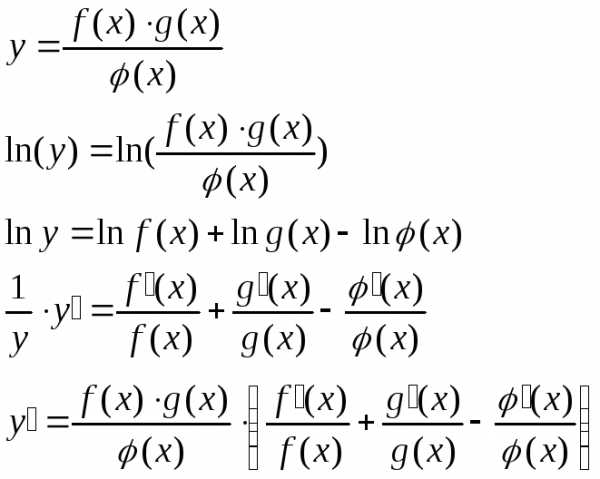
Однако производные степенных функций находят только логарифмическим дифференцированием.

Производная степенно-показательной функции равна сумме производно показательной функции, при условии

U=const, и производной степенной функции, при условии V=const.

37. Теоремы о среднем. Правило Лопиталя.

Рассмотрим способ раскрытия неопределенностей 0 / 0 и ∞ / ∞, который основан на применении производных.

Правило Лопиталя, при 0 / 0.

Пусть функции f(x) и φ(x) непрерывны и дифференцируемы в окрестности точки x₀ и обращается в нуль в этой точке: .

Пусть φ ′(x) ≠ 0 в окрестности точки x₀

Если существует предел

, то

Применим к функциям f(x) и φ(x) теорему Коши для отрезка [x₀;x], лежащего в окрестности точки x

0 , тогда

, где с лежит между x₀ и х.

При x→x₀ величина с также стремится к х₀; перейдем в предыдущем равенстве к пределу:

Так как 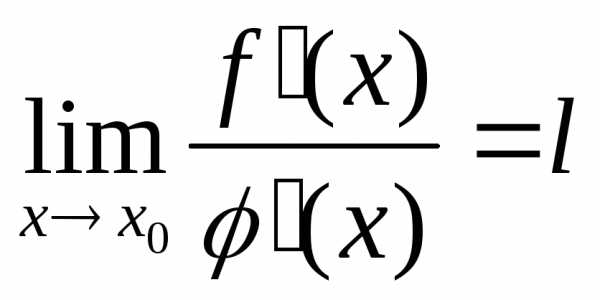, то.

Поэтому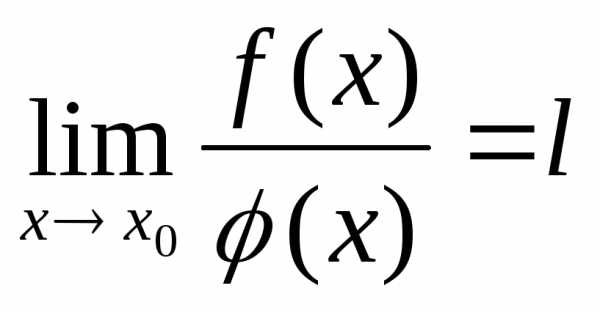

(предел отношения двух бесконечно малых равен пределу отношения их производных, если последний существует)

Правило Лопиталя, при ∞ / ∞.

Пусть функции f(x) и φ(x) непрерывны и дифференцируемы в окрестности точки x₀ (кроме точки x₀), в этой окрестности

Если существует предел

, то

Неопределенности вида 0∙∞ ; ∞-∞ ; 1^∞ ; ∞⁰ ; 0⁰сводятся к двум основным.

Например, 0∙∞

Пусть f(x)→0, φ(x)→∞ при х→х₀

38. Дифференциалы высших порядков.

Пусть y=f(x) дифференцируема функция, а ее аргумент х – независимая переменная. Тогда дифференциал dy=f ′(x)dx есть также функция х, можно найти дифференциал этой функции. Дифференциал от дифференциала есть второй дифференциал.

Производную можно рассматривать, как отношение дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.

Д

ифференциалn-ого порядка, есть дифференциал от дифференциала (n-1)-ого порядка, т.е. производную функции можно рассматривать, как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.

studfiles.net

Производная и дифференциал функции — Мегаобучалка

Производная функции, ее геометрический смысл

 

Определение. Производной функции в точке называется предел, если он существует, отношения приращения функции в точке к приращению аргумента в этой точке, когда последнее стремится к нулю:

 

,

где — приращение аргумента в точке , а — соответствующее этому приращению приращение функции в этой точке.

 

 

у

 

 

P

M

 

0 x

 

Пусть функция определена на некотором промежутке и имеет во внутренней точке этого промежутка конечную производную. Пусть — точка графика функции , соответствующая абсциссе , а — произвольная точка графика функции.

Касательной к кривой в точке называется предельное положение секущей , когда точка стремится к точке по кривой с любой стороны.

Обозначим через угол наклона секущей МР к положительному направлению оси . Тогда . Находим

,

где — угол наклона касательной к графику функции в точке .

Угол между кривыми в их общей точке определяется как угол между касательными, проведенными к этим кривым в их общей точке.

Уравнение касательной к кривой в точке имеет вид:

Уравнение нормали к кривой в точке имеет вид: .

Функция имеющая конечную производную в точке называется дифференцируемой в этой точке.

 

Односторонние производные функции в точке

 

Определение. Правой (левой) производной функции в точке называется правый (левый) предел

при условии, что этот предел существует.

Если функция имеет производную в некоторой точке , то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Во-первых функция может иметь разрыв в точке , а во- вторых, даже если функция непрерывна в точке , она может быть в ней не дифференцируема.

Например: — имеет в точке и левую и правую производную, непрерывна в этой точке, однако, не имеет в ней производной.

Теорема. (Необходимое условие существования производной) Если функция имеет производную в точке , то она непрерывна в этой точке.

Очевидно, что это условие не является достаточным.

 

Основные правила дифференцирования

 

Пусть — функции, дифференцируемые в точке . Тогда:

1)

2)

3) , если v ¹ 0

Эти правила могут быть доказаны на основе теорем о пределах.

 

Производные основных элементарных функций.

 

1) , 9) ,

2) , 10) ,

3) , 11) ,

4) , 12) ,

5) , 13) ,

6) , 14) ,

7) , 15) ,

8) , 16) .

 

Производная сложной функции

 

Теорема.Пусть , причем область значений функции входит в область определения функции .Тогда

Доказательство. Имеем

.

Переходя к пределу в обеих частях при получим:

,

(с учетом того, что если , то , т.к. – непрерывная функция)

Тогда . Теорема доказана.

 

megaobuchalka.ru

06. Понятие дифференциала и производной функции. Вычисление производн

Допустим, что на графике функции Y(X) (рис.14) производится предельный переход от точки X1 к точке X. Разность значений аргумента X – X1 =Δx называется приращением аргумента. Таким же образом можно ввести понятие приращения функции Δy = Y(X) – Y(X1). Тогда Предел приращения переменных величин X при стремлении X1 к точке X, и У1 к точке Y, если он существует, называется Дифференциалом (обозначается Dx или Dy) в этой точке (от слова differ (Англ.) – разность, следовательно дифференциал – бесконечно малая разность):

.

Для однородного пространства координат все точки равноправны, а поэтому все дифференциалы равны. Пусть Y есть функция от X , тогда приращение функции связано с приращением аргумента.

Если для любого X существует предел отношения приращения функции к приращению аргумента, то он равен отношению дифференциалов этих величин, называется производной функции Y(X) По переменной X И обозначается со штрихом Y’(X) (Или в общем случае F’(X)):

. (17)

 

 

 

 

 

 

 

 

 

 

 

Рис.14. К определению производной

Практический смысл производной заключается в том, что эта величина характеризует, во-первых,

Скорость протекания процессов. Действительно, стоит переменной X (аргументу) придать смысл времени, а функции Y – количество произведенной продукции (Q) за определенный интервал времени, как производная будет характеризовать производственную функцию:– количество товаров, произведенных за единицу времени, то есть скорость производства товаров. Если функция Y(T) характеризует путь S, пройденный за определенный отрезок времени, то производная покажет скорость движения: – путь пройденный за единицу времени. С другой стороны, на соответствующем графике функции видно, что приращение одной величины (ΔY) к приращению другой (ΔX) определяется тангенсом угла наклона касательной АВ (рис.14) к оси 0X, проведенной в той точке, в которой определяется производная. Поэтому геометрический смысл производной понятен – это (во-вторых) Тангенс угла наклона касательной к точке. График функции Y(T) описывает траекторию движения точки (тела), а касательная – скорость этого движения в каждой точке, то есть мгновенную скорость, величину которой обычно показывают спидометры в автомобиле. Для цели описания движения точек по сложным криволинейным траекториям Ньютон первым «изобрел» дифференциальное исчисление и научился рассчитывать производные.

Еще одно применение производной можно предложить, анализируя, например, топографическую карту местности (рис.15). На графике высоты горы (в сечении) проведены приращения высот через равные расстояния по оси 0H. Соответствующая карта горы отражает в направлении оси 0X крутизну этой горы. Видно, что уровни высоты горы несимметричны относительно ее вершины, слева гора спадает более круто, чем справа. Это произошло потому, что одинаковым значениям приращений высоты Δh слева и справа соответствует различное приращение координат Δx. Поэтому величина отношения Δh/Δx для левой стороны будет больше, чем для правой.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

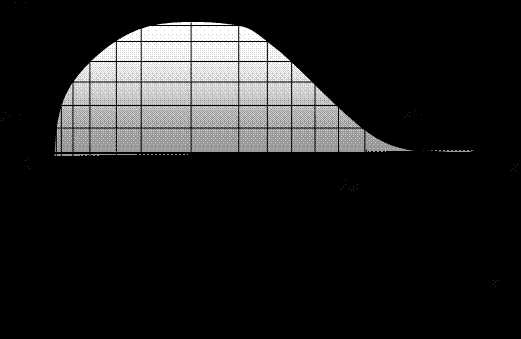Рис.15. Линии равных высот на карте горы

Крутизна горы слева больше, чем справа и такое же соотношение будут иметь пределы этих отношений, то есть производные. Таким образом, производная характеризует крутизну изменения функции. Латинский термин «градиент» по смыслу совпадает со словом «крутизна», поэтому, в третьих, Градиент есть наибольшая величина производной.

Градиенты играют основную роль в создании направленных процессов. Любое нарушение симметрии однородности (градиенты) создает потоки: передачу энергии, если температуры тел различны; создает селевые потоки, распространяющиеся в сторону низких высот. Градиенты условий в экономике создают финансовые потоки; градиент потенциала создает в проводнике электрический ток; различие в условиях жизни, какими бы параметрами эти условия не измерять, ведут к миграционным процессам и т. п. Таким образом, если Вы ищете причину какого либо направленного процесса, то ищите Нарушение симметрии или градиенты.

Производная в некоторой точке может оказаться равной нулю. Это возможно, если касательная к функции в этой точке параллельна оси 0х, что в свою очередь происходит тогда, когда функция в точке либо максимальна, либо минимальна, либо совершает перегиб (рис.16). Такие точки функции называют Точками экстремума или экстремальными точками и они определяют в экономике, в частности, наибольший или наименьший доход ( Y = R), полученный при продаже товаров ( X = Q). Допустим, что Вы проводите анализ работы рынка по результатам прибыли, полученной от продаж. Какая интерпретация событий могла бы привести к графику, изображенному на рис.16?

 

Рис.16. Экстремальные точки функции

Еще одно типичное использование производной связано с понятием Плотности. Часто встречаемое словосочетание – плотность населения связано с Отношением количества жителей в регионе к размерам площади, занимаемой регионом. Однако, полученная величина – количество жителей, приходящееся на единицу площади – не отражает деталей распределения людей, эта характеристика усредненная. Поэтому переход к детальной картине, в которой найдется место и для городов, и для поселков, и для пустынных мест требует в расчетах перехода к пределу Отношения (при стремлении размеров площади к минимальной), то есть к производной. Таким же образом, плотность вещества следует определить не просто как отношение массы вещества к величине объема, в котором это вещество распределено, а в виде производной: .

Подводя итоги вопросам использования производной, фиксируем, что производная имеет смысл Скорости (ускорения), величины Градиента, Плотности, определяет Экстремальные точки функции и геометрически характеризует Касательную в произвольной точке. Производная показывает как меняется функция при изменении аргумента На единицу его приращения.

Теперь рассмотрим примеры на вычисление производной.

1. Пусть мы имеем функцию Y(x) = x2 . Найдем производную этой функции в произвольной точке X . Приращение аргумента обозначим

ΔX = X1 – X , откуда следует, что X1 = X+ ΔX. Приращение функции обозначим ΔY = Y(X1) – Y(X) = X12 – X2. Тогда по определению производной через предел отношения приращений, будем иметь при X1 → X , то есть при ΔX→0 :

.

Окончательно записываем: .

VI. Обобщая полученный результат на любую показательную функцию, по аналогии можно записать (без вывода): (Xn)’ = Nxn-1.

3. Пусть Y = Sinx. Вычислим производную этой функции:

Окончательно получаем, что (sinx)’=cosx. При расчетах использованы соотношения: cosΔx→1 при Δx→0 и второй замечательный предел.

4. Пусть Y(X) = Ex. Вычислим соответствующую производную.

В расчетах использовано разложение экспоненциальной функции в степенной ряд (14) и переход к линейной функции (1+ΔX) при малых значениях аргумента ΔX. В результате оказалось, что производная от экспоненциальной функции совпадает с самой экспоненциальной функцией.

Другие, часто используемые производные, вычисленные на основе определения производной, стали «табличными» и занесены в любой справочник по математике. Приложение в методических рекомендациях содержит эти данные. Для вычисления производных от достаточно сложно представленных функций требуется знание основных правил дифференцирования, которые также записаны в методических рекомендациях. Остановимся на доказательстве некоторых из этих правил.

1. Правило дифференцирования произведения двух функций, зависящих от одного и того же аргумента: Y(X) = F(X)·G(X) или кратко Y = Fg. Если функции F(X) И G(X)Получили приращение, то и функция Y(X) Также получила приращение. Тогда можно записать, что Y + Δy = ( F +Δf )(G+ +Δg). Выразим отсюда величину Δy: Δy = Fg + F Δg + G Δf – Fg = F Δg+ + G Δf. Поделим левую и правую часть на приращение аргумента Δx и перейдем к пределам:

2. Правило дифференцирования отношения двух функций: Y = F/G .

Введем обозначение U = 1/G = G-1. Тогда будем иметь произведение функций Y = F U. Используя предыдущее правило, получим: Y’ = F’U + U’F. Найдем теперь производную Du/Dx.

Подстановка полученного выражения в равенство для производной искомой функции приводит к следующему результату:

.

3. Правило дифференцирования сложной функции.

По ходу выполнения действий для предыдущего правила был использован прием поиска производной от функции U, которая сама сложным образом зависит от аргумента X. Можно в общем виде записать, что U зависит от функции G, которая зависит от переменной X, то есть: U(G(X)) . Правило дифференцирования такой функции, которая называется сложной, очевидно из тех действий, которые мы уже произвели в предыдущем примере.

Пусть дана сложная функция y = u(g(f(x))) и необходимо найти ее производную по переменной X, То есть . Тогда очевидно равенство:

, которое и является правилом дифференцирования сложной функции. Например, для функции производная по переменной X рассчитывается следующим образом: вначале берется производная по экспоненте, которая равна самой экспоненте, а затем умножается на производную от показателя степени, то есть от функции F(X) по переменной X: .

Если от полученной производной, рассматривая ее как новую функцию, еще раз взять производную, то такая двойная операция от первоначальной функции называется Второй производной. Поиск второй производной можно представить по смыслу, как вычисление скорости изменения скорости, то есть как поиск Ускорения. Иногда в конкретных задачах требуется рассчитать производные более высоких порядков, чем первая или вторая, однако, технически вводить новых правил для таких действий нет необходимости.

Примеры поиска производных от различных функций приведены в методических рекомендациях.

Применим математический подход к реальной ситуации, складывающейся в каком либо регионе в момент начала эпидемии гриппа. Как известно, количество здоровых людей при этом начинает уменьшаться по экспоненциальному закону: N1 =N0E—T. Количество заболевших к моменту времени T окажется ΔN = (N0 – N0E—T) (первый «сценарий»). С другой стороны, при нормальной обстановке количество выздоравливающих людей увеличивается пропорционально времени, то есть по линейному закону: N2 = Kt + N0 (второй «сценарий»).

(?): Какая будет складываться обстановка, если продолжать лечить людей обычными методами в условиях эпидемии?

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис.17. Математический анализ эпидемиологической ситуации

На рис. 17 эта ситуация с двумя сценариями представлена в виде двух графиков, изображенных пунктиром.

Очевидно, что с течением времени, количество здоровых людей будет изменяться и это количество можно рассчитать как разность между выздоравливающими и заболевшими.

N(T) = N2(T) – Δn = Kt + N0 – N0 + N0E—T = Kt + N0E—T .

Приведенный расчет показывает, что для построения общей зависимости необходимо складывать значения функций N* = Kt и N1 = N0E—T В одинаковые моменты времени. Функция N* Отличается от N2 Тем, что из значений N2 Вычтена константа N0 , а следовательно график функции пройдет через начало координат. Результат сложения (по точкам) приводит к функции, которая имеет минимум. Это означает, что в момент TКр количество здоровых людей будет минимально или количество больных максимально. Этот критический момент можно рассчитать по условию экстремума функции – производная в этой точке обращается в нуль. Поэтому можно записать:

.

После логарифмирования получаем:

Окончательный вывод очевиден: чем эффективнее лечение, тем больше величина K и тем скорее будет пройден критический момент. Ценность математического подхода заключается не в том, что он подтверждает очевидные факты, а в том, что он позволяет делать количественный и временнòй прогноз со всеми вытекающими отсюда последствиями.

Приведенный пример можно отнести к области математического моделирования.

< Предыдущая		Следующая >

matica.org.ua

Дифференциал и производная | Математика, которая мне нравится

Определение. Пусть функция задана на множестве , . Производная функции в точке есть

   

Определение. Пусть функция задана на множестве , . Производная функции в точке есть

   

Доказательство равносильности двух определений.

   

Рассмотрим разность

   

Функция задана и

   

Если произвольным образом задать значение функции при , то последнее равенство будет выполняться и при .

Определение. Пусть , . Функция называется дифференцируемой в точке , если существует такое число и такая функция , что имеет место равенство

   

Функция, которая каждому числу ставит в соответствие число , называется дифференциалом функции в точке .

Мы доказали, что если у функции есть производная в точке , то дифференцируема в этой точке (за число можно взять число ).

Докажем, что если функция дифференцируема в точке , то у нее есть производная в точке .

   

   

Попутно мы доказали, что число в правой части равенства определяется однозначно и равно .

Обозначение. — дифференциал функции в точке .

Дифференциал — линейная функция приращения :

   

Пример.

   

Пример.

   

Пример.

   

— обозначение дифференциала тождественной функции

   

   

Обозначения.

Задачи. 1) Вычислите приращения для данных функций и данной точки , постройте соответствующие графики функций , постройте графики функций , найдите , если он существует.

а) ;

б) ;

в) ;

г) .

2) Для данных функций и данной точки вычислите производную

   

составьте выражение

   

и докажите, что , найдите .

а) ;

б) .

3) Выясните, для каких из данных функций найдется такое число , что при всех функция (при ) может быть представлена в виде , где

а) , б) .

1. ;

2. ;

3.

4) Найдите дифференциал функции и с его помощью приближенно вычислите значение данной функции в точке .

5) Приведите примеры функций, имеющих производные везде, кроме: а) одной точки; б) двух точек; в) трех точек; г) целых чисел.

6) Выясните, имеют ли данные функции производную в точке :

а)

   

б)

   

7) Найдите все значения параметров и , такие, что функция

   

а) непрерывна в ;
б) дифференцируема в .

8 ) Исследуйте функции на дифференцируемость

а) ;
б) ;
в)

   

hijos.ru

Дифференциал сложной функции

Здесь дифференциал записан в том же виде, как и в формуле для дифференциала функции независимой переменной x, т. е. , хотя аргумент u является не независимой переменной, а функцией x.

Следовательно, выражение дифференциала функции в виде произведения производной этой функции на дифференциал её аргумента справедливо независимо от того, является ли аргумент независимой переменной или функцией другой переменной. Это свойство называется инвариантностью (неизменностью) формы дифференциала.

Задание к примерам. Во всех примерах требуется вычислить дифференциал функции двумя способами: выражая его через dx и через du — дифференциал промежуточной переменной u. Проверить совпадение полученных результатов.

Потребуется таблица производных некоторых сложных функций.

Пример 1. Дана функция .

Решение.

Через dx:

Использовали правило дифференцирования степенной функции.

Через du:

Подставляя в полученное равенство и , получаем

Результаты совпадают.

Пример 2. Дана функция .

Решение.

Через dx:

Использовали правило дифференцирования сложной функции квадратного корня.

Через du:

.

Подставляя в полученное равенство и , получаем

Результаты совпадают.

Пример 3. Дана функция .

Решение.

Через dx:

Использовали правило дифференцирования сложной логарифмической функции.

Через du:

.

Подставляя в полученное равенство и , получаем

Результаты совпадают.

Пример 4. Дана функция .

Решение.

Через dx (в процессе решения для удобства преобразуем корни в степени и обратно):

Использовали общее правило дифференцирования сложной функции два раза.

Через du:

.

Подставляя в полученное равенство и
,
получаем

Результаты совпадают.

Пример 5. Дана функция .

Решение.

Через dx:

Использовали общее правило дифференцирования сложной функции и правило дифференцирования сложной логарифмической функции.

Через du:

.

Подставляя в полученное равенство и , получаем

.

Результаты совпадают.

Весь блок «Производная»

Поделиться с друзьями

function-x.ru